第三章习题分解

第三章连接课后习题参考答案第三章连接课后习题参考答案焊接连接参考答案一、概念题3．1 从功能上分类，连接有哪几种基本类型？3．2 焊缝有两种基本类型—对接坡口焊缝和贴角焊缝，二者在施工、受力、适用范围上各有哪些特点？3．3 对接接头连接需使用对接焊缝，角接接头连接需采用角焊缝，这么说对吗？3．4 h和lw相同时，吊车梁上的焊缝采用正f面角焊缝比采用侧面角焊缝承载力高？3．5 为何对角焊缝焊脚尺寸有最大和最小取值的限制？对侧面角焊缝的长度有何要求？为什么？【答】（1）最小焊脚尺寸：角焊缝的焊脚尺寸不能过小，否则焊接时产生的热量较小，致使施焊时冷却速度过快，导致母材开裂。

《规范》规定：h f≥1.5t，式中：t2——较厚焊件厚度，单2位为mm。

计算时，焊脚尺寸取整数。

自动焊熔深较大，所取最小焊脚尺寸可减小1mm；T形连接的单面角焊缝，应增加1mm；当焊件厚度小于或等于4mm时，则取与焊件厚度相同。

（2）最大焊脚尺寸：为了避免焊缝区的主体金属“过热”，减小焊件的焊接残余应力和残余变形，角焊缝的焊脚尺寸应满足12.1t h f式中： t 1——较薄焊件的厚度，单位为mm 。

（3）侧面角焊缝的最大计算长度侧面角焊缝在弹性阶段沿长度方向受力不均匀，两端大而中间小，可能首先在焊缝的两端破坏，故规定侧面角焊缝的计算长度l w ≤60h f 。

若内力沿侧面角焊缝全长分布，例如焊接梁翼缘与腹板的连接焊缝，可不受上述限制。

3．6 简述焊接残余应力产生的实质，其最大分布特点是什么？ 3．7 画出焊接H 形截面和焊接箱形截面的焊接残余应力分布图。

3．8 贴角焊缝中，何为端焊缝？何为侧焊缝？二者破坏截面上的应力性质有何区别？3．9 规范规定：侧焊缝的计算长度不得大于焊脚尺寸的某个倍数，原因何在？规范同时有焊缝最小尺寸的规定，原因何在？ 3.10 规范禁止3条相互垂直的焊缝相交，为什么。

3.11 举3～5例说明焊接设计中减小应力集中的构造措施。

《电工学复习题》第一章习题1－1 指出图1－1所示电路中A 、B 、C 三点的电位。

图1－1 题 1－1 的电路1－2 图1－2所示电路元件P 产生功率为10W ，则电流I 应为多少?1－5 图1－4所示电路中，已知电压U 1 = U 2 = U 4 = 5V ，求U 3和U CA 。

1－6 欲使图1－5所示电路中的电流I=0，U S 应为多少？（1V ） 1－7 在图1－6所示三个电路中，R 1 = 5Ω，R 2 = 15Ω，U S = 100V ，I 1 = 5A ，I 2 = 2A 。

若R 2电阻两端电压U ＝30V ，求电阻R 3 。

（17.5欧）1－8 求图1－7所示各电路中的未知量。

1－10 电路如图1－9所示，求A 点的电位。

（-5V ）1－11 求图1－10所示电路中的电压U 、电流I 。

1－12 简化图1－11所示各电路为一个等效的电压源或理想电流源。

1－13 在图1－12（a ）（b ）（c ）所示的电路中，是哪些元件在提供功率？1－14 在图1－13（a ）（b ）（c ）所示的电路中，电压U 是多少？第二章习题2-2 试用支路电流法求图2-2所示网络中通过电阻R 3支路的电流I 3及理想电流源两端的电压U 。

图中I S =2A ，U S =2V ，R 1=3Ω，R 2=R 3=2Ω。

（） 2-3 试用叠加原理重解题2-2. 2-4 再用戴维宁定理求题2-2中I 3。

2-6 图2-4所示电路中，U S1=30V ，U S2=10V ，U S3=20V ，R 1=5k Ω，R 2=2k Ω，R 3=10k Ω，I S =5mA 。

求开关S 在位置1和位置2两种情况下，电流I 分别为多少？（3.75mA ，2.5mA ）2-7 图2-5所示电路中，已知U AB =0，试用叠加原理求U S 的值。

（12.5V ）2-8 电路如图2-6所示，试用叠加原理求电流I 。

（-2.4A ） 2-9 电路如图2-7所示，试用叠加原理求电阻R 4上电压U 的表达式。

《电工学复习题》第一章习题1－1 指出图1－1所示电路中A、B、C三点的电位。

图1－1 题1－1 的电路1－2 图1－2所示电路元件P产生功率为10W，则电流I应为多少?1－5 图1－4所示电路中，已知电压U1 = U2 = U4 = 5V，求U3和U CA。

1－6 欲使图1－5所示电路中的电流I=0，U S应为多少？（1V）1－7 在图1－6所示三个电路中，R1 = 5Ω，R2 = 15Ω，U S = 100V，I1 = 5A，I2 = 2A。

若R2电阻两端电压U＝30V，求电阻R3 。

（17.5欧）1－8 求图1－7所示各电路中的未知量。

1－10 电路如图1－9所示，求A点的电位。

（-5V）1－11 求图1－10所示电路中的电压U、电流I。

1－12 简化图1－11所示各电路为一个等效的电压源或理想电流源。

1－13 在图1－12（a）（b）（c）所示的电路中，是哪些元件在提供功率？1－14 在图1－13（a）（b）（c）所示的电路中，电压U是多少？第二章习题2-2 试用支路电流法求图2-2所示网络中通过电阻R3支路的电流I3及理想电流源两端的电压U。

图中I S=2A，U S=2V，R1=3Ω，R2=R3=2Ω。

（）2-3 试用叠加原理重解题2-2.2-4再用戴维宁定理求题2-2中I3。

2-6 图2-4所示电路中，U S1=30V，U S2=10V，U S3=20V，R1=5kΩ，R2=2kΩ，R3=10kΩ，I S=5mA。

求开关S在位置1和位置2两种情况下，电流I分别为多少？（3.75mA，2.5mA）2-7 图2-5所示电路中，已知U AB=0，试用叠加原理求U S的值。

（12.5V）2-8 电路如图2-6所示，试用叠加原理求电流I。

（-2.4A）2-9 电路如图2-7所示，试用叠加原理求电阻R4上电压U的表达式。

（U=）2-10 电路如图2-8所示,已知R1=Ω，R2=R3=2Ω，U S=1V，欲使I=0，试用叠加原理确定电流源I S的值。

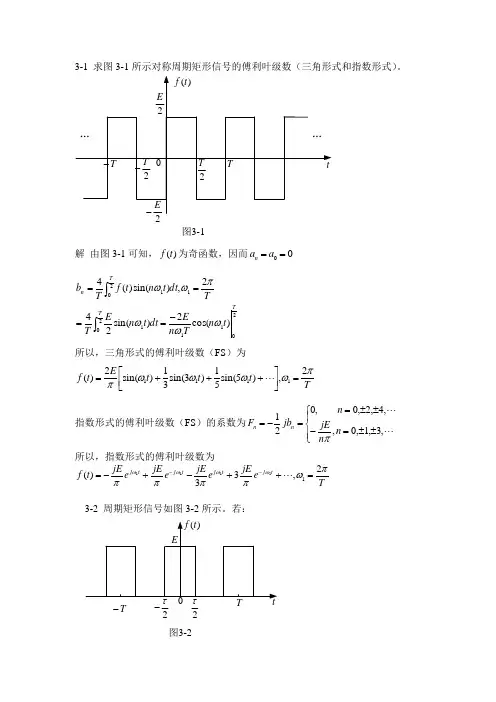
3-1 求图3-1所示对称周期矩形信号的傅利叶级数（三角形式和指数形式）。

图3-1解 由图3-1可知，)(t f 为奇函数，因而00==a a n2112011201)cos(2)sin(242,)sin()(4T T T n t n T n Edt t n E T T dt t n t f T b ωωωπωω-====⎰⎰所以，三角形式的傅利叶级数（FS ）为T t t t E t f πωωωωπ2,)5sin(51)3sin(31)sin(2)(1111=⎥⎦⎤⎢⎣⎡+++=指数形式的傅利叶级数（FS ）的系数为⎪⎩⎪⎨⎧±±=-±±==-= ,3,1,0,,4,2,0,021n n jE n jb F n n π所以，指数形式的傅利叶级数为T e jE e jE e jE e jE t f t j t j t j t j πωππππωωωω2,33)(11111=++-+-=--3-2 周期矩形信号如图3-2所示。

若：图3-22τT-2τ-重复频率kHz f 5= 脉宽 s μτ20=幅度 V E 10=求直流分量大小以及基波、二次和三次谐波的有效值。

解 对于图3-2所示的周期矩形信号，其指数形式的傅利叶级数（FS ）的系数⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛====⎰⎰--22sin 12,)(1112212211τωττωππωττωωn Sa T E n n E dt Ee T T dt e t f T F tjn TT t jn n则的指数形式的傅利叶级数（FS ）为∑∑∞-∞=∞-∞=⎪⎭⎫ ⎝⎛==n tjn n tjn n e n Sa TE eF t f 112)(1ωωτωτ其直流分量为TE n Sa T EF n ττωτ=⎪⎭⎫ ⎝⎛=→2lim100 基波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-2sin 2111τωπEF F 二次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-22sin 122τωπEF F 三次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-23sin 32133τωπE F F 由所给参数kHz f 5=可得s T s rad 441102,/10-⨯==πω将各参数的值代入，可得直流分量大小为V 110210201046=⨯⨯⨯--基波的有效值为())(39.118sin 210101010sin 210264V ≈=⨯⨯⨯- πππ二次谐波分量的有效值为())(32.136sin 251010102sin 21064V ≈=⨯⨯⨯- πππ三次谐波分量的有效值为())(21.1524sin 32101010103sin 2310264V ≈=⨯⨯⨯⨯- πππ3-3 若周期矩形信号)(1t f 和)(2t f 的波形如图3-2所示，)(1t f 的参数为s μτ5.0=，s T μ1= ，V E 1=； )(2t f 的参数为s μτ5.1=，s T μ3= ，V E 3=，分别求：（1）)(1t f 的谱线间隔和带宽（第一零点位置），频率单位以kHz 表示； （2）)(2t f 的谱线间隔和带宽； （3）)(1t f 与)(2t f 的基波幅度之比； （4）)(1t f 基波与)(2t f 三次谐波幅度之比。

第三章相互作用——力4力的合成和分解课时2力的分解基础过关练题组一对力的分解的理解1.一个力的大小为30N,将此力分解为两个分力,这两个分力的大小不可能是()A.10N、10NB.20N、40NC.200N、200ND.700N、720N2.(多选)一个力F分解为两个不为零的分力F1、F2,以下说法可能正确的是()A.F1、F2与F都在同一直线上B.F1、F2都小于F2C.F1或F2的大小等于FD.F1、F2的大小都与F相等3.将一个有确定方向的力F=10N分解成两个分力,已知一个分力有确定的方向,与F成30°夹角,另一个分力的大小为6N,则在分解时()A.有无数组解B.有两组解C.有唯一解D.无解题组二按效果分解力4.如图所示,一个半径为r、重为G的光滑均匀球,用长度为r的细绳挂在竖直光滑的墙壁上,则绳子的拉力F T和球对墙壁的压力F N的大小分别是()A.G,G2B.2G,GC.√3G,√3G3D.2√33G,√3G35.如图所示,三段不可伸长的细绳OA、OB、OC能承受的最大拉力相同,它们共同悬挂一重物,其中OB是水平的,A端、B端分别固定在水平天花板上和竖直墙上。

若逐渐增加C端所挂重物的质量,则最先断的绳()A.必定是OAB.必定是OBC.必定是OCD.可能是OB,也可能是OC6.如图所示,将绳子的一端系在汽车上,另一端系在等高的树干上,两端点间绳长为10m。

用300N的拉力把水平绳子的中点往下拉离原位置0.5m,不考虑绳子的重力和绳子的伸长量,则绳子作用在汽车上的力的大小为()A.1500NB.6000NC.300ND.1500√3N题组三力的分解的讨论7.甲、乙两人用绳子拉船,使船沿OO'方向航行,甲用1000N的力拉绳子,方向如图所示,则乙的拉力最小值为()A.500√3NB.500NC.1000ND.400N8.把一个已知力F分解,要求其中一个分力F1跟F成30°角,而大小未知;另一个分力F2=√33F,但方向未知,则F1的大小可能是()A.F2B.√32F C.2√33F D.√3F题组四力的正交分解法9.如图所示,甲、乙、丙三个物体质量相同,与地面间的动摩擦因数相同,分别受到三个大小相同方向不同的作用力F,当它们滑动时,下列说法正确的是()A.甲、乙、丙所受摩擦力相同B.甲受到的摩擦力最大C.乙受到的摩擦力最大D.丙受到的摩擦力最大10.(多选)如图所示,质量为m的物体受到推力F作用,沿水平方向做匀速直线运动,已知推力F与水平面的夹角为θ,物体与地面间的动摩擦因数为μ,则物体所受的摩擦力大小为()A.F cosθB.μmgC.μFD.μ(mg+F sinθ)能力提升练题组一对力的分解的讨论1.(2020山东师大附中高一上期末,)(多选)已知一个力F=10√3N,可分解为两个分力F1和F2,已知F1与F夹角为30°(如图所示),F2的大小为10N,则F1的大小可能是()A.5√3NB.10√3NC.10ND.20N题组二按效果分解力2.(2019河北唐山一中高一上期中,)一个体操运动员在水平地面上做倒立动作,下列哪个图中沿每只手臂向下的力最大()3.(2020浙江嘉兴一中、湖州中学高一上期中联考,)减速带是交叉路口常见的一种交通设施,车辆驶过减速带时要减速,以保障行人的安全。

第三章 平衡方程的应用习题解析3—1静定多跨梁的荷载及尺寸如图3－1所示，长度单位为m ，求支座反力和中间铰处的压力。

图3－1 题3—1图解：a)按照约束的性质画静定多跨梁BC 段受力图（见图3-2），对于BC 梁由平衡条件得到如下方程：图3－2062021660cos ,0)(201=⨯⨯-⨯=∑=NC ni i B F F M ，kN 120=NC F060sin ,001=-=∑=NC Bx ni ix F F F ， kN 9.10360sin 0==NC Bx F F060cos kN 620,001=+⨯-=∑=NC By ni iy F F F ， kN F By 60=故支座反力C 反力kN 120=NC F ，方向垂直与支撑面；中间铰处B 的压力kN 9.103=Bx F 、kN 60=By F 。

如果同学有兴趣，可以进一步计算固定端A 约束反力，按照约束的性质画AB 段受力图（见图3-3），由作用反作用定律得'Bx F Bx F =kN 9.103=、'By F By F =kN 60=。

对于BC 梁由平衡条件得到如下方程：图3-3'1,0Bx Ax ni ix F F F ==∑=kN 9.103=01=∑=ni iy F ， 'By Ay F F =kN 60=0340,0)('1=⨯-⋅-=∑=By A ni i A F m kN M F M ，A M m kN ⋅=220b) 按照约束的性质画静定多跨梁ABC 段、CD 段受力图（见图3-4），对于BC 梁由平衡条件得到如下方程：图3－40m kN 22.521m kN 54,0)(21=⋅⨯⨯-⋅-⨯=∑=ND ni i C F F M ， m kN 5.2⋅=ND F0,01==∑=Cx ni ix F F0kN 25.2,01=+⨯-=∑=ND Cy ni iy F F F ， kN 5.2=Cy F由作用反作用定律得'Cx F Cx F ==0、'Cy F Cy F =kN 5.2=。

大学物理复习题分解第一章质点运动学htz?（h?0,??0,R、1、设质点的运动方程x?Rcos?t，y?Rsin?t，2?h、ω＝常数）,求：①位置矢量的表达式；②任意时刻速度；③任意时刻加速度。

2、一质点在xoy平面上运动，运动函数为x=2t，y=4t2-8（采用国际单位制），求：①质点的轨道方程；②t=1s和t=2s 时，质点的位置、速度和加速度。

3、一质量为10kg的物体沿x轴无摩擦地运动，设t?0时物体位于原点，速度为零，求：①设物体在力F?(3?4t)N的作用下运动了3s，它的速度及加速度各为多少？②设物体在力F?(3?4x)N的作用下移动了3m，它的速度和加速度各为多少？4、有一学生在体育馆阳台上以投射角??300和速率v0?20m/s向台前操场投出一垒球。

球离开手时距离操场水平面的高度h?10m。

试问球投出后何时着地？在何处着地？5、一吊扇翼片长R?0.50m，以n?180r/min的转速转动。

关闭电源开关后，吊扇均匀减速，经tA?1.50min转动停止。

（1）求吊扇翼尖原来的转动角速度?0与线速度v0；（2）求关闭电源开关后时翼尖的角加速度、切向加速度、法向加速度和总加速度。

6、质量m?2kg质点在力F的作用下，在OX直线上运动，运动方程为：x?1t2?2t?4（F,x,t采用国际单位），求：⑴ t=2s 21末的速度v?? 和加速度a??⑵ 在t=1s到t=2s的过程中，力F的冲量I??⑶在t=1s到t=2s的过程中，力F做的功W??第二章牛顿运动定律1、质量为m的小球从高处落下，设它所受到的空气阻力与它的速度的大小成正比f当小球下落的速度vT?80m/s 时，?kv。

重力与阻力平衡，小球作匀速直线运动。

求小球下落到速度v1?1vT时，所经历的时间。

22、一个质量m为的珠子系在线的一端，线的另一端绑在墙上的钉子上，线长为l。

先拉动珠子使线保持水平静止，然后松手使珠子下落。

求线摆下?角时这个珠子的速率和线的张力。

第三章习题及答案一、关键概念1.成本计算的含义2.变动成本法3.产品成本4.期间成本5.变动成本的理论前提6.贡献式损益确定程序7.传统式损益确定程序8.利润差额9.两种成本法分析利润差额10.贡献式损益确定程序 11.传统式损益确定程序 12.广义营业利润差额 13.狭义营业利润差额二、分析思考1.变动成本法的理论前提有哪些？2.变动成本法与完全成本法在产品成本构成上有哪些不同？3.变动成本法与完全成本法相比有哪些区别？ 5.广义营业利润差额的变动规律是什么？4.变动成本法与完全成本法相比在损益确定方面与哪些不同？6.变动成本法的优点和局限性各是什么？7.在我国应用变动成本法有哪些设想？三、单项选择题1．下列各项中，能构成变动成本法产品成本内容的是（）。

A.变动成本B.固定成本C.生产成本D.变动生产成本2．在变动成本法下，固定性制造费用应当列作（）。

A.非生产成本B.期间成本C.产品成本D.直接成本3．下列费用中属于酌量型固定成本的是（）。

A.房屋及设备租金B.技术研发费C.行政管理人员的薪金D.不动产税金1．若本期完全成本法计算下的利润小于变动成本法计算下的利润，则（）。

A.本期生产量大于本期销售量B.本期生产量等于本期销售量C.期末存货量大于期初存货量D.期末存货量小于期初存货量2．在相同成本原始资料条件下，变动成本法计算下的单位产品成本比完全成本法计算下的单位产品成本（）。

A.相同 B.大 C.小 D.无法确定3．下列各项中，能构成变动成本法产品成本内容的是（）。

A.变动成本B.固定成本C.生产成本D.变动生产成本4．在Y=a+( )X中，Y表示总成本，a表示固定成本，X表示销售额，则X的系数应是（）。

A.单位变动成本B.单位边际贡献C.变动成本率D.边际贡献率5．当相关系数r→+1时，表明成本与业务量之间的关系是（）。

A.完全正相关B.基本正相关C.完全相关D.完全无关6．在变动成本法下，其利润表所提供的中间指标是（）。