下载文档原格式
1 / 2绝对值【知识梳理】1、什么叫绝对值？在数轴上，一个数所对应的点与原点的距离叫做这个数的绝对值．例如+5的绝对值等于5，记作|+5|=5；-3的绝对值等于3，记作|-3|=3．2、绝对值的特点有哪些？（1）一个正数的绝对值是它本身；例如，|4|＝4 , |＋7.1| ＝ 7.1 （2）一个负数的绝对值是它的相反数；例如，|－2|＝2,|－5.2|＝5.2 （3）0的绝对值是0．容易看出，两个互为相反数的数的绝对值相等．如|-5|=|+5|=5．若用a 表示一个数，当a 是正数时可以表示成a ＞0，当a 是负数时可以表示成a ＜0，这样，上面的绝对值的特点可用用符号语言可表示为：(1) 如果a ＞0，那么|a|＝a ； (2) 如果a ＜0，那么|a|＝－a ； (3) 如果a ＝0，那么|a|＝0。
3、绝对值在本节课中的应用――比较两个负数的大小由于绝对值是表示数的点到原点的距离，则离原点越远的点表示的数的绝对值越大．负数的绝对值越大，表示这个数的点就越靠左边，因此，两个负数比较，绝对值大的反而小．【重点难点】重点：（1）绝对值的概念； （2）化简；（3）用绝对值比较两个负数的大小。
难点：绝对值的化简；用绝对值比较两个负数的大小。
【典例解析】例1 、已知｜x ｜＝5，求x 的值。
解：因为｜x ｜＝5，所以x ＝5或x ＝－5。
﹡拓展：｜x －3|＝5，求x 的值.解：因为｜x －3|＝5所以x －3＝5或x －3=－5，则x=8或x=－2 例2、绝对值小于5的整数有哪些？解：有4+，4-，3+，3-，2+，2-，1+，1-，0。
例3、 比较87-和76-的大小． 分析 比较两个负数的大小，应先比较它们绝对值的大小，再根据“两个负数，绝对值大的反而小”来判断它们的大小．解 564987|87|==-，564876|76|==-， 56485649>，所以87-<76- 【过关试题】1、下列说法中正确的有（ ）① 互为相反数的两个数的绝对值相等；②正数和零的绝对值都等于它本身；③只有负数的绝对值是它的相反数；④一个数的绝对值相反数一定是负数。
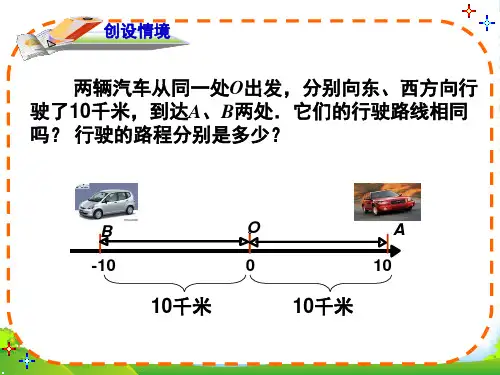
第3讲 绝对值姓名 学校 日期【知识要点】一、绝对值的概念1．定义：一个数的绝对值就是数轴上表示a 的点与原点的距离，数a 的绝对值记作a ，读作a 的绝对值。
2．绝对值的代数意义：一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值还是0。
3．绝对值的几何意义：一个数的绝对值就是表示这个数的点到原点的距离，离原点的距离越远，绝对值越大，离原点的距离越近，绝对值越小。
4绝对值的非负性：由于距离总是正数或0，故有理数的绝对值不可能是负数，即对任意有理数a ，总有a ≥0。
5．互为相反数的两个数的绝对值相等，但绝对值相等的两个数相等或互为相反数。
6．绝对值等于它本身的数一定是非负数，绝对值等于它的相反数的数一定是非正数。
二、绝对值的求法绝对值是一种运算，这个运算符号是“”，求一个数的绝对值就是想办法去掉绝对值符号，对于任意有理数a ，有 （1）(0)0(0)(0)a a a a a a >⎧⎪==⎨⎪-<⎩（2）(0)(0)a a a a a ≥⎧⎨-<⎩ （3）(0)(0)a a a a a >⎧⎨-≤⎩ 【典型例题】例1 求下列各数的绝对值。
（1）34= ； （2）13-= ； （3）144-= ； （4）132= ； 例2 （1）一个数的绝对值是3，则这个数是 。
（2）一个数的绝对值是0，则这个数是 。
（3）有没有一个数的绝对值是-4？ 。
思考：a 与0的大小关系例3 （1）若2m -=，求m 的值；（2）若a b =，则a b 与的关系是什么？例4 写出绝对值不大于3的所有整数，并求出它们的和。
例5 如果a 的相反数是最大的负整数，b 是绝对值最小的数，那么a 与b 的和是多少?例6 数b a ,在数轴上的位置如图，观察数轴，并回答：（1）比较a 和b 的大小；（2）比较a 和b 的大小； （3）判断b a a b b a b a ⨯--+,,,的符号；（4）试化简a b b a -+--经典练习一、填空题1．31-的绝对值是 ，31的绝对值是 ， 的绝对值是31．2.一个正数的绝对值为8，这个数是 ，一个负数的绝对值为8，这个数是 ．3. 的绝对值是它本身， 的绝对值是它的相反数．4.若0>a ，则=a ；若0<a ，则=a ；若0=a ，则=a ．5.若a a =，则a 0，若a a -=，则a 0．6. 的绝对值比它的本身大．7.一个数的绝对值不大于3，则满足条件的最大的负数是 ．二、选择题1．下列等式中，成立的是（ ）A 、33±=+B 、()33--=-C 、33±=±D 、3131=--2．下列计算中，错误的是（ ）A 、1257=-+-B 、04.03.034.0=---C 、535154=-- D 、311312213=---a b3．如果两个数的绝对值相等，那么这两个数必满足（ ）A 、相等B 、都是0C 、互为相反数D 、相等或互为相反数4．下列各式中，不正确的是（ ）A 、01.001.0->-B 、001.001.0->-C 、⎪⎭⎫⎝⎛--<--3131D 、2.32.3->--5．下列判断正确的是（ ）A 、若b a =，则b a =B 、若b a =，则b a =C 、若b a <，则b a <D 、若b a >，则b a >三、解答题1．试写出：（1）绝对值小于5的所有负整数 ；（2）绝对值小于5.2而又大于2.1的所有整数 ．2．已知一组数；4，－3，21-，+5.1，214-，0，－2.2．在这组数中：（1）绝对值最大的数为 ；绝对值最小的数为 ；（2）相反数最大的数为 ；相反数最小的数为 ．3．如图，直线上有三个不同的点A 、B 、C ，且AB ≠BC ，那么，到A 、B 、C 三点距离的和最小的点（ ）（A ）是B 点 （B ）是AC 的中点 （C ）是AC 外一点 （D ）有无穷多个4．对任意有理数a ，式子1a -，1a +，1a -+，1a +中，取值不为0的是 。
第一章第6课绝对值-七年级上册初一数学（人教版）1. 绝对值的概念绝对值是数学中的一个重要概念，简单来说，它表示一个数与0的距离。
对于任意一个实数a，它的绝对值记作|a|，定义如下：•如果a大于等于0，则|a|等于a本身；•如果a小于0，则|a|等于-a。
绝对值的计算结果始终为非负数。
2. 绝对值的性质绝对值有以下几个重要的性质：•非负性：对于任意一个实数a，|a|大于等于0。
•正负性：对于任意一个实数a，如果a大于0，则|a|等于a本身；如果a小于0，则|a|等于-a。
•零的绝对值：|0|等于0。
•数轴上的表示：数轴上的点a到原点0的距离就是|a|。
3. 绝对值的运算3.1. 绝对值的加法绝对值的加法遵循以下规则：对于任意两个实数a和b，有以下等式成立：|a + b| <= |a| + |b|即绝对值的加法不会增加数的绝对值，而是有可能减小。
3.2. 绝对值的减法绝对值的减法遵循以下规则：对于任意两个实数a和b，有以下等式成立：|a - b| <= |a| + |b|即绝对值的减法的结果的绝对值不会大于原来两个数的绝对值之和。
3.3. 绝对值的乘法绝对值的乘法遵循以下规则：对于任意两个实数a和b，有以下等式成立：|a * b| = |a| * |b|即绝对值的乘法相当于两个数的绝对值相乘。
4. 绝对值的应用4.1. 距离的计算绝对值可以用来计算两个数在数轴上的距离。
例如，记数轴上的点A和点B的坐标分别为a和b，则点A和点B之间的距离为|a - b|。
4.2. 数据的取模在实际问题中，我们常常需要对数据进行取模运算。
取模运算即取绝对值，可以去除数据的符号，使得结果始终为非负数。
4.3. 求解不等式绝对值可以用来求解一些简单的不等式。
例如，求解|2x - 1| < 5这个不等式，可以分为两种情况讨论：当2x - 1大于等于0时，原不等式可化简为2x - 1 < 5，解得x < 3；当2x - 1小于0时，原不等式可化简为-(2x - 1) < 5，解得x > -2。
