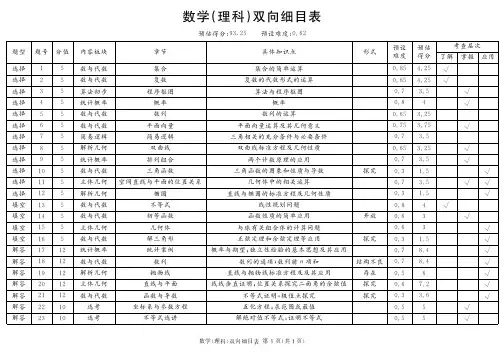
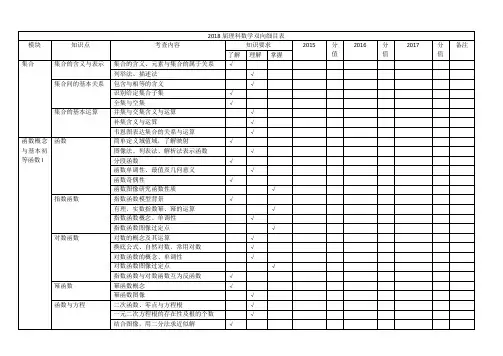
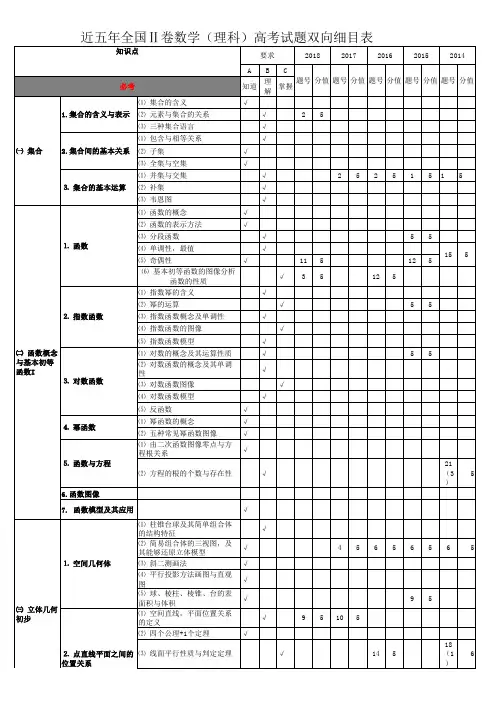
近三年全国理科数学试卷双向细目表

1如有帮助欢迎下载支持
2如有帮助欢迎下载支持
必考的知识点:复数、程序框图、三视图,函数与导数,圆锥曲线,三角函数,（排列组合、统计与概率这个整体）等
常考的知识点常用逻辑用语（注意：从没考过充要条件，多考命题真假）、球的组合体（09年考的是正方体的组合体)、集合、线性规划、数列,平面向量、二项式,解三角形、定积分、直线与圆等
注意：解答题第17题只考纯数列或纯解三角形试题，不会和其他知识组合考。

大题考数列，小题不会考数列，大题不考数列，小题会考2个数列题，三角函数多考小题等
3如有帮助欢迎下载支持。

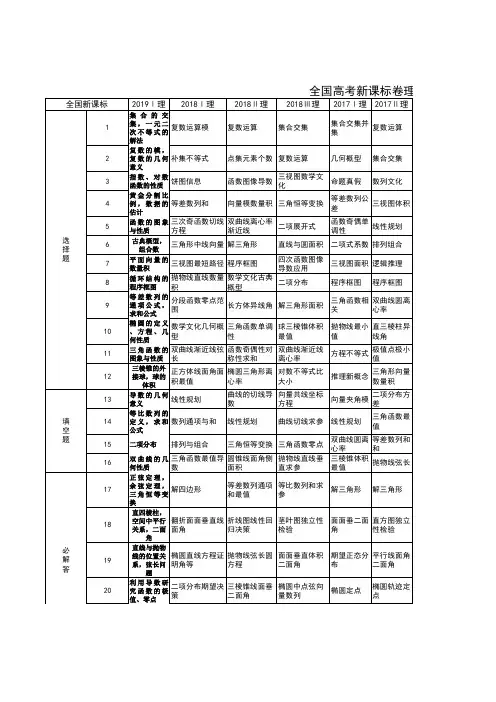
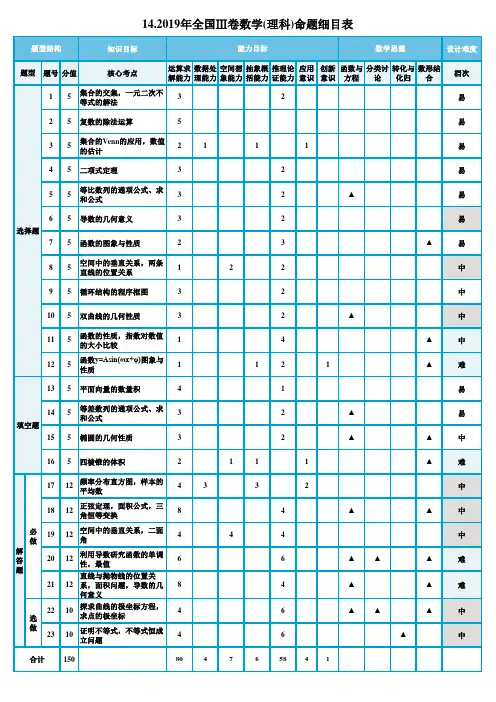
知识目标设计难度题号分值核心考点运算求解能力数据处理能力空间想象能力抽象概括能力推理论证能力应用意识创新意识函数与方程分类讨论转化与化归数形结合档次15集合的交集，一元二次不等式的解法32易25复数的除法运算5易35集合的Venn 的应用，数值的估计2111易45二项式定理32易55等比数列的通项公式、求和公式32▲易65导数的几何意义32易75函数的图象与性质23▲易85空间中的垂直关系，两条直线的位置关系122中95循环结构的程序框图32中105双曲线的几何性质32▲中115函数的性质，指数对数值的大小比较14▲中125函数y=Asin(ωx+φ)图象与性质1121▲难135平面向量的数量积41易145等差数列的通项公式、求和公式32▲易155椭圆的几何性质32▲▲中165四棱锥的体积2111▲难1712频率分布直方图，样本的平均数4332中1812正弦定理，面积公式，三角恒等变换84▲▲中1912空间中的垂直关系，二面角444中2012利用导数研究函数的单调性，最值66▲▲▲难2112直线与抛物线的位置关系，面积问题，导数的几何意义84▲▲难2210探求曲线的极坐标方程，求点的极坐标46▲▲▲中2310证明不等式，不等式恒成立问题46▲中150804765841合计解答题必做选做选择题填空题14.2019年全国Ⅲ卷数学(理科)命题细目表题型结构能力目标数学思想题型。

2023新课标全国2卷数学双向细目表一、概述随着时代的发展和教育体制的不断改革，教育教学内容也在不断更新。

在教育领域，新课标的推出是一个重要的事件，它对学生的学习内容和学习方法，以及教师的教学内容和教学方法都有着重要的指导作用。

本文根据2023年新课标全国2卷数学的双向细目表，进行了详细解读和分析，旨在帮助教师和学生更好地了解新课标的要求，有效指导教学实践。

二、2023新课标全国2卷数学双向细目表解读1. 教材选择根据新课标的要求，教材的选择应当注重贴近学生的生活和实际应用，提倡多角度、立体化的教学。

2. 学习目标新课标强调培养学生的数学思维能力和解决问题的能力，要求学生在学习数学的过程中，不仅要掌握数学的基本知识，更要具备数学的思维方式和解决问题的能力。

3. 教学内容在教学内容方面，新课标重视数学知识的系统性和整合性，提倡数学知识的跨学科性和综合性。

教学内容涵盖了数学的基本概念、基本原理和基本方法，同时还包括了一些前沿的数学知识和数学应用。

4. 学习方法新课标要求教师在教学中注重培养学生的自主学习能力，引导学生学会提出问题、探究问题和解决问题的方法，注重培养学生的团队合作精神和交流能力。

5. 教学评价新课标提倡多样化的教学评价方式，不再仅仅依靠考试成绩来评价学生的学习水平，而是要注重以课堂表现、作业与项目、综合评价等多种方式来全面评价学生的学习情况。

三、教学实践与有效策略1. 加强课堂教学的互动性在教学实践中，教师应该注重通过提问、讨论、案例分析等方式，激发学生的学习兴趣，提高学生的学习积极性，培养学生的自主学习能力。

2. 组织丰富多样的教学活动除了传统的讲授和练习，教师还应该开展更多的实验、探究、研究性学习等活动，让学生在实践中掌握知识，提高解决问题的能力。

3. 引导学生进行综合性实践活动教师应该引导学生参与数学建模、数学应用等综合性实践活动，让学生将所学知识应用到实际中去，提高数学知识的实际运用能力。

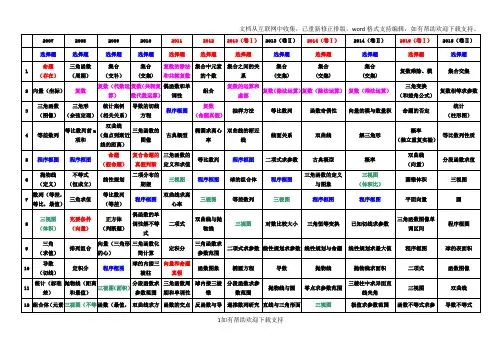
近3年新高考卷高考数学双向细目表【导语】近年来，随着新高考政策的实施，高考数学的内容和要求也发生了一些变化。

高考数学的双向细目表成为考生备考的重要内容之一。

本文将围绕近3年新高考卷和高考数学双向细目表展开深入探讨。

【1. 高考数学的变化】近3年来，高考数学的难度整体上有所增加。

新高考政策要求考生在数学方面具备更多的综合应用能力，因此考试内容更加贴近生活、灵活多变。

高考数学考试的命题也更加注重考察考生深层次的理解和解决问题的能力。

【2. 新高考数学试卷】近3年来，高考数学试卷在命题上更加突出对考生数学运用能力和实际问题解决能力的考查。

试题更加贴近生活实际，涉及更多的跨学科知识和综合运用能力。

试题内容更加灵活和多样，对考生的逻辑思维和实际问题解决能力提出更高的要求。

【3. 高考数学双向细目表的重要性】高考数学双向细目表是考生备考的重要工具，它具有指导性、全面性和灵活性。

通过对高考数学双向细目表的认真学习和分析，考生可以清晰地了解数学考试的要求和重点内容，有助于考生有的放矢、科学备考。

【4. 如何有效利用高考数学双向细目表】针对高考数学双向细目表的利用，考生可以从以下几个方面着手：（1）认真研读双向细目表，了解各个知识点的重点、难点和考点，为备考提供明确的目标和方向。

（2）结合双向细目表对平时的学习进行有效整合，重点攻克细目表中涉及的各个知识点，提高对知识点的深度和广度掌握。

（3）针对双向细目表中的重点、难点进行针对性的练习和强化，做到知识温故而意识新。

【5. 个人观点】在我的观点看来，高考数学双向细目表是考生备考的重要工具，通过认真研读和有效利用双向细目表，可以帮助考生更好地理解数学考试的要求和重点内容，为备考提供更有力的支持。

【总结回顾】回顾本文的内容，我们了解到近3年新高考数学试卷的变化和趋势，以及高考数学双向细目表的重要性和有效利用方法。

希望通过本文的阐述，考生们能够更好地应对高考数学考试，取得优异的成绩。

2023年数学学科高考双向细目表第一部分：知识与技能
1.1 数与代数
- 数的性质和运算
- 同类项与合并
- 一元一次方程与不等式
- 二元一次方程组与不等式组
- 函数与图像
- 幂指对数
- 平面向量
1.2 几何与形状
- 二维平面几何
- 三维空间几何
- 点、直线与面的位置关系
- 图形的性质与计算
- 圆的性质与计算
- 空间中的平面与直线
1.3 数据、统计与概率
- 数据的收集与整理
- 数据的分析与解释
- 概率的基本概念
- 概率计算与应用
- 统计与统计图表
第二部分：解决问题与实践应用
2.1 数学问题解决
- 解决实际问题的数学建模
- 利用数学工具解决问题
- 数学推理与论证方法
2.2 数学实践应用
- 应用数学知识解决实际问题
- 利用数学工具进行实际操作
- 数学思维与计算能力的培养
第三部分：学科素养与拓展
- 数学史和数学文化
- 数学与其他学科的关系
- 数学研究方法和论文写作
以上为2023年数学学科高考双向细目表，包含了数学学科的知识与技能、解决问题与实践应用以及学科素养与拓展三个部分。

详细列出了各个部分的具体内容，旨在指导学生备考高考并培养数学思维与计算能力。

数学试卷及双向细目表试卷题号题型分值一二12345678911112131415161718192选择题填空题4444444444444444441111三2122232425解答题121214试题难度A 易B 中C 难√√√√√√√√√√√√√√√√√√√√√√√√√学段、板块主要知识及主要思想方法七年级“整式”单项式乘以单项式、幂的运算法则六年级“一次方程” 方程根的意义、解一元一次方程八年级“函数”一次函数图像八年级”向量”向量八年级“概率”概率九年级”向量”向量六年级“一次不等式”一元一次不等式的解集七年级“整式”八年级“方程”八年级“方程”八年级“函数”利用平方差公式因式分解换元法无理方程的解函数值八年级“反比例函数”反比例函数、待定系数法八年级“一次函数” 一次函数、图形运动(平移)九年级“统计”统计七年级“平行直线”平行线性质九年级“相似三角形”相似三角形的性质九年级“相似三角形”平行线分线段成比例、平行四边形的性质九年级“锐角三角比”三角比、点和圆的位置关系“圆”八年级“二次根式” 二次根式的化简、分母有理化八年级“分式方程“ 分式方程、转化思想九年级“三角比“”锐角三角比、垂径定理、方程思想圆“九年级“统计” 图表信息处理八年级“几何证明” 特殊四边形的证明九年级“二次函数” 二次函数、待定系数法、配方法、数形结合思想等综合题三角形面积、圆与圆位置关系、相似三角形、函数思想等。