【免费下载】小学奥数四年级 乘除法算式谜添运算符号和括号

小学奥数——四年级第二讲添运算符号和括号例1：把“+”、“-”“×”、“÷”填在适当的圆圈中（每个运算符号只能用一次），并在方框中填上适当的整数，使下面的两个等式成立。

9○ 13 ○ 7 = 10014 ○ 2 ○ 5 = □【试一试】把“+”、“－”“×”、“÷”填在适当的圆圈中（每个运算符号只能用一次），并在方框中填上适当的整数，使下面的两个等式成立。

36○ 0 ○ 15 = 1521 ○ 3 ○ 5 = □例2、在下列四个4中间添上适当的运算符号和括号，组成3个不同的算式，使结果都等于2.（1） 4 4 4 4 = 2（2） 4 4 4 4 = 2（3） 4 4 4 4 = 2【试一试】在下列数字之间填上适当的运算符号和括号，使等式成立。

（1） 5 5 5 5 5 = 2（2）9 9 9 9 9 = 18例3、在下面算式适当的地方添上运算符号，使结果等于1000.5 5 5 5 5 5 5 5 5 5 5 5 = 1000【试一试】在下面算式适当的地方添上运算符号，使结果等于1000.8 8 8 8 8 8 8 8 =1000例4、在1～9这九个数字中加上“＋”、“－”两种运算符号，使其结果等于100（数的顺序不能改变。

）1 2 3 4 5 6 7 8 9 = 100【试一试】把一个乘号和七个加号添在下面的算式中合适的地方，使结果等于100（数的顺序不能改变。

）1 2 3 4 5 6 7 8 9 = 100【练一练】1、把“+”、“－”“×”、“÷”填在适当的圆圈中（每个运算符号只能用一次），并在方框中填上适当的整数，使下面的两个等式成立。

15○ 7 ○ 5 = 1005 ○ 16 ○ 8 = □2、在下列数字之间填上适当的运算符号和括号，使等式成立。

（1） 3 3 3 3 3 = 6（2） 3 3 3 3 3 = 6（3） 3 3 3 3 3 = 63、在下面算式适当的地方添上运算符号，使结果等于1999.8 8 8 8 8 8 8 8 =19994、把加号添在下面算式中合适的地方，使结果等于99（数的顺序不能改变。

方法一：逆推法例一、在等号左边的数之间添上适当的运算符号和括号，使等式成立。

1 2 3 4 5 6 7 8 =2。

用逆推的方法，从后往前尽量让大的数经过加减运算为0，然后依次求出来。

在后4位数中（5+8）-（6+7）=0，因此原式变为1 2 3 4+5-6-7+8=2，所以原式就可以变为1 2 3 4=2，很清楚就可以知道1+2+3-4=2。

解答：1+2+3-4+5-6-7+8=2 。

方法二：倒推法例二、在下面4个4中间添加上适当的运算符号和括号，组成3个不同的算式，使得数都是2。

1）4 4 4 4=22）4 4 4 4=23）4 4 4 4=2首先要考虑几种得数是2的可能性，，如16÷8=2，1+1=2，4-2=2，…然后联系题目中的具体数字，加上运算符号，使得算式等于2。

考虑4个4组成16÷8=2，这样可以把前面两个4计算成16，后面两个计算成8；2）考虑将四个四组成1+1=2，这样可以把前后两个4都计算成1；3）考虑将4个4组成4-2=2，这样可以将后3个4计算成2。

解答：1）4×4÷（4+4）=2； 2）4÷4+4÷4=2； 3）4-（4+4）÷4=2。

方法三：逼近法例三、在没有写完的算式:1 2 3 4 5 6 7 8 9=100的左边数字之间插入一些符号，使得等式成立，要求按下面3个规定，写出3个等式来：1）插入7个加号1个乘号；2）插入2个加号2个减号；3）插入2个加号2个减号。

解析：1）因为1+2+3+4+5+6+7+8+9=45，有8个加号，结果比要求的100还少55，按要求可以把其中的一个加号变成乘号；所以可以在靠近结果的8和9之间用乘号。

2）要求用4个运算符号，先确定一个接近100的数，用1，2，3写成一个三位数123，123比100多了23，剩余的6个数字之间用一个加号，两个减号凑成23。

3）要求用两个加号两个减号，但不能与2）的方法相同，那就同样用123，然后用剩下的数字在一个加号两个减号的组合下凑23。

巧添运算符号巧点晴——方法和技巧解决问题的常用方法：①计算、试验、合理地组合；②从后面开始思考的逆推法。

(1)添运算符号的题目一般来讲解法都不是唯一的,如果题中没有特别的要求,则添出一种答案就算正确;(2)添运算符号不仅可以在两个数字之间添,也可以将相邻的几个数字看成一个数,再在这个数与其相邻的数之间添.巧指导——例题精讲A级冲刺名校·基础点晴一、巧用递推法【例1】用下列各组数“凑24”。

（1）4，5，7，9 （2）3，7，8，8（3）2，2，8，8 （4）5，5，5，5（5）9，10，11，12 （6）2，4，6，13做一做1 把下列每组中的四个数凑成24。

（1）1，1，5，7 （2）3，7，7，8（3）4，4，4，4 （4）5，8，11，12【例2】添上＋、－、×、÷、（）、[ ]等符号，使算式1 2 3 4 5=1成立。

做一做2 添上＋、－、×、÷、（）等符号，使下列等式成立。

（1）1 2 3 4 5=10 （2）1 2 3 4 5=10（3）1 2 3 4 5=10 （4）1 2 3 4 5=10【例3】在下面的式里加上括号，使等式成立。

（1）6×9＋15÷3－2=21 （2）6×9＋15÷3－2=69（3）6×9＋15÷3－2=46 （4）6×9＋15÷3－2=36做一做3 在下面的算式中合适的地方，添上一个括号，使等式成立。

（1）6＋30÷15－3×4－2=2 （2）6＋30÷15－3×4－2=6 （3）6＋30÷15－3×4－2=10 （4）6＋30÷15－3×4－2=12 （5）6＋30÷15－3×4－2=14 （6）6＋30÷15－3×4－2=36B级竞赛培优·更上层楼二、合理尝试【例4】在1 2 3 4 5 6 7 8 9的某些数字之间添上加号或减号，使计算结果等于100。

一、知识点分析（1）重点、考点：掌握四则运算的概念在解决问题的过程中，掌握四则运算混合运算顺序（2）难点、xx点：对四则运算意义的理解（3）教学目标加深对四则运算意义的理解，提高计算能力，培养同学们思维的灵活性和敏捷性．二、教学内容：xx运算符号和括号【知识点梳理】添运算符号和括号，通常采用尝试探索法。

尝试探索法有两种：1、如果题目中的数比较简单，可以从等式的结果入手，推想哪些算式能够得到这个结果，然后拼凑出所求的算式。

2、如果题目中的数多，结果也较大，可以考虑先用几个数凑出接近于等式结果的数，然后在进行调整，使等式成立。

通常情况下，要根据题目的特点选择方法，有时将以下两种方法结合起来使用，更有助于问题的解决。

【例题详解】例1你能在下面4个2之间添上+、－、×、÷或（），使算式成立吗？22 =4拓展：你能在下面4个6之间添上+、－、×、÷或（），使算式成立吗？（1）66 =0（2）66 =1（3）66 =2（4）66 =3例2在下面各数之间添上+、－、×、÷或（），使算式成立12345 =10拓展在两个数之间添上运算符号，使算式成立105=22例3有2，5，6，10四个数，在它们之间添上+、－、×、÷或（），使它们的结果是24（每个数只能用一次）。

例4在下面式子中适当的地方添上+、－、×、÷，使算式成立77777 =1400拓展在下面式子中适当的地方添上两个“－”，一个“＋”和一个“（9=100【课堂练习】1、在下列算式中适当的地方添上（），使算式成立（1）1 + 2 × 3 + 4 × 5 + 6 × 7 + 8 × 9 =505（2）215－89 × 3＋111 ÷ 3－2 =872、对于下列各式，按要求添运算符号，使算式成立。

（1）在下列式子中适当的地方添上“＋”或“－”，使算式成立。

数字谜是杯赛中非常重要的一块，特别是迎春杯，数字谜是必考的，一般学生在做数字谜的时候都采用尝试的方式，但是这样会在考试中浪费很多时间．本模块主要讲乘除竖式数字谜的解题方法，学会通过找突破口来解决问题．最后通过例题的学习，总结解数字谜问题的关键是找到合适的解题突破口．在确定各数位上的数字时，首先要对填写的数字进行估算，这样可以缩小取值范围，然后再逐一检验，去掉不符合题意的取值，直到取得正确的解答．1. 数字谜定义:一般是指那些含有未知数字或未知运算符号的算式．2. 数字谜突破口：这种不完整的算式，就像“谜”一样，要解开这样的谜，就得根据有关的运算法则，数的性质（和差积商的位数，数的整除性，奇偶性，尾数规律等）来进行正确的推理，判断．3. 解数字谜：一般是从某个数的首位或末位数字上寻找突破口．推理时应注意： ⑴ 数字谜中的文字，字母或其它符号，只取0~9中的某个数字； ⑵ 要认真分析算式中所包含的数量关系，找出尽可能多的隐蔽条件；⑶ 必要时应采用枚举和筛选相结合的方法（试验法），逐步淘汰掉那些不符合题意的数字； ⑷ 数字谜解出之后，最好验算一遍．模块一、乘法数字谜【例 1】 下面是一个乘法算式：问：当乘积最大时，所填的四个数字的和是多少？5×【例 2】 下面两个算式中，相同的汉字代表相同的数字，不同的汉字代表不同的数字．⨯=美妙数学数数妙，美+妙数学=妙数数。

=美妙数学___________【例 3】 北京有一家餐馆，店号“天然居”，里面有一副著名对联：客上天然居，居然天上客。

巧的很，例题精讲知识点拨教学目标5-1-2-2.乘除法数字谜（一）×客上天然居4居然天上客【例 4】 下面算式(1)是一个残缺的乘法竖式，其中□≠2，那么乘积是多少？【例 5】 下面残缺的算式中，只写出了3个数字1，其余的数字都不是1，那么这个算式的乘积是？【例 6】 右面的算式中，每个汉字代表一个数字（0~9），不同汉字代表不同数字．美+妙+数+学+花+园= ．423805⨯美妙数学花园数学真美妙好好好美妙【例 7】 在右边的乘法算式中，字母A 、B 和C 分别代表一个不同的数字，每个空格代表一个非零数字．求A 、B 和C 分别代表什么数字？941A B CA B C⨯【例 8】 在每个方框中填入一个数字，使得乘法竖式成立．已知乘积有两种不同的得数，那么这两个得数的差是 ．【例 9】 在图中的每个方框中填入一个适当的数字，使得乘法竖式成立。

第6讲算式谜（二）一、知识要点解决算式谜题，关键是找准突破口，推理时应注意以下几点：1．认真分析算式中所包含的数量关系，找出隐蔽条件，选择有特征的部分作出局部判断；2．利用列举和筛选相结合的方法，逐步排除不合理的数字；3．试验时，应借助估值的方法，以缩小所求数字的取值范围，达到快速而准确的目的；4．算式谜解出后，要验算一遍。

二、精讲精练【例题1】在下面的方框中填上合适的数字。

练习1：在□里填上适当的数。

【例题2】在下面方框中填上适合的数字。

练习2：在□内填入适当的数字，使下列除法竖式成立。

【例题3】下面算式中的a、b、c、d这四个字母各代表什么数字？练习3：求下列各题中每个汉字所代表的数字。

1 华罗庚金杯× 3华罗庚金杯 1花红柳绿× 9柳绿花红盼望祖国早日统一×一盼盼盼盼盼盼盼盼盼【例题4】在1、2、3、4、5、6、7、8、9这九个数字中间加上“＋、－”两种运算符号，使其结果等于100（数字的顺序不能改变）。

1 2 3 4 5 6 7 8 9 = 100练习4：（1）在下面等号左边的数字之间添上一些加号，使其结果等于99（数字的顺序不能改变）。

9 8 7 6 5 4 3 2 1 = 99（2）一个乘号和七个加号添在下面的算式中合适的地方，使其结果等于100（数字的顺序不能改变）。

1 2 3 4 5 6 7 8 9 = 100（3）添上适当的运算符号和括号，使下列等式成立。

1 2 3 4 5 = 100【例题5】在下面的式子里添上括号，使等式成立。

7×9＋12÷3－2 = 23练习5：1.在下面的式子里添上括号，使等式成立。

（1）7×9＋12÷3－2 = 75（2）7×9＋12÷3－2 = 47（3）88＋33－11÷11×2 = 52.在1、2、3、4、5、6、7、8、9这九个数字中间加上“＋、－”两种运算符号，使其结果等于100（数字的顺序不能改变）。

第10讲破译乘除法竖式谜知识要点我们已经在前面的学习中接触过竖式谜了，知道了解决这类问题，要运用正确的分析推理方法，确定算式中的未知数字。

解答较复杂的竖式谜时，要先仔细审题，分析数据之间的关系，找到突破口，逐步试验，分析求解，除了要用到以前学过的首位分析法、末位分析法、进（退）位分析法，还要运用倒推法、凑整法、估值法等。

精典例题例1:如图，在下面的乘法算式中：a、b、c、d分别表示不同的数字，问abc表示的三位数是__________。

a b c×74 4 b d利用首位分析法，分析出a表示的数，再进一步倒推到个位。

模仿练习在下面的算式中，相同的汉字（字母）代表相同的数字，不同的汉字（字母）代表不同的数字，你知道每个汉字（字母）代表几吗？（1）我爱美丽成都×都9 9 9 9 9 9（2） A B C D×9D C B A精典例题例2:如图，在下图中的方框内填入合适的数，让乘法竖式成立。

× 285利用竖式中已有的数字来寻找“突破口”。

模仿练习在下图中的方框内填入合适的数，让乘法竖式成立。

×8数学会让你变成一个善于发现的孩子！- 2-精典例题例3:如图，在图中的空格内填入合适的数字，使除法竖式成立。

267根据商中的“2”和它与除数的乘积个位上的“6“来确定除数。

模仿练习如图，在图中的空格内填入合适的数字，使除法竖式成立。

8 7精典例题例4:如图，在图中的空格内填入合适的数字，使除法竖式成立。

971根据除数的最高位，可以确定商的最高位，再根据余数来确定除数的个位。

模仿练习如图，在图中的空格内填入合适的数字，使除法竖式成立。

7 4639 8数学会让你变成一个善于发现的孩子！- 4-家庭作业1. 下面的乘法算式中，不同的汉字代表不同的数字，如果赛代表9，那么其它几个字各代表什么呢？来 参 加 数 学 邀 请 赛 × 赛 来 来 来 来 来 来 来 来 来2. 如图，在下图(1)中的方框内填入合适的数，在图（2）中填入不是 8的数，让乘法竖式成立。

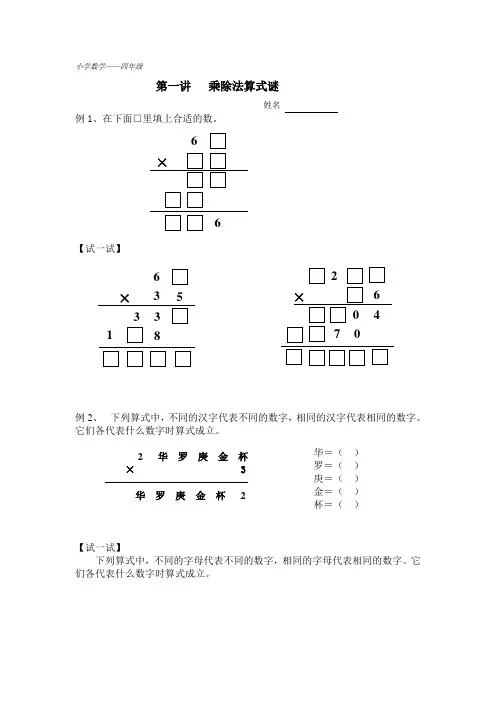
小学数学——四年级第一讲 乘除法算式谜姓名例1、在下面□里填上合适的数。

【试一试】例2、 下列算式中，不同的汉字代表不同的数字，相同的汉字代表相同的数字。

它们各代表什么数字时算式成立。

2 华 罗 庚 金 杯 ×3 华 罗 庚 金 杯 2【试一试】下列算式中，不同的字母代表不同的数字，相同的字母代表相同的数字。

它们各代表什么数字时算式成立。

华＝（ ） 罗＝（ ） 庚＝（ ） 金＝（ ） 杯＝（ ）6 66 × 35 33 81 20 0 7 4a b c d× 9 d c b a例3、 下列算式中，不同的汉字代表不同的数字，相同的汉字代表相同的数字。

它们各代表什么数字时算式成立。

【试一试】在下面的乘法算式中，汉字“七 巧 板”各代表一个互不相同的数字，已知“巧”代表7，其余两个字各代表什么数字时算式成立。

例4、 在下面□里填上合适的数，使竖式成立。

a ＝（ ）b ＝（ ）c ＝（ ）d ＝（ ）算＝（ ） 式＝（ ） 谜＝（ ） 七＝（ ） 巧＝ 7 板＝（ ）算 ×式 谜 算 式 谜 谜谜七 ×巧 板 七 巧 板板七 巧【试一试】【练一练】1、2、下列算式中，不同的汉字代表不同的数字，相同的汉字代表相同的数字。

它们各代表什么数字时算式成立。

盼 望 祖 国 早 日 统 一 × 9 盼 盼 盼 盼 盼 盼 盼 盼 盼3、算式中不同的汉字各代表哪个数字？盼＝（ ） 望＝（ ）祖＝（ ） 国＝（ ）早＝（ ） 日＝（ ）统＝（ ） 一＝（ ）6 7 09 2 × 92 14、5、下列算式中，不同的汉字代表不同的数字，相同的汉字代表相同的数字。

它们各代表什么数字时算式成立。

团 团 × 圆 圆 ＝ 和 和 美 美学＝（ ） 好＝（ ）×学 好 好0 2 好 学 1 团 = （ ） 圆=（ ） 和=（ ） 美=（ ）1。

第一讲乘除法数字谜（一）
专题简析：
解决算式谜题，关键是找准突破口，推理时应注意以下几点：
1.认真分析算式中所包含的数量关系，找出隐蔽条件，选择有特征的部分作出局部判断；
2.利用列举和筛选相结合的方法，逐步排除不合理的数字；
3.试验时，应借助估值的方法，以缩小所求数字的取值范围，达到快速而准确的目的；
4.算式谜解出后，要验算一遍。

例1.在下面的方框中填上合适的数字。

分析：由积的末尾是0，可推出第二个因数的个位是5；由第二个因数的个位是5，并结合第一个因数与5相乘的积的情况考虑，可推出第一人个因数的百位是3；由第一个因数为376与积为31□□0，可推出第二个因数的十数上是8。

题中别的数字就容易填了。

练习一。

【小学四年级奥数讲义】算式谜（二）一、知识要点解决算式谜题，关键是找准突破口，推理时应注意以下几点：1．认真分析算式中所包含的数量关系，找出隐蔽条件，选择有特征的部分作出局部判断；2．利用列举和筛选相结合的方法，逐步排除不合理的数字；3．试验时，应借助估值的方法，以缩小所求数字的取值范围，达到快速而准确的目的；4．算式谜解出后，要验算一遍。

二、精讲精练【例题1】在下面的方框中填上合适的数字。

练习1：在□里填上适当的数。

【例题2】在下面方框中填上适合的数字。

练习2：在□内填入适当的数字，使下列除法竖式成立。

【例题3】下面算式中的a、b、c、d这四个字母各代表什么数字？练习3：求下列各题中每个汉字所代表的数字。

1 华罗庚金杯× 3华罗庚金杯 1花红柳绿× 9柳绿花红盼望祖国早日统一×一盼盼盼盼盼盼盼盼盼【例题4】在1、2、3、4、5、6、7、8、9这九个数字中间加上“＋、－”两种运算符号，使其结果等于100（数字的顺序不能改变）。

1 2 3 4 5 6 7 8 9 = 100练习4：（1）在下面等号左边的数字之间添上一些加号，使其结果等于99（数字的顺序不能改变）。

9 8 7 6 5 4 3 2 1 = 99（2）一个乘号和七个加号添在下面的算式中合适的地方，使其结果等于100（数字的顺序不能改变）。

1 2 3 4 5 6 7 8 9 = 100（3）添上适当的运算符号和括号，使下列等式成立。

1 2 3 4 5 = 100【例题5】在下面的式子里添上括号，使等式成立。

7×9＋12÷3－2 = 23练习5：1.在下面的式子里添上括号，使等式成立。

（1）7×9＋12÷3－2 = 75（2）7×9＋12÷3－2 = 47（3）88＋33－11÷11×2 = 52.在1、2、3、4、5、6、7、8、9这九个数字中间加上“＋、－”两种运算符号，使其结果等于100（数字的顺序不能改变）。

5-1-1-1.算式谜（一）教学目标数字谜从形式上可以分为横式数字谜与竖式数字谜，从运算法则上可以分为加减乘除四种形式的数字谜。

横式与竖式亦可以互相转换，本讲中将主要介绍数字谜的一般解题技巧。

主要横式数字谜问题，因此，会需要利用数论的简单奇偶性等知识解决数字谜问题知识点拨一、基本概念填算符：指在一些数之间的适当地方填上适当的运算符号（包括括号），从而使这些数和运算符号构成的算式成为一个等式。

算符：指+、-、×、÷、（）、[]、｛｝。

二、解决巧填算符的基本方法（1）凑数法：根据所给的数，凑出一个与结果比较接近的数，再对算式中剩下的数字作适当的增加或减少，从而使等式成立。

（2）逆推法：常是从算式的最后一个数字开始，逐步向前推想，从而得到等式。

三、奇数和偶数的简单性质（一）定义：整数可以分为奇数和偶数两类（1）我们把1，3，5，7，9和个位数字是1，3，5，7，9的数叫奇数.（2）把0，2，4，6，8和个位数是0，2，4，6，8的数叫偶数.（二）性质：①奇数≠偶数.②整数的加法有以下性质：奇数+奇数=偶数；奇数+偶数=奇数；偶数+偶数=偶数.③整数的减法有以下性质：奇数-奇数=偶数；奇数-偶数=奇数；偶数-奇数=奇数；偶数-偶数=偶数.④整数的乘法有以下性质：奇数×奇数=奇数；奇数×偶数=偶数；偶数×偶数=偶数.例题精讲模块一、巧填算符（一）巧填加减运算符号【例1】在下面算式适当的地方添上加号，使算式成立。

88888888=1000【考点】巧填算符之凑数法【难度】3星【题型】填空【解析】要在八个8之间只添加号，使和为1000，可先考虑在加数中凑出一个较接近1000的数，它可以是888，而888＋88=976，此时，用去了五个8，剩下的三个8应凑成1000-976＝24，这只要三者相加就行了。

本题的答案是：888+88+8+8+8=1000【答案】888+88+8+8+8=1000【例2】在等号左边9个数字之间填写6个加号或减号组成等式：1 2 3 4 5 6 7 8 9＝101 【考点】巧填算符之凑数法【难度】3星【题型】填空【关键词】2006年，迎春杯，中年级，初赛，第2题【解析】（不唯一）123456789101-+-+++=++++-+=或123456789101【答案】123456789101++++-+=或123456789101-+-+++=【例3】在下面的□中填入“+”、“一”，使算式成立：1110987654210□□□□□□□□3□□=【考点】巧填算符之凑数法【难度】3星【题型】填空【关键词】2008年，第6届，希望杯，4年级，初赛，5题【解析】11+10+9-8-7-6-5-4+3-2-1=0.(答案不唯一)【答案】11+10+9-8-7-6-5-4+3-2-1=0.(答案不唯一)【巩固】在下面的□中填入“+”、“一”，使算式成立：11109876321□□□□□□5□4□□=【考点】巧填算符之凑数法【难度】3星【题型】填空【关键词】2008年，希望杯，第六届，六年级，初赛，第2题，6分【解析】11+10+9……3+2=65，所以只要将其中和为32的几项的加号改成减号即11-10-9-8+7+6-5+4+3+2=1 【答案】11-10-9-8+7+6-5+4+3+2=1【例4】在下面算式中合适的地方，只添两个加号和两个减号使等式成立。

一般是指那些含有未知数字或缺少运算符号的算式。

解决这类问题；可以根据已学过的知识；运用正确的分析推理方法；确定算式中的未知数字和运用符号。

由于这类题目的解答过程类似全平时进行的猜谜语游戏；所以；我们把这类题目称为“算式谜题”。

解答算式谜问题时；要先仔细审题；分析数据之间的关系；找到突破口；逐步试验；分析求解；通常要运用倒推法、凑整法、估值法等。

例1：在下面算式的括号里填上合适的数。

分析：根据题目特点；先看个位：7＋5=12；在和的个位（）中填2；并向十位进一；再看十位；（）+4+1的和个位是1；因此；第一个加数的（）中只能填6；并向百位进1；最后来看百位、千位；6+（）+1的和的个位是2；第二个加数的（）中只能填5；并向千位进1；因此；和的千位（）中应填8。

例2：下面各式中“巨”、“龙”、“腾”、“飞”分别代表不同的数字；相同的汉字代表相同的数字。

当它们各代表什么数字时；下列的算式成立。

分析：先看个位；3个“飞”相加的和的个位数字是1；可推知“飞”代表7；再看十位；3个“腾”相加；再加上个位进来的2；所得的和的个位是0；可推知“腾”代表6；再看百位；两个“龙”相加；加上十位进上来的2；所得和的个位是0；“龙”可能是4或9；考虑到千位上的“巨”不可能为0；所以“龙”只能代表4；“巨”只能代表1。

例3：下面各式中的“兵”、“炮”、“马”、“卒”各代表0—9这十个数字中的某一个；相同的汉字代表相同的数字。

这些汉字各代表哪些数字？分析：这道题应以“卒”入手来分析。

“卒”和“卒”相加和的个位数字仍然是“卒”；这个数字只能是0。

确定“卒”是0后；所有是“卒”的地方；都是0。

注意到百位上是“兵”+“兵”=“卒”；容易知道“兵”是5；“车”是1；再由十位上的情况可推知“马”是4；进而推得“炮”是2。

例4：将0、1、2、3、4、5、6这七个数字填在圆圈和方格内；每个数字恰好出现一次；组成一个整数算式。

分析：要求用七个数字组成五个数；这五个数有三个是一位数；有两个是两位数。

年级四年级学科奥数版本通用版课程标题乘除数字谜（二）一般来说，算式都是由一些数字和运算符号组成的，可有些算式却由汉字或英文字母组成，我们称它为文字算式。

文字算式也是一种数字谜，解答时要注意在同一道题中，相同的文字或英文字母应表示相同的数字，不同的文字或英文字母应表示不同的数字。

解文字算式谜与添运算符号、填竖式的步骤与方法基本是一样的，都要仔细观察算式的特征，认真分析，正确选择解题的突破口，最后通过尝试找寻正确答案。

例1下面算式中的a、b、c、d四个字母各代表什么数字？（各个数字不重复）分析与解：因为四位数abcd乘9的积是四位数，可知a是1；d和9相乘的积的个位是1，可知d只能是9；因为第二个因数9与第一个因数百位上的数b相乘的积不能进位，所以b只能是0（1已经用过）；再由b＝0，可推知c＝8。

故a＝１，ｂ＝０，ｃ＝８，ｄ＝９。

例2下列算式中不同的汉字代表不同的数字，相同的汉字代表相同的数字。

它们各代表什么数字时算式成立？分析与解：（1）由积的个位是2，一个因数是3，推出另一个因数的个位数“杯”是4。

（2）4×3＝12，在积的个位上写2，向十位进1，因为积的十位数“杯”为4，所以“金”×3的积的个位数是3，由此“金”是1。

（3）“金”是1，积的百位数为1，所以“庚”×3的积的末位数应是1，由此“庚”是7。

（4）7×3＝21，在积的百位上写1，向千位进2，因为积的千位数为7，所以“罗”×3的积的末位数应是5，由此“罗”是5。

（5）由积的万位数“罗”是5，可推得“华”为8。

华＝8，罗=5，庚=7，金=1，杯=4。

例3 下图的除法竖式中，相同的字母代表相同的数字，不同的字母代表不同的数字，那么被除数DEFGF 是多少？分析与解：显然1D =，由AB A IF ⨯=可知，A 不会超过3，否则得到的乘积应该是3位数，如果3A =，那么B 也不能超过3，所以B 只能是2，这样的64232=⨯=⨯B AB 与AAH 矛盾，所以3A ≠，所以2A =，根据AB B AAH ⨯=，可以尝试得出8B =时，等式成立，得到这些条件即可依次求得：5I =，6F =，9G =，0E =，所以被除数DEFGF 是10696。

巧添算符（三）98－76＋5－4＋3－2－1=232、在下面算式中适当的地方添上＋、－、×、÷使等式成立1 2 3 4 5 6 7 8=11＋2×3－4＋5－6＋7－8=13、在下面算式中适当的地方添上＋、－使等式成立1 2 3 4 5 6 7 8=141＋2＋3－4＋5＋6－7＋8=144、在下面的数字之间添上＋、－、×、÷使等式成立1 2 3 4 5 6 = 6（1＋2－3）×4×5＋6=61 2 3 4 5 6 = 101＋2×3×（4＋5）÷6=10例4：改变下式中的一个运算符号，使等式成立。

1＋2＋3＋4＋5＋6＋7＋8＋9=100【思路导航】首先不妨算一算等号左边的值等于多少，1＋2＋3＋4＋5＋6＋7＋8＋9=45，45比100小55，所以应量使等号左边的结果大一些，如果把8和9之间的“＋”改“×”，这样等式左边的值就增加了55，这样等式成立。

1＋2＋3＋4＋5＋6＋7＋8×9=100练习四1、改变一个运算符号，使等式成立。

1＋2＋3＋4＋5＋6＋7＋8＋9＋10=451＋2＋3＋4－5＋6＋7＋8＋9＋10=452、王老师在批改作业时发现小林同学抄题时丢了括号，但结果仍是正确的，请你给小林的算式添上排号。

4＋28÷4－2×3－1=4（4＋28）÷4－2×（3－1）=43、在下列算式中合适的地方添上括号，使等式成立。

1＋2×3＋4×5＋6×7＋8×9=303（1＋2×3＋4×5＋6）×7＋8×9=303。