2008年全国初中数学联赛

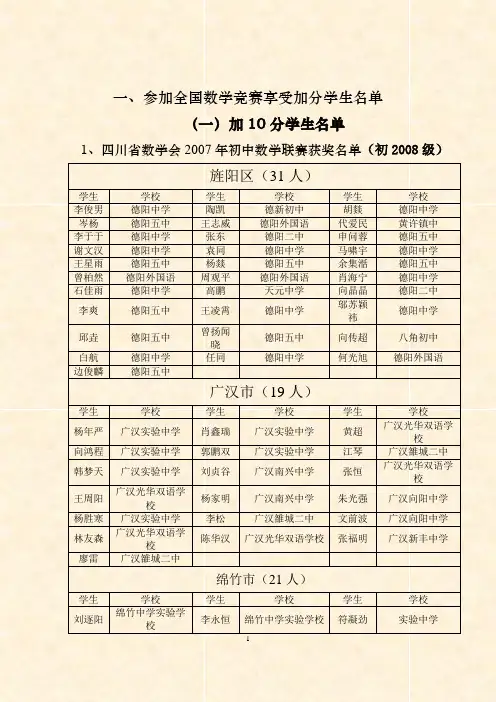
一、参加全国数学竞赛享受加分学生名单（一）加10分学生名单1、四川省数学会2007年初中数学联赛获奖名单（初2008级）旌阳区（31人）学生学校学生学校学生学校李俊男德阳中学陶凯德新初中胡燚德阳中学岑杨德阳五中王志威德阳外国语代爱民黄许镇中李于于德阳中学张东德阳二中申问蓉德阳五中谢文汉德阳中学袁同德阳中学马啸宇德阳中学王星雨德阳五中杨燚德阳五中余集湉德阳五中曾柏然德阳外国语周观平德阳外国语肖海宁德阳中学石佳雨德阳中学高鹏天元中学向晶晶德阳二中李爽德阳五中王凌霄德阳中学邬苏颖祎德阳中学邱垚德阳五中曾扬闻晓德阳五中向传超八角初中白航德阳中学任同德阳中学何光旭德阳外国语边俊麟德阳五中广汉市（19人）学生学校学生学校学生学校杨年严广汉实验中学肖鑫瑞广汉实验中学黄超广汉光华双语学校向鸿程广汉实验中学郭鹏双广汉实验中学江琴广汉雒城二中韩梦天广汉实验中学刘贞谷广汉南兴中学张恒广汉光华双语学校王周阳广汉光华双语学校杨家明广汉南兴中学朱光强广汉向阳中学杨胜寒广汉实验中学李松广汉雒城二中文前波广汉向阳中学林友森广汉光华双语学校陈华汉广汉光华双语学校张福明广汉新丰中学廖雷广汉雒城二中绵竹市（21人）学生学校学生学校学生学校刘逐阳绵竹中学实验学校李永恒绵竹中学实验学校符凝劲实验中学叶文超绵竹中学实验学校朱曼绵竹中学实验学校周甜甜实验中学陈刚绵竹中学实验学校王爽绵竹中学实验学校韩旭绵竹中学实验学校何云鹏绵竹中学实验学校李珂实验中学邓志鑫实验中学杨咏馨绵竹中学实验学校付亚丰实验中学李成军绵竹中学实验学校蒋德刚绵竹中学实验学校代路实验中学唐朝绵竹中学实验学校谢一凡绵竹中学实验学校倪庆新市中学吕秋阳实验中学什邡市（14人）学生学校学生学校学生学校刘一璠什邡中学实验学校叶子菡什邡中学实验学校曾奕什邡禾丰中学李坚什邡马井中学张尚睿什邡中学实验学校王泽全什邡雍城中学汪好什邡中学实验学校徐榕什邡方亭中学苏琪什邡雍城中学黄福泓什邡外国语学校林睿霄什邡中学实验学校曾静仪什邡外国语学校廖梦茜什邡外国语学校刘成什邡隐丰中学中江县（9人）学生学校学生学校学生学校陈波中兴刘林鑫御河中学刘健玉兴涂梨清河袁冬御河中学谭敏龙台镇中张飞龙柏林周杰永兴陈越龙台中学罗江县（6人）学生学校学生学校学生学校昌虎罗江中学王伟罗江回龙学校罗宏罗江鄢家中学张志豪罗江中学周畅罗江中学徐小茹罗江中学2、2008年全国初中数学联赛获奖名单（初2008级）旌阳区（27人）学生学校学生学校学生学校谢文汉德阳中学谢子哲德阳中学待孟桃外国语学校岑扬德阳五中杨继华德阳中学于洁德阳五中曾扬闻晓德阳五中付翔德阳中学吕施施德阳中学谭天德阳中学徐笛瑞德阳中学陈骏德阳五中袁同德阳中学张鑫德阳中学张东德阳二中李俊男德阳中学李于于德阳中学石佳雨德阳中学朱孟韬德阳中学梅熹德德阳二中周龙德阳五中邱垚德阳五中曾雪梅德阳中学肖霄德阳五中付浩书德阳中学陈曦德阳五中李智德阳五中广汉市（19人）学生学校学生学校学生学校王周阳光华学校钟学凯金雁中学李航雒三中韩梦天广汉中学谭世民光华学校黄龙向阳中学庄萌光华学校罗宇雒三中钟凯连山中学刘涛南丰中学赵子豪高坪中学贺英杰广汉中学林友森光华学校张豪雒三中邓怡向阳中学周亮光华学校曾杨静光华学校邹志豪光华学校李强雒三中中江（25人）学生学校学生学校学生学校陈越龙台中学曾峻崧玉兴镇中学李欢欢永兴镇中陈波中兴中学邹雨莎御河中学何琦御河中学彭意吉永兴镇中徐天文御河中学刘彧御河中学谭平普兴镇中谢志强兴隆镇中学蒋凤联合镇中陈茂健通济中心学校伍国凌永太镇中金冬梅永丰中心校黄俊龙御河中学曾真御河中学吴强中江中学邓震雷中江实验中学李传根悦来璧中吴雪梅悦来镇中夏洪学永兴镇中寿洪国中江中学彭蓉太平乡中周杰永兴镇中绵竹（13人）学生学校学生学校学生学校谢一帆绵竹实验学校韩旭绵竹实验学校唐朗莲土门中学叶超绵竹实验学校刘逐阳绵竹实验学校唐朝绵竹实验学校李珂绵竹实验学校雷蕾绵竹实验学校王爽绵竹实验学校邓志鑫绵竹实验学校廖国强绵竹实验学校李帙汉旺中学蒋德刚绵竹实验学校什邡（11人）学生学校学生学校学生学校刘一潘实验中学刘牧云实验中学杨杰马祖初中叶子蒸实验中学车大奇双盛初中刘海棠马井初中陈凯方亭初中刘真良实验中学雷鸣实验中学蒲聪颖实验中学吴俊杰雍城中学罗江（5人）学生学校学生学校学生学校李源罗江中学叶帅罗江中学张雄罗江中学周畅罗江中学刘瑶实验中学（二）加5分学生名单1、四川省数学会2007年初中数学联赛获奖名单（初2008级）旌阳区（30人）学生学校学生学校学生学校宋欣悦德阳中学李峰德阳中学李金圣德阳二中王缘德阳中学任宇德阳中学刘莹逸夫学校张雪婷外国语何凯德阳五中罗竞丰通江学校殷维佳德阳五中潘思翰德阳五中陈乔丹德阳中学邱桐德阳中学刘欣路德阳五中张思诗孝泉中学谢闻寿丰初中周龙德阳五中邹超德新初中朱孟韬德阳中学陈涛德阳中学朱阳洋德新初中陈兰若德阳五中余浩德阳中学李可即德阳五中冯玥德阳中学雷潇凯雯德阳中学刘开源华山南路学校杨旭德阳中学胡峰凡德阳中学何红梅和新初中广汉市（20人）学生学校学生学校学生学校杨成广汉雒城二中刘沁广汉向阳中学冯琦滢广汉实验中学赵志强广汉雒城二中艾西广汉雒城三中燕航宇广汉雒城二中张豪广汉雒城三中游华轩广汉光华双语学校向倩兰广汉实验中学罗捷广汉光华双语学校李逸广汉南兴中学李丹广汉金雁中学向逸飞广汉光华双语学校钟方尚广汉金雁中学秦雪广汉北外中学王博广汉光华双语学校陈磊广汉广兴中学龚雷雪广汉北外中学汪维正广汉实验中学贺英杰广汉实验中学绵竹市（11人）学生学校学生学校学生学校汪洋绵竹中学实验学校张云尧绵竹中学实验学校王俊汉旺中学陈阳凡观鱼中学陈琪绵竹中学实验学校赵祉君实验中学付成城南中学李雪薇实验中学宋章绵竹中学实验学校毕雪城南中学曾理绵竹中学实验学校什邡市（12人）学生学校学生学校学生学校李书焓什邡中学实验学校谭吉祥什邡双盛中学林于雅什邡外国语学校黄立锐什邡外国语学校邹维成什邡马祖中学郭明亮什邡禾丰中学肖文倩什邡中学实验学校王正一什邡外国语学校柳婷什邡双盛中学刘牧云什邡中学实验学校叶琴什邡方亭中学李莉什邡宏达中学中江县（18人）学生学校学生学校学生学校段昭霞永兴王雪御河中学彭意吉永兴雷炜涵城北中学寿洪国中江中学李建桥御河中学胡伟永兴蒋丽太安宾倩柏林段刚玉兴邹雨莎御河中学李青岳御河中学蒋中伟冯店职中袁圆玉兴卢权永兴何海鑫中江中学刘青广福中心校李佳冯店职中罗江县（9人）学生学校学生学校学生学校易超广富初中李源罗江中学廖方芳调元学校刘尧罗江东升学校刘崇安罗江中学张瑾广富学校龙怡驰新盛初中杨翎爽罗江中学廖怨婷回龙学校2、2008年全国初中数学联赛获奖名单（初2008级）旌阳区（25人）学生学校学生学校学生学校黄彦铭德阳二中陶凯德新初中刘莹德阳七中谢赐磊德阳二中何凯德阳五中余集湉德阳五中白航德阳中学陈兰若德阳五中彭仁举德阳二中杨燚德阳五中曾琛淑德阳二中肖海宁德阳中学杨汉德阳二中范星德阳五中王陵霄德阳中学雷潇凯雯德阳中学胡颂毓德阳三中林绍智德阳中学张栌兮外国语学校李秋婧德阳七中刘欣路德阳五中蒋承晋德阳中学王志威外国语学校苏铃翔东电中学付馨德阳五中广汉市（20人）学生学校学生学校学生学校谭明豪广汉中学王鹏雒二中张恒光华学校彭开民广汉中学李行博广汉中学曾传奇高坪中学冷维杰广汉中学罗朋连山中学胥遇时金雁中学汪维正广汉中学贺霄云光华学校曾莉金雁中学陈磊广兴中学高雄广汉中学罗韩广汉中学曾思思高坪中学罗捷光华学校张世奇广汉中学陈德兴广汉中学章德辉光华学校中江（24人）学生学校学生学校学生学校谢奎通济中心学校陈熙文中江实验中学陈婷婷集凤镇中张月御河中学夏柏根永兴镇中李贵涛城北中学吴家委御河中学黄斌永兴镇中刘鹏御河中学陈龙威富兴镇会棚中学杨昌龙联合镇群星朱加伟龙台镇初级中学丁煜民集凤镇中兰楠冯店镇中黄波民主唐义仟兴隆镇中学唐强中兴中学胡伟永兴镇中袁梦御河中学许瑶永安镇中段刚玉兴镇中学邓杨御河中学王春梅清凉中学李攀积金中学绵竹（13人）学生学校学生学校学生学校孙元红土门中学汪洋绵竹实验学校李雪薇绵竹实验学校陈林锦绵竹实验学校马啸宇绵竹实验学校何崇含绵竹实验学校张音洁绵竹实验学校彭飞良绵竹实验学校黄小峰绵竹实验学校邱宇杰绵竹实验学校蒲德俊绵竹实验学校林峰二职中蒋晶晶绵竹实验学校什邡（12人）学生学校学生学校学生学校周诗齐实验中学吕蕊雍城中学陆阳方亭初中汪好实验中学李泓樾外国语学校李正鹏雍城中学龙彪外国语学校郭明亮禾丰初中张露丹实验中学余林雍城中学程文马井初中杨文滔雍城中学罗江（6人）学生学校学生学校学生学校赵山回龙学校邓佳略坪初中王斌鄢家中学罗波德安初中张浩实验中学毕辉慧觉学校。

12008年全国初中数学联合竞赛试题参考答案及评分标准说明：评阅试卷时，请依据本评分标准.第一试，选择题和填空题只设7分和0分两档；第二试各题，请按照本评分标准规定的评分档次给分.如果考生的解答方法和本解答不同，只要思路合理，步骤正确，在评卷时请参照本评分标准划分的档次，给予相应的分数.第一试一、选择题（本题满分42分，每小题7分）本题共有6小题，每题均给出了代号为A ，B ，C ，D 的四个答案，其中有且仅有一个是正确的．将你所选择的答案的代号填在题后的括号内．每小题选对得7分；不选、选错或选出的代号字母超过一个（不论是否写在括号内），一律得0分．1．设213a a +=，213b b +=，且a b ≠，则代数式2211a b+的值为 （ ） A ．5 B ．7 C ．9 D ．11.【答案】B【解析】 由题设条件可知2310a a -+=，2310b b -+=，且a b ≠，所以a ，b 是一元二次方程2310x x -+=的两根，故3a b +=，1ab =，因此222222222211()23217()1a b a b ab a b a b ab ++--⨯+====． 故选B 2．如图，设AD ，BE ，CF 为三角形ABC 的三条高，若6AB =，5BC =，3EF =，则线段BE 的长为（ ）EFDCBA2A ．185B ．4C ．215D ．245【答案】D【解析】 因为AD ，BE ，CF 为三角形ABC 的三条高，易知B ，C ，E ，F 四点共圆，于是AEF ABC △∽△，故35AF EF AC BC ==，即3cos 5BAC ∠=，所以4sin 5BAC ∠=． 在Rt ABE △中，424sin 655BE AB BAC =∠=⨯=．故选D3．从分别写有数字1，2，3，4，5的5张卡片中任意取出两张，把第一张卡片上的数字作为十位数字，第二张卡片上的数字作为个位数字，组成一个两位数，则所组成的数是3的倍数的概率是 （ ）A ．15B ．310C ．25D ．12. 【答案】C【解析】 能够组成的两位数有12，13，14，15，21，23，24，25，31，32，34，35，41，42，43，45，51，52，53，54，共20个，其中是3的倍数的数为12，15，21，24，42，45，51，54，共8个．所以所组成的数是3的倍数的概率是82205=．故选C 4．在ABC △中，12ABC ∠=o ，132ACB ∠=o ，BM 和CN 分别是这两个角的外角平分线，且点M ，N 分别在直线AC 和直线AB 上，则 （ ）3A ．BM CN >B ．BM CN =C ．BM CN <D ．BM 和CN 的大小关系不确定【答案】B【解析】 ∵12ABC ∠=o ，BM 为ABC ∠的外角平分线，∴1(18012)842MBC ∠=-=o o o．又180********BCM ACB ∠=-∠=-=o o o o ，∴180844848BMC ∠=--=o o o o ，∴BM BC =．又11(180)(180132)2422ACN ACB ∠=-∠=-=o o o o，∴18018012()BNC ABC BCN ACB ACN ∠=-∠-∠=--∠+∠o o o 168(13224)=-+o o o12ABC ==∠o ，∴CN CB =. 因此，BM BC CN ==．故选B5．现有价格相同的5种不同商品，从今天开始每天分别降价10％或20％，若干天后，这5种商品的价格互不相同，设最高价格和最低价格的比值为r ，则r 的最小值为 （ ）A ．398T ⎛⎫ ⎪⎝⎭.B ．498⎛⎫ ⎪⎝⎭.C ．598⎛⎫⎪⎝⎭. D ．98.【答案】B.【解析】 容易知道，4天之后就可以出现5种商品的价格互不相同的情况．设5种商品降价前的价格为a ，过了n 天. n 天后每种商品的价格一定可以表示为4()()98110%120%1010kn kkn ka a --⎛⎫⎛⎫⋅-⋅-=⋅⋅ ⎪⎪⎝⎭⎝⎭，其中k 为自然数，且0k n ≤≤．要使r 的值最小，五种商品的价格应该分别为：981010in ia -⎛⎫⎛⎫⋅⋅ ⎪⎪⎝⎭⎝⎭，1188(1010i n i a +--⎛⎫⎛⎫⋅⋅ ⎪ ⎪⎝⎭⎝⎭，22991010i n i a +--⎛⎫⎛⎫⋅⋅ ⎪ ⎪⎝⎭⎝⎭，33981010i n i a +--⎛⎫⎛⎫⋅⋅ ⎪⎪⎝⎭⎝⎭，44981010i n i a +--⎛⎫⎛⎫⋅⋅ ⎪⎪⎝⎭⎝⎭，其中i 为不超过n 的自然数.所以r 的最小值为44498910108981010i n i i n ia a +---⎛⎫⎛⎫⋅⋅ ⎪ ⎪⎛⎫⎝⎭⎝⎭= ⎪⎝⎭⎛⎫⎛⎫⋅⋅ ⎪ ⎪⎝⎭⎝⎭．故选B ． 6．已知实数x ，y 满足(22200820082008x x y y --=，则223233x y x y -+-2007-的值为（ ）A ．2008-B ．2008C ．1-D ．1.【答案】D ．【解析】 ∵(22200820082008x x y y --=，∴222200820082008x x y y y y -=---222200820082008y y x x x x -=---由以上两式可得x y =．所以(2220082008x x -=，解得22008x =，所以522222323320073233200720071x y x y x x x x x -+--=-+--=-=．故选D ．二、填空题（本题满分28分，每小题7分）1．设51a -，则5432322a a a a a a a +---+=- ． 【答案】 2-【解析】 ∵2251351a a --==-⎝⎭，∴21a a +=， ∴()()32325432322222a a a a a a a a a a a a a a a a+--+++---+=-⋅- ()()333322212111(11)211a a a a a a a a a a a--+--===-=-++=-+=-⋅----． 2．如图，正方形ABCD 的边长为1，M ，N 为BD 所在直线上的两点，且5AM 135MAN ∠=o ，则四边形AMCN 的面积为 ．【答案】 52【解析】 设正方形ABCD 的中心为O ，连AO ，则AO BD ⊥，2AO OB = ()222223252MO AM AO ⎛⎫-- ⎪ ⎪⎝⎭O MND CBA6∴2MB MO OB =-又135ABM NDA ∠=∠=o ，13590NAD MAN DAB MAB MAB ∠=∠-∠-∠=--∠o o 45MAB AMB =-∠=∠o ，所以ADN MBA △∽△，故AD DN MB BA =，从而212AD DN BA MB =⋅=． 根据对称性可知，四边形AMCN 的面积1122522222222MAN S S MN AO ==⨯⨯⨯=⨯⨯+=⎝△． 3．已知二次函数2y x ax b =++的图象与x 轴的两个交点的横坐标分别为m ，n ，且1m n +≤.设满足上述要求的b 的最大值和最小值分别为p ，q ，则p q += ．【答案】 12【解析】 根据题意，m ，n 是一元二次方程20x ax b ++=的两根，所以m n a +=-，mn b =．∵1m n +≤，∴1m n m n ++≤≤，1m n m n -+≤≤．∵方程20x ax b ++=的判别式240a b ∆=-≥，∴22()1444a m nb +=≤≤． 22244()()()11b mn m n m n m n ==+--+--≥≥，故14b -≥，等号当且仅当12m n =-=时取得；22244()()1()1b mn m n m n m n ==+----≤≤，故14b ≤，等号当且仅当12m n ==时取得．7所以14p =，14q =-，于是12p q +=．4．依次将正整数1，2，3，…的平方数排成一串：149162536496481100121144…，排在第1个位置的数字是1，排在第5个位置的数字是6，排在第10个位置的数字是4，排在第2008个位置的数字是 ．【答案】 1【解析】 21到23，结果都只各占1个数位，共占133⨯=个数位；24到29，结果都只各占2个数位，共占2612⨯=个数位；210到231，结果都只各占3个数位，共占32266⨯=个数位；232到299，结果都只各占4个数位，共占468272⨯=个数位；2100到2316，结果都只各占5个数位，共占52171085⨯=个数位；此时还差2008(312662721085)570-++++=个数位．2317到2411，结果都只各占6个数位，共占695570⨯=个数位．所以，排在第2008个位置的数字恰好应该是2411的个位数字，即为1．第二试 （A ）一．（本题满分20分）8已知221a b +=，对于满足条件01x ≤≤的一切实数x ，不等式(1)(1)()0a x x ax bx b x bx ------≥ ①恒成立.当乘积ab 取最小值时，求a ，b 的值．【解析】 整理不等式①并将221a b +=代入，得2(1)(21)0a b x a x a ++-++≥ ②在不等式②中，令0x =，得0a ≥；令1x =，得0b ≥．易知10a b ++>，21012(1)a ab +<<++，故二次函数2(1)(21)y a b x a x a =++-++的图象（抛物线）的开口向上，且顶点的横坐标在0和1之间．由题设知，不等式②对于满足条件01x ≤≤的一切实数x 恒成立，所以它的判别式2(21)4(1)0a a b a ∆=+-++⋅≤，即14ab ≥．由方程组221,14a b ab ⎧+=⎪⎨=⎪⎩ ③ 消去b ，得42161610a a -+=，所以223a -或223a +=． 又因为0a ≥，所以62a -或62a +，9于是方程组③的解为6262a b ⎧-=⎪⎪⎨+⎪=⎪⎩或6262a b ⎧+⎪⎪⎨-⎪=⎪⎩所以ab 的最小值为14，此时,a b 的值有两组，分别为 62a -，62b +和62a +=，62b -=．二．（本题满分25分）如图，圆O 与圆D 相交于,A B 两点，BC 为圆D 的切线，点C 在圆O 上，且AB BC =．⑴ 证明：点O 在圆D 的圆周上．⑵ 设△ABC 的面积为S ，求圆D 的的半径r 的最小值．【解析】 ⑴ 连OA ，OB ，OC ，AC ，因为O 为圆心，AB BC =，所以△OBA ∽△OBC ，从而OBA OBC ∠=∠．因为OD AB ⊥，DB BC ⊥，所以9090DOB OBA OBC DBO ∠=-∠=-∠=∠o o ，所以DB DO =，因此点O 在圆D 的圆周上．⑵ 设圆O 的半径为a ，BO 的延长线交AC 于点E ，易知CE OABD10BE AC ⊥.设2AC y =(0)y a <≤，OE x =，AB l =，则222a x y =+，()S y a x =+，22222222()2222()aSl y a x y a ax x a ax a a x y=++=+++=+=+=． 因为22ABC OBA OAB BDO ∠=∠=∠=∠,AB BC =,DB DO =，所以BDO ABC △∽△，所以BD BOAB AC=，即2r a l y =，故2al r y =．所以322222224422a l a aS S a S r y y y y ⎛⎫==⋅=⋅ ⎪⎝⎭≥，即2S r 其中等号当a y =时成立，这时AC是圆O 的直径.所以圆D 的的半径r 2S三．（本题满分25分）设a 为质数，b 为正整数，且()()2925094511a b a b +=+①求a ，b 的值.【解析】 ①式即2634511509509a b a b++⎛⎫= ⎪⎝⎭，设63509a b m +=，4511509a b n +=，则 509650943511m a n ab --== ②故351160n m a -+=，又2n m =，所以2351160m m a -+=③由①式可知，2(2)a b +能被509整除，而509是质数，于是2a b +能被509整除，故m 为整数，即关于m 的一元二次方程③有整数根，所以它的判别式251172a ∆=-为完全平方数．11不妨设2251172a t ∆=-=（t 为自然数），则2272511(511)(511)a t t t =-=+-．由于511t +和511t -的奇偶性相同，且511511t +≥，所以只可能有以下几种情况：①51136,5112,t a t +=⎧⎨-=⎩两式相加，得3621022a +=，没有整数解．②51118,5114,t a t +=⎧⎨-=⎩两式相加，得1841022a +=，没有整数解． ③51112,5116,t a t +=⎧⎨-=⎩两式相加，得1261022a +=，没有整数解． ④5116,51112,t a t +=⎧⎨-=⎩两式相加，得6121022a +=，没有整数解．⑤5114,51118,t a t +=⎧⎨-=⎩两式相加，得4181022a +=，解得251a =． ⑥5112,51136,t a t +=⎧⎨-=⎩两式相加，得2361022a +=，解得493a =，而4931729=⨯不是质数，故舍去．综合可知251a =．此时方程③的解为3m =或5023m =（舍去）． 把251a =，3m =代入②式，得5093625173b ⨯-⨯==．第二试 （B ）12一．（本题满分20分）已知221a b +=，对于满足条件1x y +=，0xy ≥的一切实数对()x y ，，不等式220ay xy bx -+≥ ①恒成立.当乘积ab 取最小值时，求a ，b 的值.【解析】 由1x y +=，0xy ≥可知01x ≤≤，01y ≤≤．在①式中，令0x =，1y =，得0a ≥；令1x =，0y =，得0b ≥．将1y x =-代入①式，得22(1)(1)0a x x x bx ---+≥，即()()21210a b x a x a ++-++≥ ②易知10a b ++>，21012(1)a ab +<<++，故二次函数2(1)(21)y a b x a x a =++-++的图象（抛物线）的开口向上，且顶点的横坐标在0和1之间．由题设知，不等式②对于满足条件01x ≤≤的一切实数x 恒成立，所以它的判别式2(21)4(1)0a a b a ∆=+-++⋅≤，即14ab ≥由方程组221,14a b ab ⎧+=⎪⎨=⎪⎩ ③ 消去b ，得42161610a a -+=，所以223a -或223a +=，13又因为0a ≥，所以62a -或62a +． 于是方程组③的解为6262ab ⎧-=⎪⎪⎨+⎪=⎪⎩或6262a b ⎧+⎪⎪⎨-⎪=⎪⎩所以满足条件的a ，b 的值有两组，分别为62a -=，62b +和62a +，62b -= 二．（本题满分25分）题目和解答与（A ）卷第二题相同.三．（本题满分25分）题目和解答与（A ）卷第三题相同.第二试 （C ）一．（本题满分20分）题目和解答与（B ）卷第一题相同.二．（本题满分25分）题目和解答与（A ）卷第二题相同.三．（本题满分25分）设a 为质数，b ，c 为正整数，且满足29(22)509(41022511)2a b c a b c b c ⎧+-=+-⎨-=⎩①②14求()a b c +的值.【解析】 ①式即266341022511509509a b c a b c+-+-⎛⎫=⎪⎝⎭， 设663509a b c m +-=，41022511509a b cn +-=，则5096509423511m a n ab c ---== ③ 故351160n m a -+=，又2n m =，所以2351160m m a -+= ④由①式可知，2(22)a b c +-能被509整除，而509是质数，于是22a b c +-能被509整除，故m 为整数，即关于m 的一元二次方程④有整数根，所以它的判别式251172a ∆=-为完全平方数．不妨设2251172a t ∆=-=（t 为自然数），则2272511(511)(511)a t t t =-=+-．由于511t +和511t -的奇偶性相同，且511511t +≥，所以只可能有以下几种情况：①51136,5112,t a t +=⎧⎨-=⎩两式相加，得3621022a +=，没有整数解． ②51118,5114,t a t +=⎧⎨-=⎩两式相加，得1841022a +=，没有整数解．③51112,5116,t a t +=⎧⎨-=⎩两式相加，得1261022a +=，没有整数解． ④5116,51112,t a t +=⎧⎨-=⎩两式相加，得6121022a +=，没有整数解．15⑤5114,51118,t a t +=⎧⎨-=⎩两式相加，得4181022a +=，解得251a =． ⑥5112,51136,t a t +=⎧⎨-=⎩两式相加，得2361022a +=，解得493a =，而4931729=⨯不是质数，故舍去．综合可知251a =，此时方程④的解为3m =或5023m =（舍去）． 把251a =，3m =代入③式，得50936251273b c ⨯-⨯-==，即27c b =-．代入②式得(27)2b b --=，所以5b =，3c =，因此()251(53)2008a b c +=⨯+=．。

≤∑100k =1a 2k +1∑100k =1(a 2k +2a k +1a k +2)2=1×∑100k =1(a2k+2a k +1a k +2)2=∑100k =1(a4k+4a 2k a k +1a k +2+4a 2k +1a 2k +2)≤∑100k =1[a 4k +2a 2k (a 2k +1+a 2k +2)+4a 2k +1a 2k +2]=∑100k =1(a 4k+6a 2k a 2k +1+2a 2k a 2k +2).又∑100k =1(a 4k +2a 2k a 2k +1+2a 2k a 2k +2)≤∑100k =1a 2k2,∑100k =1a2ka 2k +1≤∑50i =1a22i -1∑50j =1a22j,故　(3S )2≤∑100k =1a2k2+4∑50i =1a22i -1∑50j =1a22j≤1+∑50i =1a 22i -1+∑50j =1a 22j2=2.从而,S ≤23≈014714<0148=1225.7.本届I M O 第6题.2008年全国初中数学联赛(江西卷) 说明:2008年全国初中数学联赛于4月13日举行,因当日与江西省其他考试的时间重叠,经与联赛组委会商议,联赛江西省赛区竞赛改于4月19日举行,并由江西另行命制一份试题.第一试一、选择题(每小题7分,共42分)1.从分数组12,14,16,18,110,112中删去两个分数,使剩下的数之和为1.则删去的两个数是( ).(A )14与18(B )14与110(C )18与110(D )18与1122.化简32+51+5的结果是( ).(A )12　(B )54　(C )38　(D )1+573.555的末尾三位数字是( ).(A )125(B )375(C )625(D )875.4.若实数x 、y 、z 满足方程组:xy x +2y =1,①yz y +2z=2,②zx z +2x=3,③则( ).(A )x +2y +3z =0(B )7x +5y +2z =0(C )9x +6y +3z =0(D )10x +7y +z=05.将正三角形每条边四等分,然后过这图1些分点作平行于其他两边的直线.则以图1中线段为边的菱形个数为( ).(A )15(B )18(C )21(D )246.某人将2008看成了一个填数游戏式:28.于是,他在每个框中各填写了一个两位数ab 与cd ,结果发现,所得到的六位数2abcd 8恰是一个完全立方数.则ab +cd =( ).(A )40(B )50(C )60(D )70二、填空题(每小题7分,共28分)1.设x +x 2+1y +y 2+4=9.则x y 2+4+yx 2+1= .图22.如图2,在边长为1的正△ABC 中,由两条含120°圆心角的弓形AOB 、AOC 及边BC 所围成的(火炬形)阴影部分的面积是 .3.一本书共有61页,顺次编号为1,2,…,61.某人在将这些数相加时,有两个两位数页码都错把个位数与十位数弄反了(形如ab 的两位数被当成了两位数ba ),结果得到的总和是2008.那么,书上这两个两位数页码之和的最大值是 .4.不超过5+36的最大整数是 .第二试一、(20分)设a 为整数,使得关于x 的方程ax 2-(a +5)x +a +7=0至少有一个有理根.试求方程所有可能的有理根.二、(25分)如图3,在四边形ABCD 中,图3E 、F 分别是边AB 、CD 的中点,P 为对角线AC 延长线上的任意一点,PF 交AD 于点M ,PE 交BC 于点N ,EF 交MN 于点K .求证:K是线段MN 的中点.三、(25分)120人参加数学竞赛,试题共有5道大题.已知第1、2、3、4、5题分别有96、83、74、66、35人做对.如果至少做对3题便可获奖,问:这次竞赛至少有几人获奖?参考答案第一试 一、1.C.由14+112=13,而12+13+16=1,故删去18与110后,可使剩下的数之和为1.2.A.32+5=38(2+5)8=12316+85　=123(1+5)3=1+52]32+51+5=12.3.A.注意到555=5×554.因为52被8除余1,所以,554被8除余1.故555被8除余5.而在125、375、625、875四个数中,只有125被8除余5.4.D.由式①、③得y =x x -2,z =6xx -3.故x ≠0.代入式②解得x =2710.所以,y =277,z =-54.检验知此组解满足原方程组.于是,10x +7y +z =0.5.C.图1中只有边长为1或2的两种菱形,每个菱形恰有一条与其边长相等的对角线,原正三角形内部每条长为1的线段,恰是一个边长为1的菱形的对角线;这种线段有18条,对应着18个边长为1的菱形;原正三角形的每条中位线恰是一个边长为2的菱形的对角线,三条中位线对应着3个边长为2的菱形.共得21个菱形.6.D.设2abcd 8=(xy )3.据末位数字特征得y =2,进而确定xy .因603=216000,703=343000,所以, 60<xy<70.故只有xy=62.而623=238328,则ab=38,cd=32,ab+cd=70.二、1.77 18.据条件式有xy+y x2+1+x y2+4+(x2+1)(y2+4)=9.①令x y2+4+y x2+1=z.则式①化为z+xy+(x2+1)(y2+4)=9,即　9-z=xy+(x2+1)(y2+4).平方得81-18z+z2=x2y2+(x2+1)(y2+4)+2xy(x2+1)(y2+4).②又z2=(x y2+4+y x2+1)2=x2(y2+4)+y2(x2+1)+2xy(x2+1)(y2+4),代入式②得81-18z=4.所以,z=7718.2.312.图4如图4,联结OA、OB、OC.线段OA将阴影的上方部分剖分成两个弓形,将这两个弓形分别按顺时针及逆时针方向绕点O旋转120°后,阴影部分便合并成△OBC,它的面积等于△ABC面积的13,即等于312.3.68.注意到1+2+…+61=1891,2008-1891=117.由于形如ab的页码被当成ba后,加得的和数将相差9|a-b|,因为a、b只能在1,2,…,9中取值,|a-b|≤8,所以,9|a-b|≤72.由于117=72+45=63+54,设弄错的两数是ab和cd.若9|a-b|=72,9|c-d|=45,则只有ab=19,而cd可以取16,27,38,49,此时,ab+ cd的最大值是68;若9|a-b|=63,9|c-d|=54,则ab可以取18,29,而cd可以取17,28,39,此时, ab+cd的最大值也是68.4.3903.注意到(5+3)6=(8+215)3.令8+215=a,8-215=b.得a+b=16,ab=4.知a、b是方程x2-16x+4=0的两个根,则有a2=16a-4,b2=16b-4;a3=16a2-4a,b3=16b2-4b.故a3+b3=16(a2+b2)-4(a+b)=16[16(a+b)-8]-4(a+b)=252(a+b)-128=3904.而0<b<1,故3903<a3<3904.因此,不超过(5+3)6的最大整数是3903.第二试一、当a=0时,方程的有理根为x=75.以下考虑a≠0的情况.此时,原方程为一元二次方程,由判别式(a+5)2-4a(a+7)≥0,即　3a2+18a-25≤0.解得-9-1563≤a≤-9+1563.整数a只能在其中的非零整数1,-1, -2,-3,-4,-5,-6,-7中取值.由方程得x=a+5±52-3(a+3)22a.①当a=1时,由式①得x=2和4;当a=-1时,方程无有理根;当a=-2时,由式①得x=1和-52;当a =-3时,方程无有理根;当a =-4时,由式①得x =-1和34;当a =-5时,方程无有理根;当a =-6时,由式①得x =12和-13;当a =-7时,由式①得x =0和27.因此,相对于不同的a 值,方程共有11个有理根.二、证法1:如图3,EF 截△PMN ,则N K K M ・MF FP ・PEEN =1.①BC 截△P A E ,则E B BA ・AC CP ・PNN E=1.故PN N E =2CPAC.所以,PE EN =2CP +AC AC .②AD 截△PCF ,则FD DC ・C A A P ・PM MF =1,PM MF =2A P AC.所以,FP MF =2A P -ACAC.③因为A P =AC +CP ,所以,2CP +AC =2A P -AC .由式②、③得PE EN =FP MF ,即MF FP ・PEEN=1.由式①得N K =K M ,即K 是线段MN 的中点.图5证法2:如图5,在PF 上取点G ,使GF =FM ,CG ∥DM ,又取C A 的中点L ,联结GC 、G N 、L E 、L F .则L E 、L F分别为△ABC 、△ACD 的中位线,有L F ∥AD ,L E ∥CB .得∠GCN =∠F L E ,CG L F =PC P L =CNL E.故△CNG △L EF ,NG ∥EF .于是,FK 是△MNG 的中位线.所以,K 是MN 的中点.三、将这120人分别编号为P 1,P 2,…,P 120,并视为数轴上的120个点.用A k (k =1,2,3,4,5)表示这120人之中未答对第k 题的人所成的组,|A k |为该组的人数.则|A 1|=24,|A 2|=37,|A 3|=46,|A 4|=54,|A 5|=85.将以上五个组分别赋予五种颜色,如果某人未做对第k (k =1,2,3,4,5)题,则将表示该人的点染第k 色.问题转化为:求出至少染有三色的点最多有几个.由|A 1|+|A 2|+|A 3|+|A 4|+|A 5|=246,知至少染有三色的点不多于2463=82个.一方面,将点P 1,P 2,…,P 85这85个点染第5色,因85>82,而为使染有三色的点数尽可能多,需在上述85个点中将尽可能多的点再加染另两色,由于|A 1|+|A 2|+|A 3|+|A 4|=161,故加染另两色的点不会多于1612=80个,即染有三色的点不多于80个.另一方面,可以具体构造一种染法,使得有80个点染有三种颜色.例如,如图6,将点P 1,P 2,…,P 85这85个点染第5色;点P 1,P 2,…,P 44以及点P 79、P 80这46个点染第3色;点P 45,P 46,…,P 81这37个点染第2色;点P 1,P 2,…,P 24这24个点染第1色;点P 25,P 26…,P 78这54个点染第4色.于是,至少染有三种颜色的点最多有80个.因此,染色数不多于两种的点至少有40个,即至少有40人获奖(他们每人至多答错两题,而至少答对三题,例如,P 81,P 82,…,P 120这40个人).图6(陶平生　提供)。

2008年全国初中数学联赛获奖名单一等奖（６０名）姓名学校姓名学校郭吕成上饶县第二中学万文奇景德镇市第二中学方亦豪景德镇市第二中学刘明宇景德镇市第二中学沈琛魁景德镇市第二中学肖一君乐平市第五中学晏诚敏江西省上高中学柳珺景德镇市一中分校喻军新余市第四中学梁毓娇江西省高安中学孙涵宇江西省高安中学王嘉琛景德镇市一中分校刘志凯吉安市朝宗实验学校王瑞琛乐平市第五中学杨煜景德镇市第二中学程禹婺源县婺源中学钟晓旭景德镇市一中分校成亚能景德镇市一中分校周宏宇南昌市第十中学罗翌新景德镇市一中分校陈白杨赣县第二中学周罗伟南昌市第十中学戴耀文景德镇市第二中学郑双越上饶县第二中学池龙景德镇市第二中学宋姗姗江西省高安中学范嘉俊景德镇市第二中学李强江西省临川第二中学周陶杰江西省临川第二中学莫少波江西省临川第二中学王博海江西省临川第二中学朱文瑜江西省高安中学谌偲翔江西省高安中学金怡泽南昌市第十中学童聿强景德镇市第二中学赵建梁婺源县婺源中学胡健宏景德镇市一中分校杨锴必景德镇市一中分校万翔鹏景德镇市一中分校谢翀江西省高安中学段训岚景德镇市第二中学龚时伟九江市同文中学陈章麒南昌市第十中学彭章景德镇市一中分校曾俊景德镇市第二中学郑荣上饶县第二中学袁鑫鹏景德镇市一中分校郭碧川吉水县第三中学陈雨贵溪市第二中学邬涛赣州市第三中学徐宏江西省临川第二中学吴艺翀鹰潭市中山学校吴志佳景德镇市第二中学汪佳璇婺源县婺源中学单铮景德镇市一中分校罗步景玉山文苑学校符豪江西省高安中学张志洋崇仁县第二中学刘宏成萍乡市第四中学刘凌焜吉安市第二中学二等奖（１２３名）姓名学校姓名学校陈佳民江西省临川第二中学王俊杰景德镇市第二中学刘鹏吉安市第八中学张翔江西省高安中学郭泽卿吉安市朝宗实验学校钟文南昌市第十中学郑程婺源县婺源中学陈星蓉石城县第二中学江雅雯景德镇市一中分校邓祖琪江西省高安中学盛博文南昌市第十中学王敬敬江西省临川第二中学郭儒乐上饶县第二中学孙津江西省高安中学曹煜永丰县恩江中学吴一鸣玉山文苑学校何致劼景德镇市一中分校张婧江西省高安中学项韬九江市同文中学冯丹颖江西省临川第二中学罗鸣樟树第三中学郑榕江西省高安中学方梦娟广丰县永丰中学江杰章上饶市第四中学李克诚江西省上高中学邹大卫景德镇市一中分校余毓敏江西省高安中学熊博奉新县第二中学金恺景德镇市一中分校万俊景德镇市第二中学程杰乐平市第五中学黄雯上饶县第六中学舒冠鑫进贤县第一中学吴雅琦江西省高安中学姚越上饶市第二中学马誉鑫南昌第二十七中学刘闽金溪县第一中学李高峰萍乡市第六中学李家恺婺源县婺源中学余阳九江市外国语学校汪建平万年县华茂学校李康荃乐平市第五中学黄诚景德镇市第二中学王博景德镇市第二中学赵杰江西省上高中学龚达巍新余市第四中学晏鹏江西省高安中学危宜萍江西省临川第二中学陶雨挺南昌铁路一中曾文华江西省临川第二中学赵继鸿乐平市第五中学鲁培江西省高安中学马晨景德镇市一中分校廖舒维南昌市第十中学曹绍平余干蓝天实验学校程振宇乐平市第五中学吴禹锟江西省高安中学刘文康景德镇市一中分校徐泽东乡县第二中学杨风波上饶县第二中学朱国栋南昌大学附属中学刘雨薇吉安市第二中学孙望舒南昌市第十中学潘俊九江市外国语学校李佳月景德镇市一中分校叶瑾瑜吉安市第二中学黄星晨贵溪市第二中学熊国帧南昌市第十中学江魏玮九江市外国语学校洪军景德镇市第二中学陈贤哲景德镇市第二中学徐承炜金溪县第一中学陈宇晖乐平市第五中学李经纬江西省宜春市第三中学易文翰九江市同文中学徐诗纯上饶县第六中学赖昕吉安市第八中学徐诗琦金溪县第一中学周佺吉水县第三中学吴丽丽江西省临川第二中学唐小龙余干蓝天实验学校欧阳力亚南昌市第十中学彭瑞光江西省高安中学蒋慧景德镇市第二中学龚辉新余市第一中学董杰江西省临川第二中学郑之成九江市外国语学校何叶冰新余市第四中学方政高安中学陈道勇上饶县第二中学王路通临川区第四中学石培涛乐平市第五中学郭朝望泰和县第三中学冷挺江西省上高中学郭磊信丰县黄泥中学吴闻九江市同文中学周浩雅上饶市第二中学刘子海吉安市朝宗实验学校胡翔上饶县第二中学杨坚江西师大附中张子巍贵溪市第二中学符绍舜上饶县第二中学江旭江西省高安中学郑浩上饶县第二中学曾芷雯南昌市第十中学徐春鹏鹰潭市第二中学尹君珺万安县第二中学彭星南昌县塔城中学钟晨嘉新余市第四中学张琼晶江西省宜春市第三中学徐辉乐平市第五中学胥啸南昌市第十中学齐玢婺源县婺源中学王恩靖乐平市第五中学梁竟宇景德镇市一中分校余一鹏婺源县婺源中学郑钊景德镇市第二中学吴雪萍大余县池江中学王赵博景德镇市一中分校余璐景德镇市一中分校刘齐瑞金市第二中学徐国秋广丰县永丰中学赖俊豪石城县第二中学三等奖（２４４名）姓名学校姓名学校王斌兴国县潋江中学杨文武弋阳县方志敏中学游世勋景德镇市第二中学李伟清宜黄县第二中学夏铭宇南丰县第二中学汪佩祺上高中学赵令华上饶县第二中学金克恒九江市外国语学校帅威九江市同文中学孙霄霓贵溪市第二中学高远南昌市广南学校付晨阳樟树第三中学罗贤亮景德镇市第二中学施雨婷南昌外国语学校黄帅景德镇市第二中学饶俊杰景德镇市第二中学陈赛昕萍乡市第四中学杨立浩兴国县潋江中学罗淞晖景德镇市第二中学梁梦吟江西省高安中学黄升上高中学李经纬萍乡市第四中学邹瞭望九江市外国语学校付彬彬南丰县第二中学倪伟焱九江市晨光中学章冬波进贤县第二中学章和夫九江市晨光中学郭泽宣九江市晨光中学蓝迪南昌市第十中学朱兴隆丰城市第一中学曾毓薇泰和县第四中学邓莹琪南昌第二十七中学刘振传永丰县恩江中学周韦博南昌市第十中学郑诗雨上饶市第二中学李颖鹏弋阳县方志敏中学罗泽坤景德镇市第二中学江文斌景德镇市第二中学项翔坚万年县第二中学郑丽霞上饶县第二中学冯冬发都昌县钱氏宗亲学校陈文万年县华兴学校黄良超贵溪市第二中学程昕瑞景德镇市第二中学梁婷东乡县第二中学叶宇哲萍乡市第四中学罗志宝新干县神政桥中学李晨辉南昌市湾里二中李琳遂川县泉江中学胡嘉文南昌大学附属中学段良平宁冈县龙江中学袁世政南昌市第一中学廖俊祺赣州市第七中学张汶喆吉安市第二中学冯瑜南昌市第一中学刘立伟南昌外国语学校邹循成石城县第二中学罗时江南昌市新城学校欧阳梓标婺源县婺源中学龚斌鄱阳县第二中学毛逢博玉山冰溪中学俞大刚婺源县婺源中学萧翔宇赣县第二中学温润石城县第二中学刘琼九江市实验中学官嘉男贵溪市第二中学李勤金溪县第一中学谢辉乐安县第一中学王司玺景德镇市第二中学周啟中瑞金市第二中学沈越吉安市第二中学万明杰南昌市第十中学周灿炜贵溪市第二中学张湲旭赣县第二中学郑济林九江市同文中学陈震涛永修县第三中学魏俊丰城市第一中学宋雪九江市同文中学俞骥昊南昌市第十中学易美琪永新县禾川中学王远飞南康市第六中学陈则贫景德镇市第二中学卢瑶江西省高安中学肖骏信丰县第二中学廖鹏崇仁县第一中学邱建维上饶市第二中学段灵修德安县共青中学晏文勇上高中学万伟进贤县第二中学陈向江西省上高中学雷斯嘉江西省高安中学陈宾九江市同文中学熊奇吉安市第五中学余月朦吉安市第二中学刘园林吉水县乌江中学吴璐芸南昌县莲塘第五中学刘欣安福县严田中学王艺超南昌市育新学校吴东昊江西师大附中丁磊丰城市第一中学张雄健南昌市第一中学周予杨南昌外国语学校王静新余市第十中学王嘉希南昌市第十中学章齐上饶市第二中学郑杨光龑乐平市第二中学刘衍民赣县第二中学杨果上犹中学蔡单景德镇市一中分校朱学林瑞金市第二中学王波文于都县第三中学蔡俊于都县第三中学刘万鹏南昌市第十中学温昱钦上犹中学吴际通贵溪市第二中学李言顺新余市第四中学段鹏湖口县凰村中学范智超景德镇市第二中学李祖泉广昌县第一中学陈阳萍乡市第四中学梅蒙九江市晨光中学王壮壮九江市外国语学校胡娅璇南昌市第十中学李睿智丰城市剑光中学易越江西省宜春中学廖望江西省宜春市第三中学文瑶万安县第二中学喻阳南昌市第十中学卢维国赣州厚德中学李帆江西师大附中黄长发高安市八景镇初级中学杨航萍乡市第二中学胡秉诚南昌市育新学校王志鵾安义县第二中学傅翀吉安市第五中学陈翌琪樟树第三中学廖松吉水县第三中学黄思成南昌市第十中学刘轶新余市第三中学熊志龙南昌市江安学校宋林泉赣县江口中学郭书旸于都县第三中学陈亮余干县第二中学查灶坤婺源思口中学江山都昌县东湖中学曾令健上犹县第二中学涂醒洲进贤县第一中学卢宇晨江西省上高中学刘智博吉水县第三中学黎云樟树第三中学陈嘉玉江西师大附中柯童南昌市育新学校徐权上饶市第二中学张健龙信丰县第四中学温开宝寻乌县博豪中学程雪妮鄱阳芝阳学校陈霖于都县第三中学陈隽景德镇市第二中学汪泽宇乐平市第五中学肖斌萍乡市第四中学朱正根萍乡市湘东云程实验学校甘灏霖萍乡市第四中学洪家铭东乡县第二中学赵雨豪萍乡市第六中学桓旭奉新县第二中学晏凌宇江西省上高中学何海明进贤县云桥中学沈雅婷九江市同文中学简嘉樟树第三中学刘辉南昌县莲塘第五中学刘挺樟树第三中学颜琛安福县城关中学张成樟树第二中学刘仁伟南昌市第二十三中学彭国琦宜春市第四中学周凯鹏吉水县第三中学陈睆清南昌市第三中学陈伟吉安市第八中学林庆国兴国县潋江中学唐树祝安远县第三中学华倩赣县江口中学朱劲涛瑞金市第三中学袁宏煜乐平市第五中学汪泽文景德镇市第二中学颜锴萍乡市莲花县城厢中学刘馨德赣县第二中学游宇翔上高中学易雪萍乡市上栗县上栗镇二中陈仔荣高安市灰埠镇初级中学徐丹九江市同文中学鄢盛尧丰城市第一中学吴海林遂川县瑶厦中学周祎晗南昌第二十八中学杨成龙南昌外国语学校董欣茹弋阳县方志敏中学方雅文南昌市第十中学高康奇鄱阳芝阳学校袁志强南康市第五中学刘衍林瑞金英才学校杨晨浩玉山冰溪中学施逸文九江市金安中学李舒玲婺源县婺源中学余涛进贤县第二中学金鑫德安县聂桥中学钟志宏江西省宜春中学徐翰超九江市第六中学李谷瑞金市第二中学吴伟林会昌实验学校郭飞飞信丰大阿中学易梦媛新余市第四中学陈浩华萍乡市第六中学程梓瑶武宁县第二中学刘叶永修县马口中学赖志坚万载县三兴初中宋成奉新县第二中学王仲钦江西省上高中学彭豪泰和县第四中学徐宗奕南昌市洪都中学陈中演樟树第三中学宋志军吉安市朝宗实验学校周煜吉水县第三中学周凌昊南昌市第三中学陈天书新余市第四中学赖清华龙南县第二中学何航广丰立达学校周雁南上犹中学胡锦江西省铜鼓第二中学王嘉程上饶县第六中学彭成吉安市朝宗实验学校王莹九江市同文中学张凌飞万安县第二中学陈吉雨南昌市育新学校梁宇修水县一中刘东园于都县第二中学郑静芳婺源江湾中学王钰芒上饶市第二中学赵洋南康市第三中学肖亮南昌县蒋巷中学吕云鹏大余新城中学胡玮伊南昌市外国语学校向万晓修水县一中叶琦玉山一中文苑学校宁可九江市晨光中学李瑾涵萍乡市第四中学。

丽水市教育局教研室文件
丽教研数字[2008] 73 号
关于公布2008年全国初中数学竞赛（丽水赛区）
获奖名单的通知
各县（市、区）教育局教研室：
2008年全国初中数学竞赛（丽水赛区）的初赛、复赛工作，在各地的大力支持下，已圆满结束。

丽水赛区全市共有324名参赛学生分获一、二、三等奖，其中一等奖47名，二等奖116名，三等奖161名。

对获一等奖学生的指导教师颁布优秀指导教师奖，评出2008年全国初中数学竞赛（丽水赛区）优胜团体5名,现予公布。

附件：1、2008年全国初中数学竞赛（丽水赛区）获奖名单
2、2008年全国初中数学竞赛（丽水赛区）优胜团体奖
二00八年五月十二日
主题词：初中数学竞赛获奖通知
校对：田用杰共印30份
附件1：2008年全国初中数学竞赛（丽水赛区）获奖名单
一等奖（47名）
二等奖（116名）
三等奖（161名）
附件2：
2008年全国初中数学竞赛（丽水赛区）优胜团体名单
市直丽水市实验学校
龙泉市龙泉市育才学校
松阳县松阳县凌霄外国语学校
遂昌县遂昌二中
缙云县缙云县实验中学。

12008年全国初中数学联合竞赛试题参考答案及评分标准说明：评阅试卷时，请依据本评分标准.第一试，选择题和填空题只设7分和0分两档；第二试各题，请按照本评分标准规定的评分档次给分.如果考生的解答方法和本解答不同，只要思路合理，步骤正确，在评卷时请参照本评分标准划分的档次，给予相应的分数.第一试一、选择题（本题满分42分，每小题7分）本题共有6小题，每题均给出了代号为A ，B ，C ，D 的四个答案，其中有且仅有一个是正确的．将你所选择的答案的代号填在题后的括号内．每小题选对得7分；不选、选错或选出的代号字母超过一个（不论是否写在括号内），一律得0分．1．设213a a +=，213b b +=，且a b ≠，则代数式2211a b+的值为 （ ） A ．5 B ．7 C ．9 D ．11.【答案】B【解析】 由题设条件可知2310a a -+=，2310b b -+=，且a b ≠，所以a ，b 是一元二次方程2310x x -+=的两根，故3a b +=，1ab =，因此222222222211()23217()1a b a b ab a b a b ab ++--⨯+====． 故选B 2．如图，设AD ，BE ，CF 为三角形ABC 的三条高，若6AB =，5BC =，3EF =，则线段BE 的长为（ ）EFDCBA2A ．185B ．4C ．215D ．245【答案】D【解析】 因为AD ，BE ，CF 为三角形ABC 的三条高，易知B ，C ，E ，F 四点共圆，于是AEF ABC △∽△，故35AF EF AC BC ==，即3cos 5BAC ∠=，所以4sin 5BAC ∠=． 在Rt ABE △中，424sin 655BE AB BAC =∠=⨯=．故选D3．从分别写有数字1，2，3，4，5的5张卡片中任意取出两张，把第一张卡片上的数字作为十位数字，第二张卡片上的数字作为个位数字，组成一个两位数，则所组成的数是3的倍数的概率是 （ ）A ．15B ．310C ．25D ．12. 【答案】C【解析】 能够组成的两位数有12，13，14，15，21，23，24，25，31，32，34，35，41，42，43，45，51，52，53，54，共20个，其中是3的倍数的数为12，15，21，24，42，45，51，54，共8个．所以所组成的数是3的倍数的概率是82205=．故选C 4．在ABC △中，12ABC ∠=o ，132ACB ∠=o ，BM 和CN 分别是这两个角的外角平分线，且点M ，N 分别在直线AC 和直线AB 上，则 （ ）3A ．BM CN >B ．BM CN =C ．BM CN <D ．BM 和CN 的大小关系不确定【答案】B【解析】 ∵12ABC ∠=o ，BM 为ABC ∠的外角平分线，∴1(18012)842MBC ∠=-=o o o．又180********BCM ACB ∠=-∠=-=o o o o ，∴180844848BMC ∠=--=o o o o ，∴BM BC =．又11(180)(180132)2422ACN ACB ∠=-∠=-=o o o o，∴18018012()BNC ABC BCN ACB ACN ∠=-∠-∠=--∠+∠o o o 168(13224)=-+o o o12ABC ==∠o ，∴CN CB =. 因此，BM BC CN ==．故选B5．现有价格相同的5种不同商品，从今天开始每天分别降价10％或20％，若干天后，这5种商品的价格互不相同，设最高价格和最低价格的比值为r ，则r 的最小值为 （ ）A ．398T ⎛⎫ ⎪⎝⎭.B ．498⎛⎫ ⎪⎝⎭.C ．598⎛⎫⎪⎝⎭. D ．98.【答案】B.【解析】 容易知道，4天之后就可以出现5种商品的价格互不相同的情况．设5种商品降价前的价格为a ，过了n 天. n 天后每种商品的价格一定可以表示为4()()98110%120%1010kn kkn ka a --⎛⎫⎛⎫⋅-⋅-=⋅⋅ ⎪⎪⎝⎭⎝⎭，其中k 为自然数，且0k n ≤≤．要使r 的值最小，五种商品的价格应该分别为：981010in ia -⎛⎫⎛⎫⋅⋅ ⎪⎪⎝⎭⎝⎭，1188(1010i n i a +--⎛⎫⎛⎫⋅⋅ ⎪ ⎪⎝⎭⎝⎭，22991010i n i a +--⎛⎫⎛⎫⋅⋅ ⎪ ⎪⎝⎭⎝⎭，33981010i n i a +--⎛⎫⎛⎫⋅⋅ ⎪⎪⎝⎭⎝⎭，44981010i n i a +--⎛⎫⎛⎫⋅⋅ ⎪⎪⎝⎭⎝⎭，其中i 为不超过n 的自然数.所以r 的最小值为44498910108981010i n i i n ia a +---⎛⎫⎛⎫⋅⋅ ⎪ ⎪⎛⎫⎝⎭⎝⎭= ⎪⎝⎭⎛⎫⎛⎫⋅⋅ ⎪ ⎪⎝⎭⎝⎭．故选B ． 6．已知实数x ，y 满足(22200820082008x x y y --=，则223233x y x y -+-2007-的值为（ ）A ．2008-B ．2008C ．1-D ．1.【答案】D ．【解析】 ∵(22200820082008x x y y --=，∴222200820082008x x y y y y -=---222200820082008y y x x x x -=---由以上两式可得x y =．所以(2220082008x x -=，解得22008x =，所以522222323320073233200720071x y x y x x x x x -+--=-+--=-=．故选D ．二、填空题（本题满分28分，每小题7分）1．设51a -，则5432322a a a a a a a +---+=- ． 【答案】 2-【解析】 ∵2251351a a --==-⎝⎭，∴21a a +=， ∴()()32325432322222a a a a a a a a a a a a a a a a+--+++---+=-⋅- ()()333322212111(11)211a a a a a a a a a a a--+--===-=-++=-+=-⋅----． 2．如图，正方形ABCD 的边长为1，M ，N 为BD 所在直线上的两点，且5AM 135MAN ∠=o ，则四边形AMCN 的面积为 ．【答案】 52【解析】 设正方形ABCD 的中心为O ，连AO ，则AO BD ⊥，2AO OB = ()222223252MO AM AO ⎛⎫-- ⎪ ⎪⎝⎭O MND CBA6∴2MB MO OB =-又135ABM NDA ∠=∠=o ，13590NAD MAN DAB MAB MAB ∠=∠-∠-∠=--∠o o 45MAB AMB =-∠=∠o ，所以ADN MBA △∽△，故AD DN MB BA =，从而212AD DN BA MB =⋅=． 根据对称性可知，四边形AMCN 的面积1122522222222MAN S S MN AO ==⨯⨯⨯=⨯⨯+=⎝△． 3．已知二次函数2y x ax b =++的图象与x 轴的两个交点的横坐标分别为m ，n ，且1m n +≤.设满足上述要求的b 的最大值和最小值分别为p ，q ，则p q += ．【答案】 12【解析】 根据题意，m ，n 是一元二次方程20x ax b ++=的两根，所以m n a +=-，mn b =．∵1m n +≤，∴1m n m n ++≤≤，1m n m n -+≤≤．∵方程20x ax b ++=的判别式240a b ∆=-≥，∴22()1444a m nb +=≤≤． 22244()()()11b mn m n m n m n ==+--+--≥≥，故14b -≥，等号当且仅当12m n =-=时取得；22244()()1()1b mn m n m n m n ==+----≤≤，故14b ≤，等号当且仅当12m n ==时取得．7所以14p =，14q =-，于是12p q +=．4．依次将正整数1，2，3，…的平方数排成一串：149162536496481100121144…，排在第1个位置的数字是1，排在第5个位置的数字是6，排在第10个位置的数字是4，排在第2008个位置的数字是 ．【答案】 1【解析】 21到23，结果都只各占1个数位，共占133⨯=个数位；24到29，结果都只各占2个数位，共占2612⨯=个数位；210到231，结果都只各占3个数位，共占32266⨯=个数位；232到299，结果都只各占4个数位，共占468272⨯=个数位；2100到2316，结果都只各占5个数位，共占52171085⨯=个数位；此时还差2008(312662721085)570-++++=个数位．2317到2411，结果都只各占6个数位，共占695570⨯=个数位．所以，排在第2008个位置的数字恰好应该是2411的个位数字，即为1．第二试 （A ）一．（本题满分20分）8已知221a b +=，对于满足条件01x ≤≤的一切实数x ，不等式(1)(1)()0a x x ax bx b x bx ------≥ ①恒成立.当乘积ab 取最小值时，求a ，b 的值．【解析】 整理不等式①并将221a b +=代入，得2(1)(21)0a b x a x a ++-++≥ ②在不等式②中，令0x =，得0a ≥；令1x =，得0b ≥．易知10a b ++>，21012(1)a ab +<<++，故二次函数2(1)(21)y a b x a x a =++-++的图象（抛物线）的开口向上，且顶点的横坐标在0和1之间．由题设知，不等式②对于满足条件01x ≤≤的一切实数x 恒成立，所以它的判别式2(21)4(1)0a a b a ∆=+-++⋅≤，即14ab ≥．由方程组221,14a b ab ⎧+=⎪⎨=⎪⎩ ③ 消去b ，得42161610a a -+=，所以223a -或223a +=． 又因为0a ≥，所以62a -或62a +，9于是方程组③的解为6262a b ⎧-=⎪⎪⎨+⎪=⎪⎩或6262a b ⎧+⎪⎪⎨-⎪=⎪⎩所以ab 的最小值为14，此时,a b 的值有两组，分别为 62a -，62b +和62a +=，62b -=．二．（本题满分25分）如图，圆O 与圆D 相交于,A B 两点，BC 为圆D 的切线，点C 在圆O 上，且AB BC =．⑴ 证明：点O 在圆D 的圆周上．⑵ 设△ABC 的面积为S ，求圆D 的的半径r 的最小值．【解析】 ⑴ 连OA ，OB ，OC ，AC ，因为O 为圆心，AB BC =，所以△OBA ∽△OBC ，从而OBA OBC ∠=∠．因为OD AB ⊥，DB BC ⊥，所以9090DOB OBA OBC DBO ∠=-∠=-∠=∠o o ，所以DB DO =，因此点O 在圆D 的圆周上．⑵ 设圆O 的半径为a ，BO 的延长线交AC 于点E ，易知CE OABD10BE AC ⊥.设2AC y =(0)y a <≤，OE x =，AB l =，则222a x y =+，()S y a x =+，22222222()2222()aSl y a x y a ax x a ax a a x y=++=+++=+=+=． 因为22ABC OBA OAB BDO ∠=∠=∠=∠,AB BC =,DB DO =，所以BDO ABC △∽△，所以BD BOAB AC=，即2r a l y =，故2al r y =．所以322222224422a l a aS S a S r y y y y ⎛⎫==⋅=⋅ ⎪⎝⎭≥，即2S r 其中等号当a y =时成立，这时AC是圆O 的直径.所以圆D 的的半径r 2S三．（本题满分25分）设a 为质数，b 为正整数，且()()2925094511a b a b +=+①求a ，b 的值.【解析】 ①式即2634511509509a b a b++⎛⎫= ⎪⎝⎭，设63509a b m +=，4511509a b n +=，则 509650943511m a n ab --== ②故351160n m a -+=，又2n m =，所以2351160m m a -+=③由①式可知，2(2)a b +能被509整除，而509是质数，于是2a b +能被509整除，故m 为整数，即关于m 的一元二次方程③有整数根，所以它的判别式251172a ∆=-为完全平方数．11不妨设2251172a t ∆=-=（t 为自然数），则2272511(511)(511)a t t t =-=+-．由于511t +和511t -的奇偶性相同，且511511t +≥，所以只可能有以下几种情况：①51136,5112,t a t +=⎧⎨-=⎩两式相加，得3621022a +=，没有整数解．②51118,5114,t a t +=⎧⎨-=⎩两式相加，得1841022a +=，没有整数解． ③51112,5116,t a t +=⎧⎨-=⎩两式相加，得1261022a +=，没有整数解． ④5116,51112,t a t +=⎧⎨-=⎩两式相加，得6121022a +=，没有整数解．⑤5114,51118,t a t +=⎧⎨-=⎩两式相加，得4181022a +=，解得251a =． ⑥5112,51136,t a t +=⎧⎨-=⎩两式相加，得2361022a +=，解得493a =，而4931729=⨯不是质数，故舍去．综合可知251a =．此时方程③的解为3m =或5023m =（舍去）． 把251a =，3m =代入②式，得5093625173b ⨯-⨯==．第二试 （B ）12一．（本题满分20分）已知221a b +=，对于满足条件1x y +=，0xy ≥的一切实数对()x y ，，不等式220ay xy bx -+≥ ①恒成立.当乘积ab 取最小值时，求a ，b 的值.【解析】 由1x y +=，0xy ≥可知01x ≤≤，01y ≤≤．在①式中，令0x =，1y =，得0a ≥；令1x =，0y =，得0b ≥．将1y x =-代入①式，得22(1)(1)0a x x x bx ---+≥，即()()21210a b x a x a ++-++≥ ②易知10a b ++>，21012(1)a ab +<<++，故二次函数2(1)(21)y a b x a x a =++-++的图象（抛物线）的开口向上，且顶点的横坐标在0和1之间．由题设知，不等式②对于满足条件01x ≤≤的一切实数x 恒成立，所以它的判别式2(21)4(1)0a a b a ∆=+-++⋅≤，即14ab ≥由方程组221,14a b ab ⎧+=⎪⎨=⎪⎩ ③ 消去b ，得42161610a a -+=，所以223a -或223a +=，13又因为0a ≥，所以62a -或62a +． 于是方程组③的解为6262ab ⎧-=⎪⎪⎨+⎪=⎪⎩或6262a b ⎧+⎪⎪⎨-⎪=⎪⎩所以满足条件的a ，b 的值有两组，分别为62a -=，62b +和62a +，62b -= 二．（本题满分25分）题目和解答与（A ）卷第二题相同.三．（本题满分25分）题目和解答与（A ）卷第三题相同.第二试 （C ）一．（本题满分20分）题目和解答与（B ）卷第一题相同.二．（本题满分25分）题目和解答与（A ）卷第二题相同.三．（本题满分25分）设a 为质数，b ，c 为正整数，且满足29(22)509(41022511)2a b c a b c b c ⎧+-=+-⎨-=⎩①②14求()a b c +的值.【解析】 ①式即266341022511509509a b c a b c+-+-⎛⎫=⎪⎝⎭， 设663509a b c m +-=，41022511509a b cn +-=，则5096509423511m a n ab c ---== ③ 故351160n m a -+=，又2n m =，所以2351160m m a -+= ④由①式可知，2(22)a b c +-能被509整除，而509是质数，于是22a b c +-能被509整除，故m 为整数，即关于m 的一元二次方程④有整数根，所以它的判别式251172a ∆=-为完全平方数．不妨设2251172a t ∆=-=（t 为自然数），则2272511(511)(511)a t t t =-=+-．由于511t +和511t -的奇偶性相同，且511511t +≥，所以只可能有以下几种情况：①51136,5112,t a t +=⎧⎨-=⎩两式相加，得3621022a +=，没有整数解． ②51118,5114,t a t +=⎧⎨-=⎩两式相加，得1841022a +=，没有整数解．③51112,5116,t a t +=⎧⎨-=⎩两式相加，得1261022a +=，没有整数解． ④5116,51112,t a t +=⎧⎨-=⎩两式相加，得6121022a +=，没有整数解．15⑤5114,51118,t a t +=⎧⎨-=⎩两式相加，得4181022a +=，解得251a =． ⑥5112,51136,t a t +=⎧⎨-=⎩两式相加，得2361022a +=，解得493a =，而4931729=⨯不是质数，故舍去．综合可知251a =，此时方程④的解为3m =或5023m =（舍去）． 把251a =，3m =代入③式，得50936251273b c ⨯-⨯-==，即27c b =-．代入②式得(27)2b b --=，所以5b =，3c =，因此()251(53)2008a b c +=⨯+=．。

2008年数学奥林匹克竞赛2008年的数学奥林匹克竞赛是中国数学界的一次盛事。

在这场比赛中，来自各个国家的数学精英齐聚一堂，争夺数学的荣誉。

本文将重点介绍在这场竞赛中的一些内容和亮点。

一、竞赛概述2008年数学奥林匹克竞赛于7月在中国浙江省杭州市举行。

来自约100个国家和地区的400多名中学生参加了比赛。

竞赛分为两天进行，每天有三个题目需要参赛者解答。

这些题目涵盖了数论、代数、几何和组合数学等各个领域。

二、2016年题目回顾以下是其中一些有代表性的题目：1. 第一天的第一题：证明存在一个22位的自然数，其中每位数字都是从1到9中选择而来，且任意相邻两位数字之差的绝对值为0或1。

2. 第一天的第二题：在直角坐标系中，给定一个点O(0, 0)，一条直线L以y=x-2为斜率经过点O，另一条直线L'垂直于直线L，并经过坐标点(60, y)，若该点到直线L的距离恰好等于6，则求y的所有可能值。

3. 第二天的第一题：在一个正方形的四个顶点上分别放置了红、黄、蓝、绿四种颜色的灯泡。

每次可以选择一个角上的灯泡，然后改变该灯泡以及相邻两个角上的灯泡的颜色（即红变黄，黄变蓝，蓝变绿，绿变红）。

问是否存在某种操作方式，使得无论从哪一种初始灯泡颜色出发，经过若干次操作后，四个角上的灯泡都变成同一颜色。

4. 第二天的第二题：证明对于任意正整数n，都存在一个长度为n的序列{a1, a2, ..., an}，满足以下条件：1）ai为1到n之间的整数，且ai与ai+1的最大公约数为ai(1≤i<n)2）a1和an是互质的这些题目既有综合性的思维题，也有需要运用数学原理的计算题。

参赛选手们需要在有限的时间内，灵活运用自己所学的数学知识和解题技巧。

三、赛事亮点2008年的数学奥林匹克竞赛不仅仅是一场数学比赛，还充满了学术交流和合作的氛围。

各国选手在竞赛之余，互相切磋，分享数学思维和解题技巧。

这种交流不仅促进了彼此的成长，也丰富了数学的发展。

2008年四川省初中数学联赛（初二组）决赛试题参考答案及评分细则一、选择题（本题满分42分，每小题7分）１、Ｄ ２、Ａ ３、Ｄ ４、Ｃ ５、Ｂ ６、Ｂ．二、填空题（本题满分28分，每小题7分）１、1 ２、45 ３、5 ４、756．三、证明：记2)(c b a A ++=，2)(c b a B -+=，2)(a c b C -+=，2)(b a c D -+=．则ca bc ab c b a A 222222+++++= ① ．．．．．．5分 ca bc ab c b a B 222222--+++= ②ca bc ab c b a C 222222-+-++= ③ca bc ab c b a D 222222+--++= ④上面４式两边相加，得)(4222c b a D C B A ++=+++ ⑤ ．．．．．．10分 如果D C B A ,,,这四个代数式的值中均小于222c b a ++，则)(4222c b a D C B A ++<+++，这与⑤矛盾．所以，D C B A ,,,这四个代数式的值中至少有一个不小于222c b a ++． ．．．．．．15分 如果D C B A ,,,这四个代数式的值中均大于222c b a ++，则)(4222c b a D C B A ++>+++，这与⑤矛盾．所以，D C B A ,,,这四个代数式的值中至少有一个不大于222c b a ++．所以，结论成立． ．．．．．．20分四、解：设x OF =，则x FB -=8，x FA +=8．由条件知DA ∥EF ∥CB ，所以ABFB AD FE =，C 即EF x AD ⨯-=816； 同理EF xBC ⨯+=816． ．．．．．．10分 所以EF xEF x x BC AD ⨯-⨯=⨯++-=+2281616)816816(． ① ．．．．．．15分 又在EFO Rt ∆中222OE OF EF =+，即222)8(EF x EF -=+， 故16822x EF -=． ② ．．．．．．20分 由①、②得16=+BC AD ． ．．．．．．25分五、（１）证明：因为＋1－2－3＋4＋5－6＋7－8＋9＝７，所以7是“可被表出的数”. ．．．．．．5分 又因为＋1＋2＋3＋4＋5＋6＋7＋8＋9＝45是奇数，而对于任意两个整数b a ,有b a +与b a -具有相同的奇偶性，因此，无论怎样填“＋”、“－”，所得代数和一定是奇数，不可能为８．所以，８是“不可被表出的数”． ．．．．．．10分（２）设填＂＋＂的数字和为x ，填＂－＂的数字和为y ．则25=-y x ．又45921=+++=+ y x ．所以35=x ，10=y ． ．．．．．．15分由此可知，填＂－＂的数之和为10．我们只要在和为10的那些数前面填＂－＂号，其余的数前面填＂＋＂号，就得到25的一种表示方法。

中国教育学会中学数学教学专业委员会“《数学周报》杯”2008 年全国初中数学竞赛试题一、选择题（共5 小题，每小题6 分，满分30 分以下每道小题均给出了代号为A 、B 、C 、D 的四个选项，其中有且只有一个选项是正确的. 请将正确选项的代号填入题后的括号里，不填、多填或错填都得0 分）1．已知实数x ，y 满足3,3242424=+=-y y x x ，则444y x+的值为（ ） （A ）7 （B ）2131+ （C ） 2137+ （D ）5 2．把一枚六个面编号分别为1，2，3，4，5，6 的质地均匀的正方体骰子先后投掷2 次，若两个正面朝上的编号分别为m ，n ，则二次函数 n mx x y ++=2的图象与x 轴有两个不同交点的概率是（ ）．（A ）125 （B ）94 （C ）3617 （D ）213．有两个同心圆， 圆周上有4 个不同的点，小圆周上有2 个不同的点，则这6 个点可确定的不同直线最少有( ) ．（A ）6 条 （B ） 8 条 （C ）10 条 （D ）12 条4．已知AB 是半径为1的圆O 的一条弦，且AB = a < 1．以AB 为一边在圆 O 内作正△ABC ，点D 为圆O 上不同于点A 的一点，且DB = AB = a ，DC 的延长线交圆O 于点E ，则AE 的长为（ ）．（A ）a 25 （B ）1 （C ）23 （D ）a5．将1，2，3，4，5 这五个数字排成一排，最后一个数是奇数，且使得其任意连续三个数之和都能被这三个数中的第一个数整除，那么满足要求的排法有（ ）．（A ）2 种 （B ）3 种 （C ）4 种 （D ）5 种二、填空题（共5 小题，每小题6 分，满分30 分）6．对于实数u ，v ，定义一种运算“*”为：u *v = uv + v ．若关于x 的方程41)*(*-=x a x 有两个不同的实数根，则满足条件的实数a 的取值范围是 ；7．小王沿街匀速行走，发现每隔6 分钟从背后驶过一辆18 路公交车，每隔 3 分钟从迎面驶来一辆18 路公交车．假设每辆18 路公交车行驶速度相同，而且 18 路公交车总站每隔固定时间发一辆车，那么发车间隔的时间是 分钟．8．如图，在△ABC 中，AB=7，AC=11，点M 是BC 的中点，AD是∠BAC 的平分线，MF ∥AD ，则FC 的长为（第8 题）9．△ABC中，AB ＝7，BC ＝8，CA＝9，过△ABC的内切圆圆心I 作DE ∥BC，分别与AB ，AC 相交于点D ，E ，则DE的长为．10．关于x ，y 的方程)(20822yxyx-=+的所有正整数解为．三、解答题（共4 题，每题15 分，满分60 分）11 （A）．在直角坐标系xOy 中，一次函数y = kx + b （k≠0）的图象与x 轴、y 轴的正半轴分别交于A ，B 两点，且使得△OAB的面积值等于3++OBOA（1）用b 表示k；（2）求△OAB 面积的最小值．11 （B）．已知一次函数xy21=，二次函数122+=xy，是否存在二次函数cbxaxy++=23，其图象经过点（－5，2），且对于任意实数x的同一个值，这三个函数对应的函数值321,,yyy，都有231yyy≤≤成立？若存在，求出函数3y的解析式；若不存在，请说明理由．12 （A）．是否存在质数p ，q，使得关于x 的一元二次方程02=+-pqxpx有有理数根？12 （B）．已知a，b 为正整数，关于x 的方程022=+-baxx的两个实数根为21,xx，关于y的方程022=++bayy两个实数根为21,yy，且满足20082211=-yxyx。

历年(95-10)年全国数学竞赛(联赛)分类题型详解 - 几何(1)选择题(30道题)1. 如果边长顺次为25、39、52与60的四边形内接于一圆，那么此圆的周长为［ ]A．62πB．63π C．64πD．65π1995年全国初中数学联赛试题答案: D详解：四个选择支表明，圆的周长存在且唯一，从而直径也存在且唯一．又由AB2＋AD2 ＝252＋602 ＝52×（52＋122）＝52×132＝(32＋42)×132 ＝392＋522 ＝BC2＋CD2故可取BD＝65为直径，得周长为65π，选D．2. 设AB是⊙O的一条弦，CD是⊙O的直径，且与弦AB相交，记M＝｜S△CAB－S△DAB｜，N＝2S△OAB，则[ ]A．M＞N B．M＝N C．M＜N D．M、N的大小关系不确定1995年全国初中数学联赛试题答案: B详解1: 不失一般性，设CE≥ED，在CE上取CF＝ED，则有OF＝OE，且S△ACE－S△ADE＝S△AEF＝2S△AOE．同理，S△BCE－S△BDE＝2S△BOE．相加，得S△ABC－S△DAB＝2S△OAB，即M＝N．选B．详解2: 若过C、D、O分别作AB的垂线（图3），CE⊥AB、DF⊥AB、OL⊥AB，垂足分别为E、F、L．连CF、DE，可得梯形CEDF．又由垂径分弦定理，知L是EF的中点．根据课本上做过的一道作业：梯形对角线中点的连线平行底边，并且等于两底差的一半，有｜CE－DF｜＝2OL．即M＝N．选B．3．如图，A是半径为1的圆O外的一点，OA=2，AB是圆O的切线，B是切点，弦BC∥OA，连结AC，则阴影部分的面积等于[ ]1996年全国初中数学联赛试题答案: B4．如果一个三角形的面积和周长都被一直线所平分，那么该直线必通过这个三角形的[ ]A．内心B．外心C．重心D．垂心1996年全国初中数学联赛试题答案: A5．如果20个点将某圆周20等分，那么顶点只能在这20个点中选取的正多边形的个数有[ ]A．4个B．8个 C．12个 D．24个1996年全国初中数学联赛试题答案: C6. 在△ABC中，已知BD和CE分别是两边上的中线，并且BD⊥CE，BD=4，CE=6，那么△ABC的面积等于（）（Ａ）12（Ｂ）14（Ｃ）16（Ｄ）181998年全国数学联赛试卷答案: C详解: 连ED，则又因为DE是△ABC两边中点连线，所以故选C．7．一个凸n边形的内角和小于1999°，那么n的最大值是（）．A．11 B．12 C．13 D．141999年全国初中数学竞赛答案: C8．在三角形ABC 中，D 是边BC 上的一点，已知AC=5，AD=6，BD=10，CD=5，那么三角形ABC 的面积是（ ）．A ．30B ．36C ．72D ．1251999年全国初中数学竞赛答案: B9．在正五边形ABCDE 所在的平面内能找到点P ，使得△PCD 与△BCD 的面积相等，并且△ABP 为等腰三角形，这样的不同的点P 的个数为（ ）．A ．2B ．3C ．4D ．51999年全国初中数学竞赛答案: D10. 设a ，b ，c 分别是△ABC 的三边的长，且cb a ba b a +++=，则它的内角∠A 、∠B 的关系是（ ）。

2008年全国初中数学联合竞赛试题（天津赛区）参考答案及评分标准说明：评阅试卷时，请依据本评分标准.第一试，选择题和填空题只设7分和0分两档；第二试各题，请按照本评分标准规定的评分档次给分.如果考生的解答方法和本解答不同，只要思路合理，步骤正确，在评卷时请参照本评分标准划分的档次，给予相应的分数.第一试一、选择题（本题满分42分，每小题7分）本题共有6小题，每题均给出了代号为D C B A ,,,的四个答案，其中有且仅有一个是正确的.将你所选择的答案的代号填在题后的括号内.每小题选对得7分；不选、选错或选出的代号字母超过一个（不论是否写在括号内），一律得0分.1．设213a a +=，213b b +=，且a b ≠，则代数式2211a b+的值为 （ ） )(A 5. )(B 7. )(C 9. )(D 11.【答】B .解 由题设条件可知2310a a -+=，2310b b -+=，且a b ≠，所以,a b 是一元二次方程2310x x -+=的两根，故3a b +=，1ab =，因此222222222211()23217()1a b a b ab a b a b ab ++--⨯+====. 故选B . 2．如图，设AD ，BE ，CF 为三角形ABC 的三条高，若6AB =，5BC =，115AE EC -=，则线段BE 的长为 （ ） )(A 185. )(B 4. )(C 215. )(D 245. 【答】D .解 根据勾股定理，有 AB 2＝AE 2+BE 2①，BC 2＝BE 2＋EC 2②，用①－②，得到AB 2－BC 2＝AE 2－EC 2＝(AE －EC )·(AE ＋CE )，所以AE ＋CE ＝(62－52)÷115＝5，从而解得AE ＝185，CE ＝75，这样BE 245==. 故选D .3．从分别写有数字1，2，3，4，5的5张卡片中任意取出两张，把第一张卡片上的数字作为十位数字，第二张卡片上的数字作为个位数字，组成一个两位数，则所组成的数是3的倍数的概率是 （ ）)(A 15. )(B 310. )(C 25. )(D 12. 【答】C . 解 能够组成的两位数有12，13，14，15，21，23，24，25，31，32，34，35，41，42，43，45，51，52，53，54，共20个，其中是3的倍数的数为12，15，21，24，42，45，51，54，共8个.所以所组成的数是3的倍数的概率是82205=. 故选C .4．在△ABC 中，12ABC ∠=︒，132ACB ∠=︒，BM 和CN 分别是这两个角的外角平分线，且点,M N 分别在直线AC 和直线AB 上，则 （ ）)(A BM CN >. )(B BM CN =.)(C BM CN <. )(D BM 和CN 的大小关系不确定.【答】B .解 ∵12ABC ∠=︒，BM 为ABC ∠的外角平分线，∴1(18012)842MBC ∠=︒-︒=︒. 又180********BCM ACB ∠=︒-∠=︒-︒=︒，∴180844848BMC ∠=︒-︒-︒=︒， ∴BM BC =.又11(180)(180132)2422ACN ACB ∠=︒-∠=︒-︒=︒，∴18018012()BNC ABC BCN ACB ACN ∠=︒-∠-∠=︒-︒-∠+∠168(13224)=︒-︒+︒12ABC =︒=∠，∴CN CB =. 因此，BM BC CN ==.故选B .5．现有价格相同的5种不同商品，从今天开始每天分别降价10％或20％，若干天后，这5种商品的价格互不相同，设最高价格和最低价格的比值为r ，则r 的最小值为 （ ）)(A 39()8. )(B 49()8. )(C 59()8. )(D 98.【答】 B .解 容易知道，4天之后就可以出现5种商品的价格互不相同的情况.设5种商品降价前的价格为a ，过了n 天. n 天后每种商品的价格一定可以表示为98(110%)(120%)()()1010k n k k n k a a --⋅-⋅-=⋅⋅，其中k 为自然数，且0k n ≤≤.要使r 的值最小，五种商品的价格应该分别为：98()()1010i n i a -⋅⋅，1198()()1010i n i a +--⋅⋅，2298()()1010i n i a +--⋅⋅，3398()()1010i n i a +--⋅⋅，4498()()1010i n i a +--⋅⋅，其中i 为不超过n 的自然数.所以r 的最小值为44498()()91010()988()()1010i n i i n i a a +---⋅⋅=⋅⋅. 故选B .6． 已知实数,x y满足(2008x y =，则223233x y x y -+-2007-的值为 （ ）)(A 2008-. )(B 2008. )(C 1-. )(D 1.【答】D .解∵(2008x y =，∴x y -==y x -==由以上两式可得x y =. 所以2(2008x =，解得22008x =，所以22222323320073233200720071x y x y x x x x x -+--=-+--=-=. 故选D .二、填空题（本题满分28分，每小题7分）1．设12a -=，则5432322a a a a a a a+---+=-2-.解 ∵2213()122a a ===-，∴21a a +=， ∴543232323222()2()2a a a a a a a a a a a a a a a a +---++--++=-⋅-33332221211(1)(11)2(1)1a a a a a a a a a a a--+--===-=-++=-+=-⋅----.2．如图，正方形ABCD 的边长为1，,M N 为BD 所在直线上的两点，且AM =135MAN ∠=︒，则四边形AMCN 的面积为52解 设正方形ABCD 的中心为O ，连AO ，则AO BD ⊥，AO OB ==,2MO ===, ∴MB MO OB =-=又135ABM NDA ∠=∠=︒，13590NAD MAN DAB MAB MAB ∠=∠-∠-∠=︒-︒-∠45=︒-MAB AMB ∠=∠，所以△ADN ∽△MBA ，故AD DNMB BA =，从而12AD DN BA MB =⋅==. 根据对称性可知，四边形AMCN 的面积115222(22222MAN S S MN AO ==⨯⨯⨯=⨯⨯⨯=△.3．已知一次函数(1)y a x a =-+（a 为整数且a ≠1）的图象与x 轴、y 轴的交点分别为A 、B ，且△OAB 的面积是正整数，则a ＝ 2 .解 不难求得A 、B 两点的坐标分别为（－1aa -，0），（0，a ），故12OABS ∆=·1a a --·a ＝12211(1)121a a a a =++-- 注意到OAB S ∆、a 均为整数，故11a -为整数，于是a －1＝1或－1，即a ＝2或0.将此两值分别代入可知a ＝0时，OAB S ∆＝0应舍去；a ＝2时，OAB S ∆＝2满足题设.故a ＝2.4．依次将正整数1，2，3，…的平方数排成一串：149162536496481100121144…，排在第1个位置的数字是1，排在第5个位置的数字是6，排在第10个位置的数字是4，排在第2008个位置的数字是 1 .解 21到23，结果都只各占1个数位，共占133⨯=个数位；24到29，结果都只各占2个数位，共占2612⨯=个数位；210到231，结果都只各占3个数位，共占32266⨯=个数位； 232到299，结果都只各占4个数位，共占468272⨯=个数位；2100到2316，结果都只各占5个数位，共占52171085⨯=个数位；此时还差2008(312662721085)570-++++=个数位.2317到2411，结果都只各占6个数位，共占695570⨯=个数位.所以，排在第2008个位置的数字恰好应该是2411的个位数字，即为1.第二试 （A ）一．（本题满分20分） 已知实数a 、b 、c 、d 使得方程()()24()()x a x b x c x d -+-=++对一切实数x 均成立，那么当代数式2222448810a b c d ab cd a b c d +++++--+++取到最小值时， a ＋b ＋c ＋d 的值为多少？解 化简原方程，得到：22()24()x b a x ab x c d x cd +---=+++因为此方程对一切实数x 均成立，故得到： b －a ＝c ＋d①－ab －24＝cd ② ……………… 5分而①2－②×2，则有：a 2＋b 2＋48＝c 2＋d 2③ ……………… 10分将①、②、③式代入所求代数式中，有： 原式＝a 2＋b 2＋a 2＋b 2＋48－24－4a －4b ＋8(b －a )＋10 ＝2a 2＋2b 2－12a ＋4b ＋34＝2(a －3) 2＋2(b ＋1) 2＋14……………… 15分故在a －3＝0,b ＋1＝0,即a ＝3,b ＝－1时，该式取到最小值14，此时c ＋d ＝－1－3＝－4，于是a ＋b ＋c ＋d ＝3＋(－1)＋(－4)＝－2 ……………… 20分二．（本题满分25分） △ABC 中，∠B ＝90°，M 为AB 上一点，使得AM ＝BC ，N 为BC 上一点，使得CN ＝BM ，连AN 、CM 交于P 点。

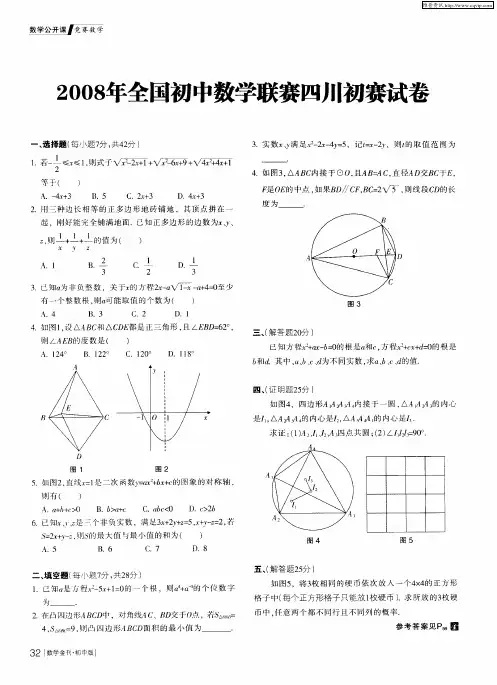
2008年全国初中数学联赛试卷（第一试)一、选择题1．设a２+1=3a，b2＋1=３b,且a≠b，则代数式＼f(1,a2)＋＼ｆ(１,ｂ2)的值为(）(Ａ） 5. (B)7.(C) 9．(D)11．2.如图，设AD，BＥ,ＣF为三角形ＡＢC的三条高,若AＢ＝６,BＣ＝5,EＦ＝3，则线段ＢＥ的长为（）(A)185. (Ｂ) 4. (C）错误!. (D) 错误!.3.从分别写有数字1,２，3，４，5的５张卡片中依次取出两张，把第一张卡片上的数字作为十位数字，第二张卡片上的数字作为个位数字,组成一个两位数，则所组成的数是3的倍数的概率是( ）(A）错误!. (B) 错误!.(Ｃ) 错误!. （D) 1２.4．在△ABＣ中，∠AＢＣ=12°，∠ACＢ=132°，BM和ＣN分别是这两个角的外角平分线,且点M,N分别在直线AC和直线AB上，则()(Ａ）ＢM>CN. (B) BM＝ＣN.(C) ＢM<CN.（D) ＢM和CN的大小关系不确定.5．现有价格相同的5种不同商品,从今天开始每天分别降价１0%或２0%,若干天后,这５种商品的价格互不相同，设最高价格和最低价格的比值为r,则r的最小值为( ）(A）(错误!）3．(Ｂ) (错误!）4. (C) (错误!)5. （Ｄ) 98.6.已知实数x,y满足(x-错误!)(y－错误!)=2008，则3x2－2ｙ2＋３x－3y-2007的值为（）(Ａ) -200８.(B) 2０08. (C）-1.(D)1.二、填空题1.设a=错误!,则错误!＝ ___＿_____.2.如图,正方形AＢＣD的边长为１,Ｍ,Ｎ为BD所在直线上的两点,且AＭ＝错误!，∠ＭＡN=135°,则四边形AMCＮ的面积为_＿＿_____＿__.３.已知二次函数y＝ｘ2＋ａx＋b的图象与x轴的两个交点的横坐标分别为ｍ，n，且│m│＋│n│＜1. 设满足上述要求的b的最大值和最小值分别为p,q，则│ｐ│+│q│＝_＿____＿__＿.4．依次将正整数1,2,3，…的平方数排成一串:149162536４９64811001211４4…,排在第1个位置的数字是1，排在第5个位置的数字是６，排在第10个位置的数字是4,排在第２008个位置的数字是__＿＿_______.第二试一、已知a2＋ｂ2＝1，对于满足条件0≤x≤１的一切实数x,不等式ａ(1－ｘ) (1－ｘ－aｘ）-ｂｘ(b-x-bｘ)≥０恒成立.当乘积ab取最小值时，求a,b的值.二、如图,圆O与圆D相交于Ａ,B两点,BＣ为圆D的切线,点Ｃ在圆O上，且AB=BC．（１）证明:点Ｏ在圆D的圆周上.（2）设△ABC的面积为S，求圆D的的半径ｒ的最小值．三、设a为质数，b为正整数,且9(2ａ＋b)2=509(４ａ+511b)求a，b的值．。

2008年全国初中数学联赛(江西卷)
陶平生
【期刊名称】《《中等数学》》
【年(卷),期】2008(000)009
【摘要】说明：2008年全国初中数学联赛于4月13日举行，因当日与江西省其他考试的时间重叠，经与联赛组委会商议，联赛江西省赛区竞赛改于4月19日举行，并由江西另行命制一份试题．
【总页数】4页(P24-27)
【作者】陶平生
【作者单位】
【正文语种】中文
【中图分类】O1
【相关文献】
1.2008年全国初中数学联赛武汉市CASIO杯选拔赛试题 [J], ;
2.2008年全国初中数学联赛浙江赛区初赛 [J],
3.2008年全国初中数学联赛武汉CASIO杯选拔赛 [J],
4.2008年全国初中数学联赛 [J], 徐胜林
5.2008年全国初中数学联赛四川省初赛 [J], 四川省数学竞赛委员会
因版权原因，仅展示原文概要，查看原文内容请购买。