菠萝中的数学建模

链接——数学建模小论文选题————————————————————————————————作者: ————————————————————————————————日期：中学数学建模小论文选题•“电影票”中的数学问题•“大风车”几何图形探讨•“粉笔中的数学”——中学数学建模教学一例•“供应站的最佳位置在哪里”的应用•“划拳”中的概率问题纠错•“剪刀”里有学问•“近体原则”在中学数学建模教学中的应用•“酒杯问题”的距离分析与变式•“烙饼”的数学建模和教学逻辑•“连环送”中折扣问题的数学探讨•“零首付”买房问题的思考和建议•“牛吃草”问题在实际生活中——传统数学模型的新应用开发•“牛奶包装盒”中的数学思考•“乡村旅游”广告中的奥秘•“直角走廊”问题的探源及拓展•“装错信封问题”的数学模型与求解•《红色警戒》中兵种战斗力的数字建模与统计研究•11名同学挑食严重程度排名•１１0巡警站的位置安排是否合理的问题•NＢA常规赛赛程的合理安排•QQ号真的能计算年龄吗•TI图形计算器在数学建模中的应用——摩天轮中的数学问题•艾滋病检测中的概率问题•按揭贷款还款方式的选择•搬家中的数学模型•变速自行车的选档问题•菠萝中的数学•彩票中的数学•彩票中奖概率分析数学建模•餐厅购菜中的数学问题•测量篮球的表面积•差点儿被忽悠•超市问题探究——收银台数与客流量的关系•潮汐问题数学模型的新探究•车辆油料调剂问题•车牌号码中的数学问题•车站选址与绝对值函数•城市犯罪案件时间特征的实例数据分析•城市交通管理中的出租车规划模型•城市生活垃圾焚烧炉的建模•乘车中的数学•乘船中的数学问题•乘上等车的学问•抽奖活动后面的数学——揭露高额奖金的欺骗性•抽签时不用争先恐后•抽烟中的数学•出租车计费问题数学建模•初中学生课桌椅高度的确定•传染病增长中的几个数学模型•串并联电路的可靠性问题•从北京汽车摇号想到的•从车轮是圆的说开去•从大江截流时间的估算谈建模•从赌博和概率到抽奖陷阱中的数学•从二氧化碳含量与人体关系看教学作息制度的合理性•从公园游览看简单的数学模型•从花坛的设计说起•从将军饮马问题说起•从拼图游戏到人类基因组计划——浅探碎片拼接中有趣的数学规律•从商场的打折到赠券的思考•打折问题•贷款购房时不同还款方式的比较•单循环赛赛程编排的数学模型•蛋糕如何分割•蛋糕作坊的经营策略——数学建模活动个案•蛋筒冰淇淋的包装设计•导数在农田喷灌喷水滴落点建模中的应用•到底几小时用一次药•道路设计与费用核算问题——一份数学建模报告•抵押贷款买房决策模型•电缆线求长的等差数列求和法•电脑福利彩票中几种现象的探究•电热水壶中的数学•电梯调度问题•叠砖问题•定点投篮中的数学问题•都江堰宝瓶口的水有多深•渡河登岸点的最佳选择•短跑运动员步幅的数学建模分析•对互联网中Fｌash的调研•对十字路口红绿灯时间的探索•对一道行程问题的研究•对一道旋转相似问题数学模型的探究•对一光线反射问题的再思考•对易拉罐优化设计模型的改进•多一张奖券中奖概率翻倍吗——小议中奖概率与奖券总数的关系•砝码问题——初等数学建模实例•帆船运动与数学——怎样保证帆船对风力的最大利用•房屋贷款中的数学建模问题•房屋家具摆设的方案•飞镖游戏中的数学知识•飞机免费托运行李的箱体大小尺寸讨论•飞机失事后救生舱氧气系统的数学建模仿真•非法传销现象之分析及研究•肥皂包装箱设计•分蛋糕的无妒忌协议•分期付款多付了多少钱•分期付款模型探讨•峰荷电价的定价模式分析•富翁的宝地•改进“洁诺”•干脆面中奖的数学调查•高考生物试题中数学模型问题的分析•高铁上座率怎么算更合理•个人复习时间分配与知识掌握•个人住房抵押贷款问题•公路交通拥堵现象的建模与分析•公路上雪的融化速度•公平的班干部选举•“关灯”游戏的数学建模与求解•关于“七星彩”中奖问题的一点探讨•关于“跳槽”的数学模型•关于５号信封设计合理性的讨论•关于北京机动车尾号限行的合理性•关于打包问题•关于多人识别系统对应密码特征数的讨论•关于高考前复习时间分配的模型•关于合适教室形状的探究•关于家用电热水器的数学模型•关于节约家用天然气问题的数学分析•关于铺地砖是贴大块地砖省钱还是贴小块地砖省钱•关于物流中最佳派车的数学模型•关于移动与联通的套餐话费节省问题的讨论•关于在学校打饭如何节省时间的分析•观精彩ＮBA建数学模型•灌溉问题“中学数学建模问题一例”•龟免赛跑的数学思考•寒假旅游费用分析建模论文•行车颠簸问题的数学模型与分析•行车时间估计和最优路线选择•喝饮料品数学•合理安排，赚更多的money•红绿灯的周期多长最好•红色旅游模型•黄壁庄水库泄洪问题的研究•火柴棍游戏的启示•机票超额预订问题•基于差分方程的人口预测模型•基于非线性规划的双炼油厂输油管线布置方案•基于活动的初中数学建模的教学实践——设计恺撒密码进行密码传送为例•基于数学建模的中国体育彩票超级大乐适中奖率的研究•基于最短路程的城市公交咨询系统的数学模型•几何中的学问•剪剪拼拼学数学•建立数学模型解物理问题•建立数学模型巧解电梯问题•建模，深刻思維转换的体操——构造“A错误!”解“不相邻”问题•键盘排列的优化•“将军饮马”模型的拓展•教室建造问题•教室内吊扇最优化安装问题•揭开拼图魔术的奥秘•节能灯节电方案•节约能源，选择小排量汽车•节约用水从我做起——关于家庭用水量的分析•截断切割的最小成本问题的探讨•解决韩信立马分油问题的两种方法•金茂大厦的高度测量•九连环序列赏析——中国古环拆装的数学模型•九连环游戏所给出的递推数列研究•酒杯中细棒的平衡位置•就地取材建立数学模型•决策中非理性因素的数学浅析•看孙悟空巧分菜园子•考察“菠萝中的数学”•可以提出更合理的方案•空瓶兑换中的数学模型•垃圾站选址问题的数学模型及应用•利用Excel在我厂建立利润模型——多产品量本利分析模型•利用灯光促进植物生长的实验•利用函数思想解决实际问题•利用数学建模解物理问题•利用图表分析法确定最优化方案•例说数学建模•例谈测量问题中的数学模型•例谈高中数学建模解析化学问题•例谈平面几何问题的三角函数建模研究•例谈数学方法解决高中物理最值问题•例谈数学建模的实际应用•淋雨模型•淋雨中的数学思考•论高层建筑的电梯使用效率问题•论个买卖问题的数学建模•旅客自用行李车的数学力学分析•旅游如何游•蚂蚁通道与数学建模•蚂蚁爬行最短路径问题•买彩票中奖概率的估算•买卖中的数学问题•卖报中的函数问题•猫运动的路线能确定吗•美国中学生数学建模竞赛获奖论文•美丽“花瓣”面积的求法•美丽的蜂窝构造•密码协议与直线方程•妙趣横生的歧中易数列——数学建模一例•哪种能源更合算•喷泉前的思考•乒乓球打法的数学分析•乒乓球赛问题•扑克牌游戏中数学模型思想的渗透与培养•汽车安全车距模型影响因素分析•汽车分期付款合算吗？•汽车转弯时由内轮差引发的交通事故原因建模与分析•铅球投掷中的数学模型•浅谈教室最优座位位置选择•浅谈趣味数学应用问题——从网络游戏话数学建模•浅析“月上柳梢头”的数学模型•浅析数学期望的实际应用•巧猜纸牌魔术•巧卖智买•巧用概率设计抽奖活动•切大葱的学问•丘成桐中学数学奖参赛论文•球类运动中的数学问题•全自动洗衣机用水设计的数学原理•让学生体验数学建模的过程——一道试题引发的思考•扰排问题的推广•热风胆展开面的画线问题•人机游戏中的数学模型•人寿理财分红类保险条款的分析•如何罚点球——隐藏在体育中的数学•如何方便快捷地到达目的地•如何利用声纳波测量海底的深度•如何判断能否被录用•如何让纸飞机飞得更远•如何选择合理的饮食结构•如何用一张纸连续分隔空间•入射角与太阳能热水器的效率•三妾争产分配方案的博弈分析及数学建模——诠释广义平均分配原则的人性化应用•三兄弟共挣多少钱•扫雷•山地车挡泥板挡泥效果的应用论文•商场中的数学•商品促销中的数学模型两例•商品需求价格弹性的数学模型及分析•商厦自动扶梯与老年人购物问题•上海外滩利用之我见•上海外滩观景人流量的计算•上网资费模型研究•烧水的铝壶底的结构与数学•设备选购决策中的数学模型•设计自行车前叉有科学•社区儿童接送服务车辆的线路优化•生活用品的购买•生活中的实例与数学建模•生活中的数学——求零存整取利息•生活中的数学问题•生活中的小问题•生猪养殖场的经营管理数学模型的分析与求解•剩下的钱哪去了•施化肥量对农作物的影响•使作业时间最省的方案设计•市场供求关系的数学模型分析•是继续亏损还是提高票价•收益大小损失风险和决策•手机话费中的数学问题•手机套餐问题的一个数学模型•输油管布置的优化模型•数列在分期付款中的应用•数学和台球的问题•数学建模两例谈•数学建模思想在中学数学应用中的举例•数学建模在公交化校车的优化线路中的运用•数学建模之观影的最佳位置•数学就在我们身边从上楼梯想到的•数学模型在包装装潢设计中的应用•数学中的“盖房与拆迁”三视图•双瓶输液中的数理问题•水温的最佳选择——高中数学教材必修一函数建模的应用范例•台球桌上的数学问题•探究出行费用•探究性学习数学建模例谈•探秘蜂房结构•探索合理的飞镖靶盘•探讨温州市出租车司机的生意经•探险家的沙漠旅行•体育课表的设置•投篮中的数学问题•投骰中的玄机•弯管制作中的数学建模和函数拟合•玩具枪瞄准器的校正•玩具与正多面体•为长辈健康提建议•卫星控制中心室内座位布局引出的数学建模问题•乌鸦能喝到水吗•物资调运中数学模型的建立•洗衣服的数学•洗衣机节水的优化模型•现实生活中最优化问题的数学模型构造•线段图助解打折销售问题•销售代理模型•小球何时能坠到杯底•小学数学建模思想在“替换”问题中的形成与应用•校园汽车减速设施合理设计初探•新旧个税的数学思考•新年联欢会的数学问题•研究性学习在生活应用中的运用——洗衣服中的数学问题•药物残留量问题•一次家务活引发的数学问题•一次研究性课题教学案例——对材料利用率的数学建模发现•一道函数应用题最值的探索之旅•一个初等模型购房贷款决策问题•一个函数最值模型在实际问题中的应用•一个环境保护问题的数学建模活动体验•一个趣味问题的数学模型•一个数学建模问题的简单解法•一个数学历史名题的模型建立及其教学设想谈免子繁殖问题•一个优美的比赛安排问题•一个游戏难题的数学建模与求解•一个有趣的房间地面面积问题•一位房地产商遇到的难题•一种魔术扑克游戏的数学建模及实现•易拉罐的设计方案•音乐中的几何变换•饮料中的学问•应用空间向量与三角函数解题的一个范例•应用数学模型研究手机“套餐”资费问题•硬币滚动中的数学•拥挤的水房——有关打水问题的数学模型•用弗米方法预测中国人口数量的变化•用概率的观点看抽奖•用数理方法预测石油价格•用数学建模方法解决哥尼斯堡七桥问题•用数学建模解决身边的经济问题案例及分析•由“阿凡提分羊”引发的思考•由糖水问题想起数学建模•由一道生活情境问题引发的思考•由转盘游戏谈概率问题•游戏与艺术的魅力•游戏中的数列问题•有趣的地毯问题•鱼池有多少条鱼•鱼火锅里的计算题•羽毛球赛中的数学问题•雨量预报方法的评价模型•雨中行走,速度越快,淋雨越少吗？从数学建模角度分析20１1年的一道高考题•雨中行走问题•预测SAＲＳ疫情影响旅游人数的数学模型•圆角方形牛奶盒的设计•圆形广场的地下灯排布问题•源于生活的一次数学建模•粤海铁路问题探究•运用初等数学建立存贮模型•运用建模方法求解与旅游有关的数学问题•在概率统计教学中如何渗透数学•在月球上跳高和跳远•怎样打包面积最小•怎样烧开水最快最省煤气•张老师买鸡蛋•招聘问题•折纸在数学教学中的应用•真的“公平交易,老少无欺”吗•正方形的花式裁剪和拼接•职工月工资及年终奖扣税函数模型分析•纸扇设计中的数学知识•质点作匀速圆周运动的必要条件和充分条件•中国古代盈不足模型及其算法的应用•中国太平洋少儿乐两全保险A款条款分析•中午食堂吃饭的数学建模•中小学生购买手机方案模型分析•中学教学楼人员疏散优化研究•中学课堂教学时间分配的数学模型•中学生数学建模能力水平的实验分析•中学生消费面面观•中学数学建模问题探究•中学数学建模一例•中学数学建模一例及其启示•中学数学建模与最值问题•重复性赛制中的数学问题•住宅选择中的数学模型•装修工的烦恼•自行车存放问题•自行车的奇想和探究•自行车轮胎问题•自助沙拉的堆叠方案分析•走进幕燕风光中的“卡片与统筹安排”活动课•租船问题趣谈•足球射门中的数学问题•足球中的数学知识•最佳选址问题。

高中生数学建模素养培养的三个路径摘要：古人云“学以致用”，学习数学的目的是应用数学解决问题。

鉴于数学是模型的科学这一特征，让高中生认识数学模型、学习数学建模并提升自身的数学建模素养，是帮助他们把握数学本质、提升知识应用能力的有效途径。

本文从“三学”——学生、学校、教学三个方面将高中生数学建模素养的培养路径总结为以下三点：体认数学建模过程，培养学生建模兴趣；开发数学建模技术，发展学生建模能力；渗透数学建模思想，提升学生建模素养。

关键词：数学核心素养；数学建模素养；数学建模；高中数学模型是借助数学解决实际问题的有力工具，是学科育人和创新人才培养的有效载体。

[1]让学生掌握数学建模的基本过程，提升高中生数学建模素养，是高中数学教学的重要任务和基本目标。

如何落实高中生数学建模素养的培养成为当今数学教育界研究的热点和难点，但归根到底还是得以学生为主体并落实到数学建模的教学上，还是得聚焦于“三学”——学生、学校和教学，基于此，本文将高中生数学建模素养的培养路径总结为以下三点：一、体认数学建模过程，培养学生建模兴趣高中生数学建模素养的培养需要以数学建模的一般过程为教学基点，让学生能够在结合自身身体经验的背景中亲身经历数学建模的过程，即让学生“体认”数学建模过程。

基于此，教师首先要让学生明白“何为数学建模”以及“为何数学建模”的根本问题。

首先，何为数学建模？让学生了解数学建模的内涵是进行数学建模教学的前提，在这里不妨把数学建模总结为“数学建模就是借助于数学概念、公式、定理等，对现实问题进行简化和抽象成数学问题，然后进行数学运算、推理，进而对得到的数据分析和预测，最后带入到实际问题中检验的过程。

”[2]教师可以借助于“削菠萝”的例子，通过介绍菠萝的刨削艺术，[3]即削好的菠萝纹路为何是螺纹状，来展示数学建模的艺术内涵。

然后，为何数学建模？事实上，学习数学在一定程度上可以说是学习“数学化”，“数学模型”的工作原理就是将复杂的问题经过“数学化”后变得简单明了。

初中数学菠萝模型教案1. 让学生了解菠萝模型（Pineapple Model）的基本概念和特点，理解其在数学教学中的应用价值。

2. 培养学生运用菠萝模型解决实际问题的能力，提高学生的数学思维水平。

3. 通过对菠萝模型的学习，激发学生对数学的兴趣，培养学生的创新意识和团队协作精神。

二、教学内容1. 菠萝模型的定义及基本特点2. 菠萝模型在数学教学中的应用3. 运用菠萝模型解决实际问题三、教学过程1. 导入：通过向学生展示一个菠萝实物，引导学生思考菠萝的形状、结构以及特点，从而引出菠萝模型。

2. 基本概念：介绍菠萝模型的定义，让学生了解菠萝模型是一种多面体，具有多个三角形面和若干个四边形面。

3. 基本特点：引导学生观察菠萝模型的特点，如：各面的形状、相邻面的关系等。

4. 应用价值：讲解菠萝模型在数学教学中的应用，如：空间几何图形的认识、立体图形的绘制等。

5. 实践操作：让学生分组合作，利用菠萝模型解决实际问题，如：计算菠萝模型的表面积、体积等。

6. 总结提升：对本节课的内容进行总结，强调菠萝模型在数学教学中的重要性，激发学生对数学的兴趣。

四、教学策略1. 采用直观教学法，让学生通过观察、操作、实践，加深对菠萝模型的认识。

2. 采用问题驱动法，引导学生主动思考、探究，提高学生的数学思维能力。

3. 采用合作学习法，培养学生的团队协作精神，提高学生的沟通能力。

4. 注重个体差异，针对不同学生的学习需求，给予适当的指导和支持。

五、教学评价1. 学生能准确说出菠萝模型的定义和特点。

2. 学生能运用菠萝模型解决实际问题，如：计算表面积、体积等。

3. 学生对菠萝模型在数学教学中的应用有深入了解。

4. 学生在团队合作中表现出良好的沟通能力和协作精神。

六、教学资源1. 实物菠萝：用于导入和新课教学。

2. 菠萝模型图纸：用于实践操作和展示。

3. 计算器：用于计算菠萝模型的表面积、体积等。

4. 多媒体教学设备：用于展示菠萝模型的图片和视频。

0.1 0.1 0.03 0.04 0.02 0.02 0.02 0.05
ቤተ መጻሕፍቲ ባይዱ
以下数据仅供本次竞赛参考，不能作为今后科研数据使用 田间地头到大市场损耗率 大市场到零售市场损耗率 0.04 0.02 0.05 0.025 0.11 0.06 0.15 0.1 0.16 0.11 0.14 0.1 0.12 0.07 0.11 0.05 0.15 0.1 0.08 0.03 0.16 0.1 0.14 0.09 0.16 0.11 0.03 0.01 0.1 0.05 0.07 0.03 0.09 0.03 0.06 0.02 0.06 0.03 0.03 0.01 0.13 0.04 0.06 0.03 0.04 0.02 0.17 0.09 0.16 0.07 0.17 0.08 0.03 0.08 0.08 0.06 0.05 0.2 0.21 0.22 0.08 0.1 0.04 0.1 0.02 0.12 0.1 0.05 0.16 0.15 0.01 0.03 0.03 0.02 0.02 0.08 0.09 0.1 0.03 0.04 0.01 0.03 0.005 0.03 0.04 0.01 0.04 0.07
食物名称胡萝卜萝卜竹笋大白菜菠菜菜花韭菜芹菜生菜蒜苗小白菜油菜圆白菜冬瓜西红柿青椒茄子黄瓜苦瓜南瓜丝瓜土豆榨菜蘑菇目耳香菇田间地头到大市场损耗率0
食物名称 胡萝卜 萝卜 竹笋 大白菜 菠菜 菜花 韭菜 芹菜 生菜 蒜苗 小白菜 油菜 圆白菜 冬瓜 西红柿 青椒 茄子 黄瓜 苦瓜 南瓜 丝瓜 土豆 榨菜 蘑菇 目耳 香菇 苹果 梨 桃子 杏子 李子 葡萄 香蕉 草莓 橙子 橘子 柚子 西瓜 哈密瓜 桑葚 柿子 大枣 荔枝 龙眼
芒果 猕猴桃 菠萝 山楂 椰子 柠檬 木瓜 枇杷

（由组委会填写）第十一届华为杯全国研究生数学建模竞赛学校青岛科技大学参赛队号10426019队员姓名1.王玉江2.陈桂兵3.严春梅（由组委会填写）第十一届华为杯全国研究生数学建模竞赛题目人体营养健康角度的中国果蔬发展战略研究摘要：水果和蔬菜是重要的农产品，主要为人体提供矿物质、维生素、膳食纤维。

因此，预测我国果蔬的消费与生产趋势，科学地规划与调整我国果蔬的中长期的种植模式，具有重要的战略意义。

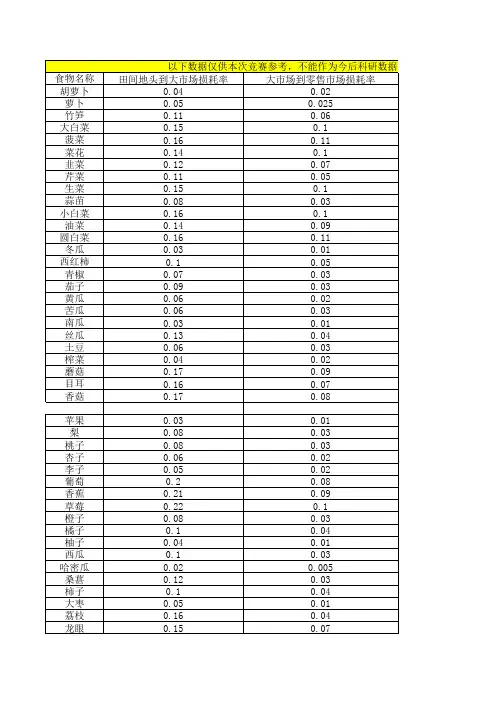
针对问题一，首先选取需要研究的主要水果、蔬菜品种，以其总计含量分别达到各自总产量的90%为约束条件，采用多目标规划（产量最多、营养含量最高、种类最少）筛选出主要的水果、蔬菜品种（水果10种、蔬菜8种，结果见表4、表5）。

随后，查询2002至2010年主要品种的产量，通过两种方法（损耗率、进出口差量）计算人均消费量，用灰色预测GM（1,1）和曲线拟合两种模型预测未来人均消费量，并分别检验拟合效果、进行误差分析，发现基于损耗率估计消费量灰色预测的效果较理想。

所以以苹果为例，综合考虑损耗率和进出口量利用灰色预测模型估计其2010至2020年的人均消费量（见表9、表12），拟合出曲线图（见图2、图6），分析其发展趋势。

针对问题二，首先依据10种营养成分在主要果蔬产品中含量的相似性，运用Spss 软件对10种营养成分进行Q型聚类降维得6大类营养成分（结果见表12），每类营养成分都筛选出一个营养成分作为代表分别是膳食纤维、维生素A、维生素C、维生素E、钙、锌。

采用正态分布中间型模型计算每种营养成分年均实际摄入量关于标准摄入量的隶属度，隶属度越接近1表明实际摄入量越趋近于标准量，以此评价2014年的营养年摄入水平。

用维生素A、C、E隶属度的乘积量化维生素这一大类营养元素趋于健康的程度，同样对钙锌采取相同的措施作为矿物质的量化值，关于时间作图可知2014至2019年中国居民的营养健康状况趋于好转，2019至2020年趋于恶化。

菠萝中的数学建模菠萝是一种美味的热带水果，含有丰富的维生素C和纤维素，深受人们喜爱。

但是，在菠萝的外观之下，隐藏着许多数学模型和计算方法。

本文将介绍菠萝中的一些数学建模，并探讨它们在农业生产和质量控制方面的应用。

一、菠萝研发模型在菠萝的种植和研发过程中，数学建模可以起到重要作用。

例如，为了改良品种和提高产量，研究人员需要确定最佳的肥料配比、灌溉量和光照条件。

这涉及到多个因素的综合评估和优化，可以使用数学模型进行分析和预测。

一种常用的数学模型是响应面分析，它可以帮助农业科学家在多个自变量条件下确定最佳的响应变量值。

对于菠萝的研发过程，自变量可以是土壤pH值、施肥量和光照时间，而响应变量可以是产量或营养价值。

通过实验数据的收集和分析，科学家可以建立一个数学模型，进而预测菠萝的最优种植条件。

二、菠萝运输模型菠萝在运输过程中容易受到挤压和震动的影响，这可能导致果实受损和质量下降。

为了避免这些问题，数学建模可以用来优化菠萝的包装和运输方式。

其中，一种常见的模型是震动模型。

震动模型可以通过模拟运输过程中的震动情况，对菠萝的受损程度进行评估。

通过测量菠萝的结构特性和弹性系数，结合运输车辆的震动参数，可以计算出果实在运输过程中所承受的压力。

根据模型的结果，可以优化包装材料和运输方式，以保护菠萝的完整性和品质。

三、菠萝糖度模型菠萝的糖度是评估其甜度和成熟度的重要指标。

为了准确测量菠萝的糖度，数学建模可以被用来开发预测模型。

一个典型的糖度模型可以基于光学测量技术和多元回归分析。

光学测量技术可以通过检测菠萝果皮的颜色和光线透射特性，来间接估计其糖度。

然后，通过与实际采样数据进行校准和优化，可以建立一个预测模型，用于非破坏性测试。

该模型可以应用于菠萝糖度的快速检测，无需破坏果实并节约时间。

这对于菠萝的仓储、销售和消费具有重要意义，以确保产品的质量和符合度。

结论通过数学建模，我们可以在菠萝的种植、运输和质量控制过程中发挥重要作用。

2012年第八届大学生数学建模竞赛C题：瓜果体积的估计问题首先想问大家一个问题：在水果店里，如果老板奖励你一次任意拿水果的机会，你将怎样选择？假如质量都是一样，但形状差异很大，又怎样合适选择呢？下面就走进我们的建模吧！摘要体积和重量常用来衡量果实大小,且以体积为更佳，如果我们能精确的估计出不同形状水果的大小，并能找到一个固定模式，当我们买水果的时候，只要我们通过测量几个长度就能估算出其体积，选择出最大的那个。

那么，我们怎样只通过软尺测量一些参数值就可以估计该瓜呢？对于我们经常见到的各种各样的瓜果，如萝卜、南瓜、茄子、番茄、香蕉、西瓜等等，虽然其形状千奇百怪，重量也有很大差异。

但当我们学习了数学和计算机后，我们就可以通过数学知识建立模型应用计算机的优点将其性质计算出来。

因此我们建立的模型思路是：取西瓜萝卜各一筐，然后分别对其形状进行分类，可得出简单结论：西瓜可以近似看成椭球体形，萝卜可以近似看成抛物线椭球体形。

对不同的西瓜其对应三半径（横半径·纵半径·竖半径，其值大小可以通过软尺测出，最好是将西瓜均匀切开，但由于经济条件就选择了体外直接测量）在变，从而其形状就不同。

因此我们分别随机选取十组具有代表性大小形状的西瓜和萝卜，最后通过积分知识估计出体积和总量大小，分别将其与排液方法秤重法对应得出的数据进行分析，应用计算机编程软件得出它们之间的关系，从而得出模型。

总之，本文中的模型具有一般性和推广性，但只对同类水果有参考价值，只要所给数据信息量足够、准确，模型求出的结果将具有更好的实际意义。

关键词：形状大小半径积分编程一问题的提出1、选定2-3种瓜果，每种瓜果制定一些测量标准（可以自己命名参数），依据其形状特征，通过你所学过的和资料上介绍的各种几何体的体积计算方法给出综合计算模型；要求有一般性模型，同时对每种瓜果要给出若干不同大小样本的理论估计值（用你的模型算出的值）；2、利用物体在液体中排开体积的较为精确计算方法分析1中模型的误差，评价模型的优劣（此问题可以利用其他测量工具，如量杯等）；3、选定2-3种瓜果，每种瓜果选取不同大小的样本若干（有条件的情况下越多越好），制定一些测量标准，测出其相关参数值（用软尺），再用排液法和秤重法分别测出这些样本相应的体积和重量，建立数据表。

菠萝中的数学建模摘要四月是菠萝上市的季节，大家都知道，吃菠萝前要削皮去籽。

削皮去籽的方法有多种，水果店的人一般是斜着削，削完后菠萝上留下的是一条条螺线，这是一个很有艺术性的过程。

我们购买水果时，希望水果商将皮和籽干净去除的同时，也非常希望保留下来的果肉是最多的(即削掉的果肉是最少的)。

尽可能少削除可食用的菠萝肉，也就是说削刀在菠萝上走的路程要尽可能短。

现在的问题就是要我们求出斜向、横向及纵向这三种削法削刀所走过的路程，比较出哪种削法的路程最短。

我们运用假设分析法，假设将菠萝的形状看成圆柱体，将菠萝的圆柱侧面展开，则形成一矩形，忽略菠萝黑籽的体积，用点表示菠萝黑籽，忽略削去菠萝果肉的厚度及宽度，用连线表示削去的菠萝果肉。

菠萝籽在展开的矩形上呈交错排列，削去的菠萝皮本来是螺旋线，展开后应该成为直线才能少削去菠萝果肉。

关键词：假设分析法勾股定理1.问题重述削皮去籽的方法有多种，水果店的人一般是斜着削，削完后菠萝上留下的是一条条螺线，这是一个很有艺术性的过程。

你认为哪种削菠萝的方法最好，能否从数学角度证明你的结论？请写出你的结论，并尽量详细地将自己的思考过程以及问题解答过程书写下来。

2.模型假设⑴假设将菠萝的形状看成圆柱体；⑵将菠萝的圆柱侧面展开，则形成一矩形；⑶忽略菠萝黑籽的体积，用点表示菠萝黑籽；⑷忽略削去菠萝果肉的厚度及宽度，用连线表示削去的菠萝果肉；⑸菠萝籽在展开的矩形上呈交错排列（如后图），削去的菠萝皮本来是螺旋线，展开后应该成为直线才能少削去菠萝果肉。

3.符号说明s：一行上的菠萝籽数目；k：一列上的菠萝籽数目；a：矩形对角线的长度。

4．问题分析及模型建立我们用化整为零的方法，仅观察如图所示的四颗菠萝籽A、B、C、D，显然这四个菠萝籽的连线构成一个菱形，我们不妨再特殊一点设其为正方形。

设对角a线AC=BD=a，则边长AD=√22图一图二图三图四假设一行上有s个菠萝籽，一列上有k个菠萝籽，这就是一般情况了。

小学课文：一只乌鸦口渴了， 小学课文：一只乌鸦口渴了，到处找水 乌鸦看见一个瓶子，瓶子里有水。 喝。乌鸦看见一个瓶子，瓶子里有水。 可是瓶子里水不多，瓶口又小， 可是瓶子里水不多，瓶口又小，乌鸦喝 不着水，怎么办呢？ 不着水，怎么办呢？ 乌鸦看见旁边有 许多小石子，想出办法来了。 许多小石子，想出办法来了。乌鸦把小 石子一个一个地放进瓶子里。 石子一个一个地放进瓶子里。瓶子里的 水渐渐升高，乌鸦就喝着水了。 水渐渐升高，乌鸦就喝着水了。
数学 建模
建立数学模型的全过程 （包括表述、求解、解释、检验等） 包括表述、求解、解释、检验等）
数学建模的一般步骤
模型准备 模型检验 模型应用
模 型 准 备
模型假设 模型分析
建立模型 模型求解
了解实际背景
明确建模目的
搜集有关信息 掌握对象特征
形成一个 比较清晰 问题’ 的‘问题’
数学建模的一般步骤
转化为数学问题
• 穿上高跟鞋后，身高为h+x厘米，下肢 穿上高跟鞋后，身高为h+x厘米， h+x厘米 l+x厘米 厘米。 长l+x厘米。 • 得到一个关于x的一次方程： 得到一个关于x的一次方程：
l+x = 0.618 h+x
问题的求解
• 解该一次方程，得： 解该一次方程，
0.618h − l x= 0.382
评价和应用
• 假如乌鸦聪明得很，能使石子彼此之间挨 假如乌鸦聪明得很， 得更紧密些，那么空隙部分也得占瓶子1/3 得更紧密些，那么空隙部分也得占瓶子1/3 左右（只是计算麻烦些， 左右（只是计算麻烦些，读者可举一实例 验证之） 验证之） • 上述计算尽管只是对特殊情况的一种粗略计算， 上述计算尽管只是对特殊情况的一种粗略计算， 但这也实在难为乌鸦了， 但这也实在难为乌鸦了，不过这不能不使我们 考虑这样一个事实，在日常生活中， 考虑这样一个事实，在日常生活中，应当怎样 地充分利用空间，减少浪费，获得更高的效益， 地充分利用空间，减少浪费，获得更高的效益， 这正是数学所需要解决的问题。 这正是数学所需要解决的问题。

·２ ６·
第 ４ 卷第 ２ 期
数学建模及其应用
表 ２ ２ ０ ０ ８－２ ０ １ １ 年主要水果的产量及其占额表
Ｖ ｏ ｌ ． ４Ｎ ｏ ． ２ Ｊ ｕ ｎ ． ２ ０ １ ５
水果 ／ 万吨 苹果 大枣 芒果 西瓜 梨 草莓 香蕉 葡萄 柿子 橙子 水果总产量 主要水果产量份额 ／％
２ ０ ０ ８年 ２ ９ ８ ４． ６ ６ ３ ６ ３． ４ １ ３ ８ ０． ０ ０ ６ ２ ８ ２． １ ７ １ ３ ５ ３． ８ １ ２ ０ ０． ０ ４ ７ ８ ３． ４ ７ ７ １ ５． １ ５ ３ １ ８． ７ ２ ３ ９ ３． ６ ９ １ ９ ２ ２ ０． １ ９ ７ １． ４ ２
数学建模及其应用vol4no2jun2015表220082011年主要水果的产量及其占额表水果万吨2008年2009年2010年2011年苹果298466316808332636359848大枣36341424784468354268芒果38000400004000043500西瓜628217647847681810688935135381142630150526157948草莓20004220602330024908香蕉783478833995605104000葡萄71515794068549090675柿子31872287562834227110橙子39369463345418058350水果总产量1922019203955121401452276818主要水果产量份额7142713071827090蔬菜聚类分析结果表类别蔬菜种类黄瓜丝瓜竹笋冬瓜表42005200620082009年主要蔬菜的产量及其占额表蔬菜产量万吨2005年2006年2008年2009年茄子22634224702372225885胡萝卜22634144301476715057菠菜15674162701662817538蘑菇3400367547024673西红柿31500324003982845266南瓜5700600063006450萝卜39352400303955040799大白菜103083105060105455105873芹菜19513206801976020814土豆70865540217078073231黄瓜38171404004219444204蔬菜总产量564515539531592404618238主要蔬菜产量份额660659648647课题集锦基于人体营养健康角度的中国果蔬发展建模2015年6月主要的蔬菜水果代表品种表代表品种主要水果苹果大枣芒果西瓜草莓香蕉葡萄柿子橙子梨主要蔬菜茄子胡萝卜菠菜蘑菇西红柿黄瓜南瓜萝卜大白菜芹菜土豆主要蔬菜水果的营养成分摄入量预测在假设蔬菜水果的营养成分不随年份改变而变化的前提下对于蔬菜水果的年人均消耗量分别从城镇和农村两方面考虑从中华人民共和国统计年鉴获取19902012年的城镇农村居民蔬菜水果年人均消费量主要水果和蔬菜的年总产量和中国总人口数

数学建模在农业科学中的应用数学建模作为一种独特的科学研究方法，已被广泛应用于各个领域，其中农业科学便是其中之一。

通过运用数学模型和相关的统计学方法，可以对农业生产和管理过程进行系统性分析和评估，为农业科学研究与决策提供定量化的支持和指导。

本文将以数学建模在农业科学中的应用为主题，探讨其对农业领域的影响和潜力。

一、气象预测模型的应用气象因素是农业生产的重要影响因素之一，气象预测模型的应用可以帮助农业从业者更准确地了解天气变化情况，据此调整农作物的种植和管理方案。

通过将气象数据与历史数据相结合，在数学模型的基础上进行预测和分析，可以提高农业生产的效率和稳定性。

例如，基于气象预测模型的作物适应性评估，可以帮助选择适宜于不同气候条件下的农作物品种，从而提高农作物的适应性和产量。

二、灾害风险评估模型的应用农业生产过程中，各种自然灾害如台风、洪涝等对农作物造成了巨大的破坏。

利用数学建模技术，可以建立灾害风险评估模型，通过对历史灾害数据和相关因素进行分析，预测未来可能发生的灾害风险，并制定相应的应对措施。

例如，基于灾害风险评估模型的土壤保水能力分析，可以帮助农业从业者判断不同地区的土壤保水能力，从而调整灌溉和排水系统，提高农作物对干旱和水涝等灾害的抵抗能力。

三、农业物流优化模型的应用在农产品生产和销售过程中，物流环节的优化对于提高农产品的质量和降低成本非常重要。

数学建模可以帮助分析农产品的生产、贮存和运输等方面的环节，运用优化算法得出最佳的物流方案。

例如，基于农业物流优化模型的货物调度策略优化，可以在保证货物的新鲜度和质量的前提下，降低运输成本，提高运输效率，推动农业产品市场的发展。

四、农业产量预测模型的应用农业产量预测是指通过分析农业生产的各个环节以及影响因素，预测未来的农产品产量，并提前做出相应的生产安排和管理措施。

数学建模技术在农业产量预测中能够发挥重要作用。

例如，基于农业产量预测模型的农作物优化种植方案，可以通过分析气候、土壤和种植技术等因素，为农业从业者提供种植建议，帮助其实现高产、高效的农业生产。

数学建模在农业科学中的应用数学建模是指利用数学方法和技术，对实际问题进行数学描述、分析和求解的过程。

在农业科学领域，数学建模在许多方面发挥着重要作用，如农田水分管理、作物生长预测、病虫害防控等。

本文将重点介绍数学建模在农业科学中的应用，并探讨其对农业生产的意义。

一、农田水分管理农田水分管理对于农业生产至关重要。

数学建模可以通过建立水分平衡模型，帮助农民科学合理地利用和调控田间水分。

首先，可以基于实际监测数据，利用数学方法拟合土壤含水量与时间的变化规律，建立土壤水分动态模型。

其次，结合气象数据和植物生理特性，预测作物对水分的需求量，并利用这些信息优化灌溉方案。

此外，数学建模还可以模拟作物根系对土壤水分的吸收和运输，评估水分利用效率，更好地解决农业灌溉问题。

二、作物生长预测作物生长预测可以帮助农民做出更好的决策，使农业生产更加高效可持续。

通过数学建模，可以建立作物生长动态模型，根据作物生长的影响因素，如气象、土壤等，预测作物产量和生长趋势。

例如，结合光合作用速率模型和气象数据，可以预测不同作物在不同环境条件下的生长速度和产量。

同时，数学建模还可以分析作物叶片面积指数、光合产物转运等参数，为作物管理提供科学依据，提高作物产量和质量。

三、病虫害防控病虫害是农业生产中的重要问题，对农作物的产量和品质造成严重影响。

数学建模可以帮助农民预测和控制病虫害的发生和传播。

首先，可以利用数学模型分析感病虫害作物和病虫害传播介体之间的关系，预测病虫害的发生概率和传播速度。

其次，可以基于病虫害历史数据，建立数学模型，评估不同防控措施的有效性，并通过优化模型，设计最佳的病虫害防控策略。

通过数学建模，可以及时预警病虫害的发生，采取针对性的防治措施，降低农业生产风险。

总结起来，数学建模在农业科学中的应用涵盖了农田水分管理、作物生长预测和病虫害防控等方面。

通过数学建模，可以提供科学依据和决策支持，帮助农民优化农业生产方式，提高农业生产的效率和质量。

数学建模c题蔬菜matlab代码近年来，随着社会经济的不断发展，蔬菜的生产和销售已成为社会关注的焦点。

对于蔬菜的产量和质量进行精确的预测和分析，有助于农业生产的科学管理和决策。

数学建模作为一种重要的分析和预测工具，被广泛应用于农业领域。

本文将介绍数学建模C题中蔬菜产量的预测问题，并提供相应的Matlab代码。

一、问题描述我们要解决的问题是：通过对历史蔬菜产量数据的分析，利用数学模型来预测未来蔬菜的产量。

具体而言，我们需要根据过去几年的蔬菜产量数据，建立一个合适的数学模型，并利用该模型预测未来几年的蔬菜产量。

二、数据分析我们首先需要收集过去几年的蔬菜产量数据。

假设我们已经收集到了这些数据，并对其进行了初步的分析。

我们可以利用Matlab对这些数据进行进一步的处理和分析。

我们需要将数据导入Matlab，并进行数据可视化和描述性统计分析。

我们可以利用Matlab的拟合工具来拟合各种数学模型，比较它们的拟合效果，并选择最合适的模型。

三、数学建模建立数学模型是解决问题的关键步骤。

在本文中，我们将采用一元线性回归模型来描述蔬菜产量与时间的关系。

回归模型通常可以用如下的数学公式表示：\[Y = aX + b\]其中，\(Y\)表示蔬菜产量，\(X\)表示时间，\(a\)和\(b\)分别表示回归系数和截距。

在Matlab中，我们可以利用regress函数来进行回归分析，并得到回归系数\(a\)和\(b\)的估计值。

我们还可以利用polyval 函数来进行预测，从而得到未来几年的蔬菜产量预测值。

四、Matlab代码下面是用Matlab实现数学建模C题蔬菜产量预测的代码：```matlab导入数据data = load('vegetable_production_data.csv');X = data(:,1); 时间Y = data(:,2); 蔬菜产量回归分析[b, bint, r, rint, stats] = regress(Y, [ones(length(X),1), X]);a = b(2);b = b(1);预测future_X = [2023; 2024; 2025]; 未来几年的时间future_Y = polyval(a, future_X) + b;disp(future_Y);```五、结果分析通过以上的分析和代码实现，我们得到了未来几年的蔬菜产量预测值。

步骤． ’
２ 数学 建模 的五个 步骤
首先 ， 学生 了解什 么是 数学 建模． 让 数学 建模
●
期 打开学 生数 学应 用 的 眼界 ， 了解 数 学建 模 的 步
骤与方法 ， 引导学生 关注生 活 中的数 学．
１ 问题提 出
是数 学学 习的一 种新 的方 式 ， 为 学生 提 供 了 自 它
在上 海 的多所 中学 里 给学 生 做 此 问题 ， 到 拿 问题后 ， 没有 老 师 的任何 提示 ， 学生 的表现 如同我
图２
我们 可 以把 世 界 分 为真 实 世 界 与 数 学世 界 ， 数 学建模 的来源 是 真 实世 界 中 的某 一 问题 ， 过 通
维普资讯
立“ 数学 建模”的专题课 程 ， 设立 “ 数学 与 日常 生活
相联 系” Ｄ系列 课程 ． 的 如何将 这些课 程转化 为教
学实践 ？ 此我 们 以 “ 萝 中 的数 学 ”为 例 ， 析 在 菠 分
“ 数学建 模”教学 的实 施 途径 ， 学 生 了解 数 学 建 让
模 的方法 ， 培育 其数 学建模 能力．
题 的答案 明显 而理所 当然 ， 因 为这样 削美 观 ” 如“ ，
“ 因为菠 萝就是这 么长的 ” “ ， 因为这 种 削法是 一代
一
决生 活 中的现实 问 题 方 面非 常 薄 弱 ， 一 现 象在 这
高 中学生 中普遍存 在．
代 传下来 的”“ ，因为这样 削速 度快 ， 失 的果 肉 损
主学 习的 空间 ， ＩＡ 将“ 学建模 ” 义 为 ５ ＰＳ 数 定 个步
骤（ 如图 ２ ： ）
菠萝是 我们 所 熟 悉 的水 果 ， ’ 吃菠 萝前 要 削 皮 去籽几乎 是人 人 皆 知． 去除 菠 萝黑 籽 的方 法 有 许

教案：初中数学——菠萝模型教学目标：1. 让学生了解菠萝模型的概念，理解其内涵和外延；2. 培养学生运用菠萝模型解决实际问题的能力；3. 培养学生合作学习、交流分享的良好习惯。

教学重点：1. 菠萝模型的概念及特点；2. 运用菠萝模型解决实际问题。

教学难点：1. 菠萝模型的抽象理解；2. 灵活运用菠萝模型解决不同问题。

教学准备：1. 教师准备PPT，内容包括菠萝模型的介绍、案例分析等；2. 学生准备笔记本，用于记录学习内容和感悟。

教学过程：一、导入（5分钟）1. 教师通过向学生展示一颗菠萝，引发学生对菠萝的好奇心，激发学习兴趣；2. 提问：同学们，你们对菠萝有什么了解？菠萝有哪些特点？二、新课导入（10分钟）1. 教师介绍菠萝模型的概念：菠萝模型是一种用于解决实际问题的数学模型，其特点是层次分明、因果关系明确；2. 讲解菠萝模型的内涵和外延：内涵是指模型所包含的基本元素和关系，外延是指模型在实际问题中的应用；3. 举例说明菠萝模型在实际问题中的应用，如：优化生产流程、合理安排时间等。

三、案例分析（15分钟）1. 教师提出一个实际问题，如：某工厂生产两种产品，A产品和B产品。

生产A 产品需要2小时，生产B产品需要3小时。

请问如何安排生产计划，才能使工厂的利益最大化？2. 学生分组讨论，运用菠萝模型分析问题，提出解决方案；3. 各组汇报讨论成果，教师点评并指导。

四、课堂练习（10分钟）1. 教师给出几个有关菠萝模型的练习题，要求学生独立完成；2. 学生解答问题，教师巡回指导。

五、总结与反思（5分钟）1. 教师引导学生回顾本节课所学内容，总结菠萝模型的特点和应用；2. 学生分享学习感悟，谈谈对菠萝模型的理解和个人体会；3. 教师总结：菠萝模型是一种实用的数学工具，希望大家能够灵活运用，解决实际问题。

教学反思：本节课通过引入菠萝模型，让学生了解其概念和应用，培养学生的实际问题解决能力。

在教学过程中，要注意关注学生的学习反馈，及时调整教学节奏和难度，确保学生能够较好地掌握菠萝模型。

数学建模水果产量预测matlab摘要：一、引言1.数学建模的背景和意义2.数学模型在各领域的应用3.数学建模与计算机技术的关系二、数学建模的基本步骤1.理解问题的实际背景和意义2.提炼问题的数学模型3.利用数学工具解决问题三、数学建模在水果产量预测中的应用1.水果产量预测的重要性2.建立水果产量预测的数学模型3.使用MATLAB 进行水果产量预测四、结论1.数学建模在解决实际问题中的价值2.数学建模与计算机技术的结合对知识经济时代的影响正文：一、引言随着计算机技术的迅速发展和应用范围的不断扩大，数学建模在各个领域中发挥着越来越重要的作用。

数学建模是一种将实际问题抽象为数学模型，并利用数学工具进行分析和求解的过程。

在这个过程中，数学模型能够解释某些客观现象、预测未来的发展规律，或为控制某一现象的发展提供最优策略或较好策略。

数学建模已经成为当代高新技术的重要组成部分，与计算机技术相结合，为知识经济时代的发展提供了强大的支持。

二、数学建模的基本步骤1.理解问题的实际背景和意义：在进行数学建模之前，首先要对问题的实际背景进行深入了解，明确问题的实际意义，掌握对象的各种信息。

2.提炼问题的数学模型：在理解问题的基础上，运用数学思想包容问题的精髓，用数学语言描述问题，建立数学模型。

这一过程要求符合数学理论和习惯，表达清晰准确。

3.利用数学工具解决问题：根据实际对象的特征和建模的目的，对问题进行必要的简化，并提出恰当的假设。

在此基础上，利用适当的数学工具解决问题，求解模型。

三、数学建模在水果产量预测中的应用1.水果产量预测的重要性：水果是人们日常生活中不可或缺的食品，其产量的预测对于农业生产和市场供应具有重要意义。

准确的产量预测能够为农民和商家提供决策依据，以确保水果的稳定供应和合理价格。

2.建立水果产量预测的数学模型：利用数学建模方法，可以建立水果产量预测的数学模型。

一般而言，水果产量受多种因素影响，如气候、土壤、种植技术等。

数学建模水果产量预测matlab【原创实用版】目录一、引言二、数学建模简介1.数学模型的定义2.数学模型的作用三、水果产量预测概述1.水果产量预测的重要性2.预测方法的发展四、MATLAB 在数学建模中的应用1.MATLAB 简介2.MATLAB 在预测模型中的作用五、数学建模在水果产量预测中的应用实例1.数据收集与处理2.建立预测模型3.模型检验与优化4.应用实例分析六、结论七、展望正文一、引言随着科技的快速发展，数学应用已经渗透到各个领域，成为解决实际问题的重要手段。

在农业领域，水果产量预测是关系国家经济、人民生活的重要问题。

为了提高预测准确性，数学建模方法在水果产量预测中的应用越来越广泛。

本文将介绍数学建模方法在水果产量预测中的应用，并以MATLAB 为例，阐述其在预测模型建立和求解过程中的关键作用。

二、数学建模简介1.数学模型的定义数学模型是一种用数学符号、式子、程序和图形等对实际课题本质属性的抽象而又简洁的刻画。

它或能解释某些客观现象，或能预测未来的发展规律，或能为控制某一现象的发展提供某种意义下的最优策略或较好策略。

2.数学模型的作用数学模型在实际应用中具有重要作用，它能帮助我们理解问题的本质，揭示现象背后的规律，为决策提供科学依据。

三、水果产量预测概述1.水果产量预测的重要性水果产量预测是农业领域中的重要问题，它关系到国家经济的发展、人民生活的改善以及农业政策的制定。

准确的产量预测能够帮助农民制定合理的生产计划，减少生产风险，提高经济效益。

2.预测方法的发展随着科学技术的发展，水果产量预测方法不断改进和完善。

从最初的经验预测到统计预测，再到现代的数学建模预测，预测准确性不断提高。

四、MATLAB 在数学建模中的应用1.MATLAB 简介MATLAB 是一种功能强大的数学软件，它提供了丰富的数学函数和图形处理功能，能够方便地解决各种数学问题。

2.MATLAB 在预测模型中的作用在建立和求解数学模型时，MATLAB 可以发挥关键作用。