淮南市2016年高中数学必修2双基限时练11

双基限时练(十一)一、选择题1．如果一条直线与一个梯形的两腰所在的直线垂直，那么这条直线与这个梯形所在平面的位置关系是( )A．垂直B．平行C．直线在平面内D．不确定解析梯形的两腰所在的直线为相交直线．答案 A2．直线l与平面α垂直，则( )A．l与平面α内的某几条直线垂直B．l与平面α内的一条直线垂直C．l与平面α内的无数条直线垂直D．l与平面α内的任意一条直线垂直答案 D3．如图，ABCD—A1B1C1D1为正方体，下面结论中错误的个数是( )①BD∥平面CB1D1；②AC1⊥BD；③AC1⊥平面CB1D1.A．0个B．1个C．2个D．3个解析由于BD∥B1D1，故①正确；由于BD⊥AC，BD⊥CC1，故BD⊥面ACC1，故BD⊥AC1，故②正确；由于AC1⊥B1D1，AC1⊥B1C，故AC1⊥面CB1D1，故①②③全正确，答案为A.答案 A4．如图△ADB和△ADC都是以D为直角顶点的等腰直角三角形，且∠BAC＝60°，下列说法中错误的是( )A．AD⊥面BDC B．BD⊥面ADCC．DC⊥面ABD D．BC⊥面ABD解析由题可知，AD⊥BD，AD⊥DC，∴AD⊥面BDC，又△ABD与△ADC均为以D为直角顶点的等腰直角三角形，∴AB＝AC，BD＝DC＝22 AB.又∠BAC＝60°，∴△ABC为等边三角形，故BC＝AB＝2BD，∴∠BDC＝90°，即BD⊥DC.∴BD⊥面ADC，同理DC⊥面ABD.∴A、B、C项均正确．答案 D5．在四面体P—ABC中，PA＝PB＝PC＝AB＝BC＝CA，D，E，F分别为AB，BC，CA的中点，下列结论中不成立的是( )A．BC∥面PDF B．DF⊥面PAEC．BC⊥面PAE D．AE⊥面APC解析∵D，F分别为AB，AC的中点，∴DF∥BC，故BC∥面PDF，故A项正确，又AB＝AC，PB＝PC，E为BC的中点，∴AE⊥BC，PE⊥BC，∴BC⊥面PAE，又DF∥BC，∴DF⊥面PAE，故B、C项正确，由于AE与AP不垂直，故AE与面APC不垂直．答案 D6.下列说法中错误的是( )①如果一条直线和平面内的一条直线垂直，那么该直线与这个平面必相交；②如果一条直线与某一平面的垂线平行，那么该直线垂直于这个平面；③如果一条直线和一个平面垂直，那么该直线垂直于平面内的任何直线；④若一条直线与平面的垂线垂直，则该直线一定在这个平面内．A．①② B．①④C．①③④ D．②④解析因为当直线与平面平行时，平面内仍存在直线与该直线垂直，故①不正确，②显然正确，根据线面垂直的定义可知，③正确；当一条直线与平面的垂线垂直时，这条直线可能在平面内也可能与平面平行，故④不正确．答案B二、填空题7．下列命题：①过平面外一点有且仅有一条直线与已知平面垂直；②若a∥b，a⊥α，则b⊥α；③若直线a与平面α的两条直线垂直，则直线a⊥α；④若a∥α，α∥β，则a∥β；⑤若a∥α，b∥α，则a∥b；⑥若a⊥α，b⊥α，则a∥b，其中正确命题有________．答案①②⑥8．在三棱锥P—ABC中，最多有________个直角三角形．解析不妨设PA⊥AB，PA⊥AC，则△A PB，△PAC为直角三角形，由线面垂直的判定定理，可得PA⊥面ABC，由线面垂直的定义，可知PA⊥BC，若∠ABC＝90°，则BC⊥AB，∴BC⊥面PAB，即∠PBC＝90°，∴△ABC，△PBC为直角三角形，故直角三角形最多有4个．答案 49．如图，在四面体ABCD中，BC＝CD，AD⊥BD，E，F分别为AB，BD的中点，则BD与面CEF的位置关系是________．解析∵E，F为AB，BD的中点，∴EF∥AD.又AD⊥BD，∴EF⊥B D.又BC＝CD，F为BD的中点，∴CF⊥BD，又EF∩CF＝F，∴BD⊥面CEF.答案BD⊥面CEF三、解答题10．如图所示，在正方体ABCD－A1B1C1D1中，E，F分别为棱B1C1，B1B的中点．求证：CF⊥面EAB.证明在平面B1BCC1中，∵E，F分别是B1C1，B1B的中点，∴△BB1E≌△CBF，∴∠B1BE＝∠BCF，∴∠BCF＋∠EBC＝90°，∴CF⊥BE.又AB⊥平面B1BCC1，CF⊂平面B1BCC1，∴AB⊥CF，又AB∩BE＝B，∴CF⊥平面EAB.11．如图所示，空间四边形ABCD中，BC＝AC，AD＝BD.作BE⊥CD于E，AH⊥BE于H，求证：AH⊥面BCD.证明取AB的中点F，连接CF，DF，∵BC＝AC，∴CF⊥AB.∵BD＝AD，∴DF⊥AB.又CF∩DF＝F，∴AB⊥面CDF.又CD面CDF，∴AB⊥CD.又BE⊥CD，AB∩BE＝B，∴CD⊥面ABE.∵AH面ABE，∴CD⊥AH.∵AH⊥BE，又BE∩CD＝E，∴AH⊥面BCD.12．如图，AB是圆O的直径，PA垂直于圆O所在平面，M是圆周上任意一点，AN⊥PM，垂足为N.求证：AN⊥平面PBM.证明设圆O所在平面为α，则已知PA⊥α，且BMα，∴PA⊥BM.又∵AB为⊙O的直径，点M为圆周上一点，∴AM⊥BM.由于PA∩AM＝A，∴BM⊥平面PAM.而AN平面PAM，∴BM⊥AN.又PM⊥AN，PM∩BM＝M，∴AN⊥平面PBM.思维探究13．已知直四棱柱ABCD—A1B1C1D1中，底面ABCD为菱形，F为BB1的中点，M为线段AC1的中点，求证：(1)直线MF∥面ABCD ； (2)MF⊥面A 1ACC 1.证明 (1)取AC 的中点O ，连接MO ， ∵M，O 为AC 1，AC 的中点，∴MO 綊12CC 1.又F 为BB 1的中点，ABCD —A 1B 1C 1D 1为直四棱柱， ∴BF 綊12CC 1.∴MO 綊BF.∴四边形MOBF 为平行四边形．∴MF∥BO，又M F⃘面ABCD ，BO 面ABCD ， ∴MF∥面ABCD.(2)∵F 为BB 1的中点，∴AF＝C 1F ，又M 为AC 1的中点，∴MF⊥AC 1. 又ABCD 为菱形，∴BO⊥AC. 又MF∥BO，∴MF⊥AC.又AC 1∩AC＝A ，∴MF⊥面A 1ACC 1.。

双基限时练(二十一)基 础 强 化1．原点到直线x ＋2y －5＝0的距离为( ) A ．1 B. 3 C ．2D. 5解析 d ＝|－5|5＝ 5.答案 D2．已知点(3，m )到直线x ＋3y －4＝0的距离为1，则m 的值为( )A. 3 B ．－ 3 C ．－33D.3或－33 解析 |3＋3m －4|2＝1，∴|3m －1|＝2. ∴m ＝3，或m ＝－33. 答案 D3．两条平行线l 1：3x －4y －1＝0，与l 2：6x －8y －7＝0间的距离为( )A.12B.35C.65D ．1 解析 l 1：6x －8y －2＝0，∴d ＝|－2＋7|62＋82＝510＝12.答案 A4．点P (m －n ，－m )到直线x m ＋yn ＝1的距离为( ) A.m 2±n 2 B.m 2－n 2 C.－m 2＋n 2 D.m 2＋n 2解析 直线方程可变为nx ＋my －mn ＝0， ∴d ＝|n (m －n )＋m (－m )－mn |m 2＋n 2＝m 2＋n 2.答案 D5．设直线l 经过点(－1,1)，当点(2，－1)到直线l 的距离最远时，直线l 的方程是( )A ．3x －2y ＋5＝0B ．2x －3y －5＝0C ．x －2y －5＝0D ．2x －y ＋5＝0 解析 当直线l 与点(2，－1)最远时，直线l 与过点(－1,1)和(2，－1)的直线垂直．过(－1,1)和(2，－1)的直线的斜率为1－(－1)－1－2＝－23，∴直线l 的斜率为32，∴l ：y －1＝32(x ＋1)，即3x －2y ＋5＝0. 答案 A6．P 点在直线3x ＋y －5＝0上，且P 到直线x －y －1＝0的距离等于2，则P 坐标为( )A ．(1,2)B ．(2,1)C ．(1,2)或(2，－1)D ．(2,1)或(－1,2)答案 C7．点A (－4,2)到直线3x ＋4y ＝2的距离为________． 解析 d ＝|3×(－4)＋4×2－2|5＝65. 答案 658．过点A (－1,2)，且与原点距离等于22的直线方程为________________________________．解析 设直线方程为y －2＝k (x ＋1)，即kx －y ＋k ＋2＝0， ∴d ＝|k ＋2|k 2＋1＝22，∴k ＝－1，或k ＝－7. ∴所求直线方程为x ＋y －1＝0，或7x ＋y ＋5＝0. 答案 x ＋y －1＝0，或7x ＋y ＋5＝0能 力 提 升9．在坐标平面内，与点A (1,2)距离为1，且与点B (3,1)距离为2的直线共有________条．解析 由题意知，所求直线斜率必存在， 设为直线y ＝kx ＋b ，即kx －y ＋b ＝0. 由d 1＝|k －2＋b |k 2＋1＝1，d 2＝|3k －1＋b |k 2＋1＝2，解得⎩⎨⎧k ＝0，b ＝3，或⎩⎪⎨⎪⎧k ＝－43，b ＝53.答案 两条10．设点P 在直线x ＋3y ＝0上，且点P 到原点的距离与点P 到直线x ＋3y －2＝0的距离相等，求点P 的坐标．解 ∵点P 在直线x ＋3y ＝0上，∴设P (－3y 0，y 0)， ∴(－3y 0)2＋y 20＝|－3y 0＋3y 0－2|12＋32，∴|y 0|＝15，即y 0＝±15，∴点P 的坐标为⎝⎛⎭⎪⎫35，－15，或⎝⎛⎭⎪⎫－35，15.11．已知直线l 过点P (1,2)，并且与点A (2,3)、B (0，－5)的距离相等，求出直线方程．解 若l 斜率存在， 设其方程为y －2＝k (x －1)，由题意得|2k －3＋2－k |k 2＋1＝|5＋2－k |k 2＋1，得k ＝4.∴l 的方程为y ＝4x －2.若l 斜率不存在，则其方程为x ＝1. 易知A 、B 到l 的距离相等．综上所求l 的方程为y ＝4x －2或x ＝1.12．已知分别过P (－2，－2)，Q (1,3)的直线l 1和l 2，分别绕点P ，Q 旋转，且保持l 1∥l 2，求两条直线的距离d 的取值范围．解 ∵P ∈l 1，Q ∈l 2，l 1∥l 2，∴d ＝|PQ |为l 1和l 2间距离最大值而当l 1和l 2无限趋近重合时，d 无限趋近0. 又∵|PQ |＝(－2－1)2＋(－2－3)2＝34，∴0＜d ≤34.品 味 高 考13．与直线l ：5x －12y ＋6＝0平行且到l 的距离为2的直线m 的方程为________．解析 设所求直线为5x －12y ＋c ＝0，则由两平行直线间的距离公式得2＝|c－6|52＋(－12)2，解得c＝32，或c＝－20.故所求直线的方程为5x－12y＋32＝0或5x－12y－20＝0.答案5x－12y＋32＝0或5x－12y－20＝0。

双基限时练(四)基础强化1．一个直角三角形绕斜边旋转360°形成的空间几何体为() A．一个圆锥B．一个圆锥和一个圆柱C．两个圆锥D．一个圆锥和一个圆台解析所形成的两个圆锥对底，其底面半径是这个直角三角形斜边上的高，这两个对底圆锥的高的和等于这个直角三角形斜边的长．答案 C2．用一个平面去截一个几何体，得到的截面是四边形，则这个几何体可能是()A．圆锥B．圆柱C．球体D．以上都可能解析球体被任何平面所截得的截面均为圆面；对圆锥，截面不能为四边形；对于圆柱，当截面过两条母线时，得到四边形．答案 B3．已知圆锥的底面面积为4π，高为2，则它的母线长为() A．1 B．2C．2 2 D．4解析圆锥的底面半径为2，故它的母线长为2 2.答案 C4．圆台两底面半径分别是2和5，母线长是310，则它的高为()A．9 B．310C．10 2 D．3解析 h ＝(310)2－(5－2)2＝9.答案 A5．设地球的半径为R ，在东经80°上有两点M 、N ，M 在北纬30°，N 在南纬15°，则M 、N 两点间的球面距离为( )A.πR 6B.πR 4C.πR 3D ．πR解析 经线圈是大圆，故经过M 、N 两点的大圆的圆心角为45°，∴M 、N 的球面距离为l ＝2π×R ×45°360°＝πR 4.答案 B6．已知球的半径为5，球心到截面的距离为3，则截面圆的面积为( )A ．4πB ．6πC ．9πD ．16π解析 截面圆的半径为r ＝52－32＝4，∴S ＝π·r 2＝16π. 答案 D7．一个圆台的母线长为5，上、下底面直径分别为2,8，则圆台的轴截面面积为________．解析 圆台的高h ＝ 52－(8－22)2＝4，∴S ＝12×(2＋8)×4＝20. 答案 208．一圆锥的轴截面的顶角为120°，母线长为1，则过该顶点的圆锥截面中最大截面面积为__________．解析因为圆锥的轴截面的顶角为120°，大于90°，所以过顶点的所有截面中，面积最大的是等腰直角三角形的截面，且其面积为母线长的平方的一半．答案12能力提升9．给出下列说法：①球面上四个不同的点一定不在同一平面内；②球的半径是球面上任意一点和球心的连线段；③球面上任意三点可能在一条直线上；④用一个平面去截球，得到的截面是一个圆面．其中正确说法的序号是________．解析作球的一个大圆，在大圆上任取四点，则这四点就在球面上，且共面，故①错误；根据球的半径的定义可知②正确；球面上任意三点一定不共线，故③错误；用一个平面去截球，一定截得一个圆面，故④正确．答案②④10．如图所示，梯形ABCD中，AD∥BC，且AD＜BC，当梯形ABCD绕AD所在直线旋转一周时，其他各边旋转围成了一个几何体，试描述该几何体的结构特征．解 如图所示，旋转所得的几何体是一个圆柱挖去两个圆锥后剩余部分构成的组合体．11.如图所示，圆台母线AB 长为20 cm ，上、下底面半径分别为5 cm 和10 cm ，从母线AB 的中点M 拉一条绳子绕圆台侧面转到B 点，求这条绳长的最小值．解 作出圆台的侧面展开图，如下图所示，由其轴截面中Rt △OPA 与Rt △OQB 相似，得OA OA ＋AB ＝510，可求得OA ＝20 cm.设∠BOB ′＝α，由于扇形弧BB ′︵的长与底面圆Q 的周长相等，而底面圆Q 的周长为2π×10 cm.扇形OBB ′的半径为OA ＋AB ＝20＋20＝40 cm ，扇形OBB ′所在圆的周长为2π×40＝80π cm.所以扇形弧BB ′︵的长度20π为所在圆周长的14.所以OB ⊥OB ′.所以在Rt △B ′OM 中，B ′M 2＝402＋302，所以B ′M ＝50 cm ，即所求绳长的最小值为50 cm.12．设地球的半径为R ，在南纬60°圈上有两点A ，B ，A 在西经90°，B 在东经90°，求A ，B 两点间纬线圈的弧长及A ，B 两点间的球面距离．解 纬度数为60°，则纬度圈小圆的半径r ＝R cos60°＝R2. 如图所示，设南纬60°圈的中心为O 1，地球球心为O ，则∠AO 1B ＝180°.∴AB ＝2AO 1＝R . ∴△AOB 为等边三角形，∴∠AOB ＝60°，∴在南纬60°圈上，AB ︵的长为180π180×R 2＝πR 2； 在球面上，A ，B 两点间的球面距离为60π180×R ＝πR 3.品 味 高 考13．给出下列说法：①正方形的直观图是一个平行四边形，其相邻两边长的比为1：2，有一内角为45°；②水平放置的正三角形的直观图是一个底边长不变，高为原三角形高的一半的三角形；③水平放置的不等边三角形的直观图是不等边三角形； ④水平放置的平面图形的直观图是平面图形． 写出其中正确说法的序号________．解析 对于①，若以该正方形的一组邻边所在的直线为x 轴、y 轴，则结论正确；但若以该正方形的两条对角线所在的直线为x 轴、y 轴，由于此时该正方形的各边均不在坐标轴上且不与坐标轴平行，则其直观图中相邻两边长的比不为1：2；对于②，水平放置的正三角形的直观图是一个底边长不变，高比原三角形高的一半还要短的三角形；对于③，只要坐标系选取的恰当，水平放置的不等边三角形的直观图可以是等边三角形．答案 ④。

高三数学练习卷11班级 姓名 学号一、填空题（每小题5分，满分50分）1．函数)9(log 23x y -=的定义域为A ，值域为B ，则=B A ]2,3(-。

2．函数x y sin 2=的单调递增区间是Z k k k ∈+-,]22,22[ππππ。

3．若22)4(sin 2cos -=-παα，则=+ααsin cos 21。

4．已知数列}{n a 满足11=a ，)2()1(321321≥-++++=-n a n a a a a n n ，则}{n a 的通项公式为⎪⎩⎪⎨⎧≥⋅==)2(!21)1(1n n n a n 。

5. 某同学准备用反证法证明如下一个问题：函数()f x 在]1,0[上有意义,且)1()0(f f =,如果对于不同的]1,0[,21∈x x ,都有|||)()(|2121x x x f x f -<-，求证：21|)()(|21<-x f x f 。

那么他的反设应该是21|)()(||||)()(|,]1,0[,21212121≥--<-∈x f x f x x x f x f x x 且使得存在。

6．已知P 是双曲线19222=-y ax 右支上的一点，双曲线的一条渐近线方程为03=-y x 。

设21F F 、分别为双曲线的左、右焦点。

若3||2=PF ，则=||1PF 5 。

7．若关于x 的方程m x x =+-5||42有四个不相等的实根，则实数m 的取值范围是)5,1(。

8．已知0>x ，0>y ，且112=+yx ，若m m y x 222+>+恒成立，则实数m 的取值范围是)2,4(-。

9．（理）如图，用C B A 、、三类不同的元件连接成系统1N ，当元 件A 正常工作且元件C B 、至少有一个正常工作时，系统1N 正常工作。

已知元件C B A 、、正常工作的概率依次为,90.0,80.0 90.0，则系统1N 正常工作的概率为792.0。

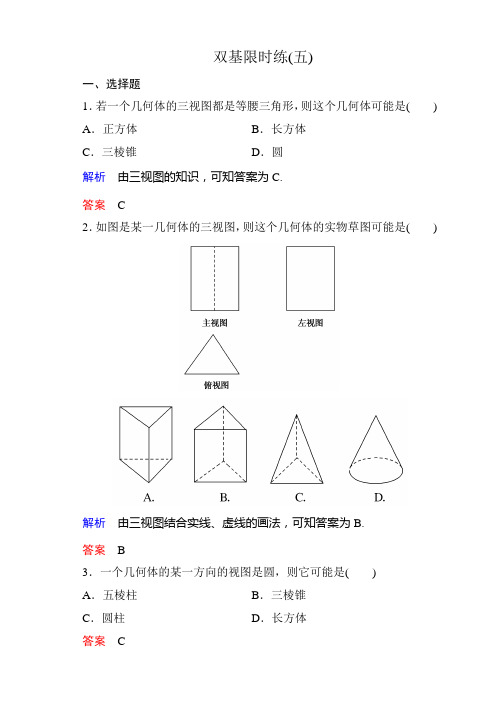
双基限时练(五)一、选择题1．若一个几何体的三视图都是等腰三角形，则这个几何体可能是() A．正方体B．长方体C．三棱锥D．圆解析由三视图的知识，可知答案为C.答案 C2．如图是某一几何体的三视图，则这个几何体的实物草图可能是()解析由三视图结合实线、虚线的画法，可知答案为B.答案 B3．一个几何体的某一方向的视图是圆，则它可能是()A．五棱柱B．三棱锥C．圆柱D．长方体答案 C4．某几何体的三视图如图所示，则该几何体是()A．棱台B．棱柱C．棱锥D．以上均不对解析由相似比，可知几何体的侧棱相交于一点．答案 A5．如果一个几何体的主视图和左视图都是矩形，则这个几何体可能是()A．长方体B．圆柱或正方体C．长方体或圆台D．长方体或圆柱解析正方体的三视图都是正方形；圆台的主视图、左视图都是等腰梯形，长方体和圆柱的主视图和左视图都是矩形．答案 D6．某几何体的主视图和左视图均如图所示，则该几何体的俯视图不可能是()解析若俯视图是A，则原几何体是两个圆柱的组合体；若俯视图是B，则原几何体是一个圆柱和一个四棱柱的组合体；若俯视图为D，则原几何体是一个底面为等腰直角三角形的直三棱柱和一个四棱柱的组合体，故选C.答案 C二、填空题7．如图所示，①②③是三个几何体的三视图，其中①对应的几何体为________，②对应的几何体为________，③对应的几何体为________．解析由三视图的知识，可知甲对应的几何体为圆柱，乙对应的几何体为三棱锥，丙对应的几何体为圆锥．答案圆柱三棱锥圆锥8．桌上放着一个半球，如图所示，则在它的三视图及右面看到的图形中，有三个图相同，这个不同的图应该是________．解析俯视图为圆，主视图与左视图均为半圆．答案俯视图9．如图是长和宽分别相等的两个矩形．给定下列三个命：①存在三棱柱，其主视图、俯视图如图；②存在四棱柱，其主视图、俯视图如图；③存在圆柱，其主视图、俯视图如图．其中是真命题的是________(只填写序号)．解析如图①②③的主视图和俯视图都与原题相同．答案①②③三、解答题10．如图是简单组合体的三视图，想象它们表示的组合体的结构特征，并作适当描述．解由三视图可知该几何体是体育器材杠铃．11．根据下列几何体的三视图，画出该几何体的直观图．该几何体上面是一个圆锥，下面是一个倒置的圆台，如图②所示．9题解析图12.某建筑由相同的若干房间组成，该楼房的三视图如图所示，问：(1)该楼房有几层？从前往后最多要经过几个房间？(2)最高一层的房间在什么位置？请画出此楼房的大致形状．解(1)由主视图和左视图可以知道，该楼房有3层；由俯视图知道，从前往后最多要经过3个房间；(2)从主视图和左视图可以知道，最高一层的房间在左侧的最后一排的房间．楼房大致形状如图所示．思维探究13．如图所示，已知几何体的三视图，用斜二测画法画出它的直观图．解由三视图可知，该几何体下方是一个长方体，上方是以长方体的上底面为底面的四棱锥，其直观图的画法如下：(1)作出长方体的直观图ABCD－A1B1C1D1，如图a所示；(2)再以上底面A1B1C1D1的对角线交点为原点建立x′，y′，z′轴，如图b所示，在z′上取点V′，使得V′O′的长度为棱锥的高，连接V′A1，V′B1，V′C1，V′D1，得到四棱锥的直观图，如图b；(3)擦去辅助线和坐标轴，遮住部分用虚线表示，得到几何体的直观图，如图c.。

双基限时练(十一)1．设自变量x ∈R ，下列各函数中是奇函数的是( ) A ．y ＝x ＋3 B ．y ＝－|x | C ．y ＝－2x 2 D ．y ＝x 3＋x答案 D2．对于定义在R 上的任意奇函数f (x )都有( ) A ．f (x )－f (－x )>0 B ．f (x )－f (－x )≤0 C ．f (x )·f (－x )≤0 D ．f (x )·f (－x )>0 解析 ∵f (－x )＝－f (x )，∴f (x )·f (－x )＝－f 2(x )≤0，故C 正确． 答案 C3．函数f (x )＝1x －x 的图象关于( ) A ．y 轴对称 B ．直线y ＝－x 对称 C ．坐标原点对称D ．直线y ＝x 对称 解析 函数f (x )的定义域关于原点对称，又∵f (－x )＝1－x＋x ＝－⎝ ⎛⎭⎪⎫1x －x ＝－f (x )，∴f (x )为奇函数，其图象关于坐标原点对称． 答案 C4．奇函数y ＝f (x )(x ∈R )的图象必定经过点( ) A ．(a ，f (－a )) B ．(－a ，f (a ))C ．(－a ，－f (a ))D.⎝ ⎛⎭⎪⎫a ，f ⎝ ⎛⎭⎪⎫1a 解析 当x ＝－a 时，f (－a )＝－f (a )， ∴过点(－a ，－f (a ))． 答案 C5．偶函数y ＝f (x )在区间[0,4]上单调递减，则有( )A ．f (－1)>f ⎝ ⎛⎭⎪⎫π3>f (－π)B ．f ⎝ ⎛⎭⎪⎫π3>f (－1)>f (－π)C ．f (－π)>f (－1)>f ⎝ ⎛⎭⎪⎫π3D ．f (－1)>f (π)>f ⎝ ⎛⎭⎪⎫π3解析 ∵y ＝f (x )为偶函数， ∴f (－1)＝f (1)，f (－π)＝f (π)．∵0<1<π3<π<4，y ＝f (x )在[0,4]上单调递减，∴f (1)>f ⎝ ⎛⎭⎪⎫π3>f (π)．∴f (－1)>f ⎝ ⎛⎭⎪⎫π3>f (－π)．答案 A6．已知x >0时，f (x )＝x －2013，且知f (x )在定义域上是奇函数，则当x <0时，f (x )的解析式是( )A ．f (x )＝x ＋2013B ．f (x )＝－x ＋2013C ．f (x )＝－x －2013D ．f (x )＝x －2013解析 设x <0，则－x >0，所以f (－x )＝－x －2013，又因为f (x )是奇函数， 所以f (x )＝－f (－x )＝x ＋2013，故选A. 答案 A7．设函数f (x )＝(x ＋1)(x ＋a )x 为奇函数，则a ＝________. 解析 由f (－x )＝－f (x )，得(－x ＋1)(－x ＋a )－x ＝(x ＋1)(x ＋a )－x，即(x －1)(x －a )＝(x ＋1)(x ＋a )(x ≠0)，∴a ＝－1. 答案 －18．已知函数f (x )为偶函数，其图象与x 轴有四个不同的交点，则这四个不同交点的横坐标之和为________．解析 由题意可知函数f (x )的图象关于y 轴对称．所以函数f (x )的图象与x 轴的四个不同交点关于y 轴对称，因此四个不同交点的横坐标之和为0.答案 09．若函数f (x )＝⎩⎪⎨⎪⎧x 2＋2x (x ≥0)g (x ) (x <0)为奇函数，则f (g (－1))＝________.解析 当x <0时，则－x >0，由f (x )是奇函数， 所以f (－x )＝－f (x )＝(－x )2－2x ＝x 2－2x ，所以f (x )＝－x 2＋2x . 即g (x )＝－x 2＋2x ，因此，f (g (－1))＝f (－3)＝－9－6＝－15. 答案 －1510．已知函数f (x )＝ax 2＋bx ＋3a ＋b 为偶函数，其定义域是[a －1,2a ]，求f (x )的值域．解 ∵f (x )＝ax 2＋bx ＋3a ＋b 是定义在区间[a －1,2a ]上的偶函数，∴⎩⎪⎨⎪⎧a －1＋2a ＝0，b ＝0，∴⎩⎨⎧a ＝13，b ＝0.∴f (x )＝13x 2＋1.∴f (x )＝13x 2＋1在⎣⎢⎡⎦⎥⎤－23，23上的值域为⎣⎢⎡⎦⎥⎤1，3127. 11．判断下列函数的奇偶性： (1)f (x )＝1x －1；(2)f (x )＝－3x 2＋1； (3)f (x )＝1－x ·1＋x|x ＋2|－2；(4)f (x )＝⎩⎪⎨⎪⎧x ＋1，x >0，1，x ＝0，－x ＋1，x <0.解 (1)f (x )＝1x －1的定义域是(－∞，1)∪(1，＋∞)，不关于原点对称，所以为非奇非偶函数．(2)f (x )＝－3x 2＋1的定义域是R ，f (－x )＝f (x )，所以为偶函数．(3)f (x )＝1－x ·1＋x|x ＋2|－2的定义域是[－1,0)∪(0,1]，所以解析式可化简为f (x )＝1－x ·1＋xx，满足f (－x )＝－f (x )，所以是奇函数． (4)函数的定义域为R . 当x >0时，－x <0，则f (－x )＝－(－x )＋1＝x ＋1＝f (x )； 当x ＝0时，f (－x )＝f (x )＝1；当x <0时，－x >0，f (－x )＝－x ＋1＝f (x )． 综上，对任意x ∈R ，都有f (－x )＝f (x )，∴f (x )为偶函数．12．(1)已知y ＝f (x )是定义在R 上的奇函数，且在R 上为增函数，求不等式f (4x －5)>0的解集；(2)已知偶函数f (x )(x ∈R )，当x ≥0时，f (x )＝x (5－x )＋1，求f (x )在R 上的解析式．解 (1)∵y ＝f (x )在R 上为奇函数，∴f (0)＝0. 又f (4x －5)>0，即f (4x －5)>f (0)， 又f (x )为增函数，∴4x －5>0，∴x >54. 即不等式f (4x －5)>0的解集为⎩⎨⎧⎭⎬⎫x |x >54. (2)当x <0时，－x >0，∴f (－x )＝－x (5＋x )＋1，又f (－x )＝f (x )， ∴f (x )＝－x (5＋x )＋1.∴f (x )＝⎩⎪⎨⎪⎧x (5－x )＋1 (x ≥0)，－x (5＋x )＋1 (x <0).。

双基限时练(十一)1．椭圆x 2m ＋y 24＝1的焦距是2，则m 的值为( ) A ．5 B ．8 C ．5或3D ．8或5解析 当焦点在x 轴上时，m ＝4＋1＝5；当焦点在y 轴上时，4＝m ＋1，∴m ＝3，综上知，m ＝5或3.答案 C2．椭圆x 225＋y 29＝1与x 29－k ＋y 225－k ＝1(0＜k ＜9)的关系为( )A ．有相等的长轴B ．有相等的短轴C ．有相同的焦点D ．有相等的焦距解析 当0<k <9时，(25－k )－(9－k )＝25－9＝16＝c 2，∴c ＝4，而焦点一个在x 轴上，一个在y 轴上，∴两椭圆的焦点不同，因此，有相同的焦距，故选D.答案 D3．已知椭圆的长轴长是短轴长的2倍，则椭圆的离心率等于( )A.13B.33C.12D.32解析 依题意2a ＝4b ，即a ＝2b ，又a 2＝b 2＋c 2，∴a 2＝14a 2＋c 2，即34a 2＝c 2，∴c 2a 2＝34，∴e ＝c a ＝32. 答案 D4．若椭圆x 216＋y 2m ＝1的离心率为13，则m 的值为( ) A.1289 B.1289或18 C ．18D.1283或6解析 当焦点在x 轴上时，a 2＝16，b 2＝m ，∴c 2＝a 2－b 2＝16－m ，∴e 2＝c 2a 2＝16－m 16＝⎝ ⎛⎭⎪⎫132，∴m ＝1289，当焦点在y 轴上时，同理可求得m ＝18.综上知m 的值为1289或18. 答案 B5．直线y ＝x ＋1被椭圆x 24＋y 22＝1所截得的线段的中点坐标为( )A.⎝ ⎛⎭⎪⎫23，53B.⎝ ⎛⎭⎪⎫43，73 C.⎝⎛⎭⎪⎫－23，13 D.⎝⎛⎭⎪⎫－132，－172解析 由⎩⎪⎨⎪⎧y ＝x ＋1，x 2＋2y 2＝4消去y ，得3x 2＋4x －2＝0.设直线与椭圆的交点A (x 1，y 1)，B (x 2，y 2)，则x 1＋x 2＝－43， ∴y 1＋y 2＝x 1＋x 2＋2＝23.∴AB 中点的坐标为⎝ ⎛⎭⎪⎫－23，13.答案 C6．已知F 1，F 2是椭圆x 2k ＋2＋y 2k ＋1＝1的左、右焦点，弦AB 过点F 1，若△ABF 2的周长是8，则椭圆的渐近线方程为________________________．解析 由题意得4k ＋2＝8，∴k ＝2.∴椭圆方程为x 24＋y 23＝1，其渐近线方程为y ＝±32x .答案 y ＝±32x7．人造地球卫星的运行轨道是以地心为一个焦点的椭圆，设地球半径为R ，卫星近地点、远地点离地面的距离分别为r 1、r 2，则卫星运行轨道的离心率是__________．解析 由题意得⎩⎪⎨⎪⎧a ＋c ＝r 2＋R ，a －c ＝r 1＋R ，∴2a ＝2R ＋r 1＋r 2,2c ＝r 2－r 1. ∴e ＝ca ＝r 2－r 12R ＋r 1＋r 2.答案 r 2－r 12R ＋r 1＋r 28．在平面直角坐标系xOy 中，设椭圆x 2a 2＋y 2b 2＝1(a >b >0)的焦距为2c .以点O 为圆心，a 为半径作圆M ，若过点P (a 2c ，0)所作圆M 的两条切线互相垂直．则该椭圆的离心率为________．解析 如图，切线P A ，PB 互相垂直，又半径OA 垂直于P A ，所以△OAP 为等腰直角三角形．∴a 2c ＝2a ，∴e ＝c a ＝22.答案 229．椭圆y 2a 2＋x 2b 2＝1(a ＞b ＞0)的两焦点为F 1(0，－c )，F 2(0，c )(c ＞0)，离心率e ＝32，焦点到椭圆上点的最短距离为2－3，求椭圆的方程．解 ∵椭圆的长轴的一个端点到焦点的距离最短， ∴a －c ＝2－ 3. 又e ＝c a ＝32， ∴a ＝2，c ＝ 3. ∴b 2＝1.∴椭圆的方程为y 24＋x 2＝1.10．直线l 过点M (1,1)，与椭圆x 24＋y 23＝1相交于A ，B 两点，若AB 的中点为M ，求直线l 的方程．解 设A (x 1，y 1)，B (x 2，y 2)， 则x 214＋y 213＝1，①x 224＋y 223＝1，②①－②得(x 1－x 2)(x 1＋x 2)4＋(y 1－y 2)(y 1＋y 2)3＝0， ∴y 1－y 2x 1－x 2＝－34·x 1＋x 2y 1＋y 2. 又M (1,1)为AB 的中点， ∴x 1＋x 2＝2，y 1＋y 2＝2. ∴直线l 的斜率为－34.∴直线l 的方程为y －1＝－34(x －1)， 即3x ＋4y －7＝0.11．椭圆过点(3,0)点，离心率e ＝63，求椭圆的标准方程． 解 当椭圆焦点在x 轴上时，则 a ＝3，c a ＝63，∴c ＝ 6. ∴b 2＝a 2－c 2＝3.故椭圆的方程为x 29＋y 23＝1. 当椭圆的焦点在y 轴上时，则b ＝3，又c a ＝63， ∴a 2－b 2a ＝63，∴a 2＝27， 故椭圆的方程为x 29＋y 227＝1.∴所求椭圆的方程为x 29＋y 23＝1或x 29＋y 227＝1.12．在平面直角坐标系xOy 中，点P 到两点(0，－3)，(0，3)的距离之和等于4，设点P 的轨迹为C .(1)求C 的方程；(2)设直线y ＝kx ＋1与C 交于A ，B 两点，k 为何值时OA →⊥OB →？此时|AB |的值是多少．解 (1)设P (x ，y )，由椭圆的定义知，点P 的轨迹C 是以(－3，0)，(3，0)为焦点，长半轴长为2的椭圆，它的短半轴长b ＝22－(3)2＝1.故曲线C 的方程为x2＋y2/4＝1(2)设A (x 1，y 1)，B (x 2，y 2)，其坐标满足⎩⎪⎨⎪⎧y ＝kx ＋1，x 2＋4y 2＝4.消去y ，并整理，得(k 2＋4)x 2＋2kx －3＝0.由根与系数的关系得x 1＋x 2＝－2k k 2＋4，x 1x 2＝－3k 2＋4.若OA →⊥OB →，则x 1x 2＋y 1y 2＝0.∵y 1y 2＝(kx 1＋1)(kx 2＋1)＝k 2x 1x 2＋k (x 1＋x 2)＋1， ∴x 1x 2＋y 1y 2＝－3k 2＋4－3k 2k 2＋4－2k 2k 2＋4＋1＝－4k 2－1k 2＋4＝0，∴k ＝±12.当k ＝±12时，x 1＋x 2＝∓417，x 1x 2＝－1217.∴|AB |＝(x 1－x 2)2＋(y 1－y 2)2＝(1＋k 2)(x 1－x 2)2.而(x 1－x 2)2＝(x 1＋x 2)2－4x 1x 2＝42172＋4×1217＝43×13172，∴|AB |＝54×43×13172＝46517.。

【名师一号】（学习方略）2015-2016学年高中数学 3.2.2直线的两点式方程双基限时练 新人教A 版必修21．过两点(2,5)，(2，－5)的直线方程是( ) A ．x ＝5 B ．y ＝2 C ．x ＝2 D ．x ＋y ＝2答案 C2．在x ，y 轴上截距分别为4，－3的直线方程是( ) A.x 4＋y －3＝1 B.x －3＋y 4＝1 C.x4－y－3＝1 D.x－4＋y3＝1 答案 A3．过(x 1，y 1)和(x 2，y 2)两点的直线方程是( ) A.y －y 1y 2－y 1＝x －x 1x 2－x 1 B.y －y 1x －x 1＝y 2－y 1x 2－x 1C ．(y 2－y 1)(x －x 1)－(x 2－x 1)(y －y 1)＝0D ．(x 2－x 1)(x －x 1)－(y 2－y 1)(y －y 1)＝0 答案 C4．直线ax ＋by ＝1与两坐标轴围成的三角形的面积是( ) A.12ab B.12|ab | C.12abD.12|ab |解析 令x ＝0，得y ＝1b ；令y ＝0，得x ＝1a .故三角形面积为S ＝12|1b ||1a |＝12|ab |.答案 D5．直线ax －y ＋a ＝0(a ≠0)在两坐标轴上截距之和是( ) A ．a －1 B ．1－a C ．a ＋1D ．a －1a解析 令x ＝0，得y ＝a ；令y ＝0，得x ＝－1，故直线在两坐标轴上截距之和为a －1. 答案 A6．若三角形ABC 的顶点A (－5,0)，B (3，－2)，C (1,2)，则经过AB ，BC 两边中点的直线方程为________．解析 AB 的中点为(－1，－1)，BC 的中点为(2,0)．因此所求的直线方程为y ＋10＋1＝x ＋12＋1，即x －3y －2＝0. 答案 x －3y －2＝07．过(5,7)及(1,3)两点的直线方程为________，若点(a,12)在此直线上，则a ＝________.解析 过点(5,7)及(1,3)两点的直线方程为y －73－7＝x －51－5，即x －y ＋2＝0.∵点(a,12)在x －y ＋2＝0上，∴a －12＋2＝0.∴a ＝10. 答案 x －y ＋2＝0 108．已知直线mx ＋ny ＋12＝0在x 轴、y 轴上的截距分别为－3和4，则m ，n 的值分别为________，________.解析 依题意知点(－3,0)，(0,4)在直线mx ＋ny ＋12＝0上，分别代入可求得m ＝4，n ＝－3.答案 4 －39．若直线(2t －3)x ＋y ＋6＝0不经过第一象限，则t 的取值范围是________． 解析 方程可化为y ＝(3－2t )x －6，∵直线不经过第一象限，∴3－2t ≤0，得t ≥32.答案 ⎣⎢⎡⎭⎪⎫32，＋∞ 10．已知直线l 的斜率为6，且在两坐标轴上的截距之和为10，求此直线l 的方程． 解 解法1：设直线方程为y ＝6x ＋b ， 令x ＝0，得y ＝b ；令y ＝0，得x ＝－b6.由题意b －b6＝10，∴b ＝12.所以所求直线方程为6x －y ＋12＝0. 解法2：设直线方程为x a ＋y b＝1，由题意得⎩⎪⎨⎪⎧a ＋b ＝10，－ba＝6.解得⎩⎪⎨⎪⎧a ＝－2，b ＝12.∴x －2＋y12＝1即所求直线方程为6x －y ＋12＝0. 11．求斜率为34，且与两坐标轴围成的三角形的周长为12的直线l 的方程．解 由题意可设直线l 的方程为y ＝34x ＋b .令y ＝0，得x ＝－43b ；令x ＝0，得y ＝b .即直线与两坐标轴的交点为(0，b )，(－43b,0)．由题意|－43b |＋|b |＋b 2＋43b 2＝12，∴|b |＋43|b |＋53|b |＝4|b |＝12.∴b ＝±3.故所求直线的方程为y ＝34x ±3.即为3x －4y ±12＝0.12．直线l 过定点A (－2,3)，且与两坐标轴围成的三角形面积为4，求直线l 的方程． 解 显然l 的斜率存在且k ≠0，可设l 的方程为y －3＝k (x ＋2)，令x ＝0，得y ＝2k ＋3； 令y ＝0，得x ＝－3k－2，即直线l 在两轴上的截距分别为－3k－2,2k ＋3.由题意得12|(－3k －2)(2k ＋3)|＝4.∴(2k ＋3)(3k ＋2)＝±8.若(2k ＋3)(3k ＋2)＝8时，k 不存在． 若(2k ＋3)(3k＋2)＝－8， 解得k 1＝－12，或k 2＝－92.∴直线l 的方程为x ＋2y －4＝0，或9x ＋2y ＋12＝0.。

双基限时练(一)一、选择题1．下面几何体的截面一定是圆面的是()A．圆柱B．圆锥C．球D．圆台答案 C2．下列说法正确的是()A．圆锥是直角三角形绕其一边旋转而成B．在圆台上、下底面圆周上各取一点，则这两点的连线是圆台的母线C．圆柱的任意两条母线所在直线互相平行D．用一平面截圆锥，截面与底面之间的部分为圆台解析由旋转的过程，可知圆柱的任意两条母线所在直线互相平行．答案 C3．如图所示，观察下面四个几何体，其中判断正确的是()A．①是圆台B．②是圆台C．③是圆锥D．④是圆台答案 C4．如图①是由下面哪个平面旋转得到的()解析由旋转的知识，可知答案为C.答案 C5．一个圆锥的母线长为20 cm，母线与轴的夹角为30°，则圆锥的高为()A．10 3 cm B．20 3 cmC．20 cm D．10 cm解析由图可知，h＝20cos30°＝103(cm)，答案为A.答案 A6．有下列四个命题：①圆柱是将矩形旋转一周所得的几何体；②以直角三角形的一边为旋转轴，旋转所得几何体是圆锥；③圆台的任意两条母线的延长线可能相交也可能不相交；④圆锥的轴截面是等腰三角形．其中错误命题的个数是( ) A ．1 B ．2 C ．3D ．4解析 ①错，以矩形某一边为轴旋转才是圆柱，以对角线为轴旋转则不是圆柱；②错，以其直角边为轴旋转才是圆锥；③错，一定相交；④正确．答案 C 二、填空题7．圆台的两底面半径分别为2 cm 和5 cm ，母线长为310 cm ，则它的轴截面面积为________．解析 圆台的高h ＝(310)2－(5－2)2＝9(cm)， S 轴截面＝(4＋10)×92＝63(cm 2)． 答案 63 cm 28．用一张4 cm ×8 cm 的矩形硬纸卷成圆柱的侧面，接头忽略不计，则轴截面面积是________．解析 若圆柱的高为8 cm ，则2πr ＝4(cm)， 2r ＝4π，轴截面面积S ＝8·4π＝32π(cm 2)， 若圆柱的高为4 cm ，则2πr ＝8(cm)， 2r ＝8π，轴截面面积S ＝4·8π＝32π(cm 2)， 故答案为32π cm 2.答案 32π cm 29．一直角梯形上底长为1，下底长为3，高为2，现绕着直角梯形的下底旋转一周，所围成的几何体的轴截面的面积为________．解析 其轴截面由两部分组成其中一个为矩形，一个为三角形，S ＝4×1＋12×4×2＝8.答案 8 三、解答题 10.如图所示，已知梯形ABCD 中，AD ∥BC ，且AD <BC ，当梯形ABCD 绕AD 所在直线旋转一周时，其他各边旋转围成一个几何体，试描述该几何体的结构特征．解 如图所示，旋转所得的几何体是一个圆柱挖去两个圆锥后剩余部分而成的组合体．11．如果一个圆锥的侧面展开图是半圆，求这个圆锥的轴截面的顶角．解 设圆锥的底面半径为r ，母线长为l ，由题意，可得πl ＝2πr ，∴r ＝l2. ∴轴截面的顶角α满足 sin α2＝r l ＝12，∴α2＝30°.∴α＝60°，即圆锥轴截面的顶角为60°.12．已知一个圆台的母线长是5 cm ，上、下底面的面积分别是9π cm 2和16π cm 2，求：(1)圆台的高；(2)截得此圆台的圆锥的母线长．解 (1)设圆台的上、下底面半径为r 、R ，高为h ， 则r ＝3，R ＝4，h ＝l 2－(R －r )2＝52－12＝ 26(cm)；(2)设圆锥母线长为l ′，则l ′－l l ′＝r R ，即l ′－5l ′＝34，l ′＝20(cm)．思 维 探 究13．一个圆锥的底面直径为4，高为8，在其中有一个高为x 的内接圆柱．(1)用x 表示圆柱的轴截面面积； (2)当x 为何值时，S 最大．解 作出圆锥和内接圆柱的轴截面，设圆柱的底面半径为r . 由三角形相似可得x 8＝2－r 2，得r ＝2－x4.(1)圆柱的轴截面面积S ＝2rx ＝2⎝ ⎛⎭⎪⎫2－x 4x ＝－12x 2＋4x ，x ∈(0,8) (2)∵S ＝－12x 2＋4x ＝－12(x －4)2＋8，x ∈(0,8)， ∴当x ＝4时，S 取得最大值8.。

双基限时练(二)一、选择题1．下列说法中正确的是()A．棱柱的各个面中，至少有两个面互相平行B．棱柱中两个互相平行的平面一定是棱柱的底面C．棱柱中侧棱的长叫做棱柱的高D．棱柱的侧面是矩形，但它的底面一定不是矩形解析据棱柱的概念，知答案为A.答案 A2．若棱台上、下底面的对应边之比为1:2，则上、下底面的面积之比为()A．1:2 B．1:4C．2:1 D．4:1解析面积之比等于对应边之比的平方，可知答案为B.答案 B3．棱台不一定具有的性质是()A．侧面都是梯形B．侧棱都相等C．两底面相似D．侧棱延长后交于一点解析据棱台的性质，知答案为B.答案 B4．以下命题正确的是()A．棱锥的各侧棱长相等B．棱柱的各侧面都是矩形C．棱台的各侧棱延长线相交于一点D．圆锥的母线长等于底面圆的周长答案 C5．一个正棱锥的底面边长与侧棱长相等，则该棱锥一定不是() A．三棱锥B．四棱锥C．五棱锥D．六棱锥解析由于正六边形的中心到顶点的距离与边长都相等，故正六棱锥的侧棱长大于底面边长．答案 D6．给出下列命题：①有两个面平行，其余各面都是平行四边形所围成的几何体一定是棱柱；②有一个面是多边形，其余各面都是三角形所围成的几何体是棱锥；③用一个平行于棱锥底面的平面去截棱锥，得到的几何体叫棱台．以上命题中真命题的个数为()A．0 B．1C．2 D．3解析对于①②不符合棱柱、棱锥的定义；对于③，用一个平行于棱锥底面的平面去截棱锥，得的几何体一个是棱台，另一个是棱锥，故③不正确．答案 A二、填空题7．四棱柱有________条侧棱；________个顶点；________个侧面．答案48 48．给出下列几个命题：①棱柱的侧面都是平行四边形；②棱锥的侧面为三角形，且所有侧面都有一个公共点；③棱台的侧棱所在直线均相交于一点；④将直角梯形绕着它的一条腰所在的直线旋转一周所得的几何体为圆台．其中正确的是________．解析①②③显然正确，对于④，只有当直角梯形绕着它的一条垂直于底边的腰所在的直线旋转一周时，所形成的几何体才是圆台，故④不正确．答案①②③9．已知正四棱锥V—ABCD，底面面积为16，一条侧棱长为211，则它的斜高为________．解析由S底＝16，知底面边长为4，又侧棱长为211，故斜高h′＝(211)2－22＝210.答案210三、解答题10．如图所示的棱柱ABCD—A1B1C1D1为正四棱柱，用平面BCEF把该棱柱分成两部分后，各部分的几何体还是棱柱吗？如果是，是几棱柱？如果不是，说明理由．解∵ABCD—A1B1C1D1为正四棱柱，∴截面BCEF右边的部分是三棱柱BFB1—CEC1，截面BCEF左边的部分也是棱柱，是一个四棱柱ABF A1—DCED1.11．如图所示的几何体所有的棱长都相等，分析此几何体的面数，顶点数和棱数，并判断该几何体是不是棱柱、棱锥、棱台的一种．解该几何体有8个面，6个顶点，12条棱，它不满足棱柱、棱锥、棱台的定义，故不是棱柱，也不是棱锥，也不是棱台，但它是一个多面体．12．已知正三棱柱ABC－A1B1C1的底面边长为1，高为4，一动点从A 点出发，沿着三棱柱的侧面绕行一周到达点A1，求动点所经过的最短路程长．解将三棱柱沿AA1将侧面展开，如图所示其中AA′＝3，A′A′1＝4，∴AA′1＝AA′2＋A′A′21＝32＋42＝5.∴动点所经过的最短路程长为5.思维探究13．已知底面是正方形，侧棱都相等的棱锥的高为3，侧棱长为7，求侧面等腰三角形底边上的高．解如图，在棱锥S－ABCD中，高OS＝3，侧棱SA＝SB＝SC＝SD ＝7，解Rt△SOA，得OA＝2，则AC＝4，∴AB＝BC＝CD＝DA＝2 2.作OE⊥AB于E，则E为AB中点．连接SE，则SE即为所求．由于SO⊥OE，在Rt△SOE中，∵OE＝12BC＝2，SO＝3，∴SE＝ 5.∴棱锥侧面等腰三角形底边上的高为 5.。