中考数学压轴题专题汇编04 因动点产生的特殊四边形问题 (解析版)

特殊四边形动点问题专题训练及答案解析（一）已知，如图，点D是△ABC的边AB的中点，四边形BCED是平行四边形，（1）求证：四边形ADCE是平行四边形；（2）当△ABC满足什么条件时，平行四边形ADCE是矩形？证明：（1）因为四边形BCED是平行四边形，所以BD=CE且BD∥CE，又因为D是△ABC的边AB的中点，所以AD=BD，即DA=CE，又因为CE∥BD，所以四边形ADCE是平行四边形．（2）当△ABC为等腰三角形且AC=BC时，四边形ADCE是矩形理由：∵AC=BC，D是△ABC的边AB的中点∴CD⊥AD，即∠ADC=90°，由（1）可知，四边形ADCE是平行四边形∴四边形ADCE是矩形．（二）如图，已知E是▱ABCD中BC边的中点，连接AE并延长AE交DC的延长线于点F．（1）求证：△ABE≌△FCE．（2）连接AC、BF，若∠AEC=2∠ABC，求证：四边形ABFC为矩形．（三）如图，O为△ABC的边AC上一动点,过点O的直线MN∥BC，设MN分别交∠ACB的内、外角平分线于点E、F。

（1）求证：OE=OF（2）若CE=12，CF=5，求OC的长（3）当点O在AC边上运动到何处时，四边形AECF是矩形？证明你的结论（4）在（3）的条件下，当△ABC满足什么条件时，四边形AECF为正方形，并说明你的理由。

（1）证明：∵CE平分∠ACB∴∠ACE＝∠BCE∵MN∥BC∴∠OEC＝∠BCE，∴∠ACE＝∠OEC，∴OE＝OC，同理：OF＝OC∴OE＝OF（2）∵CE平分∠ACB∴∠ACE＝∠ACB/2∵CF平分∠ACD∴∠ACF＝∠ACD/2∴∠ECF＝∠ACE+∠ACF＝∠ACB/2+∠ACD/2＝（∠ACB+∠ACD）/2＝180/2＝900在Rt△ECF中，EF2= CE2+ CF2= 122+ 52=169∴EF=13由（1）可知OE＝OF∴OC=EF/2=13/2(3)、当O运动到AC的中点时，AECF是矩形证明：∵O是AC的中点∴AO＝CO∵OE＝OF∴四边形AECF是平行四边形由（2）可知∠ECF＝900∴四边形AECF是矩形3、△ABC为直角三角形，且∠ACB＝90时，四边形AECF是正方形证明：∵∠ACB＝900，MN∥BC∴∠AOM＝∠ACB＝900，由（3）知四边形AECF 是矩形∴四边形AECF 是矩形（四）如图，已知平行四边形ABCD 的对角线AC 、BD 相交于点O ，AC=20cm 、BD=12cm ，两动点E 、F 同时分别以2cm/s 的速度从点A 、C 出发在线段AC 相对上运动．（1）求证：当E 、F 运动过程中不与点O 重合时，四边形BEDF 一定为平行四边形； （2）当E 、F 运动时间t 为何值时，四边形BEDF 为矩形？（1）解：连接DE ，EB ，BF ，FD∵两动点E 、F 同时分别以2cm/s 的速度从点A 、C 出发在线段AC 相对上运动． ∴AE=CF在平行四边形ABCD 中，OD=OB ，OA=OC ∴OA-AE=OC-CF 或AE-OA=CF-OC 即OE=OF∴四边形BEDF 为平行四边形．（2）当点E 在OA 上，点F 在OC 上时EF=BD=12cm ， 四边形BEDF 为矩形 ∵运动时间为t∴AE=CF=2t ∴EF=20-4t=12 ∴t=2（s ）当点E 在OC 上，点F 在OA 上时，EF=BD=12cm EF=4t-20=12 ∴t=8（s ）因此当E 、F 运动时间2s 或8s 时，四边形BEDF 为矩形．（五）如图，平行四边形ABCD 的对角线AC 、BD 相交于点O ，BD=12cm ，AC=6cm ，点E 在线段BO 上从点B 以1cm/s 的速度运动，点F 在线段OD 上从点O 以2cm/s 的速度运动．（1）若点E 、F 同时运动，设运动时间为t 秒，当t 为何值时，四边形AECF 是平行四边形． （2）在（1）的条件下，①当AB 为何值时，四边形AECF 是菱形；②四边形AECF 可以是矩形吗？为什么？OCDBAEF解：（1）连接DE，EB，BF，FD∵两动点E、F同时分别以2cm/s的速度从点A、C出发在线段AC相对上运动．∴AE=CF∵平行四边形ABCD的对角线AC、BD相交于点O，∴OD=OB，OA=OC（平行四边形的对角线互相平分）∴OA-AE=OC-CF或AE-OA=CF-OC即OE=OF∴四边形AECF为平行四边形．（对角线互相平分的四边形是平行四边形）（2）当点E在OA上，点F在OC上时EF=BD=12cm，四边形BEDF为矩形∵运动时间为t∴AE=CF=2t∴EF=20-4t=12∴t=2（s）当点E在OC上，点F在OA上时，EF=BD=12cmEF=4t-20=12∴t=8（s）因此当E、F运动时间2s或8s时，四边形AECF为矩形．（六）如图，已知在四边形ABCD中，AD∥BC，∠B=90°，AD=24cm，AB=8cm，BC=26cm，动点P从A开始沿AD边向点D以1cm/s的速度运动，动点Q从点C开始沿CB边向点B以3cm/s的速度运动，P、Q别从点A、C同时出发，当其中一点到达端点时，另一点也随之停止运动，设运动的时间为t 秒．（1）当t为何值时，四边形PQCD为平行四边形？（2）当t为何值时，四边形ABQP为矩形？（七）(1)设经过xs的时间，四边形PQCD是平行四边形因为四边形PQCD是平行四边形所以DP=CQ由已知得：DP=AD-AP=24-xCQ=3x所以24-x=3xx=6答：经过6s的时间，四边形PQCD是平行四边形（2）设经过xs的时间，四边形PQBA是矩形因为四边形PQBA是矩形所以AP=BQ由已知得：AP=XBQ=BC-CQ=26-3x所以x=26-3xx=13/2答：经过13/2s的时间，四边形PQBA是矩形。

第四节 动点产生的特殊四边形问题讲方法一、平行四边形存在性1.三定一动如图1,已知△ABC,找点D,使以点A 、B 、C 、D 为顶点的四边形为平行四边形操作:分别过点A 、B 、C 作对边BC 、AC 、AB 的平行线,交点即为所求D 点图1 图2 图32.两定两动已知线段AB,找点C 、D,使得以点A 、B 、C 、D 为顶点的四边形为平行四边形(1)如图2,AB 为边:平移型,利用一组对边平行且相等的四边形为平行四边形(2)如图3,AB 为对角线:旋转型,利用对角线互相平分的四边形为平行四边形3.计算点坐标(1)通过中点坐标公式求点的坐标(2)通过点的平移求点的坐标(3)通过两点之间距离公式根据对边相等建立等式二、菱形存在性1.转化为等腰三角形存在性,然后对称补全2.转化为菱形的判定建立等式三、矩形存在性1.转化为直角三角形存在性,然后对称补全2.转化为矩形的判定建立等式四、正方形存在性1.转化为等腰直角三角形存在性,然后对称补全2.转化为正方形的判定建立等式学思路铺垫(山东泰安中考)如图,是将抛物线y=x 2平移后得到的抛物线,其对称轴为直线x=1,与x轴的一个交点为A(-1,0),另一个交点为B,与y 轴的交点为C(1)抛物线的函数表达式为(2)点P 是抛物线上一点,点Q 是一次函数y=23x+23的图象上一点, 若四边形OAPQ 为平行四边形,这样的点P 、Q 是否存在?若存在,分别求出点P,Q 的坐标;若不存在,说明理由提示：①平行四边形OAPQ 点的位置已经确定,并且O 、A 坐标已知,可根据PQ∥AO,PQ=AO 建立等式压轴题（湖南岳阳中考)如图,抛物线y=32 x 2+bx+c 经过点B(3,0),C(0,-2),直线l:y=-32x-32交y 轴于点E,且与抛物线交于A,D 两点,P 为抛物线上一动点(不与A,D 重合(1)抛物线的解析式为(2)设F 为直线l 上的点,以E,C,P,F 为顶点的四边形能否构成平行四边形?若能,求出点F 的坐标;若不能,请说明理由提能力1.(陕西中考)如图,在同一直角坐标系中,抛物线C1:y=ax2-2x-3与抛物线C2:y=x2+mx+n关于y轴对称,C2与x轴交于A、B两点,其中点A在点B的左侧(1)抛物线C2的函数表达式为(2)在抛物线C1上是否存在一点P,在抛物线C2上是否存在一点Q,使得以AB为边,且以A、B、P、Q四点为顶点的四边形是平行四边形?若存在,求出P、Q两点的坐标;若不存在,请说明理由.2.(青海西宁中考)如图,在平面直角坐标系中,矩形OABC的顶点A,C分别在x轴,y轴的正半轴上,且OA=4,OC=3,若抛物线经过O,A两点,且顶点在BC边上,对称轴交BE于点F,点E的坐标为(0,1)(1)抛物线的解析式为(2)点M在对称轴右侧的抛物线上,点N在x轴上,请问是否存在以点A,F,M,N为顶点的四边形是平行四边形?若存在,请求出所有符合条件的点M的坐标;若不存在,请说明理由3.(四川宜宾中考)如图,抛物线y=-x2+bx+c与x轴分别交于A(-1,0),B(5,0)两点(1)则抛物线的解析式为(2)在第二象限内取一点C,作CD垂直x轴于点D,连接AC,且AD=5,CD=8,将Rt△ACD沿x轴向右平移m个单位,当点C落在抛物线上时,求m的值;(3)在(2)的条件下,当点C第一次落在抛物线上记为点E,点P是抛物线对称轴上一点,试探究:在抛物线上是否存在点Q,使以点B、E、P、Q为顶点的四边形是平行四边形?若存在,请求出点Q的坐标;若不存在,请说明理由4.(甘肃天水中考)如图,在平面直角坐标系中xOy中,抛物线y=ax2-2ax-3a(a<0)与x轴交于A,B两点(点A在点B的左侧),经过点A的直线1:y=kx+b与y轴负半轴交于C,与抛物线的另一个交点为D,且CD=4AC(1)则A、B两点的坐标为,抛物线的对称轴为(2)设P是抛物线对称轴上的一点,点Q在抛物线上,以点A、D、P、Q为顶点的四边形能否为矩形?若能,求出点P的坐标;若不能,请说明理由5.(江宁营口中考)如图,抛物线y=ax2+bx-2的对称轴是直线x=1,与x轴交于A,B两点,与y 轴交于点C,点A的坐标为(-2,0),点P为抛物线上的一个动点,过点P作PD⊥x轴于点D,交直线BC于点E.(1)求抛物线解析式为(2)若点P在第一象限内,OD=4PE,若点M为直线BC上一点,点N为平面直角坐标系内一点,是否存在这样的点M和点N,使得以点B、D、M、N为顶点的四边形是菱形?若存在,直接写出点N的坐标;若不存在,请说明理由。

2024年中考数学高频压轴题训练——二次函数压轴题（特殊四边形）()1求该抛物线的表达式；()2点P在该抛物线上，点Q在y轴上，要使以点形，求所有满足条件的点P的坐标．2．如图，已知抛物线223=--+y x x的左侧），与y轴交于点C．点E为抛物线对称轴上的一个动点：(1)当点E 在x 轴上方且CE BD ∥时，求sin DEC ∠(2)若点P 在抛物线上，是否存在以点B ，E ，C ，P 求出点P 的坐标；(3)若抛物线对称轴上有点E ，使得55AE DE +取得最小值，连接限抛物线为点M ，从请直接写出AM 的长度．3．如图，抛物线23y ax bx =+-与x 轴交于(1,0A -(1)求抛物线的解析式；(2)若点D 是抛物线上的一点，当ABD △的面积为(3)点P 是抛物线对称轴上的一点，在抛物线上是否存在一点为顶点的四边形是平行四边形？若存在，求出点Q(1)求出抛物线与直线的解析式；(2)已知点K为线段AD上一动点，过点K作AH，求AHD的最大面积；(3)若点M是x轴上的一动点，点N是抛物线上一动点，当以点顶点的四边形是平行四边形时，请你直接写出符合条件的点(1)求抛物线的解析式；(2)若点P 是抛物线第四象限上的一个动点，过点P 作PQ AC ∥交BC 于点Q ．①如图1，记APQ △面积为1,S BPQ 面积为2S ，求12S S +的面积最大值及此时点P 的坐标．②如图2，若将QP 沿直线BC 翻折得到QE ，且点E 落在线段AC 上，求此时点P 的坐标．6．如图，抛物线y ＝﹣54x 2+bx +c 与直线y ＝12x +c 相交于A （0，1），B （3，52）两点，过点B 作BC ⊥x 轴，垂足为点C ，在线段AB 上方的抛物线上取一点D ，过D 作DF 轴，垂足为点F ，交AB 于点E ．（1）求该抛物线的表达式；（2）求△ABD面积的最大值；（3）连接BD、CE，四边形BDEC能否成为平行四边形？若能，求出点D的坐标；若不能，请说明理由．7．在平面直角坐标系中，矩形OABC如图所示放置，点A在x轴上，点B的坐标为（2，'''．1）．将此矩形绕点O逆时针旋转90°，得到矩形OA B C（1）求过点A、A'、C'的抛物线的解析式；（2）将矩形OABC沿x轴正方向平移，使点C落在抛物线上，求平移的距离．12．如图，在平面直角坐标系中，点()3,4A -、()5,10B -在抛物线2y x bx c =++上，点P 为该抛物线上一点，其横坐标为m ．（1）求该抛物线的解析式；（2）当点P 与点A 关于该抛物线的对称轴对称时，求PAB 的面积；（3）当该抛物线在点B 与点P 之间部分（含点B 和点P ）的最高点与最低点的纵坐标之差为3时，求m 的值；（4）点Q 为该抛物线的对称轴上任意一点，当以点A 、B 、P 、Q 为顶点的四边形是平行四边形时，直接写出点P 的坐标．13．如图，抛物线2y x bx c =-++交x 轴于点A B ，，交y 轴于点C ，点B 的坐标为()3,0，点C 的坐标为()0,3，点C 与点D 关于抛物线的对称轴对称．(1)求抛物线的解析式；(2)若点P 为抛物线对称轴上一点，连接BD ，以PD PB 、为边作平行四边形PDNB ，是否存在这样的点P ，使得PDNB 是矩形？若存在，请求出tan BDN ∠的值；若不存在，请说明理由；(3)点Q 在y 轴右侧抛物线上运动，当ACQ 的面积与ABQ 的面积相等时，请直接写出点Q 的坐标．14．如图，在平面直角坐标系中，抛物线2y x bx c =-++与x 轴交于点()1,0A -，与y 轴交于点()0,3B ．P 是该抛物线上一点，其横坐标为m ，作点P 关于原点O 的对称点Q ．当线段PQ 不与坐标轴垂直时，以PQ 为对角线构造矩形PMQN ，该矩形的边均与某条坐标轴垂直．(1)求该抛物线对应的函数解析式；(2)当点P 是该抛物线的顶点时，求点Q 的坐标；(3)当点B 在矩形PMQN 的边上时，求m 的值；(4)当0m >，且矩形PMQN 与该抛物线有三个交点时，直接写出m 的取值范围．(1)试求抛物线的解析式；(2)直线()10y kx k =+>与y 轴交于点D ，与抛物线在第一象限交于点于点M ，记CPM CDMS m S =△△，试求m 的最大值及此时点P 的坐标；(3)在（2）的条件下，m 取最大值时，点Q 是x 轴上的一个动点，点参考答案：t。

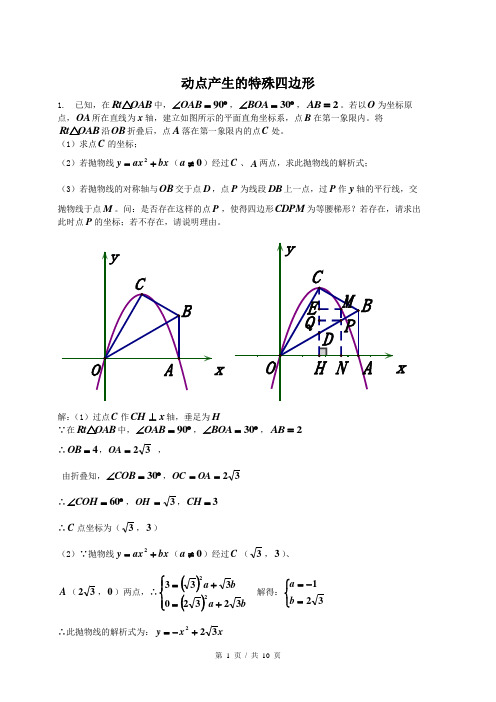
动点产生的特殊四边形1. 已知，在OAB t R △中，︒=∠90OAB ，︒=∠30BOA ，2=AB 。

若以O 为坐标原点，OA 所在直线为x 轴，建立如图所示的平面直角坐标系，点B 在第一象限内。

将OAB t R △沿OB 折叠后，点A 落在第一象限内的点C 处。

（1）求点C 的坐标；（2）若抛物线bx ax y +=2（0≠a ）经过C 、A 两点，求此抛物线的解析式；（3）若抛物线的对称轴与OB 交于点D ，点P 为线段DB 上一点，过P 作y 轴的平行线，交抛物线于点M 。

问：是否存在这样的点P ，使得四边形CDPM 为等腰梯形？若存在，请求出此时点P 的坐标；若不存在，请说明理由。

解：（1）过点C 作x CH ⊥轴，垂足为H ∵在OAB t R △中，︒=∠90OAB ，︒=∠30BOA ，2=AB ∴4=OB ，32=OA ，由折叠知，︒=∠30COB ，32==OA OC ∴︒=∠60COH ，3=OH ，3=CH∴C 点坐标为（3，3）（2）∵抛物线bx ax y +=2（0≠a ）经过C （3，3）、A （32，0）两点，∴()()⎪⎩⎪⎨⎧+=+=b a b a 3232033322解得：⎩⎨⎧=-=321b a ∴此抛物线的解析式为：x x y 322+-=xx（3）存在。

∵x x y 322+-=的顶点坐标为（3，3）即为点C ，x MP ⊥轴，设垂足为N ，t PN =，∵︒=∠30BOA ，∴3=ON t∴P （t 3，t ），作CD PQ ⊥，垂足为Q ，CD ME ⊥，垂足为E 把t x ⋅=3代入x x y 322+-=得：t t y 632+-=∴（t 3，t t 632+-），E （3，t t 632+-） 同理：Q （3，t ），D （3，1）要使四边形CDPM 为等腰梯形，只需QD CE =即()16332-=+--t t t ，解得：341=t ，12=t （舍） ∴P 点坐标为（334，34）∴ 存在满足条件的点P ，使得四边形CDPM 为等腰梯形， 此时P 点的坐为（334，34）M2. 如图，在矩形OABC 中，5=OA ，4=AB ，点D 为边AB 上一点,将△BCD 沿直线CD 折叠,使点B 恰好落在OA 边上的点E 处，分别以OC 、OA 所在的直线为x 轴，y 轴建立平面直角坐标系.(1)求OE 的长；(2)求经过O 、D 、C 三点的抛物线的解析式；(3)一动点P 从点C 出发，沿CB 以每秒2个单位长的速度向点B 运动，同时动点Q 从E 点出发，沿EC 以每秒1个单位长的速度向点C 运动，当点P 到达点B 时，两点同时停止运动.设运动时间为t 秒，当t 为何值时，DQ DP =；(4) 若点N 在(2)中的抛物线的对称轴上，点M 在抛物线上,是否存在这样的点M 与点N ，使得以M 、N 、C 、E 为顶点的四边形是平行四边形？若存在，请求出M 点的坐标;若不存在，请说明理由.解：（1）易知：3=OE（2）设m AD =，则m BD DE -==4 ∵3=OE ∴2=AE∴222)4(2m m -=+ ∴23=m ∴D （23-，5-） ∵C （4-，0），O (0，0) ∴x x y 316342+=（3）∵t CP 2= ∴t BP 25-= 易知：△DBP ≌△DEQ ∴EQ BP =∴t t =-25 ∴35=t（4）设N （2-，n ），①当四边形ECMN 是平行四边形∴M （6-，3+n ） ∴16)6(316)6(3432=-⨯+-⨯=+n ∴1M (6-,16)②若四边形ECNM 为平行四边形 ∴2M (2,16) ③若四边形EMCN 为平行四边形 ∴3M （2-，316-）3. 在直角梯形OABC 中，CB ∥OA ,︒=∠90COA ，3=CB ，6=OA ，53=BA ,分别以OA 、OC 边所在的直线为x 轴、y 轴建立直角坐标系．（1）求点B 的坐标；（2）已知D 、E 分别为线段OC 、OB 上的点，5=OD ，EB OE 2=,直线DE 交x 轴于点F ，求直线DE 的解析式；（3）若点M 是（2）中直线DE 上的一个动点，在x 轴上方的平面内是否存在另一点N ，使以O 、D 、M 、N 为顶点的四边形是菱形？若存在，请求出点N 的坐标；若不存在，请说明理由．解：（1）作x BH ⊥轴于点H ，则四边形OHBC 为矩形，∴3==CB OH ∴3=-=OH OA AH ∴622=-=AH BA BH ∴点B 的坐标为（3，6）（2）作x EG ⊥轴于点G ，则EG ∥BH ∴△OEG ∽△OBH ∴BHEGOH OG OB OE == 又EB OE 2= ∴32=OB OE ∴6332EG OG == ∴2=OG ，4=EG ∴点E 的坐标为（2，4） 又D 点坐标为（0，5） ∴直线DE 的解析式为：521+-=x y （3）存在①如图，当5====NO MN DM OD 时，四边形ODMN 为菱形，作MP ∥x 轴 ∴△MPD ∽△FOD ∴FDMDOD PD OF MP == 又F 点坐标为（10，0） ∴10=OF ∴55=FD ∴555510==PD MP ∴52=MP ，5=PD ∴M 点坐标为（52-,55+）∴N 点坐标为（52-，5）②如图，当5====MO NM DN OD 时，四边形ODNM 为菱形，延长NM 交x 轴于点P ，则x MP ⊥轴。

2020年中考数学压轴题专项训练——特殊的平行四边形1．已知四边形ABCD是正方形，点E是边BC上的任意一点，AE⊥EF，且直线EF交正方形外角的平分线CF于点F．（1）如图1，求证：AE＝EF；（2）如图2，当AB＝2，点E是边BC的中点时，请直接写出FC的长．2．如图，矩形ABCD中，E是AD的中点，延长CE，BA交于点F，连接AC，DF．（1）判断四边形ACDF的形状；（2）当BC＝2CD时，求证：CF平分∠BCD．3．在菱形A BCD中，∠ABC＝60°，延长BA至点F，延长CB至点E，使BE＝AF，连结CF，EA，AC，延长EA交CF于点G．（1）求证：△ACE≌△CBF；（2）求∠CGE的度数．4．如图，△ABC中，AD是角平分线，DE∥AC交AB于点E，DF∥AB交AC于点F．（1）试判断四边形AEDF的形状．（2）当△ABC满足条件时，EF∥BC；当△ABC满足条件时，EF＝AD．5．如图正方形ABCD，E、F分别为BC、CD边上一点．（1）若∠EAF＝45°，求证：EF＝BE+DF；（2）若该正方形ABCD的边长为1，如果△CEF的周长为2．求∠EAF的度数．6．一个六边形的花坛被分割成7个部分，其中四边形PRBA，RQDC，QPFE为正方形．记正方形PRBA，RQDC，QPFE的面积分别为S1，S2，S3，RH⊥PQ，垂足为H．（友情提示：正方形的四个内角都等于90度，四边都相等）（1）若PR⊥QR，S1＝16，S2＝9，则S3＝，RH＝；（2）若四边形PRBA，RQDC，QPFE的面积分别为25m2、13m2、36m2①求△PRQ的面积；②请判断△PRQ和△DEQ的面积的数量关系，并证明你的结论；③六边形花坛ABCDEF的面积是m2．7．已知，如图所示，正方形ABCD的边长为1，G为CD边上的一个动点（点G与C、D 不重合），以CG为一边向正方形ABCD外作正方形GCEF，连接DE交BG的延长线于点H．（1）求证：①△BCG≌△DCE．②BH⊥DE．（2）当BH平分DE时，求GC的长．8．如图，过矩形ABCD的对角线AC的中点O做EF⊥AC，交BC边于点E，交AD边于点F，分别连接AE、CF．（1）求证：四边形AECF是菱形；（2）若AB＝，∠DCF＝30°，求EF的长．9．已知：如图，在平行四边形ABCD中，G、H分别是AD、BC的中点，E、O、F分别是对角线BD上的四等分点，顺次连接G、E、H、F．（1）求证：四边形GEHF是平行四边形；（2）当平行四边形ABCD满足条件时，四边形GEHF是菱形；（3）若BD＝2AB，探究四边形GEHF的形状，并说明理由．10．如图，平行四边形ABCD中，G是CD的中点，E是边AD上的动点，EG的延长线与BC的延长线交于点F，连结C E，DF．（1）求证：四边形CEDF为平行四边形；（2）若AB＝6cm，BC＝10cm，∠B＝60°，①当AE＝cm时，四边形CEDF是矩形；②当AE＝cm时，四边形CEDF是菱形．11．如图，在四边形ABCD中，AD∥BC，AB＝8，AD＝16，BC＝22，∠ABC＝90°，点P 从点A出发，以每秒1单位的速度向点D运动，点Q从点C同时出发，以每秒v单位的速度向点B运动，其中一个动点到达终点时，另一个动点也随之停止运动，设运动时间为t秒．（1）当v＝3时，若以点P，Q和点A，B，C，D中的两个点为顶点的四边形为平行四边形，且线段PQ为平行四边形的一边，求t的值；（2）若以点P，Q和点A，B，C，D中的两个点为顶点的四边形为菱形，且线段PQ为菱形的一条对角线，请直接写出t的值．12．如图，在四边形ABCD中，AB∥CD，AC垂直平分BD，交BD于点F，延长DC到点E，使得CE＝DC，连接BE．（1）求证：四边形ABCD是菱形．（2）填空：①当∠ADC＝°时，四边形ACEB为菱形；②当∠ADC＝90°，BE＝4时，则DE＝．13．如图，在矩形ABCD中，M是BC上一点，EF垂直平分AM，分别交BC，AM，AD于点E，O，F，连接AE，MF．（1）求证：四边形AEMF是菱形；（2）若AB＝6，H为AB的中点，连接OH交AE于点P，OH+OA＝9，求△OPE的周长．14．在菱形ABCD中，P、Q分别是边BC、CD的中点，连接AP、AQ．（1）如图（1），求证：AP＝AQ；（2）如图（2），连接PQ、AC，在不添加任何辅助线的情况下，请直接写出图中所有的等腰三角形．15．如图，四边形ABCD为菱形，∠BCD＝60°，E为对角线AC上一点，且AE＝AB，F为CE的中点，接DF、BF，BG⊥BF与AC交于点G；（1）若AB＝2，求EF的长；（2）求证：CG﹣EF＝BG．参考答案1．（1）证明：如图1，在AB上截取BM＝BE，连接ME，∵∠B＝90°，∴∠BME＝∠BEM＝45°，∴∠AME＝135°＝∠ECF，∵AB＝BC，BM＝BE，∴AM＝EC，在△AME和△ECF中，∴△AME≌△ECF（ASA），∴AE＝EF；（2）解：取AB中点M，连接EM，∵AB＝BC，E为BC中点，M为AB中点，∴AM＝CE＝BE，∴∠BME＝∠BME＝45°，∴∠AME＝135°＝∠ECF，∵∠B＝90°，∴∠BAE+∠AEB＝90°，∵∠AEF＝90°，∴∠AEB+∠FEC＝90°，∴∠BAE＝∠FEC，在△AME和△ECF中，∴△AME≌△ECF（ASA），∴EM＝CF，∵AB＝2，点E是边BC的中点，∴BM＝BE＝1，∴CF＝ME＝．2．（1）解：四边形ACDF是平行四边形，理由如下：∵四边形ABCD是矩形，∴AB∥CD，∠BCD＝∠B＝90°，∴∠F AE＝∠CDE，∵E是AD的中点，∴AE＝DE，在△F AE和△CDE中，，∴△F AE≌△CDE（ASA），∴CD＝F A，又∵CD∥AF，∴四边形ACDF是平行四边形；（2）证明：∵BC＝2CD，AB＝CD，四边形ACDF是平行四边形，∴AF＝CD，BF＝BC，∴△BCF是等腰直角三角形，∴∠BCF＝45°，∴∠DCF＝45°，∴CF平分∠BCD．3．（1）证明：∵AB＝AC，∠ABC＝60°，∴△ABC是等边三角形，∴BC＝AC，∠ACB＝∠ABC，∵BE＝AF，∴BE+BC＝AF+AB，即CE＝BF，在△ACE和△CBF中，，∴△ACE≌△CBF（SAS）；（2）解：由（1）可知：△ABC是等边三角形，△ACE≌△CBF，∴∠E＝∠F，∵∠BAE＝∠F AG，∴∠E+∠BAE＝∠F+∠F AG，∴∠CGE＝∠ABC，∵∠ABC＝60°，∴∠CGE＝60°．4．解：（1）四边形AEDF是菱形；理由如下：∵DE∥AC交AB于点E，DF∥AB交AC于点F，∴四边形AEDF是平行四边形，∠EAD＝∠ADF，∵AD是△ABC的角平分线，∴∠EAD＝∠F AD，∴∠ADF＝∠F AD，∴F A＝FD，∴四边形AEDF是菱形；（2）当△ABC满足AB＝AC条件时，EF∥BC；当△ABC满足∠BAC＝90°条件时，EF ＝AD．理由如下：由（1）得：四边形AEDF是菱形，∴AD⊥EF，∵AB＝AC，AD是角平分线，∴AD⊥BC，∴EF∥BC；当∠ABC＝90°时，四边形AEDF是正方形，∴EF＝AD；故答案为：AB＝AC，∠BAC＝90°．5．（1）证明：如图，延长CD至E'，使DE'＝BE，连接AE'，∵四边形ABCD为正方形，∴AB＝AD＝CB＝CD，∠BAD＝∠B＝90°，∴∠ADE'＝90°＝∠ABE，在△ADE'和△ABE中，，∴△ADE'≌△ABE（SAS），∴AE'＝AE，∠DAE'＝∠BAE，∵∠EAF＝45°，∴∠DAF+∠B AE＝45°，∴∠DAF+∠DAE'＝∠E'AF＝45°＝∠EAF，在△E′AF和△EAF中，，∴△E′AF≌△EAF（SAS），∴E′F＝EF，∵E′F＝DE′+DF＝BE+DF，∴EF＝BE+DF；（2）延长CD至E'使DE'＝BE，连接AE'，由（1）知，△ADE'≌△ABE（SAS），∴AE'＝AE，∠DAE'＝BAE，设BE＝x，DF＝y，∵正方形ABCD的边长为1，∴CE＝1﹣x，CF＝1﹣y，∵△CEF的周长为2，∴CE+CF+EF＝2，∴1﹣x+1﹣y+EF＝2，∴EF＝x+y＝BE+DF＝DE'+DF＝E'F，在△E'AF和△EAF中，，∴△E'AF≌△EAF（SSS），∴∠E'AF＝∠EAF，∴∠DAE'+∠DAF＝∠BAE+∠DAF＝∠EAF，∵∠DAF+∠EAF+∠BAE＝90°，∴∠EAF＝45°．6．解：（1）∵PR⊥QR，∴∠PRQ＝90°，∴PR2+RQ2＝PQ2，∵S1＝16，S2＝9，∴S3＝16+9＝25，∴PR＝4，RQ＝3，PQ＝5，∵RH⊥PQ，∴PR•RQ＝PQ•RH，∴RH＝＝，故答案为：25，2.4；（2）①设PH＝a，则QH＝6﹣a，∵RH2＝PR2﹣PH2＝RQ2﹣HQ2，∴25﹣a2＝13﹣（6﹣a）2，解得：a＝4，∴RH2＝PR2﹣PH2＝25﹣16＝9，∴RH ＝3，∴S △PQR ＝×6×3＝9；②S △PRQ ＝S △DQE ，证明：延长RQ 到点M ，使QM ＝RQ ，连结PM ，∵QD ＝QM ，∠DQE ＝∠MQP ，QE ＝QP∴△DQE ≌△MQP （SAS ），∴S △DQE ＝S △MQP ，∵RQ ＝QM ，∴S △PRQ ＝S △MQP ，∴S △PRQ ＝S △DQE ；③六边形花坛ABCDEF 的面积＝25+13+36+4×9＝74+36＝110m 2． 故答案为：110．7．（1）证明：∵正方形ABCD ，∴∠BCD ＝90°，BC ＝CD ，同理：CG ＝CE ，∠GCE ＝90°，∴∠BCD ＝∠GCE ＝90°，，∴△BCG ≌△DCE （SAS ），∴∠GBC＝∠CDE，在Rt△DCE中∠CDE+∠CED＝90°，∴∠GBC+∠BEH＝90°，∴∠BHE＝180°﹣（∠GBC+∠BHE）＝90°，∴BH⊥DE；（2）若BH垂直平分DE，连接BD，∴BD＝BE，∵BD＝，∴CG＝CE＝BE﹣BC＝﹣1．8．解：（1）证明：∵O是AC的中点，且EF⊥AC，∴AF＝CF，AE＝CE，OA＝OC，∵四边形ABCD是矩形，∴AD∥BC，∴∠AFO＝∠CEO，在△AOF和△COE中，，∴△AOF≌△COE（AAS），∴AF＝CE，∴AF＝CF＝CE＝AE，∴四边形AECF是菱形；（2）∵四边形ABCD是矩形，∴CD＝AB＝，在Rt△CDF中，cos∠DCF＝，∠DCF＝30°，∴CF＝＝2，∵四边形AECF是菱形，∴CE＝CF＝2．9．（1）证明：连接AC，如图1所示：∵四边形ABCD是平行四边形，∴OA＝OC，OB＝OD，∴BD的中点在AC上，∵E、O、F分别是对角线BD上的四等分点，∴E、F分别为OB、OD的中点，∵G是AD的中点，∴GF为△AOD的中位线，∴GF∥OA，GF＝OA，同理：EH∥OC，EH＝OC，∴EH＝GF，EH∥GF，∴四边形GEHF是平行四边形；（2）解：当▱ABCD满足AB⊥BD条件时，四边形GEHF是菱形；理由如下：连接GH，如图2所示：则AG＝BH，AG∥BH，∴四边形ABHG是平行四边形，∴AB∥GH，∵AB⊥BD，∴GH⊥BD，∴GH⊥EF，∴四边形GEHF是菱形；故答案为：AB⊥BD；（3）解：四边形GEHF是矩形；理由如下：由（2）得：四边形GEHF是平行四边形，∴GH＝AB，∵BD＝2AB，∴AB＝BD＝EF，∴GH＝EF，∴四边形GEHF是矩形．10．（1）证明：∵四边形ABCD是平行四边形，∴CF∥ED，∴∠FCD＝∠GCD，∵G是CD的中点，∴CG＝DG，在△FCG和△EDG中，∴△CFG≌△EDG（ASA），∴FG＝EG，∴四边形CEDF是平行四边形；（2）①解：当AE＝7时，平行四边形CEDF是矩形，理由是：过A作AM⊥BC于M，∵∠B＝60°，AB＝6，∴BM＝3，∵四边形ABCD是平行四边形，∴∠CDA＝∠B＝60°，DC＝AB＝6，BC＝AD＝10，∵AE＝7，∴DE＝3＝BM，在△MBA和△EDC中，，∴△MBA≌△EDC（SAS），∴∠CED＝∠AMB＝90°，∵四边形CEDF是平行四边形，∴四边形CEDF是矩形，故答案为：7；②当AE＝4时，四边形CEDF是菱形，理由是：∵AD＝10，AE＝4，∴DE＝6，∵CD＝6，∠CDE＝60°，∴△CDE是等边三角形，∴CE＝DE，∵四边形CEDF是平行四边形，∴四边形CEDF是菱形，故答案为：4．11．解：（1）∵当P、Q两点与A、B两点构成的四边形是平行四边形时，∵AP∥BQ，∴当AP＝BQ时，四边形APQB为平行四边形．此时，t＝22﹣3t，t＝．当P、Q两点与C、D两点构成的四边形是平行四边形时，∵PD∥QC，∴当PD＝QC时，四边形PQCD为平行四边形．此时，16﹣t＝3t，t＝4，∵线段PQ为平行四边形的一边，故当t＝或4时，线段PQ为平行四边形的一边．（2）当PD＝BQ＝BP时，四边形PBQD能成为菱形．由PD＝BQ，得16﹣t＝22﹣3t，解得t＝3，当t＝3时，PD＝BQ＝13，AP＝AD﹣PD＝16﹣13＝3．在Rt△ABP中，AB＝8，根据勾股定理得，BP═≠13∴四边形PBQD不能成为菱形；如果Q点的速度改变为vcm/s时，能够使四边形PBQD在时刻ts为菱形，由题意得，，解得，．故点Q的速度为2cm/s时，能够使四边形PBQD在t＝6时为菱形．12．（1）证明：∵AC垂直平分BD，∴AB＝AD，BF＝DF，∵AB∥CD，∴∠ABD＝∠CD B．∵∠AFB＝∠CFD，∴△AFB≌△CFD（ASA），∴AB＝CD．又∵AB∥CD，∴四边形ABCD是平行四边形，∵AB＝AD，∴平行四边形ABCD是菱形；（2）①当∠ADC＝60°，四边形ACEB为菱形，∵∠ADC＝60°，∴∠BCE＝60°，∴△BCE是等边三角形，∴CE＝BE，∴四边形ACEB为菱形，故答案为：60；②当∠ADC＝90°，BE＝4时，DE＝4，故答案为：4．13．（1）证明：∵EF垂直平分AM，∴AE＝EM，OA＝OM．∵四边形ABCD是矩形，∴AD∥BC．∴∠AFO＝∠MEO，在△OF和△MOE中，，∴△AOF≌△MOE（AAS）．∴OF＝OE．∴四边形AEMF是平行四边形．∵AE＝EM．∴四边形AEMF是菱形；（2）解：∵O、H分别为AM、AB的中点，∴BM＝2OH，AM＝2OA，∴AM+BM＝2OA+2OH＝18．设BM＝x，则AM＝18﹣x，在Rt△ABM中，由勾股定理得：62+x2＝（18﹣x）2，解得：x＝8，∴BM＝8，AM＝10．∴OA＝AM＝5，设EM＝m，则BE＝8﹣m，AE＝EM＝m，在Rt△ABE中，由勾股定理得：62+（8﹣m）2＝m2，解得：m＝，∴AE＝EM＝在Rt△AOE中，EO＝＝＝．∵OP∥EM，∴＝＝1，∴AP＝PE，∴OP＝EM＝，∵PE＝AE＝，∴△OPE的周长＝EO+PE+OP＝++＝10．14．证明：（1）∵四边形ABCD是菱形，∴AB＝BC＝CD＝AD，∠B＝∠D，∵P、Q分别是边BC、CD的中点，∴BP＝CQ，在△ABP和△ADQ中，，∴△ABP≌△ADQ（SAS），∴AP＝AQ，（2）∵AP＝AQ，∴△APQ是等腰三角形，∵BC＝CD，∵P、Q分别是边BC、CD的中点，∴PC＝CQ，∴△PQC是等腰三角形，∵AB＝BC，AD＝CD，∴△ABC，△ACD是等腰三角形，∴图中所有的等腰三角形有△ABC，△APQ，△ACD，△CPQ．15．（1）解：连接BD交AC于O，如图所示：∵四边形ABCD是菱形，∴∠BAD＝∠BCD＝60°，AC⊥BD，OB＝OD，OA＝OC，∠OAB＝∠BAD＝30°，∴OB＝AB＝1，OA＝OB＝，∴AC＝2OA＝2，∵AE＝AB＝2，∴CE＝AC﹣AE＝2﹣2，∵F为CE的中点，∴EF＝CE＝﹣1；（2）证明：设AB＝2a，同（1）得：OB＝AB＝a，OA＝OB＝a，∴AC＝2OA＝2a，∵AE＝AB＝2a，∴CE＝AC﹣AE＝（2﹣2）a，OE＝AE﹣OA＝（2﹣）a，∵F为CE的中点，∴EF＝CE＝（﹣1）a，∴OF＝OE+EF＝（2﹣）a+（﹣1）a＝a，∴OB＝OF，∵AC⊥BD，∴△BOF是等腰直角三角形，∴∠BFG＝45°，∵BG⊥BF，∴△BFG是等腰直角三角形，∴GF＝BG，∵GF＝CG﹣CF＝CG﹣EF，∴CG﹣EF＝BG．。

中考数学压轴题专项训练：四边形存在问题一、解答题1(2023·西藏·中考真题)在平面直角坐标系中，抛物线y=-x2+bx+c与x轴交于A-3,0，B1,0两点，与y轴交于点C．(1)求抛物线的解析式；(2)如图甲，在y轴上找一点D，使△ACD为等腰三角形，请直接写出点D的坐标；(3)如图乙，点P为抛物线对称轴上一点，是否存在P、Q两点使以点A，C，P，Q为顶点的四边形是菱形？若存在，求出P、Q两点的坐标，若不存在，请说明理由．2(2023·山东枣庄·中考真题)如图，抛物线y=-x2+bx+c经过A(-1,0),C(0,3)两点，并交x轴于另一点B，点M是抛物线的顶点，直线AM与轴交于点D．(1)求该抛物线的表达式；(2)若点H是x轴上一动点，分别连接MH，DH，求MH+DH的最小值；(3)若点P是抛物线上一动点，问在对称轴上是否存在点Q，使得以D，M，P，Q为顶点的四边形是平行四边形？若存在，请直接写出所有满足条件的点Q的坐标；若不存在，请说明理由．3(2022·辽宁朝阳·中考真题)如图，在平面直角坐标系中，抛物线y=ax2+2x+c与x轴分别交于点A (1，0)和点B，与y轴交于点C(0，-3)，连接BC．(1)求抛物线的解析式及点B的坐标．(2)如图，点P为线段BC上的一个动点(点P不与点B，C重合)，过点P作y轴的平行线交抛物线于点Q，求线段PQ长度的最大值．(3)动点P以每秒2个单位长度的速度在线段BC上由点C向点B运动，同时动点M以每秒1个单位长度的速度在线段BO上由点B向点O运动，在平面内是否存在点N，使得以点P，M，B，N为顶点的四边形是菱形？若存在，请直接写出符合条件的点N的坐标；若不存在，请说明理由．4(2022·山东烟台·中考真题)如图，已知直线y=43x+4与x轴交于点A，与y轴交于点C，抛物线y=ax2+bx+c经过A，C两点，且与x轴的另一个交点为B，对称轴为直线x=-1．(1)求抛物线的表达式；(2)D是第二象限内抛物线上的动点，设点D的横坐标为m，求四边形ABCD面积S的最大值及此时D点的坐标；(3)若点P在抛物线对称轴上，是否存在点P，Q，使以点A，C，P，Q为顶点的四边形是以AC为对角线的菱形？若存在，请求出P，Q两点的坐标；若不存在，请说明理由．5(2022·湖北随州·中考真题)如图1，平面直角坐标系xOy中，抛物线y=ax2+bx+c+a<0与x轴分则点A和点B1,0，与y轴交于点C，对称轴为直线x=-1，且OA=OC，P为抛物线上一动点．(1)直接写出抛物线的解析式；(2)如图2，连接AC，当点P在直线AC上方时，求四边形PABC面积的最大值，并求出此时P点的坐标；(3)设M为抛物线对称轴上一动点，当P，M运动时，在坐标轴上是否存在点N，使四边形PMCN为矩形？若存在，直接写出点P及其对应点N的坐标；若不存在，请说明理由．6(2021·内蒙古鄂尔多斯·中考真题)如图，抛物线y=x2+2x-8与x轴交于A，B两点(点A在点B左侧)，与y轴交于点C．(1)求A，B，C三点的坐标；(2)连接AC，直线x=m-4<m<0与该抛物线交于点E，与AC交于点D，连接OD．当OD⊥AC时，求线段DE的长；(3)点M在y轴上，点N在直线AC上，点P为抛物线对称轴上一点，是否存在点M，使得以C、M、N、P为顶点的四边形是菱形？若存在，请直接写出点M的坐标；若不存在，请说明理由．7(2021·四川凉山·中考真题)如图，抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点，与y轴交于C点，AC=10，OB=OC=3OA．(1)求抛物线的解析式；(2)在第二象限内的抛物线上确定一点P，使四边形PBAC的面积最大．求出点P的坐标；(3)在(2)的结论下，点M为x轴上一动点，抛物线上是否存在一点Q．使点P、B、M、Q为顶点的四边形是平行四边形，若存在．请直接写出Q点的坐标；若不存在，请说明理由．8(2023·湖南岳阳·中考真题)已知抛物线Q1:y=-x2+bx+c与x轴交于A-3,0,B两点，交y轴于点C0,3．(1)请求出抛物线Q1的表达式．(2)如图1，在y轴上有一点D0,-1，点E在抛物线Q1上，点F为坐标平面内一点，是否存在点E,F使得四边形DAEF为正方形？若存在，请求出点E,F的坐标；若不存在，请说明理由．(3)如图2，将抛物线Q1向右平移2个单位，得到抛物线Q2，抛物线Q2的顶点为K，与x轴正半轴交于点H，抛物线Q1上是否存在点P，使得∠CPK=∠CHK？若存在，请求出点P的坐标；若不存在，请说明理由．9(2022·四川泸州·中考真题)如图，在平面直角坐标系xOy中，已知抛物线y=ax2+x+c经过A-2,0两点，直线x=3与x轴交于点C．，B0,4(1)求a，c的值；(2)经过点O的直线分别与线段AB，直线x=3交于点D，E，且△BDO与△OCE的面积相等，求直线DE 的解析式；(3)P是抛物线上位于第一象限的一个动点，在线段OC和直线x=3上是否分别存在点F，G，使B，F，G，P为顶点的四边形是以BF为一边的矩形？若存在，求出点F的坐标；若不存在，请说明理由．中考数学压轴题专项训练：四边形存在问题一、解答题1(2023·西藏·中考真题)在平面直角坐标系中，抛物线y =-x 2+bx +c 与x 轴交于A -3,0 ，B 1,0 两点，与y 轴交于点C ．(1)求抛物线的解析式；(2)如图甲，在y 轴上找一点D ，使△ACD 为等腰三角形，请直接写出点D 的坐标；(3)如图乙，点P 为抛物线对称轴上一点，是否存在P 、Q 两点使以点A ，C ，P ，Q 为顶点的四边形是菱形？若存在，求出P 、Q 两点的坐标，若不存在，请说明理由．【答案】1．(1)y =-x 2-2x +3；(2)0，0 或0，-3 或0，3-32 或0，3+32 ；(3)存在，P -1，3-17 ，Q -4，-17 或P -1，3+17 ，Q -4，17 或P -1，1 ，Q -2，2 或P -1，14 ，Q 2，3+14 或P -1,-14 ，Q 2，3-14【分析】(1)将A -3,0 ，B 1,0 代入y =-x 2+bx +c ，求出b ,c ,即可得出答案；(2)分别以点D 为顶点、以点A 为顶点、当以点C 为顶点，计算即可；(3)抛物线y =-x 2-2x +3的对称轴为直线x =-1，设P -1,t ，Q m ,n ，求出AC 2=18，AP 2=t 2+4，PC 2=t 2-6t +10，分三种情况：以AP 为对角线或以AC 为对角线或以CP 为对角线．【详解】(1)解：(1)∵A -3,0 ，B 1,0 两点在抛物线上，∴0=--3 2-3b +c 0=-12+b +c解得，b =-2c =3 ，∴抛物线的解析式为：y =-x 2-2x +3；(2)令x =0，y =3，∴C 0，3 ，由△ACD 为等腰三角形，如图甲，当以点D 为顶点时，DA =DC ，点D 与原点O 重合，∴D 0，0 ；当以点A 为顶点时，AC =AD ，AO 是等腰△ACD 中线，∴OC =OD ，∴D 0，-3 ；当以点C 为顶点时，AC =CD =OA 2+OC 2=32+32=32∴点D 的纵坐标为3-32或32+3，∴综上所述，点D 的坐标为0，0 或0，-3 或0，3-32 或0，3+32 ．(3)存在，理由如下：抛物线y =-x 2-2x +3的对称轴为：直线x =-1，设P -1,t ，Q m ,n ，∵A -3，0 ，C 0，3 ，则AC 2=-3 2+32=18，AP 2=-1+3 2+t 2=t 2+4，PC 2=-1 2+t -3 2=t 2-6t +10，∵以A 、C 、P 、Q 为顶点的四边形是菱形，∴分三种情况：以AP 为对角线或以AC 为对角线或以CP 为对角线，当以AP 为对角线时，则CP =CA ，如图1，∴t 2-6t +10=18，解得：t =3±17，∴P 1-1，3-17 或P 2-1，3+17∵四边形ACPQ 是菱形，∴AP 与CQ 互相垂直平分，即AP 与CQ 的中点重合，当P 1-1，3-17 时，∴m +02=-3-12，n +32=0+3-172，解得：m =-4,n =-17，∴Q 1-4，-17当P 2-1，3+17 时，∴m +02=-3-12，n +32=0+3+172，解得：m =-4,n =17，∴Q 2-4，17以AC 为对角线时，则PC =AP ，如图2，∴t 2-6t +10=t 2+4，解得：t =1，∴P 3-1，1 ，∵四边形APCQ 是菱形，∴AC 与PQ 互相垂直平分，即AC 与CQ 中点重合，∴m -12=-3+02，n +12=0+32，解得：m =-2,n =2，∴Q 3-2，2 ；当以CP 为对角线时，则AP =AC ，如图3，∴t 2+4=18，解得：t =±14，∴P 4-1,14 ,P 5-1,-14 ，∵四边形ACQP 是菱形，∴AQ 与CP 互相垂直平分，即AQ 与CP 的中点重合，∴-3+m 2=0-12,n +02=3±142，解得：m =2,n =3±14∴Q 42,3+14 ,Q 52,3-14 ，综上所述，符合条件的点P 、Q 的坐标为：P -1，3-17 ，Q -4，-17 或P -1，3+17 ，Q -4，17 或P -1，1 ，Q -2，2 或P -1，14 ，Q 2，3+14 或P -1,-14 ，Q 2，3-14【点睛】本题是二次函数综合题，考查了解析式的求法、等腰三角形的判定、菱形的性质、坐标与图形的性质、分类讨论等知识，熟练掌握菱形的性质和坐标与图形的性质是解题的关键．2(2023·山东枣庄·中考真题)如图，抛物线y =-x 2+bx +c 经过A (-1,0),C (0,3)两点，并交x 轴于另一点B ，点M 是抛物线的顶点，直线AM 与轴交于点D ．(1)求该抛物线的表达式；(2)若点H 是x 轴上一动点，分别连接MH ，DH ，求MH +DH 的最小值；(3)若点P 是抛物线上一动点，问在对称轴上是否存在点Q ，使得以D ，M ，P ，Q 为顶点的四边形是平行四边形？若存在，请直接写出所有满足条件的点Q 的坐标；若不存在，请说明理由．【答案】(1)y =-x 2+2x +3(2)37(3)存在，Q 1,3 或Q 1,1 或Q 1,5【分析】(1)待定系数法求出函数解析式即可；(2)作点D 关于x 轴的对称点D ，连接D M ，D M 与x 轴的交点即为点H ，进而得到MH +DH 的最小值为D M 的长，利用两点间距离公式进行求解即可；(3)分DM ，DP ，MP 分别为对角线，三种情况进行讨论求解即可．【详解】(1)解：∵抛物线y =-x 2+bx +c 经过A (-1,0),C (0,3)两点，∴-1-b +c =0c =3 ，解得：b =2c =3 ，∴y =-x 2+2x +3；(2)∵y =-x 2+2x +3=-x -1 2+4，∴M 1,4 ，设直线AM :y =kx +m (k ≠0)，则：-k +m =0k +m =4 ，解得：k =2m =2 ，∴AM :y =2x +2，当x =0时，y =2，∴D 0,2 ；作点D 关于x 轴的对称点D ，连接D M ，则：D 0,-2 ，MH +DH =MH +D H ≥D M ，∴当M ,H ,D 三点共线时，MH +DH 有最小值为D M 的长，∵D 0,-2 ，M 1,4 ，∴D M =12+4+2 2=37，即：MH +DH 的最小值为：37；(3)解：存在；∵y =-x 2+2x +3=-x -1 2+4，∴对称轴为直线x =1，设P p ,t ，Q 1,n ，当以D ，M ，P ，Q 为顶点的四边形是平行四边形时：①DM 为对角线时：1+p =0+1t +n =4+2 ，∴p =0t +n =6 ，当p =0时，t =3，∴n =3，∴Q 1,3 ；②当DP 为对角线时：0+p =1+12+t =4+n ，∴p =22+t =4+n ，当p =2时，t =-22+2×2+3=3，∴n =1，∴Q 1,1 ；③当MP 为对角线时：1+p =0+14+t =2+n ，∴p =0n -t =2 ，当p =0时，t =3，∴n =5，∴Q 1,5 ；综上：当以D ，M ，P ，Q 为顶点的四边形是平行四边形时，Q 1,3 或Q 1,1 或Q 1,5 ．【点睛】本题考查二次函数的综合应用，是中考常见的压轴题．正确的求出函数解析式，熟练掌握二次函数的性质，利用数形结合和分类讨论的思想进行求解，是解题的关键．3(2022·辽宁朝阳·中考真题)如图，在平面直角坐标系中，抛物线y =ax 2+2x +c 与x 轴分别交于点A (1，0)和点B ，与y 轴交于点C (0，-3)，连接BC ．(1)求抛物线的解析式及点B 的坐标．(2)如图，点P 为线段BC 上的一个动点(点P 不与点B ，C 重合)，过点P 作y 轴的平行线交抛物线于点Q ，求线段PQ 长度的最大值．(3)动点P 以每秒2个单位长度的速度在线段BC 上由点C 向点B 运动，同时动点M 以每秒1个单位长度的速度在线段BO 上由点B 向点O 运动，在平面内是否存在点N ，使得以点P ，M ，B ，N 为顶点的四边形是菱形？若存在，请直接写出符合条件的点N 的坐标；若不存在，请说明理由．【答案】(1)y =x 2+2x -3，(-3，0)(2)94(3)-3,-32或(-2，1)或0,3-32 【分析】(1)将A ，C 两点坐标代入抛物线的解析式求得a ，c 的值，进而得出解析式，当y =0时，求出方程的解，进而求得B 点坐标；(2)由B ，C 两点求出BC 的解析式，进而设出点P 和点Q 坐标，表示出PQ 的长，进一步得出结果；(3)要使以点P ，M ，B ，N 为顶点的四边形是菱形，只需△PMB 是等腰三角形，所以分为PM =BM ，PM =PB 和BP =BM ，结合图象，进一步得出结果．【详解】(1)解：把点A (1，0)，C (0，-3)代入y =ax 2+2x +c 得：c =-3a +2×1+c =0 ，解得：c =-3a =1 ，∴抛物线解析式为y =x 2+2x -3；令y =0，则x 2+2x -3=0，解得：x 1=1,x 2=-3，∴点B 的坐标为(-3，0)；(2)解：设直线BC 的解析式为y =kx +b k ≠0 ，把点B (-3，0)，C (0，-3)代入得：b =-3-3k +b =0 ，解得：k =-1b =-3 ，∴直线BC 的解析式为y =-x -3，设点P m ,-m +3 ，则Q m ,m 2+2m -3 ，∴PQ =-m -3 -m 2+2m -3 =-m 2-3m =-m +32 2+94，∴当m =-32时，PQ 最大，最大值为94；(3)解：存在，根据题意得：PC =2t ,BM =t ，则PB =32-2t ，如图，当BM =PM 时，∵B (-3，0)，C (0，-3)，∴OB =OC =3，∴∠OCB =∠OBC =45°，延长NP 交y 轴于点D ，∵点P ，M ，B ，N 为顶点的四边形是菱形，∴PN ∥x 轴，BN ∥PM ，即DN ⊥y 轴，∴△CDP 为等腰直角三角形，∴CD =PD =PC ⋅sin ∠OCB =2t ×22=t ，∵BM =PM ，∴∠MPB =∠OBC =45°，∴∠PMO =∠PDO =∠MOD =90°，∴四边形OMPD 是矩形，∴OM =PD =t ，MP ⊥x 轴，∴BN ⊥x 轴，∵BM +OM =OB ，∴t +t =3，解得t =32，∴P -32,-32 ，∴N -3,-32 ；如图，当PM =PB 时，作PD ⊥y 轴于D ，连接PN ，∵点P ，M ，B ，N 为顶点的四边形是菱形，∴PN ⊥BM ，NE =PE ，∴BM =2BE ，∴∠OEP =∠DOE =∠ODP =90°，∴四边形PDOE 是矩形，∴OE =PD =t ，∴BE =3-t ，∴t =2(3-t )，解得：t =2，∴P (-2，-1)，∴N (-2，1)；如图，当PB =MB 时，32-2t =t ，解得：t =6-32，∴PN =BP =BM =6-32，过点P 作PE ⊥x 轴于点E ，∴PE ⊥PM ，∴∠EON =∠OEP =∠EPN =90°，∴四边形OEPN 为矩形，∴PN =OE ，PN ⊥y 轴，∵∠OBC =45°，∴BE =PE =PB ⋅sin ∠OBC =6-32 ×22=32-3，∴OE =OB -BE =3-32-3 =6-32，∴点N 在y 轴上，∴N 0,3-32 ，综上所述，点N 的坐标为-3,-32或(-2，1)或0,3-32 ．【点睛】本题考查了二次函数及其图象的性质，用待定系数法求一次函数的解析式，等腰三角形的分类和等腰三角形的性质，菱形的性质等知识，解决问题的关键是正确分类，画出符合条件的图形．4(2022·山东烟台·中考真题)如图，已知直线y =43x +4与x 轴交于点A ，与y 轴交于点C ，抛物线y =ax 2+bx +c 经过A ，C 两点，且与x 轴的另一个交点为B ，对称轴为直线x =-1．(1)求抛物线的表达式；(2)D 是第二象限内抛物线上的动点，设点D 的横坐标为m ，求四边形ABCD 面积S 的最大值及此时D 点的坐标；(3)若点P 在抛物线对称轴上，是否存在点P ，Q ，使以点A ，C ，P ，Q 为顶点的四边形是以AC 为对角线的菱形？若存在，请求出P ，Q 两点的坐标；若不存在，请说明理由．【答案】(1)y =-43x 2-83x +4(2)S 最大=252，D -32，5(3)存在，Q -2，198【分析】(1)先求得A ，C ，B 三点的坐标，将抛物线设为交点式，进一步求得结果；(2)作DF ⊥AB 于F ，交AC 于E ，根据点D 和点E 坐标可表示出DE 的长，进而表示出三角形ADC 的面积，进而表示出S 的函数关系式，进一步求得结果；(3)根据菱形性质可得PA =PC ，进而求得点P 的坐标，根据菱形性质，进一步求得点Q 坐标．【详解】(1)解：当x =0时，y =4，∴C (0，4)，当y =0时，43x +4=0，∴x =-3，∴A (-3，0)，∵对称轴为直线x =-1，∴B (1，0)，∴设抛物线的表达式：y =a (x -1)•(x +3)，∴4=-3a ，∴a =-43，∴抛物线的表达式为：y =-43(x -1)•(x +3)=-43x 2-83x +4；(2)如图1，作DF ⊥AB 于F ，交AC 于E ，∴D m ，-43m 2-83m +4 ，E m ，43m +4 ，∴DE =-43m 2-83m +4-43m +4 =-43m 2-4m ，∴S △ADC =12DE ⋅OA =32•-43m 2-4m =-2m 2-6m ，∵S △ABC =12AB ⋅OC =12×4×4=8，∴S =-2m 2-6m +8=-2m +32 2+252，∴当m =-32时，S 最大=252，当m =-32时，y =-43×-32-1 ×-32+3 =5，∴D -32，5；(3)设P (-1，n )，∵以A ，C ，P ，Q 为顶点的四边形是以AC 为对角线的菱形，∴PA =PC ，即：PA 2=PC 2，∴(-1+3)2+n 2=1+(n -4)2，∴n =138，∴P -1，138，∵x P +x Q =x A +x C ，y P +y Q =y A +y C∴x Q =-3-(-1)=-2，y Q =4-138=198，∴Q -2，198．【点睛】本题考查了二次函数及其图象性质，勾股定理，菱形性质等知识，解决问题的关键是熟练掌握相关二次函数和菱形性质5(2022·湖北随州·中考真题)如图1，平面直角坐标系xOy 中，抛物线y =ax 2+bx +c +a <0 与x 轴分则点A 和点B 1,0 ，与y 轴交于点C ，对称轴为直线x =-1，且OA =OC ，P 为抛物线上一动点．(1)直接写出抛物线的解析式；(2)如图2，连接AC ，当点P 在直线AC 上方时，求四边形PABC 面积的最大值，并求出此时P 点的坐标；(3)设M 为抛物线对称轴上一动点，当P ，M 运动时，在坐标轴上是否存在点N ，使四边形PMCN 为矩形？若存在，直接写出点P 及其对应点N 的坐标；若不存在，请说明理由．【答案】(1)y =-x 2-2x +3(2)S 最大=758，P 点的坐标为-32,154(3)存在，P 1-1,4 ，N 10,4 ；P 2-5-1456,145-118 ，N 21-1456,0 ；P 3-5+1456,-145-118，N 31+1456,0 【分析】(1)根据已知条件，列出方程组求出a ，b ，c 的值即可；(2)方法一：设P m ,n ，四边形PABC 的面积S =S ΔPAO +S ΔPCO +S ΔBCO ，用m 表示出S ，并求出S 的最大值与此时P 点的坐标；方法二：易知A -3,0 ，C 0,3 ，故直线AC 的方程为y =x +3，设P x ,-x 2-2x +3 -3<x <0 ，表示出PQ ，并用x 表示出△APC 的面积，再表示出S ，并求出S 的最大值与此时P 点的坐标；(3)根据题目要求，分类讨论当当N 在y 轴上时；当N 在x 轴负半轴上时，设N t ,0 ，用t 表示出点P 的坐标，解出t ，写出点P 及其对应点N 的坐标．【详解】(1)解：∵OA =OC ，∴C 0,c ，A -c ，0 ，∵B 1,0 ，对称轴为直线x =-1，c >0，∴0=a +b +c -b 2a =-10=ac 2+bc +c ，解得a =-1b =-2c =3，∴抛物线的解析式为：y =-x 2-2x +3．(2)解：方法一：连接OP ，设P m ,n ，易知-3<m <0，n >0，∵AO =CO =3，BO =1，∴四边形PABC 的面积S =S ΔPAO +S ΔPCO +S ΔBCO ，∴S =12×3n +12×3⋅-m +12×3×1=32n -m +1又∵n =-m 2-2m +3，∴S =32-m 2-3m +4 =-32m +32 2+758∴当m =-32时，S 最大=758，∴此时P 点的坐标为-32,154；方法二：易知A -3,0 ，C 0,3 ，故直线AC 的方程为y =x +3设P x ,-x 2-2x +3 -3<x <0 ，∵过点P 作PQ ⊥x 轴，交AC 于点Q ，∴O x ,x +3 ，∵点P 在AC 上方，∴PQ =-x 2-2x +3-x +3 =-x 2-3，∴S ΔAPC =S ΔPAQ +S ΔPCQ =12PQ x Q -x A +12PQ x C -x Q =12PQ x C -x A =32PQ =32-x 2-3x =-32x 2-92x ，∴四边形PABC 面积S =S ΔAPC +S ΔABC =-32x 2-92x +12×4×3=-32x 2-92x +6，∴当x =-32时，S 有最大值758，∴此时P 点的坐标为-32,154．(3)存在点N ．①当N 在y 轴上时，∵四边形PMCN 为矩形，此时，P 1-1,4 ，N 10,4 ；②当N 在x 轴负半轴上时，如图所示，四边形PMCN 为矩形，过M 作y轴的垂线，垂足为D ，过P 作x 轴的垂线，垂足为E ，设N t ,0 ，则ON =-t ，∴∠CDM =∠NEP =90°，∵四边形PMCN 为矩形，∴∠MCN =∠CNP =90°，CM =NP ，∵∠MCD +∠OCN =90°，∠ONC +∠OCN =90°，∴∠MCD =∠ONC ，又∵∠CDM =∠CON =90°，∴△CMD ∽△CNO ，∴CD ON =MD OC，又∵点M 在对称轴上，C 0,3 ，∴DM =1,OC =3，∴CD -t =13，即CD =-13t ，∵∠MCD +∠CMD =90°，∠ONC +∠PNE =90°，∴∠CMD =∠PNE ，∴△CMD ≌△NPE AAS ，∴NE =MD =1，EP =CD =-13t ，∴OE =ON +EN =-t +1，∴P 点的坐标为t -1,-13t ，∵P 点在抛物线y =-x 2-2x +3上，∴-13t =-t -1 2-2t -1 +3解得t 1=1-1456，t 2=1+1456(舍)，∴P 2-5-1456,145-118，N 21-1456,0 ；③当N 在x 轴正半轴上时，如图所示，四边形PMCN 为矩形，过M 作y 轴的垂线，垂足为D ，过P 作x 轴的垂线，垂足为E ，设N t ,0 ，则ON =t ，∴∠CDM =∠NEP =90°，∵四边形PMCN 为矩形时，∴∠MCN =∠CNP =90°，CM =NP ，∵∠MCD +∠OCN =90°，∠ONC +∠OCN =90°，∴∠MCD =∠ONC ，又∵∠CDM =∠CON =90°，∴△CMD ∽△CNO ，∴CD ON =MD OC，又∵点M 在对称轴上，C 0,3 ，∴DM =1,OC =3，∴CD t =13，即CD =13t ，∵∠MCD +∠CMD =90°，∠ONC +∠PNE =90°，∴∠CMD =∠PNE ，∴△CMD ≌△NPE AAS ，∴NE =MD =1，EP =CD =13t ，∴OE =ON -EN =t -1，∴P 点的坐标为t -1,-13t ，∵P 点在抛物线y =-x 2-2x +3上，∴-13t =-t -1 2-2t -1 +3解得t 1=1-1456(舍)，t 2=1+1456，∴P 3-5+1456,-145-118 ，N 31+1456,0 ，综上：P 1-1,4 ，N 10,4 ；P 2-5-1456,145-118 ，N 21-1456,0 ；P 3-5+1456,-145-118，N 31+1456,0【点睛】本题考查用待定系数法求二次函数、二次函数综合问题，矩形的性质与判定，二次函数图象上点的坐标特征等知识点的理解和掌握，综合运用这些性质进行计算是解此题的关键．6(2021·内蒙古鄂尔多斯·中考真题)如图，抛物线y =x 2+2x -8与x 轴交于A ，B 两点(点A 在点B 左侧)，与y 轴交于点C ．(1)求A ，B ，C 三点的坐标；(2)连接AC ，直线x =m -4<m <0 与该抛物线交于点E ，与AC 交于点D ，连接OD ．当OD ⊥AC 时，求线段DE 的长；(3)点M 在y 轴上，点N 在直线AC 上，点P 为抛物线对称轴上一点，是否存在点M ，使得以C 、M 、N 、P 为顶点的四边形是菱形？若存在，请直接写出点M 的坐标；若不存在，请说明理由．【答案】(1)A (-4,0)，B (2,0)，C (0，-8)；(2)DE =6425；(3)存在，M (0,-8+5)、(0,-8-5)、(0,-12)、0,-274【分析】(1)分别令x =0、y =0即可求出A ，B ，C 三点的坐标；(2)先求出AC 解析式，用m 表示出DE 坐标，最后根据OD ⊥AC 求出m 的值即可；(3)分三种情况：CM 对角线或CN 为对角线或CP 为对角线，①当CP 为对角线时，CM ⎳PN ，CM =PN =CN ，可得出N (-1,-6)，根据CM =PN =CN =5，即可求出答案；②当CN 为对角线时，CM ⎳PN ，CM =PN =CP ，设CM =a ，则M (0,-8+a )，P (-1,-6-a )，建立方程求解即可；③当CM 对角线时，PN 与CM 互相垂直平分，设P (-1,b )，则N (1,b )，M (0,2b +8)，根据N (1,b )在直线y =-2x -8上，即可求得答案．【详解】解：(1)令x =0得y =-8，∴C 点坐标(0，-8)令y =0得：x 2+2x -8=0，解得：x 1=-4,x 2=2，∴A (-4,0)，B (2,0)；(2)设DE 交x 轴于F ，设AC 解析式为y =kx +b ，代入AC 坐标得：0=-4k +b -8=b，解得k =-2b =-8∴AC 解析式为y =-2x -8，∵直线x =m -4<m <0 与该抛物线交于点E ，与AC 交于点D ，∴D (m ,-2m -8),E (m ,m 2+2m -8),F (m ,0)，∴OF =-m ,DF =2m +8,DE =-m 2-4m ，∵OD ⊥AC ，∴∠AOD =∠ACO ，∴△FOD ∼△OCA ，∴OFDF =OC OA ，∴-m 2m +8=84，解得m =-165，∴DE =-m 2-4m =6425；(3)存在，如图2，∵y =x 2+2x -8=(x +1)2-9，抛物线对称轴为直线x =-1，∵以C 、M 、N 、P 为顶点的四边形是菱形，∴分三种情况：CM 对角线或CN 为对角线或CP 为对角线，①当CP 为对角线时，CM ⎳PN ，CM =PN =CN ，∴N 点为直线AC 与抛物线对称轴的交点，即N (-1,-6)，CN =(-1-0)2+(-6+8)2=5，∴CM =PN =5，∴M 1(0,-8+5)，M 2(0,-8-5)；②当CN 为对角线时，CM ⎳PN ，CM =PN =CP ，设CM =a ，则M (0,-8+a )，P (-1,-6-a )，∴(-1-0)2+(-6-a +8)2=a 2，解得：a =54，∴M 30,-274，③当CM 对角线时，PN 与CM 互相垂直平分，设P (-1,b )，则N (1,b )，M (0,2b +8)，∵N (1,b )在直线y =-2x -8上，∴b =-2×1-8=-10，∴M 4(0,-12)，综上所述，点M 的坐标为：M 1(0,-8+5)，M 2(0,-8-5)，M 30,-274，M 4(0,-12)．【点睛】本题考查了二次函数的综合题：熟练掌握二次函数图象上点的坐标特征、二次函数的性质和菱形的性质；会利用相似三角形处理垂直．7(2021·四川凉山·中考真题)如图，抛物线y =ax 2+bx +c (a ≠0)与x 轴交于A 、B 两点，与y 轴交于C 点，AC =10，OB =OC =3OA ．(1)求抛物线的解析式；(2)在第二象限内的抛物线上确定一点P ，使四边形PBAC 的面积最大．求出点P 的坐标；(3)在(2)的结论下，点M 为x 轴上一动点，抛物线上是否存在一点Q ．使点P 、B 、M 、Q 为顶点的四边形是平行四边形，若存在．请直接写出Q 点的坐标；若不存在，请说明理由．【答案】(1)y =-x 2-2x +3；(2)P -32,154 ；(3)-12,154 或-2-312,-154 或-2+312,-154【分析】(1)根据OB =OC =3OA ，AC =10，利用勾股定理求出OA ，可得OB 和OC ，得到A ，B ，C 的坐标，利用待定系数法求出抛物线的解析式；(2)判断出四边形PBAC 的面积最大时，△BPC 的最大面积，过点P 作y 轴的平行线交BC 于点H ，求出直线BC 的表达式，设点P x ，-x 2-2x +3 ，利用三角形面积公式S △BPC =-32x 2-92x ，即可求出S △BPC 面积最大时点P 的坐标；(3)根据平行四边形的性质进行分类讨论，求出点Q 的坐标．【详解】解：(1)∵OB =OC =3OA ，AC =10，∴OC 2+OA 2=AC 2，即3OA 2+OA 2=10 2，解得：OA =1，OC =OB =3，∴A 1，0 ，B -3，0 ，C 0，3 ，代入y =ax 2+bx +c 中，则0=a +b +c 0=9a -3b +c 3=c ，解得：a =-1b =-2c =3，∴抛物线的解析式为y =-x 2-2x +3；(2)如图，四边形PBAC 的面积=△BCA 的面积+△PBC 的面积，而△BCA 的面积是定值，故四边形PBAC 的面积最大，只需要△PBC 的最大面积即可，过点P 作y 轴的平行线交BC 于点H ，∵B -3，0 ，C 0，3 ，设直线BC 的表达式为y =mx +n ，则0=-3m +n 3=n ，解得：m =1n =3 ，∴直线BC 的表达式为y =x +3，设点P x ，-x 2-2x +3 ，则点H x ，x +3 ，S △BPC =12PH ×OB =12×-x 2-2x +3-x -3 ×3=-32x 2-92x ，∵-32<0，故S 有最大值，即四边形PBAC 的面积有最大值，此时x =-32，代入y =-x 2-2x +3得y =154，∴P -32,154；(3)由(1)、(2)得：B -3，0 ，P -32,154，根据题意设M a ,0 ，Q b ,-b 2-2b +3 ，①若BP 为平行四边形的对角线，则-3-32=a +b 154=-b 2-2b +3 ，解得：a =-4b =-12 或a =-3b =-32 (此时P 、Q 重合，不合题意，舍去)将b =-12代入抛物线得：y =154，∴Q 1-12,154； ②若BQ 为平行四边形的对角线，则-3+b =-32+a 154=-b 2-2b +3 ，解得：a =-2b =-12 或a =-3b =-32 (此时P 、Q 重合，不合题意，舍去)将b =-12代入抛物线得：y =154，∴Q 2-12,154； ③若BM 为平行四边形的对角线，则-3+a =-32+b 154-b 2-2b +3=0 ，解得：a =1+312b =-2+312 或a =1-312b =-2-312，分别将b =-2-312，b =-2+312代入抛物线，求得y =-154，∴Q 3-2+312,-154 ，Q 4-2-312,-154 ，综上：点Q 的坐标为-12,154 或-2-312,-154 或-2+312,-154．【点睛】本题是二次函数综合题，考查了二次函数的有关性质、一次函数的性质、平行四边形的性质，熟练掌握二次函数的性质是解题的关键．8(2023·湖南岳阳·中考真题)已知抛物线Q 1:y =-x 2+bx +c 与x 轴交于A -3,0 ,B 两点，交y 轴于点C 0,3 ．(1)请求出抛物线Q1的表达式．(2)如图1，在y轴上有一点D0,-1，点E在抛物线Q1上，点F为坐标平面内一点，是否存在点E,F使得四边形DAEF为正方形？若存在，请求出点E,F的坐标；若不存在，请说明理由．(3)如图2，将抛物线Q1向右平移2个单位，得到抛物线Q2，抛物线Q2的顶点为K，与x轴正半轴交于点H，抛物线Q1上是否存在点P，使得∠CPK=∠CHK？若存在，请求出点P的坐标；若不存在，请说明理由．【答案】(1)y=-x2-2x+3(2)E-2,3；F1,2(3)点P的坐标为(1,0)或(-2,3)【分析】(1)把A-3，0，C0,3代入Q1:y=-x2+bx+c，求出b=-2,c=3即可；(2)假设存在这样的正方形，过点E作ER⊥x于点R，过点F作FI⊥y轴于点I，证明△EAR≅△AOD,△FID≅△DOA，可得ER=3,AR=1,FI=1,IO=2,故可得E-2,3，F1,2；(3)先求得抛物线Q2的解析式为y=-(x+1-2)2+4=-(x-1)2+4，得出K(1,4)，H(3,0)，运用待定系数法可得直线BC的解析式为y=-x+3，过点K作KT⊥y轴于点T，连接BC，设KP交直线BC于M或N，如图2，过点C作PS⊥y轴交BK于点S，交抛物线Q1于点P，连接PK，利用等腰直角三角形性质和三角函数定义可得tan∠CHK=CKCH=232=13，进而可求得点P的坐标．【详解】(1)∵抛物线Q1:y=-x2+bx+c与x轴交于A-3,0,两点，交y轴于点C0,3，∴把A-3，0，C0,3代入Q1:y=-x2+bx+c，得，-9-3b+c=0 c=3,解得，b=-2 c=3,∴解析式为：y=-x2-2x+3；(2)假设存在这样的正方形DAEF，如图，过点E作ER⊥x于点R，过点F作FI⊥y轴于点I，∴∠AER+∠EAR=90°,∵四边形DAEF是正方形，∴AE=AD,∠EAD=90°,∴∠EAR+∠DAR=90°,∴∠AER=∠DAO,又∠ERA=∠AOD=90°,∴△AER≅△DAO，∴AR =DO ,ER =AO ,∵A -3,0 ,D 0,-1 ,∴OA =3,OD =1,∴AR =1,ER =3,∴OR =OA -AR =3-1=2,∴E -2,3 ；同理可证明：△FID ≅△DOA ，∴FI =DO =1,DI =AO =3,∴IO =DI -DO =3-1=2,∴F 1,2 ；(3)解：抛物线Q 1上存在点P ，使得∠CPK =∠CHK ．∵y =-x 2-2x +3=-(x +1)2+4，∴抛物线Q 1的顶点坐标为(-1,4)，∵将抛物线Q 1向右平移2个单位，得到抛物线Q 2，∴抛物线Q 2的解析式为y =-(x +1-2)2+4=-(x -1)2+4，∵抛物线Q 2的顶点为K ，与x 轴正半轴交于点H ，∴K (1,4)，H (3,0)，设直线BC 的解析式为y =kx +n ，把C (0,3)，H (3,0)代入得n =33k +n =0 ，解得：k =-1n =3 ，∴直线BC 的解析式为y =-x +3，过点K 作KT ⊥y 轴于点T ，连接BC ，设KP 交直线BC 于M 或N ，如图2，过点C 作PS ⊥y 轴交BK 于点S ，交抛物线Q 1于点P ，连接PK ，则T (0,4)，M (m ,-m +3)，N (t ,-t +3)∴KT =TC =1，∠KTC =90°，∴△CKT 是等腰直角三角形，∴∠KCT =45°，CK =2KT =2，∵OH =OC =3，∠COH =90°，∴△COH 是等腰直角三角形，∴∠HCO =45°，CH =2OC =32，∴∠KCH =180°-∠KCT -∠HCO =90°，∴tan ∠CHK =CK CH =232=13，∵∠CPK =∠CHK ，∴tan ∠CPK =tan ∠CHK =13，∵tan ∠BCO =OB OC=13，∴∠BCO =∠CHK ，∵BK ∥OC ，∴∠CBK =∠BCO ，∴∠CBK =∠CHK ，即点P 与点B 重合时，∠CPK =∠CHK ，∴P 1(1,0)；∵SK =1，PS =3，∴tan ∠CPK =SK PS=13，∴∠CPK =∠CHK ，∵点P 与点C 关于直线x =-1对称，∴P (-2,3)；综上所述，抛物线Q 1上存在点P ，使得∠CPK =∠CHK ，点P 的坐标为(1,0)或(-2,3)．【点睛】本题是二次函数综合题，考查了待定系数法求解析式，二次函数的性质，全等三角形的判定与性质，正方形的性质等知识，运用数形结合思想解决问题是解题的关键．9(2022·四川泸州·中考真题)如图，在平面直角坐标系xOy 中，已知抛物线y =ax 2+x +c 经过A -2,0 ，B 0,4 两点，直线x =3与x 轴交于点C ．(1)求a ，c 的值；(2)经过点O 的直线分别与线段AB ，直线x =3交于点D ，E ，且△BDO 与△OCE 的面积相等，求直线DE 的解析式；(3)P 是抛物线上位于第一象限的一个动点，在线段OC 和直线x =3上是否分别存在点F ，G ，使B ，F ，G ，P 为顶点的四边形是以BF 为一边的矩形？若存在，求出点F 的坐标；若不存在，请说明理由．【答案】(1)a =-12，c =4(2)y =-23x (3)存在这样的点F ，点F 的坐标为(2,0)或-11+2014,0 【分析】(1)将点A ,B 的坐标代入抛物线y =ax 2+x +c 可得到关于a ,c 的方程组，解方程组即可得；(2)设直线DE 的解析式为y =kx (k <0)，从而可得点E 的坐标为E (3,3k )，利用三角形的面积公式可得△OCE 的面积为-92k ，再利用待定系数法求出直线AB 的解析式，与直线DE 的解析式联立可得点D 的坐标，从而可得△BDO 的面积，然后根据△BDO 与△OCE 的面积相等建立方程，解方程可得k 的值，由此即可得出答案；(3)先求出抛物线与x 轴的另一个交点坐标为(4,0)，从而可设点F 的坐标为F (m ,0)(0≤m ≤3)，点P 的坐标为P (t ,n )(0<t <4)，再分①以BF 为一边的矩形是矩形BFGP 和②以BF 为一边的矩形是矩形BFPG 两种情况，利用相似三角形的性质和矩形的性质将t ,n 用m 表示出来，然后将点P (t ,n )代入抛物线的解析式可求出m 的值，由此即可得出答案．【详解】(1)解：∵抛物线y =ax 2+x +c 经过A -2,0 ，B 0,4 两点，∴4a -2+c =0c =4 ，解得a =-12c =4 ．(2)解：由题意，设直线DE 的解析式为y =kx (k <0)，当x =3时，y =3k ，即E (3,3k )，CE =-3k ，则△OCE 的面积为12×3×(-3k )=-92k ，设直线AB 的解析式为y =k 0x +b 0，将点A -2,0 ，B 0,4 代入得：-2k 0+b 0=0b 0=4 ，解得k 0=2b 0=4，则直线AB 的解析式为y =2x +4，联立y =2x +4y =kx ，解得x =4k -2y =4k k -2，则点D 的坐标为D 4k -2,4k k -2 ，所以△BDO 的面积为12×4×-4k -2 =82-k ，因为△BDO 与△OCE 的面积相等，所以82-k =-92k ，解得k =-23或k =83>0(不符题意，舍去)，经检验，k =-23是所列分式方程的解，所以直线DE 的解析式为y =-23x ．(3)解：抛物线y =-12x 2+x +4=-12(x -1)2+92的对称轴为直线x =1，则抛物线与x 轴的另一个交点坐标为(2×1-(-2),0)，即为(4,0)，∵B (0,4)，∴OB =4，设点F 的坐标为F (m ,0)(0≤m ≤3)，点P 的坐标为P (t ,n )(0<t <4)，由题意，分以下两种情况：①如图，当以BF 为一边的矩形是矩形BFGP 时，则OF =m ,CF =3-m ，∠BFG =90°，∴∠OFB +∠CFG =90°，∵∠OFB +∠OBF =90°，∴∠CFG =∠OBF ，在△CFG 和△OBF 中，∠CFG =∠OBF∠FCG =∠BOF =90° ，∴△CFG ∼△OBF ，∴CG OF =CF OB ，即CG m =3-m 4，解得CG =3m -m 24，∴G 3,3m -m 24 ，∵矩形BFGP 的对角线互相平分，∴m+t2=0+320+n2=4+3m-m242，解得t=3-mn=3m-m2+164，将点P(t,n)代入y=-12x2+x+4得：-12(3-m)2+3-m+4=3m-m2+164，解得m=2或m=3，当m=2时，t=3-m=3-2=1，符合题意，当m=3时，t=3-m=3-3=0，不符题意，舍去，则此时点F的坐标为(2,0)，②如图，当以BF为一边的矩形是矩形BFPG时，过点B作BQ⊥CE于点Q，则BQ=OC=3,CQ=OB=4，同理可证：△QBG∼△OBF，∴QGOF=QBOB，即QGm=34，解得QG=34 m，∴CG=CQ+QG=3m+164，∴G3,3m+164，∵矩形BFPG的对角线互相平分，∴0+t2=m+324+n2=0+3m+1642，解得t=m+3n=3m4，将点P(t,n)代入y=-12x2+x+4得：-12(m+3)2+m+3+4=3m4，解得m=-11+2014或m=-11-2014<0(不符题意，舍去)，当m=-11+2014时，t=m+3=-11+2014+3=1+2014<4，符合题意，则此时点F的坐标为-11+2014,0 ，综上，存在这样的点F，点F的坐标为(2,0)或-11+2014,0 ．【点睛】本题考查了二次函数的几何应用、相似三角形的判定与性质、矩形的性质、一元二次方程的应用等知识点，较难的是题(3)，正确分两种情况讨论，并找出相似三角形是解题关键．。

中考数学总复习《二次函数压轴题（特殊四边形）》专项提升练习题（附答案)学校:___________班级：___________姓名：___________考号：___________1．如图，已知抛物线232y a x k ⎛⎫=-+ ⎪⎝⎭经过()1,0A -，()0,4C -两点，直线m 是抛物线的对称轴．(1)求抛物线的解析式．(2)设E 是直线m 上的一个动点，当点E 到点A ，C 的距离之和最短时，求点E 的坐标．(3)已知P 为抛物线的顶点，在平面直角坐标系中是否存在一点Q ，恰好使得P ，Q ，B ，C 为顶点平行四边形，若存在，写出所有符合条件的Q 点坐标，并写出求解点Q 的坐标的其中一种情况的过程，若不存在，说明理由． 2．如图，抛物线232yax bx与x 轴交于()1,0A -和()3,0B ，与y 轴交于C 点，点C 关于抛物线的对称轴的对称点为点D ．抛物线顶点为H ．(1)求抛物线的解析式．(2)如图1，在抛物线上是否存在一点M （异于点B ）使得ACB ACM S S =△△？若存在，请求出M 的坐标，不存在，说明理由；(3)如图2，当点E 在抛物线上运动时，在直线AD 上是否存在点F ，使得以点A 、C 、E 、F 为顶点的四边形为平行四边形？若存在，请直接写出点F 的坐标；若不存在，请说明理由．3．如图，已知抛物线23y ax bx =+-（a ，b 为常数，且0a ≠）与x 轴交于()30A B ，，两点，且3OB OA =，与y 轴交于点C ，点D 为第四象限内抛物线上的动点，DE y ∥轴交BC 所在直线于点E ．(1)求抛物线的函数表达式和点C '的坐标；(2)若点F 为y 轴上一点，是否存在点D ，使得以点C ，D ，E ，F 为顶点的四边形是菱形？若存在，求出所有符合条件的点D 的坐标：若不存在，请说明理由．4．如图，在平面直角坐标系中，抛物线24y ax bx =++与x 轴分别交于()4,0A -，()2,0B 两点，与y 轴交于C 点．(1)求抛物线的解析式；(2)点P 为直线AC 上方抛物线上任意一点，过点P 作PD y ∥轴交直线AC 于点D ，过点D 作DH x ∥轴，交y 轴于点H ，求PD DH +的最大值及此时点P 的坐标；(3)将抛物线沿着水平方向向右平移2个单位长度得到新的抛物线，点E 为原抛物线与平移后的抛物线的交点，点M 为平移后的抛物线对称轴上一动点，点N 为坐标平面内一点，直接写出所有使得以点B ，E ，M ，N 为顶点的四边形是菱形的点N 的坐标，并把求其中一个点N 的坐标的求解过程写出来．5．如图，已知直线1y x =+与抛物线2y x mx n =-++交于A 、D 两点且A 点在x 轴上，抛物线与x 轴另一个交点为B ，与y 轴交于点()0,3C ．(1)求抛物线的解析式；(2)如图，直线AD 上方的抛物线上有一点F ，过点F 作FG AD ⊥于点G ，求线段FG 的最大值；(3)点M 是抛物线的顶点，点P 是y 轴上一点，点Q 是坐标平面内一点，以A ，M ，P ，Q 为顶点的四边形是以AM 为边的矩形，求点Q 的坐标．6．如图，已知直线24y x =-+分别交x 轴、y 轴于点B ．抛物线过A ，B 两点． P 是线段AB 上一动点，过点P 作PC ⊥x 轴于点C ，交抛物线于点D ．(1)若抛物线的顶点M 的坐标为19,22⎛⎫⎪⎝⎭，其对称轴交AB 于点N ．⊥求抛物线的解析式．⊥在抛物线的对称轴上找一点Q ，使AQ BQ -的值最大，试求出点Q 的坐标． ⊥是否存在点P ，使四边形MNPD 为平行四边形？若存在，求出此时点P 的坐标．(2)当点P 的横坐标为1时，是否存在这样的抛物线，使得以B ，P ，D 为顶点的三角形与AOB 相似？若存在，直接写出满足条件的抛物线的解析式；若不存在，请说明理由．7．如图1，在平面直角坐标系中，抛物线22y ax bx =++与x 轴交于()40A -，和()10B ，，与y 轴交于点C ，连接AC BC ，．(1)求该抛物线的解析式；(2)如图1，在x 轴上有一动点D ，平面内是否存在一点E ，使以点A 、D 、C 、E 为顶点的四边形是菱形？若存在，请求出点E 的坐标，若不存在，请说明理由． (3)如图2，点M 为抛物线上的一动点：⊥若点M 为直线AC 上方的抛物线上任意一点，过点M 作y 轴的平行线，交AC 于点N ，过点M 作x 轴的平行线，交直线AC 于点Q ，求MNQ △周长的最大值；⊥若点M 为抛物线上的任意一动点，且45ACM BAC ∠=︒-∠，请直接写出满足条件的点M 的坐标． 8．如图，直线443y x =+与x 轴交于点A ，与y 轴交于点C ，抛物线2)83(0y ax x c a =-+≠经过A ，C 两点，交x 轴的正半轴于点B ，连接BC ．(1)求抛物线的解析式．(2)点P 在抛物线上，连接PB ，当45PBC ∠=︒时，求点P 的坐标；(3)已知点M 从点B 出发，以每秒1个单位长度的速度沿BA 运动，同时点N 从点O 出发，以每秒3个单位长度的速度沿OC CA ，运动．当点M ，N 运动到某一时刻时，在坐标平面内是否存在点D ，使得以A ，M ，N ，D 为顶点的四边形是矩形?若存在，请直接写出点D 的坐标；若不存在，请说明理由．9．如图1，平面直角坐标系xOy 中，抛物线()230y ax bx a =++<与x 轴分别交于点()30A -,和点()10B ,，与y 轴交于点C ，P 为抛物线上一动点．(1)写出抛物线的对称轴为直线______，抛物线的解析式为______；(2)如图2，连结AC ，若P 在AC 上方，作PQ y ∥轴交AC 于Q ，把上述抛物线沿射线PQ 的方向向下平移，平移的距离为h ()0h >，在平移过程中，该抛物线与直线AC 始终有交点，求h 的最大值；(3)若P 在AC 上方，设直线AP ，BP 与抛物线的对称轴分别相交于点F ，E ，请探索以A ，F ，B ，G （G 是点E 关于x 轴的对称点）为顶点的四边形面积是否随着P 点的运动而发生变化，若不变，求出这个四边形的面积；若变化，说明理由．(4)设M 为抛物线对称轴上一动点，当P ，M 运动时，在坐标轴上是否存在点N ，使四边形PMCN 为矩形？若存在，直接写出点P 的横坐标；若不存在，请说明理由．10．如图，在平面直角坐标系中，二次函数2y ax bx c =++的图象与x 轴交于()30A ，，()10B -，两点，与y 轴交于点()03C ，．(1)求这个二次函数的解析式；(2)已知点D 是直线AC 上方的抛物线上一动点．⊥当点D 运动到什么位置时，四边形ABCD 的面积最大？求此时D 点的坐标和四边形ABCD 的最大面积； ⊥连接DO DC ，，并把DOC △沿CO 翻折，得到四边形DOD C '，那么是否存在点D ，使四边形DOD C '为菱形？若存在，请求出此时点D 的坐标；若不存在，请说明理由．11．如图，抛物线23y ax ax c =-+与x 轴交于A ，()4,0B 两点（A 在B 的左侧），与y 轴交于点(0,4)C -，直线l 是地物线的对称轴，直线l 与x 轴交于点D ．(1)求抛物线的函数表达式；(2)点M 在直线l 上，且12DM =，点P ，Q 是抛物线上的动点，点P 在点Q 的左侧，是否存在点P ，Q 使得以点D 、M 、P 、Q 为顶点的四边形是菱形？若存在，请求出点P ，Q 的坐标；若不存在，请说明理由． 12．如图，二次函数的图象交x 轴于点()2,0A -和()8,0B ，交y 轴于点()0,4C ，连接AC ，BC ，点P 是线段OB 上一动点，过点P 作直线PD AC ∥，交y 轴于点D ，交线段BC 于点E ，交x 轴上方二次函数的图象于点F ．(1)求二次函数的表达式．(2)当点P 为线段DE 的三等分点时，求点P 的坐标．(3)在线段OB 上是否存在点P ，使得四边形AEFC 为平行四边形？若存在，求出点P 的坐标；若不存在，请说明理由． 13．综合与探究如图，直线4y x =-+与x 轴交于点B ，与y 轴交于点C ，经过B ，C 两点的抛物线212y x bx c =-++与x 轴的另一个交点为点A ，连接AC ．(1)求抛物线的解析式以及点A 的坐标；(2)若点P 是直线BC 上方抛物线上的一个动点，过点P 作PQ AC ∥交直线4y x =-+于点Q ，求线段PQ 的最大值；(3)若点M 在直线BC 上运动，在坐标平面内是否存在另一个点N ，使得以A ，C ，M ，N 为顶点的四边形是菱形？若存在，请直接写出点N 的坐标；若不存在，请说明理由．14．如图，已知抛物线()230y ax ax c a =++>与x 轴交于A 、B 两点，与y 轴交于点C ，点A 在点B 左侧，点B 的坐标为()1,0，点C 的坐标为为()0,3-．(1)求抛物线的函数关系式；(2)若点D 是x 轴上的一点，在抛物线上是否存在点E ，使以A 、C 、D 、C 为顶点且以AC 为一边的四边形是平行四边形﹖若存在，请求出点E 的坐标；若不存在，请说明理由． 15．综合与探究：如图，抛物线248433y x x =+-与x 轴交于A ，B 两点（点A 在点B 的左侧），与y 轴交于点C ．(1)求点A ，B ，C 的坐标；(2)点D 是第三象限内抛物线上的动点，设点D 的横坐标为m ，求四边形ABCD 面积S 的最大值及此时点D 的坐标；(3)若点P 在抛物线对称轴上，点Q 是平面内一点，试探究，是否存在点P ，Q ，使以点A ，C ，P ，Q 为顶点的四边形是以AC 为对角线的菱形？若存在，请求出点P 的坐标；若不存在，请说明理由．参考答案：1．(1)232524y x ⎛⎫=-- ⎪⎝⎭(2)35,22E -⎛⎫⎪⎝⎭(3)59,24Q ⎛⎫ ⎪⎝⎭或145,24Q -⎛⎫- ⎪⎝⎭或119,24Q -⎛⎫ ⎪⎝⎭2．(1)21322y x x =-++．(2)存在，M 点的坐标为214,2⎛⎫-- ⎪⎝⎭(3)存在，点F 的坐标为10,2⎛⎫ ⎪⎝⎭或317517,24⎛⎫++ ⎪⎝⎭或317517,24⎛⎫-- ⎪⎝⎭或12,2⎛⎫-- ⎪⎝⎭3．(1)抛物线的函数表达式为223y x x =--，点C 的坐标为()03-，(2)存在点D ，使得以点C ，D ，E ，F 为顶点的四边形是菱形，点D 的坐标为()23-，或()32,242--4．(1)2142y x x =--+ (2)92 53,2P ⎛⎫- ⎪⎝⎭(3)()1,419-+或()1,419--或()3,19或()3,19-5．(1)223y x x =-++(2)928(3)72,2Q ⎛⎫ ⎪⎝⎭或12,2Q ⎛⎫- ⎪⎝⎭6．(1)⊥2224y x x =-++；⊥1,62Q ⎛⎫⎪⎝⎭；⊥存在 3,12P ⎛⎫ ⎪⎝⎭(2)存在，2224y x x =-++或25342y x x =-++7．(1)213222y x x --=+(2)存在 ()10,2E - ()225,2E ()325,2E - 45,22E -⎛⎫⎪⎝⎭(3)⊥625+ ⊥1(5,3)M -- 22375(,)749M -8．(1)248433y x x =--+(2)51213,20100⎛⎫- ⎪⎝⎭(3)71311362⎛⎫+-- ⎪ ⎪⎝⎭，或()33-，或11355⎛⎫-- ⎪⎝⎭，9．(1)=1x - 223y x x =--+ (2)h 的最大值为169(3)不变，这个四边形的面积为16 (4)存在，点P 的横坐标为51456-± 1-10．(1)二次函数的解析式为223y x x =-++；(2)⊥点D 的坐标为31524⎛⎫ ⎪⎝⎭，时，四边形ABCD 的最大面积值为758；⊥点D 的坐标为210322⎛⎫+ ⎪ ⎪⎝⎭，．11．(1)234y x x =--(2)存在，点P 、Q 的坐标分别是()2,6- ()5,6或()1,6- ()2,6-12．(1)213442y x x =-++(2)点P 的坐标为8011⎛⎫ ⎪⎝⎭，或1607⎛⎫⎪⎝⎭，； (3)不存在，理由见解析13．(1)抛物线的解析式为2142y x x =-++ ()20A -，； (2)PQ 的最大值为253； (3)点N 的坐标为()21010--，或()21010-+-，或()46，或()75-，．14．(1)239344y x x =+- (2)()3,3--或341,32⎛⎫-- ⎪ ⎪⎝⎭或341,32⎛⎫-+ ⎪ ⎪⎝⎭15．(1)()30A -，()10B ， ()04C -， (2)当点D 坐标为352⎛⎫-- ⎪⎝⎭，时，四边形ABCD 面积S 的最大值为252； (3)存在，P 的坐标为1318⎛⎫-- ⎪⎝⎭，。

专题04特殊平行四边形中全等相似与最值问题通用的解题思路:一、四边形与全等相似1.三角形与全等之六大全等模型:(1)一线三等角模型锐角一线三等角(2)手拉手模型(3)半角模型(4)倍长中线模型模型(6)雨伞等模型(5)平行线中等模型2.三角形与相似之四大相似模型:(1)A字模型(3)手拉手模型(2)8字模型(4)一线三等角模型B 二、四边形线段最值问题囹 1 C B D 02B （1）将军饮马模型两定一动模型一定两动模型两线段相减的最大值模型（三点共线）• B（2）费马点模型：将边以A 为顶点逆时针旋转60。

，得到AQE,连接P0则^APQ 为等边三角形,PA=PQ O1. （2023-r 东深圳•中考真题）（1）如图，在矩形ABCD 中，E 为AD 边上一点，连接BE,①若= 过C 作CFLBE 交BE 于点、F ,求证：AABE^AFCB ；②若S 矩形倔8 = 2。

时，则BECF=(2)如图，在菱形ABCD 中，cosA = |,过。

作CE1AB 交A8的延长线于点E,过E 作EF _LAD 交AD 于点、F ,若S 菱形*d =24时，求EF BC 的值.(3)如图，在平行四边形ABCD 中，匕4 = 60。

，AB = 6, AD=5,点E 在CD 上，且CE = 2,点F 为BC 上一点，连接时，过E 作EGLEF 交平行四边形ABCD 的边于点G,若EF ・EG = 70时，请直接写出AG 的长.D,E E a C C A B AB备用图2.（2022广东广州•中考真题）如图，在菱形ABCQ中，0BAD=120°,AB=6,连接8Q.⑴求BQ的长；⑵点E为线段BQ上一动点（不与点B,。

重合），点E在边AQ上，且BE二也DF,①当CE±AB时，求四边形的面积；②当四边形的面积取得最小值时，CE+右CT的值是否也最小？如果是，求CE+也CF的最小值；如果不是，请说明理由.题型一特殊平行四边形中全等相似计算1.（2024-P东汕头•一模）（1）如图1,在矩形ABCD中，E为AD边上一点，连接8E,①若BE=BC,过。

AE 并延长AE 交DC 的延长线于点F.最新资料推荐2015特殊四边形动点问题专题训练及答案解析(一)已知，如图，点D 是八ABC 的边AB 的中点,四边形BCED 是平行四边形，(1)求证：四边形ADCE!平行四边形；⑵ 当ABC 满足什么条件时，平行四边形ADCE 是矩形？证明：(1)因为四边形BCED 是平行四边形，所以 BD=CE 且 BD// CE又因为D 是八ABC 的边AB 的中点,所以AD=BD 即卩DA=CE又因为CE//卅以四边形ADCE 是平行四边形.(2)当八ABC 为等腰三角形且AC=BC 寸，四边形 ADCE 是矩形 理由：••• AC=BC D 是八ABC 的边AB 的中点… CDIAD 即/ ADC=90 ,由(1)可知，四边形ADCE 是平行四边形…四边形ADCE 是矩(T#如图，已知E 是？ ABCD 中BC 边的中点，连接 (1) 求证：△ ABE J FCE(2) 连接AC BF,若/ AEC=N ABC 求证：四边形证明：C 1 J 二四边形ABCD 为平荷四I 边瑋亠-■-AB//DC >-'「ABE 二"ECF *又YE 为BC 的中点*-■-BE =CE >在ZiABE 和GCE 中上 '上 ABE 二/ECFBE=CENEB^FEC OS 寸顶角相等)-A ABE " A FCE CC 2 } AABE^ZXFCE >AB 二匚F r 又丸BZZ CF r 四边形ABF 匚为平行四边形“——BE=EC ■ AE=EF >又，KE 匚三2/ABU ,且NAEC 为 △ ABE 的夕卜角*"AEG「ABG+AEAB >一"JABC「EAB A一・—AE二BE >AE+EF二BE+EC〉艮卩AF=BC > 则四边形为矩形・最新资料推荐（三）如图，0为八ABC的边AC上一动点，过点0的直线MN/ BC,设MN分别交/ ACB的内、外角平分线于点E、Fo求证：0E=0F若CE=12 CF=5求0C的长当点0在AC边上运动到何处时，四边形AECF是矩形？证明你的结论存 V）的峯件下.当/\ ARC満忆什么峯件时.IHH力形AFCF%7F有形・并说日日你的理比.(1)(2)(3)(4)•••/ Ad BCE••• MN/ BC •••/ 0EC=/ BCE •••/ Ad OEC •••()£二OC 同理:OM OC …0E= OF(2)v CE 平分/ ACB / \ \ /•••/ Ad ACB/2Z ------------- 4 -------- VCF 平分/ ACD / (•••/ Ad ACD/2•••/ ECF=/ ACEy ACF=/ ACB/2+/ ACD/2= ( / ACL ACD /2 = 180/2 二90。