2015-2016学年黑龙江省佳木斯二中高二(下)期中考试数学(文)试题(解析版)

2016-2017学年黑龙江省佳木斯一中高二（下）期中数学试卷（文科）一、选择题：本大题共12个小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．（5分）设集合U={0，1，2，3，4，5}，M={0，3，5}，N={1，4，5}，则M ∩（∁U N）=（）A．{5}B．{0，3}C．{0，2，3，5}D．{0，1，3，4，5}2．（5分）“（2x﹣1）x=0”是“x=0”的（）A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件3．（5分）命题“∀x∈R，x2+x+1＜0”的否定为（）A．∀x∈R，x2+x+1≥0B．∀x∉R，x2+x+1≥0C．∃x0∉R，x02+x0+1＜0D．∃x0∈R，x02+x0+1≥04．（5分）函数的定义域为（）A．B．C．D．5．（5分）若lgx﹣lgy=a，则=（）A．3a B．C．a D．6．（5分）设函数f（x）=，则满足f（x）≤2的x的取值范围是（）A．[﹣1，2]B．[0，2]C．[1，+∞）D．[0，+∞）7．（5分）函数f（x）的定义域为[0，2]，则函数f（x2）的定义域是（）A．[﹣2，2]B．[﹣，]C．[0，2]D．[0，4]8．（5分）若函数y=f（x）的导函数在区间[a，b]上是增函数，则函数y=f（x）在区间[a，b]上的图象可能是（）A．B．C．D．9．（5分）若函数f（x）=kx﹣ln x在区间（1，+∞）单调递增，则k的取值范围是（）A．（﹣∞，﹣2]B．（﹣∞，﹣1]C．[2，+∞）D．[1，+∞）10．（5分）已知方程2x2﹣（m+1）x+m=0有两个不等正实根，则实数m的取值范围是（）A．或B．或C．或D．或11．（5分）已知f（x）=x2﹣xf′（0）﹣1，则f（2017）的值为（）A．2013×2015B．2014×2016C．2015×2017D．2016×2018 12．（5分）若f（x）是定义在R上的可导函数，且对任意x∈R，满足f（x）+f'（x）＞0，则对任意实数a，b（）A．a＞b⇔e a f（b）＞e b f（a）B．a＞b⇔e a f（b）＜e b f（a）C．a＞b⇔e a f（a）＜e b f（b）D．a＞b⇔e a f（a）＞e b f（b）二、填空题（每题5分，满分20分，将答案填在答题纸上）13．（5分）若递增的一次函数f（x）满足f[f（x）]=4x+3，则f（x）=．14．（5分）已知命题p：m＜0，命题q：∀x∈R，x2+mx+1＞0成立，若“p∧q”为真命题，则实数m的取值范围是．15．（5分）已知函数f（x）=4x2﹣mx+5在区间[﹣2，+∞）上是增函数，则f （1）的取值范围是．16．（5分）已知函数f（x）=e x（x2﹣x+1）﹣m，若∃a，b，c∈R，且a＜b＜c，使得f（a）=f（b）=f（c）=0．则实数m的取值范围是．三、解答题（本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．）17．（10分）计算（Ⅰ）（Ⅱ）．18．（12分）已知命题p：关于x的方程x2﹣ax+4=0有实根；命题q：关于x的函数y=2x2+ax+4在[3，+∞）上是增函数．若p∨q为真命题，p∧q为假命题，求实数a的取值范围．19．（12分）已知函数f（x）=+﹣lnx﹣，其中a∈R，且曲线y=f（x）在点（1，f（1））处的切线垂直于直线y=x．（Ⅰ）求a的值；（Ⅱ）求函数f（x）的单调区间与极值．20．（12分）已知函数f（x）=x2，g（x）=x﹣1．（1）若存在x∈R，使f（x）＜b•g（x），求实数b的取值范围；（2）设F（x）=f（x）﹣mg（x）+1﹣m，若F（x）≥0在区间[2，5]上恒成立，求实数m的取值范围．21．（12分）已知椭圆的右焦点为F（1，0），且点在椭圆C上，O为坐标原点．（Ⅰ）求椭圆C的标准方程；（Ⅱ）设过定点T（0，2）的直线l与椭圆C交于不同的两点A、B，且∠AOB 为锐角，求直线l的斜率k的取值范围．22．（12分）已知函数f（x）=ax3++bx（a，b为常数）（1）若y=f（x）的图象在x=2处的切线方程为x﹣y+6=0，求函数f（x）的解析式；（2）在（1）的条件下，求函数y=f（x）的图象与y=﹣[f′（x）﹣9x﹣3]+m 的图象交点的个数；（3）当a=1时，∀x∈（0，+∞），lnx≤f'（x）恒成立，求b的取值范围．2016-2017学年黑龙江省佳木斯一中高二（下）期中数学试卷（文科）参考答案与试题解析一、选择题：本大题共12个小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．（5分）设集合U={0，1，2，3，4，5}，M={0，3，5}，N={1，4，5}，则M ∩（∁U N）=（）A．{5}B．{0，3}C．{0，2，3，5}D．{0，1，3，4，5}【解答】解：∵集合U={0，1，2，3，4，5}，M={0，3，5}，N={1，4，5}，∴∁U N={0，2，3}，则M∩（∁U N）={0，3}．故选：B．2．（5分）“（2x﹣1）x=0”是“x=0”的（）A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件【解答】解：若（2x﹣1）x=0 则x=0或x=．即（2x﹣1）x=0推不出x=0．反之，若x=0，则（2x﹣1）x=0，即x=0推出（2x﹣1）x=0所以“（2x﹣1）x=0”是“x=0”的必要不充分条件．故选：B．3．（5分）命题“∀x∈R，x2+x+1＜0”的否定为（）A．∀x∈R，x2+x+1≥0B．∀x∉R，x2+x+1≥0C．∃x0∉R，x02+x0+1＜0D．∃x0∈R，x02+x0+1≥0【解答】解：因为全称命题的否定是特称命题，所以命题“∀x∈R，x2+x+1＜0”的否定为：∃x0∈R，x02+x0+1≥0．故选：D．4．（5分）函数的定义域为（）A．B．C．D．【解答】解：函数，∴，解得，即﹣≤x＜，∴函数y的定义域为[﹣，）．故选：D．5．（5分）若lgx﹣lgy=a，则=（）A．3a B．C．a D．【解答】解：=3（lgx﹣lg2）﹣3（lgy﹣lg2）=3（lgx﹣lgy）=3a故选：A．6．（5分）设函数f（x）=，则满足f（x）≤2的x的取值范围是（）A．[﹣1，2]B．[0，2]C．[1，+∞）D．[0，+∞）【解答】解：当x≤1时，21﹣x≤2的可变形为1﹣x≤1，x≥0，∴0≤x≤1．当x＞1时，1﹣log2x≤2的可变形为x≥，∴x≥1，故答案为[0，+∞）．故选：D．7．（5分）函数f（x）的定义域为[0，2]，则函数f（x2）的定义域是（）A．[﹣2，2]B．[﹣，]C．[0，2]D．[0，4]【解答】解：∵f（x）的定义域为[0，2]，∴在f（x2）中0≤x2≤2，∴故选：B．8．（5分）若函数y=f（x）的导函数在区间[a，b]上是增函数，则函数y=f（x）在区间[a，b]上的图象可能是（）A．B．C．D．【解答】解：∵函数y=f（x）的导函数在区间[a，b]上是增函数，∴对任意的a＜x′＜x″＜b，有f′（a）＜f′（x′）＜f′（x″）＜f′（b），也即在a，x'，x“，b处它们的斜率是依次增大的．∴A 满足上述条件，B 存在f′（x′）＞f′（x″），C 对任意的a＜x′＜x″＜b，f′（x′）=f′（x″），D 对任意的x∈[a，b]，f′（x）不满足逐项递增的条件，故选：A．9．（5分）若函数f（x）=kx﹣ln x在区间（1，+∞）单调递增，则k的取值范围是（）A．（﹣∞，﹣2]B．（﹣∞，﹣1]C．[2，+∞）D．[1，+∞）【解答】解：f′（x）=k﹣，∵函数f（x）=kx﹣lnx在区间（1，+∞）单调递增，∴f′（x）≥0在区间（1，+∞）上恒成立．∴k≥，而y=在区间（1，+∞）上单调递减，∴k≥1．∴k的取值范围是：[1，+∞）．故选：D．10．（5分）已知方程2x2﹣（m+1）x+m=0有两个不等正实根，则实数m的取值范围是（）A．或B．或C．或D．或【解答】解：∵方程2x2﹣（m+1）x+m=0有两个不等正实根，∴△=（﹣m﹣1）2﹣8m＞0，即m2﹣6m+1＞0，求得m＜3﹣2，或m＞3+2．再根据两根之和为＞0，且两根之积为＞0，求得m＞0．综合可得，0＜m＜3﹣2，或m＞3+2，故选：C．11．（5分）已知f（x）=x2﹣xf′（0）﹣1，则f（2017）的值为（）A．2013×2015B．2014×2016C．2015×2017D．2016×2018【解答】解：∵f（x）=x2﹣xf′（0）﹣1，∴f′（x）=2x﹣f‘（0），∴f′（0）=0，f（x）=x2﹣1，∴f（2017）=2017×2017﹣1=2016×2018．故选：D．12．（5分）若f（x）是定义在R上的可导函数，且对任意x∈R，满足f（x）+f'（x）＞0，则对任意实数a，b（）A．a＞b⇔e a f（b）＞e b f（a）B．a＞b⇔e a f（b）＜e b f（a）C．a＞b⇔e a f（a）＜e b f（b）D．a＞b⇔e a f（a）＞e b f（b）【解答】解：由题意令g（x）=e x f（x），则g′（x）=e x[f（x）+f'（x）]∵f（x）+f'（x）＞0，∴g′（x）＞0，即g（x）在R上是单调递增，①若a＞b，∴g（a）＞g（b），∴e a f（a）＞e b f（b），②若e a f（a）＞e b f（b），∴g（a）＞g（b），∴a＞b∴a＞b⇔e a f（a）＞e b f（b）故选：D．二、填空题（每题5分，满分20分，将答案填在答题纸上）13．（5分）若递增的一次函数f（x）满足f[f（x）]=4x+3，则f（x）=2x+1．【解答】解：设一次函数的方程为f（x）=ax+b，因为一次函数为递增函数，所以a＞0．则由f[f（x）]=4x+3，得f[ax+b]=a（ax+b）+b=a2x+ab+b=4x+3，即，解得，即f（x）=2x+1．故答案为：2x+114．（5分）已知命题p：m＜0，命题q：∀x∈R，x2+mx+1＞0成立，若“p∧q”为真命题，则实数m的取值范围是﹣2＜m＜0．【解答】解：因为“p∧q”为真命题，所以命题p、q都是真命题，若命题q是真命题，则∀x∈R，x2+mx+1＞0横成立，所以△=m2﹣4＜0，解得﹣2＜m＜2，又命题p：m＜0，也是真命题，所以实数m的取值范围是：﹣2＜m＜0，故答案为：﹣2＜m＜0．15．（5分）已知函数f（x）=4x2﹣mx+5在区间[﹣2，+∞）上是增函数，则f （1）的取值范围是[25，+∞）．【解答】解：f（x）=4x2﹣mx+5的对称轴x=∵函数在区间[﹣2，+∞）上是增函数，∴即m≤﹣16则f（1）=9﹣m≥25故答案为：[25，+∞）16．（5分）已知函数f（x）=e x（x2﹣x+1）﹣m，若∃a，b，c∈R，且a＜b＜c，使得f（a）=f（b）=f（c）=0．则实数m的取值范围是．【解答】解：∃a，b，c∈R，且a＜b＜c，使得f（a）=f（b）=f（c）=0．说明函数f（x）有3个不同零点，即方程e x（x2﹣x+1）﹣m=0有三个根．即e x（x2﹣x+1）=m有三个根．令g（x）=e x（x2﹣x+1），g′（x）=（x2﹣x+1）•e x+（2x﹣1）•e x =x（x+1）•e x，由g′（x）＞0，得x＞0或x＜﹣1；由g′（x）＜0，得﹣1＜x＜0．∴g（x）在（﹣∞，﹣1），（0，+∞）上单调递增，在（﹣1，0）上单调递减．∴函数g（x）的极大值为f（﹣1）=，极小值为f（0）=1．由题意可得，函数g（x）的图象和直线y=m有3个交点，如图所示：故有：1＜m＜，故答案为：．三、解答题（本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．）17．（10分）计算（Ⅰ）（Ⅱ）．【解答】解：（1）原式=（2）原式==18．（12分）已知命题p：关于x的方程x2﹣ax+4=0有实根；命题q：关于x的函数y=2x2+ax+4在[3，+∞）上是增函数．若p∨q为真命题，p∧q为假命题，求实数a的取值范围．【解答】解：命题p：关于x的方程x2﹣ax+4=0有实根，则△=a2﹣16≥0，解得a≥4，或a≤﹣4．命题q：关于x的函数y=2x2+ax+4在[3，+∞）上是增函数，∴，解得a ≥﹣12．若p∨q为真命题，p∧q为假命题，∴p与q必然一真一假，∴，或，解得a＜﹣12，或﹣4＜a＜4，∴实数a的取值范围是a＜﹣12，或﹣4＜a＜4．19．（12分）已知函数f（x）=+﹣lnx﹣，其中a∈R，且曲线y=f（x）在点（1，f（1））处的切线垂直于直线y=x．（Ⅰ）求a的值；（Ⅱ）求函数f（x）的单调区间与极值．【解答】解：（Ⅰ）∵f（x）=+﹣lnx﹣，∴f′（x）=﹣﹣，∵曲线y=f（x）在点（1，f（1））处的切线垂直于直线y=x．∴f′（1）=﹣a﹣1=﹣2，解得：a=．（Ⅱ）由（Ⅰ）知：f（x）=+﹣lnx﹣，f′（x）=﹣﹣=（x＞0），令f′（x）=0，解得x=5，或x=﹣1（舍），∵当x∈（0，5）时，f′（x）＜0，当x∈（5，+∞）时，f′（x）＞0，故函数f（x）的单调递增区间为（5，+∞）；单调递减区间为（0，5）；当x=5时，函数取极小值﹣ln5．20．（12分）已知函数f（x）=x2，g（x）=x﹣1．（1）若存在x∈R，使f（x）＜b•g（x），求实数b的取值范围；（2）设F（x）=f（x）﹣mg（x）+1﹣m，若F（x）≥0在区间[2，5]上恒成立，求实数m的取值范围．【解答】解：（1）存在x∈R，使f（x）＜b•g（x），即存在x∈R，x2﹣bx+b＜0，则△＞0，即b2﹣4b＞0，所以b的取值范围为（﹣∞，0）∪（4，+∞）；（2）由题意可知x2﹣mx+1≥0在区间[2，5]上恒成立，即在区间[2，5]上恒成立，由于在[2，5]上单调递增，所以当x=2时，有最小值，所以．即实数m的取值范围为（﹣]．21．（12分）已知椭圆的右焦点为F（1，0），且点在椭圆C上，O为坐标原点．（Ⅰ）求椭圆C的标准方程；（Ⅱ）设过定点T（0，2）的直线l与椭圆C交于不同的两点A、B，且∠AOB 为锐角，求直线l的斜率k的取值范围．【解答】解：（Ⅰ）由题意，得c=1，所以a2=b2+1．因为点在椭圆C上，所以，可解得a2=4，b2=3．则椭圆C的标准方程为．（Ⅱ）设直线l的方程为y=kx+2，点A（x1，y1），B（x2，y2），由，得（4k2+3）x2+16kx+4=0．因为△=48（4k2﹣1）＞0，所以，由根与系数的关系，得．因为∠AOB为锐角，所以，即x 1x2+y1y2＞0．所以x1x2+（kx1+2）（kx2+2）＞0，即（1+k2）x1x2+2k（x1+x2）+4＞0，所以．综上，解得或．所以，所求直线的斜率的取值范围为或．22．（12分）已知函数f（x）=ax3++bx（a，b为常数）（1）若y=f（x）的图象在x=2处的切线方程为x﹣y+6=0，求函数f（x）的解析式；（2）在（1）的条件下，求函数y=f（x）的图象与y=﹣[f′（x）﹣9x﹣3]+m的图象交点的个数；（3）当a=1时，∀x∈（0，+∞），lnx≤f'（x）恒成立，求b的取值范围．【解答】解：（Ⅰ）由题意得f′（x）=3ax2+（2﹣3a）x+b，由题知∵y=f（x）的图象在x=2处的切线方程为x﹣y+6=0，∴，即，解得a=﹣1，b=3．则f（x）=﹣x3++3x．（Ⅱ）由f（x）=﹣x3++3x，可得f′（x）=﹣3x2+5x+3，则y=﹣[f′（x）﹣9x﹣3]+m=﹣（﹣3x2+5x+3﹣9x﹣3）+m=，则由题意函数f（x）的图象与y=﹣[f′（x）﹣9x﹣3]+m的图象交点的个数等价于方程﹣x3++3x=实根的个数，即m=﹣x3+x2+x根的个数．等价于g（x）=﹣x3+x2+x的图象与直线y=m的交点个数，…（6分）g′（x）=﹣3x2+2x+1=﹣（x﹣1）（3x+1），由g′（x）＞0，解得＜x＜1，此时函数递增，由g′（x）＜0，解得x＜或x＞1，此时函数递减．则函数g（x）的极小值为g（）=，极大值为g（1）=1…（8分）根据上面的讨论，作出g（x）=﹣x3+x2+x的大致图象与直线y=m的位置如图，由图知，当＜m＜1时，函数f（x）的图象与y=﹣[f′（x）﹣9x﹣3]+m的图象有三个不同交点；当m=或m=1时，函数f（x）的图象与y=﹣[f′（x）﹣9x﹣3]+m的图象有两个不同交点；当m＜或m＞1时，函数f（x）的图象与y=﹣[f′（x）﹣9x﹣3]+m的图象有1个交点．…（10分）（Ⅲ）当a=1时，f（x）=﹣x3+bx，f′（x）=3x2﹣x+b，若，∀x∈（0，+∞），lnx≤f′（x）恒成立，等价于lnx≤3x2﹣x+b，即b≥lnx﹣3x2+x在（0，+∞）上恒成立，令h（x）=lnx﹣3x2+x，只需b≥h（x）max．h′（x）=，故当x∈（0，）时，h′（x）＞0，h（x）单调递增；当x∈（，+∞）时，h′（x）＜0，h（x）单调递增．∴h（x）max=h（）=﹣ln2﹣，∴b≥﹣ln2﹣，因此b的范围是[﹣ln2﹣，+∞）．。

黑龙江省佳木斯市高二下学期数学期中考试试卷姓名:________ 班级:________ 成绩:________一、选择题：本大题共12小题，每小题5分，共60分. (共12题；共60分)1. （5分）四名同学争夺跑步、跳高、跳远三项冠军，则可能的结果数是（）A .B .C .D .2. （5分）已知f（x）=xn ，若f′（﹣1）=3，则n的值为（）A . 3B . ﹣4C . 5D . ﹣53. （5分）口袋中装有大小质地都相同，编号为1，2，3，4，5的求各一个，现从中一次性随机地取出两个球，设取出的两球中较大的编号为X，则随机变量X的数学期望是（）A . 3B . 4C . 4.5D . 54. （5分）已知，那么n等于（）A . 14B . 12C . 13D . 155. （5分）现有10张奖票，只有1张可以中奖，10个人各自从中随机抽取1张，则第一人抽中奖与第十人抽中奖的概率分别为（）A . ，B . ，C . ，D . ，6. （5分）函数f（x）的图象如图所示，下列数值排序正确的是（）A . 0＜f′（3）＜f′（4）＜f（4）﹣f（3）B . 0＜f′（3）＜f（4）﹣f（3）＜f′（4）C . 0＜f′（4）＜f′（3）＜f（4）﹣f（3）D . 0＜f（4）﹣f（3）＜f′（3）＜f′（4）7. （5分）当K2＞6.635时，认为事件A与事件B（）A . 有95%的把握有关B . 有99%的把握有关C . 没有理由说它们有关D . 不确定8. （5分） 2015年6月20日是我们的传统节日﹣﹣”端午节”，这天小明的妈妈为小明煮了5个粽子，其中两个腊肉馅三个豆沙馅，小明随机取出两个，事件A=“取到的两个为同一种馅”，事件B=“取到的两个都是豆沙馅”，则P（B|A）=（）A .B .C .D .9. （5分） (2016高二下·三门峡期中) 一排9个座位坐了3个三口之家．若每家人坐在一起，则不同的坐法种数为（）A . 3×3!B . 3×（3!）3C . （3!）4D . 9!10. （5分）等差数列中的 a1 ， a4027 是函数的极值点，则（）A . 3B . 2C . 4D . 511. （5分）已知平面上的线段l及点P，在l上任取一点Q，线段PQ长度的最小值称为点P到线段l的距离，记作d（P，l）．设l是长为2的线段，点集D={P|d（P，l）≤1}所表示图形的面积为（）A . πB . 2πC . 2+πD . 4+π12. （5分） (2015高二下·咸阳期中) 函数f（x）=2x3﹣9x2+12x+1的单调递增区间（）A . （1，2）B . （2，+∞）C . （﹣∞，1）D . （﹣∞，1）和（2，+∞）二、填空题：本大题共4小题，每小题5分，共20分。

2015-2016学年高二（下）期中数学试卷（含答案）一、选择题（共5小题，每小题5分，满分25分）1．如果直线y=x+b经过圆x2+y2+4x﹣2y﹣4=0的圆心，则b=( )A．﹣3 B．0 C．3 D．﹣22．直线x﹣2y+2=0和直线3x﹣y+7=0的夹角是( )A．30° B．60° C．45° D．135°3．设椭圆的焦点为F1、F2，直线L过点F1，且与椭圆相交于A，B两点，则△ABF2的周长为( )A．9 B．16 C．20 D．254．已知A（1，3）、B（4，﹣1）两点，则AB的距离=( )A．5 B．6 C．7 D．45．已知 A（﹣2，3）、B（4，﹣3）两点，则线段AB的中点坐标是( )A．（3，0） B．（2，3） C．（3，3） D．（1，0）二、填空题（每题5分，共40分）6．直线x﹣y﹣1=0的斜率是__________；倾斜角为__________；在y轴上的截距是__________．7．已知直线经过点A（1，2）、B（3，4），则斜率K=__________；倾斜角α=__________．8．如果直线ax﹣2y+1=0和2x﹣ay+3=0平行，则a=__________．9．已知直线（3a+2）x+（1﹣4a）y+8=0与（5a﹣2）x+（a+4）y﹣7=0垂直，则a=__________．10．过点A（2，1）且与直线2x+y﹣10=0垂直的直线l的方程是__________．11．椭圆+=1的焦点坐标是__________，长轴长=__________，短轴长=__________，焦距=__________，顶点坐标是__________，离心率e=__________，准线方程是__________．12．以点A（﹣1，2）为圆心，3为半径的圆，方程为__________．三、简答题（每题6分，共36分）13．求平行线L1：2x+3y﹣8=0和L2：2x+3y+18=0的距离．14．圆心在点C（1，3），并且和直线3x﹣4y﹣11=0相切的圆．15．求斜率为3，且和圆x2+y2=4相切的直线方程．16．求经过圆（x﹣1）2+（y﹣1）2=1外的一点P（2，3）向圆所引的切线方程．17．在椭圆中，a=5，b=4，焦点在x轴上，求椭圆方程．18．椭圆焦距为8，离心率e=0.8，求该椭圆的标准方程．一、选择题（共5小题，每小题5分，满分25分）1．如果直线y=x+b经过圆x2+y2+4x﹣2y﹣4=0的圆心，则b=( )A．﹣3 B．0 C．3 D．﹣2【考点】圆的一般方程．【专题】计算题；直线与圆．【分析】把圆的方程化为标准方程后，找出圆心坐标，代入直线y=x+b即可得出结论．【解答】解：把圆的方程化为标准方程得：（x+2）2+（y﹣1）2=9，则圆心坐标为（﹣2，1），∵直线y=x+b经过圆x2+y2+4x﹣2y﹣4=0的圆心，∴1=﹣2+b，∴b=3，故选：C．【点评】本题考查直线与圆的位置关系，考查学生的计算能力，确定圆心坐标是关键．2．直线x﹣2y+2=0和直线3x﹣y+7=0的夹角是( )A．30° B．60° C．45° D．135°【考点】两直线的夹角与到角问题．【专题】计算题；直线与圆．【分析】根据题意算出两条直线的斜率值，再利用两条直线的夹角公式加以计算，可得夹角的正切值为1，从而得到夹角的大小．【解答】解：∵直线x﹣2y+2=0的斜率k1=，直线3x﹣y+7=0的斜率k2=3，∴设两条直线的夹角为θ，由tanθ=||=1∵0°＜θ＜90°，∴θ=45°即两条直线的夹角等于45°故选：C．【点评】本题给出两条定直线，求它们的夹角大小．考查了直线的位置关系和两条直线的夹角公式等知识，属于基础题．3．设椭圆的焦点为F1、F2，直线L过点F1，且与椭圆相交于A，B两点，则△ABF2的周长为( )A．9 B．16 C．20 D．25【考点】椭圆的简单性质．【专题】整体思想；数学模型法；圆锥曲线的定义、性质与方程．【分析】利用椭圆的定义即可得出．【解答】解：∵椭圆，则a=5．∴△ABF2的周长=|AB|+|AF2|+|BF2|═|AF1|+|AF2|+|BF1|+|BF2|=2a+2a=4a=4〓5=20．故选：C．【点评】本题考查了椭圆的定义、三角形的周长，考查了推理能力与计算能力，属于中档题．4．已知A（1，3）、B（4，﹣1）两点，则AB的距离=( )A．5 B．6 C．7 D．4【考点】两点间距离公式的应用．【专题】计算题；直线与圆．【分析】根据两点间的距离公式可直接解答．【解答】解：∵两点A（1，3）、B（4，﹣1），∴A、B两点间的距离是：=5．故选：A．【点评】本题考查了两点间的距离．求直角坐标系内任意两点间的距离可直接套用两点间的距离公式．5．已知 A（﹣2，3）、B（4，﹣3）两点，则线段AB的中点坐标是( )A．（3，0） B．（2，3） C．（3，3） D．（1，0）【考点】中点坐标公式．【专题】直线与圆．【分析】根据已知中A，B点的坐标，代入中点坐标公式，可得答案．【解答】解：∵A（﹣2，3）、B（4，﹣3），∴线段AB的中点坐标是（，）=（1，0），故选：D．【点评】本题考查的知识点是中点坐标公式，难度不大，属于基础题．二、填空题（每题5分，共40分）6．直线x﹣y﹣1=0的斜率是1；倾斜角为45°；在y轴上的截距是﹣1．【考点】直线的斜率．【专题】直线与圆．【分析】化直线方程的一般式为斜截式，由此求得直线的斜率，倾斜角以及直线在y轴上的截距．【解答】解：由x﹣y﹣1=0，得y=x﹣1．∴直线x﹣y﹣1=0的斜率是1，倾斜角为45°，在y轴上的截距为﹣1．故答案为：1；45°；﹣1．【点评】本题考查直线的斜率，考查了化直线的一般方程为斜截式方程，是基础题．7．已知直线经过点A（1，2）、B（3，4），则斜率K=1；倾斜角α=．【考点】直线的斜率；直线的倾斜角．【专题】计算题；直线与圆．【分析】利用直线的斜率公式代入数值计算即得斜率，利用斜率与倾斜角的关系，可得倾斜角．【解答】解：∵直线经过点A（1，2）、B（3，4），∴k==1，∵0≤α＜π，∴α=．故答案为：1；．【点评】本题考查了由直线上的两点求其斜率的问题，考查斜率与倾斜角的关系，是基础题．8．如果直线ax﹣2y+1=0和2x﹣ay+3=0平行，则a=〒2．【考点】直线的一般式方程与直线的平行关系．【专题】直线与圆．【分析】直线直线判断的等价条件进行判断即可．【解答】解：若a=0，则两直线方程为﹣2y+1=0，2x+3=0．此时两直线不平行，若a≠0，若两直线平行，则≠，由得a2=4，则a=〒2，满足条件．故答案为：〒2【点评】本题主要考查直线平行的应用，根据系数之间的关系是解决本题的关键．9．已知直线（3a+2）x+（1﹣4a）y+8=0与（5a﹣2）x+（a+4）y﹣7=0垂直，则a=0或1．【考点】直线的一般式方程与直线的垂直关系．【专题】直线与圆．【分析】由直线的垂直关系可得a的方程，解方程可得．【解答】解：∵直线（3a+2）x+（1﹣4a）y+8=0与（5a﹣2）x+（a+4）y﹣7=0垂直，∴（3a+2）（5a﹣2）+（1﹣4a）（a+4）=0，化简可得a2﹣a=0，解得a=0或a=1故答案为：0或1【点评】本题考查直线的一般式方程和垂直关系，属基础题．10．过点A（2，1）且与直线2x+y﹣10=0垂直的直线l的方程是x﹣2y=0．．【考点】直线的一般式方程与直线的垂直关系．【专题】直线与圆．【分析】由垂直可得直线的斜率，可得点斜式方程，化为一般式即可．【解答】解：∵直线2x+y﹣10=0的斜率为﹣2，由垂直可得所求直线的斜率为，∴所求直线的方程为y﹣1=（x﹣2），化为一般式可得x﹣2y=0故答案为：x﹣2y=0【点评】本题考查直线的一般式方程和垂直关系，属基础题．11．椭圆+=1的焦点坐标是（〒3，0），长轴长=10，短轴长=8，焦距=6，顶点坐标是（〒5，0）；（0，〒4），离心率e=，准线方程是x=．21世纪教育网版权所有【考点】椭圆的简单性质．【专题】数形结合；数学模型法；圆锥曲线的定义、性质与方程．【分析】由椭圆+=1可得：a=5，b=4，c==3，即可得出．【解答】解：椭圆+=1可得：a=5，b=4，c==3，于是可得：焦点坐标是（〒3，0），长轴长=2a=10，短轴长=2b=8，焦距=2c=6，顶点坐标是（〒5，0），（0，〒4）离心率e==，准线方程是x=即x=．故答案分别为：（〒3，0）；10；8；6；（〒5，0）；（0，〒4）；；x=．【点评】本题考查了椭圆的标准方程及其性质，考查了推理能力与计算能力，属于中档题．12．以点A（﹣1，2）为圆心，3为半径的圆，方程为（x+1）2+（y﹣2）2=9．【考点】圆的标准方程．【专题】直线与圆．【分析】根据圆心坐标和半径，代入圆的标准方程，可得答案．【解答】解：以点A（﹣1，2）为圆心，3为半径的圆的标准方程为：（x+1）2+（y﹣2）2=9，故答案为：（x+1）2+（y﹣2）2=9【点评】本题考查的知识点是圆的标准方程，难度不大，属于基础题．三、简答题（每题6分，共36分）13．求平行线L1：2x+3y﹣8=0和L2：2x+3y+18=0的距离．【考点】直线的一般式方程与直线的平行关系．【专题】直线与圆．【分析】由已知中直线方程，代入平行线距离公式，可得答案．【解答】解：平行线L1：2x+3y﹣8=0和L2：2x+3y+18=0的距离d满足：d==2【点评】本题考查的知识点是平行线间距离公式，难度不大，属于基础题．14．圆心在点C（1，3），并且和直线3x﹣4y﹣11=0相切的圆．【考点】圆的切线方程．【专题】计算题；直线与圆．【分析】根据直线3x﹣4y﹣11=0为所求圆的切线，得到圆心到切线的距离等于圆的半径，故利用点到直线的距离公式求出圆心到已知直线的距离d，即为圆的半径r，根据圆心和半径写出圆的标准方程．【解答】解：∵圆心（1，3）到直线3x﹣4y﹣11=0的距离d==4，∴所求圆的半径r=4，则所求圆的方程为：（x﹣1）2+（y﹣3）2=16．【点评】此题考查了直线与圆的位置关系，涉及的知识有：点到直线的距离公式，以及圆的标准方程，当直线与圆相切时，圆心到直线的距离等于圆的半径，即d=r，熟练掌握此性质是解本题的关键．15．求斜率为3，且和圆x2+y2=4相切的直线方程．【考点】圆的切线方程．【专题】计算题；直线与圆．【分析】设所求的直线的方程为y=3x+b，根据圆心（0，0）到直线的距离等于半径求得k 的值，可得所求的直线方程．【解答】解：设所求的直线的方程为y=3x+b，即3x﹣y+k=0，则由圆心（0，0）到直线的距离等于半径可得=2，求得k=〒2，故所求的直线方程为3x﹣y〒2=0．【点评】本题主要考查直线和圆相切的性质，点到直线的距离公式的应用，用待定系数法求直线的方程，属于基础题．16．求经过圆（x﹣1）2+（y﹣1）2=1外的一点P（2，3）向圆所引的切线方程．【考点】圆的切线方程．【专题】计算题；直线与圆．【分析】由圆的方程找出圆心坐标和半径r，当切线方程的斜率不存在时，显然x=2满足题意；当切线方程的斜率存在时，设斜率为k，由P的坐标和k表示出切线方程，利用点到直线的距离公式表示出圆心到切线的距离d，根据d=r列出关于k的方程，求出方程的解，得到k的值，确定出此时切线的方程，综上，得到所有满足题意的切线方程．【解答】解：由圆（x﹣1）2+（y﹣1）2=1，得到圆心坐标为（1，1），半径r=1，当过P的切线方程斜率不存在时，显然x=2为圆的切线；当过P的切线方程斜率存在时，设斜率为k，切线方程为y﹣3=k（x﹣2），即kx﹣y﹣2k+3=0，∴圆心到切线的距离d==r=1，解得：k=，此时切线方程为3x﹣4y+6=0，综上，切线方程为x=2或3x﹣4y+6=0．【点评】此题考查了圆的切线方程，涉及的知识有：圆的标准方程，点到直线的距离公式，直线的点斜式方程，利用了分类讨论的思想，是高考中常考的题型．本题易漏掉特殊情况导致错误17．在椭圆中，a=5，b=4，焦点在x轴上，求椭圆方程．【考点】椭圆的标准方程．【专题】计算题；圆锥曲线的定义、性质与方程．【分析】椭圆方程中，由a=5，b=4，焦点在x轴，能够求出椭圆的标准方程．【解答】解：∵椭圆方程中，a=5，b=4，焦点在x轴，∴椭圆方程为．【点评】本题考查椭圆的方程，考查学生的计算能力，比较基础．18．椭圆焦距为8，离心率e=0.8，求该椭圆的标准方程．【考点】椭圆的标准方程．【专题】圆锥曲线的定义、性质与方程．【分析】由题意求出椭圆的半焦距，结合离心率求出a，则b可求，椭圆的标准方程可求．【解答】解：由题意知，2c=8，c=4，又，得a=5．∴b2=a2﹣c2=25﹣16=9．则椭圆的标准方程为或．【点评】本题考查椭圆的简单性质，考查了椭圆标准方程的求法，是基础题．。

佳二中2015—2016学年度下学期期中考试高一数学试卷命题教师：马大海 审题教师:赵新第Ⅰ卷(共60分)一、选择题（共60分，每题5分）1、已知a ，b 为非零实数，且a ＜b ，则下列结论一定成立的是（ ）A ．a 2＜b 2B ．a 3＜b 3C ．＞D ．ac 2＜bc 22、经过两点，的直线的倾斜角为（ ）A ．120°B ．150°C ．60°D ．30 3、在△ABC 中，若∠A=60°，∠B=45°，，则AC=（ ）A ．B ．C ．D ．4、等差数列{a n }中，a 4+a 8=10，a 10=6，则公差d 等于( ）A ．B ．C ．2D ．﹣5、已知数列{a n ｝满足a n+1=2a n （n≥1)，其前n 项和为S n ，则=（ ）A ．B ．C ．D ．6、已知数列{}n b 是等比数列,9b 是1和3的等差中项,则216b b =( ）A ．16B ．8C ．2D ．47、设a=3x 2﹣x+2，b=2x 2+x ，则（ ）A ．a ＞bB ．a ＜bC ．a≥bD ．a≤b8、动点P 在直线x+y —4=0上，O 为原点，则|OP|的最小值为( ）A 10B ．22C 6D ．29、已知直线l 1：x+2ay ﹣1=0，与l 2:(2a ﹣1)x ﹣ay ﹣1=0平行，则a 的值是（ )A ．0或1B ．1或C ．0或D ．10、设a ＞0，b ＞0，若是4a 与2b 的等比中项，则的最小值为( ）A ．2B ．8C ．9D ．1011、钝角三角形的三边长分别为a 、a+1、a+2，则a 的取值范围是（ ）A ．(0，3）B ．（1，3）C ．（3，4）D ．(4，6）12、已知n S 是等差数列{}n a 的前n 项和，且675S S S >>，给出下列五个命题:①0d <；②110S >;③120S <;④数列{}n S 中的最大项为11S ；⑤67a a >其中正确命题的个数是（ ）A ．5B ．4C ．3D ．1第Ⅱ卷(共90分)二、填空题（共20分,每题5分）13、过点)1,2(且在两坐标轴上截距相等的直线的方程是 ____（用一般式作答）。

高二下学期期中考试数学(文科)试题与答案高二年级下学期期中考试数学（文）试题一、选择题（本大题共12小题，每小题5分，共60分）1.复数 $2-i$ 与 $2+i$ 的商为（）A。

$1-\frac{4}{5}i$。

B。

$\frac{33}{43}+\frac{4}{5}i$。

C。

$1-\frac{1}{5}i$。

D。

$1+\frac{1}{5}i$2.设有一个回归方程为 $y=2-2.5x$，则变量 $x$ 增加一个单位时（）A。

$y$ 平均增加 $2.5$ 个单位。

B。

$y$ 平均减少$2.5$ 个单位。

C。

$y$ 平均增加 $2$ 个单位。

D。

$y$ 平均减少 $2$ 个单位3.所有金属都能导电，铁是金属，所以铁能导电，属于哪种推理（）.A。

类比推理。

B。

演绎推理。

C。

合情推理。

D。

归纳推理4.点 $M$ 的极坐标 $(5,\frac{2\pi}{3})$ 化为直角坐标为（）A。

$(-\frac{5\sqrt{3}}{2},-2)$。

B。

$(2,-2)$。

C。

$(-\frac{5}{2},2)$。

D。

$(2,2)$5.用反证法证明命题“若 $a^2+b^2=0$，则 $a$、$b$ 全为$0$（$a$、$b\in R$）”，其假设正确的是（）A。

$a$、$b$ 至少有一个不为 $0$。

B。

$a$、$b$ 至少有一个为 $0$。

C。

$a$、$b$ 全不为 $0$。

D。

$a$、$b$ 中只有一个为 $0$6.直线 $y=2x+1$ 的参数方程是（$t$ 为参数）（）A。

$\begin{cases}x=t^2\\y=2t^2+1\end{cases}$。

B。

$\begin{cases}x=2t-1\\y=4t+1\end{cases}$。

C。

$\begin{cases}x=t-1\\y=2t-1\end{cases}$。

D。

$\begin{cases}x=\sin\theta\\y=2\sin\theta+1\end{cases}$7.当 $\frac{2}{3}<m<1$ 时，复数 $m(3+i)-(2+i)$ 在复平面内对应的点位于（）A。

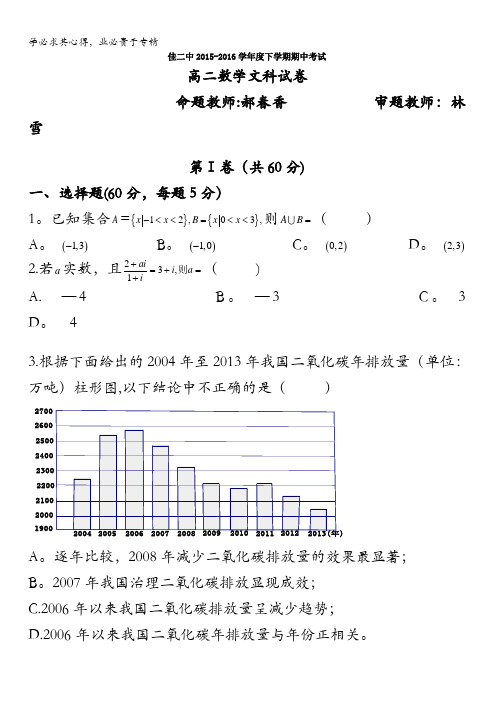
佳二中2015-2016学年度下学期期中考试高二数学文科试卷命题教师:郝春香 审题教师：林雪第Ⅰ卷（共60分)一、选择题(60分，每题5分）1。

已知集合A ={}{}12,03,x x B x x -<<=<<则A B =（）A 。

()1,3-B 。

()1,0-C 。

()0,2D 。

()2,32.若a 实数，且=+=++a i iai 则,312（ )A. —4 B 。

—3 C 。

3 D 。

43.根据下面给出的2004年至2013年我国二氧化碳年排放量（单位：万吨）柱形图,以下结论中不正确的是（ ）2700260025002400210020001900)A 。

逐年比较，2008年减少二氧化碳排放量的效果最显著；B 。

2007年我国治理二氧化碳排放显现成效； C.2006年以来我国二氧化碳排放量呈减少趋势； D.2006年以来我国二氧化碳年排放量与年份正相关。

4。

下列在曲线sin 2()cos sin x y θθθθ=⎧⎨=+⎩为参数上的点是( ）A ．1(,2 B ．31(,)42- C ． D ．5。

化极坐标方程2cos 0ρθρ-=为直角坐标方程为（ ）A ．20x y +=2或1y = B ．1x = C ．20xy +=2或1x =D ．1y =6.圆5cos ρθθ=-的圆心是（）A ．4(5,)3π-- B ．(5,)3π- C ．(5,)3π D ．5(5,)3π- 7。

极坐标方程cos 2sin 2ρθθ=表示的曲线为（ ）A ．一条射线和一个圆B ．两条直线C ．一条直线和一个圆D ．一个圆8.下列各式中，最小值等于2的是（ ) A ．xy y x + B ．4522++x xC ．1tan tan θθ+D ．22xx -+9。

不等式3529x ≤-<的解集为（ ） A ．[2,1)[4,7)- B ．(2,1](4,7]-C ．(2,1][4,7)--D ．(2,1][4,7)-10.下边程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术".执行该程序框图，若输入的,a b 分别为14,18，则输出的a 为（ ）否是 否A 。

黑龙江高二高中数学期中考试班级:___________ 姓名：___________ 分数：___________一、解答题1.已知函数．（1）求曲线在点处的切线方程；（2）直线为曲线的切线，且经过原点，求直线的方程及切点坐标．2.求下列函数的导数：（1）（2）3.设复数，试求取何实数值时，（1）是实数；（2）是纯虚数；（3）对应的点位于复平面的第四象限．4.设命题p：实数x满足x2－4Ax＋3A2<0，其中A.>0；命题q：实数x满足x2－5x＋6≤0.(1)若A＝1，且p∧q为真，求实数x的取值范围；(2)若p是q成立的必要不充分条件，求实数A的取值范围．5.设函数．（1）求函数的单调区间；（2）设是否存在极值，若存在，请求出极值；若不存在，请说明理由；（3）当时．证明：．二、选择题1.设集合，则= ()A．B．C．D．2.化简后的结果为（）A．B．C．D．3.若函数，则（）A．B．C．D．4.若在处可导，则（ ）A ．B ．C ．D ．不一定存在5.若曲线y ＝在点P 处的切线斜率为－4，则点P 的坐标是( ) A ．或B ．C ．D ．6.下列函数中,在上为增函数的是 （ ）A ．B ．C ．D ．7.已知是定义在内的可导函数，则“”是“在上为增函数”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件8.过点(0,1)且与曲线y ＝在点(3,2)处的切线垂直的直线方程为( ) A ．2x ＋y －1＝0B ．x －2y ＋2＝0C ．x ＋2y －2＝0D ．2x －y -4＝09.若函数的图象与直线相切，则（ ） A ．B ．C ．D ．10.若函数在其定义域内的一个子区间内不是单调函数，则实数的取值范围是（ ） A ．B ．C ．D ．11.设函数是定义在上的可导函数，其导函数为，且有，则不等式的解集为（ ）A ．B ．C ．D ．三、填空题1.函数在点处的切线斜率为________．2.设函数f (x )＝6x 3＋3(A.＋2)x 2＋2A.x .若f (x )的两个极值点为x 1，x 2，且x 1x 2＝1，则实数A.的值为________．3.已知不等式，照此规律，总结出第-1个不等式为________．4.直线＝分别与曲线＝2(＋1)，＝＋ln 交于A ，B ，则|AB|的最小值为________．黑龙江高二高中数学期中考试答案及解析一、解答题1.已知函数．（1）求曲线在点处的切线方程；（2）直线为曲线的切线，且经过原点，求直线的方程及切点坐标．【答案】（1）；（2）直线的方程为，切点坐标为．【解析】（1）第一步，先求函数的导数，第二步，再求，根据导数的几何意义，，最后代入直线方程，就是所求的切线方程；（2）设切点，首先求在切点处的切线方程，即求和，然后因为切线过点，所以将原点代入切线方程，转化为关于的方程，求出切点，最后再整理切线方程.试题解析：（1）在点处的切线的斜率，切线的方程为；（2）设切点为，则直线的斜率为，直线的方程为：．又直线过点，，整理，得，，，的斜率，直线的方程为，切点坐标为．【考点】本题主要考查导数的几何意义，直线方程的点斜式。

佳二中2015—2016学年度下学期期中考试高二数学理科试卷命题教师：夏 萍 审题教师: 林 雪第Ⅰ卷（共60分）一、选择题（60分，每题5分）1.若复数z 满足(1)2z i i +=（i 为虚数单位），则||z =（ ）2.如图，一环形花坛分成A B C D ，，，四块，现有4种不同的花供选种，要求在每块里种1种花，且相邻的2块种不同的花，则不同的种法总数为（ ） A ．96B ．84C ．60D ．483.甲、乙两人从4门课程中各选修2门，则甲、乙所选的课程中恰有1门相同的选法有（ ） A ．6种 B.12种 C.24种 D.30种4.设()121222104321x a x a x a a xx x ++++=+++ ,则=0a ( )A ．256B ．0C ．1-D ．15.随机变量Y ～),(p n B ，且() 3.6E Y =,16.2)(=Y D ，则此二项分布是（ ） A. (4,0.9)B B. (9,0.4)B C. (18,0.2)B D. (36,0.1)B6.设1nx ⎛⎫ ⎪⎝⎭的展开式的各项系数的和为P ，所有二项式系数的和为S ，若272P S +=，则n为（ ）A ．4B ．5C ．6D ．87.甲、乙两人独立解答某道题，解错的概率分别为a 和b ，那么两人都解对此题的概率是（ ） A ．1ab - B ．()()11a b -- C ．()()111a b --- D ．()()11a b b a -+-8.将甲、乙、丙、丁四名学生分到三个不同的班，每个班至少分到一名学生，且甲、乙两名学生不能分到同一个班，则不同分法的种数为（ ）A. 18B. 24C. 30D. 369.()()()(),0f x g x g x ≠分别是定义在R 上的奇函数和偶函数，当0x <时，()()()()f x g x f x g x ''<，且()()()30,0f x f g x -=<的解集为（ ） A ．（－∞，－3）∪（3，+∞）B ．（－3，0）∪（0，3）C ．（－3，0）∪（3，+∞）D ．（－∞，－3）∪（0，3）10.曲线32y x =+上的任意一点P 处切线的斜率的取值范围是（ ）A ．)+∞ B. )+∞ C. ()+∞ D. [)+∞ 11.310(1)(1)x x -+的展开式中，5x 的系数是（ ） A. 297-B.252-C. 297D. 20712. 若10109910103)1()1()1(+++++++=+x a x a x a a x x ，则2a = ( ) A ．48 B ．42 C ． -48 D ．-42第Ⅱ卷（共90分）二、填空题（20分，每题5分）13.已知随机变量X 服从正态分布2(0)N σ，且(20)P X -≤≤0.4=则(2)P X >= ．14.若(0)1P X p ==-，(1)P X p ==，则(23)E X -=15.甲、乙、丙3人站到共有7级的台阶上，若每级台阶最多站2人，同一级台阶上的人不区分站的位置，则不同的站法种数是 （用数字作答）16.如图，点A 的坐标为()1,0 ，点C 的坐标为()2,4 ，函数()2f x x = ，若在矩形ABCD 内随机取一点，则此点取自阴影部分的概率等于 ．三、解答题（70分，每题10~12分）17（本题10分）为推动乒乓球运动的发展，某乒乓球比赛允许不同协会的运动员组队参加.现有来自甲协会的运动员3名，其中种子选手2名；乙协会的运动员5名，其中种子选手3名.从这8名运动员中随机选择4人参加比赛.(1)设A 为事件“选出的4人中恰有2 名种子选手，且这2名种子选手来自同一个协会”求事件A 发生的概率；(2)设X 为选出的4人中种子选手的人数，求随机变量X 的分布列和数学期望18（本题12分）在四棱锥P ABCD -中，PA ⊥平面ABCD ，ABC ∆是正三角形，AC 与BD 的交点M 恰好是AC 中点，又4PA AB ==，120CDA ∠=，点N 在线段PB 上，且（1）求证：BD PC ⊥；（2）求证：//MN 平面PDC ; （3）求二面角A PC B --的余弦值．19（本题12分）已知过原点的动直线l 与圆221:650C x y x +-+=相交于不同的两点A ，B . （1）求圆1C 的圆心坐标；（2）求线段AB 的中点M 的轨迹C 的方程；（3）是否存在实数k ，使得直线:(4)L y k x =-与曲线C 只有一个交点：若存在，求出k 的取值范围；若不存在，说明理由.20（本题12分）已知2件次品和3件正品放在一起，现需要通过检测将其区分，每次随机检测一件产品，检测后不放回，直到检测出2件次品或者检测出3件正品时检测结果.（1）求第一次检测出的是次品且第二次检测出的是正品的概率（2）已知每检测一件产品需要费用100元，设X 表示直到检测出2件次品或者检测出3件正品时所需要的检测费用（单位：元），求X 的分布列和均值（数学期望）21（本题12分）衡水市为“市中学生知识竞赛”进行选拔性测试，且规定：成绩大于或等于90分的有参赛资格，90分以下（不包括90分）的则被淘汰。

2014—2015学年度下学期期末考试高二数学(文科)试卷考试说明：本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分150分，考试时间120分钟。

（1） 答题前，考生先将自己的姓名、班级填写清楚，考条粘贴到指定位置。

（2） 选择题用2B 铅笔作答。

（3） 请按照题号顺序在各题目的答题区域内作答，在草稿纸、试题上答题无效。

（4） 保持卡面清洁，不得折叠，不要弄破、弄皱，不准使用涂改液、刮纸刀。

第Ⅰ卷（共60分）一、选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的） 1．设i 是虚数单位，复数iai-+21为纯虚数，则实数a 为（ ） A. 2 B. -2 C.21- D.212．设集合{}06|2<-+∈=x x R x M ，{}2|1||≤-∈=x R x N . 则N M = （ ） A ．(-3，-2] B ．[-2，-1) C ．[-1，2) D ．[2，3)3．甲、乙、丙、丁四位同学各自对A ，B 两变量的线性相关性做试验，并用回归分析方法分别求得相关系数r 与残差平方和m 如下表：A ． 甲B ．乙C ．丙D ．丁 4．函数2()lg(31)f x x =+的定义域是 （ ）A ．1(,)3-+∞B ．1(,1)3-C ．11(,)33-D ．1(,)3-∞-5．若集合{}|lg ,S y y x x R +==∈，{}2|1,T y y x x R ==-∈，则S T = （ ）A ．SB ．TC ．φD ．以上都不对6. 下列各式中成立的一项是（ ）A ．7177)(m n mn =B ．31243)3(-=-AC ．43433)(y x y x +=+D ．3339=7．函数y ＝log 0.6(6＋x －x 2)的单调增区间是( )A ．(－∞，12]B ．[12，＋∞)C ．(－2，12]D ．[12，3)8、已知函数)(x f y =为奇函数，且当0>x 时32)(2+-=x x x f ，则当0<x 时，)(x f 的解析式为（ ）A. 32)(2-+-=x x x fB. 32)(2+-=x x x fC. 32)(2---=x x x f D. 32)(2+--=x x x f9．“a ≠1或b ≠2”是“a ＋b ≠3”的 （ ） A. 充要条件 B. 充分不必要条件 C. 必要不充分条件 D.既不充分也不必要10．已知函数错误！未找到引用源。

佳二中2015—2016学年度上学期期中考试 高二语文试卷 命题教师：胡忠慧 审题教师:任怀顺 考试说明：本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分150分，考试时间150分钟。

答题前，考生先将自己的姓名、准考证号码填写清楚； 请按照题号顺序在各题目的答题区域内作答，在草稿纸、试题上答题无效。

保持卡面清洁，不得折叠，不要弄破、弄皱，不准使用涂改液、刮纸刀。

第Ⅰ卷（共72分） 一、现代文阅读（9分，每小题3分） 阅读下面的文字，完成1－3题 书法文化即指书法本身的文化性和书法背后隐藏的文化元素。

书法背后隐藏的文化元素包括技法的哲理性、内容的诗意性、印章的渲染性等。

通过由点而线的书写产生的笔画，却有一种力的运动意味，使一个个体现了自然形体结构规律的文字，产生了俨若筋骨血肉的审美效果。

有人说：“书法是哲学的艺术。

”这个说法虽然不够准确，但在书法的技法中却包含了一种辩证美的内涵，体现了一种具有哲学意义的线条艺术，创造了一种天人合一的高妙境界。

线条在形态上表现出长短、曲直、大小、方圆、正斜，字形有一疏一密、一虚一实、一方一圆、一大一小、一离一合、一巧一拙的矛盾统一……有矛盾，才生动，有生动才会产生艺术。

当然，书法艺术的哲学意味并不只限于技法，在书法的形式图像、气韵境 界和人格修为中也表现为哲学之思。

如果点画拙劣，线条粗俗难看，很容易暴露轻浮浅薄、华而不实的老底。

内容的诗意性，既表现为文字的准确性与文学性，又表现为内容的诗意与书法的情韵相互贯通，所以文学语言和书法线条有密切的关联性。

文字的准确性是最基本的要求，然而用字的准确性并不那么简单，一方面是文字的准确性涉及文字的功底；另一方面是书法字法的准确性涉及书法研究的深度与广度。

用毛笔书写古代经典、诗词曲赋，如“无可奈何花落去，似曾相识燕归来”，“小园香径独徘徊”，总能从中找到一份情思，或从经史子集中找到先人的哲思，或从李杜苏黄的诗文中找到书法创作的灵感。