用Matlab画出信号的时域波形及频谱,观察它们的关系。18页PPT

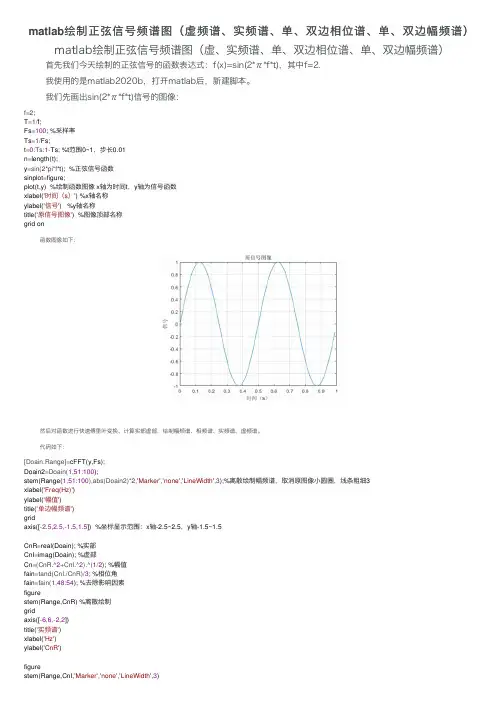
matlab 绘制正弦信号频谱图（虚频谱、实频谱、单、双边相位谱、单、双边幅频谱）matlab绘制正弦信号频谱图（虚、实频谱、单、双边相位谱、单、双边幅频谱） ⾸先我们今天绘制的正弦信号的函数表达式：f(x)=sin(2*π*f*t)，其中f=2. 我使⽤的是matlab2020b，打开matlab后，新建脚本。

我们先画出sin(2*π*f*t)信号的图像： 函数图像如下： 然后对函数进⾏快速傅⾥叶变换、计算实部虚部，绘制幅频谱、相频谱、实频谱、虚频谱。

代码如下：f=2;T =1/f;Fs =100; %采样率Ts =1/Fs;t =0:Ts:1-Ts; %t 范围0~1，步长0.01n =length(t);y =sin(2*pi*f*t); %正弦信号函数sinplot =figure;plot(t,y) %绘制函数图像 x 轴为时间t ，y 轴为信号函数xlabel('时间（s ）') %x 轴名称ylabel('信号') %y 轴名称title('原信号图像') %图像顶部名称grid on[Doain,Range]=cFFT(y,Fs);Doain2=Doain(1,51:100);stem(Range(1,51:100),abs(Doain2)*2,'Marker','none','LineWidth',3);%离散绘制幅频谱，取消原图像⼩圆圈，线条粗细3xlabel('Freq(Hz)')ylabel('幅值')title('单边幅频谱')gridaxis([-2.5,2.5,-1.5,1.5]) %坐标显⽰范围：x 轴-2.5~2.5，y 轴-1.5~1.5CnR =real(Doain); %实部CnI =imag(Doain); %虚部Cn =(CnR.^2+CnI.^2).^(1/2); %幅值fain =tand(CnI./CnR)/3; %相位⾓fain =fain(1,48:54); %去除影响因素figurestem(Range,CnR) %离散绘制gridaxis([-6,6,-2,2])title('实频谱')xlabel('Hz')ylabel('CnR')figurestem(Range,CnI,'Marker','none','LineWidth',3)axis([-2.5,2.5,-1,1])title('虚频谱')xlabel('Hz')ylabel('CnI')figurestem(Range,Cn,'Marker','none','LineWidth',3)gridaxis([-2.5,2.5,-0.5,1])title('双边幅频谱')xlabel('Hz')ylabel('|Cn|')figurestem(Range(1,48:54),-fain,'Marker','none','LineWidth',3) gridaxis([-2.5,2.5,-2.5,2.5])title('双边相频谱')xlabel('Hz')ylabel('相位⾓')figurefain2=fain(1,4:7);stem(Range(1,51:54),-fain2,'Marker','none','LineWidth',3) gridaxis([-2.5,2.5,-2.5,1.5])title('单边相频谱')xlabel('Hz')ylabel('相位⾓')figureplot(t,y)xlabel('时间（s）')ylabel('信号')title('原信号图像')grid onfunction[X,freq]=cFFT(x,Fs) %修正N=length(x);if mod(N,2)==0k=-N/2:N/2-1;elsek=-(N-1)/2:(N-1)/2;endT=N/Fs;freq=k/T;X=fft(x)/N;X=fftshift(X);end 绘制图像如下： 最后附上完整代码：f=2;T=1/f;Fs=100;Ts=1/Fs;t=0:Ts:1-Ts;n=length(t);y=sin(2*pi*f*t);sinplot=figure[Doain,Range]=cFFT(y,Fs);Doain2=Doain(1,51:100);stem(Range(1,51:100),abs(Doain2)*2,'Marker','none','LineWidth',3); xlabel('Freq(Hz)')ylabel('幅值')title('单边幅频谱')gridaxis([-2.5,2.5,-1.5,1.5])CnR=real(Doain);CnI=imag(Doain);Cn=(CnR.^2+CnI.^2).^(1/2);fain=tand(CnI./CnR)/3;fain=fain(1,48:54);figurestem(Range,CnR)gridaxis([-6,6,-2,2])title('实频谱')xlabel('Hz')ylabel('CnR')figurestem(Range,CnI,'Marker','none','LineWidth',3)gridaxis([-2.5,2.5,-1,1])title('虚频谱')xlabel('Hz')ylabel('CnI')figurestem(Range,Cn,'Marker','none','LineWidth',3)gridaxis([-2.5,2.5,-0.5,1])title('双边幅频谱')xlabel('Hz')ylabel('|Cn|')figurestem(Range(1,48:54),-fain,'Marker','none','LineWidth',3)gridaxis([-2.5,2.5,-2.5,2.5])title('双边相频谱')xlabel('Hz')ylabel('相位⾓')figurefain2=fain(1,4:7);stem(Range(1,51:54),-fain2,'Marker','none','LineWidth',3)gridaxis([-2.5,2.5,-2.5,1.5])title('单边相频谱')xlabel('Hz')ylabel('相位⾓')figureplot(t,y)xlabel('时间（s）')ylabel('信号')grid onfunction[X,freq]=cFFT(x,Fs)N=length(x);if mod(N,2)==0k=-N/2:N/2-1;elsek=-(N-1)/2:(N-1)/2;endT=N/Fs;freq=k/T;X=fft(x)/N;X=fftshift(X);end延迟T/4后的代码fo=2;T=1/fo;Fs=100;Ts=1/Fs;t=0:Ts:1-Ts;n=length(t);y=sin(2*pi*fo*t-pi/2);sinplot=figure[Doain,Range]=centeredFFT(y,Fs);Doain2=Doain(1,51:100);stem(Range(1,51:100),abs(Doain2)*2,'Marker','none','LineWidth',3); xlabel('Freq(Hz)')ylabel('幅值')title('单边幅频谱')gridaxis([-2.5,2.5,-1,1.5])CnR=real(Doain);CnI=imag(Doain);Cn=(CnR.^2+CnI.^2).^(1/2);fain=tand(CnR./CnI)*3.2;fain=fain(1,48:54);figurestem(Range,CnR,'Marker','none','LineWidth',3)gridaxis([-2.5,2.5,-1,1])title('实频谱')xlabel('Hz')ylabel('CnR')figurestem(Range,CnI)gridaxis([-6,6,-2,2])title('虚频谱')xlabel('Hz')ylabel('CnI')figurestem(Range,Cn,'Marker','none','LineWidth',3)gridaxis([-2.5,2.5,-0.5,1])title('双边幅频谱')xlabel('Hz')ylabel('|Cn|')figurestem(Range(1,48:54),abs(fain),'Marker','none','LineWidth',3)gridaxis([-2.5,2.5,-4,4])title('双边相频谱')xlabel('Hz')figurefain2=fain(1,4:7);stem(Range(1,51:54),abs(fain2),'Marker','none','LineWidth',3)gridaxis([-2.5,2.5,-4,4])title('单边相频谱')xlabel('Hz')ylabel('相位⾓')figureplot(t,y)xlabel('时间（s）')ylabel('y')title('原信号图像')grid onfunction[X,freq]=centeredFFT(x,Fs)N=length(x);if mod(N,2)==0k=-N/2:N/2-1; % N evenelsek=-(N-1)/2:(N-1)/2; % N oddendT=N/Fs;freq=k/T; %the frequency axisaccordinglyX=fft(x)/N;X=fftshift(X);End⽂件链接： （matlabxinhao1⽂件是本⽂所提到的信号，matlabxinhao2是将本⽂提到的信号延迟T/4之后的信号绘图。

目录目录………………………………………………………………………………………………正文…………………………………………………………………………………………………1 基本波形………………………………………………………………………………1.1正弦波…………………………………………………………………………1.2三角波和锯齿波………………………………………………………………1.3方波和不对称方波……………………………………………………1.4伪码……………………………………………………………………………………2调幅………………………………………………………………………………2.1常规双边带调幅（AM）……………………………………………………………2.2抑制载波双边带调幅(DSB)……………………………………………………………2.3 单边带调幅（SSB）…………………………………………………………………3.4振幅键控（ASK）……………………………………………………………………3调频………………………………………………………………………………3.1单音频调频……………………………………………………………………………3.2锯齿波调频……………………………………………………………………………3.3 三角波调频…………………………………………………………………………3.4 移频键控（FSK）………………………………………………………………………4 调相……………………………………………………………………………………………4.1 方波调相…………………………………………………………………………………4.2 伪码调相…………………………………………………………………………………一、 基本波形（1）正弦波)t 2sin()(θ+***=m f pi t sm f 为正弦波频率，θ为初始相位理论频谱：)]()([)(m m j S ωωδωωδπω--+=m ω为正弦波角频率，且m m f *2πω= 时域波形：图1-1-1 正弦波的时域波形（横坐标为时间t ，纵坐标为幅度） 图1-1-1为正弦波的时域波形。

辽宁科技大学毕业设计（论文）第I页基于MATLAB的信号波形与频谱分析摘要本文利用MATLAB软件进行信号频谱分析的设计，并通过GUI界面(图形用户界面)实现信号频谱分析的动态设计。

用户可与计算机交互式地进行对象参数的设置、控制算法的选取、以及对离散信号与连续信号的动态频谱分析。

并利用MATLAB内嵌的Simulink模块，实现系统的信号频谱分析，满足不同用户的不同要求。

MATLAB的GUIDE是专门用于图形用户界面（GUI）程序设计的快速开发环境，本文从介绍GUIDE入手结合具体的软件图形界面实例，给出了利用GUIDE制作图形用户界面的基本方法。

通过本文的研究得出利用GUIDE设计的仿真界面不仅可以对离散信号与连续信号的动态频谱进行相关分析，而且还可以对此问题作进一步的预测和分析。

基于GUIDE技术制作的图形用户界面，具有友好性，开放性，方便科研人员不断地研究和扩充。

关键词频谱分析；GUI；SIMULINK；MATLAB辽宁科技大学毕业设计（论文）第II页AbstractUsing MATLAB software for signal spectrum analysis of the design, and through the GUI interface (graphical user interface) signal spectrum analysis of the dynamic design. Users can interactively with the computer targeting parameters for the establishment, control algorithm selection, and the discrete signals and continuous signal analysis of the dynamic spectrum. MATLAB and Simulink embedded module, the signal system to achieve spectral analysis, meet the needs of different users with different needs.MATLAB GUIDE is devoted to the graphical user interface (GUI) design procedures for the rapid development environment, This paper introduced GUIDE start from the context of the specific examples of graphical interface software, GUIDE is produced using a graphical user interface methods. Through this paper, the study of the use of simulation GUIDE interface design can not only right for discrete signal and the signal dynamic spectrum analysis, but also the issue for further analysis and forecasts. GUIDE technology based on the production of graphical user interface is friendly and open, facilitate researchers continue to study and expanded.Keywords Spectrum Analysis ；GUI；SIMULINK；MATLAB辽宁科技大学毕业设计（论文）第III页目录摘要 (I)Abstract.................................................................................................I I 第1章绪论 . (1)1.1 MATLAB应用软件简介 (1)1.2课题研究的内容 (2)1.2.1信号的频谱分析 (2)1.2.2信号频谱分析的原理 (3)1.2.3频谱分析与显示原理 (3)1.2.4对三阶交调进行模拟分析 (3)1.2.5伪彩色编码的动态频谱图显示 (4)1.2.6宽带频谱图与窄带频谱图 (5)1.3 GUI界面设计实现 (5)1.4 SIMULINK (6)1.4.1 SIMULINK模型与文件 (7)1.4.2 SIMULINK仿真原理 (7)第2章MATLAB工具箱的概述及GUI界面的简介 (8)2.1引言 (8)2.2句柄图形及图形用户界面 (8)2.3 GUIDE (8)2.4编制回调程序 (10)2.5主界面 (10)2.6子界面 (11)2.7基于MATLAB信号处理工具箱的数字滤波器设计与仿真 (11)2.8带通滤波器设计实例 (12)第3章GUI界面下噪声信号的频谱分析与实现 (14)3.1概述 (14)3.2 MATLAB信号处理工具箱介绍及功能 (14)3.2.1MATLAB工具箱介绍 (14)辽宁科技大学毕业设计（论文）第IV页3.2.2工具箱功能 (15)3.3通风机噪声信号的采集方法 (17)3.4噪声信号的频谱分析 (18)3.5GUI界面下噪声频谱分析的实现 (19)结论 (22)致谢 (23)参考文献 (24)附录A (25)附录B (27)辽宁科技大学毕业设计（论文）第1页第1章绪论1.1 MATLAB应用软件简介MATLAB是一种功能强大的科学计算和工程仿真软件，它的交互式集成界面能够帮助用户快速地完成数值分析、矩阵运算、数字信号处理、仿真建模、系统控制和优化等功能。

基于matlab 的时域信号采样及频谱分析一：主要设计方法与步骤：1. 画出连续时间信号0sin()()t u t Ω-at x(t)=Ae 的时域波形及其幅频特性曲线，其中，幅度因子444.128A =，衰减因子222.144a =，模拟角频率0222.144Ω=；2. 对信号()x t 进行采样，得到采样序列0()sin()()ant x n Ae nT u n -=Ω，050n ≤≤，其中，1sT f =为采样间隔，通过改变采样频率可改变T ，画出采样频率分别为200H z ，500Hz ，1000Hz 时的采样序列波形；3. 对不同采样频率下的采样序列进行频谱分析，绘制其幅频和相频曲线，对各频率下采样序列()x n 和()x t 的幅频曲线有无差别，如有差别说明原因；4. 设系统单位抽样响应为5()()h n R n =，求解当输入为()x n 时的系统响应()y n ，画出()x n ，()h n ，()y n 的时域波形及幅频特性曲线，并利用结果验证卷积定理的正确性（此内容将参数设置为444.128A =，222.144a =，0222.144W =，1000fs =）； 5. 用FFT 对信号()x n ，()h n ，()y n 进行频谱分析，观察与4中结果有无差别； 6. 由采样序列()x n 恢复出连续时间信号1()x t ，画出其时域波形，对比1()x t 与原来的连续时间信号()x t 的时域波形，计算并记录两者最大误差。

二：详细程序及仿真波形分析1.连续时间信号()x t 及其200/500/1000Hz Hz Hz 频率抽样信号函数()x n % 绘制信号x(n)的幅度谱和相位谱 clcclear all close alln=0:50 % 定义序列的长度是50A=input('请入A 的值A:') % 设置信号的有关参数 a=input('请入a 的值a:')w0=input('请入w0的值w0:') T1=0.005 T2=0.002 T3=0.001 T0=0.001x=A*exp(-a*n*T0).*sin(w0*n*T0) y1=A*exp(-a*n*T1).*sin(w0*n*T1) y2=A*exp(-a*n*T2).*sin(w0*n*T2) y3=A*exp(-a*n*T3).*sin(w0*n*T3) close allsubplot(2,1,1)stem(n,x) % 绘制x(n)的图形 grid ontitle('离散时间信号') subplot(2,1,2) plot(n,x) grid ontitle('连续时间信号')05101520253035404550离散时间信号5101520253035404550-50050100150连续时间信号figure(2)subplot(3,1,1) stem(n,y1) grid ontitle('200Hz 理想采样信号序列') subplot(3,1,2) stem(n,y2) grid ontitle('500Hz 连续时间信号') subplot(3,1,3) stem(n,y3)grid ontitle('1000Hz 连续时间信号')5101520253035404550200Hz 理想采样信号序列05101520253035404550500Hz 连续时间信号051015202530354045501000Hz 连续时间信号k=-25:25W=(pi/12.5)*k w=W/piY1=y1*exp(-j*pi/12.5).^(n'*k) figure (3) subplot(2,1,1) plot(w,abs(Y1)) gridxlabel('w') ylabel('幅度')title('200Hz 理想采样信号序列的幅度谱') axis([-2 2 0 1000]) subplot(2,1,2) plot(w,angle(Y1)) gridxlabel('w') ylabel('幅角')title('200Hz 理想采样信号序列的相位谱')-2-1.5-1-0.500.51 1.5205001000w幅度-2.5-2-1.5-1-0.50.511.52-4-2024w幅角200Hz 理想采样信号序列的相位谱Y2=y2*(exp(-j*pi/12.5)).^(n'*k) figure (4) subplot(2,1,1) plot(w,abs(Y2)) gridxlabel('w') ylabel('幅度')title('500Hz 理想采样信号序列的幅度谱') axis([-2 2 0 1000]) subplot(2,1,2) plot(w,angle(Y2)) gridxlabel('w') ylabel('幅角')title('500Hz 理想采样信号序列的相位谱')-2-1.5-1-0.500.51 1.5205001000w幅度-2.5-2-1.5-1-0.50.511.52-4-2024w幅角500Hz 理想采样信号序列的相位谱Y3=y3*(exp(-j*pi/12.5)).^(n'*k) figure (5) subplot(2,1,1) plot(w,abs(Y3)) gridxlabel('w') ylabel('幅度')title('1000Hz 理想采样信号序列的幅度谱') axis([-2 2 0 1000]) subplot(2,1,2) plot(w,angle(Y3)) gridxlabel('w') ylabel('幅角')title('1000Hz 理想采样信号序列的相位谱')-2-1.5-1-0.500.51 1.5205001000w幅度-2.5-2-1.5-1-0.50.511.52-4-2024w幅角1000Hz 理想采样信号序列的相位谱分析：采样频率为1000Hz 时没有失真，500Hz 时有横线，产生失真，200Hz 时横线加长，失真加大。

利用Matlab绘制正弦信号的频谱图并做相关分析一、作业要求：1、信号可变（信号的赋值、相位、频率可变）；2、采样频率fs可变；3、加各种不同的窗函数并分析其影响；4、频谱校正；5、频谱细化。

二、采用matlab编写如下程序：clear;clf;fs=100;N=1024; %采样频率和数据点数A=20;B=30;C=0.38;n=0:N-1;t=n/fs; %时间序列x=A*sin(2*pi*B*t+C); %信号y=fft(x,N); %对信号进行傅里叶变换yy=abs(y); %求得傅里叶变换后的振幅yy=yy*2/N; %幅值处理f=n*fs/N; %频率序列subplot(3,3,1),plot(f,yy); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图1：fs=100，N=1024');grid on;%两种信号叠加，x=A*sin(2*pi*B*t+C)+2*A*sin(2*pi*1.5*B*t+2.5*C); %信号y=fft(x,N); %对信号进行傅里叶变换yy=abs(y); %求得傅里叶变换后的振幅yy=yy*2/N; %幅值处理f=n*fs/N; %频率序列subplot(3,3,2),plot(f,yy); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图2：fs=100,N=1024，两种信号叠加');grid on;%加噪声之后的图像x=A*sin(2*pi*B*t+C)+28*randn(size(t));y=fft(x,N);yy=abs(y);yy=yy*2/N; %幅值处理subplot(3,3,3),plot(f(1:N/2.56),yy(1:N/2.56));xlabel('频率/\itHz');ylabel('振幅');title('图3：fs=100,N=1024混入噪声');grid on;%改变采样点数N=128N=128;n=0:N-1;t=n/fs; %时间序列x=A*sin(2*pi*B*t+C); %信号y=fft(x,N); %对信号进行傅里叶变换yy=abs(y); %求得傅里叶变换后的振幅yy=yy*2/N; %幅值处理f=n*fs/N; %频率序列subplot(3,3,4),plot(f(1:N/2.56),yy(1:N/2.56)); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图4：fs=100，N=128');grid on;%改变采样频率为200Hz时的频谱fs=400;N=1024;n=0:N-1;t=n/fs;x=A*sin(2*pi*B*t+C); %信号y=fft(x,N); %对信号进行快速傅里叶变换yy=abs(y); %求取傅里叶变换的振幅yy=yy*2/N; %幅值处理f=n*fs/N;subplot(3,3,5),plot(f(1:N/2.56),yy(1:N/2.56)); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图5：fs=400，N=1024');grid on;%加三角窗函数fs=100;N=1024; %采样频率和数据点数n=0:N-1;t=n/fs; %时间序列x=A*sin(2*pi*B*t+C); %信号window=triang(N);%生成三角窗函数x=x.*window';%加窗函数y=fft(x,N); %对信号进行傅里叶变换yy=abs(y); %求得傅里叶变换后的振幅yy=yy*2/N; %幅值处理f=n*fs/N; %频率序列subplot(3,3,6),plot(f(1:N/2.56),2*yy(1:N/2.56)); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图6：fs=100,N=1024,加三角窗函数');grid on;%加海明窗函数后的频谱fs=100;N=1024;n=0:N-1;t=n/fs;x=A*sin(2*pi*B*t+C); %信号window=hamming(N);%生成海明窗函数x=x.*window';%加窗函数y=fft(x,N); %对信号进行快速傅里叶变换yy=abs(y); %求取傅里叶变换的振幅yy=yy*2/N; %幅值处理f=n*fs/N;subplot(3,3,7),plot(f(1:N/2.56),1.852*yy(1:N/2.56)); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图7：fs=100，N=1024,加海明窗函数');grid on;%加汉宁窗函数后的频谱fs=100;N=1024;n=0:N-1;t=n/fs;x=A*sin(2*pi*B*t+C); %信号window=hanning(N);%生成汉宁窗函数x=x.*window';%加窗函数y=fft(x,N); %对信号进行快速傅里叶变换yy=abs(y); %求取傅里叶变换的振幅yy=yy*2/N; %幅值处理f=n*fs/N;subplot(3,3,8),plot(f(1:N/2.56),2*yy(1:N/2.56)); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图8：fs=100，N=1024,加汉宁窗函数');grid on;三、运行结果如下：四、分析与结论：1）从所做图像可以看出，信号的幅值均小于真实值，说明在截断信号时存在泄露。

目录目录………………………………………………………………………………………………正文…………………………………………………………………………………………………1 基本波形………………………………………………………………………………1.1正弦波…………………………………………………………………………1.2三角波和锯齿波………………………………………………………………1.3方波和不对称方波……………………………………………………1.4伪码……………………………………………………………………………………2调幅………………………………………………………………………………2.1常规双边带调幅（AM）……………………………………………………………2.2抑制载波双边带调幅(DSB)……………………………………………………………2.3 单边带调幅（SSB）…………………………………………………………………3.4振幅键控（ASK）……………………………………………………………………3调频………………………………………………………………………………3.1单音频调频……………………………………………………………………………3.2锯齿波调频……………………………………………………………………………3.3 三角波调频…………………………………………………………………………3.4 移频键控（FSK）………………………………………………………………………4 调相……………………………………………………………………………………………4.1 方波调相…………………………………………………………………………………4.2 伪码调相…………………………………………………………………………………一、 基本波形（1）正弦波)t 2sin()(θ+***=m f pi t sm f 为正弦波频率，θ为初始相位理论频谱：)]()([)(m m j S ωωδωωδπω--+=m ω为正弦波角频率，且m m f *2πω= 时域波形：图1-1-1 正弦波的时域波形（横坐标为时间t ，纵坐标为幅度） 图1-1-1为正弦波的时域波形。

利用Matlab绘制正弦信号的频谱图并做相关分析一、作业要求：1、信号可变（信号的赋值、相位、频率可变）；2、采样频率fs可变；3、加各种不同的窗函数并分析其影响；4、频谱校正；5、频谱细化。

二、采用matlab编写如下程序：clear;clf;fs=100;N=1024; %采样频率和数据点数A=20;B=30;C=0.38;n=0:N-1;t=n/fs; %时间序列x=A*sin(2*pi*B*t+C); %信号y=fft(x,N); %对信号进行傅里叶变换yy=abs(y); %求得傅里叶变换后的振幅yy=yy*2/N; %幅值处理f=n*fs/N; %频率序列subplot(3,3,1),plot(f,yy); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图1：fs=100，N=1024');grid on;%两种信号叠加，x=A*sin(2*pi*B*t+C)+2*A*sin(2*pi*1.5*B*t+2.5*C); %信号y=fft(x,N); %对信号进行傅里叶变换yy=abs(y); %求得傅里叶变换后的振幅yy=yy*2/N; %幅值处理f=n*fs/N; %频率序列subplot(3,3,2),plot(f,yy); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图2：fs=100,N=1024，两种信号叠加');grid on;%加噪声之后的图像x=A*sin(2*pi*B*t+C)+28*randn(size(t));y=fft(x,N);yy=abs(y);yy=yy*2/N; %幅值处理subplot(3,3,3),plot(f(1:N/2.56),yy(1:N/2.56));xlabel('频率/\itHz');ylabel('振幅');title('图3：fs=100,N=1024混入噪声');grid on;%改变采样点数N=128N=128;n=0:N-1;t=n/fs; %时间序列x=A*sin(2*pi*B*t+C); %信号y=fft(x,N); %对信号进行傅里叶变换yy=abs(y); %求得傅里叶变换后的振幅yy=yy*2/N; %幅值处理f=n*fs/N; %频率序列subplot(3,3,4),plot(f(1:N/2.56),yy(1:N/2.56)); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图4：fs=100，N=128');grid on;%改变采样频率为200Hz时的频谱fs=400;N=1024;n=0:N-1;t=n/fs;x=A*sin(2*pi*B*t+C); %信号y=fft(x,N); %对信号进行快速傅里叶变换yy=abs(y); %求取傅里叶变换的振幅yy=yy*2/N; %幅值处理f=n*fs/N;subplot(3,3,5),plot(f(1:N/2.56),yy(1:N/2.56)); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图5：fs=400，N=1024');grid on;%加三角窗函数fs=100;N=1024; %采样频率和数据点数n=0:N-1;t=n/fs; %时间序列x=A*sin(2*pi*B*t+C); %信号window=triang(N);%生成三角窗函数x=x.*window';%加窗函数y=fft(x,N); %对信号进行傅里叶变换yy=abs(y); %求得傅里叶变换后的振幅yy=yy*2/N; %幅值处理f=n*fs/N; %频率序列subplot(3,3,6),plot(f(1:N/2.56),2*yy(1:N/2.56)); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图6：fs=100,N=1024,加三角窗函数');grid on;%加海明窗函数后的频谱fs=100;N=1024;n=0:N-1;t=n/fs;x=A*sin(2*pi*B*t+C); %信号window=hamming(N);%生成海明窗函数x=x.*window';%加窗函数y=fft(x,N); %对信号进行快速傅里叶变换yy=abs(y); %求取傅里叶变换的振幅yy=yy*2/N; %幅值处理f=n*fs/N;subplot(3,3,7),plot(f(1:N/2.56),1.852*yy(1:N/2.56)); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图7：fs=100，N=1024,加海明窗函数');grid on;%加汉宁窗函数后的频谱fs=100;N=1024;n=0:N-1;t=n/fs;x=A*sin(2*pi*B*t+C); %信号window=hanning(N);%生成汉宁窗函数x=x.*window';%加窗函数y=fft(x,N); %对信号进行快速傅里叶变换yy=abs(y); %求取傅里叶变换的振幅yy=yy*2/N; %幅值处理f=n*fs/N;subplot(3,3,8),plot(f(1:N/2.56),2*yy(1:N/2.56)); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图8：fs=100，N=1024,加汉宁窗函数');grid on;三、运行结果如下：四、分析与结论：1）从所做图像可以看出，信号的幅值均小于真实值，说明在截断信号时存在泄露。

中文摘要利用DFT分析信号频谱的基本流程，阐述了频谱分析过程中误差形成的原因及减小分析误差的主要措施。

实例列举了基于MATLAB GUI编制的信号分析系统，集成了常用的信号分析方法，系统界面友好，使用方便，与传统处理方法相比效率更高。

关键词：MATLAB GUI；信号分析；频谱分析Analysis of Signal Waveform and FrequencySpectrum Based on MATLABAbstractThe use of DFT analysis of signal spectrum basic process , elaborated spectral analysis in the process of formation and reduce error analysis error measures. The examples cited MATLAB GUI system based on the signal analysis system, integrated with the commonly used method of signal analysis, the system friendly interface, convenient use, compared with the traditional processing approaches more efficient.Key words: MATLAB GUI; signal analysis; spectrum analysisI目录中文摘要 (I)Abstract (I)引言 (3)1.信号的概述 (3)1.3 信号频谱的误差分析 (5)2.信号的频谱分析 (6)2.1 软件介绍 (7)2.1.1 MATLAB软件介绍 (7)2.1.2 GUI软件介绍 (7)2.2 信号的频谱分析 (7)2.2.1 信号谱分析的原理 (7)2.2.2 信号谱编程思路 (8)3.信号系统频谱分析实例 (9)3.1系统设计 (9)4.结论 (17)参考文献 (18)致谢 (19)II引言信号的频谱分析是利用傅里叶分析的方法，求出与时域描述相对应的频域描述，从中找出信号时域波形相对应的频率函数，从中找出描述该信号频谱结构的变化规律，以达到特征提取的目的。

matlab时域宽度,MATLAB对信号的时域与频域分析%信号的时域和频域分析%信号的频域分析，计算⽅波的DFS(离散傅⾥叶变换)，在60的时窗宽度上⽅波宽度分别为%5到12，并且画出x(n)和DFS(x(n))的杆状图L=5;N=60;k=[-N/2:N/2];xn=[zeros(1,(N-L+1)/2),ones(1,L),zeros(1,(N-L-1)/2)];n=[0:N-1];subplot(221)stem(n,xn);gridaxis([0 60 -0.3 1.3]);title('xn');p=0:N-1;WN=exp(-j*2*pi/N);nk=n'*p;WNnk=WN.^nk;Xk=xn*WNnk;magXk=abs([Xk(N/2+1:N) Xk(1:N/2+1)]);subplot(222)stem(k,magXk);gridaxis([-N/2 N/2 -0.5 5.5]);xlabel('k');ylabel('spectrum');title('DFS:L=5,N=60');L=12;N=60;k=-N/2:N/2;xn=[zeros(1,(N-L+1)/2),ones(1,L),zeros(1,(N-L-1)/2)];n=0:N-1;subplot(223)stem(n,xn);gridaxis([0 60 -0.3 1.3]);title('xn');p=[0:N-1];WN=exp(-j*2*pi/N);nk=n'*p;magXk=abs([Xk(N/2+1:N) Xk(1:N/2+1)]);subplot(224)stem(k,magXk);gridaxis([-N/2 N/2 -0.5 13]);xlabel('k');ylabel('spectrum');title('DFS:L=12,N=60');%频谱分析的若⼲问题%不同时窗正弦信号频谱的分析%1Hz的正弦波仅取10个周期及50个周期，都做4096点FFT，⽐较两者的频谱t=0:0.1:10; %取10或50(将10变成50即可)个周期的进⾏变换y1=sin(2*pi*t);Y1=fft(y1,4096); %4096点的快速傅⾥叶变换Y=fftshift(Y1);c=[0:2047]/409;plot(c,abs(Y(2049:4096)))axis([0 2 -5 60]);title('sin(t)周期 T=10')grid%加窗函数后的频谱特征分析%不加窗函数是正弦谱线与矩形窗频谱的卷积；加窗函数是正弦谱线于汉明窗频谱的卷积%后者的旁瓣⼩得多，但是主谱线宽⼀些t=0.1:0.1:20; %取20个周期y=sin(2*pi*t); %定义1Hz的正弦波w=hamming(200); %定义200长的汉明窗y=y.*w';Y1=fft(y,4096); %4096点的快速傅⾥叶变换Y=fftshift(Y1);c=[0:2047]./409.6;plot(c,abs(Y(2049:4096)))axis([0 3 -5 60]);title('sin(t) 加窗频谱');grid%CZT线性调频Z变换%应⽤CZT变换不在频率轴上均匀采样，对关⼼的部分加⼤采样密度，可以提⾼关⼼部分的f1=13.2;f2=13.41;f3=15;fs=60;n=0:N-1;t=2*pi*n/fs;e=fs/N;n1=0:e:(fs/2)-e;x=sin(f1*t)+sin(f2*t)+sin(f3*t); %三个不同频率正弦信号相加Y1=abs(fft(x)); %⼀般傅⾥叶频谱分析subplot(121)plot(n1,(Y1(1:N/2)));title('fft');grid;M=60; %CZT变换的长度f0=12.6;q=0.05;A=exp(j*2*pi*f0/fs); %CZT变换的起点W=exp(-j*2*pi*q/fs); %CZT变换的倾斜率Y3=czt(x,M,W,A); %CZT变换做频谱分析n2=f0:q:f0+(M-1)*q;subplot(122)plot(n2,abs(Y3));title('czt');grid%常见信号的频谱分析%基础波形 fft(快速傅⾥叶变换)，fftshift(移动傅⾥叶变换的系数)n=2048;t=1:2048;y=zeros(1,n);y(1,[1020:1035])=1; %定义宽度为15的⽅波y1=[zeros(1,1000),ones(1,60),zeros(1,988)];%定义宽度为60的⽅波subplot(121)plot(t,y,'b',t,y1,'r')axis([850 1200 -0.2 1.3]);title('⽅形图');gridsubplot(122)Y2=fft(y,2048);Y3a=fftshift(Y3);w=-1024:1023;semilogy(w,abs(Y2a),'b',w,abs(Y3a),'r')axis([-500 500 -5 80]);title('⽅波频谱');axis([-250 250 1 100]);grid;%三⾓波n=2048;t=1:2048;y=[zeros(1,800),[1:500],zeros(1,748)]; %定义三⾓波subplot(121)plot(t,y)axis([0 2100 -30 560]);title('三⾓波');gridsubplot(122)Y1=fft(y,2048);Y=fftshift(Y1);c=-1024:1023;yw=log(abs(Y)+eps);plot(c,yw,'r')axis([-104 104 7 12]);title('三⾓波频谱');grid on;%冲击函数n=400;delta=4*pi/n;t=-2*pi:delta:2*pi;y=sinc(t); %定义冲击函数subplot(121)plot(t,y)axis([-7 7 -0.4 1.3]);title('sinc(t)');gridsubplot(122)c=-1024:1023;plot(c,abs(Y))axis([-500 500 -5 40]);title('sinc(t)的频谱');grid%调制信号%双边带调幅fs=1000;t=0:1/fs:.4;fc=250;y=0.4*cos(pi*20*t);x=modulate(y,fc,fs,'amdsb-tc'); %双边带调幅subplot(121)plot(t,x)legend('调幅双边带波形');gridsubplot(122)p=fft(x,1024);p1=fftshift(p);w=0:511;p2=abs(p1);plot(w,p2(1:512));grid;legend('调幅双边带频谱')axis([100 400 -10 100])%⽤直⽅图表⽰调频信号谱m=5; %⽤直⽅图表⽰调制指数为5的调频信号谱分析n=1:10;y1(n)=besseli(n,(i*m),1);z1=real(y1./(i.^(n)));z2=fliplr(z1);y0=besseli(0,(i*m),1);z0=real(y0);z=[z2 z0 z1];axis([-10 10 -.1 .8]);gridtitle('m=5')^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ %四种数字调制⽅法(ASK FSK PSK OQPSK)的频谱图%产⽣码元宽度为64的随机序列%m⽂件n=1:8192;m=1:128;x(n)=randint(1,8192,2);x=[x(n)]';y(n)=zeros(1,8192);z(m)=zeros(1,128);for n=1:8192form=1:128if n==64*m-63z(m)=x(n);if m==ceil(n/64)y([(64*m-63):(64*m)]')=z(m);endendendendn=1:8192;rm2=y(n);%ASK调制n=[1:(2^13)];x1=cos(n.*1e9*2*pi/4e9);run('rm2');X2=rm2;x2=X2';x=x1.*X2;b=.42+.5*cos(2*pi*(n-(2^12))/(2^13))+0.08*...cos(4*pi*(n-(2^12))/(2^13));X=b.*x;x3=[ones(1,64) zeros(1,8128)];y1=X(1:(2^13));y4=x1.*x3;Y1=fft(y1,(2^13));magY1=abs(Y1(1:1:(2^12)+1))/(200);u=(2*w1/pi)*1e9;figure(1)subplot(211)plot(u,magY1,'b',u,magY4,'r');gridtitle('ASKr');axis([4e8,1.6e9,0,1.1])X2=b.*X2;y2=X2(1:(2^13));Y2=fft(y2,(2^13));magY2=abs(Y2(1:1:(2^12)+1))/(200);k1=0:(2^12);w1=(2*pi/(2^13))*k1;u=(2*w1/pi)*1e9;Y3=fft(x3,(2^13));magY3=abs(Y3(1:1:(2^12)+1))/(40); subplot(212)semilogy(u,magY2,'b',u,magY3,'r');gridtitle('ASKr-modulation');axis([0 1.2e9 3e-4 3]);figure(2)subplot(211);plot(n,x2);axis([0 720 -0.2 1.2])subplot(212);plot(n,x);axis([0 720 -1.2 1.2])%FSK调制频谱分析n=[1:(2^13)];d=.13;run('rm2');x2=((2*rm2)-1);x5=cos(.5*n.*((1e8*2*pi/4e8)-d));x4=cos(.5*n.*((1e8*2*pi/4e8)+d));x=cos(.5*n.*((1e8*2*pi/4e8)+d*x2));b=.42+.5*cos(2*pi*(n-(2^12))/(2^13))+0.08*...cos(4*pi*(n-(2^12))/(2^13));X=b.*x;x3=[ones(1,64) zeros(1,8128)];y1=X(1:(2^13));y4=x4.*x3;y5=x5.*x3;Y1=fft(y1,(2^13));magY1=abs(Y1(1:1:(2^12)+1))/(200*2); Y4=fft(y4,(2^13));magY4=abs(Y4(1:1:(2^12)+1))/(70);Y5=fft(y5,(2^13));magY5=abs(Y5(1:1:(2^12)+1))/(70);subplot(211)plot(u,magY1,'b',u,magY4,'r',u,magY5,'g');gridtitle('FSKr');axis([1e8 1e9 0 .65]);X2=b.*x2;y2=X2(1:(2^13));Y2=fft(y2,(2^13));magY2=abs(Y2(1:1:(2^12)+1))/(50*6); k1=0:(2^12);w1=(2*pi/(2^13))*k1;u=(2*w1/pi)*1e9;Y3=fft(x3,(2^13));magY3=abs(Y3(1:1:(2^12)+1))/(30); subplot(212)plot(u,magY2,'b',u,magY3,'r');gridtitle('FSKr-modulation');axis([0 1.2e9 0 2.3])figure(2)subplot(211);plot(n,x2);axis([0 320 -1.2 1.2])subplot(212);plot(n,x);axis([0 320 -1.2 1.2])%PSK调制n=[1:(2^13)];x1=cos(n.*1e9*2*pi/4e9);run('rm2');x2=(2*rm2)-1;x=x1.*x2;b=.42+.5*cos(2*pi*(n-(2^12))/(2^13))+0.08*...cos(4*pi*(n-(2^12))/(2^13));X=b.*x;x3=[ones(1,64) zeros(1,8128)];y1=X(1:(2^13));y4=x1.*x3;Y1=fft(y1,(2^13));magY1=abs(Y1(1:1:(2^12)+1))/(300); Y4=fft(y4,(2^13));magY4=abs(Y4(1:1:(2^12)+1))/(30);k1=0:(2^12);w1=(2*pi/(2^13))*k1;u=(2*w1/pi)*1e9;figure(1)subplot(211)y2=X2(1:(2^13));Y2=fft(y2,(2^13));magY2=abs(Y2(1:1:(2^12)+1))/(300); k1=0:(2^12);w1=(2*pi/(2^13))*k1;u=(2*w1/pi)*1e9;Y3=fft(x3,(2^13));magY3=abs(Y3(1:1:(2^12)+1))/(30); subplot(212)plot(u,magY2,'b',u,magY3,'r');gridtitle('PSKr-modulation');axis([0 1.2e9 0 2.3])figure(2)subplot(211);plot(n,x2);title('PSKr');axis([0 1200 -1.2 1.2])subplot(212);plot(n,x);axis([100 275 -1.2 1.2])%谱估计 tfe 从输⼊输出中估计传递函数%估计传输函数h=fir1(30,.2,boxcar(31)); %使⽤矩形窗x=randn(16384,1); %输⼊信号y=filter(h,1,x); %输出信号z=tfe(x,y,1024,[],[],512);n=[1:length(z)];p=log10(abs(z)+eps);plot(n,p);grid%互功率谱密度 csd已知⼆信号求互功率谱密度h=fir1(30,.2,hamming(31)); %使⽤汉明窗h1=ones(1,10)/sqrt(10);r=randn(16384,1);x=filter(h1,1,r);y=filter(h,1,x);z=csd(x,y,1024,10000,triang(500),0,[]); %使⽤三⾓窗n=[1:length(z)];p=log10(abs(z)+eps);plot(n,p);gridx=randn(16384,1);y=filter(h,1,x);z=psd(y,1024,10000,kaiser(512,5),0,.95); %使⽤凯塞窗n=[1:length(z)];p=log10(abs(z)+eps);plot(n,p);grid。

利用Matlab绘制正弦信号的频谱图并做相关分析一、作业要求：1、信号可变（信号的赋值、相位、频率可变）；2、采样频率fs可变；3、加各种不同的窗函数并分析其影响；4、频谱校正；5、频谱细化。

二、采用matlab编写如下程序：clear;clf;fs=100;N=1024; %采样频率和数据点数A=20;B=30;C=0.38;n=0:N-1;t=n/fs; %时间序列x=A*sin(2*pi*B*t+C); %信号y=fft(x,N); %对信号进行傅里叶变换yy=abs(y); %求得傅里叶变换后的振幅yy=yy*2/N; %幅值处理f=n*fs/N; %频率序列subplot(3,3,1),plot(f,yy); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图1：fs=100，N=1024');grid on;%两种信号叠加，x=A*sin(2*pi*B*t+C)+2*A*sin(2*pi*1.5*B*t+2.5*C); %信号y=fft(x,N); %对信号进行傅里叶变换yy=abs(y); %求得傅里叶变换后的振幅yy=yy*2/N; %幅值处理f=n*fs/N; %频率序列subplot(3,3,2),plot(f,yy); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图2：fs=100,N=1024，两种信号叠加');grid on;%加噪声之后的图像x=A*sin(2*pi*B*t+C)+28*randn(size(t));y=fft(x,N);yy=abs(y);yy=yy*2/N; %幅值处理subplot(3,3,3),plot(f(1:N/2.56),yy(1:N/2.56));xlabel('频率/\itHz');ylabel('振幅');title('图3：fs=100,N=1024混入噪声');grid on;%改变采样点数N=128N=128;n=0:N-1;t=n/fs; %时间序列x=A*sin(2*pi*B*t+C); %信号y=fft(x,N); %对信号进行傅里叶变换yy=abs(y); %求得傅里叶变换后的振幅yy=yy*2/N; %幅值处理f=n*fs/N; %频率序列subplot(3,3,4),plot(f(1:N/2.56),yy(1:N/2.56)); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图4：fs=100，N=128');grid on;%改变采样频率为200Hz时的频谱fs=400;N=1024;n=0:N-1;t=n/fs;x=A*sin(2*pi*B*t+C); %信号y=fft(x,N); %对信号进行快速傅里叶变换yy=abs(y); %求取傅里叶变换的振幅yy=yy*2/N; %幅值处理f=n*fs/N;subplot(3,3,5),plot(f(1:N/2.56),yy(1:N/2.56)); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图5：fs=400，N=1024');grid on;%加三角窗函数fs=100;N=1024; %采样频率和数据点数n=0:N-1;t=n/fs; %时间序列x=A*sin(2*pi*B*t+C); %信号window=triang(N);%生成三角窗函数x=x.*window';%加窗函数y=fft(x,N); %对信号进行傅里叶变换yy=abs(y); %求得傅里叶变换后的振幅yy=yy*2/N; %幅值处理f=n*fs/N; %频率序列subplot(3,3,6),plot(f(1:N/2.56),2*yy(1:N/2.56)); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图6：fs=100,N=1024,加三角窗函数');grid on;%加海明窗函数后的频谱fs=100;N=1024;n=0:N-1;t=n/fs;x=A*sin(2*pi*B*t+C); %信号window=hamming(N);%生成海明窗函数x=x.*window';%加窗函数y=fft(x,N); %对信号进行快速傅里叶变换yy=abs(y); %求取傅里叶变换的振幅yy=yy*2/N; %幅值处理f=n*fs/N;subplot(3,3,7),plot(f(1:N/2.56),1.852*yy(1:N/2.56)); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图7：fs=100，N=1024,加海明窗函数');grid on;%加汉宁窗函数后的频谱fs=100;N=1024;n=0:N-1;t=n/fs;x=A*sin(2*pi*B*t+C); %信号window=hanning(N);%生成汉宁窗函数x=x.*window';%加窗函数y=fft(x,N); %对信号进行快速傅里叶变换yy=abs(y); %求取傅里叶变换的振幅yy=yy*2/N; %幅值处理f=n*fs/N;subplot(3,3,8),plot(f(1:N/2.56),2*yy(1:N/2.56)); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图8：fs=100，N=1024,加汉宁窗函数');grid on;三、运行结果如下：四、分析与结论：1）从所做图像可以看出，信号的幅值均小于真实值，说明在截断信号时存在泄露。

信号的频谱分析及MATLAB实现
一、信号频谱分析介绍
信号的频谱分析，又称信号的谱分析或谱分析，是一种分析信号按频率分布的重要技术。

频谱分析可以揭示信号中功率分布的情况，以及信号的噪声水平、低频成分、高频成分、端频成分的大小和具体位置、信号的频谱结构等信息。

（1）实验步骤。

1）准备信号；
2）使用fft函数提取信号的频率谱；
3）使用plot函数绘制信号的频谱图；
4）观察信号的频谱特征。

（2）MATLAB代码
%信号频谱分析
fs = 8000; % 采样频率
t = 0:1/fs:1; % 时间定义
x = sin(2*pi*100*t); % 信号x
X = fft(x); % 进行FFT转换
%频谱绝对值
X_abs = abs(X);
nf = length(X_abs); % 频谱长度，计算频率
f = (0:nf-1)*fs/nf; % 频率定义
%绘制频谱图
plot(f, X_abs);
xlabel('frequency/Hz');
ylabel('amplitude/mv');
title('Signal Spectrum');
通过分析，可以看出，信号频率主要集中在100Hz，其峰值为1.2mv，除此以外，分布范围有200~700Hz，峰值不大。

三、结论
本次实验分析了信号的频谱分析及其在MATLAB中的应用，利用MATLAB的fft函数可以很快速地实现信号的频谱分析。

利用Matlab绘制正弦信号的频谱图并做相关分析一、作业要求：1、信号可变（信号的赋值、相位、频率可变）；2、采样频率fs可变；3、加各种不同的窗函数并分析其影响；4、频谱校正；5、频谱细化。

二、采用matlab编写如下程序：clear;clf;fs=100;N=1024; %采样频率和数据点数A=20;B=30;C=0.38;n=0:N-1;t=n/fs; %时间序列x=A*sin(2*pi*B*t+C); %信号y=fft(x,N); %对信号进行傅里叶变换yy=abs(y); %求得傅里叶变换后的振幅yy=yy*2/N; %幅值处理f=n*fs/N; %频率序列subplot(3,3,1),plot(f,yy); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图1：fs=100，N=1024');grid on;%两种信号叠加，x=A*sin(2*pi*B*t+C)+2*A*sin(2*pi*1.5*B*t+2.5*C); %信号y=fft(x,N); %对信号进行傅里叶变换yy=abs(y); %求得傅里叶变换后的振幅yy=yy*2/N; %幅值处理f=n*fs/N; %频率序列subplot(3,3,2),plot(f,yy); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图2：fs=100,N=1024，两种信号叠加');grid on;%加噪声之后的图像x=A*sin(2*pi*B*t+C)+28*randn(size(t));y=fft(x,N);yy=abs(y);yy=yy*2/N; %幅值处理subplot(3,3,3),plot(f(1:N/2.56),yy(1:N/2.56));xlabel('频率/\itHz');ylabel('振幅');title('图3：fs=100,N=1024混入噪声');grid on;%改变采样点数N=128N=128;n=0:N-1;t=n/fs; %时间序列x=A*sin(2*pi*B*t+C); %信号y=fft(x,N); %对信号进行傅里叶变换yy=abs(y); %求得傅里叶变换后的振幅yy=yy*2/N; %幅值处理f=n*fs/N; %频率序列subplot(3,3,4),plot(f(1:N/2.56),yy(1:N/2.56)); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图4：fs=100，N=128');grid on;%改变采样频率为200Hz时的频谱fs=400;N=1024;n=0:N-1;t=n/fs;x=A*sin(2*pi*B*t+C); %信号y=fft(x,N); %对信号进行快速傅里叶变换yy=abs(y); %求取傅里叶变换的振幅yy=yy*2/N; %幅值处理f=n*fs/N;subplot(3,3,5),plot(f(1:N/2.56),yy(1:N/2.56)); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图5：fs=400，N=1024');grid on;%加三角窗函数fs=100;N=1024; %采样频率和数据点数n=0:N-1;t=n/fs; %时间序列x=A*sin(2*pi*B*t+C); %信号window=triang(N);%生成三角窗函数x=x.*window';%加窗函数y=fft(x,N); %对信号进行傅里叶变换yy=abs(y); %求得傅里叶变换后的振幅yy=yy*2/N; %幅值处理f=n*fs/N; %频率序列subplot(3,3,6),plot(f(1:N/2.56),2*yy(1:N/2.56)); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图6：fs=100,N=1024,加三角窗函数');grid on;%加海明窗函数后的频谱fs=100;N=1024;n=0:N-1;t=n/fs;x=A*sin(2*pi*B*t+C); %信号window=hamming(N);%生成海明窗函数x=x.*window';%加窗函数y=fft(x,N); %对信号进行快速傅里叶变换yy=abs(y); %求取傅里叶变换的振幅yy=yy*2/N; %幅值处理f=n*fs/N;subplot(3,3,7),plot(f(1:N/2.56),1.852*yy(1:N/2.56)); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图7：fs=100，N=1024,加海明窗函数');grid on;%加汉宁窗函数后的频谱fs=100;N=1024;n=0:N-1;t=n/fs;x=A*sin(2*pi*B*t+C); %信号window=hanning(N);%生成汉宁窗函数x=x.*window';%加窗函数y=fft(x,N); %对信号进行快速傅里叶变换yy=abs(y); %求取傅里叶变换的振幅yy=yy*2/N; %幅值处理f=n*fs/N;subplot(3,3,8),plot(f(1:N/2.56),2*yy(1:N/2.56)); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图8：fs=100，N=1024,加汉宁窗函数');grid on;三、运行结果如下：四、分析与结论：1）从所做图像可以看出，信号的幅值均小于真实值，说明在截断信号时存在泄露。

利用MATLAB进行时域分析时域分析是信号处理中的重要一环，它可以帮助我们了解信号的时域特性和动态行为。

MATLAB是一个功能强大的数学软件，其中的信号处理工具箱可以方便地进行时域分析。

首先，我们需要将信号载入到MATLAB中。

MATLAB支持多种载入信号的方式，如读取文件、生成随机信号或者使用MATLAB中的内置信号。

如果有信号文件，我们可以使用`audioread`函数将音频文件加载到MATLAB中。

如下所示的代码将导入名为`audio.wav`的文件并存储为`y`变量：```matlab[y, Fs] = audioread('audio.wav');```其中，`y`是一个包含音频数据的向量，`Fs`是采样率。

第二步是绘制信号波形。

通过使用`plot`函数，我们可以可视化信号的时域波形。

以下代码将绘制信号`y`的波形：```matlabt = (0:length(y)-1)/Fs; % 计算时间轴plot(t, y);xlabel('Time (s)');ylabel('Amplitude');title('Time Domain Analysis');```这将绘制信号`y`的时间波形，其中x轴表示时间，y轴表示信号的幅度。

接下来，我们可以计算信号的功率谱密度（PSD）。

功率谱密度是用于描述信号频谱特性的一种方法。

MATLAB提供了`pwelch`函数用于计算功率谱密度。

以下代码计算信号`y`的功率谱密度：```matlab[p,f] = pwelch(y,[],[],[],Fs); % 计算功率谱密度plot(f, 10*log10(p));xlabel('Frequency (Hz)');ylabel('Power Spectral Density (dB/Hz)');title('Power Spectral Density');```这将绘制信号`y`的功率谱密度图，其中x轴表示频率，y轴表示功率谱密度。

利用Matlab绘制正弦信号的频谱图并做相关分析一、作业要求：1、信号可变（信号的赋值、相位、频率可变）；2、采样频率fs可变；3、加各种不同的窗函数并分析其影响；4、频谱校正；5、频谱细化。

二、采用matlab编写如下程序：clear;clf;fs=100;N=1024; %采样频率和数据点数A=20;B=30;C=0.38;n=0:N-1;t=n/fs; %时间序列x=A*sin(2*pi*B*t+C); %信号y=fft(x,N); %对信号进行傅里叶变换yy=abs(y); %求得傅里叶变换后的振幅yy=yy*2/N; %幅值处理f=n*fs/N; %频率序列subplot(3,3,1),plot(f,yy); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图1：fs=100，N=1024');grid on;%两种信号叠加，x=A*sin(2*pi*B*t+C)+2*A*sin(2*pi*1.5*B*t+2.5*C); %信号y=fft(x,N); %对信号进行傅里叶变换yy=abs(y); %求得傅里叶变换后的振幅yy=yy*2/N; %幅值处理f=n*fs/N; %频率序列subplot(3,3,2),plot(f,yy); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图2：fs=100,N=1024，两种信号叠加');grid on;%加噪声之后的图像x=A*sin(2*pi*B*t+C)+28*randn(size(t));y=fft(x,N);yy=abs(y);yy=yy*2/N; %幅值处理subplot(3,3,3),plot(f(1:N/2.56),yy(1:N/2.56));xlabel('频率/\itHz');ylabel('振幅');title('图3：fs=100,N=1024混入噪声');grid on;%改变采样点数N=128N=128;n=0:N-1;t=n/fs; %时间序列x=A*sin(2*pi*B*t+C); %信号y=fft(x,N); %对信号进行傅里叶变换yy=abs(y); %求得傅里叶变换后的振幅yy=yy*2/N; %幅值处理f=n*fs/N; %频率序列subplot(3,3,4),plot(f(1:N/2.56),yy(1:N/2.56)); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图4：fs=100，N=128');grid on;%改变采样频率为200Hz时的频谱fs=400;N=1024;n=0:N-1;t=n/fs;x=A*sin(2*pi*B*t+C); %信号y=fft(x,N); %对信号进行快速傅里叶变换yy=abs(y); %求取傅里叶变换的振幅yy=yy*2/N; %幅值处理f=n*fs/N;subplot(3,3,5),plot(f(1:N/2.56),yy(1:N/2.56)); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图5：fs=400，N=1024');grid on;%加三角窗函数fs=100;N=1024; %采样频率和数据点数n=0:N-1;t=n/fs; %时间序列x=A*sin(2*pi*B*t+C); %信号window=triang(N);%生成三角窗函数x=x.*window';%加窗函数y=fft(x,N); %对信号进行傅里叶变换yy=abs(y); %求得傅里叶变换后的振幅yy=yy*2/N; %幅值处理f=n*fs/N; %频率序列subplot(3,3,6),plot(f(1:N/2.56),2*yy(1:N/2.56)); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图6：fs=100,N=1024,加三角窗函数');grid on;%加海明窗函数后的频谱fs=100;N=1024;n=0:N-1;t=n/fs;x=A*sin(2*pi*B*t+C); %信号window=hamming(N);%生成海明窗函数x=x.*window';%加窗函数y=fft(x,N); %对信号进行快速傅里叶变换yy=abs(y); %求取傅里叶变换的振幅yy=yy*2/N; %幅值处理f=n*fs/N;subplot(3,3,7),plot(f(1:N/2.56),1.852*yy(1:N/2.56)); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图7：fs=100，N=1024,加海明窗函数');grid on;%加汉宁窗函数后的频谱fs=100;N=1024;n=0:N-1;t=n/fs;x=A*sin(2*pi*B*t+C); %信号window=hanning(N);%生成汉宁窗函数x=x.*window';%加窗函数y=fft(x,N); %对信号进行快速傅里叶变换yy=abs(y); %求取傅里叶变换的振幅yy=yy*2/N; %幅值处理f=n*fs/N;subplot(3,3,8),plot(f(1:N/2.56),2*yy(1:N/2.56)); %绘出随频率变化的振幅xlabel('频率/\itHz');ylabel('振幅');title('图8：fs=100，N=1024,加汉宁窗函数');grid on;三、运行结果如下：四、分析与结论：1）从所做图像可以看出，信号的幅值均小于真实值，说明在截断信号时存在泄露。

实验目的：熟悉MA TLAB 软件的相关函数的使用方法、各种信号的时域波形。

实验内容：1、用MA TLAB 软件绘制各类典型信号的时域波形并且给出程序源代码。

（1）指数信号、 指数序列； （2）单位阶跃函数、 单位阶跃序列； （3）单位脉冲信号； 单位抽样序列；（4）矩形信号，矩形序列信号， 矩形宽度自定； （5）正弦信号、 正弦序列，其中振幅和频率自选； 2、 假设存在一个单边离散指数序列][n s ， 参数自选； ][n d 为随机噪声，方差和均值自选； 绘制][n s ，][n d 和][][][n d n s n x +=的图形3、绘制你所采集的电信号的时域波形（部分即可）， 进行必要的说明和分析4、选作提高： 编写一个程序， 运行后可以在键盘上依次任意输入两个序列，计算两个序列的线性卷积，并输出计算结果。

（相关函数：input ， conv ）实现方案：（1）指数信号、指数序列1、指数信号分为实指数信号和复指数信号，其中实指数信号的基本形式为 atKe =f(t)。

其中，K 、a 为实数。

当a>0时，实指数信号随时间按指数式增长；当a<0时，实指数信号随时间按指数式衰减；当a=0时，实指数信号不随时间变化，转化为直流信号。

MATLAB 中用exp 函数来表示实指数信号，语句表示为 y=K*exp(a*t).下面用MA TLAB 命令产生单边递增指数信号)(32t u e t ，当0<=t<=5的波形图。

MATLAB 源程序为：K=3;a=2; t=0:0.01:5; y=K*exp(a*t); plot(t,y),grid on程序运行后，产生如下图所示的波形。

2、复指数信号复指数信号的基本形式为)sin()cos()()(t jKe t Ke Ke Ke t f t t j st ωωσσωσ+===+其中， ωσj s += 是复变量；σ、ω为实数。

当 ω=0 时，st Ke 为一个实指数信号；当0>σ 0≠ω时，stKe 的实部和虚部分别是按指数规律衰减的正弦振荡；当0<σ0≠ω时，stKe 的实部和虚部均为等幅的正弦振荡。