2019年4月湘赣十四校(湖南长郡中学、江西南昌二中等)2019届高三下学期第二次联考语文试题

2019届湘赣·十四校高三联考第一次考试数学（文科）试卷注意事项:1.答题前,考生须认真核对条形码上的姓名、考生号、考场号和座位号,并将其贴在指定位置,然后用0.5毫米黑色字迹签字笔将自己所在的县(市、区)、学校以及自己的姓名、考生号、考场号和座位号填写在答题卡和试卷的指定位置,并用2B铅笔在答题卡的“考生号”处填涂考生号。

2.第Ⅰ卷每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号。

写在试卷、草稿纸或答题卡上的非答题区域均无效。

3.第Ⅱ卷必须用0.5毫米黑色字迹签字笔作答,答案必须写在答题卡各题目指定区域内相应的位置;如需改动,先画掉原来的答案,然后再写上新的答案;不能使用涂改液、胶带纸、修正带。

不按以上要求作答的答案无效。

4.考试结束后,将本试卷和答题卡一并交回。

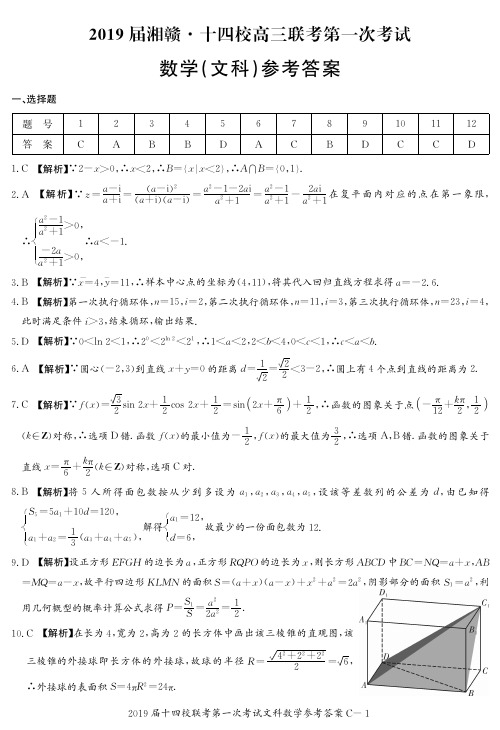
第Ⅰ卷一、选择题（本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的）1.已知集合，集合，则（）A. B. C. D.【答案】C【解析】【分析】求解出集合表示的范围，然后根据交集定义来求解.【详解】由得：又本题正确选项：【点睛】本题考查集合的基本运算中的交集运算，属于基础题.2.设复数在复平面内对应的点位于第一象限，则的取值范围是（）A. B. C. D.【答案】A【解析】【分析】将整理为，可知实部和虚部均大于零，得到不等式组，求得取值范围.【详解】对应的点在第一象限本题正确选项：【点睛】本题考查复数的基础运算和几何意义，属于基础题.3.已知下表所示数据的回归直线方程为，则实数的值为（）A. 2.6B. -2.6C. -2.8D. -3.4【答案】B【解析】【分析】根据最小二乘法：，求得平均数后代入回归直线即可求得结果.【详解】由题意得：；本题正确选项：【点睛】本题考查利用最小二乘法求解回归直线问题，关键在于明确回归直线必过，因此代入点即可求解出.4.执行如图所示的程序框图，则输出的值为（）A. 7B. 23C. 47D. 63 【答案】B【解析】【分析】根据程序框图条件，依次进行赋值推导，直到输出结果为止.【详解】当时，可知，又，循环当时，可知，又，循环当时，可知，又，输出则本题正确选项：【点睛】本题考查程序框图的运算，属于基础题.5.已知实数，，，则，，的大小关系是（）A. B. C. D.【答案】D【解析】【分析】根据的范围，依次求解出所处的范围，得到大小关系.【详解】，，本题正确选项：【点睛】本题考查与对数有关的比较大小问题，关键在于能够通过临界值对进行区分，从而得到大小关系，属于基础题.6.圆上到直线的距离等于2的点有（）A. 4个B. 3个C. 2个D. 1个【答案】A【解析】【分析】首先判断出圆心到直线的距离，然后判断，与的关系，从而确定点的个数.【详解】圆的圆心为，半径为圆心到直线的距离可知，由上图可知，圆上到直线距离等于的点共有个本题正确选项：【点睛】本题考查直线与圆的位置关系，由位置关系判断到直线距离为定值的点的个数，解题关键在于确定圆心到直线的距离，再进一步判断.7.已知函数，则（）A. 它的最小值为-1B. 它的最大值为2C. 它的图象关于直线对称D. 它的图象关于点对称【答案】C【解析】【分析】将整理成，然后依次判断各个选项，得到正确结果.【详解】选项：最小值为，所以错误；选项：由知，最大值为，所以错误；选项：当时，，而是的对称轴，所以是的对称轴，所以正确；选项：当时，，而是的对称中心，当时，，所以是的对称中心，所以错误.本题正确选项：【点睛】本题考查型的函数的值域及性质，关键在于能够通过整体代入的方式，与图像进行整体对应，从而快速判断出结果.8.《莱茵德纸草书》是世界上最古老的数学著作之一，书中有一道这样的题目：把120个面包分给5个人，使每人所得成等差数列，且使较多的三份之和的是较少的两份之和，则最少的一份面包个数为（）A. 46 B. 12 C. 11 D. 2【答案】B【解析】【分析】将问题转化为等差数列的问题，通过和，求解出即可.【详解】设每个人所得面包数，自少而多分别为：且成等差数列由题意可知：，设公差为，可知：所以最少的一份面包数为本题正确选项：【点睛】本题考查利用等差数列求解基本项的问题，关键在于将文字描述的内容转化为等差数列中的关系式，利用通项公式和求和公式求解出基本项.9.如图，分别沿长方形纸片和正方形纸片的对角线、剪开，拼成如图所示的平行四边形，且中间的四边形为正方形.在平行四边形内随机取一点，则此点取自阴影部分的概率是（）A. B. C. D.【答案】D【解析】【分析】假设正方形边长和长方形的长和宽，根据图形导出，然后分别求解出平行四边形面积和阴影部分的面积，利用几何概型求解出结果.【详解】由题意可知：设正方形边长为，长方形长为，宽为则，即，又，即平行四边形面积为阴影部分面积为：所求概率本题正确选项：【点睛】本题考查几何概型中的面积型的概率求解，关键在于能够通过图形得到之间的关系，从而能将几何概型的式子进行化简.10.如图，网格纸上小正方形的边长为1，粗线画出的是某三棱锥的三视图，则该三棱锥的外接球的表面积为（ ）A. B. C. D.【答案】C 【解析】 【分析】根据三视图可知原几何体可通过长方体切割得到，可知长方体的外接球即为三棱锥的外接球，外接球半径为长方体体对角线的一半，求解出半径即可求出表面积. 【详解】通过三视图还原，可知三棱锥为如下图所示的，可通过切割长方体得到所以长方体的外接球即为三棱锥的外接球又，，所以外接球半径：球的表面积为：本题正确选项：【点睛】本题考查空间几何体的三视图和外接球问题，关键在于能够通过割补的方式，将几何体放回长方体中，从而确定半径的长度. 11.若函数的值域为，则实数的取值范围为（ ） A.B.C.D.【答案】C 【解析】 【分析】先求出在上的值域，可知要想的整体值域为，在上的最大值为，最小值大于等于，由此求出临界点，得到的取值范围.【详解】当时，又对称轴为，当时，值域为且时，当时，，令，解得在上单调递增，在上单调递减又当时，本题正确选项：【点睛】本题考查通过分段函数、利用函数的值域求解参数范围问题，解题关键是确定最值的范围和临界点.12.在中，角，，的对边分别为，，，若，且恒成立，则的取值范围是（）A. B.C. D.【答案】D【解析】【分析】由边角关系式可得，再结合余弦定理得到，代入可得，利用基本不等式可得；将恒成立的不等式转化为与有关的不等式，利用二次函数图像特点，求解出的范围.【详解】又又，当且仅当时取等号设，即当时，恒成立设则可知可得：本题正确选项：【点睛】本题考查解三角形中边角关系式化简、基本不等式、二次函数成像问题.利用边角关系式求得的范围是解决问题的关键；难点在于通过二次函数图像来得到关于的不等式，讨论二次函数图像通常从以下三个方面来讨论：①判别式；②对称轴；③区间端点值符号.第Ⅱ卷本卷包括必考题和选考题两部分.第13～21题为必考题，每个试题考生都必须作答.第22、23题为选考题，考生根据要求作答.二、填空题（本大题共4小题，每小题5分，共20分.把答案填在答题卡中对应题号后的横线上）13.已知向量，的夹角为，且，，则__________．【答案】1【解析】【分析】对进行平方运算，代入已知量即可得到结果.【详解】本题正确结果：【点睛】本题考查复合向量模长的计算，先求出模长的平方是解题的关键，属于基础题.14.已知实数，满足，则目标函数的最大值为__________．【答案】10【解析】【分析】画出可行域，转化为求解在轴截距的最大值的问题，找到成立的点，代入即可求解. 【详解】由约束条件可得可行域如下图所示：将转化为，则当在轴截距最大时，取最大值由下图可知：当过点时，截距最大又本题正确结果：【点睛】本题考查线性规划求解最值得问题，属于基础题.15.已知直线与函数的图象恰有四个公共点，，，，则__________．【答案】-2【解析】【分析】利用数形结合可得直线与余弦函数图象在处相切，且∈，利用相切得a＝，利用公共点得a＝，从而得，进而得解.【详解】直线y＝a(x+2)过定点（－2,0），如下图所示，由图可知，直线与余弦函数图象在x4处相切，且∈，即a(x4+2)＝－cos，所以，a＝又，即直线的斜率为：a＝，因此a＝＝，即＋＝＋＝－－2＝－2.故答案为：－2.【点睛】本题主要考查了函数与方程的应用，着重考查了学生的数形结合能力，属于难题.16.已知抛物线：的焦点为双曲线：的顶点，直线过点且与抛物线交于点，（点在点的右侧），设直线的斜率为，为原点，若与的面积和为5，则__________．【答案】【解析】【分析】根据双曲线的顶点为抛物线焦点，可以得到抛物线方程；假设直线后与抛物线联立，利用弦长公式和点到直线距离表示出；再通过点坐标表示出，利用面积之和等于构造出方程，求解出的值. 【详解】由题意得：双曲线顶点为即设，则与联立可得：设，则，则则到距离又，可知解得：本题正确结果：【点睛】本题考查直线与抛物线的综合问题，常见的解题思路是将直线与抛物线联立，通过韦达定理表示出已知或者所求的等量或不等量关系，然后进行相应的求解.三、解答题（共70分.解答应写出文字说明、证明过程或演算步骤）17.已知函数的所有正数零点构成递增数列.（1）求数列的通项公式；（2）设，求数列的前项和.【答案】（1）；（2）.【解析】（1）根据正零点坐标得到数列为等差数列，利用等差数列首项和公差求解出通项；（2）通过导出的通项公式，然后采用错位相减法求解出前项和.【详解】（1）令，得则有的所有正零点构成递增数列是以为首项，公差为的等差数列（2）由（1）可知……①……②②①有：【点睛】本题考查等差数列通项公式的求解和错位相减法求和，解题关键是能够通过解析式判断出需要用错位相减法求和，错位相减法试用于通项公式为等差与等比乘积的形式；具体方法为：列出后，再乘以等比部分的公比，然后作差求解出，最后整理出.18.如图，四棱锥的底面是边长为4的正方形，，.（1）证明：平面；（2）求四面体体积的最大值.【答案】（1）详见解析；（2）.【分析】（1）首先证明平面，利用得到平面，从而证得，又，可证得结论；（2）设，利用四面体体积公式将体积表示成关于的函数，利用均值不等式得到最值.【详解】（1）四边形是正方形，又，平面又平面则有又，平面（2）设，则四面体的体积（当且仅当即时取等号）四面体的体积最大值为【点睛】本题考查线面垂直的证明、椎体体积最值问题，处理最值问题时，关键在于能够将体积表示为某变量的函数关系式，然后利用基本不等式或函数值域的求解方法求解出最值.19.随着人们生活水平的提高，越来越多的人愿意花更高的价格购买手机.某机构为了解市民使用手机的价格情况，随机选取了100人进行调查，并将这100人使用的手机价格按照，，…，分成6组，制成如图所示的频率分布直方图：（1）求图中的值；（2）求这组数据的平均数和中位数（同一组中的数据用该组区间的中间值作代表）；（3）利用分层抽样从手机价格在和的人中抽取5人，并从这5人中抽取2人进行访谈，求抽取出的2人的手机价格在不同区间的概率.【答案】（1）；（2）平均数3720，中位数3750；（3）.【解析】【分析】（1）利用矩形面积之和为，构造方程解出；（2）根据频率分布直方图估计平均数和中位数的方法，直接计算即可；（3）首先确定来自和的人数，然后采用列举法求解出结果.【详解】（1）由题意知：解得（2）平均数（元）前三组的频率之和为前四组的频率之和为故中位数落在第四组.设中位数为，则，解得（3）由图知手机价格在和的人数之比为，故用分层抽样抽取的人中，来自区间的有人，设为，来自的有人，设为则从这人中抽取出人的取法有，，，，，，，，，，共种其中抽取出的人的手机价格在不同区间的有，，，，，，共种故抽取出的人的手机价格在不同区间的概率【点睛】本题考查统计中利用频率分布直方图计算频率和估计总体数据问题、古典概型的问题，关键在于能够掌握用样本估计总体的方法和求解古典概型的基本方法：列举法.20.椭圆：的左焦点为且离心率为，为椭圆上任意一点，的取值范围为，.（1）求椭圆的方程；（2）如图，设圆是圆心在椭圆上且半径为的动圆，过原点作圆的两条切线，分别交椭圆于，两点.是否存在使得直线与直线的斜率之积为定值？若存在，求出的值；若不存在，说明理由.【答案】（1）；（2）时，直线与直线的斜率之积为定值.【解析】【分析】（1）利用离心率得到的关系；然后表示出，通过的范围得到，由得到，从而求得方程；（2）假设圆的方程，利用直线与圆相切，得到关于的方程，从而得到的表达式，从而得到当时，为定值，求得结果.【详解】（1）椭圆的离心率椭圆的方程可写为设椭圆上任意一点的坐标为则，，，椭圆的方程为（2）设圆的圆心为，则圆的方程为设过原点的圆的切线方程为：，则有整理有由题意知该方程有两个不等实根，设为，则当时，当圆的半径时，直线与直线的斜率之积为定值【点睛】本题考查椭圆标准方程的求解、椭圆问题中的定值问题，解题关键在于能够列出关于所求定值的变量关系式，通过消元的方式，消除关系式中的变量，最终求得所求的定值.21.已知函数.（1）若时，函数有极大值为-2，求；（2）若对任意实数，都有，求的最小值.【答案】（1）1；（2）0.【解析】【分析】（1）求解出的值，代入，得到，求解出；（2）由可知，根据的范围讨论可知：；利用得到，所以；令，则的最小值即为，通过导数运算可知的最小值为.【详解】（1）当时，有极大值为由知经检验满足题意（2）函数的定义域为，<1>当时，当时在上单调递增令，则可知不恒成立，舍去<2>当时，当时在上单调递增令，则可知不恒成立，舍去<3>当时，当时；当时在上单调递增，在上单调递减的最大值为即设令，则当时在上单调递减当时在上单调递增的最小值为综上所述，当，时的最小值为【点睛】本题考查利用极值求函数解析式、恒成立问题的求解，解题关键是能够把恒成立问题转变为最值求解的问题，通过构造新函数、导数等方法求得最值.请考生在第22、23题中任选一题作答，如果多做，则按所做的第一题计分.22.已知曲线的极坐标方程为，直线：，直线：.以极点为原点，极轴为轴的正半轴建立平面直角坐标系.（1）求直线，及曲线的直角坐标方程；（2）若直线与曲线交于，两点，直线与曲线交于，两点，求的面积.【答案】（1）直线：，直线：，曲线：；（2）.【解析】【分析】（1）利用直角坐标和极坐标的互化原则直接转化即可；（2）根据极坐标的关系，求解出和，利用三角形面积公式直接求得结果.【详解】（1）直线的直角坐标方程为：直线的直角坐标方程为：，且曲线的直角坐标方程为：即（2）曲线的极坐标方程为：当时，当时，【点睛】本题考查极坐标和直角坐标的互化、极坐标应用问题，关键在于能够利用极坐标的求解出三角形两邻边的长度，直接求得结果.23.已知函数.（1）当时，求不等式的解集；（2）若时，不等式恒成立，求的取值范围.【答案】（1）；（2）.【解析】【分析】（1）分别在，，三个范围中求解不等式，得到结果；（2）将原问题转化为恒成立，根据的不同取值情况，讨论结果.【详解】（1）当时，，当时，当时，不成立当时，综上所述：不等式的解集为：（2）当时，，即恒成立当时，，满足题意当时，，满足题意当时，令，则，不合题意综上所述：的取值范围为：【点睛】本题考查含绝对值不等式的求解及不等式中的恒成立问题，关键在于能够通过零点讨论的方式，将绝对值去除，从而求得结果.。

2019届湘赣·十四校高三联考第二次考试英语试题总分：150分时量：120分钟考试时间：2019年4月7日15：00——17：00第一部分听力（共两节，满分30分）做题时，先将答案标在试卷上。

录音内容结束后，你将有两分钟的时间将试卷上的答案转涂到答题卡上。

第一节（共5小题；每小题1.5分，满分7.5分）听下面5段对话。

每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳选项。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

例: How much is the shirt?A.￡19.15B.￡9.18C.￡9.15答案是C1. What will the speakers do tonight?A. Watch TV.B. Go to the movies.C. Enjoy a concert.2. Where does the conversation probably take place?A. At the airport.B. On the plane.C. In a coffee shop.3. When will the woman probably arrive in Hong Kong?A. On November 28th.B. On November 14th.C. On November 1st.4. What makes the woman disappointed about the restaurant?A. The food.B. The environment.C. The service.5. What is the woman asking for?A. A long dress.B. A fancy dress.C. A bright-color dress.第二节（共15小题；每小题1.5分，满分22.5分）听下面5段对话或独白。

2019届湘赣・十四校高三联考第一次考试生物试卷1.下列有关植物细胞中叶绿体与细胞核的一些相同之处，正确的是A. 能进行遗传信息的复制、转录和翻译B. 有双层膜结构，能合成生物大分子C. 内有DNA和RNA，能合成和消耗ATPD. 同时存在于除根细胞之外的其他植物细胞中【答案】B【解析】【分析】1、细胞核包括核膜（将细胞核内物质与细胞质分开）、染色质（主要成分：DNA和蛋白质）、核仁（与某种RNA的合成以及核糖体的形成有关）、核孔（实现核质之间频繁的物质交换和信息交流）。

细胞核是遗传物质贮存和复制的场所，是细胞遗传和代谢的控制中心。

2、叶绿体包括双层膜、基粒（由类囊体堆叠形成，其上有色素和酶，并大大扩展了膜面积）、基质（内含有少量DNA、RNA、核糖体和多种酶）。

是绿色植物进行光合作用的场所。

【详解】A. 两者都含有DNA，都能进行遗传信息的复制、转录。

叶绿体内有核糖体，能进行翻译，而细胞核不能，A错误。

B. 两者都有双层膜结构，都能进行DNA复制和转录，从而能合成生物大分子DNA、RNA，B正确。

C. 两者都含有DNA和RNA，叶绿体中光反应能合成ATP，暗反应能消耗ATP，但细胞核不能合成和消耗ATP，C错误。

D. 细胞核存在于除高等植物成熟筛管细胞外的几乎所有植物细胞中，而叶绿体仅存在于叶肉细胞等部分植物细胞中，D错误。

2.下列有关遗传的叙述，正确的是A. 基因的表达过程中反密码子与终止密码子发生配对B. 复制与转录过程中均发生蛋白质与DNA的结合与释放C. 转录与翻译过程中不会发生蛋白质与DNA的结合与释放D. 雌雄配子结合过程中伴随非等位基因的自由组合【解析】【分析】密码子是mRNA上决定一个氨基酸的3个相邻的碱基，共有64种，其中有3种是终止密码子，不编码氨基酸。

tRNA有61种，其一端的3个碱基构成反密码子，能识别密码子，并转运相应的氨基酸，且一种tRNA 只能识别一种密码子，转运一种氨基酸。