诚仁中学2016-2017学年度第二学期期中考试.docx

2016-2017学年内蒙古巴彦淖尔市磴口县诚仁中学八年级下学期期中数学试卷一、单1.若在实数范围内有意义，则x的取值范围是（??）A、x＞0B、x＞3C、x≥3D、x≤3+2.下列二次根式，不能与合并的是（??）A、B、C、D、﹣+3.下列运算正确的是（）A、﹣=B、=2C、﹣=D、=2﹣+4.在三边分别为下列长度的三角形中，是直角三角形的是（??）A、9，12，14B、2，C、4，3，D、4，3，5+5.如图，直线l上有三个正方形a，b，c，若a，c的面积分别为5和11，则b的面积为（）A、4B、6C、16D、55+6.如图，矩形ABCD中，AB=3，两条对角线AC、BD所夹的钝角为120°，则对角线BD的长为（）A、3B、6C、D、+7.如图，菱形ABCD中，E，F分别是AB，AC的中点，若EF=3，则菱形ABCD的周长是（??）A、12B、16C、20D、24+8.平行四边形、矩形、菱形、正方形都具有的性质是（）A、对角线互相平分B、对角线互相垂直C、对角线相等D、轴对称图形+9.一艘轮船以16海里/时的速度离开港口向东南方向航行，另一艘轮船在同时同地以12海里/时的速度向西南方向航行，它们离开港口3小时相距（??）海里．A、60 B、30 C、20 D、80+如图，四边形ABCD中，AB=BC，∠ABC=∠CDA=90°，BE⊥AD于点E，且四边形ABCD的面积为16，则BE=（??）A、2B、3C、4D、5+二、填空题11. ﹣（）2= ．+12.如图，一旗杆离地面6m处折断，旗杆顶部落在离旗杆底部8m处，旗杆折断之前的高度是m．+13.已知直角三角形三边长分别为3，4，m，则m=+14.若y= + +2，则x y= ．+15.平面直角坐标系内点P（﹣2，0），与点Q（0，3）之间的距离是．+已知一个直角三角形的两条直角边分别为6cm，8cm，那么这个直角三角形斜边上的高为?cm．+17.如图，在?ABCD中，已知AD=8cm，AB=6cm，DE平分∠ADC，交BC边于点E，则BE= cm．+18.如图，折叠形ABCD的一边AD，点D落在BC边上的点F处，AE是折痕，已知A B=8cm，BC=10cm．则CE= cm．+19.已知菱形的一条对角线长为12，面积为30，则这个菱形的另一条对角线的长为．+20.如图，正方形ABCD的边长为4，点P在DC边上且DP=1，点Q是AC上一动点，则DQ+PQ的最小值为．+三、计算题21.计算：(1)、+2 ﹣（+ ）(2)、÷×(3)、（7+4 ）（7﹣4 ）+四、解答题22.如图所示，△ABC中，∠B=45°，∠C=30°，AB=求：AC的长．+23.如图所示，O是矩形ABCD的对角线的交点，作DE∥AC，CE∥BD，DE、CE相交于点E．求证：(1)、四边形OCED是菱形．(2)、连接OE，若AD=4，CD=3，求菱形OCED的周长和面积．+24.已知，如图，正方形ABCD的对角线AC，BD相交于点O，正方形A′B′C′D′的顶点A′与点O重合，A′B′交BC于点E，A′D′交CD于点F．(1)、求证：OE=OF；(2)、若正方形ABCD的对角线长为4，求两个正方形重叠部分的面积为．+。

内蒙古巴彦淖尔市磴口县诚仁中学2015-2016学年七年级语文下学期期中试题（考试时间：120分钟，总分：150分）一、语文积累与运用（本大题1-6小题每小题2分，第7小题12分,共24分）1、下列加点字的注音全都正确的一项是（）（2分）A、花圃．（pú）省．（shěng）悟田垄．（lǒng）脑髓．（suǐ）B、踌躇．（chú）澎湃．（pài）亘．古（gèn）骊．歌（lì）C、讪．笑（shàn）哺．育（bǔ）踱．步（duó）污秽．（suì）D、瞬．息（shùn）嫉．妒（jí）炽．痛（chì）泥泞．（nìn g）2、下列词语没有错别字的一项是（）（2分）A、幽寂锋芒毕露妇儒皆知一拍既合B、仰慕慷慨淋漓马革裹尸戛然而止C、狂澜潜心惯注铤而走险杂乱无章D、晦暗气冲斗牛契而不舍浑身解数3、下列语句中加点成语运用有误的一项是（）（2分）A、这场有赌球性质的比赛无不让有良知的球迷们义愤填膺．．．．，扼腕长叹。

B、“神十”飞天，王亚平通过天地互动的形式，为我们上了一堂叱咤风云．．．．的太空课。

C、闻一多“说”了。

说得真痛快，动人心，鼓壮志，气冲斗牛．．．．，声震天地。

D、神舟发射基地的广大官兵，个个身怀绝技，却因工作的机密而鲜为人知．．．．。

4.指出下面没有语病的一句是( ) （2分）A．为了防止类似事故发生，我们一定要加强管理，采取严密的防患措施。

B. 经调查，某社区18岁以下青少年吸烟人数前年高达120人，经过广泛宣传教育，今年已下降到60人，正好减少一倍。

C、通过这次语文综合性学习，使我们从一个侧面感受到了戏剧的魅力。

D、能否贯彻落实科学发展观，是构建和谐社会，促进经济可持续发展的重要保证。

5．下列句子排序最恰当的一项是（）（2分）①因为音乐是人类的共同语言，一切艺术都具有音乐因素。

②音乐与建筑是两种不同的艺术形式。

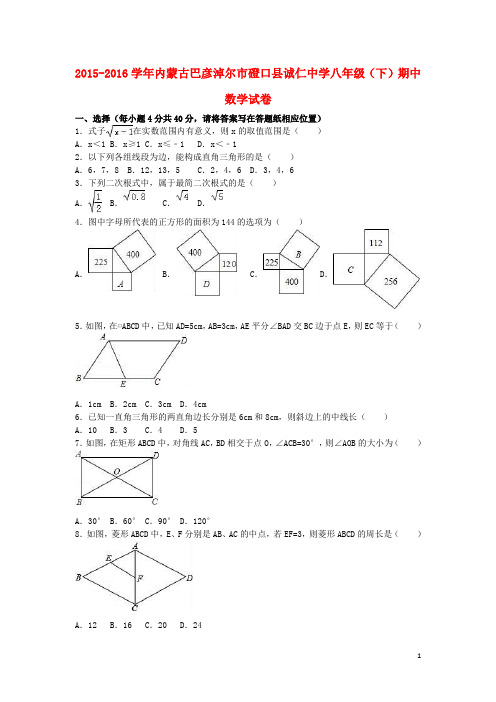
2015-2016学年内蒙古巴彦淖尔市磴口县诚仁中学八年级（下）期中数学试卷一、选择（每小题4分共40分，请将答案写在答题纸相应位置）1．式子在实数范围内有意义，则x的取值范围是（）A．x＜1 B．x≥1 C．x≤﹣1 D．x＜﹣12．以下列各组线段为边，能构成直角三角形的是（）A．6，7，8 B．12，13，5 C．2，4，6 D．3，4，63．下列二次根式中，属于最简二次根式的是（）A．B．C．D．4．图中字母所代表的正方形的面积为144的选项为（）A．B．C．D．5．如图，在▱ABCD中，已知AD=5cm，AB=3cm，AE平分∠BAD交BC边于点E，则EC等于（）A．1cm B．2cm C．3cm D．4cm6．已知一直角三角形的两直角边长分别是6cm和8cm，则斜边上的中线长（）A．10 B．3 C．4 D．57．如图，在矩形ABCD中，对角线AC，BD相交于点O，∠ACB=30°，则∠AOB的大小为（）A．30° B．60° C．90° D．120°8．如图，菱形ABCD中，E、F分别是AB、AC的中点，若EF=3，则菱形ABCD的周长是（）A．12 B．16 C．20 D．249．如图是一个圆柱形饮料罐，底面半径是5，高是12，上底面中心有一个小圆孔，则一条到达底部的直吸管在罐内部分a的长度（罐壁的厚度和小圆孔的大小忽略不计）范围是（）A．12≤a≤13 B．12≤a≤15 C．5≤a≤12 D．5≤a≤1310．如图，将n个边长都为2的正方形按如图所示摆放，点A1，A2，…A n分别是正方形的中心，则这n个正方形重叠部分的面积之和是（）A．n B．n﹣1 C．（）n﹣1D． n二、填空（每小题4分共40分，请将答案写在答题纸相应位置）11．二次根式是一个整数，那么正整数a最小值是______．12．如图，ABCD是对角线互相垂直的四边形，且OB=OD，请你添加一个适当的条件______，使ABCD成为菱形（只需添加一个即可）13．如图，已知OA=OB，那么数轴上点A所表示的数是______．14．如图，正方形OABC的边长为6，点A、C分别在x轴，y轴的正半轴上，点D（2，0）在OA上，P是OB上一动点，则PA+PD的最小值为______．15．已知y=+﹣3，则2xy的值为______．16．直角三角形有两边长为3和4，则斜边长为______．17．计算：（ +）2015×（﹣）2015=______．18．已知菱形的两条对角线长为8cm和6cm，那么这个菱形的周长是______cm，面积是______cm2．19．﹣ =______．20．在实数范围内分解因式x3﹣3x=______．三、解答题21．计算（1）（2）（3）（7+4）（7﹣4）﹣（3﹣1）2．（4）先化简，再求值：﹣，其中x=+1，y=﹣1．22．已知：如图，四边形ABCD四条边上的中点分别为E、F、G、H，顺次连接EF、FG、GH、HE，得到四边形EFGH（即四边形ABCD的中点四边形）．（1）四边形EFGH的形状是______．（2）证明你的结论．23．某港口位于东西方向的海岸线上．“远航”号、“海天”号轮船同时离开港口，各自沿一固定方向航行，“远航”号每小时航行16海里，“海天”号每小时航行12海里．它们离开港口一个半小时后相距30海里．如果知道“远航”号沿东北方向航行，能知道“海天”号沿哪个方向航行？为什么？四．选做题24．如图，平行四边形ABCD中，AB=3cm，BC=5cm，∠B=60°，G是CD的中点，E是边AD 上的动点，EG的延长线与BC的延长线交于点F，连结CE，DF．（1）求证：四边形CEDF是平行四边形；（2）①当AE=______cm时，四边形CEDF是矩形；②当AE=______cm时，四边形CEDF是菱形．（直接写出答案，不需要说明理由）25．如图：平行四边形ABCD中，∠ABC的平分线交AD于E，∠BCD的平分线交AD于F，且AB=3，DE=2，（1）求平行四边形ABCD的周长．（2）求证：BE⊥CF（3）若CF=2，求BE的长．2015-2016学年内蒙古巴彦淖尔市磴口县诚仁中学八年级（下）期中数学试卷参考答案与试题解析一、选择（每小题4分共40分，请将答案写在答题纸相应位置）1．式子在实数范围内有意义，则x 的取值范围是（ ）A ．x ＜1B ．x ≥1C ．x ≤﹣1D ．x ＜﹣1【考点】二次根式有意义的条件．【分析】根据二次根式中的被开方数必须是非负数列出不等式，解不等式得到答案．【解答】解：由题意得，x ﹣1≥0，解得，x ≥1，故选：B ．2．以下列各组线段为边，能构成直角三角形的是（ ）A ．6，7，8B ．12，13，5C ．2，4，6D ．3，4，6【考点】勾股定理的逆定理．【分析】欲求证是否为直角三角形，这里给出三边的长，只要验证两小边的平方和等于最长边的平方即可得出答案．【解答】解：A 、62+72≠82，故本选项错误；B 、52+122=132，故本选项正确；C 、22+42≠62，故本选项错误；D 、32+42≠62，故本选项错误；故选B ．3．下列二次根式中，属于最简二次根式的是（ ）A ．B ．C ．D ．【考点】最简二次根式．【分析】判定一个二次根式是不是最简二次根式的方法，就是逐个检查最简二次根式的两个条件是否同时满足，同时满足的就是最简二次根式，否则就不是．【解答】解：A 、被开方数含分母，故A 错误；B 、被开方数含分母，故B 错误；C 、被开方数含能开得尽方的因数，故C 错误；D 、被开方数不含分母；被开方数不含能开得尽方的因数或因式，故D 正确；故选：D ．4．图中字母所代表的正方形的面积为144的选项为（ ）A ．B ．C ．D ．【考点】勾股定理．【分析】两条直角边长的平方之和一定等于斜边长的平方，而边长的平方恰是正方形的面积，从而根据选项提供的面积即可得出答案．【解答】解：A、A代表的正方形的面积为400﹣225=175；B、D代表的正方形的面积为400﹣120=280；C、B代表的正方形的面积为400+225=625；D、C代表的正方形的面积为256﹣112=144．故选D．5．如图，在▱ABCD中，已知AD=5cm，AB=3cm，AE平分∠BAD交BC边于点E，则EC等于（）A．1cm B．2cm C．3cm D．4cm【考点】平行四边形的性质．【分析】由平行四边形的性质和角平分线定义得出∠AEB=∠BAE，证出BE=AB=3cm，得出EC=BC ﹣BE=2cm即可．【解答】解：∵四边形ABCD是平行四边形，∴BC=AD=5cm，AD∥BC，∴∠DAE=∠AEB，∵AE平分∠BAD，∴∠BAE=∠DAE，∴∠AEB=∠BAE，∴BE=AB=3cm，∴EC=BC﹣BE=5﹣3=2cm；故选：B．6．已知一直角三角形的两直角边长分别是6cm和8cm，则斜边上的中线长（）A．10 B．3 C．4 D．5【考点】勾股定理；直角三角形斜边上的中线．【分析】根据勾股定理计算出直角三角形的斜边长，然后再根据在直角三角形中，斜边上的中线等于斜边的一半可得答案．【解答】解：斜边长为=10（cm），则斜边上的中线长为=5（cm），故选：D．7．如图，在矩形ABCD中，对角线AC，BD相交于点O，∠ACB=30°，则∠AOB的大小为（）A．30° B．60° C．90° D．120°【考点】矩形的性质．【分析】根据矩形的对角线互相平分且相等可得OB=OC，再根据等边对等角可得∠OBC=∠ACB，然后根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解．【解答】解：∵矩形ABCD的对角线AC，BD相交于点O，∴OB=OC，∴∠OBC=∠ACB=30°，∴∠AOB=∠OBC+∠ACB=30°+30°=60°．故选：B．8．如图，菱形ABCD中，E、F分别是AB、AC的中点，若EF=3，则菱形ABCD的周长是（）A．12 B．16 C．20 D．24【考点】菱形的性质；三角形中位线定理．【分析】根据三角形的中位线平行于第三边并且等于第三边的一半求出BC，再根据菱形的周长公式列式计算即可得解．【解答】解：∵E、F分别是AB、AC的中点，∴EF是△ABC的中位线，∴BC=2EF=2×3=6，∴菱形ABCD的周长=4BC=4×6=24．故选：D．9．如图是一个圆柱形饮料罐，底面半径是5，高是12，上底面中心有一个小圆孔，则一条到达底部的直吸管在罐内部分a的长度（罐壁的厚度和小圆孔的大小忽略不计）范围是（）A．12≤a≤13 B．12≤a≤15 C．5≤a≤12 D．5≤a≤13【考点】勾股定理的应用．【分析】最短距离就是饮料罐的高度，最大距离可根据勾股定理解答．【解答】解：a的最小长度显然是圆柱的高12，最大长度根据勾股定理，得： =13．即a的取值范围是12≤a≤13．故选：A．10．如图，将n个边长都为2的正方形按如图所示摆放，点A1，A2，…A n分别是正方形的中心，则这n个正方形重叠部分的面积之和是（）A．n B．n﹣1 C．（）n﹣1D． n【考点】正方形的性质；全等三角形的判定与性质．【分析】根据题意可得，阴影部分的面积是正方形的面积的，已知两个正方形可得到一个阴影部分，则n个这样的正方形重叠部分即为（n﹣1）个阴影部分的和．【解答】解：由题意可得一个阴影部分面积等于正方形面积的，即是×4=1，5个这样的正方形重叠部分（阴影部分）的面积和为：1×4，n个这样的正方形重叠部分（阴影部分）的面积和为：1×（n﹣1）=n﹣1．故选：B．二、填空（每小题4分共40分，请将答案写在答题纸相应位置）11．二次根式是一个整数，那么正整数a最小值是 2 ．【考点】二次根式的定义．【分析】根据二次根式的乘法，可得答案．【解答】解：由二次根式是一个整数，那么正整数a最小值是2，故答案为：2．12．如图，ABCD是对角线互相垂直的四边形，且OB=OD，请你添加一个适当的条件OA=OC ，使ABCD成为菱形（只需添加一个即可）【考点】菱形的判定．【分析】可以添加条件OA=OC，根据对角线互相垂直平分的四边形是菱形可判定出结论．【解答】解：OA=OC，∵OB=OD，OA=OC，∴四边形ABCD是平行四边形，∵AC⊥BD，∴平行四边形ABCD是菱形，故答案为：OA=OC．13．如图，已知OA=OB，那么数轴上点A所表示的数是﹣．【考点】勾股定理；实数与数轴．【分析】首先根据勾股定理得：OB=．即OA=．又点A在数轴的负半轴上，则点A对应的数是﹣．【解答】解：由图可知，OC=2，作BC⊥OC，垂足为C，取BC=1，故OB=OA===，∵A在x的负半轴上，∴数轴上点A所表示的数是﹣．故答案为：﹣．14．如图，正方形OABC的边长为6，点A、C分别在x轴，y轴的正半轴上，点D（2，0）在OA上，P是OB上一动点，则PA+PD的最小值为2．【考点】轴对称-最短路线问题；坐标与图形性质．【分析】过D点作关于OB的对称点D′，连接D′A交OB于点P，由两点之间线段最短可知D′A即为PA+PD的最小值，由正方形的性质可求出D′点的坐标，再根据OA=6可求出A点的坐标，利用两点间的距离公式即可求出D′A的值．【解答】解：过D点作关于OB的对称点D′，连接D′A交OB于点P，由两点之间线段最短可知D′A即为PA+PD的最小值，∵D（2，0），四边形OABC是正方形，∴D′点的坐标为（0，2），A点坐标为（6，0），∴D′A==2，即PA+PD的最小值为2．故答案为2．15．已知y=+﹣3，则2xy的值为﹣15 ．【考点】二次根式有意义的条件．【分析】根据非负数的性质列式求出x的值，再求出y的值，然后代入代数式进行计算即可得解．【解答】解：根据题意得，2x﹣5≥0且5﹣2x≥0，解得x≥且x≤，所以，x=，y=﹣3，所以，2xy=2××（﹣3）=﹣15．故答案为：﹣15．16．直角三角形有两边长为3和4，则斜边长为4或5 ．【考点】勾股定理．【分析】直角三角形中斜边为最长边，无法确定边长为4的边是否为斜边，所以要讨论（1）边长为4的边为斜边；（2）边长为4的边为直角边．【解答】解：（1）当边长为4的边为斜边时，该直角三角形中斜边长为4；（2）当边长为4的边为直角边时，则根据勾股定理得斜边长为=5，故该直角三角形斜边长为4cm或5cm，故答案为 4或5．17．计算：（ +）2015×（﹣）2015= 1 ．【考点】二次根式的混合运算．【分析】根据幂的乘方和积的乘方的运算法则求解．【解答】解：原式=[（+）（﹣）]2015=1．故答案为：1．18．已知菱形的两条对角线长为8cm和6cm，那么这个菱形的周长是20 cm，面积是24 cm2．【考点】菱形的性质；勾股定理．【分析】根据菱形的对角线互相垂直平分求出两对角线长的一半，然后利用勾股定理求出菱形的边长，再根据周长公式计算即可得解；根据菱形的面积等于对角线乘积的一半列式计算即可得解．【解答】解：∵菱形的两条对角线长为8cm和6cm，∴菱形的两条对角线长的一半分别为4cm和3cm，根据勾股定理，边长==5cm，所以，这个菱形的周长是5×4=20cm，面积=×8×6=24cm2．故答案为：20，24．19．﹣ = ﹣3 ．【考点】二次根式的性质与化简．【分析】根据二次根式的性质化简，根据相反数的概念解答即可．【解答】解：﹣ =﹣|﹣3|=﹣3，故答案为：﹣3．20．在实数范围内分解因式x3﹣3x= x（x+）（x﹣）．【考点】实数范围内分解因式．【分析】先提取公因式x，再把3写成（）2的形式，然后利用平方差公式继续分解因式．【解答】解：x3﹣3x=x（x2﹣3），=x[x2﹣（）2]，=x（x+）（x﹣）．故答案为：x（x+）（x﹣）．三、解答题21．计算（1）（2）（3）（7+4）（7﹣4）﹣（3﹣1）2．（4）先化简，再求值：﹣，其中x=+1，y=﹣1．【考点】二次根式的混合运算；分式的化简求值．【分析】（1）先把各二次根式化为最简二次根式，然后合并即可；（2）根据二次根式的乘除法则运算；（3）利用完全平方公式和平方差公式计算；（4）先通分，再化简得到原式=，然后把x、y的值代入计算即可．【解答】解：（1）原式=4+2﹣﹣=2；（2）原式==；（3）原式=49﹣48﹣（45﹣6+1）=1﹣46+6=6﹣45；（4）原式===，当x=+1，y=﹣1，原式==2．22．已知：如图，四边形ABCD四条边上的中点分别为E、F、G、H，顺次连接EF、FG、GH、HE，得到四边形EFGH（即四边形ABCD的中点四边形）．（1）四边形EFGH的形状是平行四边形．（2）证明你的结论．【考点】中点四边形．【分析】连接BD，根据三角形的中位线定理得到EH∥BD，EH=BD，FG∥BD，FG═BD，推出，EH∥FG，EH=FG，根据一组对边平行且相等的四边形是平行四边形得出四边形EFGH是平行四边形；【解答】解：（1）四边形EFGH的形状是平行四边形．（2）证明：如图，连结BD．∵E、H分别是AB、AD中点，∴EH∥BD，EH=BD，同理FG∥BD，FG=BD，∴EH∥FG，EH=FG，∴四边形EFGH是平行四边形；23．某港口位于东西方向的海岸线上．“远航”号、“海天”号轮船同时离开港口，各自沿一固定方向航行，“远航”号每小时航行16海里，“海天”号每小时航行12海里．它们离开港口一个半小时后相距30海里．如果知道“远航”号沿东北方向航行，能知道“海天”号沿哪个方向航行？为什么？【考点】勾股定理的应用；方向角．【分析】根据路程=速度×时间分别求得PQ、PR的长，再进一步根据勾股定理的逆定理可以证明三角形PQR是直角三角形，从而求解．【解答】解：根据题意，得PQ=16×1.5=24（海里），PR=12×1.5=18（海里），QR=30（海里）．∵242+182=302，即PQ2+PR2=QR2，∴∠QPR=90°．由“远航号”沿东北方向航行可知，∠QPS=45°，则∠SPR=45°，即“海天”号沿西北方向航行．四．选做题24．如图，平行四边形ABCD中，AB=3cm，BC=5cm，∠B=60°，G是CD的中点，E是边AD 上的动点，EG的延长线与BC的延长线交于点F，连结CE，DF．（1）求证：四边形CEDF是平行四边形；（2）①当AE= 3.5 cm时，四边形CEDF是矩形；②当AE= 2 cm时，四边形CEDF是菱形．（直接写出答案，不需要说明理由）【考点】平行四边形的判定与性质；菱形的判定；矩形的判定．【分析】（1）证△CFG≌△EDG，推出FG=EG，根据平行四边形的判定推出即可；（2）①求出△MBA≌△EDC，推出∠CED=∠AMB=90°，根据矩形的判定推出即可；②求出△CDE是等边三角形，推出CE=DE，根据菱形的判定推出即可．【解答】（1）证明：∵四边形ABCD是平行四边形，∴CF∥ED，∴∠FCG=∠EDG，∵G是CD的中点，∴CG=DG，在△FCG和△EDG中，，∴△FCG≌△EDG（ASA）∴FG=EG，∵CG=DG，∴四边形CEDF是平行四边形；（2）①解：当AE=3.5时，平行四边形CEDF是矩形，理由是：过A作AM⊥BC于M，∵∠B=60°，AB=3，∴BM=1.5，∵四边形ABCD是平行四边形，∴∠CDA=∠B=60°，DC=AB=3，BC=AD=5，∵AE=3.5，∴DE=1.5=BM，在△MBA和△EDC中，，∴△MBA≌△EDC（SAS），∴∠CED=∠AMB=90°，∵四边形CEDF是平行四边形，∴四边形CEDF是矩形，故答案为：3.5；②当AE=2时，四边形CEDF是菱形，理由是：∵AD=5，AE=2，∴DE=3，∵CD=3，∠CDE=60°，∴△CDE是等边三角形，∴CE=DE，∵四边形CEDF是平行四边形，∴四边形CEDF是菱形，故答案为：2．25．如图：平行四边形ABCD中，∠ABC的平分线交AD于E，∠BCD的平分线交AD于F，且AB=3，DE=2，（1）求平行四边形ABCD的周长．（2）求证：BE⊥CF（3）若CF=2，求BE的长．【考点】平行四边形的性质．【分析】（1）由平行四边形ABCD中，∠ABC的平分线交AD于E，可得△ABE是等腰三角形，即可求得AD的长，继而求得答案；（2）由平行四边形ABCD中，∠ABC的平分线交AD于E，∠BCD的平分线交AD于F，易证得∠CBE+∠BCF=90°，继而证得结论；（3）首先过点E作EN∥CF，交BC的延长线于点N，然后由勾股定理求得BE的长．【解答】（1）解：∵四边形ABCD是平行四边形，∴AD∥BC，∴∠AEB=∠CBE，∵BE平分∠ABC，∴∠ABE=∠CBE，∴∠ABE=∠AEB，∴AE=AB=3，∴AD=AE+DE=3+2=5，∴平行四边形ABCD的周长为：2（AB+AD）=2×（3+5）=16；（2）证明：设BE与CF交于点M，∵四边形ABCD是平行四边形，∴AB∥CD，∴∠ABC+∠BCD=180°，∵BE平分∠ABC，CF平分∠BCD，∴∠CBE=∠ABC，∠BCF=∠BCD，∴∠CBE+∠BCF=90°，∴∠BMC=90°，即BE⊥CF；（3）解：过点E作EN∥CF，交BC的延长线于点N，∵AD∥BC，∴四边形EFCN是平行四边形，∴CN=EF，EN=CF=2，∵AB=AE=3，同理：CD=DF=AB=3，∴EF=AE+DF﹣AD=3+3﹣5=1，∴CN=1，∴BN=BC+CN=5+1=6，在Rt△BEN中，BE==4．。

最大最全最精的教育资源网诚仁中学 2016-2017 学年度第二学期期中考试七年级历史试题（考试时间 60 分钟，满分 100 分）姓名：班级：准考据号：一、选择题 (共 25 小题，每题 2 分，请将1～25题所选答案填涂到答题卡上，不然不得分)1. 一致是历史发展的必定趋向。

在中国古代历史上曾先后出现过三次全国性的大一致(秦、隋、元 )，此中，达成隋朝一致的人物是A. 武则天B. 隋文帝C. 唐太宗D. 唐玄宗2.以下历史事件与隋炀帝有关的是A. 创办皇帝制度B. 开凿大运河C. 轻徭薄赋D. 虚心纳谏3.以下不属于隋的贡献的是A. 结束三国两晋南北朝分裂场面B. 创办科举制C.开通大运河，促使南北经济文化的沟通和发展D.是我国诗歌发展的黄金期间4.魏征被哪一皇帝比作一面“知得失”的镜子A. 秦始皇B. 商纣王C. 隋炀帝D. 唐太宗5.唐玄宗先期出现的盛世场面称为A. 贞观之治B. 开元盛世C. 文景之治D. 康乾盛世6.假如说唐代是中国历史上一个绚烂的乐章，那么“开元盛世”就是乐章里的最强音。

它的出现是几代人共同努力的结果。

“几代人”主要指A ．唐高祖、唐太宗、唐玄宗 B. 唐太宗、唐高宗、唐中宗C. 唐高宗、武则天、唐玄宗D. 唐太宗、武则天、唐玄宗7.“惜秦皇汉武，略输文采；唐宗宋祖，稍逊风骚“。

毛泽东在此诗中说起的古代开国帝王有A ．秦皇、汉武B 唐宗、宋祖 C. 秦皇、宋祖 D. 汉武、唐宗8.隋唐期间创办和完美的增强皇权的制度A ．三省六部制 B. 推恩令 C. 中书省 D. 三公九卿制9.玄奘西行、鉴真东渡的史实充足表现了唐代对外交往的特色是A. 关国B. 高度繁华C. 封建落伍D. 外开放10. 唐代是我国歌作的黄金代。

以下被称“ 仙”的是A. 李白B. 杜甫C. 杜牧D. 愈11.新是一个民族的不懈力，以下属于唐代明的是①雕版印刷②火③活字印刷④交子A. ①②B. ②③④C. ①③④D. ②③12.史：“始置州通判⋯⋯ 故常与知州争。

2016-2017学年内蒙古巴彦淖尔市磴口县诚仁中学八年级（上）期中物理试卷一、选择题（共47分）（1-----13题为单项选择题；14----15题为多项选择题）1．（3分）下列几种估测最符合实际情况的是（）A．人步行的速度约为5m/s B．全新的2B铅笔长约18cmC．课桌的高度约为1.5 m D．一张试卷的厚度大约1mm2．（3分）关于声音的说法正确的是（）A．噪声不是由物体振动产生的B．一切正在发声的物体都在振动C．只要物体振动，我们就能听见声音D．声音的传播速度在固体中一定比在液体中快3．（3分）热现象在一年四季中随处可见，下列说法中正确的是（）A．春天的早晨经常出现大雾，这是凝华现象B．夏天揭开冰棒包装后会看到冰棒冒“白气”，这是升华现象C．秋天的早晨花草上出现小露珠，这是液化现象D．初冬的早晨地面上会出现白色的霜，这是凝固现象4．（3分）男低音独唱时由女高音轻声伴唱，则男低音比女高音（）A．音调低，响度大 B．音调低，响度小C．音调高，响度大 D．音调高，响度小5．（3分）关于运动和静止，下列说法错误的是（）A．拖拉机和联合收割机以同样的速度前进时，以拖拉机为参照物，联合收割机是静止的B．站在正在上升的观光电梯上的乘客认为电梯是静止的，是因为他以身边的乘客为参照物C．站在地球上的人觉得地球同步通信卫星在空中静止不动，是因为他以自己为参照物D．飞机在空中加油时若以受油机为参照物，加油机是运动的6．（3分）小沈阳在2009年春晚小品“不差钱”中模仿歌手刀郎的声音，观众感觉很像。

从物理学角度看，小沈阳主要是模仿了刀郎歌声的（）A．音速B．音调C．响度D．音色7．（3分）用图象表示物体运动规律，图中表示同一运动规律的是（）A．甲图和丙图B．甲图和丁图C．乙图和丙图D．乙图和丁图8．（3分）有一支用过后未甩的体温计，其示数为39℃．用这支体温计先后去测两个体温分别是38℃和40℃的病人的体温，体温计显示的示数分别是（）A．38℃，39℃B．39℃，40℃C．38℃，40℃D．39℃，39℃9．（3分）一短跑运动员在5s内跑完了50m，汽车行驶的速度是54km/h，羚羊奔跑的速度是20m/s，那么三者速度从小到大的顺序是（）A．运动员、汽车、羚羊B．汽车、羚羊、运动员C．羚羊、汽车、运动员D．运动员、羚羊、汽车10．（3分）将耳朵贴在长铁管的一端，让另外一个人敲一下铁管的另一端，则能听见（）A．两次响声，它们依先后次序是由铁管，空气传来B．两次响声，它们依先后次序是由空气，铁管传来C．无数次响声，声波在铁管内被管壁无数次地反射D．无法判断11．（3分）下列做法不能使水的蒸发加快的是（）A．用电热吹风机将湿头发吹干B．用扫帚把地面的积水向周围扫开C．把粮食拿到向阳的地方晒D．把水果用保鲜膜包好放在冷藏柜里12．（3分）如果你家附近建筑工地在施工，影响你的学习和休息，为了减小噪声的干扰，下列做法不合理的是（）A．关紧门窗B．打开门窗，让空气加快流通C．戴上耳罩D．告知有关部门督促施工单位合理安排施工时间13．（3分）一代伟人毛泽东在《沁园春•雪》中写到：“北国风光，千里冰封，万里雪飘”，形成这种自然景象的主要物态变化是（）A．熔化和汽化B．凝固和凝华C．凝固和液化D．汽化和升华14．（4分）下列说法中错误的是（）A．真空可以传播声音B．蝙蝠在飞行时会发出次声波，根据回声定位原理来飞行C．冰棍周围的“白气”是冰熔化成的小水滴D．霜叶红于二月花不是描述物体机械运动的15．（4分）下列说法中正确的是（）A．用久了的电灯灯丝变细是升华现象B．秋天的早晨，大雾逐渐散去是液化现象C．被水蒸气烫伤比沸水烫伤更严重是因为水蒸气液化时要放出热量D．人出汗后，微风吹过感到凉爽，是因为汗液蒸发加快，带走更多的热量二、实验探究题（2’×22=44’）16．（6分）（1）物体的宽度是cm；（2）停表的读数是s；（3）温度计的示数是。

2016-2017学年内蒙古巴彦淖尔市磴口县诚仁中学九年级（上）期中数学试卷一、选择题（共40分．每小题4分，共10小题）1．（4分）下列方程中是关于x的一元二次方程的是（）A．B．ax2+bx+c=0C．（x﹣1）（x+2）=1 D．3x2﹣2xy﹣5y2=02．（4分）方程x2﹣2x=0的解为（）A．x1=1，x2=2 B．x1=0，x2=1 C．x1=0，x2=2 D．x1=，x2=23．（4分）A是双曲线y=﹣上一点，过点A向x轴作垂线，垂足为B，向y轴作垂线，垂足为C，则四边形OBAC的面积为（）A．6 B．5 C．10 D．﹣54．（4分）某超市一月份的营业额为36万元，三月份的营业额为48万元，设每月的平均增长率为x，则可列方程为（）A．48（1﹣x）2=36 B．48（1+x）2=36 C．36（1﹣x）2=48 D．36（1+x）2=48 5．（4分）一元二次方程2x2﹣5x+1=0的根的情况是（）A．有两个不相等的实数根B．有两个相等的实数根C．没有实数根D．无法确定6．（4分）关于x的一元二次方程（a﹣5）x2﹣4x﹣1=0有实数根，则a满足（）A．a≥1 B．a＞1且a≠5 C．a≥1且a≠5 D．a≠57．（4分）已知反比例函数y=的图象如图，则函数y=kx﹣2的图象是图中的（）A．B．C．D．8．（4分）抛物线y=2（x﹣3）2+1的顶点坐标是（）A．（3，1） B．（3，﹣1）C．（﹣3，1）D．（﹣3，﹣1）9．（4分）抛物线y=3x2向右平移1个单位，再向下平移2个单位，所得到的抛物线是（）A．y=3（x﹣1）2﹣2 B．y=3（x+1）2﹣2 C．y=3（x+1）2+2 D．y=3（x﹣1）2+210．（4分）已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，有下列4个结论：①abc＞0；②﹣b＜a+c；③4a+2b+c＞0；④b2﹣4ac＞0；其中正确的结论有（）A．1个 B．2个 C．3个 D．4个二、填空题（共32分．每小题4分，共8小题）11．（4分）把方程3x（x﹣1）=（x+2）（x﹣2）+9化成ax2+bx+c=0的形式为．12．（4分）若x=﹣2是关于x的一元二次方程x2﹣mx+8=0的一个解，则m的值是．13．（4分）已知m和n是方程2x2﹣5x﹣3=0的两根，则=．14．（4分）如图，在直角△OAB中，∠AOB=30°，将△OAB绕点O逆时针旋转100°得到△OA1B1，则∠A1OB=°．15．（4分）时钟上的时针不停地旋转，从上午8时到上午11时，时针旋转的角度是．16．（4分）已知二次函数y=x2+bx+3的对称轴为x=2，则b=．17．（4分）若函数y=（m﹣3）是二次函数，则m=．18．（4分）若将二次函数y=x2﹣2x+3配方为y=（x﹣h）2+k的形式，则y=．三、解答题（共48分）19．（10分）解方程（1）x2﹣4x+1=0（2）3（x﹣2）2=x（x﹣2）．20．（7分）学校要组织一次篮球赛，赛制为每两队之间都赛一场，计划安排28场比赛，应邀请多少支球队参加比赛．21．（6分）用配方法把二次函数y=x2﹣3x﹣4化成y=a（x﹣h）2+k的形式，并写出该函数图象的开口方向、对称轴和顶点坐标．22．（6分）关于x的一元函数y=﹣2x+m和反比例函数y=的图象都经过点A （﹣2，1）．（1）求一次函数和反比例函数的解析式；（2）求一次函数与反比例函数的另一个交点B的坐标；（3）求△AOB的面积．23．（6分）已知y=y1﹣y2，y1与x2成正比例，y2与x﹣1成反比例，当x=﹣1时，y=3；当x=2时，y=﹣3．（1）求y与x之间的函数关系；（2）当x=时，求y的值．24．（6分）已知二次函数的图象顶点是（2，﹣1），且经过（0，1），求这个二次函数的解析式．25．（7分）如图，已知二次函数y=﹣+bx+c的图象经过A（2，0）、B（0，﹣6）两点．（1）求这个二次函数的解析式；（2）设该二次函数的对称轴与x轴交于点C，连接BA、BC，求△ABC的面积．2016-2017学年内蒙古巴彦淖尔市磴口县诚仁中学九年级（上）期中数学试卷参考答案与试题解析一、选择题（共40分．每小题4分，共10小题）1．（4分）下列方程中是关于x的一元二次方程的是（）A．B．ax2+bx+c=0C．（x﹣1）（x+2）=1 D．3x2﹣2xy﹣5y2=0【解答】解：A、原方程为分式方程；故A选项错误；B、当a=0时，即ax2+bx+c=0的二次项系数是0时，该方程就不是一元二次方程；故B选项错误；C、由原方程，得x2+x﹣3=0，符合一元二次方程的要求；故C选项正确；D、方程3x2﹣2xy﹣5y2=0中含有两个未知数；故D选项错误．故选：C．2．（4分）方程x2﹣2x=0的解为（）A．x1=1，x2=2 B．x1=0，x2=1 C．x1=0，x2=2 D．x1=，x2=2【解答】解：x2﹣2x=0，x（x﹣2）=0，x=0，x﹣2=0，x1=0，x2=2，故选：C．3．（4分）A是双曲线y=﹣上一点，过点A向x轴作垂线，垂足为B，向y轴作垂线，垂足为C，则四边形OBAC的面积为（）A．6 B．5 C．10 D．﹣5【解答】解：∵点A在双曲线y=﹣上，且AC⊥y轴，AB⊥x轴，=|k|=5．∴S矩形OBAC故选：B．4．（4分）某超市一月份的营业额为36万元，三月份的营业额为48万元，设每月的平均增长率为x，则可列方程为（）A．48（1﹣x）2=36 B．48（1+x）2=36 C．36（1﹣x）2=48 D．36（1+x）2=48【解答】解：二月份的营业额为36（1+x），三月份的营业额为36（1+x）×（1+x）=36（1+x）2，即所列的方程为36（1+x）2=48，故选：D．5．（4分）一元二次方程2x2﹣5x+1=0的根的情况是（）A．有两个不相等的实数根B．有两个相等的实数根C．没有实数根D．无法确定【解答】解：∵△=（﹣5）2﹣4×2×1=25﹣8=17＞0，∴方程有有两个不相等的实数根．故选：A．6．（4分）关于x的一元二次方程（a﹣5）x2﹣4x﹣1=0有实数根，则a满足（）A．a≥1 B．a＞1且a≠5 C．a≥1且a≠5 D．a≠5【解答】解：由已知得：，解得：a≥1且a≠5．故选：C．7．（4分）已知反比例函数y=的图象如图，则函数y=kx﹣2的图象是图中的（）A．B．C．D．【解答】解：由反比例函数y=的图象知，k＞0，又∵﹣2＜0，∴一次函数y=kx﹣2的图象位于一、三、四象限，故选：A．8．（4分）抛物线y=2（x﹣3）2+1的顶点坐标是（）A．（3，1） B．（3，﹣1）C．（﹣3，1）D．（﹣3，﹣1）【解答】解：由y=2（x﹣3）2+1，根据顶点式的坐标特点可知，顶点坐标为（3，1）．故选：A．9．（4分）抛物线y=3x2向右平移1个单位，再向下平移2个单位，所得到的抛物线是（）A．y=3（x﹣1）2﹣2 B．y=3（x+1）2﹣2 C．y=3（x+1）2+2 D．y=3（x﹣1）2+2【解答】解：抛物线y=3x2向右平移1个单位，再向下平移2个单位，所得到的抛物线是y=3（x﹣1）2﹣2，故选：A．10．（4分）已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，有下列4个结论：①abc＞0；②﹣b＜a+c；③4a+2b+c＞0；④b2﹣4ac＞0；其中正确的结论有（）A．1个 B．2个 C．3个 D．4个【解答】解：∵抛物线开口朝下，∴a＜0，∵对称轴x=1=﹣，∴b＞0，∵抛物线与y轴的交点在x轴的上方，∴c＞0，∴abc＜0，故①错误；根据图象知道当x=﹣1时，y=a﹣b+c＜0，∴a+c＜b，故②错误；根据图象知道当x=2时，y=4a+2b+c＞0，故③正确；根据图象知道抛物线与x轴有两个交点，∴b2﹣4ac＞0，故④正确．正确的有③④．故选：B．二、填空题（共32分．每小题4分，共8小题）11．（4分）把方程3x（x﹣1）=（x+2）（x﹣2）+9化成ax2+bx+c=0的形式为2x2﹣3x﹣5=0．【解答】解：方程整理得：3x2﹣3x=x2﹣4+9，即2x2﹣3x﹣5=0．故答案为：2x2﹣3x﹣5=0．12．（4分）若x=﹣2是关于x的一元二次方程x2﹣mx+8=0的一个解，则m的值是﹣6．【解答】解：把x=﹣2代入方程x2﹣mx+8=0得4+2m+8=0，解得m=﹣6．故答案为﹣6．13．（4分）已知m和n是方程2x2﹣5x﹣3=0的两根，则=﹣．【解答】解：∵m和n是方程2x2﹣5x﹣3=0的两根，∴m+n=﹣=﹣=，m•n==﹣，∴+===﹣故答案为﹣．14．（4分）如图，在直角△OAB中，∠AOB=30°，将△OAB绕点O逆时针旋转100°得到△OA1B1，则∠A1OB=70°．【解答】解：∵将△OAB绕点O逆时针旋转100°得到△OA1B1，∠AOB=30°，∴△OAB≌△OA1B1，∴∠A1OB1=∠AOB=30°．∴∠A1OB=∠A1OA﹣∠AOB=70°．故答案为：70．15．（4分）时钟上的时针不停地旋转，从上午8时到上午11时，时针旋转的角度是90°．【解答】解：∵周角为360°，时针12小时转一周，∴每小时对应的角度为：360°÷12=30°．∵时针从上午8时到上午11时走了三个小时，∴时针旋转的角度是：30°×3=90°．故答案为：90°．16．（4分）已知二次函数y=x2+bx+3的对称轴为x=2，则b=﹣4．【解答】解：∵对称轴为x=2，∴﹣=2，∴b=﹣4．17．（4分）若函数y=（m﹣3）是二次函数，则m=﹣5．【解答】解：∵y=（m﹣3）是二次函数，∴，解得m=﹣5．故答案为﹣5．18．（4分）若将二次函数y=x2﹣2x+3配方为y=（x﹣h）2+k的形式，则y=（x ﹣1）2+2．【解答】解：y=x2﹣2x+3=（x2﹣2x+1）+2=（x﹣1）2+2故本题答案为：y=（x﹣1）2+2．三、解答题（共48分）19．（10分）解方程（1）x2﹣4x+1=0（2）3（x﹣2）2=x（x﹣2）．【解答】解：（1）x2﹣4x+1=0x2﹣4x+4=﹣1+4（x﹣2）2=3x﹣2=±解得：x1=2+，x2=2﹣．（2）3（x﹣2）2=x（x﹣2）（x﹣2）[3（x﹣2）﹣x]=0（x﹣2）（2x﹣6）=0解得：x1=2，x2=3．20．（7分）学校要组织一次篮球赛，赛制为每两队之间都赛一场，计划安排28场比赛，应邀请多少支球队参加比赛．【解答】解：设要邀请x支球队参加比赛，由题意，得x（x﹣1）=28，解得：x1=8，x2=﹣7（舍去）．答：应邀请8支球队参加比赛．21．（6分）用配方法把二次函数y=x2﹣3x﹣4化成y=a（x﹣h）2+k的形式，并写出该函数图象的开口方向、对称轴和顶点坐标．【解答】解：y=x2﹣3x﹣4=（x﹣）2﹣，则函数图象的开口方向向上，对称轴是x=，顶点坐标（，﹣）．22．（6分）关于x的一元函数y=﹣2x+m和反比例函数y=的图象都经过点A （﹣2，1）．（1）求一次函数和反比例函数的解析式；（2）求一次函数与反比例函数的另一个交点B的坐标；（3）求△AOB的面积．【解答】解：（1）把A（﹣2，1）代入函数关系式得到m=﹣3，n=﹣3∴一次函数的解析式为y=﹣2x﹣3，反比例函数的解析式为y=﹣；（2）解方程组，得：，，∴B的坐标为（，﹣4）；（3）∵一次函数的解析式为y=﹣2x﹣3，∴y=0时，x=﹣，则CO=，=S△AOC+S△BOC==．∴S△AOB23．（6分）已知y=y1﹣y2，y1与x2成正比例，y2与x﹣1成反比例，当x=﹣1时，y=3；当x=2时，y=﹣3．（1）求y与x之间的函数关系；（2）当x=时，求y的值．【解答】解：（1）设y1=ax2，y2=，则y=ax2﹣，把x=﹣1，y=3；x=2，y=﹣3分别代入得，解得，所以y与x之间的函数关系为y=x2﹣；（2）当x=时，y=x2﹣=×（）2﹣=1﹣5（+1）=﹣5﹣4．24．（6分）已知二次函数的图象顶点是（2，﹣1），且经过（0，1），求这个二次函数的解析式．【解答】解：设二次函数的解析式是y=a（x﹣2）2﹣1，把（0，1）代入，得4a=2，即a=，∴该二次函数的解析式是y=（x﹣2）2﹣1．25．（7分）如图，已知二次函数y=﹣+bx+c的图象经过A（2，0）、B（0，﹣6）两点．（1）求这个二次函数的解析式；（2）设该二次函数的对称轴与x轴交于点C，连接BA、BC，求△ABC的面积．【解答】解：（1）把A（2，0）、B（0，﹣6）代入y=﹣+bx+c，得：解得，∴这个二次函数的解析式为y=﹣+4x﹣6．（2）∵该抛物线对称轴为直线x=﹣=4，∴点C的坐标为（4，0），∴AC=OC﹣OA=4﹣2=2，∴S=×AC×OB=×2×6=6．△ABC。

2015-2016学年内蒙古巴彦淖尔市磴口县诚仁中学七年级（下）期中数学试卷一、选择题（每小题3分，共36分）1．（3分）在数﹣3.14，，，π，，0.1010010001…中无理数的个数有（）A．3个B．2个C．1个D．4个2．（3分）下列说法正确的是（）A．﹣5是25的平方根B．25的平方根是﹣5C．﹣5是（﹣5）2的算术平方根D．±5是（﹣5）2的算术平方根3．（3分）方程组的解是（）A．B．C．D．4．（3分）如图，直线a∥b，直线c是截线，如果∠1=50°，那么∠2等于（）A．50°B．150°C．140°D．130°5．（3分）三个实数﹣，﹣2，﹣之间的大小关系是（）A．﹣＞﹣＞﹣2B．﹣＞﹣2＞﹣C．﹣2＞﹣＞﹣D．﹣＜﹣2＜﹣6．（3分）若x轴上的点P到y轴的距离为3，则点P的坐标为（）A．（0，3）B．（0，3）或（0，﹣3）C．（3，0）D．（3，0）或（﹣3，0）7．（3分）下列说法中正确的是（）A．在同一平面内，两条直线的位置只有两种：相交和垂直B．有且只有一条直线垂直于已知直线C．如果两条直线都与第三条直线平行，那么这两条直线也互相平行D．从直线外一点到这条直线的垂线段，叫做这点到这条直线的距离8．（3分）把点A（﹣2，1）向上平移2个单位，再向右平移3个单位后得到B，点B的坐标是（）A．（﹣5，3）B．（1，3）C．（1，﹣3）D．（﹣5，﹣1）9．（3分）一个正方形在平面直角坐标系中三个顶点的坐标为（﹣2，﹣3），（﹣2，1），（2，1），则第四个顶点的坐标为（）A．（2，2）B．（3，2）C．（2，﹣3）D．（2，3）10．（3分）下列语句中，假命题的是（）A．如果A（a，b）在x轴上，那么B（b，a）在y轴上B．如果直线a、b、c满足a∥b，b∥c，那么a∥cC．两直线平行，同旁内角互补D．相等的两个角是对顶角11．（3分）已知点P（x，y）在第四象限，且x2=9，|y|=5，则P点的坐标是（）A．（﹣3，﹣5）B．（5，﹣3）C．（3，﹣5）D．（﹣3，5）12．（3分）已知点A（2，﹣3）关于x轴对称的点的坐标为点B（2m，m+n），则m﹣n的值为（）A．﹣5B．﹣1C．1D．5二、填空（每小题3分，共21分）13．（3分）的相反数为，绝对值为．14．（3分）﹣343的立方根是；立方根是﹣0.2的数是．15．（3分）在x轴上，到原点距离为的坐标是．16．（3分）若（a﹣1）2+|b﹣9|=0，则的平方根是．17．（3分）若是方程x﹣ky=1的解，则k=．18．（3分）若点B（a，b）在第三象限，则点C（﹣a+1，3b﹣5）在第象限．19．（3分）若x2m+3+y4n﹣1=6是二元一次方程，则m=，n=．三、解答题：（63分）20．（12分）计算（1）（2）﹣（3）||﹣||21．（20分）解方程（1）3x2﹣4=23（2）4（2﹣x）2=9（3）（4）．22．（7分）若一个正数的平方根是2a+3和3a﹣8．求这个正数．23．（8分）如图，四边形ABCD为平行四边形，OD=3，CD=AB=5，点A坐标为（﹣2，0）（1）请写出B、C、D各点的坐标；（2）求四边形ABCD的面积．24．（8分）如图，已知∠DAB+∠D=180°，AC平分∠DAB，且∠CAD=25°，∠B=95°．（1）求∠DCA的度数；（2）求∠DCE的度数；（3）求∠BCA的度数．25．（8分）已知实数a、b在数轴上对应点的位置如图：（1）比较a﹣b与a+b的大小；（2）化简|b﹣a|+|a+b|．2015-2016学年内蒙古巴彦淖尔市磴口县诚仁中学七年级（下）期中数学试卷参考答案与试题解析一、选择题（每小题3分，共36分）1．（3分）在数﹣3.14，，，π，，0.1010010001…中无理数的个数有（）A．3个B．2个C．1个D．4个【考点】26：无理数．【解答】解：，π，0.1010010001…是无理数，故选：A．2．（3分）下列说法正确的是（）A．﹣5是25的平方根B．25的平方根是﹣5C．﹣5是（﹣5）2的算术平方根D．±5是（﹣5）2的算术平方根【考点】21：平方根；22：算术平方根．【解答】解：A、﹣5是25的平方根，说法正确；B、25的平方根是﹣5，说法错误；C、﹣5是（﹣5）2的算术平方根，说法错误；D、±5是（﹣5）2的算术平方根，说法错误；故选：A．3．（3分）方程组的解是（）A．B．C．D．【考点】98：解二元一次方程组．【解答】解：，①+②得：3x=6，即x=2，把x=2代入①得：y=1，则方程组的解为，故选：D．4．（3分）如图，直线a∥b，直线c是截线，如果∠1=50°，那么∠2等于（）A．50°B．150°C．140°D．130°【考点】JA：平行线的性质．【解答】解：∵直线a∥b，∠1=50°，∴∠1=∠3=50°，∴∠2=180°﹣∠3=180°﹣50°=130°．故选：D．5．（3分）三个实数﹣，﹣2，﹣之间的大小关系是（）A．﹣＞﹣＞﹣2B．﹣＞﹣2＞﹣C．﹣2＞﹣＞﹣D．﹣＜﹣2＜﹣【考点】2A：实数大小比较．【解答】解：∵﹣2=﹣，又∵＜＜∴﹣2＞﹣＞﹣．故选：C．6．（3分）若x轴上的点P到y轴的距离为3，则点P的坐标为（）A．（0，3）B．（0，3）或（0，﹣3）C．（3，0）D．（3，0）或（﹣3，0）【考点】D1：点的坐标．【解答】解：∵P在x轴上，∴P的纵坐标为0，∵P到y轴的距离是3，∴P的横坐标为3或﹣3，∴点P坐标是（3，0）或（﹣3，0）．故选：D．7．（3分）下列说法中正确的是（）A．在同一平面内，两条直线的位置只有两种：相交和垂直B．有且只有一条直线垂直于已知直线C．如果两条直线都与第三条直线平行，那么这两条直线也互相平行D．从直线外一点到这条直线的垂线段，叫做这点到这条直线的距离【考点】J1：相交线；J3：垂线；J5：点到直线的距离；J8：平行公理及推论．【解答】解：A、在同一平面内，两条直线的位置只有两种：相交和平行，垂直是相交的一种情况，故A错误；B、一条直线的垂线有无数条，故B错误；C、根据平行公理的推论，如果两条直线都与第三条直线平行，那么这两条直线也互相平行，故C正确；D、点到直线的距离指的是线段的长度，而非垂线段，故D错误．故选：C．8．（3分）把点A（﹣2，1）向上平移2个单位，再向右平移3个单位后得到B，点B的坐标是（）A．（﹣5，3）B．（1，3）C．（1，﹣3）D．（﹣5，﹣1）【考点】Q3：坐标与图形变化﹣平移．【解答】解：∵A（﹣2，1）向上平移2个单位，再向右平移3个单位后得到B，∴1+2=3，﹣2+3=1；点B的坐标是（1，3）．故选：B．9．（3分）一个正方形在平面直角坐标系中三个顶点的坐标为（﹣2，﹣3），（﹣2，1），（2，1），则第四个顶点的坐标为（）A．（2，2）B．（3，2）C．（2，﹣3）D．（2，3）【考点】D5：坐标与图形性质．【解答】解：∵正方形的两个顶点为：（﹣2，﹣3），（﹣2，1），∴正方形的边长为：1﹣（﹣3）=4，∵第三个点的坐标为：（2，1），∴第四个顶点的坐标为：（2，﹣3）．故选：C．10．（3分）下列语句中，假命题的是（）A．如果A（a，b）在x轴上，那么B（b，a）在y轴上B．如果直线a、b、c满足a∥b，b∥c，那么a∥cC．两直线平行，同旁内角互补D．相等的两个角是对顶角【考点】D1：点的坐标；J2：对顶角、邻补角；J8：平行公理及推论；JA：平行线的性质；O1：命题与定理．【解答】解：A、∵A（a，b）在x轴上，∴b=0，∴B（b，a）在y轴上，故选项正确；B、∵直线a、b、c满足a∥b，b∥c，∴a∥c，故选项正确；C、根据平行线的性质知道两直线平行，同旁内角互补，故选项正确；D、相等的两个角不一定是对顶角，故选项错误．故选：D．11．（3分）已知点P（x，y）在第四象限，且x2=9，|y|=5，则P点的坐标是（）A．（﹣3，﹣5）B．（5，﹣3）C．（3，﹣5）D．（﹣3，5）【考点】D1：点的坐标．【解答】解：∵点P（x，y）在第四象限，且x2=9，|y|=5，∴x=3，y=﹣5，∴P（3，﹣5）．故选：C．12．（3分）已知点A（2，﹣3）关于x轴对称的点的坐标为点B（2m，m+n），则m﹣n的值为（）A．﹣5B．﹣1C．1D．5【考点】P5：关于x轴、y轴对称的点的坐标．【解答】解：∵点A（2，﹣3）关于x轴对称的点的坐标为点B（2m，m+n），∴2m=2，m+n=3，解得：m=1，n=2，m﹣n=1﹣2=﹣1，故选：B．二、填空（每小题3分，共21分）13．（3分）的相反数为﹣2，绝对值为﹣2．【考点】28：实数的性质．【解答】解：的相反数为：﹣（2﹣）=﹣2，绝对值为：|2﹣|=﹣2，故答案为：﹣2，﹣2．14．（3分）﹣343的立方根是﹣7；立方根是﹣0.2的数是0.8．【考点】24：立方根．【解答】解：=﹣7，（﹣0.2）3=﹣0.8故答案为：﹣7，0.8．15．（3分）在x轴上，到原点距离为的坐标是（，0），（﹣，0）．【考点】D1：点的坐标．【解答】解：∵在x轴上，到原点距离为，∴此点可以为：（，0），（﹣，0）．故答案为：（，0），（﹣，0）．16．（3分）若（a﹣1）2+|b﹣9|=0，则的平方根是±3．【考点】16：非负数的性质：绝对值；1F：非负数的性质：偶次方；21：平方根．【解答】解：∵（a﹣1）2+|b﹣9|=0，∴a﹣1=0，b﹣9=0，∴a=1，b=9，∴，∴9的平方根是±3，故答案为：±3．17．（3分）若是方程x﹣ky=1的解，则k=﹣1．【考点】92：二元一次方程的解．【解答】解：把代入方程得：2+k=1，解得：k=﹣1，故答案为：﹣118．（3分）若点B（a，b）在第三象限，则点C（﹣a+1，3b﹣5）在第四象限．【考点】D1：点的坐标．【解答】解：∵点B（a，b）在第三象限，∴a＜0，b＜0，∴﹣a+1＞0，3b﹣5＜0，则点C（﹣a+1，3b﹣5）满足点在第四象限的条件，故点C（﹣a+1，3b﹣5）在第四象限．19．（3分）若x2m+3+y4n﹣1=6是二元一次方程，则m=﹣1，n=．【考点】91：二元一次方程的定义．【解答】解：∵x2m+3+y4n﹣1=6是二元一次方程，∴2m+3=1，4n﹣1=1．解得：m=﹣1，n=．故答案为：﹣1；．三、解答题：（63分）20．（12分）计算（1）（2）﹣（3）||﹣||【考点】2C：实数的运算．【解答】解：（1）原式=9﹣5=4；（2）原式=3﹣6+3=0；（3）原式=﹣﹣+=0．21．（20分）解方程（1）3x2﹣4=23（2）4（2﹣x）2=9（3）（4）．【考点】21：平方根；98：解二元一次方程组．【解答】解：（1）x2=9，x=±3，所以x1=3，x2=﹣3；（2）2（2﹣x）=±3，所以x1=，x2=；（3），①×2+②得5x=30，解得x=6，把x=6代入①得6﹣y=7，解得x=﹣1，所以方程组的解为；（4）方程组整理为，①﹣②得4y=28，解得y=7，把y=7代入①得3x﹣7=8，解得x=5，所以方程组的解为．22．（7分）若一个正数的平方根是2a+3和3a﹣8．求这个正数．【考点】21：平方根．【解答】解：∵一个正数的平方根是2a+3和3a﹣8，∴2a+3+3a﹣8=0，解得：a=1，2a+3=5，这个正数为52=25．23．（8分）如图，四边形ABCD为平行四边形，OD=3，CD=AB=5，点A坐标为（﹣2，0）（1）请写出B、C、D各点的坐标；（2）求四边形ABCD的面积．【考点】D5：坐标与图形性质；L5：平行四边形的性质．【解答】解：（1）∵OD=3，∴D（0，3），∵CD=AB=5，点A坐标为（﹣2，0），∴C的坐标为（5，3），B（3，0）；（2）平行四边形ABCD的面积=AB•OD=5×3=15．24．（8分）如图，已知∠DAB+∠D=180°，AC平分∠DAB，且∠CAD=25°，∠B=95°．（1）求∠DCA的度数；（2）求∠DCE的度数；（3）求∠BCA的度数．【考点】JB：平行线的判定与性质．【解答】解：（1）∵∠DAB+∠D=180°，∴AB∥CD，∴∠ACD=∠BAC，∵AC平分∠DAB，∴∠DAC=∠BAC，∴∠DAC=∠DCA，∵∠CAD=25°，∴∠DCA=25°；（2）∵AB∥CD，∴∠ECD=∠B；∵∠B=95，∴∠DCE=95°；（3）∵AB∥CD，∴∠BCD+∠B=180，∴∠BCA=180°﹣95°﹣25°=60°．25．（8分）已知实数a、b在数轴上对应点的位置如图：（1）比较a﹣b与a+b的大小；（2）化简|b﹣a|+|a+b|．【考点】15：绝对值；29：实数与数轴；2A：实数大小比较．【解答】解：由图可知，a＞0，b＜0，且|a|＜|b|，（1）∵（a﹣b）﹣（a+b）=a﹣b﹣a﹣b=﹣2b＞0，∴a﹣b＞a+b；（2）因为b﹣a＜0，a+b＜0，所以|b﹣a|+|a+b|=a﹣b﹣a﹣b=﹣2b．。

诚仁中学2016-2017学年度第二学期期中考试七年级历史试题（考试时间60分钟，满分100分）姓名：班级：准考证号：一、选择题(共25小题，每题2分，请将1～25题所选答案填涂到答题卡上，否则不得分)1. 统一是历史发展的必然趋势。

在中国古代历史上曾先后出现过三次全国性的大统一(秦、隋、元)，其中，完成隋朝统一的人物是A. 武则天B. 隋文帝C. 唐太宗D.唐玄宗2. 下列历史事件与隋炀帝有关的是A. 创立皇帝制度B. 开凿大运河C. 轻徭薄赋D. 虚心纳谏3. 下列不属于隋的贡献的是A. 结束三国两晋南北朝分裂局面B. 创立科举制C. 开通大运河，促进南北经济文化的交流和发展D. 是我国诗歌发展的黄金时期4. 魏征被哪一皇帝比作一面“知得失”的镜子A.秦始皇B. 商纣王C. 隋炀帝D. 唐太宗5. 唐玄宗前期出现的盛世局面称为A. 贞观之治B. 开元盛世C. 文景之治D. 康乾盛世6. 如果说唐朝是中国历史上一个辉煌的乐章，那么“开元盛世”就是乐章里的最强音。

它的出现是几代人共同努力的结果。

“几代人”主要指A．唐高祖、唐太宗、唐玄宗 B. 唐太宗、唐高宗、唐中宗C. 唐高宗、武则天、唐玄宗D. 唐太宗、武则天、唐玄宗7. “惜秦皇汉武，略输文采；唐宗宋祖，稍逊风骚“。

毛泽东在此诗中提及的古代开国帝王有A．秦皇、汉武B唐宗、宋祖C. 秦皇、宋祖 D. 汉武、唐宗8. 隋唐时期创立和完善的加强皇权的制度A．三省六部制 B. 推恩令 C. 中书省 D. 三公九卿制9.玄奘西行、鉴真东渡的史实充分体现了唐朝对外交往的特点是A. 闭关锁国B. 高度繁荣C. 封建落后D. 对外开放10. 唐朝是我国诗歌创作的黄金时代。

下列被称为“诗仙”的是A. 李白B. 杜甫C. 杜牧D. 韩愈11. 创新是一个民族的不懈动力，下列属于唐朝发明的是①雕版印刷②火药③活字印刷④交子A. ①②B. ②③④C. ①③④D. ②③12. 史书记载：“始置诸州通判……故常与知州争权。