陕西省西安市昆仑中学高考数学一轮复习讲义 第6课时 映射、函数及其表示 理
- 格式:doc
- 大小:911.00 KB
- 文档页数:8

课题:数列求和教学目标:1.熟练掌握等差数列与等比数列的求和公式; 2.能运用倒序相加、错位相减、拆项相消等重要的数学方法进行求和运算;3.熟记一些常用的数列的和的公式. 教学重点:特殊数列求和的方法.(一) 主要知识:1.等差数列与等比数列的求和公式的应用;2.倒序相加、错位相减,分组求和、拆项求和等求和方法;(二)主要方法:1.基本公式法:()1等差数列求和公式:()()11122n n n a a n n S na d +-==+ ()2等比数列求和公式:()111,11,111n n n na q S a q a a qq qq =⎧⎪=-⎨-=≠⎪--⎩ ()3()()2221121216n n n n +++=++L ;()4()23333112314n n n ++++=+⎡⎤⎣⎦L ; ()50122n nn n n n C C C C ++++=L .2.错位相消法:给12n n S a a a =+++L 各边同乘以一个适当的数或式,然后把所得的等式和原等式相减,对应项相互抵消,最后得出前n 项和n S .一般适应于数列{}n n a b 的前n 向求和,其中{}n a 成等差数列,{}n b 成等比数列。
3.分组求和:把一个数列分成几个可以直接求和的数列,然后利用公式法求和。
4.拆项(裂项)求和:把一个数列的通项公式分成两项差的形式,相加过程中消去中间项,只剩下有限项再求和. 常见的拆项公式有:()1若{}n a 是公差为d 的等差数列,则111111n n n n a a d a a ++⎛⎫=- ⎪⎝⎭; ()2()()1111212122121n n n n ⎛⎫=- ⎪-+-+⎝⎭;()3()()()()()1111122112n n n n n n n ⎡⎤=-⎢⎥+++++⎣⎦;()41a b=-;()51k=;()611m m mn n n C C C -+=-;()7()!1!!n n n n ⋅=+-;()811,1,2n nn S n a S S n -=⎧=⎨-⎩≥ 5.倒序相加法:根据有些数列的特点,将其倒写后与原数列相加,以达到求和的目的。

课题:集合的概念教学目标:集合、子集的概念,能利用集合中元素的性质解决问题,掌握集合问题的常规处理方法. 教学重点:集合中元素的3个性质,集合的3种表示方法,集合语言、集合思想的运用. 教学过程:(一)主要知识:1.集合、子集、空集的概念;两个集合相等的概念2. 集合中元素的3个性质,集合的3种表示方法;3. 若有限集A有n个元素,则A的子集有2n个,真子集有2n一1,非空子集有2n -1个, 非空真子集有2n -2个.4. 空集是任何集合的子集,空集是任何非空集合的真子集5. 若A B, B C,则A C6. A A U B,A「IB A,A D B A U B.7. A B= A U B=B;A B= A“B=A.(二)主要方法:1. 解决集合问题,首先要弄清楚集合中的元素是什么,即元素分析法的掌握.2. 弄清集合中元素的本质属性,能化简的要化简;3. 抓住集合中元素的3个性质,对互异性要注意检验;4. 正确进行“集合语言”和普通“数学语言”的相互转化.(三)典例分析:I、可题1:已知集合M ={xx=3 n,n e1}, N={xx = 3 n+1, n^z }, Phxx=3 n—1, n Z?,且a M , b N , c P,设d=a—b c,贝yAd M B. d N C. d P D. d MUN问题2:设集合A={xx=a2+2a+4}, B=<yy=b2—4b+7}.1若a,R , b R,试确定集合A与集合B的关系;2 若a N , b R, 的关系.问题3:2008年第29届奥运会将在北京召开,现有三个实数的集合,既可以表示为「a,b,",也可以表示为〈a2,a b,0 ?,则a2008 - b2008二______________N ={x|x = £舟,k Z}问题4:(02新课程)设M={x|x=:2 {,匕Z},则A. M 二N B. M = N C. M Y N D. M 门N =:_问题5:①若A =| x2• ax • 1 =0, x • R1 , B - ",2?,且A。

课题:抛物线教学目标:理解抛物线的定义,抛物线的标准方程,抛物线的几何性质。
教学重点: 抛物线的定义、四种方程及几何性质;四种方程的运用及对应性质的比较、辨别和应用,抛物线的几何性质的应用.(一) 主要知识及主要方法:1.(课本115P )P (0p >)的几何意义是抛物线的焦准距(焦点到准线的距离).2.(课本115P )抛物线的通径:通过焦点并且垂直于对称轴的直线与抛物线两交点之间的线段叫做抛物线的通径.通径的长为2p ,通径是过焦点最短的弦.(二)典例分析:问题1.求满足下列条件的抛物线的标准方程,并求对应抛物线的准线方程:()1过点P ()3,2-;()2焦点在直线240x y --=上;()3顶点在原点,对称轴为x 轴,抛物线上的点()3,M m -到焦点的距离等于5;()4顶点在原点,对称轴为x 轴且截直线210x y -+=问题2.()1在抛物线24y x =上找一点M ,使MA MF+最小,其中()3,2A ,()1,0F ,求M 点的坐标及此时的最小值;()2已知抛物线22y x =和定点103,3A ⎛⎫ ⎪⎝⎭,抛物线上有一动点P ,P 到点A 的距离为1d ,P 到抛物线准线的距离为2d ,求12d d +的最小值及此时P 点的坐标.问题3.()1(05全国Ⅱ)抛物线24x y =上一点A 的纵坐标为4,则点A 与抛物线焦点的距离为 .A 2 .B 3 .C 4 .D 5()2(07海南)已知抛物线22y px =(0)p >的焦点为F ,点111222()()P x y P x y ,,,,333()P x y ,在抛物线上,且2132x x x =+, 则有.A 123FP FP FP += .B 222123FPFP FP += .C 2132FP FP FP =+ .D 2213FPFP FP =g()3定长为3的线段AB 的端点A 、B 在抛物线2y x =上移动,求线段AB 的中点M 到y 轴距离的最小值.()4(06全国Ⅰ)抛物线2y x =-的点到直线4380x y +-=距离的最小值是.A 43.B 73.C 85.D 3问题4.(98全国)直线1l 和2l 相交于点M ,12l l ⊥,点1N l ∈.以A 、B 为端点的曲线段C 上的任一点到2l 的距离与到点N 的距离相等.若AMN △为锐角三角形,17AM =,3AN =,且6BN =.建立适当的坐标系,求曲线段C 的方程.问题5.(05全国Ⅲ) 设()11A x y ,,()22B x y ,两点在抛物线22y x =上,l 是AB的垂直平分线。

课题:指数函数教学目标:1•掌握指数函数;2•掌握指数函数的图象和性质教学重点:指数函数的图象及性质的简单应用.(一)主要知识:指数函数的图象和性质:1. y=a x(a 0且a=1)的定义域为R,值域为.2. y=a x(a 0且a=1)的单调性:a 1时,y = a x在R上为增函数;0 ::: a :::1时,y = a*在R上是减函数.3. y = a x(a - 0且a = 1)的图像特征:a 1时,图象像一撇,过点0,1 - 且在y轴左侧a越大,图象越靠近y轴(如图1);0 :a <1时,图象像一捺,过点0,1 ,且在y轴左侧a越小,图象越靠近y轴(如图2);y =a x与y =a "的图象关于y轴对称(如图3).图1 图2 图3(二)主要方法:1. 指数方程,指数不等式:常要转化为同底数的形式,在利用指数函数的单调性求解;2. 确定与指数有关的函数的单调性时,常要注意针对底数进行讨论;3. 要注意运用数形结合思想解决问题.(三)典例分析:问题 1 1 (05福建)函数f(x)=a x J b的图象如图,其中a、b为常数,则下列结论正确的是A. a 1, b < 0B. a 1,b 0C. 0 :: a ::1,b 0D. 0 ■a :: 1,b :: 0(2 股x>0,且a x£b x£1(a>0,b>0),贝y a 与b 的关系是A. b ::: a ::: 1B. a ::: b ::: 1C. 1 :::b :: aD. 1 ::: a ::: b3若函数y =2」“ •m的图象不经过第一象限,贝U m的取值范围是A. m _ -2B. m^. -2C. m _ -1D. m〕::「1x(4 )( 06山东模拟)设f(x) = 3 -1 , ccbva且f (c) a f (a) a f (b),则下列关系式一定成立的是 A. 3c. 3b B. 3b3a C. 3c3a2 D. 3c- 3^:: 2x — 2问题2. ( 06上海模拟)已知函数f(x)二a x(a 1),x十11证明函数f (x)在(-1,7)上为增函数;2用反证法证明f(x)=O没有负数根问题3 .要使函数y =1 +2x +a 4x在(—比, 1上y > 0恒成立,求a的取值范围I、可题4. (04全国川理)解方程:4%十1一2x=11(四)巩固练习:(1羊*1. 不等式3"的解集为13丿2 f [" ................2. 函数v 的递减区间为;最大值是12丿(五)课后作业:1.如图为指数函数(1)y 二a x,(2)y 二b x,(3)y 二c x,(4)y 二d x,则a,b,c,d 与1 的大小关系为A. a :: b ::: 1■c::dC. 1 :: a :: b :: cB. b a :: 1 :: d :: c:::2.若函数f(x) =2»4_m的图象与x轴有交点,则实数m的范围是3.已知函数f (x^ ax2 bx c a 0,满足f (1 一x) = f (1 • x),贝U f (2x)与f (3x) 的大小关系是A. f (2x) f (3x)B. f(2x p: f(3x)C. f (2x) > f(3x)D. f(2x) w f (3x)4.若直线y=2a与函数y=a x—1(a=0且a^1)的图象有两个公共点,贝U a的范围是5.已知函数y =4x -3 2x3的值域为1,7 1,则x的范围是A. 2,4 1B.(- :,6.函数y = 2 的定义域为___________ ,值域为_______________7.设a • 0, a = 1,如果函数y = a2x 2 a x -1在L 1,1】上的最大值为14,求a的值/ 、x_28.已知八’1求函数『八的值域x -Xa —a9.已知f(x) x x0 a 1 . 1证明:f(x)是定义域上的减函数; a +a2求f (x)的值域.(a 0,且a=1) . 1求f (x)的定义域;10.已知f(x)a x -12讨论f(x)的奇偶性;3求a的范围,使f(x) 0在定义域上恒成立(六)走向高考:1. (06山东)函数y =1 • a x 0 ::: a 1的反函数的图象大致是(A) (B) ( C) ( D)A. B. C. D.2. ( 04湖北文)若函数f (x)二a x• b -1 ( a 0,且a =1)的图象经过第二、四象限,则一定有 A. 0 :: a :: 1且b 0 ; B. a 1且b 0C. Ovacl 且b£0 ;D. a>1 且b£03. (05全国川文)设3x=扌,则① 0 ■ b ::: a :② a ::: b ::: 0 :③ 0 :: a :: b :④ b ■ a ■ 0 :⑤ a = b 其中不可能成立的关系式有y = x 3与y 二- 的图象的交点为 y 2 B. (1,2) C. (2,3)A. 一2 :: x :: -1B. —3 :: x :: -2C. -1 ::: x ::: 0D. 0 .. x :: 1 4. ( 07山东)已知集合 M -「-1,1 ,A^-1,1? B^-1? 1 x-W f N =?x -<2 <4, X E Z ',则 M“N = I 2 ? J C. {0} D. {—1,0}5. ( 07北京)函数A. (0, •::) x f (x) = 3 ( 0 ::: x w 2 )的反函数的定义域为B. (1,9]C. (0,1)D.[9,::)6. ( 05江西)已知实数A. 1个B.2个C.3个D.4个7.( 07山东)设函数是 A (0,1) (x 0, y °),则x 0所在的区间 D. (3,4) a 、b 满足等式x8. ( 04全国川理)已知函数y = f(x)是奇函数,则当X—0时,f(x) = 3 -1,设f (x) 的反函数是y =g(x),则g(-8) 口9.( 05全国I)设0 :::a :::1 ,函数f (x) =log a(a2x -2a x -2),则使f (x) :::0 的x 的取值范围是A.(-::,0)B. (0, ::)C. (_::,log a3)D.(log a3,::)10. ( 06 天津)如果函数f (x) =a x(a x-3a2-1) ( a 0且a=1)在区间〔0,= 上是增函数,那么实数a的取值范围为A. 0,2B.弓,1C. 0,J3D. 2,13」.3丿- ]2丿。
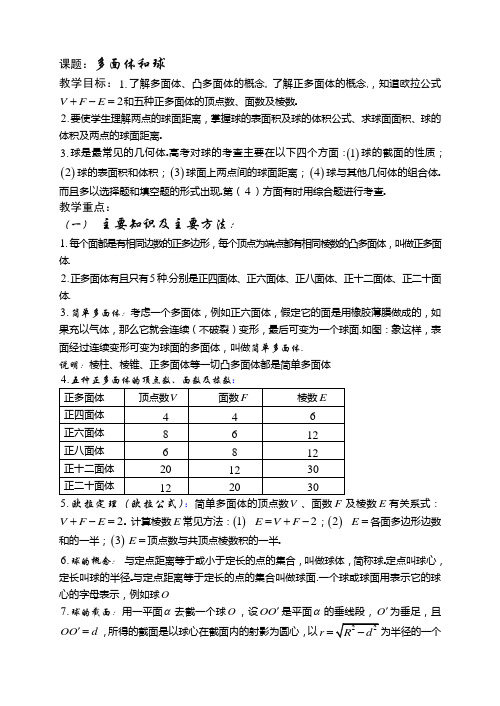
课题:多面体和球教学目标:1.了解多面体、凸多面体的概念 了解正多面体的概念,知道欧拉公式2V F E +-=和五种正多面体的顶点数、面数及棱数2.要使学生理解两点的球面距离,掌握球的表面积及球的体积公式、求球面面积、球的体积及两点的球面距离.3.球是最常见的几何体.高考对球的考查主要在以下四个方面:()1球的截面的性质;()2球的表面积和体积;()3球面上两点间的球面距离;()4球与其他几何体的组合体.而且多以选择题和填空题的形式出现.第(4)方面有时用综合题进行考查. 教学重点:(一) 主要知识及主要方法:1.每个面都是有相同边数的正多边形,每个顶点为端点都有相同棱数的凸多面体,叫做正多面体.2.正多面体有且只有5种.分别是正四面体、正六面体、正八面体、正十二面体、正二十面体.3.简单多面体:考虑一个多面体,例如正六面体,假定它的面是用橡胶薄膜做成的,如果充以气体,那么它就会连续(不破裂)变形,最后可变为一个球面.如图:象这样,表面经过连续变形可变为球面的多面体,叫做简单多面体.说明:棱柱、棱锥、正多面体等一切凸多面体都是简单多面体5.欧拉定理(欧拉公式):简单多面体的顶点数V 、面数F 及棱数E 有关系式:V F E +-= 计算棱数E 常见方法:()1 2E V F =+-;()2 E =各面多边形边数和的一半;()3E =顶点数与共顶点棱数积的一半.6.球的概念: 与定点距离等于或小于定长的点的集合,叫做球体,简称球定长叫球的半径与定点距离等于定长的点的集合叫做球面.一个球或球面用表示它的球心的字母表示,例如球O7.球的截面:用一平面α去截一个球O ,设OO '是平面α的垂线段,O '为垂足,且OO d '=,所得的截面是以球心在截面内的射影为圆心,以r =为半径的一个圆,截面是一个圆面.球面被经过球心的平面截得的圆叫做大圆,被不经过球心的平面截得的圆叫做小圆 8.两点的球面距离:球面上两点之间的最短距离,就是经过两点的大圆在这两点间的一段劣弧的长度,我们把这个弧长叫做两点的球面距离.l R ϕ=(ϕ为球心角的弧度数).9.球的表面积和体积公式:24S R π=,343V R π=. (二)典例分析:问题1.()1(05辽宁)棱长为a 的正方体,连结相邻面的中心,以这些线段为棱的八面体的体积为 .A 23a .B 24a .C 26a .D 212a()2已知一个正四面体和一个正八面体的棱长相等且为1,把它们拼起来,使一个表面重合,所得的多面体有多少个面?问题2.()1(07天津)一个长方体的各顶点均在同一球的球面上,且一个顶点上的三条棱的长分别为1,2,3,则此球的表面积为()2(07全国Ⅰ文)正四棱锥S ABCD -,点,,,,S A B C D都在同一个球面上,则该球的体积为()3(07江西文)四面体ABCD的外接球球心在CD上,且2CD=,3AB=,在外接球面上两点A、B间的球面距离是.Aπ6.Bπ3.C2π3.D5π6()4(06陕西)水平桌面α上放有4个半径均为2R的球,且相邻的球都相切(球心的连线构成正方形).在这4个球的上面放1个半径为R的小球,它和下面4个球恰好都相切,则小球的球心到水平桌面α的距离是问题3.(07四川)设球O的半径是1,A、B、C是球面上三点,已知A 到B 、C 两点的球面距离都是2π,且二面角B OA C --的大小为3π,则从A 点沿球面经B 、C 两点再回到A 点的最短距离是 .A 67π .B 45π .C 34π .D 23π问题4.三棱锥A BCD -的两条棱6AB CD ==,其余各棱长均为5,求三棱锥的内切球半径和外接球半径.问题5.已知球的半径为R ,在球内作一个内接圆柱,这个圆柱底面半径与高为何值时,它的侧面积最大?侧面积的最大值是多少?(三)课后作业:1.正方体、正多面体、凸多面体、简单多面体是什么关系?2.已知凸多面体每个面都是五边形,每个顶点都有三条棱相交,试求该凸多面体的面数、顶点数和棱数.3.一个广告气球被一束入射角为 的平行光线照射,其投影是一个长半轴为5m的椭圆,则制作这个广告气球至少需要的面料是4.在球面上有四个点P 、A 、B 、C ,如果PA 、PB 、PC 两两互相垂直,且PA PB PC a ===,那么这个球面的面积是 .A 22a π .B 23a π .C 24a π.D 26a π5.北纬30︒的圆把北半球面积分为两部分,这两部分面积的比为.A 1:1 .B 2:1 .C .D6.已知过球面上A 、B 、C 三点的截面和球心的距离等于球半径的一半, 且2AB BC CA ===,则球面面积是.A 9π16 .B 3π8 .C 4π .D 9π647.正八面体的相邻两个面所成二面角的大小为.A 1arccos 3 .B 1arccos 3π- .C 1arccos 23π- .D 1arccos 3-(四)走向高考:8.(07陕西)一个正三棱锥的四个顶点都在半径为1的球面上,其中底面的三个顶点在该球的一个大圆上,则该正三棱锥的体积是 .A 433 .B 33 .C 43 .D 1239.(07辽宁)若一个底面边长为2,的正六棱柱的所有顶点都在一个平面上,则此球的体积为10.(07全国Ⅱ)一个正四棱柱的各个顶点在一个直径为2cm 的球面上。

课题:映射与函数教学目标:了解映射的概念,在此基础上加深对函数概念的理解;能根据函数的三要素判断两个函数是否为同一函数;理解分段函数的意义.教学重点:函数是一种特殊的映射,而映射是一种特殊的对应;函数的三要素中对应法则是核心,定义域是灵魂.(一)主要知识:1. 映射与函数的概念;2. 函数的三要素及表示法,两个函数相同的条件;3. 正确理解函数值的含义,掌握函数值的求法,会灵活解决有关函数值的问题;特别是涉及分段函数或复合函数的值的问题•(二)主要方法:1. 对映射有两个关键点:一是有象,二是象惟一,缺一不可;2. 对函数三要素及其之间的关系给以深刻理解,这是处理函数问题的关键;3. 理解函数和映射的关系,函数式和方程式的关系.(三)典例分析:问题1.已知集合P =^x Q<x<4} , Q={x0^x^2},下列不.表.示.从P到Q的映射是A. f : x > y =2xB. f : x》y=3xC. f : x—;y =£xD. f : x—y = x问题2. (05黄岗模拟)下列从M到N的各对应法则f i(i =1,2,3,4 )中哪些是映射?哪些是函数?哪些不是映射?为什么?1 M -{直线Ax By ^0}, N 二R , f1:求直线Ax By C =0 的斜率;2 M ={直线Ax By 0 }, N -0 —::J , f2:求直线Ax By C = 0 的倾斜角;3当M=N=R , f3:求M中每个元素的正切;4 M二N = x 一0 ?, f4:求M中每个元素的算术平方根.5 M ={平面〉内的矩形}, N ={平面〉内的圆}, f s :作矩形的外接圆(此小题为编者自拟)问题3. 1已知x,y在映射f作用下的象是x y,xy .①求-2,3在f作用下的象②若在f作用下的象是2,3,求它的原象2设集合A和B都是实数集,映射f : A》B把集合A中的元素x映射到集合B中的元素x3 -x 1,则在映射f下,象1的原象组成的集合是A 4 BJ-1,0,V C.(0 D.「—2,—1,0l问题4. 下列各对函数中,相同的是丄2 / ------A. f(x) =x, g(x) =:〔x2B. f(x) =、1-x2, g(x)=1-x , x 1-1,11C. y = f(x), g(x) = f(x+1) , x^RD. f(x) = lg(打,g(x)=lg2,x问题5.①(05浙江文)设f (x) = x T - x ,则f -f (;)]=A. -2B. 0C. 4D. 1笑(05山东)函数sin(兀x2), 一1 c x < 0, 卄一八一“小f(xH x;,若f 1 f a =2,$xJL,xZ0.则a的所有可能值为A. 1 B•血 C. 1 丘 D. 1 丘2 ,2 ,2问题 6.矩形ABCD的长AB =8,宽AD =5,动点E、F分别在BC、CD上,且CE二CF二x , 1将厶AEF的面积S表示为x的函数f(x),求函数S=f(x)的解析式;2求S的最大值.(四)巩固练习:21. 1 A 二 R , B ={ y | y 0}, f : x — y =|x| ;2 A ={x |x _2,x 二 N }, B -〔y | y _ 0,y 二 N ?, f : x —; y = x 2-2x 2 ;3 A = {x | x 0}, B = {y | y R}, f : x —; y 二 x .上述三个对应 ______________ 是A 到B 的映射.1 12. 给定映射f : (x, y)r (2x y,xy),点(一,)的原象是 _______________ __ _____6 6 3.下列函数中,与函数 y 二x 相同的函数是2A y = — B. y=(、. x)2 C.y=lg10xD.y = 2xx-3,(^10)□上4.设函数f (x),则f (5)=lf(f(x+5)),(x<10)5. ( 06湖北八校一联)设 f ,g 都是由表一映射f 的对应法则 则与f1相同的是 A 6. ( 06灌云模拟)设 M Ma,b,c?,从M 到N 的映射f 满足f (a) • f(b) 一 f(c),试确定这样的映射 f 的个数为A. 1B. 2C.3D.4(五) 课后作业:1.设A =「x|O 乞x 乞2},B =「y|1乞2二在下图中,能表示从集合 A 到集合B 的映射是原象 1 2 3 4 象4 3 2 1lOg2X原象1 2 3 4 象 3 4 2 1A 到A 的映射,其对应法则如下表(从上到下)表二 映射f 的对应法则B. g 〔f(2)lC. g 〔f(3)lD.g[f(4)] A.B .z z = (x, y ),x, y € R,x2+ y2—12y + 27 兰0〉到集合B = R 的映射2.已知从集合A =:2f : z > -,则该映射的象集为xA一::,_-、3 U .3, :: B. 卜-』3, -3 C. -.3, .3 D.以上都不对3. ( 04北京东城模拟)设映射 2—X - 2x是实数集M到实数集N的映射,若对于实数p • N,在M中不存在原象,则p的取值范围是A. 1, ::B. 1, ::C. 一::,1D. -::,114.设集合A」1,2,3,B-4,5,6?,定义映射 f : A > B,使对任意2 2X - f (x) X f (x)是奇数,则这样的映射f的个数为A. 7B. 9C. 10D. 1825.若g(x) =1 -2x, f (g(x))晋& = 0),则f(A )A. 1B. 3C. 15D. 306•已知f(x) = P "王0),则不等式x+(x + 2)f(x+2)兰5的解集是[-1 (xcO)2x +17.设A=R , B=R , f : x 是A—;B 的映射,21设a • A,则a在B中的象是什么?s在映射f的象是什么?2设r A,那么t 1在B中的象是什么?3设s,A,若s-1在映射f下的象为5,则s应是多少?(六)走向高考:1. ( 06陕西)为确保信息安全,信息需加密传输,发送方由明文T 密文(加密),接收方由密文 T 明文(解密),已知加密规则为:明文 a 、b 、c 、d 对应密文a 2b , 2b c , 2c 3d , 4d .例如:明文1,2,3,4对应密文5,7,18,16.当接收方收到密文14,9,23,28时,则解密得 到的明文为A. 4,6,1,7B. 7,6,1,4C. 6,4,1,7D. 1,6,5,72. ( 06浙江)函数f : “,2,3丨一;;1,2,3 [满足f(f(x)) = f(x),则这样的函数个数共有A. 1个B. 4个C. 8个D.10个3. ( 06广东文)对于任意的两个实数对(a,b)和(c,d),规定:(a,b)=(c,d),当且仅当 a 二c,b =d ;运算":”为:(a,b) : (Gd) =(ac 「bd,bc ad); 运算“二”为:(a,b)二(c,d) =(a c,b d),设 p,q R ,若(1,2): (p,q)=(5,0),则(1,2)二(p,q)=A. (4,0)B. (2,0)C. (0,2)D. (0,-4)4. ( 03全国)已知f 5『(x ) =lgx ,则f(2)二( )A. lg2B. lg 32C. lg丄1 D.-lg23252e x",x :25. ( 06山东文)设1 f (X ) 2,则 f (f (2))的值为[log 3 (x -1 ,x_2A. 0B. 1C. 2D. 36. ( 07北京)已知函数f (x) , g(x)分别由下表给出:则f[g(1)]的值为___________ ;满足f[g(x)] g[f(x)]的x 的值是 ______________。
课题:函数的图像考纲要求:1.熟练掌握基本函数的图象;2.能正确地从函数的图象特征去讨论函数的主要性质;3.能够正确运用数形结合的思想方法解题. 教材复习一、作图方法:描点法和利用基本函数图象变换作图;1.描点法作图:方法步骤:(1)确定函数的定义域;(2)化简函数的解析式;(3)讨论函数的性质即奇偶性、周期性、单调性、最值(甚至变化趋势);(4)描点连线,画出函数的图象.2.图象变换作图: ①平移变换:(1)水平平移:函数()y f x a =+的图像可以把函数()y f x =的图像沿x 轴方向向左(0)a >或向右(0)a <平移||a 个单位即可得到;(2)竖直平移:函数()y f x a =+的图像可以把函数()y f x =的图像沿x 轴方向向上(0)a >或向下(0)a <平移||a 个单位即可得到. ②对称变换:(1)函数()y f x =-的图像与函数()y f x =的图像关于y 轴对称; (2)函数()y f x =-的图像与函数()y f x =的图像关于x 轴对称; (3)函数()y f x =--的图像与函数()y f x =的图像关于原点对称;(4)函数1()y f x -=的图像与函数()y f x =的图像关于直线y x =对称; (5)函数()y f x =的图像与函数)2(x a f y -=的图像关于直线a x =称. ③翻折变换:(1)函数()y f x =的图像可以将函数()y f x =的图像的x 轴下方部分沿x 轴翻折到x 轴上方,去掉原x 轴下方部分,并保留()y f x =的x 轴上方部分即可得到; (2)函数()y f x =的图像可以将函数()y f x =的图像右边沿y 轴翻折到y 轴左边替代原y 轴左边部分并保留()y f x =在y 轴右边部分即可得到. ④伸缩变换:(1)函数()y af x =(0)a >的图像可以将函数()y f x =的图像中的每一点横坐标不变纵坐标伸长(1)a >或压缩(01a <<)为原来的a 倍得到;(2)函数()y f ax =(0)a >的图像可以将函数()y f x =的图像中的每一点纵坐标不变横坐标伸长(1)a >或压缩(01a <<)为原来的1a 倍得到.二、具有对称性的抽象函数:①函数()f x 对于定义域内的任意x ,都有()()f a x f b x +=-,则()f x 是关于直线2a b x +=对称的函数;②函数()f x 对于定义域内的任意x ,都有()()f a x f b x +=--,则()f x 是关于直线2,0a b +⎛⎫⎪⎝⎭对称的函数;③()f x 关于点(),a b 对称⇔()2f x b =-(2)f a x -.基本知识方法:1.获得函数图像的两种途径:描点法和利用基本函数图象变换作图;2.三种图象变换:平移变换、对称变换和伸缩变换;3.识图:分布范围、变化趋势、对称性、周期性等等方面.4.函数图像选择题快速解题的六个依据:①定义域;②值域;③奇偶性(更广即对称性);④单调性;⑤特殊值;⑥最值(甚至变化趋势,渐近线等).典例分析: 考向一:作图问题1.分别画出下列函数的图象:()1321x y x +=-; ()212xy ⎛⎫= ⎪⎝⎭;()3221y x x =--;()4)(log 21x y -=; ()5lg y x =; ()6lg 1y x =+.考向二 知图选式与知式选图问题2:()1函数()y f x =与()y g x =的 图像分别如图①②所示:则函数()()y f x g x =⋅的图像可能是()2(07福建文)图中的图象所表示的函数的解析式为.A 312y x =- (02)x ≤≤.B 33122y x =-- (02)x ≤≤ .C 312y x =-- (02)x ≤≤ .D 11y x =--(02)x ≤≤()3(2013四川)函数231x x y =-的图象大致是考向三 有关对称问题问题3:()1设()f x 是(),-∞+∞上的奇函数,对任意实数x ,都有(2)()f x f x +=-,当11x -≤≤时,3()f x x =;①求证:直线1x =是函数()f x 图像的一条对称轴; ②当[1,5]x ∈时,求函数()f x 的解析式()2(06全国Ⅱ)函数()y f x =的图像与函数2()log (0)g x x x =>的图像关于原点对称,则()f x 的表达式为 .A 21()(0)log f x x x=> .B 21()(0)log ()f x x x =<- .C 2()log (0)f x x x =-> .D 2()log ()(0)f x x x =--<()3(2013新课标Ⅰ)若函数()()22()1f x x x ax b =-++的图像关于直线2x =-对称,.A.B.C.D则()f x 的最大值是考向四 函数图象的应用问题4:()1(2010湖北)若直线y x b =+与曲线3y =b 的取值范围是: .A 1,1⎡-+⎣ .B 1⎡-+⎣ .C 1⎡⎤-⎣⎦.D 1⎡⎤-⎣⎦()2(03全国)使()2log 1x x -<+成立的x 的取值范围是课后作业:1.函数25++=x x y 图象关于点P 中心对称,则点P 坐标是.A ()2,1-- .B ()2,1- .C ()2,1- .D ()2,12.如图,定义在[)1,-+∞上的函数的图像由一条线段和抛物线的一部分组成,则()f x 的解析式是3.若直线y x b =+与函数21y x =-的图象有两个不同的交点,则b 的范围是4.已知函数2()2f x x x =-,方程()f x a =有6个不同的实根,则实数a 的取值范围是 .A 1a <- .B 10a -<< .C 01a << .D 1a >5.(2013衡水中学第三次调研)函数()log 1a y x =+()1a >的图像大致是6.已知函数2()4f x x =-,()g x 是定义在()(),00,-∞+∞U 上的奇函数,当0x >时,2()log g x x =,则函数()()y f x g x =的大致图象为.A .B .C .D.A .B .C .D7.函数()f x 的部分图像如图所示,则函数()f x 的解析式是 .A ()sin f x x x =+ .B cos ()xf x x=.C ()cos f x x x = .D ()()()23f x x x x ππ=--走向高考:1.(08全国)函数1()f x x x=-的图像关于 .A y 轴对称.B 直线x y -=对称 .C 坐标原点对称 .D 直线x y =对称2(05北京春) 函数x x f 2log )(=的图象是3.(05北京文)为了得到函数321x y -=-的图象,只需把函数2x y =上所有点.A 向右平移3个单位长度,再向下平移1个单位长度.B 向左平移3个单位长度,再向下平移1个单位长度 .C 向右平移3个单位长度,再向上平移1个单位长度 .D 向左平移3个单位长度,再向上平移1个单位长度4.(2013北京)函数()f x 的图象向右平移1个单位长度,所得图象与x y e =关于y 轴对称,则()f x = A.1x e + B. 1x e - C. 1x e -+ D. 1x e --5.(04全国Ⅱ文)函数x y e =-的图象.A 与x y e =的图象关于y 轴对称; .B 与x y e =的图象关于坐标原点对称;.C 与x y e -=的图象关于y 轴对称;.D 与x y e -=的图象关于坐标原点对称.6.(高考)如果函数sin 2cos 2y x a x =+的图像关于8x π=-对称,那么a =.A .B .C 1 .D 1-7.(02上海)函数],[|,|sin ππ-∈+=x x x y 的大致图象是y yπ π π- O π x -π Oπ xπ- (A )y y ππ π- O π x -π O π xπ- -π (C )8.(07四川)函数x x g x x f -=+=122)(log 1)(与在同一直角坐标系下的图象大致是.A .B .C .D 9.(2013山东)函数cos sin y x x x =+的图象大致是10.(09山东)函数x xx x e e y e e--+=-的图像大致为11.(06上海文)若曲线21x y =+与直线y b =没有公共点,则b 的取值范围是12.(2011海南)已知函数()y f x =的周期为2,当[1,1]x ∈-时2()f x x =,那么函数()y f x =的图象与函数lg y x =的图象的交点共有 .A 10个 .B 9个 .C 8个 .D 1个。
课题:集合间的基本关系考纲要求:① 理解集合之间包含与相等的含义,能识别给定集合的子集.② 在具体情境中,了解全集与空集的含义教材复习集合间的基本关系:1、子集:A 是B 的子集,符号表示为 或B A ⊇2、真子集:A 是B 的真子集,符号表示为 或3、相等关系:A B ⊆且B A ⊆⇔4、不含任何元素的集合叫做 ,记作 ,并规定空集是任何集合的子集,是任何非空集合的5、集合A 有n 个元素,则集合A 的子集个数有 个,真子集个数有 个 基本知识方法1、子集、真子集的应用;2、集合相等的应用3、注意集合特征的使用典例分析:问题1:设全集U R = ,集合{}1M x x =|<-,}{1N x x =|>则下列关系中正确的是 .A M N = .B N M ⊂ .C M N ⊂ .D U N C M =∅问题2:设集合11,,,2442k k M x x k Z N x x k Z ⎧⎫⎧⎫==+∈==+∈⎨⎬⎨⎬⎩⎭⎩⎭, 则M N .问题3:设集合2{1,,},{,,}A a b B a a ab ==,且A B =,求实数,a b问题4:已知{1A x x =<-或5},{4}x B x a x a >=≤<+,若A B Ý,则实数a 的范围.走向高考:1.(08广东文)第二十九届夏季奥林匹克运动会将于2008年8月8日在北京举行.若集合A ={参加北京奥运会比赛的运动员},集合B ={参加北京奥运会比赛的男运动员},集合C ={参加北京奥运会比赛的女运动员},则下列关系正确的是A .AB ⊆ B .BC ⊆ C .A B C =D .B C A = 2.(08山东)满足1234{,,,}M a a a a ⊆,且12312{,,}{,}M a a a a a = 的集合M 的个数A. 1B. 2C.3D.43.(07 北京)已知集合{}1≤-=a x x A ,{}0452≥+-=x x x B ,若A B =∅ , 则实数a 的取值范围是 4.(07全国Ⅰ)设a 、b R ∈,集合{1,,}{0,,}b a b a b a+=,则b a -= .A 1 .B 1- .C 2 .D 2-课后练习作业:1.若A B B = ,则A B ;若A B B = 则A ;B A B A B .2.设集合11,,,3663k k P x x k Z Q x x k Z ⎧⎫⎧⎫==+∈==+∈⎨⎬⎨⎬⎩⎭⎩⎭,则P Q3.符合{}a ⊂≠{,,}P a b c ⊆的集合P 的个数是4.集合{}{}35,A x x B x x a =-<=<,且A B ⊆,则a 的范围是。
课题:函数的值域与最值教学目标:理解函数值域的意义;掌握常见题型求值域的方法,了解函数值域的一些应用.教学重点: 求函数的值域与最值的基本方法。
(一) 主要知识:1.函数的值域的定义;2.确定函数的值域的原则:定义域优先原则3.求函数的值域的方法.(二)主要方法:求函数的值域的方法常用的有:直接法,分离常数法,换元法,配方法,判别式法,不等式法,利用某些函数的有界性法,数形结合法,函数的单调性法,利用导数法,利用平移等.(三)典例分析:问题1.求下列函数的值域:()1232y x x =-+; ()2y ;()3312x y x +=-; ()423y x =-;()552log x y -=+[]2,10x ∈;()6y x =()7|1||4|y x x =-++; ()81313x x y -=+; ()922221x x y x x -+=++;()102211()212x x y x x -+=>-;()111sin 2cos x y x-=-;()12y =问题2.()1求函数()212log 45y x x =-+的值域;()2已知 3()2log f x x =+,[]1,3x ∈,求函数[]()22()y f x f x =+的值域; ()3若函数()f x 的值域为34,89⎡⎤⎢⎥⎣⎦,求()y f x =.问题3.已知函数21ax b y x +=+的值域为[]1,4-,求常数a 、b 的值(四)巩固练习:1.函数221xx y =+的值域为2.若函数()log a f x x =在[2,4]上的最大值与最小值之差为2,则a =3.已知32()26f x x x a =-+(a 是常数),在[]2,2-上有最大值3,那么在[]2,2-上的最小值是 .A 5- .B 11- .C 29- .D 37-(五)课后作业:1.求下列函数的值域:()1y =x x --+12 ([]0,1x ∈);()2y =x -5+12log x ; ()3y x =()0x ≥;()42221x y x -=+; ()535,05,0128,1x x y x x x x +≤⎧⎪=+<≤⎨⎪-+>⎩2.函数131x y =-的值域是 .A (),1-∞- .B (,0)(0,)-∞+∞U .C ()1,-+∞ .D (,1)(0,)-∞-+∞U3.已知函数2()4f x x x =+,则(2cos 1)f θ-的值域是4.函数2()23f x x mx =-+在区间[]0,2上的值域为[]2,3-,则m 的值为( ).A .B 94 .C .D 945.(07江苏通州一中质检)函数y =的最小值为6.(07江苏)已知函数3()128f x x x =-+在区间[]33-,上的最大值与最小值分别为 M 、m ,则M m -=_____.7.若函数21()2f x x x a =-+的定义域和值域均为[]1,b ()1b >,求a 、b 的值8.函数248136(1)x x y x ++=+()1x >-的最小值是( ) .A 1 .B 32.C 2 .D 39.(06长春四市一模)函数231x y x x =++()0x <的值域是 .A [)3,0-.B []3,1- .C (],3-∞- .D (),0-∞10.(06新海中学模拟)函数21y x =-的定义域是()[),12,5-∞U ,则其值域是 .A ()1,0,22⎛⎤-∞ ⎥⎝⎦U .B (],2-∞ .C [)1,2,2⎛⎫-∞+∞ ⎪⎝⎭U .D ()0,+∞11.求函数2234x x y +=-⋅()10x -≤≤的值域12.定义在R 上的函数()y f x =的值域为[],a b ,则函数()y f x a =+的值域为.A []2,a a b + .B []0,b a -.C [],a b .D [],a a b -+13.已知(199)f x +=2443x x ++()x R ∈,那么函数()f x 的最小值为14.若()f x 的值域为()0,2,则()(2007)1g x f x =--的值域为.A ()1,3-.B ()1,1- .C ()2008,2006-- .D 以上都不对15.(07江西)设函数24log (1)(3)y x x =+-≥,则其反函数的定义域为16.已知函数11()f x a x=-()0,0a x >>. ()1若()f x 在[],m n 上的值域是[],m n ,求a 的取值范围,并求相应的,m n 的值; ()2若()f x ≤2x 在()0,+∞上恒成立,求a 的取值范围(六)走向高考:1.(06全国Ⅱ)函数191()n f x x n ==-∑的最小值为.A 190 .B 171 .C 90 .D 452.(04湖北)函数()log (1)[0,1]x a f x a x =++在上的最大值与最小值之和为a ,则a 的值为 .A 41 .B 21 .C2 .D 43.(04湖北文)已知52x ≥,则245()24x x f x x -+=-有 .A 最大值54 .B 最小值54.C 最大值1 .D 最小值14.(07重庆文)函数()f x 的最小值为5.(06安徽)设0a >,对于函数()sin (0)sin x a f x x xπ+=<<,下列结论正确的是.A 有最大值而无最小值 .B 有最小值而无最大值.C 有最大值且有最小值 .D 既无最大值又无最小值6.(06陕西文)函数21()1f x x =+()x R ∈的值域是 .A ()0,1 .B (]0,1 .C [)0,1 .D []0,17.(06上海文)若曲线21x y =+与直线y b =没有公共点,则b 的取值范围为8.(06福建文)已知()f x 是二次函数,不等式()0f x <的解集是()0,5,且()f x 在区间[]1,4-上的最大值是12.(Ⅰ)求()f x 的解析式;(Ⅱ)是否存在在自然数m ,使得方程37()0f x x+=在区间(,1)m m +内有且只有两个不等的实数根?若存在,求出所有m 的值;若不存在,说明理由.。