质点运动学动力学作业问题
- 格式:ppt
- 大小:710.50 KB
- 文档页数:32



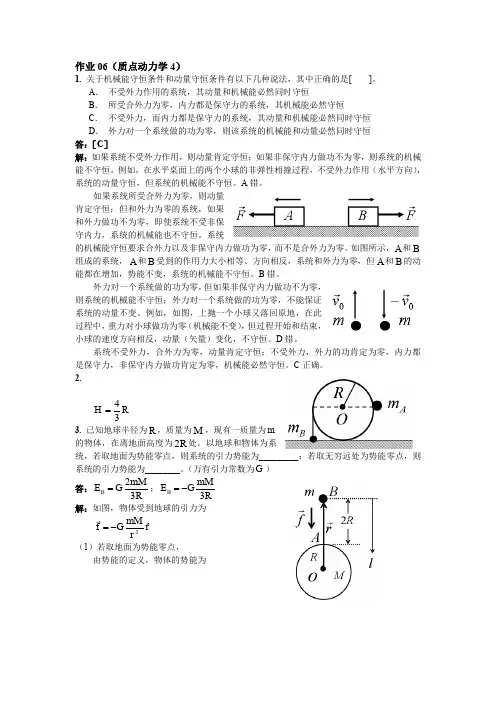
作业06(质点动力学4)1. 关于机械能守恒条件和动量守恒条件有以下几种说法,其中正确的是[ ]。
A . 不受外力作用的系统,其动量和机械能必然同时守恒B . 所受合外力为零,内力都是保守力的系统,其机械能必然守恒C . 不受外力,而内力都是保守力的系统,其动量和机械能必然同时守恒D . 外力对一个系统做的功为零,则该系统的机械能和动量必然同时守恒答:[C ]解:如果系统不受外力作用,则动量肯定守恒;如果非保守内力做功不为零,则系统的机械能不守恒。
例如,在水平桌面上的两个小球的非弹性相撞过程,不受外力作用(水平方向),系统的动量守恒,但系统的机械能不守恒。
A 错。
如果系统所受合外力为零,则动量肯定守恒;但和外力为零的系统,如果和外力做功不为零,即使系统不受非保守内力,系统的机械能也不守恒。
系统的机械能守恒要求合外力以及非保守内力做功为零,而不是合外力为零。
如图所示,A 和B 组成的系统,A 和B 受到的作用力大小相等、方向相反,系统和外力为零,但A 和B 的动能都在增加,势能不变,系统的机械能不守恒。
B 错。
外力对一个系统做的功为零,但如果非保守内力做功不为零,则系统的机械能不守恒;外力对一个系统做的功为零,不能保证系统的动量不变。
例如,如图,上抛一个小球又落回原地,在此过程中,重力对小球做功为零(机械能不变),但过程开始和结束,小球的速度方向相反,动量(矢量)变化,不守恒。
D 错。
系统不受外力,合外力为零,动量肯定守恒;不受外力,外力的功肯定为零,内力都是保守力,非保守内力做功肯定为零,机械能必然守恒。
C 正确。
2.R H 34= 3. 已知地球半径为R ,质量为M ,现有一质量为m的物体,在离地面高度为R 2处。
以地球和物体为系统,若取地面为势能零点,则系统的引力势能为_________;若取无穷远处为势能零点,则系统的引力势能为________。
(万有引力常数为G )答:R mM G E B 32=;RmM G E B 3-= 解:如图,物体受到地球的引力为r rmM G f ˆ2-= (1)若取地面为势能零点,由势能的定义,物体的势能为R mM G l d l R mM Gl fd l d f E R A B A B B 32)3(202)()()()(=-==⋅=⎰⎰⎰(2)若取无穷远处为势能零点,由势能的定义,物体的势能为R mM G r d r mM Gr fd l d f E R B B B 332)()()()(-=-=-=⋅=⎰⎰⎰∞∞∞4. 如图所示,一水平放置的轻弹簧,劲度系数为k ,其一端固定,另一端系一质量为m 的滑块A ,A 旁又有一质量相同的滑块B 。

作业04(质点动力学2)1. 质量为m 、速度大小为V 的质点受到某个力作用后,其速度的大小未变,但方向改变了θ,则这个力的冲量大小为[ ]。
A.)2/cos(2θmvB. )2/sin(2θmvC. )2/cos(θmvD. )2/sin(θmv 答:[B ]解:如图,由动量定理,冲量等于动量的变化 im v j m v i m v i m v j m v i m v v m v m v m I -+=-+=-=∆=θθθθsin cos sin cos /// 冲量的大小为 )2/s i n (2c o s 22s i n )c o s (222θθθθv m mv v v v m I I =-=+-==2. 一质量为kg m 60=的人静止站在一条质量为kg M 300=、且正以12-⋅=s m V 的速率向湖岸驶进的小木船上,湖水是静止的,其阻力不计。
现在人相对于船以一水平速度v 沿船的前进方向向河岸跳去,该人起跳后,船速减为原来的一半,v 应该是[ ]A. 12-⋅s mB. 13-⋅s mC. 15-⋅s mD. 16-⋅s m答:[C ]解:以地面为参考系。
人与船为系统。
人相对于地面的起跳速度为v V +,起跳后,船向岸边运动的速度为2/V ;原来人与船以水平速度V 一起向岸边运动。
水平方向不受外力 V M m MV v V m )(21)(+=++,)(5602230022-⋅=⨯⨯==s m m MV v 也可以原船为参考系(也是惯性系),人与船为系统。
人相对于原船的起跳速度为v ,起跳后,船相对于原船的运动速度为2/V -;在原船参考系中,起跳前,人与船静止。
水平方向不受外力,由动量守恒,得到VM mv 210-=,)(5602230022-⋅=⨯⨯==s m m MV v 3. 下列叙述中正确的是[ ]A. 质点的动量不变,则动能也不变。
B 质点的动能不变,则动量也不变C. 质点的动量变化,则动能也一定变化。

第一章质点运动学一、选择题1、一质点在xoy 平面内运动,其运动方程为x2,式中 a、、at , y b ct b c 均为常数。
当运动质点的运动方向与x 轴成 450角时,它的速率为 [ B ] 。
A. a;B.2a;C. 2c;D.a24c 2。
2、设木块沿光滑斜面从下端开始往上滑动,然后下滑,则表示木块速度与时间关系的曲线是图 1-1 中的 [ D ]。
v v v vt t t tA B C D图1-13、一质点的运动方程是r R cos ti Rsin tj ,R、为正常数。
从t=/到 t=2/ 时间内该质点的路程是[ B]。
A .2R;B.R;C. 0;D.R。
4、质量为 0.25kg 的质点,受F t i(N) 的力作用, t=0 时该质点以v =2 j m/s 的速度通过坐标原点,该质点任意时刻的位置矢量是[B]。
A . 2 t2i +2j m;B. 2 t3i2tj m;3C.3t4 i2t 3 j ;D.条件不足,无法确定。
43二、填空题1、一质点沿 x 轴运动,其运动方程为x52t t 2(x以米为单位,t以秒为单位)。
质点的初速度为2m/s,第 4 秒末的速度为-6m/s,第 4 秒末的加速度为2。
-2m/s2、一质点以(m/s)的匀速率作半径为5m的圆周运动。
该质点在5s 内的平均速度的大小为2m/s,平均加速度的大小为2m / s2。
53、一质点沿半径为 0.1m的圆周运动,其运动方程为2t 2(式中的θ以弧度计,t以秒计),质点在第一秒末的速度为0.2m/s,切向加速度为0.2m/s2。
4、一质点沿半径1m的圆周运动,运动方程为θ=2+3t 3,其中θ以弧度计,t 以秒计。
T=2s时质点的切向加速度为36m/s 2;当加速度的方向和半径成45o 角时角位移是3rad 。
85、飞轮半径 0.4m ,从静止开始启动,角加速度β=0.2rad/s 2。
t=2s 时边缘各点的速度为0.16m/s ,加速度为 0.102m/s 2。





第二章 习题解答2-17 质量为2kg 的质点的运动学方程为 j t t i t r ˆ)133(ˆ)16(22+++-= (单位:米,秒), 求证质点受恒力而运动,并求力的方向大小。
解:∵j i dt r d a ˆ6ˆ12/22+== , j i a m F ˆ12ˆ24+== 为一与时间无关的恒矢量,∴质点受恒力而运动。
F=(242+122)1/2=125N ,力与x 轴之间夹角为:'34265.0/︒===arctg F arctgF x y α2-18 质量为m 的质点在o-xy 平面内运动,质点的运动学方程为:j t b i t a r ˆsin ˆcos ωω+= ,a,b,ω为正常数,证明作用于质点的合力总指向原点。
证明:∵r j t b i t a dt r d a 2222)ˆsin ˆcos (/ωωωω-=+-== r m a m F2ω-==, ∴作用于质点的合力总指向原点。
2-19在图示的装置中两物体的质量各为m 1,m 2,物体之间及物体与桌面间的摩擦系数都为μ,求在力F 的作用下两物体的加速度及绳内张力,不计滑轮和绳的质量及轴承摩擦,绳不可伸长。
解:以地为参考系,隔离m 1,m 2,受力及运动情况如图示,其中:f 1=μN 1=μm 1g , f 2=μN 2=μ(N 1+m 2g)=μ(m 1+m 2)g. 在水平方向对两个质点应用牛二定律:②①a m T g m m g m F a m g m T 221111)(=-+--=-μμμ①+②可求得:g m m gm F a μμ-+-=2112将a 代入①中,可求得:2111)2(m m g m F m T +-=μ2-20天平左端挂一定滑轮,一轻绳跨过定滑轮,绳的两端分别系上质量为m 1,m 2的物体(m 1≠m 2),天平右端的托盘上放有砝码. 问天平托盘和砝码共重若干,天平才能保持平衡?不计滑轮和绳的质量及轴承摩擦,绳不伸长。
1第七章 质点动力学 习题解答7-1 质量为40 g 的小球M 以初速度v =8 j (m/s)从点A (0, 0, 0.3m)抛出后,受到沿i 方向恒定的电磁力作用,其大小F = 0.8 kN ,如图所示。
求小球M 到达xy 平面点B 时,点B 的坐标和小球的速度。
解:取小球M 为研究对象,小球所受到的主动力为 k i F mg F R -=由质点运动微分方程R F m =r ,写出投影式F x m = ,0=ym ,mg z m -= 初始条件为000====t t y x ,3.00==t z ;000====t t z x,v y t ==0 解得质点的速度方程为t mFx= ,v y = ,gt z -= 质点的运动方程为 22t m F x =,vt y =,3.022+-=t gz 当0=z 时,小球到达xy 平面,由03.022=+-=t g z 解得s 247.01=t ,于是小球到达xy 平面时的各速度分量为m/s 7.494811===t mFxt t ,m/s 81===v y t t ,m/s 425.211-=-==gt z t t . 各坐标为m 2.6122211===t m F x t t ,m 979.111===vt y t t ,m 137.23.02211-=+-==t gz tt .7-2 图示A ,B 两物体的质量分别为m A 和m B ,二者用一细绳连接,此绳跨过一定滑轮,滑轮半径为r 。
运动开始时,两物体的高度差为h ,且m A > m B ,不计滑轮质量。
求由静止释放后,两物体达到相同高度时所需的时间。
解:分别取A 和B 物体为研究对象,受力图如图示,列出动力学方程TA A A A F W x m -= , TB B B B F W x m -= , 式中g m W A A =,g m W B B =,根据题意,有TB TA F F =,B A x x -=,B A xx -= 初始条件00==t A x ,h x t B ==0,00==t A x,00==t B x . 解以上初值问题,得题7-2图题7-2受力图2g m m m m xBA B A A +-= , ()22gt m m m m x B A BA A +-=g m m m m x B A B A B +--= , ()h gt m m m m x B A BA B ++--=22令B A x x =,即()()h gt m m m m gt m m m m B A BA B A B A ++--=+-2222解得当两物体达到相同高度时 ()()gm m h m m t B A B A -+=...7-3 质量为m 的质点M 受到引力F = -k 2m r 的作用,其中k 为常量,运动开始时,质点M在轴x 上,OM 0 = b ,初速度v 0与轴x 的夹角为β,如图所示。
第七章 质点动力学本章要点一、质点运动的动力学建模 1动力学基本定律:牛顿三定律. 2质点运动微分方程矢量形式 ∑==ni i t m 122d d F r;形式直角坐标 ∑∑∑======n i zi n i yi n i xi F t zm F t y m F t x m 122122122d d d d d d ,,;自然坐标形式 ∑∑∑======ni i ni i ni ti F F v mF t s m 1b 1n 21220,,d d ρ.式中n t F F ,和b F 分别是作用于质点的各力F i 在切线、主法线和副法线上的投影;ρ为运动轨迹在该点处的曲率半径;v 是质点的速度。
二、质点运动的动力学分析 1 质点动力学的两类基本问题质点动力学基本问题可分为两类:一类是已知质点的运动,求作用于质点的力;另一类是已知作用于质点的力,求质点的运动。
求解质点动力学第一类基本问题只需求两次导数得到质点的加速度,代入到质点运动方程中,得到一代数方程组,即可求解。
求解质点动力学第二类基本问题在数学上归结为求解微分方程的定解问题。
还要根据已知的初始条件确定积分常数。
此外,有些质点动力学问题是第一类和第二类问题的综合。
解题要领1) 解题步骤:(1) 根据题意选取某质点为研究对象;(2) 分析作用在质点上的主动力和约束反力;(3) 根据质点的运动特征,建立适当的坐标系。
(4)选择适当的形式建立运动微分方程,第二类问题还要确定初始条件;(4)求解运动微分方程。
2) 最好将要建立运动微分方程的“一般状态”下速度投影的正向为坐标轴方向,要特别注意当阻力与速度的奇次方成正比时在轴上的投影,注意各力在坐标轴上投影的正负号。
3) 在3维空间,质点运动微分方程有3个投影式,只能够解3个未知量。
2 单自由度系统的线性振动(1) 单自由度系统的自由振动的微分方程:02=+x xn ω ,在初始条件:0000,v x x x t t ==== 下的解为)sin(ϕω+=t A x n其中⎪⎪⎭⎫ ⎝⎛=+==002220arctan ,,v x v x A mk n n n ωϕωω 这里A 为振幅,ϕ为初相位,ωn 为固有频率。
质点运动学及动力学练习题一 判断题1.质点作圆周运动,其加速度一定与速度垂直。
( )2.物体作直线运动,法向加速度必为零。
( )3.物体作曲线运动,法向加速度必不为零,且轨道最弯处,法向加速度最大。
( )4.某时刻质点速度为零,切向加速度必为零。
( )5.在单摆和抛体运动中,加速度保持不变。
( )6.某人器自行车以速率V 向正东方向行驶,遇到由北向南刮来的风,(设风速也为V ),则他感到风是从东北方向吹来的。
( )7.质点沿x 方向作直线运动,其 v - t示。
判断下列说法的正误:(1)21t t 时加速度为零。
( )(2)在0 ~ t 2 秒内的位移可用图中v – t 曲线与t 轴所围面积表示,t 轴上、下部分的面积均取正值。
( )(3)在0 ~ t 2 秒内的路程可用图中v – t 曲线与t 轴所围面积表示,t 轴上、下部分的面积均取正值。
( )8.某质点的运动方程为 x =3t -5t 3+6 (SI) ,则该质点作变加速直线运动,加速度沿X 负方向。
( )9.物体的运动方向和合外力方向一定相同。
( )t10.物体受到几个力的作用,一定产生加速度。
()11.物体运动的速度很大,所受到的合外力也很大。
()12.物体运动的速率不变,所受到的合外力为零。
()13.小力作用在一个静止的物体上,只能使它产生小的速度。
()14.小球从距地面高为h处以初速度v0水平抛出,与地面碰撞后又反弹回同样的高度,速度仍为水平方向,大小为v0在这一过程中小球的动量受恒。
()15.物体m被放在斜面M上,如把m和M看成一个系统,判断在下列何种情形下,系统的水平方向分动量是守恒的?(1)m与M间无摩擦,而M与地面间有摩擦。
()(2)m与M间无摩擦,而M与地面间无摩擦。
()(3)两处都没有摩擦。
()(4)两处都有摩擦。
()16.不受外力作用的系统,动量和机械能必然同时守恒。
()17.内力都为保守力,而它受的合外力为零,该系统的动量和机械能都必然守恒。
第二章 质点动力学习题解答2-1 如题图2-1中(a)图所示,质量为m 的物体用平行于斜面的细线联结置于光滑的斜面上,若斜面向左方作加速运动,当物体刚脱离斜面时,它的加速度的大小为( D )(A) g sin θ (B) g cos θ (C) g tan θ (D) g cot θ2-2 用水平力F N 把一个物体压着靠在粗糙的竖直墙面上保持静止.当F N 逐渐增大时,物体所受的静摩擦力F f 的大小( A )(A) 不为零,但保持不变 (B) 随F N 成正比地增大(C) 开始随F N 增大,达到某一最大值后,就保持不变 (D) 无法确定2-3 一段路面水平的公路,转弯处轨道半径为R ,汽车轮胎与路面间的摩擦因数为μ,要使汽车不至于发生侧向打滑,汽车在该处的行驶速率( C )(A) 不得小于gR μ (B) 必须等于gR μ(C) 不得大于gR μ (D) 还应由汽车的质量m 决定2-4 如习题2-4图所示,一物体沿固定圆弧形光滑轨道由静止下滑,在下滑过程中,则( B )(A) 它的加速度方向永远指向圆心,其速率保持不变 (B) 它受到的轨道的作用力的大小不断增加 (C) 它受到的合外力大小变化,方向永远指向圆心 (D) 它受到的合外力大小不变,其速率不断增加2-5 习题2-5图所示,系统置于以a =1/4 g 的加速度上升的升降机内,A 、B 两物体质量相同均为m ,A 所在的桌面是水平的,绳子和定滑轮质量均不计,若忽略滑轮轴上和桌面上的摩擦,并不计空气阻力,则绳中张力为( A )(A) 5/8mg (B) 1/2mg (C) mg (D) 2mg 2-6 对质点组有以下几种说法: (1) 质点组总动量的改变与内力无关; (2) 质点组总动能的改变与内力无关; (3) 质点组机械能的改变与保守内力无关. 下列对上述说法判断正确的是( C )习题2-4图A习题2-5图B(A) 只有(1)是正确的 (B) (1)、(2)是正确的 (C) (1)、(3)是正确的 (D) (2)、(3)是正确的2-7 有两个倾角不同、高度相同、质量一样的斜面放在光滑的水平面上,斜面是光滑的,有两个一样的物块分别从这两个斜面的顶点由静止开始滑下,则( D )(A) 物块到达斜面底端时的动量相等 (B) 物块到达斜面底端时动能相等(C) 物块和斜面(以及地球)组成的系统,机械能不守恒 (D) 物块和斜面组成的系统水平方向上动量守恒 2-8 对功的概念有以下几种说法:(1) 保守力作正功时,系统内相应的势能增加; (2) 质点运动经一闭合路径,保守力对质点作的功为零;(3) 作用力和反作用力大小相等、方向相反,所以两者所作功的代数和必为零. 下列上述说法中判断正确的是( C )(A) (1)、(2)是正确的 (B) (2)、(3)是正确的 (C) 只有(2)是正确的(D) 只有(3)是正确的2-9 如图所示,质量分别为m 1和m 2的物体A 和B ,置于光滑桌面上,A 和B 之间连有一轻弹簧。
第一章 质点运动学一 、填空题1.一质点作半径为 m 的圆周运动,它通过的弧长s 按规律 s = t + 2 t 2 变化。
则它在2 s 末的切向加速度为 m/s 2。
法向加速度为 m/s 2。
( 4 , 81 ) 解:t dt ds 41+==υΘ 4==∴dt d a t υ 2221681)41(t t r t r a n ++=+==∴υ 2.一质点沿x 轴作直线运动,运动方程为324t t x -=,则1 s 末到3 s 末的位移为 m 。
则1 s 末到3 s 末的平均速度为 m/s 。
(-44 -22 )解:44)1()3(-=-=∆x x x 221344-=--=∆∆=t x υ 3.已知质点的运动方程为j t t i t t r ρρρ)314()2125(32++-+=(SI ),当t = 2 s 时,质点的速度 为υϖ m/s , 质点的加速度=a ρ m/s 2 j ρ8, j i ρρ4+- 解:j j t i t dt r d s t ρρρρρ8/)4()2(22=++-===υ j i j t i dt d a s t ρρρρρρ4/22+-=+-===υ 4.一质点的运动方程为 262t t x +=(SI ),质点在4 s 时的速度大小为 m/s 。
加速度大小为 m/s 2 ( 50 , 12) 解:50/1224=+===s t t dt dx υ 12==dtd a υ 5.一质点沿半径R = 1 m 的圆周运动,其路程与时间的关系为 222t s +=(m ),那么,从开始计时到总加速度a 恰好与半径成45°角时,质点所经过的路程s = m 。
解:t dt ds 4==υ 4==∴dtdv a t 22216116t t R v a n === 由题意:n t a a = 2164t =∴ 得 s t 5.0= 故 m s s s 5.0)0()5.0(=-=6.一质点在半径为 m 的圆周上运动,其角位置为 256t +=θ(SI ),则t = s 时质点的速度的大小 v = m/s 。