立体几何8个定理

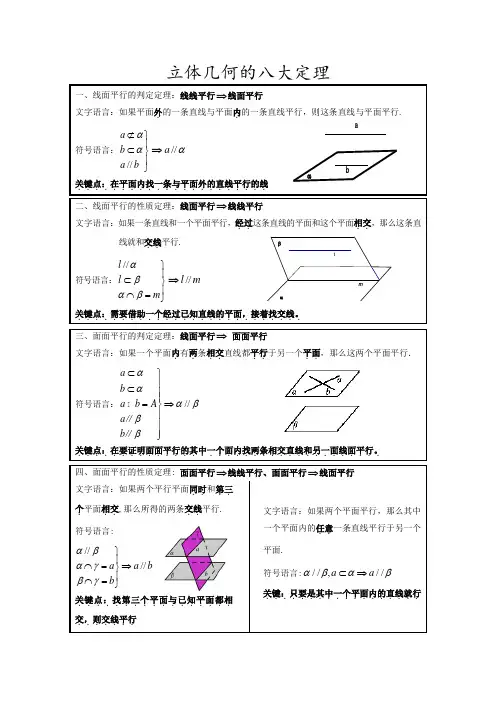
lmβααba立体几何的八大定理一、线面平行的判定定理：线线平行⇒线面平行文字语言：如果平面外．的一条直线与平面内．的一条直线平行，则这条直线与平面平行. 符号语言：//a b a b αα⊄⎫⎪⊂⎬⎪⎭⇒//a α关键点：在平面内找一条与平面外的直线平行的线．．．．．．．．．．．．．．．．．．．．．． 二、线面平行的性质定理：线面平行⇒线线平行文字语言：如果一条直线和一个平面平行，经过．．这条直线的平面和这个平面相交．．，那么这条直线就和交线．．平行. 符号语言：//l l m αβαβ⎫⎪⊂⎬⎪⋂=⎭⇒//l m关键点：需要借助一个经过已知直线的平面，接着找交线。

．．．．．．．．．．．．．．．．．．．．．．．．．． 三、面面平行的判定定理：线面平行⇒ 面面平行文字语言：如果一个平面内．有两．条相交．．直线都平行．．于另一个平面．．，那么这两个平面平行． 符号语言：//a b a b A a b αααβββ⊂⎫⎪⊂⎪⎪=⇒⎬⎪⎪⎪⎭∥∥ 关键点：在要证明面面平行的其中一个面内找两条相交直线和另一面线面平行。

．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．． 四、面面平行的性质定理: 面面平行⇒线线平行、面面平行⇒线面平行 文字语言：如果两个平行平面同时．．和第三．．个．平面相交．．,那么所得的两条交线．．平行. 符号语言:////a a b b αβαγβγ⎫⎪⋂=⇒⎬⎪⋂=⎭关键点：找第三个平面与已知平面都相．．．．．．．．．．．．．．．．．交，则交线平行．．．．．．．文字语言：如果两个平面平行，那么其中一个平面内的任意．．一条直线平行于另一个平面.符号语言://,//a a αβαβ⊂⇒ 关键：只要是其中一个平面内的直线就行．．．．．．．．．．．．．．．．．．nmAαaBA l βαaβα五、线面垂直的判定定理：线线垂直⇒线面垂直文字语言：如果一条直线和一个平面内．的两．条相交．．直线垂直．．，那么这条直线垂直于这个平面. 符号语言：,a ma n a m n A m n ααα⊥⎫⎪⊥⎪⇒⊥⎬⋂=⎪⎪⊂⊂⎭关键点：在平面内找两条相交直线与所要证的直线垂直．．．．．．．．．．．．．．．．．．．．．．．． 六、线面垂直的性质定理：线面垂直⇒线线垂直文字语言：若一条直线垂直于一个平面，则这条直线垂直平面内的任意．．一条直线. 符号语言：l l a a αα⊥⎫⇒⊥⎬⊂⎭关键点：往往线面垂直中的线线垂直需要用这个定理推出．．．．．．．．．．．．．．．．．．．．．．．．． 七、平面与平面垂直的判定定理：线面垂直⇒面面垂直文字语言：如果一个平面经过．．另一个平面的一条垂线，则这两个平面互相垂直. （如果一条直线垂直于一个平面，并且有另一个平面经过这条直线，那么这两个平面垂直）符号表示：a a ααββ⊥⎫⇒⊥⎬⊂⎭关键．．点：在需要证明的两个平面中找线面垂直．．．．．．．．．．．．．．．．．．八、平面与平面垂直的性质定理：面面垂直⇒线面垂直文字语言：如果两个平面互相垂直，那么在一个平面内垂直．．于它们的交线．．的直线垂直于另一个平面.符号语言：l AB AB AB lαβαββα⊥⎫⎪=⎪⇒⊥⎬⊂⎪⎪⊥⎭关键点：先找交线，再在其中一个面内找与交线垂直的线。

lmβααba立体几何的八大定理一、线面平行的判定定理：线线平行⇒线面平行文字语言：如果平面外．的一条直线与平面内．的一条直线平行，则这条直线与平面平行. 符号语言：//a b a b αα⊄⎫⎪⊂⎬⎪⎭⇒//a α关键点：在平面内找一条与平面外的直线平行的线．．．．．．．．．．．．．．．．．．．．．． 二、线面平行的性质定理：线面平行⇒线线平行文字语言：如果一条直线和一个平面平行，经过．．这条直线的平面和这个平面相交．．，那么这条直线就和交线．．平行. 符号语言：//l l m αβαβ⎫⎪⊂⎬⎪⋂=⎭⇒//l m关键点：需要借助一个经过已知直线的平面，接着找交线。

．．．．．．．．．．．．．．．．．．．．．．．．．． 三、面面平行的判定定理：线面平行⇒ 面面平行文字语言：如果一个平面内．有两．条相交．．直线都平行．．于另一个平面．．，那么这两个平面平行． 符号语言：//a b a b A a b αααβββ⊂⎫⎪⊂⎪⎪=⇒⎬⎪⎪⎪⎭∥∥ 关键点：在要证明面面平行的其中一个面内找两条相交直线和另一面线面平行。

．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．． 四、面面平行的性质定理: 面面平行⇒线线平行、面面平行⇒线面平行 文字语言：如果两个平行平面同时．．和第三．．个．平面相交．．,那么所得的两条交线．．平行. 符号语言:////a a b b αβαγβγ⎫⎪⋂=⇒⎬⎪⋂=⎭关键点：找第三个平面与已知平面都相．．．．．．．．．．．．．．．．．交，则交线平行．．．．．．．文字语言：如果两个平面平行，那么其中一个平面内的任意．．一条直线平行于另一个平面.符号语言://,//a a αβαβ⊂⇒ 关键：只要是其中一个平面内的直线就行．．．．．．．．．．．．．．．．．．nmAαaBA l βαaβα五、线面垂直的判定定理：线线垂直⇒线面垂直文字语言：如果一条直线和一个平面内．的两．条相交．．直线垂直．．，那么这条直线垂直于这个平面. 符号语言：,a ma n a m n A m n ααα⊥⎫⎪⊥⎪⇒⊥⎬⋂=⎪⎪⊂⊂⎭关键点：在平面内找两条相交直线与所要证的直线垂直．．．．．．．．．．．．．．．．．．．．．．．． 六、线面垂直的性质定理：线面垂直⇒线线垂直文字语言：若一条直线垂直于一个平面，则这条直线垂直平面内的任意．．一条直线. 符号语言：l l a a αα⊥⎫⇒⊥⎬⊂⎭关键点：往往线面垂直中的线线垂直需要用这个定理推出．．．．．．．．．．．．．．．．．．．．．．．．． 七、平面与平面垂直的判定定理：线面垂直⇒面面垂直文字语言：如果一个平面经过．．另一个平面的一条垂线，则这两个平面互相垂直. （如果一条直线垂直于一个平面，并且有另一个平面经过这条直线，那么这两个平面垂直）符号表示：a a ααββ⊥⎫⇒⊥⎬⊂⎭关键点：．．．．在需要证明的两个平面中找线面垂直．．．．．．．．．．．．．．．．八、平面与平面垂直的性质定理：面面垂直⇒线面垂直文字语言：如果两个平面互相垂直，那么在一个平面内垂直．．于它们的交线．．的直线垂直于另一个平面.符号语言：l AB AB AB lαβαββα⊥⎫⎪=⎪⇒⊥⎬⊂⎪⎪⊥⎭关键点：先找交线，再在其中一个面内找与交线垂直的线。

立体几何的八个判定定理立体几何的八个判定定理是指由英国数学家约翰·威尔逊（John Wallis）在17th century所提出的一套定理。

其中包括：（1）贝瑟尔定理：任意一个平面三角形的内角之和等于180度。

（2）杨氏定理：任意一个对角相交的多边形，其内部角之和等于其外部角之和。

（3）特斯克定理：在同样边上的三个面有关的角相加等于180度。

（4）柯尔定理：在同样边上的四个面有关的角相加等于360度。

（5）高斯定理：任意一个多面体的角之和等于360度乘以面的数量。

（6）伯尔定理：任意一个多边形的角之和大于360度。

（7）双旋定理：任意一个多面体的内角之和等于多边形的角之和减去多边形的边的数量。

（8）欧几里得定理：任意一个多面体的角之和等于多边形的角之和加上多边形的边的数量乘以180度。

贝瑟尔定理是最重要的立体几何判定定理，表明任意一个平面三角形的三个内角之和都等于180度。

这个定理是用来表示平面三角形的构成的，而这个定理也被用来表示一个多边形的构成。

杨氏定理是贝瑟尔定理的推广，即任意一个对角相交的多边形，其内部角之和等于其外部角之和。

特斯克定理是杨氏定理的一个特殊情况，表示在同样边上的三个面有关的角相加等于180度。

柯尔定理也是杨氏定理的一个特殊情况，表示在同样边上的四个面有关的角相加等于360度。

高斯定理是一个重要的立体几何判定定理，即任意一个多面体的角之和等于360度乘以面的数量。

这个定理与贝瑟尔定理的相似之处在于，它们都可以用来表明多面体的构成，它们都表示了一个多面体的性质。

伯尔定理是高斯定理的一个推广，表明任意一个多边形的角之和大于360度。

双旋定理是一个重要的立体几何判定定理，表明任意一个多面体的内角之和等于多边形的角之和减去多边形的边的数量。

欧几里得定理也是一个重要的立体几何判定定理，表明任意一个多面体的角之和等于多边形的角之和加上多边形的边的数量乘以180度。

总的来说，立体几何的八个判定定理是一个重要的数学工具，它们不仅可以帮助人们更好地理解多面体和多边形的构造，还可以帮助人们解决一些复杂的问题，比如求解三角形的面积，求解多面体的体积等等。

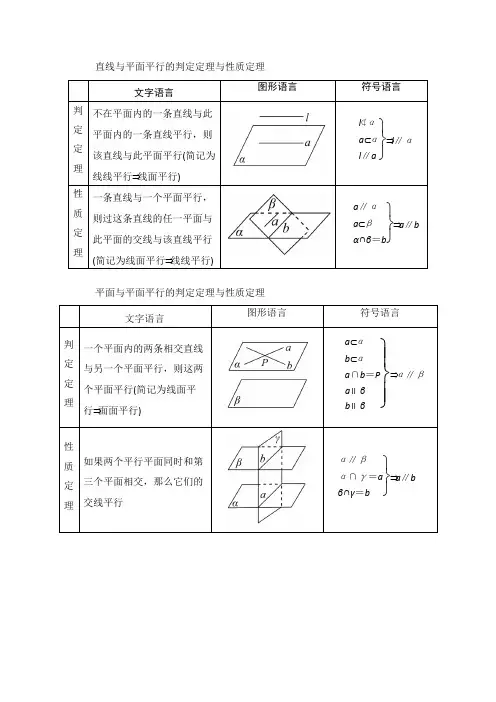
直线与平面平行的判定定理与性质定理文字语言图形语言符号语言判定定理不在平面内的一条直线与此平面内的一条直线平行，则该直线与此平面平行(简记为线线平行⇒线面平行)⎭⎬⎫l⊄αa⊂αl∥a⇒l∥α性质定理一条直线与一个平面平行，则过这条直线的任一平面与此平面的交线与该直线平行(简记为线面平行⇒线线平行)⎭⎬⎫a∥αa⊂βα∩β＝b⇒a∥b平面与平面平行的判定定理与性质定理文字语言图形语言符号语言判定定理一个平面内的两条相交直线与另一个平面平行，则这两个平面平行(简记为线面平行⇒面面平行)⎭⎪⎬⎪⎫a⊂αb⊂αa∩b＝Pa∥βb∥β⇒α∥β性质定理如果两个平行平面同时和第三个平面相交，那么它们的交线平行⎭⎬⎫α∥βα∩γ＝aβ∩γ＝b⇒a∥b直线与平面垂直的判定定理及性质定理文字语言图形语言符号语言判定定理一条直线与平面内的两条相交直线都垂直，则该直线与此平面垂直⎭⎬⎫a，b⊂αa∩b＝Ol⊥al⊥b⇒l⊥α性质定理垂直于同一个平面的两条直线平行⎭⎬⎫a⊥αb⊥α⇒a∥b平面与平面垂直的判定定理及性质定理文字语言图形语言符号语言判定定理一个平面过另一个平面的一条垂线，则这两个平面互相垂直⎭⎬⎫l⊂βl⊥α⇒α⊥β性质定理两个平面互相垂直，则一个平面内垂直于交线的直线垂直于另一个平面⎭⎬⎫α⊥βl⊂βα∩β＝al⊥a⇒l⊥α。

符号语言
判定定理
一个平面内的两条相交直线与另一个平面平行，则这两个平面平行(简记为线面平行⇒面面平行)
⇒α∥β
性质定理
如果两个平行平面同时和第三个平面相交，那么它们的交线平行
⇒a∥b
直线与平面垂直的判定定理及性质定理
文字语言
图形语言
符号语言
判定定理
一条直线与平面内的两条相交直线都垂直，则该直线与此平面垂直
⇒l⊥α
性质定理
垂直于同一个平面的两条直线平行
⇒a∥b
平面与平面垂ቤተ መጻሕፍቲ ባይዱ的判定定理及性质定理
文字语言
图形语言
符号语言
判定定理
一个平面过另一个平面的一条垂线，则这两个平面互相垂直
⇒α⊥β
性质定理
两个平面互相垂直，则一个平面内垂直于交线的直线垂直于另一个平面
⇒l⊥α
文字语言
图形语言
符号语言
判定定理
不在平面内的一条直线与此平面内的一条直线平行，则该直线与此平面平行(简记为线线平行⇒线面平行)
⇒l∥α
性质定理
一条直线与一个平面平行，则过这条直线的任一平面与此平面的交线与该直线平行(简记为线面平行⇒线线平行)
⇒a∥b
平面与平面平行的判定定理与性质定理
文字语言
图形语言

立体几何公式定理大全、公理定理（一）平面基本性质公理1：如果一条直线上的两点在一个平面内，那么这条直线上的所有的点都在这个平面内。

公理2：过不在同一条直线上的三个点，有且只有一个平面。

推论1：经过一条直线和这条直线外一点，有且只有一个平面。

推论2：经过两条相交直线，有且只有一个平面。

推论3：经过两条平行直线，有且只有一个平面。

公理3：如果两个平面有一个公共点，那么它们有且只有一条通过这个点的公共直线。

公理4：平行于同一条直线的两条直线互相平行。

等角定理：如果一个角的两边和另一个角的两边分别平行，那么这两个角相等或互补。

（二）空间中两条直线的位置关系空间两直线的位置关系：空间两条直线只有三种位置关系：平行、相交、异面1、按是否共面可分为两类：（1）共面：平行、相交（2）异面：异面直线的定义：不同在任何一个平面内的两条直线或既不平行也不相交。

异面直线判定定理：过平面内一点与平面外一点的直线，与平面内不经过该点的直线是异面直线。

两异面直线所成的角：过空间任意一点引两条直线分别平行于两条异面直线，它们所成的锐角（或直角）就是异面直线所成的角。

范围为0 , 90两异面直线间距离: 公垂线段（有且只有一条） 2、若从有无公共点的角度看可分为两类：（1）有且仅有一个公共点——相交直线；（2）没有公共点——平行或异面三）平行关系1．线面平行定义：直线和平面没有公共点判定定理：如果平面外一条直线和这个平面内的一条直线平行，那么这条直线和这个平面平行性质定理：如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线和交线平行。

2．面面平行定义：空间两平面没有公共点判定定理：如果一个平面内有两条相交直线都平行于另一个平面，那么这两个平面平行。

性质定理引理：两个平面互相平行则其中一个平面内的直线平行于另一个平面。

性质定理：如果两个平行平面同时和第三个平面相交，那么交线平行。

（四）垂直关系1线面垂直定义：如果一条直线a和一个平面内的任意一条直线都垂直，我们就说直线a和平面互相垂直.直线a叫做平面的垂线，平面叫做直线a的垂面。

立体几何证明8条定理立体几何是几何学的一个分支，研究的是在三维空间中的图形和体的性质。

在立体几何中有许多定理，其中一些重要的定理包括平行线定理、垂直线定理、欧拉定理、等角定理、切线定理、割线定理、同位角定理和三角形内角和定理等。

下面将详细讨论这些定理：1.平行线定理：如果两条平行线被一组平行线截断，那么它们的对应线段成比例。

这个定理可以用于证明两条线平行。

2.垂直线定理：如果两条直线相交，且其中一条直线垂直于另一条直线，那么相交处的四个角都是直角。

这个定理可以用于证明两条线垂直。

3.欧拉定理：在任意一个凸多面体中，顶点数、棱数和面数之间存在一个关系：顶点数加上面数等于棱数加上2、这个定理被应用于立体几何中的多面体的计算。

4.等角定理：如果两条线分别与一条平行线相交，且其中一对内错角（相对于平行线的两条线之间的两个角）或一个内错角和一个外错角（与平行线的两条线相交形成的一对内角和一对外角）相等，那么这两条线是平行线。

这个定理可以用于证明平行线。

5.切线定理：给定一个圆和一个与圆相切且通过切点的直线，那么切线的切点与切线所跨越的弦的两个端点之间的角是直角。

这个定理可以用于证明圆的性质。

6.割线定理：给定一个圆和一个与圆相交的直线，那么直线与圆的切线所跨越的弦的两个端点之间的角相等。

这个定理也可以用于证明圆的性质。

7.同位角定理：如果两条平行线被一条截线截断，那么同位角（相对于平行线的两条线的每一对内角）相等。

这个定理可以用于证明平行线。

8.三角形内角和定理：三角形的三个内角的度数之和等于180度。

这个定理是三角形的基本性质，可以用于证明其他三角形的性质。

这些定理是立体几何中的一些基本定理，通过运用它们可以推导出其他一些更复杂的定理。

这些定理不仅在几何学中有重要的应用，而且在物理学、工程学等其他学科中也有广泛的应用。

立体几何经典定理概述(八大定理)立体几何经典定理概述（八大定理）本文将概述立体几何中的八大经典定理。

立体几何是研究三维空间中的图形和形体的数学学科，定理是在研究过程中得出的具有重要意义的数学命题。

1. 欧拉定理欧拉定理是立体几何中最著名的定理之一。

它规定了三维物体的面、顶点和边的关系。

具体来说，如果一个多面体满足面+顶点-边=2的关系，那么它就是一个封闭的多面体。

欧拉定理形象地描述了三维世界中多面体的特性。

2. 柯西定理柯西定理是关于立体几何中平行四边形的定理。

它指出，对于一个平行四边形，其对角线互相平分彼此。

这个定理在解决平行四边形的性质和关系时非常有用，能够帮助我们更好地理解平面几何的性质。

3. 形心定理形心定理是关于多边形形心的定理。

形心是多边形中所有顶点的连线的交点，该定理指出，任意多边形的形心一定在多边形的重心和质心连线的上面。

形心定理可以帮助我们确定多边形的形心位置，从而研究多边形的性质和变形。

4. 二等分线定理二等分线定理是关于立体几何中等分线的定理。

它规定了等分线在多面体中的特性，即等分线和相应的两个面以及它们的交点构成的平面垂直。

这个定理在解决多面体的等分线问题时非常有用，能够帮助我们进一步理解多面体的性质。

5. 范恩艾克线定理范恩艾克线定理是关于球面上切线和交角的定理。

它指出，在球面上，任意切线与相应交角的正弦值等于球心到交点的距离和切线长的比值。

这个定理在解决球面上的切线和交角问题时非常有用，能够帮助我们研究球面的性质和切线关系。

6. 斯坦纳定理斯坦纳定理是关于三维空间中图的生成树的定理。

生成树是一个无圈连通图的子图，其中包含了所有顶点并且边的数量最少。

斯坦纳定理指出，在三维空间中的图中，生成树的条数等于顶点数减去连通分量的数量。

这个定理在解决三维空间图的生成树问题时非常有用。

7. 勾股定理勾股定理是立体几何中最基础的定理之一。

它规定了直角三角形边长之间的关系，即直角三角形的两个直角边的平方和等于斜边的平方。

立体几何性质定理集锦
一、空间点、线、面之间的位置关系
公理1：如果一条直线上的两点在这个平面内，那么这条直线在这个平面内。

公理2：过不在一条直线上的三点，有且只有一个平面。

推论：过直线及直线外一点，有且只有一个平面。

推论：过两条平行直线有且只有一平面。

推论：过两条相交平面有且只有一个平面。

公理3：如果两个不重合的平面有一个公共点，那么它们有且只有一条过交点的公共直线。

公理4：（直线平行的传递性）平行于同一条直线的两条直线平行。

二、平行与垂直的判定和性质定理
1、直线与平面平行的判定定理：平面外一条直线与平面内一条直线平行，则该直线与此平
面平行。

2、直线与平面平行的性质定理：一条直线与一个平面平行，则过这条直线的任一平面与此
平面的交线与该直线平行。

3、平面与平面平行的判定定理：一个平面内的两条相交直线与另一平面平行，则这两个平
面平行。

4、平面与平面平行的性质定理：如果两个平行平面同时和第三个平面相交，那么它们的交
线平行。

5、直线与平面垂直的判定定理：一条直线与一个平面内的两条相交直线都垂直，则该直线
与此平面垂直。

6、直线与平面垂直的性质定理：
（1）一条直线垂直一个平面，则这条直线垂直这个平面内的所有直线。

（2）垂直同一条直线的两个平面平行。

7、平面与平面垂直的判定定理：一个平面过另一个平面的垂线，则这两个平面垂直。

8、平面与平面垂直的性质定理：两个平面垂直，则一个平面内垂直于交线的直线与另一个
平面垂直。

立体几何八大定理总结《立体几何八大定理总结——那些让我又爱又恨的家伙们》嘿，同学们！今天咱就来唠唠立体几何的八大定理。

别小看它们，这可真是让咱又爱又恨呐！先说线面平行定理吧，它就像个调皮的小精灵，总在那儿晃悠，告诉你一条线和平一个面没交点，这线就和那面平行啦。

有时候我就想，这线咋就这么“安分守己”呢，没交点就平行，咋就这么直接呢。

然后是面面平行定理，这俩面平行就像好朋友，有着相同的“性格”，一组相交线分别平行，嘿，它们就平行了。

感觉就像找朋友似的，条件对上号了，就成了。

线面垂直定理可厉害咯，一条线垂直一个面里的两条相交线，它就和这面垂直啦。

就像个超级英雄，只要打倒两条“小怪兽”线，就能征服整个面。

面面垂直定理呢，像两个打架的武林高手，一个面经过另一个面的垂线，它们就扭打在一起啦，形成了垂直。

还记得三垂线定理不？就像是个魔术，斜线在平面上的投影和平面内的一条直线垂直，那斜线和这直线也垂直。

这简直太神奇了吧，有种变戏法的感觉。

体积那些定理也让人印象深刻啊，特别是三棱锥的体积，计算起来就像解谜题一样，找好底和高，就能算出那小块立体空间的大小。

有时候算错了，哎哟，那感觉就像好不容易搭的积木倒了一样。

这些定理啊，有时候就像迷宫里的线索，得好好琢磨，一旦弄明白了，那简直豁然开朗，就像找到了迷宫的出口，爽歪歪！学这些定理的时候，那真是绞尽脑汁，做题做到头大。

但等你真正掌握了，那成就感爆棚啊！感觉自己就是个立体几何小专家。

总之，立体几何八大定理啊，就是我们学习路上的小伙伴，有时候调皮捣蛋让你头疼，但最终会让你变得更强大。

和它们好好相处吧，相信不久的将来，我们都能在立体几何的世界里游刃有余啦！哈哈！现在，同学们，继续加油，和这些定理大战三百回合吧！。

立体几何点线面定理1.公理一：一条直线的两点在一个平面内，那么这条直线上的所有的点都在这个平面内。

2.公理二：如果两个平面有两个公共点,它们有无数个公共点，而且这无数个公共点都在同一条直线上。

3.公理三：经过不在同一直线上的三点有且只有一个平面。

4.推论一：经过直线和直线外一点有且只有一个平面。

5.推论二：经过两条相交直线有且只有一个平面。

6.推论三：经过两条平行直线有且只有一个平面。

7.异面直线判定定理：平面内一点与平面外一点的确定的直线，与此平面内不经过该点的直线是异面直线。

8.公理四：平行于同一条直线的两条直线平行。

9.等角定理：如果一个角的两边和另一个角的两边分别平行并且方向相同，那么这两个角相等。

10.等角定理推论：如果两条相交直线和另两条相交直线分别平行，那么这两组直线所成的锐角（或直角）相等。

11.直线与平面垂直的判定定理一：过平面外一点有且只有一条直线与已知平面垂直。

12.直线与平面垂直的判定定理二：过直线上一点，有且只有一个平面与已知直线垂直。

13.直线与平面垂直的判定定理三：如果一条直线和一个平面内的两条相交直线都垂直，那么这条直线垂直于这个平面。

14. 直线与平面垂直的性质定理四：如果一条直线垂直于已知平面，另一条直线平行于这条直线，那么另一条直线也垂直于已知平面。

15.直线与平面垂直的性质定理五：如果两条直线同垂直于一个平面，那么这两条直线平行。

16.射影长定理：从平面外一点向这个平面所引的垂线段和斜线段中，斜线段相等的射影相等，射影相等的斜线段相等，斜线段较长的射影也较长，射影较长的斜线段也较长，垂线段最短。

17.最小角定理：斜线与平面所成的角是斜线与平面内任意一条直线中所成的角中最小的。

18.三垂线定理：平面内的一条直线，如果与穿过这个平面的一条斜线在这个平面上的射影垂直，那么它也和这条斜线垂直。

19.三垂线定理的逆定理：如果平面内一条直线和穿过该平面的一条斜线垂直，那么这条直线也垂直于这条斜线在平面内的射影。

立体几何公式大全基本概念公理1：如果一条直线上的两点在一个平面内,那么这条直线上的所有的点都在这个平面内。

公理2：如果两个平面有一个公共点，那么它们有且只有一条通过这个点的公共直线。

公理3: 过不在同一条直线上的三个点，有且只有一个平面。

推论1: 经过一条直线和这条直线外一点,有且只有一个平面. 推论2：经过两条相交直线,有且只有一个平面。

推论3：经过两条平行直线，有且只有一个平面。

公理4 ：平行于同一条直线的两条直线互相平行。

等角定理：如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等.空间两直线的位置关系：空间两条直线只有三种位置关系：平行、相交、异面1、按是否共面可分为两类：(1）共面：平行、相交（2）异面:异面直线的定义：不同在任何一个平面内的两条直线或既不平行也不相交。

异面直线判定定理：用平面内一点与平面外一点的直线,与平面内不经过该点的直线是异面直线.两异面直线所成的角：范围为 ( 0°，90°） esp。

空间向量法两异面直线间距离：公垂线段(有且只有一条) esp.空间向量法2、若从有无公共点的角度看可分为两类：（1）有且仅有一个公共点-—相交直线;（2）没有公共点-—平行或异面直线和平面的位置关系: 直线和平面只有三种位置关系：在平面内、与平面相交、与平面平行①直线在平面内-—有无数个公共点②直线和平面相交——有且只有一个公共点直线与平面所成的角:平面的一条斜线和它在这个平面内的射影所成的锐角。

esp.空间向量法(找平面的法向量)规定：a、直线与平面垂直时，所成的角为直角，b、直线与平面平行或在平面内，所成的角为0°角由此得直线和平面所成角的取值范围为［0°，90°]最小角定理: 斜线与平面所成的角是斜线与该平面内任一条直线所成角中的最小角三垂线定理及逆定理: 如果平面内的一条直线,与这个平面的一条斜线的射影垂直，那么它也与这条斜线垂直esp。

立体几何公式大全基本概念公理1:如果一条直线上的两点在一个平面内,那么这条直线上的所有的点都在这个平面内。

公理２:如果两个平面有一个公共点，那么它们有且只有一条通过这个点的公共直线。

ﻫ公理3: 过不在同一条直线上的三个点,有且只有一个平面。

推论１：经过一条直线和这条直线外一点,有且只有一个平面。

推论２:经过两条相交直线，有且只有一个平面。

推论3:经过两条平行直线,有且只有一个平面。

ﻫ公理４：平行于同一条直线的两条直线互相平行。

ﻫ等角定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等。

ﻫ空间两直线的位置关系:空间两条直线只有三种位置关系：平行、相交、异面1、按是否共面可分为两类：（1）共面: 平行、相交ﻫ(2)异面：异面直线的定义：不同在任何一个平面内的两条直线或既不平行也不相交。

ﻫ异面直线判定定理:用平面内一点与平面外一点的直线，与平面内不经过该点的直线是异面直线。

两异面直线所成的角:范围为（０°，90° ) esp.空间向量法两异面直线间距离：公垂线段(有且只有一条) ｅsp.空间向量法ﻫ2、若从有无公共点的角度看可分为两类:(1)有且仅有一个公共点——相交直线;(2)没有公共点——平行或异面ﻫ直线和平面的位置关系：直线和平面只有三种位置关系:在平面内、与平面相交、与平面平行①直线在平面内——有无数个公共点②直线和平面相交——有且只有一个公共点ﻫ直线与平面所成的角:平面的一条斜线和它在这个平面内的射影所成的锐角。

ﻫesp.空间向量法(找平面的法向量)规定：a、直线与平面垂直时,所成的角为直角，b、直线与平面平行或在平面内，所成的角为0°角由此得直线和平面所成角的取值范围为[０°,9０°］ﻫ最小角定理：斜线与平面所成的角是斜线与该平面内任一条直线所成角中的最小角三垂线定理及逆定理: 如果平面内的一条直线,与这个平面的一条斜线的射影垂直，那么它也与这条斜线垂直ﻫeｓp.直线和平面垂直直线和平面垂直的定义:如果一条直线a和一个平面内的任意一条直线都垂直，我们就说直线a和平面互相垂直.直线ａ叫做平面的垂线，平面叫做直线a的垂面。

立体几何中的八大定理1.直线与平面平行的判定定理和性质定理文字语言图形语言符号语言判定定理平面外一条直线与的一条直线平行，则该直线与此平面平行(线线平行⇒线面平行)//lα⎫⎪⎪⇒⎬⎪⎪⎭性质定理一条直线与一个平面平行，则过这条直线的任一平面与此平面的与该直线平行(简记为“线面平行⇒线线平行”)//l b⎫⎪⎪⇒⎬⎪⎪⎭2.平面与平面平行的判定定理和性质定理文字语言图形语言符号语言判定定理一个平面内的两条直线与另一个平面平行，则这两个平面平行(简记为“线面平行⇒面面平行”),//,αβ⎫⎪⎪⇒⎬⎪⎪⎭性质定理如果两个平行平面同时和第三个平面，那么它们的平行//a b⎫⎪⎪⇒⎬⎪⎪⎭3.直线与平面垂直的判定定理及性质定理文字语言图形语言符号语言判定定理一条直线与一个平面内的两条直线都垂直，则该直线与此平面垂直,,lα⎫⎪⎪⇒⊥⎬⎪⎪⎭性质定理垂直于同一个平面的两条直线//a b⎫⎪⇒⎬⎪⎭4.平面与平面垂直的判定定理与性质定理文字语言图形语言符号语言判定定理一个平面过另一个平面的，则这两个平面互相垂直αβ⎫⎪⇒⊥⎬⎪⎭性质定理两个平面互相垂直，则一个平面内垂直于的直线垂直于另一个平面lα⎫⎪⎪⇒⊥⎬⎪⎪⎭。

数学立体几何八大定理
1. 柿子定理：一个作为平面多边形底面的凸多面体的侧面积等
于这个凸多面体表面积的一半加上这个多面体面数目乘以它的底面积。

2. 欧拉定理：一个简单凸多面体的面数、顶点数和边数满足公式：面
数+顶点数=边数+2。

3. 狄利克雷定理：如果一个立体角的每个边界面都可以划分成互不相
交有限个平凡的平面角，则这个立体角为平凡的。

一个立体角被称为
平凡的，当且仅当它可以被划分成三角形。

4. 菲赫斯定理：一个多面体的每条棱所在的平面相交于一点（称为多
面体的菲赫斯点）。

5. 球冠切割定理：一个球的表面可以被三个平面分割成球冠。

6. 萨公定理：任何一个超过120度的立体角可以被切割成平凡的立体角。

7. 凸多面体的交角定理：凸多面体中任意两个面交角的余角的总和等
于360度。

8. 柯西・切比雪夫定理：如果两个凸多面体的交集不为空，则它们的
交界面至少有一点。

立体几何（三）线面位置关系的八大定理一、直线与平面平行的判定定理：文字语言：如果平面外的一条直线与平面内的一条直线平行，则这条直线与平面平行图形语言：符号语言：ab a//a//b作用：线线平行线面平行典例：在正方体ABCD A1B1C1D1中，M ,N 分别是A1B,CC1的中点，求证：MN //平面ABCD二、直线与平面平行的性质定理：文字语言：如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线就和交线平行。

图形语言：l //符号语言：l l //mm作用：线面平行线线平行典例：如图，AB// ,AC // BD,C ,D ，求证：AC BD三、平面与平面平行的判定定理 文字语言：如果一个平面内有两条相交直线都平行于另一个平面，那么这两个平面平行．图形语言：符号语言：aba b A //a ∥b ∥作用：线线平行 面面平行典例：如图，在三棱柱 ABC A 1 B 1C 1中，点 D,E 分别是 BC 与B 1C 1的中点，四、平面与平面平行的性质定理 : 文字语言：如果两个平行平面同时和第三个平面相交 图形语言 : //作用 : 面面平行 线线平行典例：如图， // // ，直线 a 与 b 分别交 , , 于点 A,B,C 和点D,E,F ，AB DE 求证： BC EF求证：平面 A 1EB // 平面 ADC 1 符号语言 : a a//b bC 1ECD, 那么所得的两条交线平行五、直线与平面垂直的判定定理：文字语言：如果一条直线和一个平面内的两条相交直线垂直，图形语言：符号语言：am anamnAm ,n作用：线线垂直线面垂直典例：已知四棱锥P ABCD , PD 底面ABCD ，底面ABCD为正方形，且PD CD ，E,F 分别为PB, PC的中点，求证：（1）AC 平面PBD （2）PA AB（3）PC 平面ADFE六、直线与平面垂直的性质定理：文字语言：若两条直线垂直于同一个平面，则这两条直线平行图形语言：符号语言：aa//bb作用：线面垂直线线平行那么这条直线垂直于这个平面mn七、平面与平面垂直的判定定理： 文字语言：如果一个平面经过另一个平面的一条垂线，则这两个平面互相垂直。