状态空间表示法例题

电气系统状态空间表达式例题状态空间表达式是描述线性时不变系统动态行为的一种数学模型，它基于系统的状态变量和控制变量来描述系统的动态行为：
假设有一个电气系统，其动态行为可以用以下微分方程描述：
dx/dt = Ax + Bu
y = Cx + Du
其中，x 是系统的状态变量，u 是系统的控制输入，y 是系统的输出。

A、B、C 和 D 是系统的系数矩阵，它们描述了系统内部状态变量之间的动态关系以及系统对控制输入和输出的响应。

根据状态空间表达式，我们可以将上述微分方程转换为以下形式：
x' = Ax + Bu
y = Cx + Du
其中，x' 是新的状态变量，它包含了系统状态的导数。

这个形式的状态空间表达式包含了系统的动态行为，可以通过控制输入 u 来影响系统的状态变量 x 和输出 y。

需要注意的是，具体的系数矩阵 A、B、C 和 D 取决于具体的电气系统，需要根据系统的具体参数和特性来确定。

第9章线性系统的状态空间分析与综合r例题解析例9-1 对于图9-1所示的质量一弹簧系统，当外力F (t)作用时，系统产生运动, 质量及弹簧弹性系数见图示。

如不计摩擦，试：(1)以质量m2的位移y(t)为输出，外力F(t)为输入，列写系统的运动方程；(2)求从F(s)到y(s)的传递函数；(3 )以框图表示上述系统；(4)自选一定数目的状态变量，建立上述系统的状态方程和输出方程。

图9-1质量一弹簧系统解：(1 )设质量块m的位移为乙根据牛顿定律有F(t) kjz y) gz 1)同理对质量块m有kjz y) k2y m2y 2)联立式1)和2)消去中间变量z，得出系统微分方程：m1 m2y(4)[(k1 k2 )m1 k1m2] y k1k2y k1F (t) 3)(2)对式3)进行拉氏变换可得-258 •迪一4 --------------------- ------------ 2—4)F (s) m1m2s [(k1 k2)m1 k1m2 ]s k1k2-259 •(3)对式(1)进行拉氏变换可得Z(s)k i、Y(s) F(s) m1s2k15)同样处理式2)有Y(s) k12Z(s) m s k k6)k1 *图9-2 系统结构图x1z x1 x2 zx3 y x3 x4 y由式1)X2 z k1 X11X3 F(t) m1m1m1 k t k? &x3x-i因此有k1 x m1k2m210 k1 010 mh1 x m1 F(t)n 00 0 0m2由式5)，式6)可以画出系统结构图，如图9-2所示。

(4)设状态变量由式2) x4yy 0 0 1 Ox-260 •-261 •例9-2 在图9-3所示系统中，若选取x i , x 2 , X 3作为状态变量，试列写其状态空间 表达式，并写成矩阵形式•图9-3解：由结构图可得2 u X 1) (s 3) x 22(X 2X 3) s(s 1)X 1X 3SX jy X 1整理可得系统状态空间方程表达式X 1 X 3X 22为 3x 2 2uX 32X 2 3X 3y X 1写成矩阵的形式0 1 0x 2 3 0 x 2 u23例9-3 设系统微分方程为y 7 y 14y 8y u 8u 15u系统初始条件为零，试：（1） 采用传递函数直接分解法，建立系统的状态空间表达式，并画出状态图; （2） 采用传递函数并联分解法，建立系统的状态空间表达式，并画出状态图。

第2章 “控制系统的状态空间描述”习题解答2.5 系统的结构如图P2.5所示。

以图中所标记的1x 、2x 、3x 作为状态变量，推导其状态空间表达式。

其中，u 、y 分别为系统的输入、输出，1α、2α、3α均为标量。

3x 2x 图P2.5系统结构图解 图P2.5给出了由积分器、放大器及加法器所描述的系统结构图，且图中每个积分器的输出即为状态变量，这种图形称为系统状态变量图。

状态变量图即描述了系统状态变量之间的关系，又说明了状态变量的物理意义。

由状态变量图可直接求得系统的状态空间表达式。

着眼于求和点①、②、③，则有①：2111x x x +=α& ②： 3222x x x +=α&③：u x x +=333α&输出y 为1y x du =+，得11122233310001001x a x x a x u x a x ⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦&&& []123100x y x du x ⎡⎤⎢⎥=+⎢⎥⎢⎥⎣⎦2.8 已知系统的微分方程 (1) u y y y y 354=+++&&&&&&；(2) u u y y -=+&&&&&&32； (3) u u y y y y 75532+=+++&&&&&&&&&。

试列写出它们的状态空间表达式。

(1) 解 选择状态变量1y x =，2yx =&，3y x =&&，则有：122331231543x x x x x x x x u y x =⎧⎪=⎪⎨=---+⎪⎪=⎩&&& 状态空间表达式为：[]112233123010000105413100x x x x u x x x y x x ⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦⎣⎦⎣⎦⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦&&&(2) 解 采用拉氏变换法求取状态空间表达式。

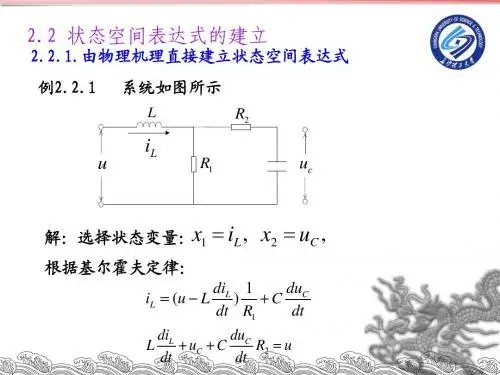
人工智能导论状态空间表示open表close表例题人工智能导论：状态空间表示与open表、close表在人工智能领域，状态空间表示是一种描述问题的形式化模型，它以状态为基本单位，通过状态之间的转移关系来描述问题的结构及其解空间。

而open表和close表则是在搜索问题解空间时常用的数据结构，用于记录搜索过程中的状态和路径信息，以便进行有效的搜索和剪枝。

本文将介绍状态空间表示的基本概念，以及open表和close 表的作用和例题应用。

一、状态空间表示1. 什么是状态空间表示？状态空间是指问题的所有可能状态的集合，而状态空间表示则是将问题中的状态、动作和转移关系用数学形式表示出来，以便进行问题分析、求解和模拟。

状态空间表示有助于我们更好地理解问题的结构、约束和解空间，从而选择合适的搜索策略和算法进行求解。

2. 怎样表示状态空间？状态空间表示通常使用图或者矩阵等形式进行表达，其中节点代表问题的状态，边或者转移函数表示状态之间的转移关系。

在八数码问题中，每个状态都可以用一个3x3的矩阵表示出来，矩阵中的数字代表每个位置的数码，而移动操作则对应着矩阵中数码的交换操作。

3. 状态空间表示的意义和价值状态空间表示可以帮助我们更好地理解问题的结构和特性，有助于问题分析和算法设计。

通过状态空间表示，我们可以清晰地描述问题的起始状态、目标状态和状态转移规则，为搜索和规划提供了明确的方向和约束。

二、open表和close表1. open表和close表的作用在搜索问题的解空间时，我们通常需要记录已访问的状态以及其相关信息，以便进行有效的搜索和避免重复访问。

这就引出了open表和close表这两种数据结构，它们分别用于记录待访问状态和已访问状态，以保证搜索的完整性和高效性。

2. open表和close表的结构和操作open表通常采用队列、堆栈或者优先队列等数据结构来实现，用于存储待访问状态及其相关信息，并根据搜索策略进行状态的出队和入队操作。

计算和证明题.1 已知机械系统如图9-7所示，21,m m 为质量块，1m 受外力)(t F 作用。

弹簧的弹性系数如图示，如不计摩擦，自选一定数目的状态变量，建立系统的状态空间描述。

提示：设中间变量质量块1m 的位移为z ，根据牛顿定律有zm y z k t F 11)()(=-- ① 同理对质量块2m 有ym y k y z k 221)(=-- ② 设状态变量z x =1 12x zx == y x =3 34x y x == 由式① 13111112)(m t F x m k x m k z x++-== 由式② 32211214x m k k x m k y x+-== 因此有)(001000100000001143212212111114321t F m x x xx m k k m k m k m k x x x x ⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡+--=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡ []⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=43210100x x x x y .2 已知系统结构图如图9-8所示。

试写出系统的状态方程和输出方程（要求写成矢量形式）。

提示：[]xy u x x 01101212=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--= .3 已知系统的微分方程，试建立其相应的状态空间描述，并画出相应的状态结构图。

（1）u u u y y y y 86375++=+++（2）u u u y y y y 23375++=+++提示：（1）[]x u x x 168100573100010=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=y ，状态结构图略 （2）[]ux u x x +---=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=54110057310001y ，状态结构图略。

.4判断下列矩阵是否满足状态转移矩阵的条件，如果满足，试求与之对应的A 阵。

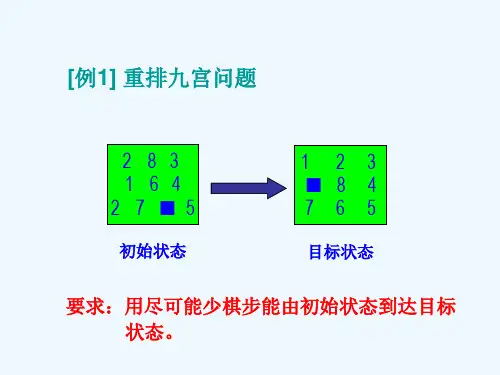
第一章 系统的状态空间模型习题1一网络系统如图所示，设Uc 和L I 为状态变量。

试求系统的状态方程。

习题2已知系统的状态空间表达式为：⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡21321.3.2.1101110200040014u u x x x x x x⎥⎦⎤⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡=21321300001Y Y x x x Y 试绘出系统的状态空间图。

习题3如图系统的状态结构图，x1,x2,x3为状态变量，u, y 为输入输出。

第二章 状态方程的解习题1已知系统的A 阵为：① ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡032100010 ② ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡072100030 试求At e 。

习题2F= ⎥⎦⎤⎢⎣⎡--5610 G=⎥⎦⎤⎢⎣⎡11 试求系统当u （k ）=3的解。

第三章 能控性和能观性习题1能控且能观的两个系统1S ，2S ： 1S ：11111.u b x A x +=， 111x c y = 其中，⎥⎦⎤⎢⎣⎡--=43101A ，⎥⎦⎤⎢⎣⎡=101b ，[]121=c ，2S ：22222.u b x A x +=，222x c y = 12-=A ，12=b ，12=c① 试求对于⎥⎦⎤⎢⎣⎡=21x x x 的状态方程。

② 考察图中系统得能控性及能观性。

③ 求关于1S ，2S 这两个子系统得传递函数，并验证②。

习题2直流电动机系统如下：RL ① 以w 为输出时的状态能控性及输出能观性；② 以转角θ为输出时系统的能观性。

第四章 动态系统的确定性分析习题1⎪⎩⎪⎨⎧--==2.31.22.1x x x x x 试确定e x 的稳定性。

习题2⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-=⎥⎥⎦⎤⎢⎢⎣⎡21.2.1211x x K x x试用李雅普诺夫理论求系统稳定时K 的取值范围 第五章 极点配置与观测器设计习题1试为下面系统设计一个全阶观测器，使闭环极点配置在-4和-5上。