第2章 船舶静置在波浪中的剪力和弯矩计算

第一章 总纵强度计算外力的确定§1.1船舶在静水中的剪力和弯矩一、概述1. 计算模型：自由-自由梁承受垂向载荷（两端处的N M ==0）[图示坐标系、载荷曲线以及微元体受力平衡]2. 静水载荷：q x w x b x ()()()=−单位长度垂向力重力浮力q x w x b x ()()()=−3. 静水剪力和弯矩（符号惯例同“结构力学”）由平衡状态下 w x b x ()()⎧⎨⎩⎫⎬⎭⇒q x ()⎯⎯⎯⎯⎯⎯⎯→N x M x ()()⎧⎨⎩⎫⎬⎭⎯边界条件微元体平衡ξ，可以采用以下2种方法之一计算（设x 轴原点取在船艉）： (1)积分法N x q x dxM x N x dx q x dx x q d x x x x x()()()()()()()====−⎧⎨⎪⎩⎪∫∫∫∫∫002000ξξ 说明：①当载荷分段解析时，相应的积分也需要分段进行；②式中的积分亦可由相应曲线下的面积表示。

(2)截面法取艉端至指定截面的一段船体为“隔离体”，根据平衡条件确定截面的剪力和弯矩。

二、重量曲线1. 船体重量组成——全船性重量、局部性重量（参阅书图1-3）2. 绘制重量曲线w x ()的方法和应遵循的原则 (1)绘制方法——先分后合[分：将船体重量划分为全船性重量与若干项局部性重量，分别处理；合：在同一站距内合并各项重量](2)原则静力等效（重量及重心纵向位置保持不变）分布范围大体一致⎧⎨⎩3. 举例（静力等效原则可以提供2个方程式） 例1：全船性重量（参阅书图1-5）[3个待定参数abc；静力等效原则可以提供2个方程式（应用负面积法）；根据统计资料直接给出b]例2：局部性重量（参阅书图1-6）[静力等效2条件→，P q L 11=ΔP q L 22=Δ]三、浮力曲线1. 对问题的分析（图示）⎯⎯⎯⎯⎯⎯←⎯⎯⎯⎯⎯←=)()()()()(图平衡水线图邦戎曲线：：剖面吃水船体单位长度浮力WL x d x x b γω⎭⎬⎫⎩⎨⎧⎯⎯⎯⎯⎯⎯⎯⎯←型值表）邦戎曲线（或型线图或），全船重量及重心位置（（浮态）船体在静水中平衡位置重力与浮力平衡条件g x W 2. 确定平衡水线的原理和方法(1)原理：全船重力与浮力相平衡（2个平衡方程）求解关于首、尾吃水和的（非线性）联立方程：d f d a f d d f d d f a f a1100(,)(,)==⎧⎨⎪⎩⎪ (2)逐步近似法（调整“倾差”）——求解上述联立方程的数值方法之一 ①等容倾斜原理：船体绕漂心F(水线面之形心)旋转任意角ψ（ψψ≈≈−tan x x Rg bm a ），其排水体积保持不变。

船舶剪力弯矩计算
船舶剪力和弯矩是船体结构力学计算中的重要参数，用于评估船舶在不同工况下的结构强度。

下面是船舶剪力和弯矩的计算方法：
1. 载荷计算：首先需要确定船舶的运载条件，包括船舶吃水线、载货量、货物分布、燃油和水污染物负荷等。

根据这些信息，可以计算出载荷的大小和分布情况。

2. 应力分析：根据船舶的结构形式和载荷情况，可以采用材料力学的原理计算出船舶结构的应力分布情况。

剪力和弯矩是应力的两个重要参数，决定了船舶结构的强度。

3. 剪力计算：剪力是指作用于一物体两个相邻截面上的力之间的内力。

船舶的剪力主要是由船舶在水中的浮力和引起船身产生剪切力的水流压力引起的。

剪力的计算可以通过应力平衡方程来进行计算。

4. 弯矩计算：弯矩是指作用于物体上的力矩。

船舶的弯矩主要是由载荷引起的。

弯矩的计算可以通过将整个船体划分为若干截面，然后根据力和力矩的平衡条件来进行计算。

总结起来，船舶剪力和弯矩的计算是基于船舶结构的应力分析和力的平衡条件进行的。

通过计算剪力和弯矩，可以评估船舶结构的强度，从而确保船舶在不同工况下的安全运行。

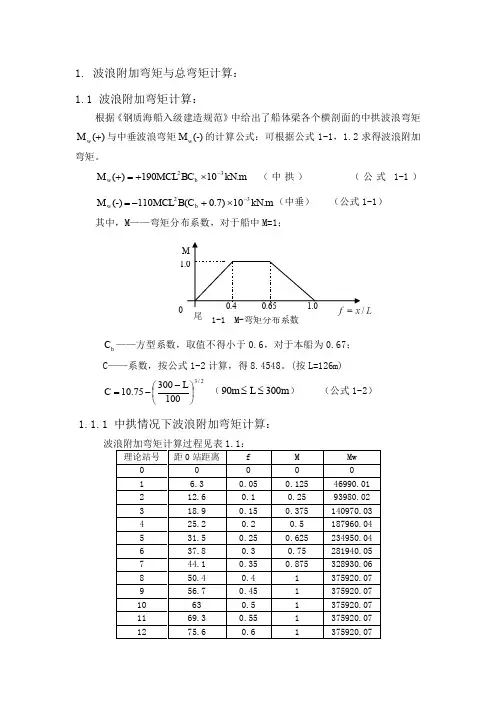
1. 波浪附加弯矩与总弯矩计算： 1.1 波浪附加弯矩计算：根据《钢质海船入级建造规范》中给出了船体梁各个横剖面的中拱波浪弯矩)(+w M 与中垂波浪弯矩)-(w M 的计算公式：可根据公式1-1，1.2求得波浪附加弯矩。

m kN BC CL M b w .10M 190)(32-⨯+=+ （中拱） （公式1-1）m kN C B CL M b w .10)7.0(M 110)-(32-⨯+-=（中垂） （公式1-1）其中，M ——弯矩分布系数，对于船中M=1；图1-1 M-弯矩分布系数 b C ——方型系数，取值不得小于0.6，对于本船为0.67；C ——系数，按公式1-2计算，得8.4548。

(按L=126m) 2/310030075.10⎪⎭⎫ ⎝⎛--=L C （m L m 30090≤≤） （公式1-2）1.1.1 中拱情况下波浪附加弯矩计算：1.0M1.00.65 0.4尾1.1.2 中拱情况下总弯矩计算：根据条件，可以近似将船体的静水弯矩当作是波浪附加弯矩的1/3，所以，可以得出总弯矩是波浪附加弯矩的4/3倍。

1.1.3中垂情况下波浪弯矩的计算1.1.4中垂情况下总弯矩计算2. 总弯曲应力计算与稳定性校核根据中横剖面图，计算剖面抗弯几何特性，见下页表1.5。

参考轴取船底板上表面，可求得：A=9390.3cm 2、B=4536030.6cm 3、C=3837423286cm 4。

参考轴距中和轴距离⊿=B/A=483.0549226cm,I=2(C-⊿2 A)= 3292542712cm 4任意构件距中和轴距离Z i ’=Zi-⊿由此求得中横剖面各构件剖面模数W i =I/ Z i ’表1.52.1 计算总弯曲应力：总弯曲应力按下式计算： cws W M M +=σ由表6.1得最小剖面模数Wc 为5469839.086cm 3,因此在中拱情况下最大总弯曲应力为91.63N/mm 2 ，在中垂情况下最大总弯曲应力为108.48N/mm 2，远小于许用应力。

船舶静止在波浪上的外力计算一、整体计算过程（计算思路）两个假设：1、假设船舶以波速在波浪的前进方向上航行，即船与波的相对速度为零；2、假设船体是在重力和浮力作用下静平衡于波浪上的一根梁。

计算思路：1、船舶外力计算的目的是进行强度校核，应保证：[]max σσ≤其中，max σ为船体断面最大正应力，[]σ为许用应力。

2、应力计算根据梁的弯曲理论由下式给出：M Z Iσ=⋅ 其中，M 为计算断面的弯矩；I 为横断面绕水平中和轴的惯性矩；Z 为计算应力点到中和轴的距离。

3、船体梁在载荷作用下纵纵弯曲产生的弯矩有两部分构成：静水力弯矩和波浪附加弯矩：s M M M ω=+整体计算步骤：1、计算不同装载状态下静水弯矩和波浪附加弯矩以及静水剪力和波浪附加剪力；2、计算总纵弯矩；3、计算船体断面的最大正应力；4、根据许用应力进行强度校核。

波浪要素和装载状态：1、计算波浪附加弯矩时，标准波浪的波形取为坦谷波；2、应考虑四种装载状况：满载出港、到港，压载出港、到港二、各部分计算过程详解1、静水弯矩计算两个必要条件：1）船体浮力等于重力；2）重心和浮心在同一铅垂线 静水弯矩计算核心公式：()()()()()()()00x x q x x b x N x q x dx M x N x dx ω=-⎧=⎪⎨⎪=⎩⎰⎰ 静水力弯矩计算步骤：1) 绘制重量曲线；2) 绘制浮力曲线；3) 求出重量曲线和浮力曲线的差值()q x ，作为船体梁的载荷强度；4) 根据上面的公式计算静水弯矩。

重量曲线绘制方法：绘制重量曲线时，必须根据静力等效原则合理分布，满足以下四个要点：重量不变，重心不变，范围一致，均匀分布围长法：核心是假设船体结构单位长度重量与剖面围长成比例；抛物线法：核心是假定船体与舾装品总重量构成的重量曲线可以用抛物线和矩形之和来表示；梯形法：将船体重量近似地用梯形曲线表示；局部性重量：根据静力等效原则进行合理分布。

浮力曲线绘制方法：浮力曲线由邦戎曲线得出，由于船舶并非处于平浮状态，所以必须进行纵倾调整，调整方法为解析法和逐步近似法，其中逐步近似法计算过程： ● 按给出的平均吃水m d ，浮心纵向坐标b x ，水线面漂心f x 以及纵稳心半径R ，计算首尾吃水：22g b f m f g b a m f x x L d d x R x x L d d x R -⎫⎛⎫=+- ⎪⎪⎝⎭⎪⎬-⎛⎫⎪=-+ ⎪⎪⎝⎭⎭● 确定首尾吃水后，利用邦戎曲线求出对应吃水线时的浮力曲线，可计算出排水体积1V 和浮心纵向坐标1b x 的第一次近似值；● 将求的的两个数值与给定的排水体积0V 及重心纵向坐标g x 比较，相差较大时，必须作第二次近似计算，由下式确定新的首尾吃水：'01'0122g b fm f g b a m f x x V V L d d x A R x x V V L d d x A R -⎫-⎛⎫=++- ⎪⎪⎝⎭⎪⎬--⎛⎫⎪=+-+ ⎪⎪⎝⎭⎭ 校核误差在下式范围内时，即可停止近似计算，由邦戎曲线得出最终的浮力曲线：0.05%~0.01%g bx x L -≤在得出重量曲线和浮力曲线后，由重量曲线和浮力曲线之差得出载荷曲线，应满足以下性质：()()()()()()0000000L L L L L Lg b q x dx x dx b x dx W B xq x dx x x dx xb x dx W x B x ωω=-=-==-=⋅-⋅=⎰⎰⎰⎰⎰⎰2、波浪附加弯矩计算船舶在波浪中的浮力曲线()b x ω是由静水中的浮力曲线()s b x 与波浪中由吃水变化引起的浮力变化量()b x ∆之和构成：()()()s b x b x b x ω=+∆船舶在波浪中的浮力变化量必须满足下列两式：()()0000LL b x dx x b x dx ⎫∆=⎪⎬⎪⋅∆=⎭⎰⎰ 船舶在波浪中的附加弯矩可以得出： ()()()()()0000xx x x N x b x dxM x N x dx b x dxdx ωωω⎫=-∆⎪⎬⎪==-∆⎭⎰⎰⎰⎰ 由于坦谷波波形因素，船舶在波浪中要有一定的下沉或上升，距尾垂线x 下沉量由下式给出： 0x x ζζψ=+⋅利用麦卡尔法，基于船侧直壁假设，可以得出：Bi Ai Ci Ai i Ai i ωωωωωωζε-=+∆=+⋅ ()0Bi Ai Ci Ai i x ωωωωζψε-=+⋅+ 根据以上条件，即可以得出波浪中附加弯矩的计算式：()()()()000xx x N x x dxM x x dxdx ωωγωγω⎫=-∆⎪⎬⎪=-∆⎭⎰⎰⎰ 3、总纵弯矩计算及强度校核将静水弯矩和波浪附加弯矩之和记作总纵弯矩，再由应力校核公式进行强度校核： s M M M ω=+[]max σσ≤。

第一章总纵强度计算外力的确定§1.1船舶在静水中的剪力和弯矩§1.2船舶静置于波浪中的剪力和弯矩§1.3船体波浪剪力和弯矩的数值计算§1.1船舶在静水中的剪力和弯矩一、概述二、重量曲线三、浮力曲线四、剪力弯矩的计算返回一、概述1. 计算模型：认为船舶是在重力和浮力作用下平衡于波浪上的一根梁q(x)=w(x)-b(x)q(x)单位长度垂向力；w(x)重力；b(x)浮力静水载荷、重力向下为正，浮力向上为正3、静水剪力和弯矩(1)剪力和弯矩符号，以下为一个船体梁断面建议大家复习一下微元体，由于选取的方式不同，将导致同一处的剪力或弯矩的大小相同，符号不同。

一般取左端面为准计算出剪力弯矩。

(2)积分法计算，设x 轴原点取在船艉⎪⎩⎪⎨⎧===∫∫∫∫dx dx x q dx x N x M q(x)dx x N x x00)()()()(计算思路：在平衡状态下，由w(x),b(x)得到q(x ）,通过微元体平衡，边界条件，得到N （x ）,M(x).返回二、重量曲线1. 船体重量组成—全船性重量、局部性重量一个重量分布曲线图2. 绘制重量曲线的方法——先分后合分：将船体重量划分为全船性重量与若干项局部性重量，分别处理；合：在同一站距内合并各项重量原则：a:静力等效—不改变重力大小及其对船肿的力矩大小。

b:分布范围大体一致全船性重量的分配方法1、围长法假设船体结构单位长度重量和剖面围长成比例。

A xlW xw h) () (⋅=船主体结构重量的总和，tfX剖面处围长，m船体全表面积2、抛物线法假定船体和舾装品构成的曲线可用抛物线和矩形之和表示。

总重量的一半作为均匀分布，另一半按抛物线分布。

用于无平行中体船。

3、梯形法重量分布用梯形曲线表示。

用于中间肥，两头尖瘦且中部有平行中体的船。

局部性重量的分布方法1、分布在两个理论站距内的重力⎩⎨⎧⋅=Δ⋅−+=aP L P P P P P 2/)(2121静力等效方程2、分布在三个理论站距内的重力先近似确定其中一个站距内的重力，然后可以比较简单地利用静力等效原则直接列出两个方程，从而求得不同理论站距内的分布载荷强度第一步：以1.5ΔL代替ΔL，使用静力等效方程求得P1、P2；第二步：将P1、P2分别向其相邻的两个理论站距内分布；最后，对中间理论站距迭加来自P1、P2的相应分布值。

7800DWT多用途船船舶结构设计计算书计算工况：选取空载（压载）到港状态进行计算且该工况在静水中处于中拱状态。

一、设计资料7800DWT多用途船1．主要数据： 2、满载到港状态下的有关参数：计算船长：L = 126.00m总重量：W = 5491.7t海水密度：ρ = 1.025t/m3浮心纵向坐标：x b = 1.680m重心纵向坐标：x g = 0.839m船宽： B = 22.00m水线面面积： A = 1520.068m2平均吃水: d m = 3.782m重力加速度：g = 9.80m/s2 纵稳心半径: R = 210.2m漂心纵向坐标: x f = 1.788m122．波型与波浪要素波型：坦谷波 波长：λ=L=108m 波高：h=5.0m 半波高：r=h/2=2.5m 坦谷波垂向坐标值采用余弦级数展开式：))4cos(1()2cos(2x r x r yλπλπλπ-+=各理论站从坦谷波面到波轴线垂向坐标值b y ，按上式计算得出下表：二、 剪力与弯矩计算 1、 绘制邦戎曲线(1）根据型线图中的横剖面图量取各站横剖面轮廓线与各水线相交面的面积，如下表所示：34（2）把量取的各值在邦戎曲线中根据站线和水线按比例1：20000取点画图，连接各点得邦戎曲线。

(下图Y 轴比例为7：1 ；X 轴比例为1:1)2、船舶在静水中的平衡位置计算(1)船舶在静水中艏吃水df和艉吃水da在邦戎曲线图上作出该水线，量取各理论站横剖面浸水面积，利用梯形积5分计算该船在该水线下的浮力B与浮心纵向坐标Xb；67(2)第一次近似计算： 首吃水:RX XX L d db gf m f --+=)2(1=m 573.32.210680.1839.0)788.12108(782.3=-⨯-+尾吃水:RX XX L d d b gf m a -+-=)2(1=m 005.42.210680.1839.0)788.12108(782.3=-⨯+-浮 力：B1=ρ*g*△L*∑（3）= 53459.35KN浮力纵向坐标：Xb1=△L*∑（4）/∑（3）= 0.571 精度检查：%5.08.9*7.549135.534598.9*7.54911>-=-WB W%1.0108571.0839.01>-=-LXb Xg不满足精度要求，所以，需要进行第二次近似计算。

《船舶强度与结构设计》课程设计题目：1500m3耙吸式挖泥船总强度计算书学院专业年级姓名学号目录第一章计算说明 (1)1.1 计算内容 (1)1.2 主要技术参数 (1)第二章剪力和弯矩计算 (1)2.1 重力分布和浮力分布计算 (1)2.2 静水剪力和弯矩计算 (3)2.3 波浪附加剪力弯矩计算及剪力弯矩合成 (7)第三章总纵弯曲应力计算 (11)3.1 剖面参数 (11)3.2 总纵弯曲应力计算 (13)第四章临界应力计算和构件稳定性校核 (14)4.1 纵骨架式甲板临界应力计算及校核 (14)4.2 甲板纵桁临界应力计算及校核 (15)4.3 纵骨临界应力计算及校核 (15)第五章极限弯矩计算 (16)5.1 极限弯矩下各构件应力计算 (16)5.2 极限弯矩计算 (17)第六章计算结果分析及结论 (18)第一章 计算说明本计算书是1500m 3耙吸式挖泥船总强度计算书，计算出了中拱状态下的船体的静水剪力、弯矩，波浪附加剪力、附加弯矩，合成剪力、合成弯矩，并计算了总弯曲应力，以及校核了是否满足设计要求。

1.1计算内容(1) 静水弯矩、剪力 (2) 波浪附加弯矩、附加剪力 (3) 剪力、弯矩合成(4) 计算总弯曲应力、受压构件的稳定性校核 (5) 计算结果分析及结论 (6) 计算状态：中拱1.2主要技术参数船长：78米；满载排水量：5020吨；平均吃水：5.4米；站距：9.3=∆L 米，波高：4米；重心在舯前：813.0=g x 米;艏吃水:77.5=f T 米;尾吃水:23.5=a T 米。

主尺度：船长：78米，船宽：14.5米，型深：6.3米，设计吃水5.1米，肋距：0.6米，强框架间距：1.8米，纵骨跨度1.8米。

海水密度ρ=1025 kg/m 3，重力加速度g=9.81m/s 2，船体钢材屈服强度σy=235N/mm 2第二章 剪力和弯矩计算2.1重力分布和浮力分布计算静水剪力弯矩计算资料：表2：静水平衡状态各站横剖面浸水面积（m2）根据表1的数据将重量单位t转换为KN，绘制站间重量分布曲线p(x)：图1：重量分布曲线依据表2计算静水浮力，取相邻两站号横剖面浸水面积的平均值作为此站距间的浸水面积A，根据理论站间浮力公式F=ρgΔLA计算出各站间的静水浮力，计算过程如表3所示：表3：静水浮力计算图2：静水浮力分布曲线2.2静水剪力和弯矩计算载荷分布曲线q(x)=p(x)−b(x)，各站间重量减去浮力得载荷值，由此绘制载荷分布曲线：图3：载荷分布曲线静水剪力是载荷分布的一次积分，即N(x)=∫q(x)dxx静水弯矩是剪力的一次积分，载荷的二次积分，即M(x)=∫N(x)dxx0=∫∫q(x)dxdxxx利用表格进行剪力和弯矩的计算，第20站剪力不为0且N(20)N max=2.92%，需要进行剪力修正：ΔN i=i20N20 N i’=N i+ΔN i使船艏艉的剪力为0，同样第20站弯矩也不为0，M(20)M max=3.07%，再次进行弯矩修正：ΔM i=i20M20 M i’=M i+ΔM i计算过程如表4所示：表4：静水剪力和弯矩计算56由上表修正后的数据，绘制站间静水剪力和弯矩图：图4：静水剪力分布曲线图5：静水弯矩分布曲线2.3波浪附加剪力弯矩计算及剪力弯矩合成波浪附加剪力弯矩计算资料：2波浪附加浮力按如下公式计算：Δb(x)=b w (x)−b s (x)其中b w (x)为波浪中平衡时的浮力曲线，b s (x)为静水中平衡时的浮力曲线 波浪附加剪力是附加浮力负数的一次积分：N w (x)=∫[b s (x)−b w (x)]dx x=∫[−Δb(x)]dx x浮力与浸水体积成正比，因此站号上静水浮力与波浪中浮力之差可以用浸水面积之差来表示：N w (x)=γ∫[F s (x)−F c (x)]dx x=γ∫ΔF i (x)dx x其中F si (x)是静水中浸水面积分布曲线，F ci (x)是波面下浸水面积分布曲线 波浪附加弯矩是附加剪力的一次积分，附加浮力的二次积分：M w (x)=∫N w (x)dx x 0=∫∫[−Δb(x)]dxdx x 0x 0同样也可以用浸水面积曲线来表示M w (x)=γ∫∫ΔF i (x)dxdx x 0x 0下面列表计算，在计算过程中，发现波浪附加剪力和附加弯矩同样在船艏处不闭合，N w(20)N wmax=1.59%，M w(20)M wmax=6.59%，采用相同的方法进行线性修正，以确保船艏艉剪力和弯矩都为0。

船舶与海洋工程结构物强度知到章节测试答案智慧树2023年最新哈尔滨工程大学第一章测试1.不同类型的海洋平台的载荷工况都一样（）参考答案:错2.军船和民船的装载工况是相同的。

（）参考答案:错3.海洋平台结构的破坏模式主要是屈服破坏和疲劳破坏。

（）参考答案:错4.强度分析主要包括外载荷计算、内力分析、强度校核标准。

（）参考答案:对5.长方形梁截面的惯性矩与（）无关。

参考答案:粱的长度6.以下为全船性的外力的是（）。

参考答案:波浪压力;船体结构重量7.载荷随时间的变化性质分类有（）。

参考答案:不变载荷;动变载荷;静变载荷;冲击载荷8.虽然海洋平台的结构形式较多，但其总强度的模型主要有（）。

参考答案:三维空间梁模型;三维空间模型9.海洋平台受到的间接自然环境载荷包括以下（）参考答案:惯性力;系泊力10.造成海损事故的原因主要有（）。

参考答案:恶劣海况;意外事故;人为因素;强度不足第二章测试1.静置在波浪上的船体载荷曲线有两条性质，分别是：沿着船长分布的整个载荷曲线与轴线之间所包含的面积之和为0；上述面积对轴上任意一点的静力矩之和为零。

（）参考答案:对2.波长远大于船长或者远小于船长的情况下，浮力的分布与在静水中的浮力分布相差很小（）。

参考答案:对3.船体结构的响应分析是指（）。

参考答案:确定结构剖面中的应力或变形4.静置法中，船与波的相对速度为（）。

参考答案:=05.船舶静置在波浪上的总纵弯矩等于船舶在静水中的弯矩和船舶静置在波浪上的波浪附加弯矩之（）。

参考答案:和6.船舶在中垂状态下，（）在船中，此时船中浮力较（）。

参考答案:波谷；小7.进行平衡水线调整时，需要满足以下（）条件。

参考答案:船体的排水体积不变;重力和浮力相等;重力和浮力的力矩相等8.绘制船体重量曲线时，需要遵循以下（）原则。

参考答案:重量的重心位置不变;重量的分布范围大体一致;重量的大小不变9.船舶静置在波浪上的波浪附加弯矩，其值的大小与下列（）因素有关。

船舶静水剪力和弯矩的计算及分析船舶静水剪力和弯矩是船舶稳定性分析的关键性要素，它们可以帮助船舶企业或设计者了解船舶的屈服状态及其结构性能。

此外，这些计算结果还可以帮助船舶设计者实现最优设计。

船舶静水剪力计算可以采用水动力过程，帮助船舶分析师对船舶行驶过程中受力状况进行分析，绘制拖拉力曲线，并计算船舶设计师所需要的力矩和力矩。

船舶弯矩计算可以帮助船舶分析师准确地模拟船舶碰撞、拖曳斜堤以及转向的情况，以及在船舶行驶过程中的耗能。

船舶静水剪力和弯矩的计算包括三个主要步骤： firstly, 进行船舶航行路线的分析，确定船舶在路线不同时间点的航行参数，并计算相应的拖拉力、弯矩和功率； secondly, 计算改变船舶航行路线和参数时的拖拉力、弯矩和功率； three, 绘制最后的静水剪力和弯矩图表，并对计算结果分析。

此外，船舶静水剪力和弯矩的计算还与船舶结构特性有关，不同船舶的结构特性可能会影响到计算的结果。

因此，在计算过程中，应该考虑到不同结构特性会对静水剪力和弯矩造成的影响，从而提高计算精度。

综上所述，船舶静水剪力和弯矩的计算和分析，对于船舶制造业具有重要的意义，它能够帮助船舶设计者准确地测试船舶在不同航行参数下的动力性能，并且能够有效地提高船舶制造设计的精度。

同时，为
了确保结果的准确性，必须注意不同的船舶结构特性对计算结果的影响。