第六讲不重复的路——一笔画问题

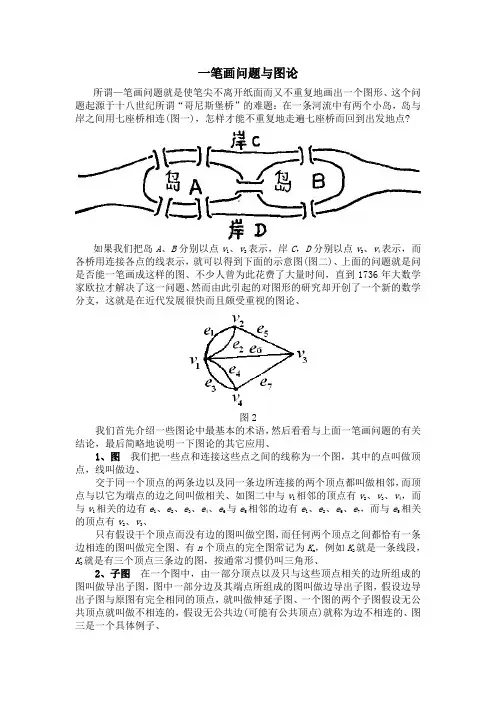
一笔画问题与图论所谓—笔画问题就是使笔尖不离开纸面而又不重复地画出一个图形、这个问题起源于十八世纪所谓“哥尼斯堡桥”的难题：在一条河流中有两个小岛，岛与岸之间用七座桥相连(图一)，怎样才能不重复地走遍七座桥而回到出发地点?如果我们把岛A、B分别以点v l、v2表示，岸C，D分别以点v3、v4表示，而各桥用连接各点的线表示，就可以得到下面的示意图(图二)、上面的问题就是问是否能一笔画成这样的图、不少人曾为此花费了大量时间，直到1736年大数学家欧拉才解决了这一问题、然而由此引起的对图形的研究却开创了一个新的数学分支，这就是在近代发展很快而且颇受重视的图论、图2我们首先介绍一些图论中最基本的术语，然后看看与上面一笔画问题的有关结论，最后简略地说明一下图论的其它应用、1、图我们把一些点和连接这些点之间的线称为一个图，其中的点叫做顶点，线叫做边、交于同一个顶点的两条边以及同一条边所连接的两个顶点都叫做相邻，而顶点与以它为端点的边之间叫做相关、如图二中与v l相邻的顶点有v2、v3、v4，而与v l相关的边有e l、e2、e3、e4、e6与e5相邻的边有e l、e2、e6、e7，而与e5相关的顶点有v2、v3、只有假设干个顶点而没有边的图叫做空图，而任何两个顶点之间都恰有一条边相连的图叫做完全图、有n个顶点的完全图常记为K n，例如K2就是一条线段，K就是有三个顶点三条边的图，按通常习惯仍叫三角形、32、子图在一个图中，由一部分顶点以及只与这些顶点相关的边所组成的图叫做导出子图，图中一部分边及其端点所组成的图叫做边导出子图，假设边导出子图与原图有完全相同的顶点，就叫做伸延子图、一个图的两个子图假设无公共顶点就叫做不相连的，假设无公共边(可能有公共顶点)就称为边不相连的、图三是一个具体例子、子图是一个相对的概念，假设H是G的子图，那么G可称为H的上图、通过子图来研究较复杂的图是图论中一个基本方法、3、顶点的度在一个图中与任一顶点v有关的边的数目，叫做这个顶点的度，记作d(v)，如图三中的G，d(v l)=2，d(v2)=5，d(v3)=4，d(v4)=2，d(v5)=3、这样一来，我们就看到在计算各个顶点的度时，实际上就是计算了边的数目，但每一条边在它的两个顶点处各计算一次，从而我们可以得到：定理一任一个图中各顶点的度数之总和等于其边数的二倍、由此事实，我们知道图中顶点度数之和为偶数，从而奇数度顶点的个数必为偶数、4、连通性在一个图中，我们从任一顶点v0出发，经过与之相关的一条边el到达另一个顶点v l，再经过与v l相关的一条边e2到达v2，……，如此继续下去，便得到一个顶点和边交替出现的序列v0e l v l e2v2……e k v k、当其中所经过的边彼此皆不相同时，我们就叫做一条迹，这时其中诸顶点有可能相同，假设连顶点也都彼此不同，这种迹就叫做路，起点与终点闭合的路又叫做圈、这些都是一些特殊的边导出子图，如图三中的G，假设取v l av2cv3dv2f v5gv3就是—条迹，而v l av2f v5gv3就是—条路，假设取v l av2f v5gv3bv l就得到一个圈、一条迹可以删去一段而成为路、图3一个图中的任意两点都存在一条连接这两点的路，那么称这个图是连通的、对于一个不连通的图，我们可以把它分成假设干个连通的分支、有了这些概念以后，我们就来看看上面的一笔画问题、为了表达方便起见，我们把包含图中所有的边的迹叫做欧拉迹，首尾闭合的欧拉迹叫做欧拉途、如果一个图含有一个欧拉途就说明从任一顶点山发，可以经过每一条边恰好一次并且回到出发点，换言之，它可以一笔画成、这种含有欧拉途的图就叫做欧拉图、不难证明下面两个定理：定理二 一个连通图是欧拉图的充分必要条件是它不含奇数度顶点、定理三 一个连通图含有欧拉迹的充分必要条件是最多有两个奇数度顶点、 由这两个定理可知，一个图可以一笔画成的充分必要条件是，或者不含奇数度顶，或者恰含有两个奇数度顶点、即使复杂的图，也不消一分钟就可以看出它是否能够一笔画成、在我们上面提到的七桥问题中，相应的图的四个顶点皆是奇数度的，所以无法—笔画成，即使不要求回到原出发点，也无法—笔画成、 一笔画问题只是图论中一个很小的侧面、事实上，我们在画出—个图的时候，可以赋予图中的顶点和边以各种不同的含义，从而也就可以用来研究五花八门的问题、下面举几个简单的例子、例— 在世界各国中，必能找到这样两个国家，它们与同样数目的国家有外交关系、我们用顶点表示国家，两国间有外交关系的就用边相连，这样一来就只须证明在任意—个这种图中必有两个顶点有相同的度数，事实上，设诸顶点以v l ，v 2，……v n 表示，假设各顶点的度数皆不相同，那么它们分别是0，1，2，…，(n -1)这n 个数、但这是不可能的，因为既然有0度的顶点就不可能再有n -1度的顶点，故必有两个顶点具有相同的度数、可见与之相应的两国与同样数目的国家有外交关系、例二 平面上有n 个点，其任意两点之间的距离不小于1，试证至多存在3n 对点，其距离恰是l 、以v l ，v 2，…，v n 表示平面上这n 个点，我们规定某两点v i 与v j 的距离恰是1时才用边相连，在如此所得到的图中，边的数日就是距离恰是1的顶点的对数、与任一顶点v 相邻的顶点必在以v 为圆心，1为半径的圆周上，但题设这些点之间的距离又不小于1，所以至多只能有六个顶点与v 相邻，换言之，对于任意1≤i ≤n 皆d 〔v i 〕≤6，于是，1()6ni i d v n =≤∑由定理一，左边就是图中边数的二倍，所以边数≤3n ，即至多有3n 对点距离恰是1、例三 在随意凑集的六个人中，一定能找列三个人，他们或者彼此认识，或者彼此不认识、这是一个Ramsey 问题，曾经是著名的难解问题之一，现在用图论方法很齐易解决、我们用六个点表示六个人，两个人认识就将扪应的两点用线连起来、于是这个问题就转化成下述形式：在任何一个六个顶点的图中，必有三个顶点存在，它们或者连成—个三角形，或者彼此不相邻、设v 是某一顶点，那么其余五个顶点中与v 相邻的顶点数和与v 不相邻的顶点数中必有一个是超过3的、不妨设u 1，u 2，u 3，是与v 相邻的，假设u l ，u 2，u 3中有某两点是相邻的，那么它们与v 将构成——个三角形，假设u 1，u 2，u 3中任意两点都不相邻，那么它们就是题中所要求的三点、下面我们再来看看图论中所研究的其它—些问题、邮路：利用欧拉途的概念可以解决所谓邮递路线问题、我们知道，邮递员总想从邮局出发以最短的路程走遍每一条街道，最后回到邮局，如果这位邮递员所负责的街道可以画成一个欧拉图，那么只须求出其欧拉途就一定是最理想的邮路了、而对于欧拉图要求出其中的欧拉途是不成问题的、但当街道画出一个非欧拉图时，情形就比较复杂了、这时须引入“重量”的概念而转化成求欧拉途的问题、当合理地规定图中的每一条边的重量以后，我们就得到一个所谓“赋重图”、这里的重量可以表示路程的长短，也可以表示运费的多少，也可以表示造价的高低，如此等等，于是有许多实际问题便可转化成求赋重图中的最轻通路问题、图论中已经建立了一些有效的方法、可靠性：要建立一个交通或通讯系统，就要设法使假设干个点之间皆有通路相连，并且还力求使总的造价是比较少的、这一类问题在图论中已通过对一种特殊的子图——“树”的研究得以解决、另一方面，如果在—种交通或通讯系统中任意两点之间都只有一条路相通，那么这种系统是很不可靠的，一旦有一处发生故障，就可能仗整个系统陷于瘫痪，于是图论中又进一步研究了连通的可靠性问题，这主要是将连通程度数量化、货郎担问题：我们把包含图中每一个顶点的路叫做哈密顿路，假设是闭的就叫做哈密顿圈，相应的图就叫做哈密顿图、与欧拉途不同的是哈密顿圈只要求走遍每一个顶点，并不要走遍每条边，著名的货郎担问题与此有关、这个问题是：寻找一条最短路线，使一个货郎不走回头路而走遍几个村镇，这是一个看起来简单却尚未得到解决的问题，没有一个有效方法可以用来判断一个图是否为哈密顿图、印刷电路：当我们设计一种印刷电路时，必须要求有关的电路图是一个平面图，由于我们在画出一个图的时候，其边的长短以及准确位置是无关紧要的，只是关心某条边是连接哪两个顶点而已、所以—个图是否为一个平面图并不是一眼就能看出来的、某些图乍看起来不是平面的，但可以重新画出使成平面图、这在图论中叫做平面嵌入，并且已经找到一些有效方法可以判断任意给出的图是否为平面图，以及如果是平面图怎样进行平面嵌入、四色问题：我们可以把图的顶点或边涂以各种颜色，并研究任意一个图最少要几种颜色)才能合理地进行上色(即使得相邻的顶点或边颜色不同)、著名的四色问题与此有关，四色问题是一种猜想：任一平面图只须四种颜色即可将顶点染色，使每每两相邻顶点皆有不同颜色、这与地图的染色是密切相关的、在图论中图论是一门比较新的学科，它当然可以尽量采取近代数学的概念及方法，诸如集合、映射、矩阵等等来处理其内容，还可以建立图与图之间的一些运算关系、用它可以解决的问题无法估量、图论的内容是丰富的，方法是新颖的，上面罗列的仅是其【一】二而已、。

一笔画问题画一个图案，如果用笔既不重复也不遗漏，纸不离笔，一笔画成，那么就称这个图案是一笔画图案.现在我们来研究的问题是：（1）怎样的图案才能一笔画成？（2）如果一个图案能一笔画成，那么该从哪里起笔到哪里收笔？需提醒大家的是，这些问题与图案中的“奇点”的个数有关.何谓奇点呢？我们知道，任何图案都是由线条（直线或曲线）连成的.在图案中，由三条或三条以上的方向各不相同的线连接在一起的点叫做图案点，通过图案点的线是奇数条就称奇点（当然，通过图案点的线是偶数条就称偶点，现在只需回答前面的问题而与偶点无关）.例如，在下面各图案中的奇点个数见统计表（请读者对照图案辨认奇点）.统计表：接着就请读者朋友拿起你的笔来逐个试画以上各图案，看能否一笔画成，将结论填在统计表内.并注意体会能一笔画的图案应该怎样画.最后，请根据上表归纳出前面两个问题的答案.【规律】（1）奇点数为0或2的图案可以一笔画成.奇点数多于2的图案不能一笔画成.（2）画奇数为0的图案时，可以选择任意点起笔都能一笔画成；画奇数为2的图案时，必须选择其中的一个奇点起笔，而到另一个奇点收笔才能一笔画成.【练习】1.下面各图案，能一笔画出来吗？试一试.2.容易看出，下面的两个图案都不能一笔画成，请在每个图案上各补画一条线就能使新图案一笔画成了.会吗？3.这是大数学家欧拉曾经研究过的一个著名数学问题----七桥问题.东普士的多尼斯堡城中有一条横贯城区的河流，河上有两个岛，两岸和两岛之间共架有七座桥、如下图所示：问人们能不重复地走遍这七座桥吗?4.回龙州公园的游览点与路线示意图如下.如果要使游人游完所有的游览点而不重复行走的路线，请问入口处和出口处应该设在什么位置?如果一个图形可以用笔在纸上连续不断而且不重复地一笔画成，那么这个图形就叫一笔画。

显然，在下面的图形中，(1)(2)不能一笔画成，故不是一笔画，(3)(4)可以一笔画成，是一笔画。

同学们可能会问：为什么有的图形能一笔画成，有的图形却不能一笔画成呢？一笔画图形有哪些特点？关于这个问题有一个著名的数学故事——哥尼斯堡七桥问题。

在行测考试中，图形推理中的一笔画问题，一直都是考生在考试中容易失分的题目。

其实主要问题存在于几个方面。

一、考生无法判断，什么样的图形考查的是一笔画;二、对一笔画图形的判断方法不了解。

接下来，中公教育专家卢志喜会从这两个方面给大家揭开一笔画的神秘面纱。

一、什么样的图形是一笔画图形定义：一笔画图形是一个图形从起点到终点可由一笔画成而中间没有间断，一笔画图形点可以重复，而线不可以重复。

一笔画图形具有两个比较明显的特点。

①图形相异;②图形简单;③图形一部分。

因此考生在复习图形推理时，除了要掌握相异图形常考的考点，点、线之外，还要掌握一笔画。

在复习备考的过程中首先要掌握一些简单的一笔画图形。

例如：长方形、正方形、三角形、五角星、圆。

当出现这些基本图形，或者在简单图形上增减了部分线条时，有一定的敏感性。

二、如何判断一个图形是否是一笔画图形方法一、奇偶点判断法奇点：从一个点引出的线条数为奇数;偶点：从一点引出的线条数为偶数。

规律：⒈凡是奇点数为2或者0的图形，一定可以一笔画成。

画时必须把一个奇点为起点，另一个奇点终点。

(利用奇点数判断，图形必须是一部分，比如“回”，奇点数为0，但是不能一笔画)2.其他情况的图都不能一笔画出。

(有偶数个奇点除以二便可算出此图需几笔画成。

)利用奇偶点法判断下列几个图形是否为一笔画图形，非一笔画图形需几笔画成?分析：图形1.奇点数为2，偶点为2，可以一笔画成。

图2.奇点为0，偶点为3，可一笔画。

图3.奇点为6，偶点为0，三笔可画成。

图4.奇点为0，偶点为10，可一笔画。

图5.奇点为4，偶点为5，可2笔画。

图6.奇点为4，可2笔画。

奇偶点判断法规律适合一切一笔画图形。

方法二、区域连通法规律：1、平面内区域可以构成两两连通的区域(表示图形没有单独的出头的线条)，且区域之间属于单连通，这样的图形可以一笔画。

(单连通表示从一个区域到另一个区域只有唯一的路径，且经过的区域不能重复)利用区域连通法，判断下列几个图形是否为一笔画图形?分析：首先对图形进行区域划分，如下：图1.区域1到区域2是单连通，可以一笔画。

一笔画问题的判定法则
一笔画问题是一种经典的智力游戏，玩家需要用一笔连通所有的点，但不能重复经过同一个点。

在解决问题时，有一些判定法则可以帮助玩家更快地找到解答。

1. 判断顶点度数：顶点度数指的是一个点与多少条线段相连。

如果一个点的度数为奇数，则这个点必须作为起点或终点；如果一个点的度数为偶数，则这个点可以通行过去。

2. 判断连通性：判断图形是否连通是解决一笔画问题的关键。

如果图形不连通，则需要用多笔画才能将所有点连通。

而在连通的情况下，有些顶点是必须通过的，有些顶点则可以绕路绕开。

3. 判断欧拉路径和欧拉回路：欧拉路径指的是经过每条边一次的路径，而欧拉回路指的是在欧拉路径的基础上回到起点。

对于连通的无向图，如果存在欧拉路径，则所有点的度数均为偶数。

对于连通的有向图，如果存在欧拉路径，则所有点的入度等于出度。

4. 判断哈密顿回路：哈密顿回路指的是经过每个点一次的回路。

对于无向图，判断哈密顿回路可以使用Dirac定理：如果图中每个点的度数都大于等于n/2(n为顶点数)，则图中存在哈密顿回路。

对于有向图，需要用到Ore定理：如果对于所有不相邻的点u和v，都有deg(u)+deg(v)>=n，则有向图存在哈密顿回路。

以上是几种判断一笔画问题的方法，不同的方法适用于不同的情况。

在实际解决问题时，可以根据具体情况选择合适的方法。

- 1 -。

如果用笔在纸上连续不断又不重复，一笔画成某种图形，这种图形就叫一笔画。

那么是不是所有的图形都能一笔画成呢？这一讲我们就一起来学习一笔画的规律。

能否一笔画成，先看是不是连通图形，不连通图形一定不能一笔画成。

连通图形，关键在于判别奇点、偶点的个数。

一、只有偶点，可以一笔画，并且可以以任意一点作为起点。

二、只有两个奇点，可以一笔画，但必须以这两个奇点分别作为起点和终点。

三、奇点超过两个，则不能一笔画。

对于一些比较复杂的路线问题，可以先转化为简单的几何图形，然后根据判定是否能一笔画的方法进行解答。

【例1】下面这些图形，哪个能一笔画？哪个不能一笔画？（1）（2）（3）（4）【例2】下面这些图形，哪个能一笔画？哪个不能一笔画？（1）（2）（3）（4）【例3】下面的各个小图形都是由点和线组成的．请你仔细观察后回答：例题精讲知识框架一笔画问题发现不同①与一条线相连的有哪些点?②与二条线相连的有哪些点?③与三条线相连的有哪些点?④与四条线或四条以上的线相连的有哪些点?【例4】下面各图能否一笔画成？（1）（2）（3）【例5】下面这几个字都能一笔写出来吗?【例6】下面这几个字母都能一笔写出来吗?【例7】下面的图形，哪些能一笔画出？哪些不能一笔画出？【例8】下图中，至少要画几笔才能画成？【随练1】德国有个城市叫哥尼斯堡．城中有条河，河中有个岛，河上架有七座桥，这些桥把陆地和小岛连接起来，这样就给人们提供了一个游玩的好去处(见下图)．俗话说，“人是万物之灵”，他们就是在游玩时候想出了这样一个问题：如果在陆地上可以随便走，而对每座桥只许通过一次，那么一个人要连续地走完这七座桥怎么个走法?好动脑筋的小朋友请先不要接着往下读，你也试一试，走一走．【随练2】在我国著名数学家陈景润写的《数学趣谈》一书中，有下面的这样一道题，大意是说：在法国的首都巴黎有一条河，河中有两个小岛，那里的人们建了15座桥把两个小岛和河岸连接起来，如下图所示，请你说一说，从任一岸出发，一次连续地通过所有的桥到达另一岸，可能吗?(每座桥只能走一次)课堂检测AB CD【作业1】 下面的图形都是由点和线组成的．请你仔细观察后回答：①与一条线相连的有哪些点?②与三条线相连的有哪些点?③与四条线或四条以上的线相连的有哪些点?【作业2】 下面各图能否一笔画成？（1）（2） （3） （4）【作业3】 下面这几个字母都能一笔写出来吗?【作业4】 下面这几个字都能一笔写出来吗?【作业5】 下图中，至少要画几笔才能画成？PONMLKJIHGFEDCBA家庭作业。

益智游戏“一笔画”的技巧当你还是个小学生的时候，也许就接触过“一笔画”的智力游戏了。

对于一个已知的几何图形，要求用笔不间断、不重复路线的方法一次性把它画完，就是“一笔画”。

现在有人把它做成手机触屏游戏，在互联网上流传。

不懂技巧的人玩起来就像迷路的司机，开着车转来转去，却始终找不到正确的方向，感觉很费神。

其实，“一笔画”是个古老的问题，欧洲人把它叫做“邮递员问题”。

邮递员面对错综复杂的城市街道，需要把邮件送达到分散在街道上的各个地方的客户手上，为了少走冤枉路，出发前需要对途经路线进行一个合理的规划，其中需要用到的知识就是“一笔画”。

在介绍一笔画技巧之前，我们先来了解两个基本概念：“奇数端点”和“偶数端点”，看下面的图形：上图中：以A为端点，只有AC 一条射线；以E为原点，有EF、EJ、ERJ三条射线；以G为端点有GC、GF、GH、GJ、GK五条射线，因为以它们为端点的射线条数都为奇数，所以称它们为“奇数端点”。

同理把B、C、D、F、H、J、K、L、M称为“偶数端点”。

概念：以图形中任意一点为端点的射线数量如果为奇数，这个端点就是“奇数端点”；如果为偶数，这个端点就是“偶数端点”。

（在这个概念中提到的射线允许是曲线，如上图中的ERJ和ISK）对于任意图形，它的“奇数端点”数量只有两种可能：0个或偶数个。

即是说你永远也不可能画出一个有奇数个“奇数端点”的图形。

【不信你自己拿纸笔试画一下，看看你能否画出一个只有1个（或3个、5个、7个……）奇数端点的图形】。

而偶数端点可以是任意个，比如下面的这个圆，你可以把它看成是没有偶数端点的图形（左边），也可以把它看成是有无数个偶数端点的图形（右边），了解了“奇数端点”和“偶数端点”的概念后，下面我们来研究“一笔画”，研究一笔画的重点是研究“奇数端点”，而“偶数端点”可以忽略。

定理一：只有0个或2个“奇数端点”的图形才能被一笔画成。

根据定理一，不管多复杂的图形，只要算一下它的“奇数端点”数量，就立即可以知道它是否可以一笔画成了。

益智游戏“一笔画”的技巧当你还是个小学生的时候,也许就接触过“一笔画”的智力游戏了。

对于一个已知的几何图形，要求用笔不间断、不重复路线的方法一次性把它画完，就是“一笔画"。

现在有人把它做成手机触屏游戏,在互联网上流传.不懂技巧的人玩起来就像迷路的司机，开着车转来转去，却始终找不到正确的方向，感觉很费神。

其实，“一笔画”是个古老的问题，欧洲人把它叫做“邮递员问题”。

邮递员面对错综复杂的城市街道,需要把邮件送达到分散在街道上的各个地方的客户手上，为了少走冤枉路，出发前需要对途经路线进行一个合理的规划，其中需要用到的知识就是“一笔画”。

在介绍一笔画技巧之前，我们先来了解两个基本概念：“奇数端点”和“偶数端点”,看下面的图形：上图中：以A为端点，只有AC 一条射线；以E为原点，有EF、EJ、ERJ三条射线;以G为端点有GC、GF、GH、GJ、GK五条射线，因为以它们为端点的射线条数都为奇数，所以称它们为“奇数端点”。

同理把B、C、D、F、H、J、K、L、M称为“偶数端点”。

概念：以图形中任意一点为端点的射线数量如果为奇数，这个端点就是“奇数端点"；如果为偶数，这个端点就是“偶数端点"。

（在这个概念中提到的射线允许是曲线，如上图中的ERJ和ISK）对于任意图形，它的“奇数端点"数量只有两种可能：0个或偶数个。

即是说你永远也不可能画出一个有奇数个“奇数端点"的图形。

【不信你自己拿纸笔试画一下,看看你能否画出一个只有1个(或3个、5个、7个……)奇数端点的图形】。

而偶数端点可以是任意个,比如下面的这个圆，你可以把它看成是没有偶数端点的图形(左边)，也可以把它看成是有无数个偶数端点的图形（右边），了解了“奇数端点”和“偶数端点”的概念后，下面我们来研究“一笔画”，研究一笔画的重点是研究“奇数端点”，而“偶数端点”可以忽略。

定理一：只有0个或2个“奇数端点”的图形才能被一笔画成。