《几何证明选讲》习题附答案

BCDO AP1.如图，点P 在圆O 直径AB 的延长线上，且PB=OB=2,PC 切圆O 于C 点，CD ⊥AB 于D 点，则PC= ， CD=.2．如图，AB 是⊙O 的直径，P 是AB 延长线上的一点，过P 作⊙O 的切线，切点为C ，,32=PC 若∠CAP ＝30°，则⊙O 的直径AB ＝___________答案43．已知圆O 的半径为3，从圆O 外一点A 引切线AD 和割线ABC ，圆心O 到AC 的距离为22，3AB =，则切线AD 的长为 _____。

解：依题意，BC =，∴AC =5，2AD =.AB AC =15，∴AD =154．如图，PA 切O 于点A ，割线PBC 经过圆心O ，OB=PB=1, OA 绕点O 逆时针旋转60°到OD ，则PD 的长为 .解：∵PA 切O 于点A ，B 为PO 中点，∴AB=OB=OA, ∴60AOB ∠=,∴120POD ∠=, 在△POD中由余弦定理，得2222cos PD PO DO PO DO POD =+-⋅∠=1414()72+-⨯-=∴PD 5．如图，在⊙O 中，AB 为直径，AD 为弦，过B 点的切线与ADAD=DC ，则sin ∠ACO=_________解：由条件不难得ABC ∆为等腰直角三角形，设圆的半径为1，则1OB =，2BC =，OC =sin BCO ∠==，s co BCO ∠= ∴ sin ∠ACO=0sin(45BCO -∠）=10106．如图，PT 是O 的切线，切点为T ，直线PA 与O 交于A 、B 两点，TPA ∠的平分线分别交直线TA 、TB 于D 、E 两点，已知2PT =，PB =，则PA = ，TEAD= ．；7．已知AB 是圆O 的直径，EF 切圆O 于C ，AD ⊥EF 于D ，AD ＝2，AB ＝6，则AC 长为_______. 、23；8．已知AB 是半圆O 的直径，点C 在半圆上，CD AB ⊥于点D ，且4AD DB =，设COD θ∠=，则cos 2θ＝ ．解：()44,AD DB OC OD OC OD =∴+=- 即35OC OD =，22237cos 22cos 12121525OD OC θθ⎛⎫⎛⎫=-=⨯-=⨯-=- ⎪ ⎪⎝⎭⎝⎭9．如图，圆O 是ABC ∆的外接圆，过点C 的切线交AB 的延长线于点D ，CD =3AB BC ==。

高中数学-《几何证明选讲》知识点归纳与练习（含答案）一、相似三角形的判定及有关性质平行线等分线段定理平行线等分线段定理：如果一组平行线在一条直线上截得的线段相等，那么在其他直线上截得的线段也相等。

推理1:经过三角形一边的中点与另一边平行的直线必平分第三边。

推理2 :经过梯形一腰的中点，且与底边平行的直线平分另一腰。

平分线分线段成比例定理平分线分线段成比例定理：三条平行线截两条直线，所得的对应线段成比例。

推论：平行于三角形一边的直线截其他两边（或两边的延长线）所得的对应线段成比例。

相似三角形的判定及性质相似三角形的判定：定义：对应角相等，对应边成比例的两个三角形叫做相似三角形。

相似三角形对应边的比值叫做相似比（或相似系数）。

由于从定义岀发判断两个三角形是否相似，需考虑6个元素，即三组对应角是否分别相等，三组对应边是否分别成比例，显然比较麻烦。

所以我们曾经给岀过如下几个判定两个三角形相似的简单方法：（1 ）两角对应相等，两三角形相似；（2 ）两边对应成比例且夹角相等，两三角形相似；（3 ）三边对应成比例，两三角形相似。

预备定理：平行于三角形一边的直线和其他两边（或两边的延长线）相交，所构成的三角形与三角形相似。

判定定理1 :对于任意两个三角形，如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似。

简述为：两角对应相等，两三角形相似。

判定定理2 :对于任意两个三角形，如果一个三角形的两边和另一个三角形的两边对应成比例，并且夹角相等，那么这两个三角形相似。

简述为：两边对应成比例且夹角相等，两三角形相似。

判定定理3 :对于任意两个三角形，如果一个三角形的三条边和另一个三角形的三条边对应成比例，那么这两个三角形相似。

简述为：三边对应成比例，两三角形相似。

引理：如果一条直线截三角形的两边（或两边的延长线）所得的对应线段成比例，那么这条直线平行于三角形的第三边定理：（1）如果两个直角三角形有一个锐角对应相等，那么它们相似；（2 ）如果两个直角三角形的两条直角边对应成比例，那么它们相似。

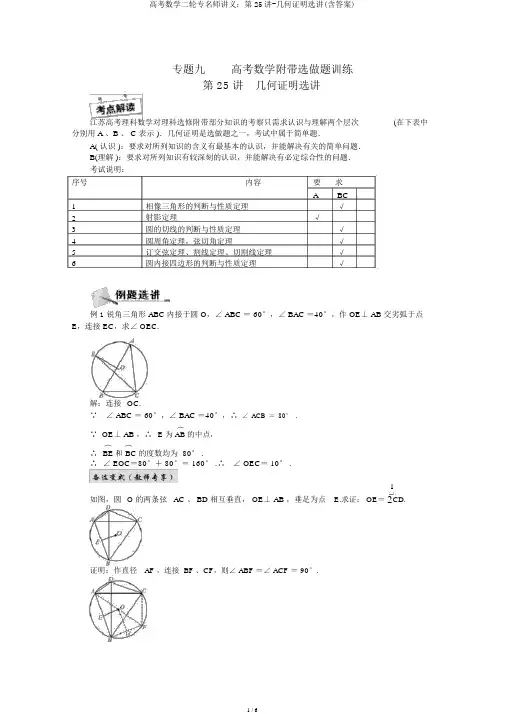
专题九高考数学附带选做题训练第 25 讲几何证明选讲江苏高考理科数学对理科选修附带部分知识的考察只需求认识与理解两个层次(在下表中分别用 A 、B 、 C 表示 )．几何证明是选做题之一，考试中属于简单题．A( 认识 )：要求对所列知识的含义有最基本的认识，并能解决有关的简单问题．B(理解 )：要求对所列知识有较深刻的认识，并能解决有必定综合性的问题．考试说明：序号内容要求A BC1相像三角形的判断与性质定理√2射影定理√3圆的切线的判断与性质定理√4圆周角定理，弦切角定理√5订交弦定理、割线定理、切割线定理√6圆内接四边形的判断与性质定理√例 1 锐角三角形ABC内接于圆O，∠ABC＝60°，∠BAC＝40°，作OE⊥AB交劣弧于点E，连接 EC，求∠ OEC.解：连接OC.∵ ∠ ABC ＝ 60°，∠ BAC ＝40°，∴∠ ACB＝80° .︵∵ OE⊥ AB ，∴ E 为 AB 的中点，︵︵∴BE和 BC 的度数均为 80° .∴∠ EOC＝80°＋ 80°＝ 160° .∴ ∠ OEC＝ 10° .1如图，圆O 的两条弦AC 、 BD 相互垂直， OE⊥ AB ，垂足为点 E.求证： OE＝2CD.证明：作直径AF ，连接 BF 、CF，则∠ ABF ＝∠ ACF ＝ 90°.1又 OE ⊥AB ， O 为 AF 的中点，则 OE ＝2BF. ∵ AC ⊥BD ，∴ ∠DBC ＋∠ ACB ＝90°.又 AF 为直径，∠ BAF ＋∠ BFA ＝ 90°，∠ AFB ＝∠ ACB ， ∴ ∠ DBC ＝∠ BAF ，即有 CD ＝ BF.1进而得 OE ＝ 2CD.︵ ︵例 2如图，已知圆上的弧AC ＝BD ，过 C 点的圆的切线与BA 的延伸线交于E 点．证明：(1) ∠ ACE ＝∠ BCD ；(2) BC 2＝ BE ·CD.︵ ︵证明： (1) 由于 AC ＝BD ，所以∠ ABC ＝∠ BCD. 由于 EC 与圆相切于点 C ，故∠ ACE ＝∠ ABC ， 所以∠ ACE ＝∠ BCD.(2) 由于∠ ECB ＝∠ CDB ，∠ EBC ＝∠ BCD ， 所以 △ BDC ∽△ ECB ，故 BC ＝CD，即 BC 2＝ BE ·CD.BE BC如图， D 、 E 分别为 △ABC 边 AB 、AC 的中点，直线 DE 交 △ABC 的外接圆于 F 、 G 两点．若 CF ∥AB. 证明：(1) CD ＝BC ；(2) △ BCD ∽△ GBD.证明： (1) 如图，由于 D 、 E 分别为 AB 、AC 的中点，所以 DE ∥ BC.又 CF ∥AB ，故四边形 BCFD 是平行四边形，所以 CF ＝ BD ＝ AD.而 CF ∥AD ，连接 AF ，所以四边形 ADCF 是平行四边形，故 CD ＝ AF. 由于 CF ∥ AB ，所以 BC ＝ AF ，故 CD ＝BC.(2) 由于 FG ∥BC ，故 GB ＝CF.由(1) 可知 BD ＝ CF ，所以 GB ＝ BD.所以∠ BGD ＝∠ BDG.由 BC ＝CD 知，∠ CBD ＝∠ CDB. 又∠ DGB ＝∠ EFC ＝∠ DBC ， 故△ BCD ∽△ GBD.例 3 如图， AB 是圆 O 的直径， C 、F 是圆 O 上的两点， OC ⊥AB ，过点 F 作圆 O 的切线 FD 交 AB 的延伸线于点 D. 连接 CF 交 AB 于点 E.求证： DE 2＝ DB ·DA.证明：连接 OF ，由于 DF 切圆 O 于 F ，所以∠ OFD ＝ 90°，所以∠ OFC ＋∠ CFD ＝ 90°.由于 OC ＝ OF ，所以∠ OCF ＝∠ OFC.又 CO ⊥ AB 于 O ，所以∠ OCF ＋∠ CEO ＝90°，所以∠ CFD ＝∠ CEO ＝∠ DEF ，所以 DF ＝ DE. 又 DF 是圆 O 的切线，所以 DF 2＝ DB ·DA ， 即 DE 2＝ DB ·DA.如图，在 △ABC 中，已知 CM 是∠ ACB 的均分线，△ AMC 的外接圆交 BC 于点 N ，且 BN ＝ 2AM. 求证： AB ＝ 2AC.证明：在 △ABC 中，由于 CM 是∠ ACB 的均分线，所以AC ＝AM. ① BC BM由于 BA 与 BC 是圆 O 过同一点B 的割线，所以 BM ·BA ＝ BN ·BC ，即 BABC ＝ BM BN.又 BN ＝ 2AM ，所以BA ＝2AM.②BC BM由①②，得 AB ＝ 2AC.例 4 如图，四边形 ABCD 中，AB 、DC 的延伸线交于点 E ，AD 、BC∠ AED 、∠ AFB 的角均分线交于点 M ，且 EM ⊥ FM. 求证：四边形 ABCD的延伸线交于点内接于圆．F ，证明：连接 EF ，由于 EM 是∠ AEC 的角均分线， 所以∠ FEC ＋∠ FEA ＝ 2∠FEM. 同理，∠ EFC ＋∠ EFA ＝ 2∠ EFM.而∠ BCD ＋∠ BAD ＝∠ ECF ＋∠ BAD＝ (180°－∠ FEC －∠ EFC) ＋ (180°－∠ FEA －∠ EFA)＝ 360°－ 2(∠ FEM ＋∠ EFM)＝ 360°－ 2(180°－∠ EMF) ＝ 2∠ EMF ＝ 180°，即∠ BCD 与∠ BAD 互补．所以四边形ABCD 内接于圆．如图，已知 AP 是圆 O 的切线， P 为切点， AC 是圆 O 的割线，与圆 O 交于 B、 C 两点，圆心O 在∠ PAC 的内部，点 M 是 BC 的中点．(1)证明： A 、P、 O、 M 四点共圆；(2)求∠ OAM ＋∠ APM 的大小．(1)证明：连接 OP、 OM ，由于 AP 与圆 O 相切于点P，所以 OP⊥ AP.由于 M 是圆 O 的弦 BC 的中点，所以OM ⊥ BC.于是∠ OPA＋∠ OMA ＝ 180°，由圆心 O 在∠ PAC 的内部，可知四边形 APOM 的对角互补，所以 A 、 P、 O、 M 四点共圆．(2)解：由 (1) 得 A 、P、 O、 M 四点共圆，所以∠ OAM ＝∠ OPM. 由 (1) 得 OP⊥ AP.由圆心 O 在∠ PAC 的内部，可知∠ OPM ＋∠ APM ＝ 90°，所以∠ OAM ＋∠ APM ＝ 90° .1.(2013 江·苏卷 )如图， AB 和 BC 分别与圆 O 相切于点 D、 C， AC 经过圆心 O，且 BC ＝2OC.求证： AC ＝ 2AD.证明：连接OD ，∵AB 、BC 分别与圆O 相切于点 D 、C，∴ ∠ ADO ＝∠ ACB ＝ 90°.∵ ∠ A＝∠ A ，∴Rt△ ADO ∽ Rt△ ACB ，BC AC∴OD＝AD .∵ BC ＝ 2OC＝2OD ，∴ AC ＝2AD. 2. 如图，在四边形 ABCD 中，△ ABC ≌△BAD. 求证： AB ∥ CD.证明：由△ABC ≌△ BAD ，得∠ ACB ＝∠ BDA ，故 A 、B 、 C、 D 四点共圆，进而∠ CAB ＝∠ CDB.再由△ ABC ≌△ BAD ，得∠ CAB ＝∠ DBA.所以∠ DBA ＝∠ CDB ，所以 AB ∥ CD.3.如图， AB 是圆 O 的直径， D 、E 为圆上位于 AB 异侧的两点，连接 BD 并延伸至点 C，使 BD ＝ DC ，连接 AC 、 AE 、 DE.求证：∠ E＝∠ C.证明：连接AD ，∵ AB 是圆 O 的直径，∴ ∠ ADB ＝ 90°，∴AD ⊥ BD.∵BD ＝ DC，∴AD 是线段 BC 的中垂线，∴AB ＝ AC，∴∠B＝∠ C.又 D 、E 为圆上位于 AB 异侧的两点，∴ ∠B＝∠ E.∴ ∠ E＝∠ C.(此题还可连接OD，利用三角形中位线来求证∠ B ＝∠ C)4.(2014 江·苏卷 )如图， AB 是圆 O 的直径， C、 D 是圆 O 上位于 AB 异侧的两点．证明：∠OCB＝∠ D.证明：由于 B 、 C 是圆 O 上的两点，所以OB ＝ OC.故∠ OCB ＝∠ B.由于 C、 D 是圆 O 上位于 AB 异侧的两点，故∠ B 、∠ D 为同弧所对的两个圆周角，所以∠ B＝∠ D.所以∠ OCB＝∠ D.(此题模拟高考评分标准，满分10 分)(2014 ·州期末泰 )如图， AB 是圆 O 的一条直径，C、D 是圆 O 上不一样于 A 、B 的两点，过B 作圆 O 的切线与AD 的延伸线订交于点M ， AD 与 BC 订交于 N 点， BN ＝ BM. 求证：(1)∠ NBD ＝∠ DBM ；(2)AM 是∠ BAC 的角均分线．证明： (1) ∵ AB 是圆 O 的直径，∴∠ADB＝90° .而BN＝BM，∴ △ BNM为等腰三角形BD 为∠ NBM 的角均分线DBC ＝∠ DBM.(5 分 )∠DBM ＝∠ DAB(2) BM 是圆 O 的切线，∠ CBD ＝∠ CAD T DAB ＝∠ DAC T AM 是∠ CAB 的角∠ DBC ＝∠ DBM均分线． (10 分 )已知点 C 在圆 O 直径 BE 的延伸线上， CA 切圆 O 于 A 点，∠ ACB 的均分线分别交 AE 、AB 于点 F 、 D.(1) 求∠ ADF 的度数；(2) AC的值．若 AB ＝AC ，求 BC解： (1) ∵ AC 为圆 O 的切线， ∴ ∠B ＝∠ EAC.又 DC 是∠ ACB 的均分线， ∴ ∠ACD ＝∠ DCB ，∴ ∠B ＋∠ DCB ＝∠ EAC ＋∠ ACD ，即∠ ADF ＝∠ AFD.又 BE 为圆 O 的直径，∴ ∠ BAE ＝ 90°，1∴ ∠ ADF ＝ (180 °－∠ BAE) ＝ 45°.(2) ∵ ∠B ＝∠ EAC ，∠ ACB ＝∠ ACB ，∴ △ACE ∽△ BCA ，∴ AC ＝ AE .BC AB又 AB ＝AC ，∴ ∠B ＝∠ ACB ， ∴ ∠ B ＝∠ ACB ＝∠ EAC.由∠ BAE ＝90°及三角形内角和知∠ B ＝ 30°.AC AE3 ∴ 在 Rt △ ABE 中，＝＝ tanB ＝ tan30 °＝BC AB3 .。

高中数学选修 4-1《几何证明选讲》练习题（三）一、选择题：本大题共 12 小题，每题 5 分，共 60 分，在每个小题给出的四个选项中，只有一项为哪一项切合题目要求的 ．1．已知三角形的3 条中位线分别为 3cm 、4cm 、 6cm ，则这个三角形的周长是（）．A ． 3cmB ． 26cmC ． 24cmD ． 65cm2．要做甲、乙两个形状同样 (相像 )的三角形框架 ,已知三角形框架甲的三边分别为50cm 、 60cm 、80cm ，三角形框架乙的一边长为 20cm ，那么切合条件的三角形框架乙共有 （）．A ．1种B ．2 种C ．3 种D ．4 种3．在 RtABC 中， CD 是斜边上的高线， AC ∶BC=3 ∶ 1，则 SABC ∶ S ACD 为（ ）．A ．4∶3B ．9∶1C ． 10∶ 1D ．10∶94．如图，在正方形ABCD 中， E 为 AB 中点， BF ⊥ CE 于 F ，那么 S △BFC :S 正方形ABCD =（ ）．A ．1：3B ． 1：4C ． 1：5D ．1：65．在 △ ABC 中，∠ A ∶∠ B ∶∠ C ＝ 1∶2∶ 3，CD ⊥ AB 于 D ， AB ＝ a ，则 DB ＝（）aaC ．a D ．3aA ．B ．24436．若梯形的中位线被它的两条对角线三均分，则梯形的上底 a 与下底 b(a<b)的比是（）．1122A ．2B ． 3C ． 3D ． 57．如图，在正方形ABCD 中， E 是 BC 的中点， F 是 CD 上一点，且 CF1CD ，4以下结论： ① BAE 30AD，② △ABE ∽△ AEF ， ③ AEEF ，④ △ADF ∽△ECF ．此中正确的个数为（ ）FA ． 1B ． 2C ． 3D ． 4BEC8．直角梯形的一条对角线把梯形分红两个三角形，此中一个是边长为30 的等边三角形，则这个梯形的中位线长是（ ）．A ．15B ．22.5C ．45D ．909．以下图，在 △ABC 中， AC=5 ，中线 AD=4 ，则 AB 边的取值范围是（）．A ．1 AB 9B ． 3 AB 13C ． 5AB 13D ． 9AB13D CFAEB10 ABCD中， AE : EB m : n，若AEF的面积等于 a ，则CDF．如图，平行四边形的面积等于（）．m 2 n 2(m n)2D ．( m n)2A ． 2 aB ． 2 aC ．2a 2anmmn11．如图，在梯形 ABCD 中， AD //BC ，对角线 AC ⊥BD ，AD且 AC=12 ，BD=9 ，则此梯形的中位线长是（）．A ． 10B ．2115D ． 12BCC ．2212．如图，设 P 为ABC 内一点，且 2 1CAPAB AC，55则ABP 的面积与ABC 的面积之比等于（ ）． P1B ．2 31A ．5 C ．D ．552AB二、填空题：本大题共 4 小题，每题 5 分，共 20 分，把答案填在题中横线上．13．若两个相像三角形的周长比为3: 4 ，则它们的三角形面积比是 ____________ ．14．如图，在梯形 ABCD 中， AD //BC ， AC ⊥ BA ， AD=DC=5 ，则 BC 的长是 __________ ．15．已知： △ ABC 中， AD 是 BC 边上的中线，E 是 AD 的中点， BE 的延伸线交AC 于点 F ，则AF____________ ．AC16．在 △ABC 中， AB9，AC 6 ，点 M 在 AB 上且 AM 3 ，点 N 在 AC 上，联络 MN ，使△ AMN 与原三角形相像，则 AN ＝ ___________三、解答题：本大题共 6小题，共 70分，解答应写出文字说明，证明过程或演算步骤 ．17．如图，在ABC 中， AD 为 BC 边上的中线， F 为 AB 上随意一点， CF 交 AD 于点 E ，求证： AE BF 2DE AF ．（ 10 分）CDEA F B18．如图，正方形DEMF内接于△ ABC，若S ADE1， S正方形DEFM 4 ，求 S ABC（12分）AD P EB M Q F C例 2 图19．已知：如图，△ＡＢＣ中，ＡＤ均分∠ＢＡＣ，ＡＤ的垂直均分线交ＡＢ于点Ｅ，交ＡＤ于点Ｈ，交ＡＣ于点Ｇ，交ＢＣ的延伸线于点Ｆ，求证：ＤＦ２＝ＣＦ ?ＢＦ．（ 12分）20．如图，CD是 Rt△ ABC的斜边AB上的高， E 是BC上随意一点，EF⊥AB于 F．求证：AC 2AD AF CD EF ．（12 分）21．如图，在Rt△ABC中，∠ACB90 ，CD AB ，垂足为 D ，设 BC a ， AC b ，111AB c ． CD b ，试说明：2b 2h2．（ 12分）aCb h aA c D B22． 如图，在△ ABC 中，BAC90 ， AD 是BC 边上的高，E 是 BC 边上的一个动点（不与B ，C 重合）， EFAB ，EGAC ，垂足分别为F ，G ．（ 1）求证：EGCG；AD CD（ 2） FD 与 DG 能否垂直？若垂直，请给出证明；若不垂直，请说明原因；（ 3）当 AB AC 时， △ FDG 为等腰直角三角形吗？并说明原因． （ 12 分）AFGBD EC答案与分析：1-5 BCCCA 6-10AABBC 11-12 CA13． 9:1614． 101915．16． 2，或3 217．证明：过 D 作 DG // AB ，交 CF 于 G ，∴AEF DEG ， CDG CBF ，AEDE DG CD ∴，BF，AFDGCB ∵ D 为BC 的中点， CD1 CB ，2DG 1 ， DG 1BF ，BF 2 2AE 2DEAE BF 2DE AF ．AF，即 BF18．解：∵正方形的面积为 4，∴ DE ＝ MF ＝ 2,过 A 点作 AQ ⊥BC 于 Q ，交 DE 于 P ，∵SADE1，∴ AP ＝1，∵DE ∥ BC ，∴△ ADE ∽△ ABC ，∴ APDE ，即 1 2 AQBC 3 BC∴BC ＝6，故 S ABC ＝919．证明：连ＡＦ，∵ＦＨ垂直均分ＡＤ，∴ＦＡ＝ＦＤ，∠ＦＡＤ＝∠ＦＤＡ，∵ＡＤ均分∠ＢＡＣ，∴∠ＣＡＤ＝∠ＢＡＤ，∴∠ＦＡＤ－∠ＣＡＤ＝∠ＦＤＡ－∠ＢＡＤ，∵∠Ｂ＝∠ＦＤＡ－∠ＢＡＤ，∴∠ＦＡＣ＝∠Ｂ，又∠ＡＦ∴△ＡＦＣ∽△ＢＦＡ，∴ＡＦ＝C Ｆ，ＢＦ ＡＦ∴ＡＦ ２＝ＣＦ ?ＢＦ，∴ＤＦ ２＝ＣＦ ?ＢＦ．20．证明： AC 2 AD AB ,AC 2 AD AFAD (AB AF) AD BF由于 Rt ADCRt EFB ,因此 ADEF ,CDBF则ADBFCD EF ，AC 2 AD AFCD EF ,即 AC 2 AD AF CD EF ．11121．解：等式 a 2b 2 h 2 建立．原因以下：∵ ACB 90 ,CD AB ，C 公共，∴1ab1AB h ， AB 2a 2b 2 ，2 2 ∴ ab c h ，∴ a 2 b 2 c 2 h 2 ，∴ a 2 b 2(a 2 b 2 )h 2 ，∴a 2b 2 (a 2b 2 )h 2，a 2b 2h2a 2b 2 h 2∴1 a 2b 2，h2a 2b2∴11 1．h 2a 2b 222．证明：在四边形AFEG 中，∵ FAG AFEAGE 90 ，∴ 四边形 AFEG 为矩形， ∴ AFEG ，（ 1）易证∴AFAD EG CG ，而 AFEG ，AD CD CG；CD（ 2） △ ABC 为直角三角形， ADBC ，∴ FADC ， 即 △ AFD ∽△CGD ，∴ ADFCDG ，又CDG ADG 90∴ADFADG90，，即FDG 90 ，∴ FD DG ； （ 3）当 ABAC 时， △ FDG 为等腰直角三角形，原因以下：AB AC ，BAC 90 ，∴ AD DC又由于 △ AFD ∽△ CGD∴FD AD1， FD DGGD DC又 FDG 90∴ △FDG ,△ FDG 为等腰直角三角形．。

高中数学选修 4-1《几何证明选讲》练习题（一）1．如图，已知在△ ABC 中， CD ⊥AB 于 D 点， BC 2＝ BD ·AB ，则∠ ACB ＝______. 分析： 在△ ABC 与△ CBD 中，由 BC 2＝ BD ·AB ，得 BC ＝ AB，且∠ B ＝∠ B ， BD BC因此△ ABC ∽△ CBD.则∠ ACB ＝∠ CDB ＝ 90°. 答案： 90°2．如图，已知在△ ABC 中，∠ ACB ＝ 90°， CD ⊥ AB 于 D ， AC ＝ 6，DB ＝ 5，则 AD 的长为 ________．分析：在 Rt △ABC 中，∠ ACB ＝ 90°， CD ⊥ AB ，∴ AC 2＝ AB ·AD.设 AD ＝ x ，则 AB ＝ x ＋ 5，又 AC ＝ 6， ∴ 62＝ x(x ＋ 5)，即 x 2 ＋5x － 36＝0. 解得 x ＝4 或 x ＝－ 9( 舍去 )，∴ AD ＝ 4. 答案： 43．如下图， 已知在△ ABC 中，∠C ＝ 90°，正方形 DEFC 内接于△ ABC ，DE ∥ AC ，EF ∥ BC ，AC ＝1， BC ＝ 2，则 AF ∶ FC 等于 ________．分析： 设正方形边长为 x ，则由△ AFE ∽△ ACB ，AF FE x 1－ x可得 AC ＝ CB ，即 2＝1 ，因此 x ＝2，于是 AF ＝1.3 FC 2 答案： 124．如图， 平行四边形 ABCD 中，AE ∶ EB ＝ 1∶ 2，△ AEF 的面积为 6，则△ ADF的面积为 ________．分析： 由题意可得△ AEF ∽△ CDF ，且相像比为 1∶ 3，由△ AEF 的面积为 6，得△ CDF 的面积为54，由题意易知SADF ∶ S CDF ＝ 1∶ 3，因此 S ADF ＝ 18.△△ △答案： 185．如图，△ ABC 中，∠ BAC ＝ 90°， AB ＝ 4 cm ， AC ＝3 cm ， DE ∥ BC 且 DE 把△ABC 的周长分为相等的两部分，则 DE ＝ ________.分析： ∵∠ BAC ＝ 90°， ∴ BC ＝ 5 cm.设 AD ＝ x cm ，AE ＝ y cm ，则 x ＋ y ＝ 6.①∵ DE ∥ BC ，得 AD＝ AE ，即 x ＝ y.②ABAC43 由①②得 x ＝24，y ＝18，77∴ DE ＝ x 2＋ y 2＝307 cm.30答案：7cm6．在△ ABC 中，点 D 在线段 BC 上，∠ BAC ＝∠ ADC ，AC ＝ 8，BC ＝ 16，则 CD 为 ________．分析： ∵∠ BAC ＝∠ ADC ，∠ C ＝∠ C ，∴△ ABC ∽△ DAC ，22∴BC ＝AC，∴ CD ＝AC＝ 8＝4.ACCDBC 16答案：4和7．如图，已知在梯形 BD 订交于点 P ，ABCD中，上底长为2，下底长为6，高为4，对角线AC(1)若 AP 长为 4，则 PC ＝ ________；(2)△ ABP 和△ CDP 的高的比为 ______． 分析： (1) ∵AB ∥ CD ， ∴△ APB ∽△ CPD ，∴ AP CP ＝ CD AB ，即 CP 4＝ 26，解得 PC ＝12.(2)由 (1) 及△ ABP 和△ CDP 的高的比等于它们的相像比， 得这两个三角形的高的比为1∶3.答案：(1)12(2)1∶ 38． (2010 ·东卷广 )如图，在直角梯形 ABCD 中， DC ∥AB ， CB ⊥AB ，AB ＝AD ＝ a ， CD＝ a，点 E ， F 分别为线段 AB ，AD 的中点，则 EF ＝ ________. 2分析：连结 DE ，因为 E 是 AB 的中点，故 a BE ＝ .2又 CD ＝a， AB ∥ DC ， CB ⊥ AB ，∴四边形 EBCD 是矩形．2在 Rt △ADE 中， AD ＝a ， F 是 AD 的中点，故 EF ＝a.2【答案】a2AE 29．如图，已知 AD ∥EG ∥ BC ， AD ＝ 6，BC ＝ 9， AB ＝ 3，则 GF 的长为 ________．分析： ∵ AD ∥ EG ∥BC ，EG AE EF BE∴BC＝AB ， AD ＝BA.∵ AE＝2，∴BE＝1，EF 1 EG 2∴ AD ＝ 3， BC ＝ 3. 又∵ AD ＝ 6， BC ＝ 9， ∴ EF ＝ 2， EG ＝ 6， ∴ GF ＝ EG －EF ＝4.答案： 410．如图，在直角梯形AB ＝ 6，在 AB 上选用一点ABCD P ，使△中，上底 AD ＝ 3，下底 BC ＝ 3 3，与两底垂直的腰和△PBC 相像，这样的点 P 有 ________个． PAD分析： 设 AP ＝ x ，AD AP(1)若△ ADP ∽△ BPC ，则 BP ＝ BC ，即 3 ＝ x，因此 x 2－ 6x ＋ 9＝ 0，解得 x ＝ 3. 6－ x 3 3(2)若△ ADP ∽△ BCP ，则AD＝ AP， BC BP即 3 ＝x ，解得 x ＝3， 3 3 6－ x 2因此切合条件的点 P 有两个． 答案： 两11．如图，在△ ABC 中， AD ⊥ BC 于 D ，DE ⊥AB 于 E ， DF ⊥AC 于 F. 求证： AE ·AB ＝ AF ·AC . 证明： ∵AD ⊥BC ，∴△ ADB 为直角三角形，又∵ DE ⊥ AB ，由射影定理知，AD 2＝ AE ·AB.同理可得 AD 2＝ AF ·AC ，∴ AE ·AB ＝ AF ·AC .12．如下图，在△ ABC 中， AD 为 BC 边上的中线， F 为 AB 上随意一点， CF 交 AD 于点E.求证： AE ·BF ＝ 2DE ·AF.证明： 过点 D 作 AB 的平行线 DM 交 AC 于点 M ，交 FC 于点 N. 在△ BCF 中， D 是 BC 的中点， DN ∥ BF ，1 ∴ DN ＝ 2BF.∵ DN ∥AF ，∴△ AFE ∽△ DNE ，∴AE ＝DE . AF DN1 AE 2DE又 DN ＝2BF ，∴ AF ＝ BF ， 即 AE ·BF ＝2DE ·AF .13．如图，△ ABC 中， AB ＝ AC ， AD 是中线， P 为 AD 上一点， CF ∥ AB ， BP 延伸线交 AC ，CF 于 E ， F ，求证： PB 2＝ PE ·PF.证明：如图，连结 PC ，易证 PC ＝PB ，∠ ABP ＝∠ ACP.∵ CF ∥ AB ，∴∠ F ＝∠ ABP ， 进而∠ F ＝∠ ACP ，又∠ EPC 为△ CPE 与△ FPC 的公共角， 进而△ CPE ∽△ FPC ，∴CP ＝ PE， FP PC∴ PC 2＝ PE ·PF ，又 PC ＝ PB ，∴ PB 2＝ PE ·PF .14．已知： 在 Rt △ABC 中， ∠ ACB ＝ 90°，M 是 BC 的中点， CN ⊥ AM ，垂足是 N ，求证： AB ·BM ＝AM ·BN.2证明：∵ CM ＝ MN ·AM ，∴ BM 2＝ MN ·AM ，∴ BM AM ＝ MN BM ，又∵∠ BMN ＝∠ AMB ，∴△ AMB ∽△ BMN ，∴ AB BN ＝ AM BM ，∴ AB ·BM ＝ AM ·BN.15．如图，在等腰三角形 ABC 中， AB ＝ AC ，底边 BC 上的高 AD ＝ 10 cm ，腰 AC 上的高 BE ＝ 12 cm.(1)求证：AB ＝5； BD 3(2)求△ ABC 的周长 . 【分析方法代码 108001159】 分析： (1) 证明：在△ ADC 和△ BEC 中，∵∠ ADC ＝∠ BEC ＝ 90°，∠ C ＝∠ C ，∴△ ADC ∽△ BEC ，∴AC ＝ AD ＝ 10＝ 5.BCBE126∵ AD 是等腰三角形 ABC 底边 BC 的高线， ∴ BC ＝ 2BD ，又 AB ＝ AC ， ∴ AC ＝ AB 5 AB 5 BC 2BD＝ ，∴ BD ＝ .6 3 5(2)设 BD ＝ x ，则 AB ＝ 3x ，在 Rt △ABD 中，∠ ADB ＝ 90°， 依据勾股定理，得 AB 2 ＝BD 2 ＋AD 2，∴53x 2＝ x 2＋102，解得 x ＝ 7.5.5∴ BC ＝ 2x ＝ 15， AB ＝ AC ＝ 3x ＝ 12.5，∴△ ABC 的周长为 40 cm.16．如右图， 在平行四边形 ABCD 中，过点 B 作 BE ⊥ CD ，垂足为 E ，连结 AE ， F 为 AE 上一点，且∠ BFE ＝∠ C.(1)求证：△ ABF ∽△ EAD . (2)若 AB ＝ 4，∠ BAE ＝ 30°， AD ＝ 3，求 BF 的长． 分析： (1) 证明：∵ AB ∥ CD ，∴∠ BAF ＝∠ AED .又∵∠ BFE ＝∠ C ，∠ BFE ＋∠ BFA ＝∠ C ＋∠ EDA ， ∴∠ BFA ＝∠ ADE . ∴△ ABF ∽△ EAD .4＝8 3， (2)∵ AE ＝ sin 60° 3BF ABAB3 3又AD ＝ AE ，∴ BF ＝AE ·AD ＝ 2 .17．如图， 梯形 ABCD 中，AD ∥ BC ，EF 经过梯形对角线的交点 O ，且 EF ∥ AD .(1)求证： OE ＝OF ；OE OE (2)求 AD ＋ BC 的值；112 (3)求证： AD ＋BC ＝EF . 【分析方法代码 108001160】 分析： (1) 证明：∵ EF ∥ AD ，AD ∥ BC ，∴ EF ∥ AD ∥ BC.OE AE OF DF∵ EF ∥ BC ，∴ BC ＝AB ， BC ＝ DC .AE DF ∵ EF ∥ AD ∥ BC ，∴ AB ＝ DC .∴ OE ＝ OF，∴ OE ＝ OF.BC BCOE BE (2)∵ OE ∥ AD ，∴ AD ＝ AB .由 (1)知， OE BC ＝AEAB ，∴OE ＋ OE ＝BE ＋AE ＝ BE ＋ AE ＝ 1.AD BC AB AB ABOE OE2OE 2OE(3)证明：由 (2)知 AD ＋ BC ＝ 1，∴ AD ＋ BC ＝2.又 EF ＝ 2OE ，∴ EF＋ EF＝ 2， AD BC∴1＋1＝2AD BC EF.18．一块直角三角形木板， 如下图， ∠ C ＝ 90°，AB ＝ 5 cm ，BC ＝ 3 cm ，AC ＝ 4 cm.依据需要， 要把它加工成一个面积最大的正方形木板， 设计一个方案， 应如何裁才能使 正方形木板面积最大，并求出这个正方形木板的边长． 分析： 如图 (1)所示，设正方形 DEFG 的边长为 x cm ，过点 C 作 CM ⊥ AB 于 M ，交DE 于N ，因为 S △ABC ＝ 1AC ·BC ＝1AB ·CM ，2 2因此 AC ·BC ＝ AB ·CM ，12即 4×3＝ 5·CM ，因此 CM ＝ 5 .因为 DE ∥AB ，因此△ CDE ∽△ CAB .12因此 CN ＝ DE ，即 5 － x.＝ x CM AB 125560因此 x ＝37.如图 (2)所示，设正方形 CDEF 的边长为 y cm ，因为 EF ∥ AC ，因此△ BEF ∽△ BAC .BF EF 3－ y y12因此 BC ＝ AC ，即 3 ＝4，因此 y ＝ 7.60 12 60因为 x ＝37， y ＝ 7 ＝35，因此 x<y.因此当按图 (2) 的方法裁剪时，正方形面积最大，其边长为12cm.7。

数学几何选讲试题答案及解析1.（本小题满分10分）选修4－1：几何证明选讲如图，圆O的半径OB垂直于直径AC,M为AO上一点，BM的延长线交圆O于N，点是线段延长线上一点，连接PN,且满足（Ⅰ）求证：是圆O的切线；(Ⅱ)若圆O的半径为，OA=OM，求MN的长.【答案】（Ⅰ）见解析(Ⅱ) 2【解析】（Ⅰ）证明：如图，连接ON，∵，则，……2分又，则.,∴，……4分∴，故是圆O的切线．……5分(Ⅱ) .在△BOM中，，,延长BO交圆O于点D，连接DN，由条件知△BOM∽△BND,于是,，即MN=BN-BM=6-4=2.……10分【考点】本题考查切线的判定定理、三角形相似等基础知识，意在考查学生推理证明和逻辑思维能力.2.如图，，是圆的两条弦，它们相交于的中点，若，，,求圆的半径.【答案】1【解析】解：由，,，得 5分又为中点，，， 10分【考点】本题考查圆的基本性质，相交弦定理等知识，意在考查推理论证能力.3.（本小题满分10分）选修4－1：几何证明选讲如图，Δ是内接于圆，,直线切于点，弦，与相交于点．（1）求证：≌；（2）若求．【答案】（1）见解析（2）【解析】（1）在ΔABE和ΔACD中，∵，∠ABE=∠ACD．又∠BAE=∠EDC，∵BD∥MN，∴∠EDC=∠DCN，∵直线是圆的切线，∴∠DCN=∠CAD，∴∠BAE=∠CAD，∴Δ≌Δ（角、边、角）． 5分（2）∵∠EBC=∠BCM，∠BCM=∠BDC，∴∠EBC=∠BDC=∠BAC，BC=CD=4，又∠BEC=∠BAC+∠ABE=∠EBC+∠ABE=∠ABC=∠ACB，∴BC=BE=4．设AE=，易证ΔABE∽ΔDEC，∴，从而.又，，∴，解得.因此. 10分【命题意图】本题考察弦切角定理、等腰三角形的性质、三角形相似等基础知识，意在考察学生推理证明和逻辑思维能力.4.如图，已知△ABC的两条角平分线AD和CE相交于H，∠B＝60°，F在AC上，且AE＝AF.（1）证明：B、D、H、E四点共圆；（2）证明：CE平分∠DEF.【答案】（1）见解析（2）见解析【解析】（1）在△ABC中，因为∠ABC＝60°，所以∠BAC＋∠BCA＝120°.因为AD、CE是角平分线，所以∠HAC＋∠HCA＝60°，故∠AHC＝120°，于是∠EHD＝∠AHC＝120°.因为∠EBD＋∠EHD＝180°，所以B、D、H、E四点共圆．（2）连结BH，则BH为∠ABC的平分线，得∠HBD＝30°.由（1）知B、D、H、E四点共圆，所以∠CED＝∠HBD＝30°.又∠AHE＝∠EBD＝60°，由已知可得EF⊥AD.可得∠CEF＝30°.所以CE平分∠DEF.【点评】熟记圆的切线性质、圆周角定理、切割线定理、相交弦定理，这些知识点是解决有关圆的问题的关键，要好好理解．5.如图, 弦AB与CD相交于内一点E, 过E作BC的平行线与AD的延长线相交于点P. 已知PD＝2DA＝2, 则PE＝ .【答案】【解析】本题考查平面几何证明，利用三角形相似即可求解，属于容易题。

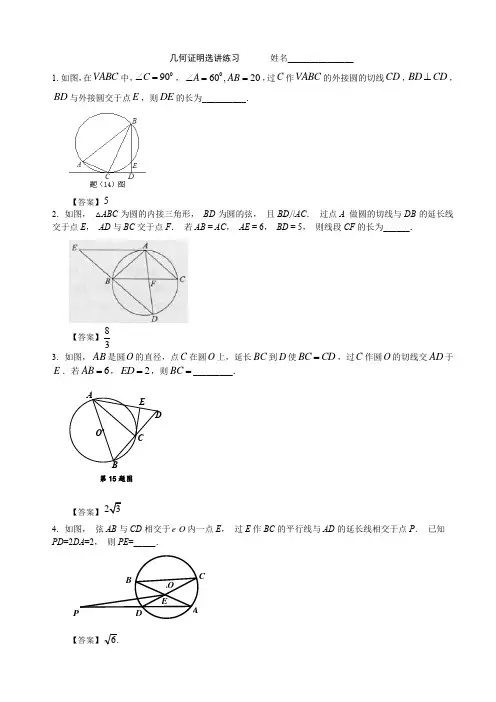
几何证明选讲练习 姓名_______________1．如图，在中，，，过作的外接圆的切线，，与外接圆交于点，则的长为__________．【答案】2．如图， △ABC 为圆的内接三角形， BD 为圆的弦， 且BD //AC ． 过点A 做圆的切线与DB 的延长线交于点E ， AD 与BC 交于点F ． 若AB = AC ， AE = 6， BD = 5， 则线段CF 的长为______．【答案】833．如图，AB 是圆O 的直径，点C 在圆O 上，延长BC 到D 使BC CD =，过C 作圆O 的切线交AD 于E ．若6AB =，2ED =，则BC =_________．【答案】4．如图， 弦AB 与CD 相交于O 内一点E ， 过E 作BC 的平行线与AD 的延长线相交于点P ． 已知PD =2DA =2， 则PE =_____．【答案】.6 ABC 090C ∠=060,20A AB ∠==C ABC CD BD CD ⊥BD EDE5.A ED CB O 第15题图5．如图2，O 中，弦,AB CD 相交于点,2P PA PB ==，1PD =，则圆心O 到弦CD 的距离为____________．【答案】23 6．如图，圆O 上一点C 在直线AB 上的射影为D ，点D 在半径OC 上的射影为E ．若3AB AD =，则CEEO的值为___________．【答案】8 7．如图，AB 为圆O 的直径，P A 为圆O 的切线，PB 与圆O 相交于D ．若PA=3，916PD DB =：：，则PD=_________；AB=___________．【答案】95；4 解三角形练习1．如图，△ABC 中，AB=AC=2，BC=点D在BC 边上，∠ADC=45°，则AD 的长度等于______．【命题意图】本题考查运用正余弦定理解三角形，是中档题．【解析】（法1）过A 作AE ⊥BC,垂足为E ，∵AB=AC=2，BC=∴E 是BC 的中点，且EC=O D EBACRt AEC ∆中，AE=又∵∠ADE=45°，∴DE=1，∴AD=（法2） ∵AB=AC=2，BC=由余弦定理知，cos C =2222AC BC AB AC BC +-⨯∴C=30°， 在△ADC 中，∠ADE=45°，由正弦定理得，sin sin AD AC C ADC=∠， ∴AD=sin sin AD C ADC ∠=12⨯2．如图，在△ABC 中，D 是边AC 上的点，且AB AD =，2AB =，2BC BD =，则sin C 的值为（ ）A．3 B．6 C3 D6【答案】D【解析】设BD a =,则由题意可得:2,BC a =2AB AD a ==,在ABD ∆中,由余弦定理得： 222cos 2AB AD BD A AB AD +-==⋅2232a a ⨯-=13，所以sin A=，在△ABC 中，由正弦定理得，sin sin AB BC C A =，所以2sin C =，解得sin CD ． 3．,EF 是等腰直角ABC ∆斜边AB 上的三等分点，则tan ECF ∠=（ ）A ．1627B ．23 CD ．34【答案】D4．在△ABC 中， 4ABC π∠=，AB 3BC =，则sin BAC ∠ =（ ） （A ）（B ）（C ）（D ）【答案】C5．ABC ∆中，90C ∠=，M 是BC 的中点，若31sin =∠BAM ，则=∠BAC sin ________．【答案】36．在△ABC 中，已知AB=4，AC=7，BC 边的中线27=AD ，求边BC 的长．7．如图，在四边形ABCD 中，AC 平分∠DAB ，∠ABC=60°，AC=7，AD=6，S △ADC =2315，求AB 的长．排列组合练习题1．有6位同学在毕业聚会活动中进行纪念品的交换，任意两位同学之间最多交换一次，进行交换的两位同学互赠一份纪念品，已知6位同学之间共进行了13次交换，则收到份纪念品的同学人数为（ ） 或 或 或 或【解析】选①设仅有甲与乙，丙没交换纪念品，则收到份纪念品的同学人数为人②设仅有甲与乙，丙与丁没交换纪念品，则收到份纪念品的同学人数为人．2．将字母排成三行两列，要求每行的字母互不相同，每列的字母也互不相同，则不同的排列方法共有A ．12种B ．18种C ．24种D ．36种答案A【命题意图】本试题考查了排列组合的用用．4()A 13()B 14()C 23()D 24D 261315132C -=-=4244,,,,,a a b b c c【解析】利用分步计数原理，先填写最左上角的数，有3种，再填写右上角的数为2种，在填写第二行第一列的数有2种，一共有．3．现有16张不同的卡片，其中红色、黄色、蓝色、绿色卡片各4张，从中任取3张，要求这些卡片不能是同一种颜色，且红色卡片至多1张，不同取法的种数为（A ）232 (B)252 (C)472 (D)484解析：,答案应选C ． 另解：． 4． 两人进行乒乓球比赛，先赢三局着获胜，决出胜负为止，则所有可能出现的情形（各人输赢局次的不同视为不同情形）共有（ ）A ．10种B ．15种C ．20种D ．30种【解析】甲赢和乙赢的可能情况是一样的，所以假设甲赢的情况如下：若两人进行3场比赛，则情况只有是甲全赢1种情况；若两人进行4场比赛，第4场比赛必为甲赢前3场任选一场乙赢为种情况；若两人进行5场比赛，第5场比赛必为甲赢前4场任选一场乙赢为种情况；综上，甲赢有10种情况，同理，乙赢有10种情况，则所有可能出现的情况共20种，故选C ．5．若从1，2，2，…，9这9个整数中同时取4个不同的数，其和为偶数，则不同的取法共有A ．60种B ．63种C ．65种D ．66种【解析】1，2，2，…，9这9个整数中有5个奇数，4个偶数．要想同时取4个不同的数其和为偶数，则取法有：4个都是偶数：1种；2个偶数，2个奇数：种； 4个都是奇数：种．∴不同的取法共有66种．【答案】D6．某艺校在一天的6节课中随机安排语文、数学、外语三门文化课和其他三门艺术课个1节，则在课表上的相邻两节文化课之间最多间隔1节艺术课的概率为 （用数字作答）．【解析】概率为 语文、数学、英语三门文化课间隔一节艺术课，排列有种排法，语文、数学、英语三门文化课相邻有种排法，语文、数学、英语三门文化课两门相邻有种排法． 32212⨯⨯=472885607216614151641122434316=-=--⨯⨯=--C C C C 472122642202111241261011123212143431204=-+=⨯⨯+-⨯⨯=+-C C C C C 313=C 624=C 225460C C =455C =3____53344A A 3312122223A C C A C3故所有的排法种数有在课表上的相邻两节文化课之间最多间隔1节艺术课的概率为5。

几何证明选讲（2011-2015全国卷文科）（一）新课标卷1.（2011.全国新课标22）（本小题满分10分）选修4-1：几何证明选讲如图，D ，E 分别为ABC ∆的边AB ，AC 上的点，且不与ABC ∆的顶点重合．已知AE 的长为m ，AC 的长为n ，AD ，AB 的长是关于x 的方程2140x x mn -+=的两个根． （I ）证明：C ，B ，D ，E 四点共圆；（II ）若90A ∠=︒，且4,6,m n ==求C ，B ，D ，E 所在圆的半径．2.（2012.全国新课标22）（本小题满分10分）选修4-1：几何证明选讲如图，D ，E 分别为△ABC 边AB ，AC 的中点，直线DE 交△ABC 的外接圆于F ，G 两点，若CF//AB ，证明： (Ⅰ)CD=BC ； (Ⅱ)△BCD ∽△GBDFGDE AB C（二）全国Ⅰ卷1.（2013.全国1卷22）（本小题满分10分）选修4—1：几何证明选讲如图，直线AB为圆的切线，切点为B，点C在圆上，∠ABC的角平分线BE交圆于点E，DB垂直BE交圆于D。

（Ⅰ）证明：DB=DC；（Ⅱ）设圆的半径为1，BC=3，延长CE交AB于点F，求△BCF外接圆的半径。

2.（2014.全国1卷22）（本小题满分10分）选修4-1，几何证明选讲如图，四边形ABCD是O的内接四边形，AB的延长线=.与DC的延长线交于点E，且CB CE∠=∠；（I）证明：D E=，（II）设AD不是O的直径，AD的中点为M，且MB MC ∆为等边三角形.证明：ABC3.（2015.全国1卷22）（本小题满分10分）选修4-1：几何证明选讲如图AB 是O 直径，AC 是O 切线，BC 交O 与点E . （I ）若D 为AC 中点，证明：DE 是O 切线； （II ）若3OACE = ，求ACB ∠的大小.（三）全国Ⅱ卷1.（2013.全国2卷22）(本小题满分10分)选修4—1：几何证明选讲如图，CD 为△ABC 外接圆的切线，AB 的延长线交直线CD 于点D ，E ，F 分别为弦AB 与弦AC 上的点，且BC·AE＝DC·AF ,B ，E ，F ，C 四点共圆． (1)证明：CA 是△ABC 外接圆的直径．(2)若DB=BE=EA,求过B ，E ，F ，C 四点的圆的面积与△ABC 外接圆面积的比值2.（2014.全国2卷22）（本小题满分10分）选修4-1：几何证明选讲如图，P 是⊙O 外一点，PA 是切线，A 为切点，割线PBC 与⊙O 相交于点B ，C ，PC=2PA ，D 为PC 的中点，AD 的延长线交⊙O 于点E ，证明: （I ）BE=EC ；（II ）AD ·DE=2PB 2。

几何证明选讲试题及参考答案几何证明是属于宣讲的一个知识点，关于这些的是试题有哪些呢?下面就是学习啦给大家的几何证明选讲试题内容，希望大家喜欢。

(1)四边形BCDE的外接圆是不是连接四边形中任意三点的三角形的外接圆?答案是肯定的!(2)三角形的外接圆半径与解三角形中的哪个定理联系很紧密?——正弦定理正弦定理的表达形式： = = =2R,其中这里边的R，就是三角形的外接圆半径。

那么，我们只要找到三角形的一边长和该边所对的角，就能将半径求出，而不需做出圆心。

解题过程：在△ABC中，连接DE、CD,根据AE=4，AC=6易知， .则DE2 =AE2+AD2 所以DE=2 ，又在△ADC中，sin∠ACD= = = 所以在三角形DCE中， =2R=10 所以R=5 .这种解题方法的掌握，是在有了扎实的基本功基础上的巧妙联想和合理推测证明，有利于学生知识体系的构建和基础知识的提升。

线、角、相交线、平行线规律1如果平面上有n(n≥2)个点，其中任何三点都不在同一直线上，那么每两点画一条直线，一共可以画出n(n-1)条。

规律2平面上的n条直线最多可把平面分成〔n(n+1)+1〕个部分。

规律3如果一条直线上有n个点，那么在这个图形中共有线段的条数为n(n-1)条。

规律4线段(或延长线)上任一点分线段为两段，这两条线段的中点的距离等于线段长的一半。

规律5有公共端点的n条射线所构成的交点的个数一共有n(n-1)个。

规律6如果平面内有n条直线都经过同一点，则可构成小于平角的角共有2n(n-1)个。

规律7如果平面内有n条直线都经过同一点，则可构成n(n-1)对对顶角。

规律8平面上若有n(n≥3)个点，任意三个点不在同一直线上，过任意三点作三角形一共可作出n(n-1)(n-2)个。

规律9互为邻补角的两个角平分线所成的角的度数为90°。

规律10平面上有n条直线相交，最多交点的个数为n(n-1)个。

规律11互为补角中较小角的余角等于这两个互为补角的角的差的一半。

高二数学几何选讲试题答案及解析于点，过点作两1.如图，已知⊙与⊙相交于、两点，过点A作⊙的切线交⊙O2圆的割线，分别交⊙、⊙于点、，与相交于点.（1）求证：；（2）若是⊙的切线，且，，求的长．【答案】（1）证明见解析；（2）【解析】（1）圆的切线的性质定理圆的切线垂直于过切点的半径，推论1经过圆心且垂直于切线的直线必过切点，推论2经过切点且垂直于切线的直线必过圆心；（2）圆的切线的性质定理经过半径的外端并且垂直于这条半径的直径是圆的切线；若已知条件中直线与圆的公共点不明确，则应过圆心作直线的垂线，得到垂线段，设法证明这条垂线段的长等于圆的半径；（3）掌握与圆有关的比例线段，如相交弦定理，割线定理，切割线定理，切线长定理.试题解析：解：（I）∵AC是⊙O的切线，∴∠BAC＝∠D，1又∵∠BAC＝∠E，∴∠D＝∠E，∴AD∥EC. 5分（II）设BP＝x，PE＝y，∵PA＝6，PC＝2，∴＝12 ①∵AD∥EC，∴，∴②由①、②解得（∵x>0，y>0）∴DE＝9＋x＋y＝16，∵AD是⊙O的切线，∴AD2＝DB·DE＝9×16，∴AD＝12. 11分2【考点】（1）证明直线与直线平行；（2）求切线长.2.如图，在△ABC中，AB=8，AC=7，BC=6，D是AB的中点，∠ADE=∠ACB，则DE=_________．【答案】.【解析】首先由知，∽，所以.然后因为AB=8，D是AB的中点，所以.又AC=7，BC=6，所以，即.【考点】相似三角形的性质.3.如图，AC为⊙O的直径，OB⊥AC，弦BN交AC于点M．若OC=，OM=1，则MN=_________．【答案】1.【解析】因为AC为⊙O的直径，OB⊥AC，且OC=，OM=1，所以，. 设，由相交弦定理知，即，所以，即.【考点】与圆有关的比例线段.4.如图，四边形是圆的内接四边形，延长和相交于点，若，，则的值为（）A．B．C．D．【答案】B【解析】四边形是圆的内接四边形，它的两对对角互补，进而得到∽，因而有，故选择B.【考点】平面几何中的圆与四边形.5.如图在△中,∥,,交于点,则图中相似三角形的对数为( ).A．1B．2C．3D．4【答案】B【解析】,;又,,故选B.【考点】相似三角形.6.如图所示，△ABC内接于⊙O，AB＝AC，直线XY切⊙O于点C，BD∥XY，AC、BD相交于E.(1)求证：△ABE≌△ACD；(2)若AB＝6 cm，BC＝4 cm，求AE的长．【答案】（1）见解析；（2）.【解析】（1）欲证三角形全等，需牢牢掌握这种证明方法和所需要的条件.本小题,(已知)，下寻找另外的边和角，考虑到这里有圆，所以运用同弧所对应的圆周角相等可得(弧所对)，接着证明(其他角和边不好证，同时这里有弦切角可以利用).（2）欲求,因,则可转化为求,考虑到，需将联系起来就得考虑三角形相似.注意到,.试题解析：(1)证明因为XY是⊙O的切线，所以.因为，所以，∴. 2分因为，所以. 4分因为，又因为，所以. 5分(2)解因为，，所以， 7分所以，即 8分因为，，所以.所以AE. 10分【考点】（1）三角形全等的证明；（2）三角形相似的证明与应用；（3）圆性质的应用.7.如图，已知圆中两条弦AB与CD相交于点F，E是AB延长线上一点，且DF＝CF＝，AF∶FB∶BE＝4∶2∶1，若CE与圆相切，求线段CE的长.【答案】【解析】利用相交弦定理可得到的等量关系，并结合已知条件可计算出,利用切割线定理可得到的等量关系，并结合前面所得可得结果.试题解析：由相交弦定理得，由于，可解得，所以.由切割线定理得，即.【考点】相交弦定理，切割线定理.8.若一个直角三角形的一条直角边为3 cm，斜边上的高为2.4 cm，则这个直角三角形的面积为A．7.2 cm2B．6 cm2C．12 cm2D．24 cm2【答案】B【解析】长为3 cm的直角边在斜边上的射影为＝1.8 (cm)，故由射影定理知斜边长为＝5 (cm)，∴三角形的面积为×5×2.4＝6 (cm2)．9.如图，在直角梯形ABCD中，DC∥AB，CB⊥AB，AB＝AD＝a，CD＝，点E，F分别为线段AB，AD的中点，则EF＝________.【答案】【解析】连接BD、DE，由题意可知DE⊥AB，DE＝a，即BC＝DE＝a，∴BD＝＝a，∴EF＝BD＝.10.如图所示，圆内的两条弦AB、CD相交于圆内一点P，已知PA＝PB＝4，PC＝PD.求CD 的长．【答案】10【解析】解设CD＝x，则PD＝x，PC＝x.由相交弦定理，得PA·PB＝PC·PD，∴4×4＝x·x，x＝10.∴CD＝10.11.如图所示，PA是⊙O的切线，切点为A，PA＝2.AC是⊙O的直径，PC与⊙O交于点B，PB＝1，则⊙O的半径r＝________.【答案】【解析】依题意，△PBA∽△ABC，所以＝，即r＝＝＝.12.如图所示，P、Q分别在BC和AC上，BP∶CP＝2∶5，CQ∶QA＝3∶4，则等于A．3∶14B．14∶3C．17∶3D．17∶14【答案】B【解析】过Q点作QM∥AP交BC于M，则＝＝，又∵＝，∴＝.又＝＝，＝＝，∴＝，∴＝.13.如图所示，点D、E分别在AB、AC上，下列条件能判定△ADE与△ACB相似的有①∠AED＝∠B②＝③＝④DE∥BCA．1个 B．2个 C．3个 D．4个【答案】C【解析】由判定定理1知①正确，由判定定理2知②正确，由预备定理1知④正确，③不符合相似三角形的判定定理，故不正确，从而选C.14.如图所示，在直角梯形ABCD中，AB＝7，AD＝2，BC＝3.设边AB上的一点P，使得以P、A、D为顶点的三角形和以P、B、C为顶点的三角形相似，那么这样的点P有A．1个 B．2个C．3个 D．4个【答案】C【解析】设AP＝x，则PB＝7－x.(1)若△PAD∽△PBC，则＝，即＝，得x＝<7，符合条件．(2)若△PAD∽△CBP，即＝，x2－7x＋6＝0，解得x1＝1，x2＝6也符合条件，故满足条件的点P 有3个．15. 在四边形ABCD 中，∠A ＝135°，∠B ＝∠D ＝90°，BC ＝2，AD ＝2，则四边形ABCD 的面积是______． 【答案】4【解析】因∠B ＝∠D ＝90°，于是设想构造直角三角形，延长BA 与CD 的延长线交于E ，则得到Rt △BCE 和Rt △ADE ，由题目条件知，△ADE 为等腰直角三角形，所以DE ＝AD ＝2，所以S △ADE ＝×2×2＝2. 又可证Rt △EBC ∽Rt △EDA ， 所以＝2＝2＝3.∴S △EBC ＝3S △EDA ，∴S 四边形ABCD ＝S △EBC －S △ADE ＝4.16. 如图所示，D 为△ABC 中BC 边上的一点，∠CAD ＝∠B ，若AD ＝6，AB ＝8，BD ＝7，求DC 的长．【答案】9【解析】解 ∵∠CAD ＝∠B ，∠C ＝∠C ， ∴△CAD ∽△CBA.∴＝＝.∴AC ＝，AC ＝.∴＝.设CD ＝x ， 则＝，解得x ＝9.故DC ＝9.17. 如图所示，已知⊙O 的两条弦AB 、CD 相交于AB 的中点E ，且AB ＝4，DE ＝CE ＋3，则CD 的长为________．【答案】5【解析】由相交弦定理知 EA·EB ＝EC·ED. (*)又∵E 为AB 中点，AB ＝4，DE ＝CE ＋3， ∴(*)式可化为22＝EC(CE ＋3)＝CE 2＋3CE ， ∴CE ＝－4(舍去)或CE ＝1.∴CD ＝DE ＋CE ＝2CE ＋3＝2＋3＝5.18. 如图所示，已知BC 是⊙O 的弦，P 是BC 延长线上一点，PA 与⊙O 相切于点A ，∠ABC ＝25°，∠ACB＝80°，求∠P的度数．【答案】55°【解析】解因为PA与⊙O相切于点A，所以∠PAC＝∠ABP＝25°.又因为∠ACB＝80°，所以∠ACP＝100°.又因为∠PAC＋∠PCA＋∠P＝180°，所以∠P＝180°－100°－25°＝55°.19.(拓展深化)如图所示，△ABC内接于⊙O，AB＝AC，直线XY切⊙O于点C，BD∥XY，AC、BD相交于E.(1)求证：△ABE≌△ACD；(2)若AB＝6 cm，BC＝4 cm，求AE的长．【答案】(1)见解析 (2)cm【解析】(1)证明因为XY是⊙O的切线，所以∠1＝∠2.因为BD∥XY，所以∠1＝∠3，∴∠2＝∠3.因为∠3＝∠4，所以∠2＝∠4.因为∠ABD＝∠ACD，又因为AB＝AC，所以△ABE≌△ACD.(2)解因为∠3＝∠2，∠ABC＝∠ACB，所以△BCE∽△ACB，＝，AC·CE＝BC2.因为AB＝AC＝6 cm，BC＝4 cm，所以6·(6－AE)＝16.所以AE＝cm.20.如图所示，在Rt△ABC中，∠C＝90°，AC＝4，BC＝3，以BC上一点O为圆心作⊙O与AB相切于E，与AC相切于C，又⊙O与BC的另一个交点为D，则线段BD的长为A．1B．C．D．【答案】C【解析】⊙O与AC相切于C，则∠ACB＝90°，又AC＝4，BC＝3，∴AB＝5，连接OE，且设⊙O的半径为R，则由△OEB∽△ACB，∴OB＝＝R，∴BC＝OC＋OB＝R＋R＝R＝3，∴R＝，∴BD＝BC－2R＝3－＝.21.若两条直线(a＋2)x＋(1－a)y－3＝0，(a－1)x＋(2a＋3)y＋2＝0与两坐标轴围成的四边形有一个外接圆，则实数a＝________.【答案】1或－1【解析】由圆内接四边形的性质，知(a＋2)(a－1)＋(1－a)·(2a＋3)＝0，整理得a2＝1，∴a＝±1. 22.(拓展深化)如图，已知△ABC中的两条角平分线AD和CE相交于H，∠B＝60°，F在AC上，且AE＝AF.(1)证明：B、D、H、E四点共圆；(2)证明：CE平分∠DEF.【答案】见解析【解析】证明(1)在△ABC中，因为∠B＝60°，所以∠BAC＋∠BCA＝120°.因为AD，CE是角平分线，所以∠HAC＋∠HCA＝60°，故∠AHC＝120°.于是∠EHD＝∠AHC＝120°.因为∠EBD＋∠EHD＝180°，所以B、D、H、E四点共圆．(2)连接BH，则BH为∠ABC的平分线，得∠HBD＝30°.由(1)知B、D、H、E四点共圆．所以∠CED＝∠HBD＝30°.又∵∠AHE＝∠EBD＝60°，由已知可得EF⊥AD，可得∠CEF＝30°，所以CE平分∠DEF.23.如图，点A、B、C是圆O上的点，且AB＝4，∠ACB＝30°，则圆O的面积等于A．4π B．8πC．12π D．16π【答案】D【解析】连接OA、OB，∵∠ACB＝30°，∴∠AOB＝60°，又∵OA＝OB，∴△AOB为等边三角形，又AB＝4，∴OA＝OB＝4，∴S＝π·42＝16π.⊙O24.在Rt△ABC中，∠BAC＝90°，AD⊥BC，垂足为D.若BC＝m，∠B＝α，则AD的长为A．m sin2α B．m cos2αC．m sin αcos α D．m sin αtan α【答案】C【解析】由射影定理，得AB2＝BD·BC，AC2＝CD·BC，即m2cos2α＝BD·m，m2sin2α＝CD·m，即BD＝mcos2α，CD＝msin2α.又∵AD2＝BD·DC＝m2cos2αsin2α，∴AD＝mcos αsin α.故选C.25.如图，在正方形ABCD中，E为AB的中点，AF⊥DE于点O，则等于________．【答案】【解析】在Rt△DAO及Rt△DEA中，∠ADO为公共角，∴Rt△DAO∽Rt△DEA，∴＝，即＝.∵E为AB的中点，∴＝＝，∴＝.26. (拓展深化)如图，M为线段AB的中点，AE与BD交于点C，∠DME＝∠A＝∠B＝α.且DM交AC于F，ME交BC于G，(1)写出图中三对相似三角形，并证明其中的一对；(2)连接FG，如果α＝45°，AB＝4，AF＝3，求FG的长．【答案】(1)△AMF∽△BGM，△DMG∽△DBM，△EMF∽EAM，证明见解析 (2)【解析】解(1)△AMF∽△BGM，△DMG∽△DBM，△EMF∽EAM.以下证明：△AMF∽△BGM.∵∠AFM＝∠DME＋∠E＝∠A＋∠E＝∠BMG，∠A＝∠B，∴△AMF∽△BGM.(2)当α＝45°时，可得AC⊥BC且AC＝BC.∵M为AB的中点，∴AM＝BM＝2.又∵△AMF∽△BGM，∴＝∴BG＝＝＝.又AC＝BC＝4×sin 45°＝4，∴CG＝4－＝.∵CF＝4－3＝1，∴FG＝＝＝.27.如图所示，已知DE∥BC，BF∶EF＝3∶2，则AC∶AE＝________，AD∶DB＝________.【答案】3∶22∶1【解析】∵DE∥BC，∴＝＝.∵BF∶EF＝3∶2，∴＝＝.∴AC∶AE＝3∶2.又DE∥BC，得AB∶AD＝3∶2，即＝.∴＝.即＝＝2，即＝2.∴AD∶BD＝2∶1.28.如图，以梯形ABCD的对角线AC及腰AD为邻边作平行四边形ACED，DC的延长线交BE于点F，求证：EF＝BF.【答案】见解析【解析】证明如图所示，连接AE交DC于O.∵四边形ACED是平行四边形．∴O是AE的中点．∵在梯形ABCD中，DC∥AB，在△EAB中，OF∥AB，又∵O是AE的中点，∴F是EB的中点，∴EF＝BF.29.如图甲,四边形是等腰梯形,.由4个这样的等腰梯形可以拼出图乙所示的平行四边形,则四边形中度数为 ( )A．B．C．D．【答案】C【解析】由于上底和两腰长已知，故要求梯形面积，关键是要找出底边上和高，由于图形中无法再分析出边与边的关系，所以我们可以从角的方向入手，求梯形的内角。