青岛科技大学 2012-2013 电路分析A2(A卷)
- 格式:pdf
- 大小:178.84 KB
- 文档页数:4

青岛科技大学2006年研究生入学考试(A )考试科目:电子技术(答案全部写在答题纸上)一、填空题(20分,每空1分) 1. 判断下列说法是否正确在答题纸上写明题号,用“√”和“×”表示判断结果。
(1) 在P 型半导体中如果掺入足够量的五价元素,可将其改型为N 型半导体。
( ) (2) 电路中各电量的交流成份是交流信号源提供的;( )(3) 现测得两个共射放大电路空载时的电压放大倍数均为-100,将它们连成两级放大电路,其电压放大倍数应为10000。
( )(4) 运放的输入失调电压U IO 是两输入端电位之差。
( ) (5) 运放的输入失调电流I IO 是两输入端电流之差。
( )(6) 若放大电路的放大倍数为负,则引入的反馈一定是负反馈。
( )(7)负反馈放大电路的放大倍数与组成它的基本放大电路的放大倍数量纲相同。
( ) (8)若放大电路引入电压负反馈,则负载电阻变化时,输出电压基本不变。
( )(9)在运算电路中,集成运放的反相输入端均为虚地。
( ) (10)凡是运算电路都可利用“虚短”和“虚断”的概念求解运算关系。
( )(11)只要电路引入了正反馈,就一定会产生正弦波振荡。
( )(12)若U 2为电源变压器副边电压的有效值,则半波整流电容滤波电路和全波整流电容滤波电路在空载时的输出电压均为22U 。
( )2. 在图1所示电路中, 已知 V C C =12V ,晶体管的β=100,'b R =100k Ω。
填空:要求先填文字表达式后填得数。
(1)当iU &=0V 时,测得U B E Q =0.7V ,若要基极电流I B Q =20μA ,则'b R 和R W 之和R b =( )≈( )k Ω; 而若测得U C E Q =6V ,则R c =( )≈( )k Ω。
(2)若测得输入电压有效值i U =5mV 时,输出电压有效值'o U =0.6V , 则电压放大图 1倍数uA &=( )≈( ) 。
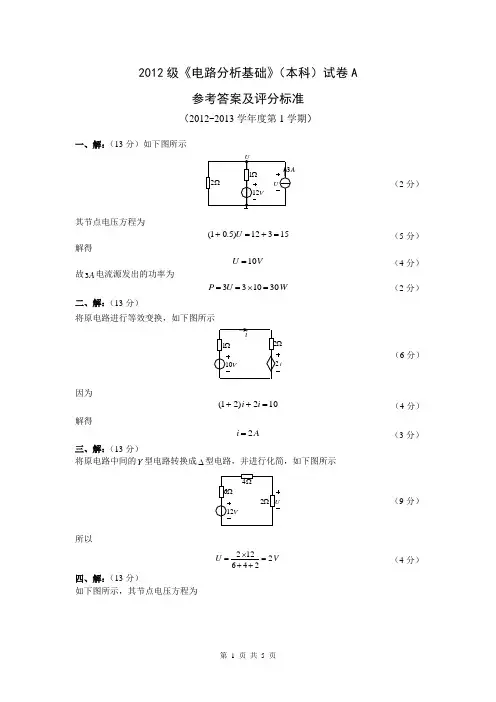
2012级《电路分析基础》(本科)试卷A参考答案及评分标准(2012-2013学年度第1学期)一、解:(13分)如下图所示其节点电压方程为 15312)5.01(=+=+U解得V U 10=故A 3电流源发出的功率为W U P 301033=⨯==二、解:(13分)将原电路进行等效变换,如下图所示 因为102)21(=++i i解得A i 2=三、解:(13分)将原电路中间的Y 型电路转换成∆型电路,并进行化简,如下图所示所以V U 2246122=++⨯=四、解:(13分)如下图所示,其节点电压方程为(4分)4(6分)(3分)(4分) (9分)(4分) (2分)(2分)(5分)⎪⎪⎩⎪⎪⎨⎧=⎪⎭⎫ ⎝⎛+++-⨯-==-⎪⎭⎫⎝⎛+++⨯-02121212112214282121212112212121u u u u 整理得⎩⎨⎧=+-=-1232032121u u u u 解得V u 91=,V u 72=。
因为A u i 5.1291221211=-=-=A u i 5.2271221222=-=-=所以A i i i 45.25.121=+=+=故V 12电压源发出的功率为W i P 4841212=⨯==五、解:(12分)将电阻R 开路,对所余一端口进行戴维宁等效,如下图所示由左上图可得V u oc 3912221821261812=-=+⨯-+⨯=由右上图可得Ω=+=+=54112//62//2eq R将戴维宁等效电源接上电阻R ,如下图所示由上图可得(2分)(1分)(1分) (1分)(1分) (2分)(5分)(3分)(1分)(3分)(2分)ΩΩ2ΩΩΩΩ253=+=R R U解得Ω=10R六、解:(12分)将原电路改画成如下电路将负载断开,对断开后的电路进行戴维宁等效。
1. 求开路电压oc u如上图所示,其网孔电流方程为⎩⎨⎧-=+-=-1012440482121i i i i 整理得⎩⎨⎧-=+-=-5621022121i i i i 解得A i 5.51=,A i 12=。

三、是非判断题(本大题共5小题,每小题2共101、2、3XXXXX常熟理工学院诚题12春参考答案及评分标准学年第学期课程名称:电路分析基础使用班级:制作人:年月日一、填空题(每空1分,共10分)1、吸收:发出;2、理想电流源;理想电压源;3、n~l, b~n+l4、夕卜;内;5、相等;相差120°二、单项选择题(本大题共5小题,每小题2分,共10分)1、A2、B3、C4、A5、B四、计算题(本大题共6小题,共70分)1、(12 分)(B)(A)解6 V电压源作用时.电路可化简如题3・6僻图00所示.用节点电压法分析•有(十+土)。
=号一%24-亨U,= —V求得再由的=6+17',得(5分)求得G +加=5 —%顷=4 V (5分)\7 分5 A电流源作用时,电路可化简如题3・6解图(b)所示.用节点法分析•有由登加定理得u = ir+cr = (42、(12 分)解:r~i|Ji?i=5on丫上一K =220 V J尸5on n^L^son由戴维宁定理可得Uoc = 220 V= 110 V (2 分)%Rg = 5O//5O n = 25 n (2 分)故“=” A r 1. 47 A (2 分)十XXL Zb 十uU由诺顿定理求得农 H 攀A = 4.4A (2 分)Req = 25" (2 分)故九= IxX天套Ql.47 A (2分)乙。
十Ov— 2Q © 3Q(3(2A =应用行列式法解得8118-2181118= 162162(5127()结点编号如图所示,选结点④为参考点。
在列方程时,受控电流源按独立电流源对待,即12V电压源不计入方程中。
列出结点电压方程Ki = 6_ 如扁1 + 弓+ § + 1)""2 — J U H3=°+"*+(土 + 如〃3=十1/ =族+』/在结点④列KCL方程有'13'从中解得用结点电压表示控制量L的辅助方程L T・5"〃2把"〃I =6, ' =1.5"〃2代入其余两个方程中并加以整理可得方程1 1“〃2 ~U n3 = * 2U,“+7%3 =18所以结点电压为电流/, = 1 .5"〃2 = 1 .5 x 2 =34(25、(12 分)解:I- J^U,a -凯2 +(2 + /8力〃3 =八=1匕3(f(4分)由三要素法得T=RC=(3//6//2)X2=2S(1 U C0) = u c(°°)+ 伍C(°+ )-"c(8)k r =3 + (6-3)很=3 + 3。

5图6图7 所示电路,已知当,1V S U ==S I 。
求当,时,3V S U =2A S I =U图 9所示双口网络的Z ,Y ,H 参数。
(20分)Ω2Ω21I 2I青 岛 科 技 大 学二O 一O 年硕士研究生入学考试试题考试科目:电路注意事项:1.本试卷共八道大题(共计12个小题),满分150分;2.本卷属试题卷,答题另有答题卷,答案一律写在答题卷上,写在该试题卷上或草纸上均无效。
要注意试卷清洁,不要在试卷上涂划;3.必须用蓝、黑钢笔或签字笔答题,其它均无效。
﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡ 一、简答题 (5小题, 共36分)1.理想电压源和电阻并联的等效电路是什么?从两个不同角度说明结论的正确性。
(6分)2.说明电阻Y -△转换化简电阻的原理。
(6分)3.互易定理成立的条件是什么?如果网络N 内含有耦合电感元件,那么互易定理还成立吗?说明理由。
(8分)4.给出含耦合的两个电感元件并联的等效电感公式,并加以证明。
(8分)5.画出用二瓦特计法测量三相功率的电路来,并以负载为三角形联接为例,证明结论。
(8分)二、求图1所示电路的输入电阻。
(15分)ab R第 1 页(共 3 页)图1三、在图2所示电路中,用戴维宁定理和回路电流法分别求电流。
(各12分,共24分)1I四、在图3所示正弦稳态电路中,已知,,,Ω==1021R R Ω=101L ωΩ=51Cω求:(1) 闭合,断开时的电流;(5分)V U 100=1S 2S I(2) 、都闭合时的电流及电流表的读数。
(10分)1S 2S I五、在图4中网络N 仅由电阻组成,根据图(a)和(b)的已知情况,求图(c)中的电流和(15分) 1I 2I第 2 页(共 3 页)图2图3图4六、图5所示电路中,V ,,,,t u s 100cos 2100=H L 4.01=H L 6.02=H M 2.0=F C μ500=,调节,使负载获最大有功功率。

(答案要注明各个要点的评分标准)一、填空题(每小题3分,共15分)1. 2;2. 2;3. t4. 1;5. 2M.二、选择题(每小题3分,共15分)1. A ;2. C ;3. D ;4. D ;5. A.三、计算题(每小题10分,共20分)1.解:1111234514916182764=1111123414916182764=12 ………………………… 10分2. 解: ()2A E B A -= ……………………………3分()2234232110110121123A E A ⎛⎫ ⎪-=- ⎪ ⎪--⎝⎭~r 1003860102960012129⎛--⎫⎪-- ⎪ ⎪-⎝⎭………8分 1386(2)2962129B A E A ---⎛⎫⎪∴=-=-- ⎪ ⎪-⎝⎭………………………10分四、计算题(第1题10分,第2题15分,第3题15分,共40分)1、解对矩阵[]12345A ααααα= 进行初等行变换可得11012121360112401111A ---⎡⎤⎢⎥-⎢⎥=⎢⎥⎢⎥--⎣⎦11012011240112401111---⎡⎤⎢⎥⎢⎥→⎢⎥⎢⎥--⎣⎦ 11012011240003500000---⎡⎤⎢⎥⎢⎥→⎢⎥⎢⎥⎣⎦…………………………8分 向量组 124ααα 是一个极大无关向量组。
…………………………10分2、解:方程组的增广矩阵()2211111,111111111~r B A b λλλλλλλλλλ⎛⎫⎛⎫ ⎪ ⎪== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭()()()()222223211110110110111002111~~λλλλλλλλλλλλλλλλλλλ⎛⎫⎛⎫ ⎪⎪------ ⎪ ⎪ ⎪⎪ ⎪---+--+⎝⎭⎝⎭…5分 (1) 若2λ≠-且1λ≠,()()3R A R B ==方程组有唯一解。
………8分 (2) 若()()2,R A R B λ=-<,方程组无解。
第 页(共26页) 1 青 岛 科 技 大 学
二○一六年硕士研究生入学考试试题
考试科目:电路
注意事项:1.本试卷共12道大题(共计12个小题),满分150分;
2.本卷属试题卷,答题另有答题卷,答案一律写在答题卷上,写在该试题卷上或草纸上均无效。
要注意试卷清洁,不要在试卷上涂划;
3.必须用蓝、黑钢笔或签字笔答题,其它均无效。
﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡
﹡﹡
1、图1所示三相对称电路(感性)中,当S 打开时,A 2电流表读数为3
A ,且2P =1P 。
求:(1)当S 打开时,其它二个电流表的读数;(2)若将S 闭合,则图中各电流表和功率表的读数分别(用1
P 表示)是多少?(12分)。
A1
A2
A3W1**
W2**A B C
Z Z Z S
图1 图2
2、图2电路中1i =0.6A ,求i 和X R 。
(10分)
3、在图3(b)所示电路中,2A I =且S 6A I =,求图3(a)电路的I 。
(10分)
4、图4所示正弦稳态电路中,U=15V ,I=5A ,R=5Ω。
求:(1)I L 及L ω,(2)电路的S 、P 、
Q 、cos ϕ 。
(12分)
5、在图5所示电路中,如果换路前电路已处于稳态,开关在位置1上,换路后合到位置2。

2012-20132 线性代数 (A 卷)数理学院 全校相关专业(答案写在答题纸上,写在试题纸上无效)一、填空题(每小题3分,共15分)1.设1221304012107301---=D ,则D 的代数余子式=23A ;2.设C B A ,,均为n 阶方阵,且E ABC =,则=T T CA B )( ;3.设A 为四阶方阵,且2-=A ,*A 是A 的伴随矩阵,则=*A ;4.n 元线性方程组b Ax =有解的充分必要条件为 ;5.设三阶方阵A 的特征值为1,-1,2,则=-1A .二、选择题(每小题3分,共15分)1.设B A ,均为n 阶方阵,则下列各式中正确的是 ;)A ()()22B A B A B A -=-+ )B ()222B A AB =)C 由BC AC =必可推出B A = )D ()()E A E A E A -+=-22.设A 为n 阶方阵,且E A =2,则 ;)A A 的行列式为1 )B A 的特征值都为1 )C A 的秩为n )D A 一定是对称矩阵3.向量组s ααα,,,21 线性无关的充分条件是 ;)A s ααα,,,21 均不为零向量)B s ααα,,,21 中任意两个向量对应分量不成比例)C s ααα,,,21 中任意一个向量均不能由其余1-s 个向量线性表出 )D s ααα,,,21 中有一部分线性无关课程考试试题学期 学年 拟题学院(系): 适 用 专 业:4.设B A ,均为n 阶矩阵,且A 与B 相似,则下列结论中不正确的是 ;)A )()(B r A r = )B B E A E -=-λλ )C B E A E -=-λλ )D B A =5.二次型32312123222132142244),,(x x x x x x x x x x x x f +--++=λ为正定二次型,则λ的取值范围为 .)A 12λ-<< )B 22<<-λ )C 2-<λ )D 2>λ三、计算题1.(10分)计算行列式1111111111111111--+---+---=x x x x D ;2.(10分)矩阵⎪⎪⎪⎭⎫ ⎝⎛-----=100110011A ,求满足方程X A AX 2-=的矩阵X ;3. (15分)λ为何值时,方程组⎪⎩⎪⎨⎧=+-+=--=+-+λ43214324321312222x x x x x x x x x x x 无解?有解?有解时求其通解. 四、计算题1. (10分)求向量组:()T 00111=α,()T 01112-=α,()T01223-=α,()T 21044--=α,()T 21035-=α的秩及一个最大无关组;2.(15分)求正交变换Py x =将二次型22212312123(,,)334f x x x x x x x x =+-+化为标准形. 五、证明题(每小题5分,共10分)1.设n 阶矩阵A 满足O E A A =--422,证明:E A +可逆,且E A E A 3)(1-=+-;2.已知321,,ααα是齐次线性方程组0=Ax 的基础解系,若211ααβ+=,322ααβ+=133ααβ+=,证明:321,,βββ也是齐次线性方程组0=Ax 的基础解系.参考答案一、 填空题:(每小题3分,共15分)1. 26;2. E3. -84. ),()(b A R A R =5. 21- 二、选择题:(每小题3分,共15分)1). D 2).C 3).C 4).B 5) A 三、计算题:1. 解: 1111111111111111-----+---=x x x x D ……………5分xx x xx x x-----=00000001111……………7分 xx x x x x x------=0000001111=4x ……………10分 2.解:由A X E A =+)2(……………2分⎪⎪⎪⎭⎫ ⎝⎛-------=+100100110110011011),2(A E A ……………5分⎪⎪⎪⎭⎫ ⎝⎛------100100210010221001~……………9分⎪⎪⎪⎭⎫⎝⎛------=∴100210221X ……………10分3. 解:B= ⎪⎪⎪⎭⎫ ⎝⎛----λ31111111022221 ……………2分 ⎪⎪⎪⎭⎫ ⎝⎛-----211101*********~λ ……………5分 ⎪⎪⎪⎭⎫ ⎝⎛----100001111022221~λ ……………9分 所以 1)1≠λ时,方程组无解 ……………12分1)1=λ时,方程组有解,B ⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎭⎫ ⎝⎛---000001111004001~000001111022221~得等价方程组⎩⎨⎧++=-=1443241x x x x x ,特解⎪⎪⎪⎪⎪⎭⎫⎝⎛=*0010η对应的齐次方程组的基础解系⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=1014011021ξξ,通解为*++=ηξξ2211k k x ……………15分四、计算题1.11243112000111100022-⎛⎫ ⎪⎪ ⎪-- ⎪--⎝⎭11243000430111100022-~-⎛⎫ ⎪ ⎪ ⎪-- ⎪--⎝⎭11243011110002200001~-⎛⎫ ⎪-- ⎪ ⎪-- ⎪⎝⎭………………7分123454(,,,)R ααααα=, ………9分1245,,αααα,是一个最大无关组 ………10分2.解:⎪⎪⎪⎭⎫⎝⎛--=100032023A ………2分λλλλ-----=-10032023E A ()()512---=λλ,得特征值121==λλ,53=λ ………6分当121==λλ时,解()0=-x E A ,⎪⎪⎪⎭⎫ ⎝⎛-⎪⎪⎪⎭⎫ ⎝⎛--=-000000011~000022022E A即,21x x =,得基础解系⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=100,01121ξξ,单位化得⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛=100,0212121p p ………10分当53=λ时,解()05=-x E A ,⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛-----=-000100011~4000220225E A得 ⎝⎛=-=0321x x x ,得⎪⎪⎪⎭⎫ ⎝⎛-=0113ξ,单位化得 ⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-=021213p ………12分 所以得正交变换Py x =,其中⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=0102102121021P , ………14分化二次型为标准型2322215y y y f ++= ………15分六、证明题(2个小题,每小题5分,共10分)1.证明: 由O E A A =--422得E E A A A =--+332,即()()E E A E A A =+-+3即()()E E A E A =+-3,………4分所以E A +可逆,且()E A E A 31-=+-. ………5分2.证明:1)3,2,1,0==i A i α ()3,2,1,0==+=+=∴i A A A A k i k i i ααααβ i β∴是0=Ax 的解 ………2分2) ⎪⎪⎪⎭⎫⎝⎛=110011101),,(),,(321321αααβββ,而021********≠=又321,,ααα是基础解系,所以线性无关,3),,(321=αααR所以3),,(),,(321321==αααβββR R ,所以321,,βββ也线性无关 ………4分 综上,321,,βββ是0=Ax 的基础解系。



(答案要注明各个要点的评分标准)一、简答题 (本大题共6个小题,每题5分,共30分)1.维持晶闸管导通的条件是使晶闸管的电流大于能保持晶闸管导通的最小电流,即维持电流。
(2.5分)要使晶闸管由导通变为关断,可利用外加电压和外电路的作用使流过晶闸管的电流降到接近于零的某一数值以下,即降到维持电流以下,便可使导通的晶闸管关断。
(2.5分)2.答:逆变运行时,一旦发生换流失败,外接的直流电源就会通过晶闸管电路形成短路,或者使变流器的输出平均电压和直流电动势变为顺向串联,由于逆变电路内阻很小,形成很大的短路电流,称为逆变失败或逆变颠覆。
(2.5分)防止逆变失败的方法有:采用精确可靠的触发电路,使用性能良好的晶闸管,保证交流电源的质量,留出充足的换向裕量角β等。
(2.5分)3.答:按照逆变电路直流测电源性质分类,直流侧是电压源的逆变电路称为电压型逆变电路,直流侧是电流源的逆变电路称为电流型逆变电路(1分)电压型逆变电路的主要特点是:(2分)①直流侧为电压源,或并联有大电容,相当于电压源。
直流侧电压基本无脉动,直流回路呈现低阻抗。
②由于直流电压源的钳位作用,交流侧输出电压波形为矩形波,并且与负载阻抗角无关。
而交流侧输出电流波形和相位因负载阻抗情况的不同而不同。
③当交流侧为阻感负载时需要提供无功功率,直流侧电容起缓冲无功能量的作用。
为了给交流侧向直流侧反馈的无功能量提供通道,逆变桥各臂都并联了反馈二极管。
电流型逆变电路的主要特点是:(2分)①直流侧串联有大电感,相当于电流源。
直流侧电流基本无脉动,直流回路呈现高阻抗。
②电路中开关器件的作用仅是改变直流电流的流通路径,因此交流侧输出电流为矩形波,并且与负载阻抗角无关。
而交流侧输出电压波形和相位则因负载阻抗情况的不同而不同。
③当交流侧为阻感负载时需要提供无功功率,直流侧电感起缓冲无功能量的作用。
因为反馈无功能量时直流电流并不反向,因此不必像电压型逆变电路那样要给开关器件反并联二极管。
图621/U U 。
求出H 图7 所示电路,已知当1V S U =,=S I 。
求当3V S U =,2A S I =时,U图 9所示双口网络的Z ,Y ,H 参数。
(20分)Ω2Ω21I 2I四、在图3所示正弦稳态电路中,已知1求:(1) 1S 闭合,2S 断开时的电流图2图3图4图5 图6青 岛 科 技 大 学二○一一年硕士研究生入学考试试题考试科目:电路注意事项:1.本试卷共7道大题(共计10个小题),满分150分;2.本卷属试题卷,答题另有答题卷,答案一律写在答题卷上,写在该试题卷上或草纸上均无效。
要注意试卷清洁,不要在试卷上涂划;3.必须用蓝、黑钢笔或签字笔答题,其它均无效。
﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡﹡ 一.简答题(38分)1.试举两例,说明叠加定理在电路分析中的应用(8分); 2.在图1正弦稳态电路中,已知2A 的读数为5A ,求1A 和3A 表的读数(10分);3.求图2所示电路的网络函数)()(2s U s H,并求出零、极点(8分);图1 图24.在图3所示三相对称电路中,已知电源线电压为380V ,电流表的读数为17.3A ,三相功率为6KW 。
试求:(1)每相负载的阻抗;(2)当A 线断开时,图中各电流表的读数和三相功率(12分)。
二.在图4正弦稳态电路中,已知V U s 250=,A I I c 101==,Ω=15R ,求:1I 、c x 及1R ;(2)电路消耗的有功功率、无功功率和功率因数。
(20分)三.图5所示电路中,当Ω=3α ,Ω=6R 时,I=2A ;当Ω=2α ,Ω=8R 时,用戴维宁定理和直接列方程两种方法求此时的电流I (25分)。
四.图6电路中N 由电阻元件所组成,已知图6(a )中,A I 12=,请分别用互易定理的三种图3图4图5五.图7所示电路中,分别用回路电流法和结点电压法列写电路方程(不求解)(22分)。
(1)青岛科技⼤学⾼数试卷10-11⾼数A2A卷2010/20112 ⾼等数学A2( A 卷)数理学院机电,信息,应物等专业(答案写在答题纸上,写在试题纸上⽆效)⼀、填空题(每⼩题3分,共15分)1.设arctany z x =,则zx= 。
2.⼀阶线性微分⽅程23x dyy e dx+=的通解为。
3.设L 是椭圆周221x y +=,则曲线积分2(21) Lx x ds ++? 。
4.函数()sin f x x x =展开为x 的幂级数是。
5.已知向量(2,1,1),(1,1,3)a b ==-,则a b ?= 。
⼆、选择题(每⼩题3分,共15分)1.函数(,)f x y =0,0)处()。
()A 偏导数存在 ()B 连续但偏导数不存在 ()C 可微 ()D 连续且偏导数存在2.⼆重积分31(,)xxdx f x y dy ?交换积分次序可化是()。
()A 1(,)y dy f x y dx ? ()B 10(,)ydy f x y dx ?()C 10(,)ydy f x y dx ? ()D 1(,)ydy f x y dx ?3.曲⾯21z x y =+在点(1,1,2)处的切平⾯⽅程是()。
()A 210x y z +--= ()B 210x y z +--= ()C 10x y z +--= ()D 10x y z ++-= 4.若级数1nn a∞=∑收敛,则级数20()nn n aa ∞+=+∑()。
()A 绝对收敛 ()B 发散 ()C 收敛 ()D 敛散性不能确定5.以4为周期的函数在[2,2)-上的表达式为24,20()2,02x x f x x x +-≤的和函数为(),s x 则(2)s =()。
课程考试试题学期学年拟题学院(系): 适⽤专业:()A 1 ()B 2 ()C 0 ()D 3.三、(共21分)1、(7分)设(2,2)z f x y x y =-+,其中f 具有⼆阶连续偏导数,求2,z zx x y。
2011~20121 数字电子技术基础自动化与电子工程学院 信息091-3班(答案写在答题纸上,写在试题纸上无效)一、填空题(每空1分,共20分)1、数值之间的转换(1)(17.2)10=( )2 (2)(1C.A )16=( )2 (3)(1101010.01)2=( )16 (4)(10101.1)2=( )102、对于JK 触发器的两个输入端,当输入信号相反时构成 触发器,当输入信号相同时构成 触发器。
3、A / D 转换器是将输入的 信号转换为输出的 信号器件。
4、英文简写SRAM 称为 存储器;英文简写DRAM 称为 存储器。
5、衡量半导体存储器的主要技术指标为 和 。
6、已知逻辑函数为'''C B BC A Y +=,根据反演定理其'Y = ; 根据对偶定理其Y D = 。
7、如图1表示的是二极管 门电路,其输出Y= 。
8、4位倒T 型电阻网络D/A 转换器,其输出模拟电压的计算公式为 ,当V REF =-8v ,当V REF =-8v ,D n =1011时, V O = v 。
9、触发器在外信号作用下,两个稳定状态可相互 ,触发器具有 功能,常用来保存二进制信息。
二、化简题(共15分)1、(8分)将逻辑函数C)B )(A C B (A )'C B A Y ++++++=''(化简为最简与非-与非式,并画出全部由与非门组成的逻辑电路图。
2、(7分)用卡诺图化简逻辑函数∑107653=)m ,m ,m ,m ,m ()C ,B ,A (Y ,给定约束条件为m 0+m 1+m 2+m 4+m 8=0,并画出其逻辑电路图。
图1课程考试试题学期 学年 拟题学院(系): 适 用 专 业:三、分析题(共35分)1、(10分)由双4选1数据选择器74LS153构成的逻辑电路如下图2所示,A 1A 0为地址输入端,D 3 D 2 D 1 D 0为数据输入端,Y 为输出端,写出Y 1,Y 2的逻辑表达式,并列真值表分析说明其逻辑功能。
青岛科技大学电力电子技术2012《电力电子技术》B卷2011/20122 《电力电子技术》B 卷自动化与电子工程学院电气工程及其自动化审批人:(答案写在答题纸上,写在试题纸上无效)一、填空题(每空1分,共20分)1. 电力电子技术是使用对进行变换和控制的技术。
2. 按照驱动电路加在电力电子器件控制端和公共端之间信号的性质,可以将电力电子器件(电力二极管除外)分为和;电力MOSFET 和IGBT 为典型常用的全控型电力电子器件,二者都属于驱动型器件。
3. 晶闸管的通态平均电流I T (A V ),是指__ ___波在一个周期内的___ __值。
4. 一般来讲,换流方式可分为器件换流、、和四种。
5. 一只额定电流为100A 的晶闸管允许通过的电流的有效值是。
6. 对三相全控桥式整流电路,必须采用_ ____脉冲或___ ___脉冲触发。
7. 同步信号为锯齿波的触发电路,偏移电压的作用是,控制电压的作用是。
8. 有源逆变电路的交流侧接,而无源逆变电路的交流侧接。
9. 直流斩波电路的功能是。
10. 在每半个周波内通过对进行控制,可以方便地调节,这种电路称为交流调压电路。
二、简答题(每题5分,共30分)1. 对以下电力电子器件分别按照被控制的程度以及驱动信号的性质进行分类:普通晶闸管、GTR 、GTO 、电力MOSFET 、IGBT 。
2. 在电路中,若流过晶闸管的电流有效值为100A ,晶闸管承受的最大正反向电压为300V ,考虑一定的裕量,试确定晶闸管的额定电压和额定电流。
3. 什么是有源逆变?其产生的条件是什么?课程考试试题学期学年拟题学院(系):适用专业:4. 什么是同步调制?什么是异步调制?说出它们各自的优缺点。
5. 高频化的意义是什么?为什么提高开关频率可以减小滤波器的体积和重量?6. 简述单相交-交变频电路的构成和基本工作原理。
三、分析与计算题(共30分)1. (10分)分析图1所示单相半桥电压型逆变电路的工作原理,画出V1、V2的驱动信号u GE1、u GE2以及输出电压i o 和u o 的工作波形。
07-081 电路分析(A 卷)自动化及电子工程学院 自化 测控 自专 测专 电气(答案写在答题纸上,写在试题纸上无效)一、填空题(每空2分,共24分)1. 图1所示正弦交流电路,o SU 030∠= ,Ω+=50100j z ,理想变压器的变比5=n ,求负载L Z = (L Z 可任意变动)时可以获得最大功率,最大功率=max P 。
2. 正序对称三相电源作星形连接,若相电压o AN U 2200=∠ ,则线电压CAU = _________V。
图1 图2 图33. 电路如图2所示,电流I 2= A 。
4. 已知电感L 与电容C 串联,已知电流为()10030A 0L i =14.1cos t +,L =100mH ,C =10mF 。
感抗X L = Ω;电感两端电压L U = ;容抗X C = Ω,电容两端电压CU = V ;L C u u += V 。
5.已知图3所示,电流表A 1和A 2的读数都是5A 。
若Z 1=Z 2,则A 0的读数是 。
若Z 1=R ,Z 2= jωL ,则A 0的读数 。
3.若A 0的读数是0,则Z 1和Z 2满足 。
二、求下列二端网络的等效电路 (写出主要步骤,各5分,共10分)课程考试试题学期 学年 拟题学院(系): 适 用 专 业:图4 图5三、计算题 (共计66分)1. 在图6所示交流电路中,100=UV ,6=I A ,10=L I A ,10=ωrad/s ,U 和I 同相。
求:(1)电流C I ;(2)C L R ,,的值。
(16分)图6 图72. 用结点电压法和电源等效方法求图7电路的I (各10分,共20分)Ω 10Ω10Ω8Ω20V+ -I 1 I5A +U - 8Ω2Ω 2Ω2I1AZ abj X c Ra b+-ABCΩ图8 图93. 用叠加定理求图8电路的I 1,I 和U 。
(15分)4. 图9所示三相对称交流电路中,U L =380V ,试求线电流 A I 及电路的P 和Q 。
信息工程学院2012—2013学年度第二学期期末考试《电路分析》A 卷参考答案及评分标准”一、单项选择题(每小题1分,共20分)二、电路理论分析应用题(每题10分,共20分) 1.电路如图10所示,试求电流I 。
(10分)各部得分如下:解:解:以i 1, i 2和αi 3为网孔电流, 用观察法列出网孔 1和网孔2的网孔方程分别为:(5分)补充两个受控源控制变量与网 孔电流i 1和i 2关系的方程:(2分)代入μ =1,α =1和两个补充方程到网孔方程中, 解得网孔电流i 1=4A, i 2=1A 和αi 3 =3A (3分)2.用结点分析法求下图所示电路的结点电压u 1、u 2和电流i 。
(10分)解:选定6V 电压源电流i 的参考方向。
计入电流变量i 列出两个结点方程:(6分)补充方程 (2分) 解(2分)题号12 3 4 5 6 7 8 9 10 答案 B A C D A B C D D C 题号1112 13 14 15 16 17 18 19 20 答案 BAABCDDCBA1321321)2()6()2(V 16)2()2()6(u i i i i i i μαα-=Ω-Ω+Ω-=Ω-Ω-Ω21311)2(i i i i u -=Ω=A 2)S 5.0(A 5)S 1(21-=-=+i u i u V621=-u u 1AV,2,V 421=-==i u u三、网络定理应用题(每题6分,共18分)1.试用叠加定理求解下图所示电路中的电压u .(6分)。
要求:(1)画出u s 电压源单独作用的电路图,求出u’.(2分) (2)画出i s 电流源单独作用的电路图,求出u”. (2分)(3)求出总电压u (2分)2.右图所示电路,用戴维宁定理求Uab 和R 0 并画出等效单口电路。
(6分) 解:(1)求出开路电压:V U ab 0522208128=⨯-+⨯+= (2分)求出内阻:Ω=+++⨯=8.8228128120R (1分)R 0=4.8+2+2=8.8Ω(2)画出等效电路图:(3分)3.图示电路中负载电阻R L解:(1)断开电路求出开路电压:(2分))(S 2S 424i R u R R R u u u "'++=+=S 4242S 424 i R R R R u u R R R u "'+=+=- + Uoc=0V Uab R 0=8.8Ω-+V U U ab oc 396339636=⨯+-⨯+== 9V 电压源失效求出R 0 (2分) Ω=+=+⨯++⨯=422636363630R(2)求出R L 的值及最大功率 (2分) R L =R 0=4Ω 最大功率:W R P uoc 5625.04434202max =⨯==四、动态电路分析应用题(每题10分,共20分)1.下图所示电路原处于稳定状态。