半导体载流子浓度
- 格式:ppt
- 大小:3.00 MB
- 文档页数:18

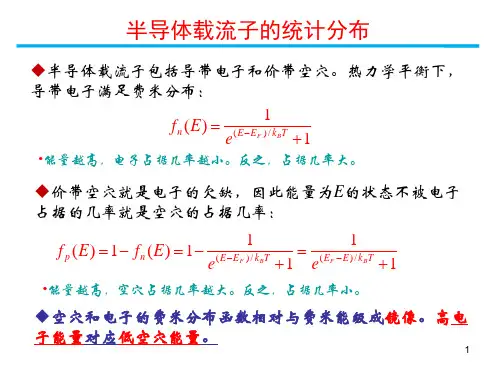
四、杂质半导体的载流子浓度1、半导体的分类 以材料分 以能带结构分 以纯度分 以杂质浓度分 元素半导体 化合物半导体(III-V, II-VI, 多元) 直接带隙半导体 间接带隙半导体 本征半导体 杂质半导体impurity atoms, Boltzemann Statistics) 重掺杂半导体(impurity band, Fermi Statistics) (单)晶态半导体轻掺杂半导体(no interaction between以晶体结构分 多晶半导体 非晶半导体2、杂质能级被电子(或空穴)占据的几率 • 单电离杂质 • 浅能级杂质III、V族 • 轻掺杂ND: 施主杂质浓度 --- 已电离nD+; 未电离nD; nD+ + nD = ND NA: 受主杂质浓度 --- 已电离pA-; 未电离pA; p A - + pA = N A 能带中的一个能级:可以容纳自旋相反的两个电子; 杂质能级:只能容纳一个电子,自旋任意; 离化施主能级只能接受一个电子因此:电子占据施主能级的几率: 空穴占据受主能级的几率: 当: ED-EF>>koT, fD(E) ~ 0, nD ~0, nD+ ~NDgD =2, gA = 4当: ED-EF =0, fD(E) = 2/3, nD =2ND/3, nD+ ~ND/3 当: EF-ED >> koT, fD(E) ~ 1, nD ~ ND, nD+ ~0 1、施主能级上的电子浓度: 2、受主能级上的空穴浓度: 3、电离施主浓度: 4、电离受主浓度:3、电中性条件 半导体中 正电荷数 = 负电荷数本征半导体: p = n 杂质半导体: p+nD+ = n+pA离化的施主、受主是固定的,不参与导电 电子、空穴分别位于导带、价带,参与导电 p + ND –nD = n + NA - pA 本征 n type p type p=n n = p + N D – nD p = n + NA -pA4、n型半导体的载流子浓度(只含一种施主杂质)掺杂有施主杂质的硅样品中,电子浓度n随温度的变化低温杂质电离区:低温弱电离 --- 中间 电离区; 杂质饱和电离区:强电离 --- 过渡区; 高温本征激发区:高温本征激发; 0K n=0 p=0 无本征激发 无杂质电离 300K 600Kn = ND n = p = ni p = ni2/ND 本征激发 杂质全部电离由于杂质的电离能比半导体的禁带宽度小很多,杂质电 离和本征激发发生在不同的温度范围,从而载流子在不同 温度的来源不同。






半导体载流子浓度计算公式(二)半导体载流子浓度计算公式前言半导体载流子浓度是指在半导体材料中的电子(n型半导体)或空穴(p型半导体)的浓度。
准确计算半导体载流子浓度对于电子学领域的研究和应用至关重要。
本文将介绍几个常用的半导体载流子浓度计算公式,并给出相关的例子说明。
1. 等效载流子浓度(Intrinsic Carrier Concentration)等效载流子浓度是指在杂质和外加电场都不影响半导体材料时的载流子浓度。
根据经验公式,等效载流子浓度的计算公式如下:[](其中,[](例子:假设某半导体材料的禁带宽度为,在室温下(300K),计算等效载流子浓度。
根据上述公式,代入相应的数值计算可得: []( 2. n型半导体载流子浓度(Electron Concentration in n-type Semiconductor)n型半导体载流子浓度是指在n型半导体中电子的浓度。
根据斯文特方程,n型半导体载流子浓度的计算公式如下:[](其中,[](例子:假设某n型半导体的等效载流子浓度为1e10/cm^3,在室温下(300K),费米能级与内禀能级的差为,计算n型半导体载流子浓度。
根据上述公式,代入相应的数值计算可得: [](3. p型半导体载流子浓度(Hole Concentration in p-type Semiconductor)p型半导体载流子浓度是指在p型半导体中空穴的浓度。
根据斯文特方程,p型半导体载流子浓度的计算公式如下:[](其中,[](例子:假设某p型半导体的等效载流子浓度为5e12/cm^3,在室温下(300K),费米能级与内禀能级的差为,计算p型半导体载流子浓度。
根据上述公式,代入相应的数值计算可得: [](总结本文介绍了常用的半导体载流子浓度计算公式,并通过例子进行了解释说明。
这些公式在半导体材料的研究和应用中具有重要的意义,帮助我们准确计算半导体中电子和空穴的浓度,为电子学领域的发展做出贡献。


半导体材料在电子学和光学器件领域中具有非常重要的地位,而半导体载流子浓度与电导率之间的关系是决定半导体材料性能的重要因素之一。
在本文中,我们将从半导体材料的基本特性和电导率的定义出发,深入探讨半导体载流子浓度与电导率的关系,帮助读者更全面地理解这一重要的物理概念。
一、半导体材料的基本特性半导体是介于导体和绝缘体之间的材料,其电导率介于导体和绝缘体的电导率之间。
半导体材料的电导率受到两种载流子的影响,即自由电子和空穴。
在纯净的半导体晶体中,自由电子和空穴的浓度几乎相等,因此其电导率较低。
然而,通过掺杂或施加外加电压,可以改变半导体材料中的载流子浓度,从而改变其电导率。
二、载流子浓度与电导率的关系1. 载流子浓度对电导率的影响载流子浓度是半导体材料中自由电子和空穴的数量,它直接影响着半导体材料的电导率。
当半导体材料中的载流子浓度较低时,由于自由电子和空穴的数量有限,它们在外加电场的作用下移动的速度较慢,因此半导体材料的电导率较低。
当半导体材料中的载流子浓度较高时,自由电子和空穴的数量增多,它们在外加电场的作用下移动的速度加快,因此半导体材料的电导率也随之增大。
2. 掺杂对载流子浓度的影响通过向半导体材料中引入掺杂物,可以有效地改变半导体材料中的载流子浓度。
N型半导体是指在半导体晶体中掺杂了大量的施主杂质,使得半导体材料中的自由电子浓度远远大于空穴浓度。
相反,P型半导体是指在半导体晶体中掺杂了大量的受主杂质,使得半导体材料中的空穴浓度远远大于自由电子浓度。
三、个人观点和理解从上述分析可以看出,半导体载流子浓度与电导率之间存在着密切的关系。
在实际的半导体器件中,通过精确控制半导体材料中的载流子浓度,可以实现对器件电性能的精确调控,从而满足不同应用场景的需求。
深入理解半导体载流子浓度与电导率的关系对于半导体器件的设计和制造具有重要的意义。
四、总结与回顾在本文中,我们从半导体材料的基本特性出发,探讨了半导体载流子浓度与电导率的关系。

宽禁带半导体的本征载流子浓度列举了有代表性的宽禁带半导体本征载流子浓度的理论公式,简要叙述了温度与禁带宽度变化的关系,讨论了本征载流子浓度对电力电子器件参数特性的影响,并通过与硅材料的对比说明了宽禁带半导体的优异性能。
标签:宽禁带半导体;本征载流子;禁带宽度;电力电子器件半导体材料的发展已历经三代,即分别以硅(Si)和砷化镓(GaAs)为代表的第一、第二代半导体材料,和以碳化硅(SiC)、氮化镓(GaN)为代表的第三代半导体材料,也称宽禁带半导体材料。
由于其具有更宽的禁带宽度、更高的击穿电场强度、更高的热导率、更高的电子饱和漂移速度等独特的参数特性,因而在电力电子器件、光电器件、射频微波器件、激光器和探测器等方面,显示出广阔的发展前景,已成为目前世界各国半导体研究的重点。
在这其中,电力电子器件是在高电压、大电流和高温下工作的,本征载流子浓度等温度敏感参数对器件的特性有着显著的影响,而宽禁带半导体材料比硅材料在这方面有着明显的优势,了解和把握这一点,对于研究宽禁带电力电子器件的参数特性显得十分必要。
1 本征载流子浓度的理论公式根据半导体物理学,半导体的本征载流子浓度ni由下式给出:2 温度对禁带宽度的影响研究表明:随着温度的上升,禁带宽度将随之减小。
文献[2]、[4]给出了硅和其它半导体禁带宽度与温度之间关系的表达式:文献[2]给出了不同半导体材料禁带宽度参数,见表2。
其中Eg(0)为00K 时的禁带宽度,α、β均为温度变化系数。
3 Eg与ni对电力电子器件参数特性的影响3.1 Eg对击穿电压的影响在描述半导体的雪崩击穿电压VB与材料禁带宽度Eg和杂质浓度NB的关系时,文献[5]引用了S.M.Sze公式:VB=60(Eg/1.1)1.5(NB/1016)-0.75 (8)对于p+n结,当NB=1014cm-3时,分别将Si的Eg=1.12eV、4H-SiC的Eg=3.23eV代入式(8),计算出Si的雪崩击穿电压为1900V,而4H-SiC的雪崩击穿电压可达9500V,是Si的5倍。
半导体材料的掺杂机制与载流子浓度半导体材料是现代电子技术和信息产业中不可或缺的重要组成部分,其性能与掺杂机制以及载流子浓度密切相关。
在半导体材料中引入杂质,即掺杂,可以改变其电子能带结构,从而控制材料的导电性能。
本文将介绍半导体材料的掺杂机制及其对载流子浓度的影响。
一、掺杂机制在半导体材料中进行掺杂,通常是向其晶体结构中引入少量的杂质原子。
这些杂质原子与半导体材料中的原子有差异,即它们在晶格中的位置和电子结构与半导体材料的原子不同。
根据掺杂的杂质类型,可以将掺杂分为两类:N-型和P-型掺杂。
1. N-型掺杂N-型掺杂是指在半导体材料中引入能够提供自由电子的杂质原子,如磷、砷等。
这些杂质原子具有多余的外层电子,当它们替代了半导体材料中的部分原子后,会形成额外的自由电子。
这样,掺杂后的半导体材料就具有较高的载流子浓度,成为N-型半导体。
2. P-型掺杂P-型掺杂是指在半导体材料中引入能够提供缺失电子的杂质原子,如硼、铝等。
这些杂质原子具有较少的外层电子,当它们替代了半导体材料中的部分原子后,会形成额外的空穴。
这样,掺杂后的半导体材料就具有较高的空穴浓度,成为P-型半导体。
二、载流子浓度的影响掺杂机制直接影响半导体材料中的载流子浓度,进而影响材料的导电性能。
载流子浓度是指单位体积内存在的自由电子或空穴的数量。
掺杂后的半导体材料中自由电子和空穴数目的增加,会使得材料的导电性能增强。
1. N-型半导体的载流子浓度在N-型半导体中,掺杂杂质原子提供了额外的自由电子。
这些自由电子具有较高的浓度,因此N-型半导体的载流子浓度较高。
这使得N-型半导体具有较好的导电性能,可用于制造导电性能要求较高的器件,如场效应管、发光二极管等。
2. P-型半导体的载流子浓度与N-型半导体类似,P-型半导体掺杂杂质原子提供了额外的空穴。
这些空穴具有较高的浓度,因此P-型半导体的载流子浓度较高。
P-型半导体在导电性能上与N-型半导体不同,但同样可以用于制造各种器件。
本征半导体温度升高后两种载流子浓度
在本征半导体中,当温度升高时,会导致两种载流子(即电子和空穴)的浓度增加。
具体来说,当温度升高时,载流子的能量会增加,从而使载流子能够跨越能带缝隙,进入能带中,从而增加载流子的浓度。
但是,这种效应是有一定的限制的。
当温度升高到一定程度时,载流子的能量会增加到一个阈值,此时载流子就会开始被激活到半导体中的缺陷或者杂质中,从而使载流子浓度减少。
这种效应称为能带填满效应。
在本征半导体中,当温度升高时,两种载流子的浓度都会增加。
具体来说,当温度升高时,半导体材料中的原子能够更容易地释放出电子和空穴,从而使载流子浓度增加。
这种效应可以通过载流子浓度函数来描述。
载流子浓度函数是一个表示载流子浓度随温度变化的函数,其中横坐标为温度,纵坐标为载流子浓度。
通常情况下,载流子浓度函数是一条单调递增的曲线,表示随着温度的升高,载流子浓度也会增加。
但是,需要注意的是,在某些情况下,载流子浓度函数并不是单调递增的。
例如,在本征半导体中,当温度升高到一定程度时,载流子浓度会出现下降的趋势,这是因为在这个温度范围内,载流子的能量会增加到一个阈值,此时载流子就会开始被激活到半导体中的缺陷或者杂质中,从而使载流子浓度减少。
这种效应称为能带填满效应。