仪器杨氏弹性模量测量仪光杠杆

实验二杨氏弹性模量的测定实验报告一、实验目的1、学会用伸长法测量金属丝的杨氏弹性模量。

2、掌握光杠杆测量微小长度变化的原理和方法。

3、学会用逐差法处理实验数据。

二、实验原理杨氏弹性模量是描述固体材料抵抗形变能力的物理量。

假设一根粗细均匀的金属丝，长度为 L，横截面积为 S，受到外力 F 作用时伸长了ΔL。

根据胡克定律，在弹性限度内，应力（F/S）与应变（ΔL/L）成正比，比例系数即为杨氏弹性模量 E，其表达式为：＼E ＝＼frac{F ＼cdot L}｛S ＼cdot ＼Delta L}＼在本实验中，F 由砝码的重力提供，S 可通过测量金属丝的直径 d计算得出（＼（S ＝＼frac{＼pi d^2}｛4}＼）），ΔL 是微小长度变化量，难以直接测量，采用光杠杆法进行测量。

光杠杆是一个带有可旋转支脚的平面镜，其前足尖放在固定平台上，后足尖置于待测金属丝的测量端，平面镜与金属丝平行。

当金属丝伸长ΔL 时，光杠杆后足尖随之下降ΔL，带动平面镜转过一个小角度θ。

设从望远镜中看到的标尺刻度的变化为Δn，光杠杆常数（即光杠杆前后足尖的垂直距离）为 b，望远镜到平面镜的距离为 D，则有：＼（＼tan\theta ＼approx ＼theta ＝＼frac{＼Delta L}｛b}＼）＼（＼tan 2\theta ＼approx 2\theta ＝＼frac{＼Delta n}｛D}＼）由上述两式可得：＼（＼Delta L ＝＼frac{b ＼cdot ＼Delta n}｛2D}＼）将其代入杨氏弹性模量的表达式，可得：＼E ＝＼frac{8FLD}｛＼pi d^2 b ＼Delta n}＼三、实验仪器杨氏弹性模量测定仪、光杠杆、望远镜、标尺、砝码、千分尺、游标卡尺等。

四、实验步骤1、调整仪器调节杨氏弹性模量测定仪底座的水平调节螺丝，使立柱铅直。

将光杠杆放在平台上，使平面镜与平台面垂直，前、后足尖位于同一水平面内。

实验6 用光杠杆测量金属的弹性模量（311）一、实验目的1．学习用光杠杆测量微小长度变化的原理，掌握放大法.2．理解视差，掌握消除视差的调整方法.3．学会用逐差法处理数据，掌握对测量结果的标准不确定度进行评定.二、实验仪器杨氏模量测定仪、钢丝、砝码、游标卡尺、卷尺三、实验原理设金属丝的长度为L ，横截面积为S ，沿长度方向受到作用力F 时，金属丝发生弹性形变，伸长(或缩短)△L .比值F ／S 是单位横截面上的作用力，称为正应力；比值 △L/L 是相对伸长，称为线应变.胡克定律告诉我们：在物体的弹性限度内正应力与线应变成正比F LES L∆= (9-1) 比例系数E 称为弹性模量(曾称杨氏模量)，单位名称为帕[斯卡]，单位符号为Pa.实验证明，弹性模量与温度有关，与物体本身材料的化学成分、结构、加工制造方法有关，而与外力、物体的形状及大小无关，是表征固体性质的一个重要物理量.固体中纵波的波速、固体材料的很多力学性质都与弹性模量有关，据此可以提供测弹性模量的不同方法.本实验就是从(9-1)式出发来测量弹性模量。

[装置介绍](9-1)式中F 、S 、L 的测量很容易解决，而△L 很小，用一般工具不易测准，因此可采用光杠杆法。

其装置如图9-1(a )所示，其细部见图9-1(b ):待测金属丝②的上端固定在支架①的顶部，下端固定在“口”形框⑤的上端，“口”形框下端的丝口接砝码托⑦，在托上放置砝码.可上下移动的平台⑥固定在支架的中部，平台上有一个矩形孔，“口”形框穿过此孔并可以在孔中上下自由移动.平面镜③安装在有三只尖脚的镜座④上，前两只尖脚放在平台上，第三只主杆尖脚卡在“口”形框内侧底面中央的接砝码托丝口的凹处，可以随着金属丝的伸长而上下移动.将水准仪放在平台上，调节支架底部的三个螺钉使平台水平.将平面镜的镜面转到与水平面垂直，望远镜⑨正对平面镜，调节目镜与叉丝距离调节手轮⑩和调焦手轮○11，从望远镜中可以看到由平面镜反射过来的标尺⑧的像. 平面镜与镜座构成了光杠杆(见图9-1（b ）).光杠杆测微小伸长量的原理见图9-3.当金属丝伸长△L 时，光杠杆的长为b 的主杆尖脚也随之下落△L ,带动平面镜M 转过α角而至M'，镜面的法线0on 也转过α角至1on .根据反射定律，0121n on n on α∠=∠=，从标尺的n 2处发出的光线将反射到n 0，从望远镜中看到的是经平面镜反射过来的标尺上n 2处的刻线.由图9-2可以看出图9-1 用光杠杆测量弹性模量装置图tan L b α∆=02tan 2n n on α=因为02n n 是在望远镜中观察到的标尺上刻线的变化，即02n n n =∆，设0on D =，由于α角很小，因此tan L b αα∆≈=2tan 2n Dαα∆≈=消去α得2bL n D∆=∆ (9-2) 从图9-2可以看出，o 相当于杠杆的支点，b+D 相当于杠杆本身，只是D 由光线所代替，所以称为光杠杆。

光杠杆的使用与杨氏模量的测定(最全)word资料光杠杆的使用与杨氏模量的测定【实验目的】1、学习微小长度变化的测量方法；2、测定钢丝样品的杨氏模量。

【实验仪器】杨氏模量装置一套、米尺、千分尺。

【实验原理】任何弹性物体在外力作用下都会发生形变。

一长度为L 、横截面积为S 的均匀金属 丝，在受到沿长度方向上的外力F 作用时，伸长量为δ，在弹性形变的限度内，根据胡克定律，其受到的拉伸应力S F 与伸长的应变L δ成正比，即 LE SF δ= （1） 比例系数E 称为该金属的杨氏模量。

又设金属丝直径为d ，则241d S π=，代入上式得 δπ24d FL E = （2） 其中，δ是一个微小量，采用放大法，用光杠杆来测量。

光杠杆原理如下图所示：一个直立的平面镜装在三足底板的一端，三足尖321,,f f f 构成等腰三角形。

1f 至32f f 的垂线长为Z ，并以前足32f f 为光点转轴，后足1f 的高低若发生微小的变化，通过平面镜反射，经较长的光程作为杠杆指示反映在标尺上。

先调节平面镜的法线水平，镜尺与平面镜距离为D 。

望远镜水平对准平面镜，从望远镜中可以看到竖尺由平面镜反射的像，望远镜中的叉丝对准竖尺某一刻度线进行读数0A ，如果加砝码（mg F =）后被测物体向下的位移为δ，光杠杆后足也随之下降δ，使平面镜微微仰起，于是1f 以32f f 为轴，以Z 为半径旋转θ角。

因为Z <<δ，所以θ角较小，有Z δθ≈。

望远镜中叉丝原来对准竖尺上的刻度为0A ，平面镜移动后，根据光的反射定律，镜面旋转θ角，反射线将旋转2θ角，这时叉丝对准的新刻度m A ，当D L <<，有D A A m 02-=θ 所以 )(20A A DZ m -=δ （3） 代入（2）式，可得 ZA A d mgLD E m )(802-=π （4） [实验内容] 1、安置好光杠杆及尺读望远镜并调节好，从望远镜中能清晰地看到直尺的像并选则好0A 的值。

杨氏模量的测定【实验目的】1．学习用拉伸法测定金属丝的杨氏弹性模量；2．掌握光杠杆法测定微小长度变化的原理，并掌握使用方法；3．学会用逐差法和作图法处理数据。

【仪器和用具】杨氏模量测定仪（包括主体支架、光杠杆、望远镜标尺组）、螺旋测微器、钢卷尺、砝码组等。

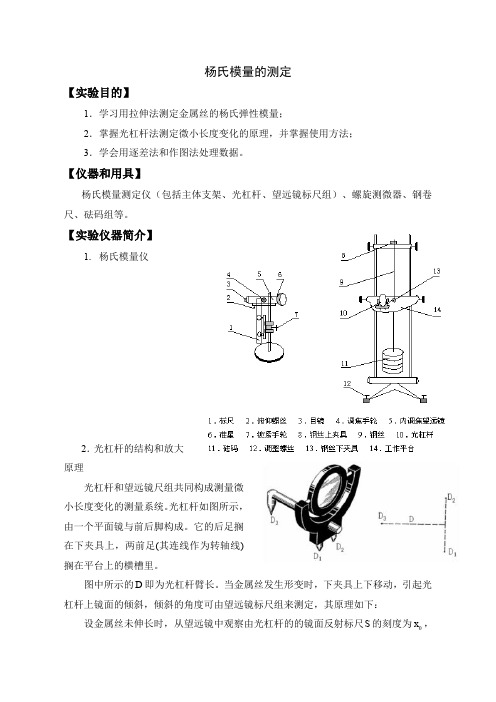
【实验仪器简介】1. 杨氏模量仪2．光杠杆的结构和放大原理光杠杆和望远镜尺组共同构成测量微小长度变化的测量系统。

光杠杆如图所示，由一个平面镜与前后脚构成。

它的后足搁在下夹具上，两前足(其连线作为转轴线)搁在平台上的横槽里。

图中所示的D即为光杠杆臂长。

当金属丝发生形变时，下夹具上下移动，引起光杠杆上镜面的倾斜，倾斜的角度可由望远镜标尺组来测定，其原理如下：x，设金属丝未伸长时，从望远镜中观察由光杠杆的的镜面反射标尺S的刻度为当金属丝伸长L ∆后，光杠杆镜面由M 转到M '的位置，即转过α角，后足3D 绕两前足尖的连线也转过了α角，如图所示，金属丝伸长L ∆之后，从望远镜读到的标尺刻度为1x ，刻度的变量为：01x x h -=∆。

光杠杆系统的放大原理图当镜面转过α角时，镜面的法线也转过了α角(BOB '∠)，则入射光线与反射光线之间的角度应改变α2(BOB ''∠)，设镜面到标尺S 的距离为R ，在α角比较小的情况下，由图知：D L tg ∆=≈αα，Rh tg ∆=≈αα22 从上两式中消去α得：h RDL ∆=∆2 因为D R >>，所以用光杠杆测h ∆就能把微小伸长量L ∆放大DR2倍,即利用光杠杆就可把测量微小的长度变化量L ∆转换成测量数值较大的标尺读数变化量h ∆，这就是光杠杆系统的放大原理。

【实验原理】取一粗细均匀的金属丝，长为L ，截面积为42d S π=，d 为截面直径，将其上端固定，下端悬挂质量为m 的砝码，测金属丝内产生单位面积的强力，即应力SF =δ，单位长度的伸长应变LL∆=ε，虎克定理指出，在弹性限度内，应力与应变成正比，即LLyS F ∆= ，称为金属材料的杨氏弹性模量，它完全由材料的性质所决定，是表征材料力学性能的一个物理量。

金属丝杨氏弹性模量的测定及其实验数据【实验目的】1.学习静态拉伸法测金属丝的杨氏模量。

2.掌握用光杠杆法测量微小长度变化的原理和方法。

3.利用有效的多次测量，及相应处理方法来减小误差。

【实验仪器】杨氏模量测量仪，光杠杆，望远镜尺组，米尺，游标卡尺【实验原理】根据胡克定律，金属丝的杨氏弹性模量， L是一个微小长度变化量，当金属丝直径为0.5毫米时， L约为10-5米。

实验中采用光杠杆镜尺法测量。

利用光杠杆镜尺法由几何原理可得，光杠杆的放大倍数为β=2D/b，一般D=1.5—2.0米，b=7.0厘米，所以放大倍数约为40倍。

通过在增加（减）砝码的同时测出标尺读数Xi和其他的长度量L、D、d、b，就能求得金属丝的杨氏弹性模量Y. 【实验内容】1.调整支架，使金属丝处于铅直位置2.调光杠杆和望远镜，使能在望远镜中看清标尺像，并无视差。

3.通过增减砝码，测出相应的标尺读数Xi′和Xi″（共加五个砝码），由Xi= Xi′/ Xi″，用逐差法求出?Xi。

重复一次。

4.测出L、D、d、b，重复六次，求出杨氏模量，【注意事项】1.仪器一经调好，测量开始，切勿碰撞移动仪器，否则要重新调节，老师检查数据前也不要破坏调节好的状态，否则一旦有错误，将难以查找原因或补作数据。

2.望远镜、光杠杆属精密器具，应细心使用操作。

避免打碎镜片，勿用手或他物触碰镜片。

3.调节旋钮前应先了解其用途，并预见到可能产生的后果或危险，不要盲目乱调，以免损坏仪器，调节旋钮时也不要过分用力，防止滑丝。

4．用螺旋测微计测量钢丝直径时，要端平测微计，避免钢丝弯曲，【数据处理】1.增减重量时钢丝伸缩量的记录数【思考题】1.在本实验中，为什么可以用不同精确度的量具测量多种长度量?为什么有些需要多次测量，有些单次测量就可以？2. 如何用十几个砝码即快又精确地测量出金属丝的平均伸长量，应该用什么方法来计算?3.光杠杆法可测微小长度变化，其主要是采用了光放大原理，放大率为β=2D/b 。

竭诚为您提供优质文档/双击可除光杠杆法测杨氏模量实验报告篇一：杨氏模量实验报告南昌大学物理实验报告实验名称：学院：机电工程学院专业班级：能源与动力工程152学生姓名：王启威学号：5902615035实验地点：106座位号：实验时间：第九周星期一下午4点开始篇二：金属材料杨氏模量的测定实验报告浙江中医药大学学生物理实验报告实验名称金属材料杨氏模量的测定学院信息技术学院专业医学信息工程班级一班报告人学号同组人学号同组人学号同组人学号理论课任课教师实验课指导教师实验日期20XX年3月2日报告日期20XX年3月3日实验成绩批改日期浙江中医药大学信息技术学院物理教研室篇三：大学物理实验-拉伸法测钢丝的杨氏模量(已批阅) 系学号姓名日期实验题目：用拉伸法测钢丝的杨氏模量13+39+33=85实验目的：采用拉伸法测定杨氏模量，掌握利用光杠杆测定微小形变地方法。

在数据处理中，掌握逐差法和作图法两种数据处理的方法实验仪器:杨氏模量测量仪（包括光杠杆，砝码，望远镜，标尺），米尺，螺旋测微计。

实验原理：在胡克定律成立的范围内，应力F/s和应变ΔL/L之比满足e=（F/s）/（ΔL/L）=FL/（sΔL）其中e为一常量，称为杨氏模量，其大小标志了材料的刚性。

根据上式，只要测量出F、ΔL/L、s就可以得到物体的杨氏模量，又因为ΔL很小，直接测量困难，故采用光杠杆将其放大，从而得到ΔL。

实验原理图如右图：当θ很小时，其中l是光杠杆的臂??tanL/l，长。

由光的反射定律可以知道，镜面转过θ，反射光线转过2θ，而且有：tan2??2??故：?Ll?b(2D)bD，即是?L?bl(2D)那么e?2DLFslb，最终也就可以用这个表达式来确定杨氏模量e。

实验内容：1．调节仪器（1）调节放置光杠杆的平台F与望远镜的相对位置，使光杠杆镜面法线与望远镜轴线大体重合。

（2）调节支架底脚螺丝，确保平台水平，调平台的上下位置，使管制器顶部与平台的上表面共面。

金属杨氏弹性模量的测定【实验目的】1. 用拉伸法测量金属丝的杨氏弹性模量。

2. 掌握用光杠杆测量微小长度的原理及方法。

【实验仪器】杨氏模量仪、望远镜尺组、光杠杆、螺旋测微计、卷尺、钢直尺、砝码。

【注意事项】1．光杠杆易碎，小心勿摔。

2．望远镜调节要细心，调焦旋钮旋到头后，切勿过量旋转以免损坏。

【实验内容及实验步骤】1．杨氏模量仪的铅直和夹子的自由滑动已基本调好，可不再调。

2．光杠杆及望远镜尺组的调节(操作难点)①位置调节：调节望远镜光轴水平且与光杠杆镜面中心基本等高；调节望远镜光轴与光杠杆镜面垂直。

②找标尺像：眼睛沿望远镜筒上方缺口准星方向向平面镜看去，找镜中标尺的像，可左右移动望远镜位置，直到找到像为止。

③望远镜调节：调望远镜目镜，使观察到的十字叉丝线清晰；调望远镜调焦旋钮，使看到的标尺像清晰。

继续微调望远镜调焦旋钮到消除视差。

④微调平面镜镜面俯仰角度，直到标尺像的零刻线和十字叉丝线相差小于1cm；细调望远镜俯仰调节螺丝，使二者相差小于1mm。

光杠杆和望远镜系统调好的标志：视场中标尺的像清晰，零刻线和十字准线水平线重合或相差小于1mm。

调节仪器完毕后，需经教师检查作为给出操作分的依据。

3.测量：根据新版教材P209—P210的数据表格，完成数据测量。

4.实验报告要求：计算杨氏模量最佳估值和不确定度，给出测量结果表达式。

【实验指导】1．用“外视法”观察寻找标尺像。

这是本实验仪器调节的关键。

因为望远镜本身的视场很小，一开始就从望远镜中观察，很可能看不到平面镜反射回来的标尺像，而从望远镜上方对着平面镜看去，视场较大，比较容易观察到标尺像。

（如果从望远镜外面看不到标尺像，则从望远镜里面不可能找到标尺像。

）因此，一般要先用“外视法”调节。

如果从望远镜上方看不到标尺像，可在望远镜的左右两边寻找。

例如：在望远镜的左边能看到标尺像，这时可将望远镜的支架向左移动到眼睛能看到标尺像的位置。

反之，支架向右移动。

望远镜经过这样左右移动调节以后，若还看不到标尺像，可能是竖直方向上的问题，这时可轻轻转动一下平面镜即可。

杨氏模量光杠杆
杨氏模量光杠杆是一种用于测量物质刚度的仪器。

其原理是利用光学测量技术和力学基本原理，将样品作为光杠杆的一端，另一端相对固定，通过测量光杠杆的弯曲位移和施加在样品上的外力来计算杨氏模量。

杨氏模量是描述物质刚度的物理量，通常用来表征固体的弹性特性。

在材料科学、力学、工程等领域中具有广泛的应用。

使用杨氏模量光杠杆可以快速准确地测量各种材料的杨氏模量，包括金属、非金属、生物组织等。

杨氏模量光杠杆的优点在于其非侵入性和非接触性，不会对样品产生损伤，并且可以进行动态测量。

此外，它还可以测量微小尺寸的样品，如纳米材料和细胞等。

杨氏模量光杠杆技术的应用领域包括材料研究、生物医学工程、新型能源材料、电子器件制造等。

随着科技不断进步，杨氏模量光杠杆技术也将不断发展和完善，为各种领域的研究提供更加精确和可靠的工具。

- 1 -。

光杠杆法测量杨氏模量,实验报告参考（朱星...佛山科学技术学院实验报告课程名称大学物理实验实验项目光杠杆法测量杨氏模量专业班级姓名学号指导教师成绩日期 200 年月日一、实验目的二、实验器材三、实验原理1．定义“应力与应变的比值，这个比值称为材料的杨氏模量（或称弹性模量），以E 表示。

即LL E S F ?= （4-1）在国际单位制中，杨氏模量E 的单位为N/m 2。

它与外力F 、物体的长度L 和截面积S 无关，而取决于固体材料本身的性质。

图4-2 光杠杆原理示意图R2.若金属丝直径为d ，则其截面积42d S π=,代入（4-1）可得L d FLE ?=24π (4-2)本次实验的目的就是利用式（4-2）测量金属丝的杨氏模量。

3. 关键：准确测定微小伸长量ΔL 。

本实验采用的是光杠杆法。

四、实验步骤1.杨氏模量测量仪的调节2．测量钢丝的杨氏模量五、实验数据和数据处理（按“补充材料”要求做）六.实验结果七.分析讨论（实验结果的误差来源和减小误差的方法、实验现象的分析、问题的讨论等）八.思考题（P.51：思考题第1，2题）1．材料相同，粗细不同的两根钢丝，它们的杨氏模量是否相同？长度不同，其杨氏模量是否相同？2．采用什么操作方法和数据处理方法，才可以消除钢丝伸长滞后效应带来的系统误差？参考答案：1.答：相同。

它与外力F 、物体的长度L 和截面积S 无关，而取决于固体材料本身的性质。

2. 答：由于钢丝在加外力F作用后，要经过一段时间才能达到稳定伸长量，这种现象称为钢丝伸长滞后效应，这段时间叫做驰豫时间。

因此,①每次加砝码后，需经较长的时间才能得到F与δr的对应值，否则将带来误差;②采用加、减载测量再取平均值的测量方法（消除系统误差的抵消测量法）：加载测量，由于滞后效应会使测量值小于准确值（因为还未到驰豫时间就读数），而减载测量，则会使测量值大于准确值，故取两者的平均值，可有效地消减滞后效应带来的误差。