下载文档原格式
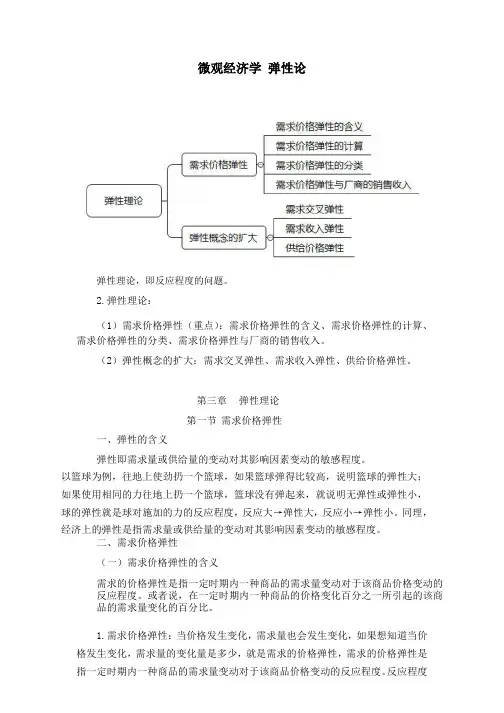
微观经济学弹性论弹性理论，即反应程度的问题。
2.弹性理论：（1）需求价格弹性（重点）：需求价格弹性的含义、需求价格弹性的计算、需求价格弹性的分类、需求价格弹性与厂商的销售收入。
（2）弹性概念的扩大：需求交叉弹性、需求收入弹性、供给价格弹性。
第三章弹性理论第一节需求价格弹性一、弹性的含义弹性即需求量或供给量的变动对其影响因素变动的敏感程度。
以篮球为例，往地上使劲扔一个篮球，如果篮球弹得比较高，说明篮球的弹性大；如果使用相同的力往地上扔一个篮球，篮球没有弹起来，就说明无弹性或弹性小，球的弹性就是球对施加的力的反应程度，反应大→弹性大，反应小→弹性小。
同理，经济上的弹性是指需求量或供给量的变动对其影响因素变动的敏感程度。
二、需求价格弹性（一）需求价格弹性的含义需求的价格弹性是指一定时期内一种商品的需求量变动对于该商品价格变动的反应程度。
或者说，在一定时期内一种商品的价格变化百分之一所引起的该商品的需求量变化的百分比。
1.需求价格弹性：当价格发生变化，需求量也会发生变化，如果想知道当价用百分数表示，比如价格变化 1%，导致需求量变化百分之多少，即需求的价格弹性。
2.需求价格弹性系数（）=-需求量的变动率，e 表示弹性，d 表示需求，该公价格的变动率式非常重要，需要记住。
需求量在上、价格在下，按照“需求价格弹性”的顺序记忆即可。
该公式上下都是变动率（变动百分比），上面是需求量变动的百分比，下面是价格变动的百分比。
公式前面有一个负号，如果不看负号公式为需求量的变动率，价格与需求量成反比，那么需求量的变动率的值是负数，比如价格上价格的变动率价格的变动率涨 10%，导致需求量下降 20%，得出需求量的变动率为-20%，价格的变动率为 10%，计算得出−10%20%=-2。
经济学中不太喜欢负数，为了便于比较大小，在公式前面加了一个负号，负负得正，取这个数的绝对值，意味着需求价格弹性系数大于 0。
3.掌握的考点：（1）需求价格弹性的含义需要理解，无需死记硬背，就是需求量的变动对价格变动的反应程度。
《弹性理论基础》课后答案
一、原题
1.什么是弹性理论？
2.弹性理论的基本原理是什么？
3.弹性理论的应用有哪些？
二、答案
1.弹性理论是一种物理学理论，它描述了物体在受到外力作用时的变形和变形后的恢复情况。
它是一种描述物体受力变形的数学模型，可以用来描述物体在受力作用时的变形情况，以及变形后的恢复情况。
2.弹性理论的基本原理是：物体在受到外力作用时，会发生变形，但是当外力消失时，物体会恢复原状。
这种变形和恢复的过程受到物体的弹性性质的影响，即物体的弹性系数。
3.弹性理论的应用非常广泛，主要应用于工程学、力学、材料学、地质学等领域。
在工程学中，弹性理论可以用来计算建筑
物、桥梁、桥梁等结构物的受力情况，以及结构物的强度和稳定性。
在力学中，弹性理论可以用来计算物体在受力作用时的变形情况，以及变形后的恢复情况。
在材料学中，弹性理论可以用来研究材料的弹性性质，以及材料在受力作用时的变形情况。
在地质学中，弹性理论可以用来研究地壳的变形情况，以及地壳在受力作用时的变形情况。
现代企业弹性理论一、前言现代企业在面对快速变化的市场和技术环境时，需要具备一定的弹性来适应外部的挑战和机遇。
本文将探讨现代企业弹性理论在实践中的应用和意义。
二、弹性理论概述弹性理论是指企业在面临外部变化时，能够迅速调整战略、组织结构和业务模式以适应新形势的能力。
企业弹性可以分为战略弹性、组织弹性和业务弹性三个层面。
2.1 战略弹性战略弹性是指企业能够根据市场需求和竞争环境随时调整战略方向和重点，保持竞争优势和市场敏感度。
2.2 组织弹性组织弹性是指企业内部机构和人员能够快速适应新的组织结构、流程和文化，以提高效率和适应新的工作方式。
2.3 业务弹性业务弹性是指企业产品与服务能够灵活调整以满足不断变化的市场需求，包括产品创新、市场定位和客户服务等方面。
三、现代企业弹性理论的重要性现代企业弹性理论的重要性在于帮助企业应对不确定性和挑战，提高市场竞争力和适应能力。
以下是几点现代企业弹性理论的重要性：3.1 适应快速变化的市场环境随着科技和市场的快速发展变化，企业需要不断调整策略和业务模式，弹性理论可以帮助企业更好地应对市场动态。
3.2 增强组织协同性和创新能力弹性理论能够激发组织内部的创新文化和团队合作精神，提高组织的协同性和创新能力。
3.3 提高客户满意度和忠诚度通过业务弹性和服务的灵活性，企业可以更好地满足客户需求并提高客户满意度和忠诚度。
四、现代企业弹性理论的实践案例4.1 亚马逊公司亚马逊公司是一个以客户为中心的企业，通过弹性的业务模式和快速的创新能力取得了成功。
亚马逊能够实时调整产品、服务和配送方式来满足客户需求，成为全球领先的电商平台之一。
4.2 谷歌公司谷歌公司以其强大的组织弹性和创新文化闻名。
谷歌鼓励员工尝试新想法和项目，快速测试并调整，使得公司能够持续保持领先地位并推动科技进步。
五、结论现代企业弹性理论是企业在快速变化的市场中生存和发展的重要保障，企业需要不断提升自身的弹性能力，灵活适应外部环境的变化。
弹性理论在经济学中的应用弹性理论是经济学中一种重要的分析工具，它可以帮助我们理解经济现象的变化规律，以及经济政策对经济的影响。
本文将介绍弹性理论在经济学中的应用，并探讨其意义和价值。
一、弹性理论的基本概念弹性是指两个经济变量之间的变化关系，即一个变量的变化会引起另一个变量的相应变化。
在经济学中，弹性可以分为需求弹性、供给弹性、交叉弹性、收入弹性等。
弹性理论的基本思想是通过比较不同变量之间的关系，来评估经济政策的效果和预测经济趋势。
二、弹性理论在经济学中的应用1.需求弹性在经济学中的应用需求弹性是指在一定时间内，一种商品的价格不变时，消费者对这种商品的需求量发生变化所引起的价格变动的比率。
需求弹性的大小取决于商品的性质、价格、消费者的收入水平、消费习惯等因素。
在经济学中，需求弹性常常被用来评估价格变动对销售量的影响，以及制定合理的价格策略。
例如，当一种商品的需求量对价格变动的反应较大时，商家可以通过降低价格来增加销售量；反之，则可以通过提高价格来获得更高的利润。
2.供给弹性在经济学中的应用供给弹性是指在一定时间内，一种商品的价格不变时，生产者对该商品的生产量发生变化所引起的价格变动的比率。
供给弹性的大小取决于生产者的成本、利润、生产技术等因素。
在经济学中，供给弹性常常被用来评估生产者对价格变动的反应程度，以及制定合理的生产计划。
例如，当生产者的生产成本对价格变动的反应较大时，商家可以通过提高价格来增加利润；反之，则可以通过降低成本来提高生产效率。
3.交叉弹性在经济学中的应用交叉弹性是指两个经济变量之间的变动关系，即一个变量的变化会引起另一个变量的相应变化。
在经济学中，交叉弹性常常被用来评估不同经济变量之间的相互影响程度，以及制定合理的经济政策。
例如，政府可以通过调整税收政策来影响消费和投资，从而影响经济增长率。
在这种情况下，政府可以根据交叉弹性的大小来制定合理的税收政策，以实现经济的稳定增长。
三、弹性理论的意义和价值弹性理论是一种重要的经济学分析工具，它可以帮助我们更好地理解经济现象的变化规律和经济政策的效果。
第二章需求分析价格上升意味着收益的增加。
收益=P×Q，当Q一定时，P上升---利润的增加。
有时，价格的上升，意味着收益的减少。
由于P上升，转为购买其他厂商的产品。
我们需要了解价格的变化量对需求量的敏感性的度量。
这就是本章要学习的内容：弹性理论。
供需法则说明了当P变化时，需求和供给的方向变化，不能说明其变化的数量。
只“定性分析”而非“定量分析”，弹性理论可以说明这种量的变化程度：定量需求分析。
第一节弹性的一般原理1、弹性的概念弹性（Elasticity）是物理学中的概念，泛指物体对外界作用力的反应能力。
经济分析中引用弹性的概念，测算因变量变化率对自变量变化率的反应的敏感程度。
通常对y=f(x)这一函数的弹性系数E。
则有：()()变化的百分比自变量变化的百分比因变量xyE=例（a）（b）（c）图1（a）、（b）、（c）三种情况，价格变化率相同，而需求量的变化率却是不相等。
（a）最小，（c）为最大，（b）为二者之间。
说明，三者在这一价格区间的（P0、P1）弹性不同。
2、弹性分析的重要意义弹性分析对企业管理决策有着重要的意义。
价格上升5%，对销售额有什么影响？销售额增加20%，价格需下降多少？如果大米和彩电同时涨价20%，为什么人们可能继续买大米而暂时放弃买彩电等等。
弹性分析与边际分析一样都是管理经济学中的重要分析工具。
弹性理应用最广泛莫过于需求弹性和供给弹性。
第二节、需求弹性需求量受众多的因素的影响，最主要： （1）该商品的自身价格变化称为需求价格弹性。
（2）该商品相关商品的价格变化，称为需求交叉价格弹性。
（3）消费者实际收入的变化，称为需求收入弹性。
1、需求的价格弹性在需求量与价格这两个经济变量中，价格是自变量，需求量是因变量。
一、需求价格弹性的定义：价格变化所引起的需求量变动的程度，或者说是需求量变动对价格变动的反应程度。
Q P P Q PP QQEd ⋅∆∆=∆∆==价格变动的百分比需求数量变化的百分比（1）Ed 被定义为自变量变动（ΔP ）的百分比（P P ∆）与因变量变动（ΔQ ）的百分比（QQ∆）这两个百分比的比率。
弹性理论与价格弹性计算经济学中的弹性理论是研究市场供需关系中价格和数量的变动对于市场反应的敏感程度。
价格弹性是弹性理论中的一个重要概念，它衡量了市场参与者对于价格变动的敏感程度。
本文将介绍弹性理论的基本概念，并探讨价格弹性的计算方法。
一、弹性理论的基本概念1. 价格弹性的定义价格弹性是指市场参与者对于价格变动的敏感程度。
当价格弹性大于1时，表示市场参与者对于价格变动的反应较为敏感，需求或供应的变动幅度大于价格变动幅度；当价格弹性小于1时，表示市场参与者对于价格变动的反应较为不敏感，需求或供应的变动幅度小于价格变动幅度；当价格弹性等于1时，表示市场参与者对于价格变动的反应与价格变动幅度相等。
2. 弹性的分类根据变动的不同，弹性可分为需求弹性和供应弹性。
需求弹性衡量了市场参与者对于价格变动的敏感程度，供应弹性则衡量了市场参与者对于价格变动的生产或供应能力的敏感程度。
3. 弹性的影响因素弹性的大小受多种因素影响。
首先，替代品的可用性是影响需求弹性的重要因素。
如果存在大量替代品，市场参与者更容易选择其他产品，需求弹性较大。
其次，商品的必需性也会影响弹性。
对于必需品，市场参与者对于价格变动的反应较为不敏感，需求弹性较小。
此外，时间因素也会影响弹性。
长期来看，市场参与者有更多的时间来调整其行为，需求或供应的弹性较大。
二、价格弹性的计算方法价格弹性的计算方法有多种，其中最常用的是价格弹性的百分比变动法和价格弹性的边际收益法。
1. 价格弹性的百分比变动法价格弹性的百分比变动法是通过计算需求量或供应量的百分比变动与价格的百分比变动之比来计算价格弹性。
具体计算公式如下：价格弹性 = (需求量变动的百分比 / 价格变动的百分比)例如，当需求量下降10%而价格上升5%时，价格弹性为-2。
这意味着需求量的变动幅度是价格变动幅度的两倍。
2. 价格弹性的边际收益法价格弹性的边际收益法是通过计算边际收益与价格的比值来计算价格弹性。
弹性理论弹性理论法的发展一般认为，弹性理论法最早是由Poulos提出的。
其实Poulos只是弹性理论法的集大成者，而不是首创者。
早在Poulos之前，已有学者采用Mindlin解求解桩基问题。
Nishida（1957）就采用Mindlin解求解了单桩的端阻力问题。
其后，在1963年，D.Appolonia（1963）等人用Mindlin解完整地研究了桩基础的沉降问题，并对下卧层是基岩的情况进行了修正。
在上述前人的基础上，Poulos将Mindlin解推广到群桩情况，并由其本人及合作者将这两种方法逐步完善起来。
Poulos&Davis（1968）提出了刚性单桩的弹性理论解法，其基本方法是将桩身分段，利用Mindlin解求出土体的柔度矩阵，根据下式求出桩身侧摩阻力和桩端阻力：(1)式中，分别为桩身和桩端的位移；，分别为桩侧摩阻力和桩端阻力；，为单位桩侧摩阻力产生的桩身和桩端位移；，为单位桩端阻力产生的桩身和桩端位移。
同年Poulos（1968）将刚性单桩解推广至刚性群桩，在计算群桩沉降时，Poulos建议采用相互作用系数法（α系数法），即在单桩计算结果的基础上，运用弹性理论叠加原理，把在弹性介质两根桩的计算结果按相互作用系数方法扩展至群桩。
其数学表达式为：（2）其中α系数法的表达式为：第根桩作用单位荷载在第根桩上产生的附加沉降第根桩作用单位荷载产生的沉降（3）W1.。
i。
k。
n 和P1.。
i。
k。
n分别为桩顶沉降和桩顶荷载；f1.。
i。
k。
n为柔度系数，即本桩作用单位荷载时产生的沉降。
随后，Poulos&Davis（1969）将桩身基本微分方程用差分法表示，从而将弹性半空间刚性群桩解推广至可压缩性群桩。
Poulos关于桩基的解均是基于土体理性均值，各向同性的假设前提下的。
为考虑土体的非均质性和各向异性，不少学者提出了各自的解决方案。
Poulos（1979）认为土体的非均质性不影响土体在荷载作用下的应力，求取位移解时采用位移求取点和荷载作用点之间弹性模量的平均值，即令Eij =（Ei+Ej）/2.Lee（1990）同样认为土体的应力不受非均质性的影响，但计算Eij时不仅考虑i层和j层的弹性模量，还考虑其余各层的弹性模量和层厚的影响，因此更为合理一些。
对于一种比较简单和常见的非均质土，即土层剪切模量随深度线性变化的Gibson土，Banerjee&Davies（1978）经试算，提出将土层分为两层弹性模量不变的土层，并将其应用于边界元。
Rajapakse（1990）运用积分变换技术求解了基于Gibson土的解析解（对应于弹性半空间的Mindlin 解），并将其运用于桩基问题中。
对于土体的各向异性，Lee（1991）采用Small&Booker（1986）的方法，得到了单桩的横观各向同性成层地基中的解。
Butterfield&Banerjee（1971）采用了类似的方法做了大量的工作，其理论较Poulos法更为严格。
Butterfiel认为Poulos的几个假设影响了解的精度，比如Poulos假设桩端光滑，桩端阻力均匀，桩侧忽略径向力等，因此Butterfiel对桩底单元进行了细分，考虑了不同径向距离处桩端阻力不一致的情况，并引入桩侧径向力，采用虚构应力函数的方法进行求解。
该方法可以直接对刚性桩求解，但对较柔的桩，则需要用迭代法解决。
由于采用Mindlin解求解桩基沉降问题涉及到Mindlin解的两次积分，计算过程较为繁复。
因此，不少学者在简化计算方面做了一些工作，其中影响比较大的是Geddes积分。
Geddes（1969）针对桩侧摩阻力均布、三角形分布的情况给出了Mindlin解沿桩长的积分。
基于同样的原因，Novak&EI Sharnoby（1985）提出用点荷载代替桩侧荷载和桩端荷载，以避免基于Mindlin解的两次积分。
当采用弹性理论法求解群桩系统时，上述方法都是采用Poulos提出的相互作用系数方法。
但是，由于采用相互作用系数法时，忽略了其他桩桩体插入对桩与桩相互作用的影响，因此存在过高估计桩与桩相互作用系数的问题，故Novak& EI Sharnoby提出采用简化的直接群桩分析法，既可以考虑桩体插入的影响，又不至于计算过于复杂，但在分析过程中同样如Poulos方法，需要将桩身分段。
接着，EI Sharnoby（1990）针对端承桩问题，再次证实了采用相互作用系数方法分析存在的问题。
我国学者在应用弹性理论计算群桩沉降方面也做了不少工作。
楼晓明（1990）分析了群桩基础的共同作用。
考虑到地基土并非是均质各向同性的线弹性体，他们通过减小桩土之间相互作用范围的办法来修正弹性理论分析结果。
刘前曦等（1997）同样认为土体的非均质性不影响土体中应力的分布，应力分析采用Bousinessq和Geddes弹性理论界，澄江计算采用分层总和法，沉降计算中假定桩土地基为弹性半空间，且单桩沉降与相邻地基土沉降相协调。
杨敏等（1998）采用Geddes积分求解群桩系统，并认为桩侧荷载超过土体剪切强度后桩土将发生滑移，即将土体视为理想弹塑性体，以此模拟群桩中部分桩、土单元上的荷载达到极限承载力的情况，并将分析结论应用于减少桩用量的实践中。
从发表的文献来看，我国在弹性理论基础上发展的计算理论大多采用Poulos提出的相互作用系数法。
此外，国内外学者还发表了不少基于弹性理论的混合解法，比如Pells（1979）提出的Mindlin解与有限元解的联合解法；Chow（1986），Lee（1991），张保良等（1997）基于荷载传递法和弹性理论法的混合解法。
弹性理论法基本假定群桩沉降分析的假定与单桩的相同。
1.土是均匀、连续、各向同性的线弹性半空间体；2.土体性质不因桩体的存在而变化（忽略桩对土的加强效应)，于是可以用弹性连续介质理论去模拟地基土体荷载响应；3.桩土界面普遍满足弹性即界面不发生滑移和屈服，沿界面诸相邻点的桩位移应与土位移相等；弹性理论法的思路弹性理论法通常把桩分成若干个均匀的受载单元，采用弹性半空间体内集中荷载作用下的Mindlin解计算土体位移，由桩体位移和土体位移协调条件建立平衡方程，从而求解桩体位移和应力。
弹性理论法用于群桩沉降分析弹性理论方法用于群桩沉降分析的主要依据是Mindlin解，而Mindlin解给出的是均质弹性半空间内作用单位竖向荷载时的位移解与应力解。
因此，群桩沉降计算就分别以位移基本解或应力基本解为出发点，形成了两种不同的分析方法:以位移解为基础的位移法和以应力解为基础的应力法。
发展了一种简化弹性理论位移法。
该法以位移解为基本解，假定桩侧摩阻力为线性分布的，在位移基本解的积分中舍去高阶无穷小量。
该方法主要进行桩一土体系柔度矩阵的计算，其分块矩阵形式为：（4）是对称矩阵，然后根据桩—土体系静力平衡方程：（5）按照上式可获得考虑桩—土相互作用的群桩沉降计算结果，其中，为桩—土体系的竖向位移向量；是与为对应的节点反力向量。
弹性理论法按其应用模式的不同又可分为以下几种具体的应用方式：一．叠加法以Poulos,Buterfield,Davis,Geddes等的群桩沉降弹性分析理论为基础的计算体系中，叠加法是比较成熟和应用较广的一种简化方法，详细阐述了其原理和计算过程，该法在忽略桩对土位移的加强效应简单的假定基础上，把单桩的分析扩展到桩群。
叠加法计算群桩沉降利用格德斯单桩荷载下的应力系数，将群桩中每一根桩由自身荷载引起的沉降和受其他桩荷载影响所产生的沉降叠加起来求得群桩沉降。
（1）带刚性承台群桩的沉降计算对于高层建筑和筒仓等的桩筏、桩箱基础和桥墩桩基，由于基础承台与上部结构的共同作用，其承台可近似视为刚性的。
对于平面尺寸不太大的独立桩基同样可看做刚性的。
刚性承台下各桩的沉降量相等，各桩的荷载依位置不同而异。
我们称单位荷载下单桩的沉降为柔度系数 ，由k桩自身单位荷载引起的沉降记为 ，由j桩单位荷载对k桩影响所引起的沉降记为 ，由此对于由n 根桩组成的群桩，桩k的沉降可利用叠加原理可表示为：（6a）式中：—桩j承受的荷载；—桩k受桩j影响的柔度系数，即j桩作用单位荷载对k桩引起的沉降；可按有限压缩层地基模型，利用Geddes（盖得斯）单桩荷载作用下的应力系数计算，但Geddes解未考虑桩径的影响。
因此，群桩中所有桩的沉降可用矩阵形式表示为：(6b)式中：—为桩沉降向量s1= s2=……= s i=……= s n =s；—为群桩柔度系数矩阵；—为桩荷载向量；；；Qj——群桩中j桩顶荷载；压缩层位均匀土层时： （7a）压缩层为成层土时： （7b）式中， 为单位荷载作用于j桩对k桩轴线桩端一下产生的竖向应力；，分别为桩端平面一下压缩层范围内土的压缩模量和成层土第l 层的压缩模量；将（7）带入（6）可得n个位移协调方程。
根据外荷载P与各桩桩顶荷载之和相平衡的条件，得：（8）联立（6）和（8），便得到包括n个单桩桩顶荷载Qi和群桩沉降s共（n+1）个未知数的（n+1）个方程，经整理可表示为：（9）解式（9），便可求得群桩各桩桩顶荷载Q和群桩沉降s。
i当现场进行了原型单桩试验时，可利用其确定单桩在单位荷载下自身的沉降。
表示：为区别于式（7）由压缩模量确定的柔度系数，以刚度系数Kij(10)式中，，分别为单桩设计荷载和设计荷载下的沉降；考虑试桩沉降的完成系数，对于砂土可取 ；一般粘性土，可取 ；饱和软土，可取 。
（2）带柔性承台群桩的沉降计算对于油罐等柔性结构的桩基、大面积堆载场地的桩基等均可视为柔性承台群桩，平面尺寸很大的独立柱桩基也可近似按带柔性承台群桩看待。
此时，各桩的桩顶荷载相等，承台沉降呈碟形。
桩顶荷载为 Q=（11）群桩中i桩的沉降为：（12）上式表示为矩阵形式：（13）式中， 为桩群中i桩的柔度系数，按式（7）确定；当有试桩资料时，可按式（10）确定 。
，由此可绘出柔性承台的挠度曲线。
解式（13）可得群桩中各桩桩顶沉降si（3）叠加法的计算群桩沉降的讨论采用上述弹性理论叠加法计算群桩沉降要注意一下几个问题：1）该法在计算中假定土体为各向同性均质的半无限弹性体，忽略桩群在土中的“加筋效应”和“遮帘效应”，即在考虑桩与桩的相互影响时，仅仅对各桩的应力、变形进行叠加，并未考虑桩的存在所带来的影响。
这对于某些加工硬化型土，如非密实的粉土、砂土可能会引起较大误差；2）该法未考虑承台分担荷载对于减小沉降的作用，也未考虑承台土反力对桩侧、桩端应力和变形的影响；3）该法未考虑桩径的影响。
格德斯解系将桩端应力简化为一集中力，将桩侧剪应力简化为沿桩轴线的若干集中力，据此求得桩端以下任一点的竖向应力系数。
该应力系数比分布于具有一定尺度界面上的桩端压应力和桩侧剪应力在同一点的应力系数要打。
