基本初等函数一思维导图
- 格式:doc
- 大小:64.50 KB
- 文档页数:1


初中数学函数思维导图(合集)(11页)页码:1/11封面初中数学函数思维导图合集副思维导图助力数学学习,掌握函数知识作者:[你的名字]日期:[填写日期]页码:2/11目录1. 引言2. 函数概念3. 函数类型3.1 线性函数3.2 二次函数3.3 反比例函数3.4 幂函数3.5 指数函数3.6 对数函数4. 函数性质4.1 单调性4.2 奇偶性4.3 周期性4.4 极值5. 函数图像6. 函数应用7. 函数解题技巧8. 常见函数问题页码:3/11引言数学函数是初中数学中的重要内容,它不仅是高中数学的基础,也是解决实际问题的重要工具。
掌握函数知识,对于提高数学成绩和解决实际问题具有重要意义。
本思维导图合集旨在帮助初中生系统地学习和掌握函数知识,提高数学思维能力和解题技巧。
页码:4/11函数概念线性函数:一次函数,形式为y=ax+b,其中a和b是常数。
二次函数:二次函数,形式为y=ax^2+bx+c,其中a、b和c是常数。
反比例函数:形式为y=k/x,其中k是常数。
幂函数:形式为y=ax^n,其中a和n是常数。
指数函数:形式为y=a^x,其中a是常数。
对数函数:形式为y=logax,其中a是常数。
页码:5/11函数类型线性函数:一次函数,形式为y=ax+b,其中a和b是常数。
它是一条直线,斜率为a,截距为b。
二次函数:二次函数,形式为y=ax^2+bx+c,其中a、b和c是常数。
它的图像是一个抛物线,开口向上或向下,取决于a的正负。
反比例函数:形式为y=k/x,其中k是常数。
它的图像是一个双曲线,随着x的增大,y的值逐渐减小。
幂函数:形式为y=ax^n,其中a和n是常数。
它的图像可以是直线、抛物线、双曲线等,取决于n的值。
指数函数:形式为y=a^x,其中a是常数。
它的图像是一个递增或递减的曲线,取决于a的正负。
对数函数:形式为y=logax,其中a是常数。
它的图像是一个递增或递减的曲线,取决于a的正负。
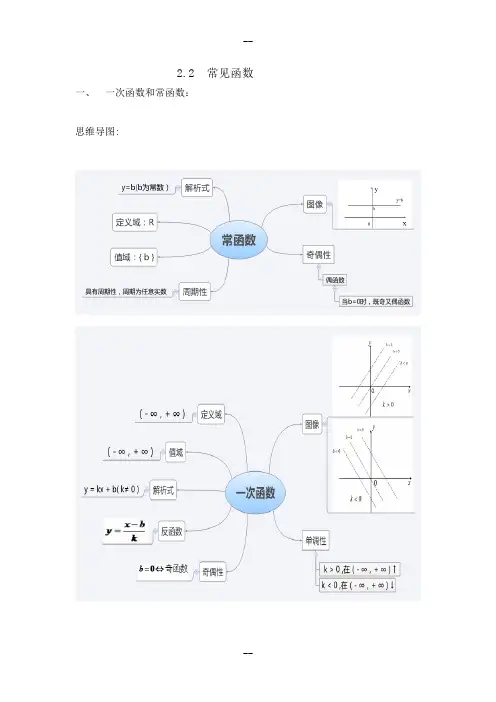
2.2常见函数一、一次函数和常函数:思维导图:(一) 、一次函数 (二)、常函数 定义域:(- ∞,+ ∞) 定义域: (- ∞,+ ∞) 值 域:(- ∞,+ ∞) 正 k=0 反 值 域:{ b }解析式:y = kx + b ( k≠ 0 ) 解析式:y = b ( b 为常数)图 像:一条与x 轴、y 轴相交的直线 图 像:一条与x 轴平行或重合的直线b x x o x b=0b<0b=0 b>0b<0K > 0 k < 0单调性: k > 0 ,在(- ∞,+ ∞)↑ 单调性:在(- ∞,+ ∞)上不单调k < 0 ,在(- ∞,+ ∞)↓奇偶性:奇函数⇔=0b 奇偶性: 偶函数 非奇非偶⇔≠0b周期性: 非周期函数 周期性:周期函数,周期为任意非零实数反函数:在(- ∞,+ ∞)上有反函数 反函数:在(- ∞,+ ∞)上没有反函数反函数仍是一次函数例题:-- 二、二次函数1、定义域:(- ∞,+ ∞)2、值 域: ),44[,02+∞-∈>ab ac y a]44,(,02ab ac y a --∞∈<3、解析式:)0(2≠++=a c bx ax y 4、图 像:一条开口向上或向下的抛物线开口向下,开口向上;正负:增大,开口缩小绝对值:随着,00<>a a a a正半轴相交与负半轴相交与y c y c c,0,0><对称轴:ab x 2-=对称轴: ;)44,2(2ab ac ab --顶点: 轴交点个数图像与x ac b →-=∆42:与x 轴交点的个数。
两个交点,0>∆一个交点,0=∆无交点,0<∆5、单调性:↑+∞-↓--∞>),2[]2,(,0ab ab a↓+∞-↑--∞<),2[]2,(,0ab ab a6、奇偶性:偶函数⇔=0b 7、周期性:非周期函数8、反函数:在(- ∞,+ ∞)上无反函数,上及其子集上有反函数或在),2[]2,(+∞---∞ab ab例题:三、反比例函数和重要的分式函数(一)、反比例函数 (二)、分式函数bax dcx y ++= 定义域:(- ∞,0)∪(0,+ ∞) 定义域:),(),(+∞---∞aba b 值 域:(- ∞,0)∪(0,+ ∞) 值 域: ),(),(+∞-∞a c a c解析式:)0()(≠=k xk x f 解析式:)(a bx b ax d cx y -≠++=图 像:以x 轴、y 轴为渐进线的双曲线 图 像:以abx -=和a c y =为渐近线的双曲线y y0 x 0 xk > 0 k < 0单调性: k>0,(- ∞,0)↓,(0,+ ∞)↓ 单调性:在),(a b --∞和),(+∞-ab上 k<0,(- ∞,0)↑,(0,+ ∞)↑ 单调性相同 奇偶性:奇函数 奇偶性:非奇非偶 对称性:关于原点对称 对称性:关于点),(aca b -成中心对称周期性:非周期函数 周期性:非周期函数 反函数:在定义域上有反函数, 反函数:在定义域有反函数,反函数是其本身。

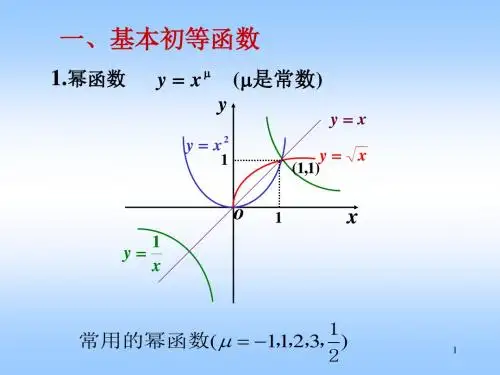
基本初等函数总结表格基本初等函数是数学中的重要概念,它们是解析函数的一种,具有简单的形式和基本的性质。
在学习数学的过程中,我们经常会接触到各种各样的基本初等函数,它们在数学建模、物理、化学等领域都有着重要的应用。
为了更好地理解和掌握基本初等函数,下面我们将对常见的基本初等函数进行总结,并制作成表格,以便大家更加直观地了解它们的特点和性质。
首先,我们来看一下常见的基本初等函数及其表达式、定义域和值域。
1. 线性函数。
表达式,y = kx + b。
定义域,(-∞, +∞)。
值域,(-∞, +∞)。
2. 幂函数。
表达式,y = ax^n (a ≠ 0, n为正整数)。
定义域,(-∞, +∞)。
值域,。
当n为奇数时,值域为(-∞, +∞)。
当n为偶数时,值域为[0, +∞)。
3. 指数函数。
表达式,y = a^x (a > 0, a ≠ 1)。
定义域,(-∞, +∞)。
值域,(0, +∞)。
4. 对数函数。
表达式,y = log_a(x) (a > 0, a ≠ 1)。
定义域,(0, +∞)。
值域,(-∞, +∞)。
5. 三角函数。
正弦函数,y = sinx。
余弦函数,y = cosx。
正切函数,y = tanx。
定义域,(-∞, +∞)。
值域,[-1, 1]通过以上表格,我们可以清晰地了解到各种基本初等函数的特点和性质。
线性函数具有直线图像,定义域和值域都是整个实数集;幂函数的图像呈现出不同的形状,其值域受到幂指数n的影响;指数函数和对数函数是互为反函数的函数对,其值域和定义域分别是正实数集和整个实数集;三角函数则是周期函数,其定义域是整个实数集,值域在[-1, 1]之间。
除了上述基本初等函数外,还有一些其他常见的基本初等函数,如双曲函数、反比例函数等,它们都有着各自独特的特点和性质。
通过学习和掌握这些基本初等函数,我们可以更好地理解数学知识,解决实际问题,甚至在日常生活中也能够运用到这些知识。

高一数学函数思想导图总结高一数学函数思想导图总结一、函数的基本概念1. 函数的定义:函数是一种特殊的关系,它把一个数集的每个元素都对应到另一个数集的唯一元素。
2. 自变量与因变量:自变量是已知的数值,在函数中起到输入的作用;因变量是待求的数值,在函数中起到输出的作用。
3. 函数的图像:函数的图像是自变量和因变量之间的对应关系在平面上的表示,可通过给定的函数表达式绘制出来。
二、函数的性质1. 定义域和值域:定义域是自变量的取值范围,值域是因变量的取值范围。
2. 奇偶性:奇函数满足 f(-x) = -f(x),偶函数满足 f(-x) = f(x),可以通过函数的图像来判断其奇偶性。
3. 单调性:函数的单调性描述了函数图像上的任意两点之间的高低变化趋势,可以通过函数的导数来判断。
4. 周期性:周期函数满足 f(x+T) = f(x),其中 T 为正数,函数的图像在一定区间内重复出现。
三、基本函数1. 常数函数:f(x) = c,其中 c 为常数,函数图像平行于 x 轴。
2. 一次函数:f(x) = kx + b,其中 k 和 b 均为常数,函数图像是一条直线。
3. 二次函数:f(x) = ax^2 + bx + c,其中 a、b 和 c 为常数,函数图像是抛物线。
4. 绝对值函数:f(x) = |x|,函数图像在原点处有拐点。
5. 幂函数:f(x) = x^n,其中 n 为整数,函数图像的形状与 n的正负相关。
6. 指数函数:f(x) = a^x,其中 a 为正常数且不等于 1,函数图像在点 (0, 1) 处经过。
四、复合函数1. 复合函数的定义:将两个或多个函数相互结合,得到一个新函数,新函数的自变量是原函数的因变量。
2. 复合函数的运算:复合函数的运算按照从内到外的顺序进行,即先求内函数值再求外函数值。
3. 复合函数的性质:复合函数的定义域由内外函数的定义域决定,复合函数的周期取内外函数周期的最小公倍数。



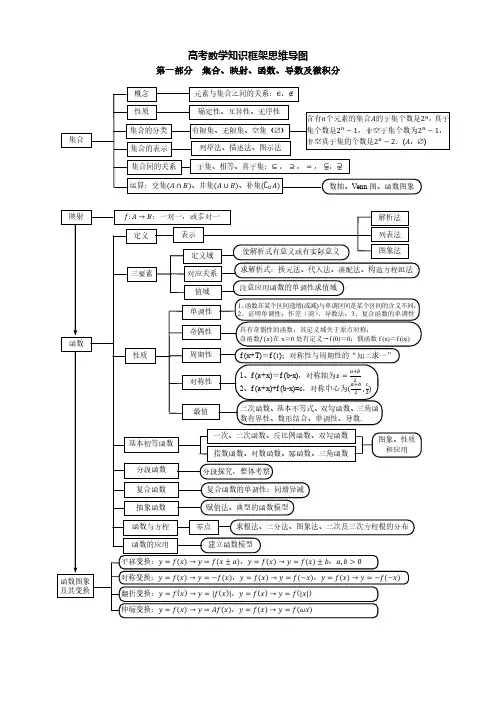
基本不等式实际是对勾函数的特例,可以考虑利用对勾实际应用题考虑解析式有意义且考虑实际问题有意义
解析式表示的斜率、截距、距离等几何意义一般适用含有绝对值的函数
6种基本函数及其加减形式
形如f[g(x)]
确定函数的定义域.
将复合函数分解成基本初等函数y =f(u),u =g(x).分别确定这两个函数的单调区间.如果一个函数的图像沿一个点旋转180度,所得的图像能与原函数图像完全重合,则称该函数具备对称性中的中心对称,对称轴是两个横坐标的中点
对称中心为函数对称两点的中点,可以利用中点坐标
如果一个奇函数f(x)在原点处有定义,即f(0)有意义,那么一定有奇偶性的判断利用奇偶性求解析式公
众
么
难。