振幅、加速度、振动频率三者的关系式

振幅、振速、振动加速度？振动一般可以用以下三个单位表示：mm、mm/s、mm/s2。

振幅、振动速度（振速）、振动加速度。

振幅是表象，速度和加速度是转子激振力的程度。

mm振动位移：一般用于低转速机械的振动评定；mm/s振动速度：一般用于中速转动机械的振动评定；mm/s2 振动加速度：一般用于高速转动机械的振动评定。

工程实用的振动速度是速度的有效值，表征的是振动的能量；加速度是用的峰值，表征振动中冲击力的大小。

振幅理解成路程，单位是mm；把振速理解成速度，单位是mm/s；振动加速度理解成运动加速度，单位mm/s2。

速度描述的是运动快慢；振速就是振动快慢，一秒内能产生的振幅。

振幅相同的设备，它的振动状态可能不同，所以引入了振速。

位移、速度、加速度都是振动测量的度量参数。

就概念而言,位移的测量能够直接反映轴承\固定螺栓和其它固定件上的应力状况。

例如:通过分析透平机上滑动轴承的位移,可以知道其轴承内轴杆的位置和摩擦情况。

速度反映轴承及其它相关结构所承受的疲劳应力。

而这正是导致旋转设备故障的重要原因。

加速度则反映设备内部各种力的综合作用。

表达上三者均为正弦曲线,分别有90度,180度的相位差。

现场应用上,对于低速设备(转速小于1000RPM)来说,位移是最好的测量方法。

而那些加速度很小,其位移较大的设备,一般采用折衷的方法,即采用速度测量,对于高速度或高频设备,有时尽管位移很小,速度也适中,但其加速度却可能很高的设备采用加速度测量是非常重要的手段。

另外还需要了解传感器的工作原理及应用选择,提及一点,例如采用涡流传感器测量的位移和应用加速度传感器通过两次积分输出的位移所得到的东西是完全不一样的。

涡流传感器测量轴承与轴杆之间的相对运动,加速度传感器测量轴承顶部的振动,然后转换成位移。

如整个轴承振动的很厉害,轴与轴承的相对运动很小,涡流传感器就不能反应出这样的状态,而加速度传感器则可以。

两种传感器测量两种不同的现象。

何谓振幅振动速度振速振动加速度振动一般可以用以下三个单位表示：mm、mm/s、mm/s2。

振幅、振动速度（振速）、振动加速度。

振幅是表象，速度和加速度是转子激振力的程度。

mm振动位移：一般用于低转速机械的振动评定； mm/s振动速度：一般用于中速转动机械的振动评定；mm/s2 振动加速度：一般用于高速转动机械的振动评定。

工程实用的振动速度是速度的有效值，表征的是振动的能量；加速度是用的峰值，表征振动中冲击力的大小。

振幅理解成路程，单位是mm；把振速理解成速度，单位是mm/s；振动加速度理解成运动加速度，单位mm/s2。

速度描述的是运动快慢；振速就是振动快慢，一秒内能产生的振幅。

振幅相同的设备，它的振动状态可能不同，所以引入了振速。

位移、速度、加速度都是振动测量的度量参数。

就概念而言,位移的测量能够直接反映轴承固定螺栓和其它固定件上的应力状况。

例如:通过分析透平机上滑动轴承的位移,可以知道其轴承内轴杆的位置和摩擦情况。

速度反映轴承及其它相关结构所承受的疲劳应力。

而这正是导致旋转设备故障的重要原因。

加速度则反映设备内部各种力的综合作用。

表达上三者均为正弦曲线,分别有90度,180度的相位差。

现场应用上,对于低速设备(转速小于1000RPM)来说,位移是最好的测量方法。

而那些加速度很小,其位移较大的设备,一般采用折衷的方法,即采用速度测量,对于高速度或高频设备,有时尽管位移很小,速度也适中,但其加速度却可能很高的设备采用加速度测量是非常重要的手段。

另外还需要了解传感器的工作原理及应用选择,提及一点,例如采用涡流传感器测量的位移和应用加速度传感器通过两次积分输出的位移所得到的东西是完全不一样的。

涡流传感器测量轴承与轴杆之间的相对运动,加速度传感器测量轴承顶部的振动,然后转换成位移。

如整个轴承振动的很厉害,轴与轴承的相对运动很小,涡流传感器就不能反应出这样的状态,而加速度传感器则可以。

两种传感器测量两种不同的现象。

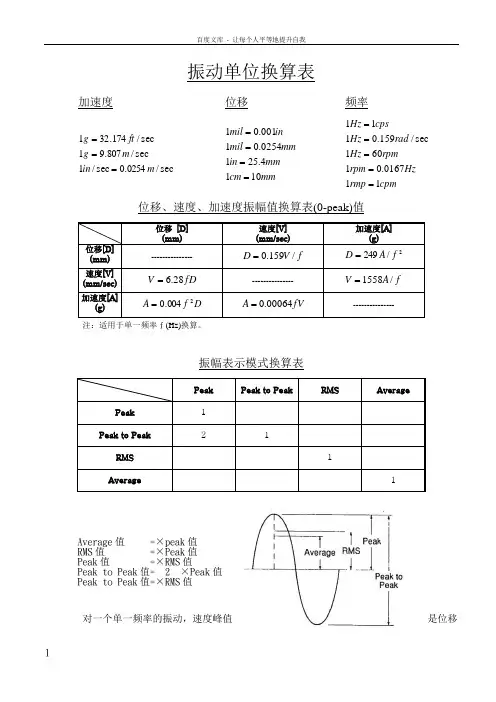
振动单位换算表加速度位移频率sec/0254.0sec /1sec /807.91sec /174.321m in m g ft g ===mmcm mm in mm mil inmil 1014.2510254.01001.01==== cpmrmp Hz rpm rpm Hz rad Hz cpsHz 110167.01601sec/159.0111=====位移、速度、加速度振幅值换算表(0-peak)值位移 [D] (mm) 速度[V] (mm/sec)加速度[A](g)位移[D] (mm) ---------------fV D /159.0=2/249f A D =速度[V] (mm/sec) fD V 28.6= ---------------f A V /1558=加速度[A](g)D f A 2004.0=fV A 00064.0=---------------注：适用于单一频率f (Hz)换算。

振幅表示模式换算表Peak Peak to PeakRMS AveragePeak 1 Peak to Peak2 1 RMS 1 Average1Average 值 =×peak 值 RMS 值 =×Peak 值 Peak 值 =×RMS 值Peak to Peak 值= 2 ×Peak 值 Peak to Peak 值=×RMS 值对一个单一频率的振动，速度峰值是位移峰值的2πf倍，加速度峰值又是速度峰值的2πf倍。

当然要注意位移一般用的峰峰值，速度用有效值，加速度用峰值。

还要注意现场测量的位移是轴和轴瓦的相对振动，速度和加速度测的是轴瓦的绝对振动。

假设一个振动的速度一定，是5mm/s，大家可以自己算下如果是低频振动，其位移会很大，但加速度很小。

高频振动位移则极小，加速度很大。

所以一般在低频区域都用位移，高频区域用加速度，中频用速度。

振动加速度计算公式
振动是物体在固定点或轴线周围做有规律地往复运动。

振动加速度是描述物体振动情况的一个物理量，表示单位时间内物体所获得的速度变化量。

首先，简谐振动的运动方程可以表示为：
x = Acos(ωt + φ)
其中，x为物体的位移，A为振幅，ω为角频率，t为时间，φ为相位常数。

其次，速度是位移对时间的导数，即
v = dx/dt = -Aωsin(ωt + φ)
再次，加速度是速度对时间的导数，即
a = dv/dt = -Aω^2cos(ωt + φ)
根据上述推导，振动加速度计算公式为：
a = -Aω^2cos(ωt + φ)
在上述公式中，A表示振幅，ω表示角频率，t表示时间，φ表示相位常数。

振幅决定了振动的幅度大小，角频率则影响振动的周期，相位常数则决定了振动的起始位置。

此外，还有一种计算振动加速度的方法是使用泰勒级数。

泰勒级数是一种将函数在其中一点展开成无穷级数的方法，通过求取一定阶数的导数来逼近其中一函数的值。

对于振动加速度，可以使用泰勒级数展开cos函数来计算。

根据泰勒
级数展开可得到：
cos(x) = 1 - (x^2/2!) + (x^4/4!) - (x^6/6!) + ...
通过对cos(x)函数进行泰勒级数展开，并截取一定阶数的项，可以
计算出振动加速度的近似值。

综上所述，振动加速度的计算公式可以根据物体振动特性得出，根据
简谐振动的运动方程和泰勒级数展开可以求得振动加速度的精确或近似值。

这些计算方法能够帮助我们更好地理解和描述振动现象。

振动试验机--最大加速度、振幅的计算方法、功能News振动试验机--最大加速度、振幅的计算方法、功能发布时间：2010-4-19 点击次数：7363次振动试验机用途：振动试验机是检测产品在运送、使用中产生碰撞及振动,为了避免这种事态的发生我们就要提早知道产品或产品中的部件的耐振寿命。

一、振动试验机计算公式：1、振动试验机最大加速度20g最大加速度=0.002×f2（频率HZ）×D（振幅mmp-p）举例:10HZ最大加速度=0.002×102×5=1g在任何頻率下最加速度不可大于20g2、振动试验机最大振幅＜5mm最大振幅=20/（0.002×f2）举例：100Hz最大振幅=20/（0.002×1002）=1mm在任何频率下振幅不可大于5mm3、频率越大振幅越小二、振动试验机型号：定频：垂直LD-L 水平LD-HL 垂直+水平LD-TL（50HZ）调频：垂直LD-F 水平LD-HF 垂直+水平LD-TF（1～600HZ）垂直LD-W 水平LD-HW 垂直+水平LD-TW（1～3000HZ）垂直LD-T 水平LD-HT 垂直+水平LD-TT（1～5000HZ）三、振动试验机技术参数：1、标准型台体尺寸：垂直500*500*150:mm、水平500*500*250:mm2、振动方向：垂直（上下）/水平（左右）3、承重量：100kg4、振幅可调范围：0～5mm、最大加速度：＜20g5、加速度与振幅换算1G=9.8m/s26、振动波形：正弦波/半弦波7、时间设定范围：1-65000S（以秒为单位）8、运行次数：1-65000次任意设定9、精密度：频率可显示到0.01Hz、精密度0.1Hz10、调频功能：在频率范围內任意设定频率11、扫频功能：（上限频率/下限频率/时间范围）可任意设定真正标准来回扫频12、可程式功能：15段每段可任意设定（频率/时间）可循环13、对数功能：①下频到上频②上频到下频③下频到上频再到下频--3种模式对数/可循环14、显示振幅加速度：如需看出振幅、加速度、最大加速度、准确数值需另购测量仪（另购）15、全功能电脑控制：485通讯接口如要连接电脑做控制,储存,记录,打印之功能需另够介面卡程式电脑（另购）16、电源电压：AC220V/50HZ、AC380V/50HZ注：定频50HZ振动试验机无调频，扫频，可程式，倍频，对数等功能。

振动常用术语1. 机械振动物体相对于平衡位置所作的往复运动称为机械振动。

简称振动。

例如，机器箱体的颤动、管线的抖动、叶片的摆动等都属于机械振动。

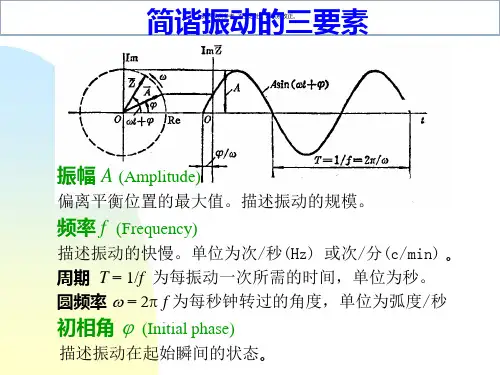
振动用基本参数、即所谓“振动三要素” —振幅、频率、相位加以描述。

3. 振幅3.1 振幅振幅是物体动态运动或振动的幅度。

振幅是振动强度和能量水平的标志，是评判机器运转状态优劣的主要指标。

3.2 峰峰值、单峰值、有效值振幅的量值可以表示为峰峰值（pp）、单峰值（p）、有效值（rms）或平均值（ap）。

峰峰值是整个振动历程的最大值，即正峰与负峰之间的差值；单峰值是正峰或负峰的最大值；有效值即均方根值。

只有在纯正弦波(如简谐振动)的情况下，单峰值等于峰峰值的1/2，有效值等于单峰值的0.707倍，平均值等于单峰值的0.637倍；平均值在振动测量中很少使用。

它们之间的换算关系是：峰峰值＝2×单峰值＝2×21/2×有效值。

此换算关系并无多大的实用价值，只是说明振幅在表示为峰峰值、峰值、有效值时，数值不同、相差很大。

3.3 振动位移、振动速度、振动加速度振幅分别用振动位移、振动速度、振动加速度值加以描述、度量，三者相互之间可以通过微分或积分进行换算。

在振动测量中，除特别注明外，习惯上，振动位移的量值为峰峰值，单位是微米[μm]或密耳[mil]；振动速度的量值为有效值，单位是毫米/秒[mm/s]或英寸/秒[ips]；振动加速度的量值是单峰值，单位是重力加速度[g]或米/秒平方[m/s2]，1[g] = 9.81[m/s2]。

可以认为，在低频范围内，振动强度与位移成正比；在中频范围内，振动强度与速度成正比；在高频范围内，振动强度与加速度成正比。

因为频率低意味着振动体在单位时间内振动的次数少、过程时间长，速度、加速度的数值相对较小且变化量更小，因此振动位移能够更清晰地反映出振动强度的大小；而频率高，意味着振动次数多、过程短，速度、尤其是加速度的数值及变化量大，因此振动强度与振动加速度成正比。

振幅和频率的关系公式振幅和频率是物理学中重要的概念，它们是描述物体振动特征的两个基本参数。

振幅表示物体振动时偏离平衡位置的最大距离，而频率则表示物体振动的周期性，即每秒钟振动的次数。

在物理学中，振幅和频率的关系可以用一个简单的公式来描述，这个公式是：振幅 = 峰值 / 2其中，峰值表示波形的最大值，也就是振动时物体偏离平衡位置的最大距离。

这个公式表明，振幅和峰值之间的关系是简单的线性关系，只需要将峰值除以2即可得到振幅。

另一方面，频率表示物体每秒钟振动的次数，通常用赫兹（Hz）来表示。

频率和周期的关系是：频率 = 1 / 周期周期是指物体振动一个完整的往复运动所需要的时间，通常用秒（s）来表示。

这个公式表明，频率和周期之间的关系也是简单的倒数关系。

振幅和频率的关系公式可以用来计算物体振动的一些基本参数。

例如，如果我们知道物体振动的频率和振幅，就可以计算出物体振动的最大速度和最大加速度。

最大速度等于振幅乘以频率，最大加速度等于振幅乘以频率的平方。

这些参数对于研究物体振动的性质和应用都非常重要。

振幅和频率的关系公式还可以用来解释一些自然现象。

例如，当我们听到声音时，声音的响度和音调就是由振幅和频率决定的。

响度表示声音的强度，它与声音的振幅成正比。

音调表示声音的高低，它与声音的频率成正比。

因此，当我们听到高音时，声波的频率较高，振幅较小；当我们听到低音时，声波的频率较低，振幅较大。

总之，振幅和频率是物理学中非常重要的概念，它们描述了物体振动的基本特征。

振幅和频率的关系公式可以用来计算物体振动的一些基本参数，也可以用来解释一些自然现象。

在学习物理学和应用物理学中，我们需要深入理解振幅和频率的概念，这将有助于我们更好地理解和应用物理学知识。

单频正弦振动加速度公式(一)单频正弦振动加速度公式1. 单频正弦振动加速度公式的定义单频正弦振动加速度公式是用于计算物体在单频正弦振动状态下的加速度的公式。

单频正弦振动是指物体在一个恒定的频率下做周期性的正弦振动。

2. 单频正弦振动加速度公式的表达式单频正弦振动加速度公式的表达式如下所示：a = A * w^2 * cos(wt + φ)其中，a表示加速度，A表示振幅，w表示角频率，t表示时间，φ表示相位角。

3. 单频正弦振动加速度公式的解释和示例•加速度与振幅的关系：加速度与振幅A成正比，即振幅越大，加速度也越大。

例如，一个弹簧在做正弦振动时，振幅越大，弹簧受到的加速度也越大。

•加速度与角频率的关系：加速度与角频率w的平方成正比，即角频率越大，加速度也越大。

例如，一个摆钟在做正弦振动时，摆动的频率越快（即角频率越大），钟摆的加速度也越大。

•加速度与相位角的关系：相位角φ对加速度具有影响。

相位角可以用来描述物体在振动周期中的位置。

例如，在一个质点以单频正弦振动运动时，当相位角为0时，即初始位置为最大位移点，此时加速度为正向最大值；当相位角为π/2时，即初始位置为最小位移点，此时加速度等于零。

相位角的变化会导致加速度的大小和方向的改变。

总结：单频正弦振动加速度公式描述了物体在单频正弦振动状态下的加速度。

该公式可以帮助我们计算和分析振动系统的加速度特性，对实际工程问题具有重要的应用价值。

在实际应用中，我们可以利用单频正弦振动加速度公式来计算和预测振动系统的加速度情况，从而设计和优化相关的工程结构和设备。

例如，在建筑工程中，可以通过计算加速度来评估建筑物的振动性能，以确保建筑物在自然灾害或其他外力作用下的安全性。

以上是关于单频正弦振动加速度公式的相关内容，希望对您有所帮助。