(河北专版)中考数学第二编中档题突破专项训练篇中档题型训练(八)统计与概率知识的应用课件
- 格式:pdf
- 大小:4.60 MB
- 文档页数:32

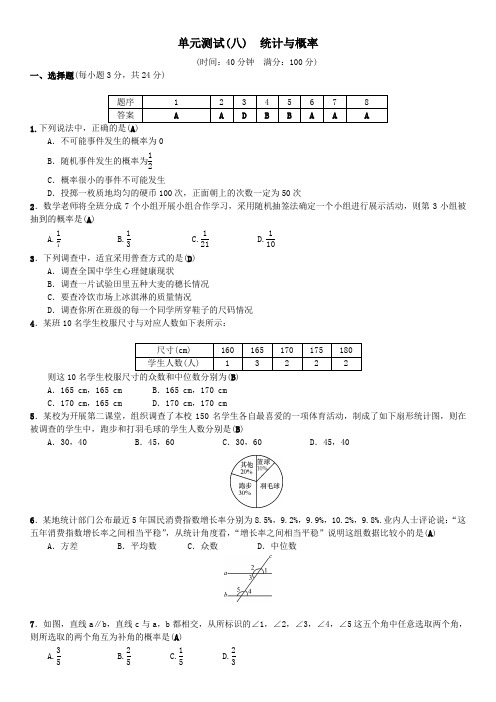
单元测试(八) 统计与概率(时间:40分钟 满分:100分)一、选择题(每小题3分,共24分)1.下列说法中,正确的是(A )A .不可能事件发生的概率为0B .随机事件发生的概率为12C .概率很小的事件不可能发生D .投掷一枚质地均匀的硬币100次,正面朝上的次数一定为50次2.数学老师将全班分成7个小组开展小组合作学习,采用随机抽签法确定一个小组进行展示活动,则第3小组被抽到的概率是(A )A.17B.13C.121D.1103.下列调查中,适宜采用普查方式的是(D )A .调查全国中学生心理健康现状B .调查一片试验田里五种大麦的穗长情况C .要查冷饮市场上冰淇淋的质量情况D .调查你所在班级的每一个同学所穿鞋子的尺码情况 4.某班10名学生校服尺寸与对应人数如下表所示:则这10名学生校服尺寸的众数和中位数分别为(B ) A .165 cm ,165 cm B .165 cm ,170 cm C .170 cm ,165 cm D .170 cm ,170 cm5.某校为开展第二课堂,组织调查了本校150名学生各自最喜爱的一项体育活动,制成了如下扇形统计图,则在被调查的学生中,跑步和打羽毛球的学生人数分别是(B )A .30,40B .45,60C .30,60D .45,406.某地统计部门公布最近5年国民消费指数增长率分别为8.5%,9.2%,9.9%,10.2%,9.8%.业内人士评论说:“这五年消费指数增长率之间相当平稳”,从统计角度看,“增长率之间相当平稳”说明这组数据比较小的是(A )A .方差B .平均数C .众数D .中位数7.如图,直线a ∥b ,直线c 与a ,b 都相交,从所标识的∠1,∠2,∠3,∠4,∠5这五个角中任意选取两个角,则所选取的两个角互为补角的概率是(A )A.35B.25C.15D.238.已知某校女子田径队23人年龄的平均数和中位数都是13岁,但是后来发现其中一位同学的年龄登记错误,将14岁写成15岁,经重新计算后,正确的平均数为a 岁,中位数为b 岁,则下列结论中正确的是(A )A .a <13,b =13B .a <13,b <13C .a >13,b <13D .a >13,b =13 二、填空题(每小题4分,共16分)9.在一次抽奖活动中,中奖概率是0.12,则不中奖的概率是0.88.10.一个不透明的口袋里装有若干除颜色外其他完全相同的小球,其中有6个黄球,将口袋中的球摇匀,从中任意摸出一个球记下颜色后再放回,通过大量重复上述实验后发现,摸到黄球的频率稳定在30%,由此估计口袋中共有小球20个.11.已知一组数据0,1,2,2,x ,3的平均数是2,则这组数据的方差是53.12.A ,B ,C 三人玩篮球传球游戏,游戏规则是:第一次传球由A 将球随机地传给B ,C 两人中的某一人,以后的每一次传球都是由上次的传球者随机地传给其他两人中的某一人,则三次传球后,球恰好在A 手中的概率为14.三、解答题(共60分)13.(14分)甲、乙两人都握有分别标记为A ,B ,C 的三张牌,两人做游戏,游戏规则是:若两人出的牌不同,则A 胜B ,B 胜C ,C 胜A ;若两人出的牌相同,则为平局.(1)用树状图或列表的方法,列出甲、乙两人一次游戏的所有可能的结果; (2)求出现平局的概率. 解:(1)画树状图得:则共有9种等可能的结果. (2)∵出现平局的有3种情况, ∴出现平局的概率为39=13.14.(14分)“泰微课”是学生自主学习的平台,某初级中学共有1 200名学生,每人每周学习的数学泰微课都在6至30个之间(含6和30),为进一步了解该校学生每周学习数学泰微课的情况,从三个年级随机抽取了部分学生的相关学习数据,并整理、绘制成统计图如下:每周学习数学泰微课 人数的条形统计图 每周学习数学泰微课人数分布扇形统计图根据以上信息完成下列问题: (1)补全条形统计图;(2)估计该校全体学生中每周学习数学泰微课在16至30个之间(含16和30)的人数. 解:(1)补全条形统计图如图.(2)估计该校全体学生中每周学习泰微课在16至30个之间的约有1 200×12+24+126÷10%=960(人).15.(16分)某小区超市一段时间每天订购80个面包进行销售,每售出1个面包获利润0.5元,未售出的每个亏损0.3元.(1)若今后每天售出的面包用x(0<x ≤80)表示,每天销售面包的利润用y(元)表示,写出y 与x 的函数关系式:y =0.8x -24;(2)商店连续m 天对该超市的面包销售情况进行了统计,并制成了频数分布直方图(每个组距包含左边的数,但不包含右边的数)和扇形统计图如下.请结合两图提供的信息,解答下列问题:①m 的值为30;②求在m 天内日销售利润少于32元的天数;(3)(2)中m 天内日销售面包个数70≤x<80这个组内的销售情况如下表:请计算该组内平均每天销售面包的个数. 解:(2)当y<32时,0.8x -24<32,∴x<70.由图可知,日销量在60~70个占20%,则30×20%=6, ∴销售利润少于32元的天数为3+6=9(天).(3)70×1+72×2+73×3+75×4+78×3+79×21+2+3+4+3+2=75(个).答:该组内平均每天销售面包的个数为75个. 16.(16分)为了了解七年级学生上学期参加社会实践活动的情况,随机抽查了某市七年级200名学生参加社会实践活动的天数,并根据抽查结果制作了如下不完整的条形统计图.根据以上信息,解答下列问题:(1)求条形统计图中参加社会实践活动天数为6天所对应的人数及被调查的200名学生参加社会实践活动天数的平均数;(2)被调查的学生参加社会实践活动天数的众数为5,中位数为5;(3)在此次调查活动中,A ,B ,C ,D 四位同学说他们中有两人被抽查了,请你用列表法或画树状图法,求出恰好抽到A 与B 两位同学的概率;(4)某市有七年级学生10万人,请你估计该市七年级学生参加社会实践活动不少于5天的人数.某市七年级200名学生参加社会实践活动天数的条形统计图解:(1)参加社会实践活动天数为6天所对应的人数为200-20-30-60-40=50(人),被调查的200名学生参加社会实践活动天数的平均数为3×20+4×30+5×60+6×50+7×40200=5.3.(3)列表如下:一共有12,∴P(恰好抽到A与B两位同学)=212=16.(4)10×200405060++=7.5(万人).答:估计该市七年级学生参加社会实践活动不少于5天的人数约为7.5万人.。

专项训练(八) 统计与概率一、选择题(2021,张家口模拟)以下说法正确的选项是(C)A.三角形的外心到三边的距离相等“任意画出一个等边三角形,它是轴对称图形〞是随机事件“任意画出一个平行四边形,它是中心对称图形〞是必然事件对飞机乘客的安检应采用抽样调查【解析】三角形的内心到三边的距离相等,应选项A错误.“任意画出一个等边三角形,它是轴对称图形〞是必然事件,应选项B错误.“任意画出一个平行四边形,它是中心对称图形〞是必然事件,应选项C正确.对飞机乘客的安检应采用全面调查,应选项D错误.(2021,怀化)以下说法正确的选项是(A)调查舞水河的水质情况,采用抽样调查的方式数据2,0,-2,1,3的中位数是-2可能性是99%的事件在一次试验中一定会发生D.从2000名学生中随机抽取 100名学生进行调查,样本容量为2000名学生【解析】 A. 调查舞水河的水质情况,采用抽样调查的方式,故这个选项正确.B. 数据2,0,-2,1,3的中位数是1,故这个选项错误. C.可能性是99%的事件在一次试验中不一定会发生,故这个选项错误. D.从2000名学生中随机抽取100名学生进行调查,样本容量为100,故这个选项错误.(2021,青岛改编)甲、乙两组数据的折线图如下图,设甲、乙两组数据的方差2 2 2 2分别为s甲,s乙,那么s甲与s乙的大小关系为(A)第3题图22B. 2 2A.s 甲>s乙 s 甲=s 乙2 2 D.不能确定C.s 甲<s乙【解析】从题图看出乙组数据的波动较小,故乙组数据的方差较小,即2 2 s 甲>s乙.在猜某一商品价格的游戏中,参与者事先不知道该商品的价格,主持人要求他从如图所示的四张卡片中任意拿走一张,使剩下的卡片从左到右连成一个三位数,该数就是他猜的价格.假设商品的价格是360元,那么他一次就能猜中的概率是(C)1第4题图1B.1A.3212C.4D.3【解析】可能出现的情况有:当拿走3时,剩下的数是560;当拿走5时,剩下的数是360;当拿走 6时,剩下的数是350;当拿走0时,剩下的数是356.出现这4种结果的可能性1相等,其中他一次就能猜中的结果只有1种,故其概率是4.5.(2021,抚顺)抚顺市中小学机器人科技大赛中,有7名学生参加决赛,他们决赛的成绩各不相同.其中一名参赛选手想知道自己能否进入前4名,他除了要知道自己的成绩外还要知道这7名学生成绩的( A)A.中位数B.众数C.平均数D.方差【解析】因为一共有7名学生,且他们的成绩各不相同,所以第4名的成绩是中位数.要判断是否进入前4名,应知道中位数的大小.(2021,黔西南州改编)某校准备从甲、乙、丙、丁四个科创小组中选出一组,参加区青少年科技创新大赛,下面表格反映的是各组平时成绩(单位:分)的平均数x及方差s2.如果要选出一个成绩较好且状态稳定的组去参赛,那么应选的组是(C)甲乙丙丁x7887s21A.甲组B.乙组C.丙组D.丁组7.【解析】因为乙组、丙组的平均数比甲组、丁组大,而丙组的方差比乙组的小,所以丙组的成绩较好且状态稳定,所以应选的组是丙组.(2021,湖州)某居委会组织两个检查组,分别对“垃圾分类〞和“违规停车〞的情况进行抽查.各组随机抽取辖区内某三个小区中的一个进行检查,那么两个组恰好抽到同一个小区的概率是(C)21B.1A.6 91D.2C.33【解析】将三个小区分别记为A,B,C.列表如下:A B CA(A,A)(B,A)(C,A)B(A,B)(B,B)(C,B)C(A,C)(B,C)(C,C)从表中可以看出,一共有9种等可能的结果,其中两个组恰好抽到同一个小区的结果有33 1种,所以两个组恰好抽到同一个小区的概率是=.3(2021,唐山路北区模拟)某校男子足球队的年龄分布情况如下表:年龄/岁131415161718人数268321那么这些队员年龄的众数和中位数分别是(A)A.15,15B.15,14C.16,15D.14,15【解析】同一年龄人数最多的是15岁,共8人,所以众数是名队员中,按照年龄从小到大排列,第11名队员与第12名队员的年龄都是15岁,所以中位数是(15+15)÷215.(2021,北京改编,导学号5892921)从甲地到乙地有A,B,C三条不同的公交线路.为了解早顶峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:min)的数据,统计如下:公交车用时/min30≤35<40<45<公交车用时t t t t合计的频数≤35≤40≤45≤50线路A59151166124500B5050122278500C4526516723500那么早顶峰期间,从甲地到乙地“公交车用时不超过45min〞的概率最大的线路是(C)A.AB.BC.CD.都一样【解析】∵A线路上的公交车用时不超过59+151+166=,B线45min的概率为50050+50+122路上的公交车用时不超过45min的概率为=,C线路上的公交车用时不超500过45min的概率为45+265+16745min的概率最=,∴C线路上的公交车用时不超过500大.二、填空题3A 区 10.(2021,成都)在一个不透明的盒子中,装有除颜色外完全相同的乒乓球共16个,从3中随机摸出一个乒乓球.假设摸到黄色乒乓球的概率为8,那么该盒子中装有黄色乒乓球的个数是6. 3【解析】 由题意,得该盒子中装有黄色乒乓球的个数是 16×8=6. (2021,承德模拟)某公司25名员工年薪的具体情况如下表:年薪/万元 30 14 9 6 43 员工数/人1234564那么该公司全体员工年薪的中位数比众数多.【解析】一共有25个数据,将这组数据按从小到大的顺序排列后,处于中间位置的是4,所以这组数据的中位数是4.这组数据中 是出现次数最多的,所以众数是3.5.所以中位数比众数多4-=0.5.(2021,舟山)小明和小红玩抛硬币游戏,连续抛两次,小明说:“假设两次都是正面, 1那么你赢;假设两次都是一正一反,那么我赢.〞小红赢的概率是〔 〕,该游戏 不公平 ( 填4 “公平〞或“不公平〞 ). 【解析】 因为抛两次硬币,所有时机均等的结果为正正,正反,反正,反反,所以出现1 2 1 两次正面的概率为 4,一正一反的概率为 4=2.因为二者概率不相等,所以游戏不公平.三、 解答题 13.(2021 ,遵义)某超市在端午节期间开展优惠活动,凡购物者都可以通过转动转盘 图所示)的方式享受折扣优惠.本次活动共有两种方式,方式一:转动转盘甲,指针指向域时,所购置物品享受九折优惠.指针指向其他区域无优惠;方式二:同时转动转盘甲和转盘乙,假设两个转盘的指针指向每个区域的字母相同,那么所购置物品享受八折优惠,其他情况无优惠.在每个转盘中,指针指向每个区城的可能性相同 (假设指针指向分界线,那么重新转动转 盘).(1)假设顾客选择方式一,那么享受九折优惠的概率为〔 1〕;4假设顾客选择方式二,请用画树状图法或列表法列出所有可能,并求顾客享受八折优惠的概率.第13题图4(如【思路分析】(1)转动转盘甲共有4种等可能的结果,其中指针指向A区域的结果只有1种,利用概率公式计算可得.(2)画树状图得出所有等可能的结果,从中确定指针指向每个区域的字母相同的结果数,利用概率公式计算可得.1解:(1)4(2)画树状图如答图.第13题答图从树状图中可以看出,一共有12种等可能的结果,其中指针指向每个区域的字母相同的2 1结果有2种,所以指针指向每个区域的字母相同的概率,即顾客享受八折优惠的概率为=.12 6(2021,江西)今年某市为创评“全国文明城市〞称号,周末团市委组织志愿者进行宣传活动.班主任梁老师决定从4名女班干部(小悦、小惠、小艳和小倩)中通过抽签方式确定2名女生去参加.抽签规那么:将4名女班干部的姓名分别写在4张完全相同的卡片正面,把4张卡片反面朝上,洗匀后放在桌面上,梁老师先从中随机抽取一张卡片,记下姓名,再从剩余的3张卡片中随机抽取第二张,记下姓名.(1)该班男生小刚被抽中是不可能事件,小悦被抽中是随机事件(填“不可能〞“必1〕;然〞或“随机〞);第一次抽取卡片小悦被抽中的概率为〔4试用画树状图或列表的方法表示这次抽签所有可能的结果,并求出小惠被抽中的概率.【思路分析】(1)根据随机事件和不可能事件的概念及概率公式解答可得.(2)列举出所有等可能的结果,看所求的结果数占总数的多少即可.解:(1)不可能随机1 4(2)记小悦、小惠、小艳和小倩这四位女同学分别为A,B,C,D.列表如下:A B C DA(B,A)(C,A)(D,A) B(A,B)(C,B)(D,B) C(A,C)(B,C)(D,C) D(A,D)(B,D)(C,D)从表中可以看出,一共有12种等可能的结果,其中小惠被抽中的结果有6种,567 1所以小惠被抽中的概率为=.2(2021,承德模拟)九年级教师对试卷讲评课中学生参与的深度与广度进行评价调查,根据调查结果将学生参与类别分为主动质疑、独立思考、专注听讲、讲解题目四种.评价组随机抽取了假设干名九年级学生的参与情况,绘制成如下图的条形统计图和扇形统计图(均不完整).第15题图在这次评价调查中,一共抽查了560名学生;(2)在扇形统计图中,参与类别“主动质疑〞所在的扇形的圆心角的度数为54°;请将条形统计图补充完整;如果全市有6000名九年级学生,那么在试卷评讲课中,“独立思考〞的九年级学生约有多少人?【思路分析】(1)根据“专注听讲〞的人数是224,所占的百分比是40%,即可求得抽查的总人数.(2)利用360°乘对应的百分比即可求解.(3)利用总人数减去其他各类别的人数,即可求得“讲解题目〞的人数,从而补全条形统计图.(4)利用6000乘对应的百分比即可.解:(1)560(2)54°(3)如答图所示.6第15题答图168(4)在试卷讲评课中,“独立思考〞的九年级学生约有6000×560=1800(人).某班级要从甲、乙两位同学中选派一人参加“秀美山河〞知识竞赛.老师对他们的五次模拟成绩(单位:分)进行了整理,计算出甲成绩的平均数是80,甲、乙成绩的方差分别是320,40,但制作的统计图(如图)表尚不完整.甲、乙两人模拟成绩统计表第一次第二次第三次第四次第五次甲成绩/分901009050a乙成绩/分8070809080根据以上信息,请你解答以下问题:a=70;请完成图中表示甲成绩变化情况的折线;求乙成绩的平均数;从平均数和方差的角度分析,谁将被选中.第16题图【思路分析】(1)根据平均数公式即可求得a的值.(2)根据(1)中计算的结果即可作出甲成绩变化情况的折线.(3)利用平均数公式即可求解.(4)首先比拟平均数,选择平均数大的;假设平均数相同,那么比拟方差,选择方差小,比拟稳定的.解:(1)70(2)如答图所示.7第16题答图1(3)x 乙=×(80+70+80+90+80)=80.因为甲、乙成绩的平均数相同,乙成绩的方差小于甲成绩的方差, 所以乙的成绩比甲的成绩稳定. 所以乙将被选中.(2021,张家口模拟,导学号5892921)垫球是排球队常规训练的重要工程之一.以下图(如图)表中的数据是甲、乙、丙三人每人 10 次垫球测试的成绩.测试规那么为连续接球10个,每垫球到位1个记1分.运发动甲测试成绩表测试序号1 2 3 4 5 6 7 8 9 10 成绩/分7687758787第17题图 写出运发动甲测试成绩的众数和中位数; 在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁 更适宜?为什么? (参考数据:三人成绩的方差分别为2 22s 甲= ,s 乙= ,s 丙=0.81) 甲、乙、丙三人相互之间进行垫球练习,每个人的球都等可能地传给其他两人,球最先从甲手中传出,第三轮结束时球回到甲手中的概率是多少?8河北省中考数学复习第六章统计与概率专项训练(八)统计与概率试题(含解析)11 / 1111【思路分析】(1)观察表格可知运发动甲测试成绩的众数和中位数都是 7.(2) 易求得x 甲=7,x 乙=7,x 丙=,根据题意判断. (3)画出树状图,即可解决问题. 解:(1)运发动甲测试成绩的众数是 7,中位数是 7. (2)∵x 甲=(5+6+7×5+8×3)÷10=7,x 乙=(6×2+7×6+8×2)÷10=7,x 丙=(5×2+6×4+7×3+8)÷10= ,2x 甲=x 乙>x 丙.32s 甲>s 乙,∴选运发动乙更适宜. 画树状图如答图所示.第17题答图由树状图中可以看出,一共有 8种等可能的结果,其中第三轮结束时球回到甲手中的结 2 1果有2种,∴第三轮结束时球回到甲手中的概率是=.849。

单元测试 ( 八)范围 : 统计与概率限时:45分钟满分:100分一、选择题 (每题 3 分, 共 30 分)1.小伟掷一枚质地均匀的骰子, 骰子的六个面上分别刻有 1 到 6 的点数 , 以下事件是随机事件的是()A.掷一次骰子 , 骰子向上一面的点数大于0B.掷一次骰子 , 骰子向上一面的点数为7C.掷三次骰子 , 骰子向上一面的点数之和恰好为18D.掷两次骰子 , 骰子向上一面的点数之积恰好是112.昨年某市有近 5 万名考生参加中考, 为认识这些考生的数学成绩, 从中抽取1000 名考生的数学成绩进行统计剖析, 以下说法正确的选项是()A.这 1000 名考生是整体的一个样本B.近 5 万名考生是整体C.每位考生的数学成绩是个体D. 1000 名考生的数学成绩是样本容量3.以下说法中正确的选项是()A.“翻开电视 , 正在播放《新闻联播》”是必定事件B.一组数据的颠簸越大, 方差越小C.数据 1,1,2,2,3的众数是3D.想认识某种饮猜中含色素的状况, 宜采纳抽样检查4 二十四节气是中国古代办感人民长久经验累积的结晶, 它与日间时长亲密有关 , 当春分、秋分时 , 日夜时长大概相等 ;.当夏至时 , 日间时长最长.依据图 D8 1, 在以下选项中日间时长低于11 小时的节气是() -图 D8-1A.惊蛰B.小满C.立秋 D .大寒5.一个暗箱里装有10 个黑球 ,8个红球,12个白球,每个球除颜色外都同样, 从中随意摸出一球, 不是白球的概率是()A.B.C.D.6.某校将举办一场“中国汉字听写大赛”, 要求各班选举一名同学参加竞赛, 为此 , 九年级某班组织了五轮班级选拔赛,在这五轮选拔赛中, 甲、乙两名同学的均匀分都是96 分 , 甲的成绩的方差是1, 乙的成绩的方差是0. 8.依据以上数据 , 下列说法正确的选项是()A.甲的成绩比乙的成绩稳固B.乙的成绩比甲的成绩稳固C.甲、乙两人的成绩同样稳固D.没法确立甲、乙两人的成绩谁更稳固7.已知一组数据 :6,2,8,x,7,它们的均匀数是6, 则这组数据的中位数是()A.7B.6C.5D.48.如图D8- 2 所示 , 暗影是两个同样菱形的重合部分, 假定能够随机在图中取点, 那么这个点取在暗影部分的概率是()A.B.C.D.9.在不透明的袋子中有黑棋子 10 枚和白棋子若干 ( 它们除颜色外都同样 ), 现随机从中摸出 10 枚记下颜色后放回 , 这样连续做了10 次 , 记录了以下的数据 :次数 1 2 3 4 5 67 8 9 10黑棋子数1302342113依据以上数据 , 预计袋中的白棋子的数目为()A.60枚B.50枚 C .40枚D.30枚10.小明和小亮玩一种游戏: 三张大小、质地都同样的卡片上分别标有数字1,2,3,现将标有数字的一面朝下, 小明从中任意抽取一张 , 记下数字后放回洗匀, 而后小亮从中随意抽取一张, 计算小明和小亮抽得的两个数字之和, 若和为奇数 , 则小明胜 , 若和为偶数 , 则小亮胜.获胜概率大的是()A.小明 B .小亮C.同样 D .没法确立二、填空题 (每题 5 分, 共 20 分)11.一个样本的50 个数据分别落在 5 个组内 , 第 1,2,3,4组数据的个数分别是2,8,15,5,则第5组数据的频数为,频次为.12.在一个不透明的口袋中有除颜色外其余都同样的红球、黄球、蓝球共200 个, 某位同学经过多次摸球试验后发现, 其中摸到红色球和蓝色球的频次稳固在35%和 55%,则口袋中可能有黄球个.13.某校拟招聘一名优异数学教师, 现有甲、乙、丙三名教师入围, 三名教师笔试、面试成绩以下表所示, 综合成绩依据笔试占 60%,面试占 40%进行计算 , 学校录取综合成绩得分最高者, 则被录取教师的综合成绩为.教师甲乙丙成绩笔试80 分82 分78 分面试76 分74 分78 分14.有两组卡片 , 第一组的三张卡片上分别写有数字3,4,5,第二组的三张卡片上分别写有数字1,3,5,现从每组卡片中各随机抽出一张 , 用抽取的第一组卡片上的数字减去抽取的第二组卡片上的数字, 差为正数的概率为.三、解答题 (共 30 分)15. (15 分 ) 某班 13 位同学参加每周一次的卫生大打扫, 按学校的卫生要求需要达成总面积为60 m2的三个项目的任务,三个项目的面积比率和每人每分钟达成状况如图D8-3所示 :图 D8-3(1)从统计图中可知 : 擦玻璃的面积占总面积的百分比为, 每人每分钟擦课桌椅2 m;(2)扫地和拖地的面积是m2;(3)他们一同达成扫地和拖地任务后 , 把这 13 人分红两组 , 一组去擦玻璃 , 一组去擦课桌椅 , 假如你是卫生委员 , 该怎样分派这两组的人数 , 才能最快地达成任务 ?16. (15分)(1)在射击竞赛中, 七位选手的成绩( 单位 : 环 ) 分别为8,5,7,8,6,8,5,则这组数据的众数和中位数分别是环和环 .(2) 某学校正部分学生进行了抽样检查, 就学生对射击运动的喜爱程度(A: 喜爱 ;B: 一般 ;C: 不喜爱 ;D: 无所谓 ) 进行数据统计 , 并绘制了以下两幅不完好的统计图.①此次检查的样本容量为;②条形统计图中存在的错误是( 填 A,B,C 中的一个 );③在图②中补画条形统计图中不完好的部分;④若从该校被检查的喜爱射击运动的学生中抽取10 人进行射击训练, 则喜爱射击运动的小明被抽中的概率是多少?图 D8-4参照答案1.C 2.C 3.D 4.D 5.D 6.B7 A[分析]由题意得 628 765,解得:7, 这组数据依据从小到大的次序摆列为:2,6,7,7,8, 则中位数为7.故.+ + +x+ = ×x=选 A.8. C [ 分析 ]设暗影部分的面积是x,则整个图形的面积是7x, 则这个点取在暗影部分的概率是= ,应选 C.9. C [ 分析 ]依据试验供给的数据得出: 黑棋子所占整体的比率为(1 +3+0+2+3+4+2+1+1+3) ÷100=20%,因此白棋子所占整体比率为1- 20%=80%.设白棋子有x 枚 . 由题意,得=80%,解得 x=40,经查验 x=40是原方程的解且切合实质, 即袋中的白棋子数目约为40 枚.应选 C.10.B [ 分析 ]画树形图,得共有 9种状况 , 和为偶数的有 5种, 因此小亮胜的概率是, 那么小明胜的概率是, 因此获胜概率大的是小亮.11. 200. 4[ 分析 ] 依据题意, 得第 1,2,3,4 组数据的个数分别是 2,8,15,5,共 (2 +8+15+5) =30, 样本容量为50, 故第 5组的频数是50- 30=20, 频次是=0. 4.12. 20[ 分析 ] ∵某位同学经过多次摸球试验后发现, 此中摸到红色球和蓝色球的频次稳固在35%和 55%,∴摸到黄球的概率 =1- 35%- 55%=10%,∴口袋中黄球的个数=200×10%=20,即口袋中可能有黄球20 个.故答案为 20.13. 78. 8 分[ 分析 ] ∵甲的综合成绩为80×60%+76×40%=78. 4( 分 ), 乙的综合成绩为 82×60%+74×40%=78. 8( 分), 丙的综合成绩为 78×60%+78× 40%=78( 分 ),∴被录取的教师为乙 , 其综合成绩为78. 8 分.14.[分析]列表,得第一组差345第二组123430125- 2- 10全部等可能的状况有9 种, 此中差为正数的状况有 5 种 , 则P= .15.解 :(1)依据题意,得擦玻璃的面积占总面积的百分比是1- 55%- 25%=20%;每人每分钟擦课桌椅m2.故答案为 20%.(2) 扫地和拖地的面积是60×55%=33(m2) .故答案为 33.(3)设擦玻璃 x 人,则擦课桌椅(13 -x )人 .依据题意 , 得x ∶(13 -x )=20%∶25%,解得 x=8,经查验 x=8是原方程的解且切合题意.13- 8=5( 人 ) .答: 擦玻璃 8 人, 擦课桌椅 5 人能最快达成任务.16.解 :(1) 这组数据依据从小到大的次序摆列为5,5,6,7,8,8,8,则众数为 8 环, 中位数为 7 环.故答案为 8 7.(2) ①由条形统计图知A类有 40人 , 由扇形统计图知它占抽查人数的20%,∴此次检查的样本容量为40÷ 20%=200.故答案为 200.②C 类所占的百分比为1-40% 20% 15% 25%,因此 C 类共有 20025% 50( 人 ),∴C 错误.故答案为 C--=×=.③D 类的共有 200×15%=30( 人 ),补全条形统计图以下图:④200 人中喜爱射击运动的学生有40 人 , 小明被抽中的概率为10÷40= .。