2013年11月19初中毕业会考适应性考试和答案6

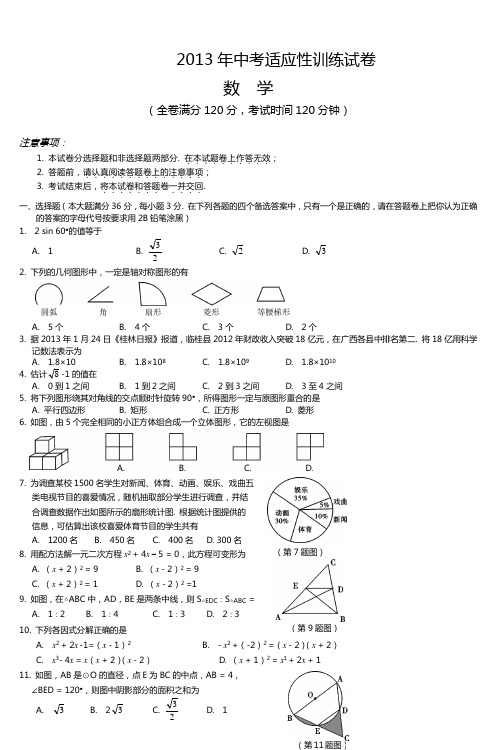
2013年中考适应性训练试卷数 学（全卷满分120分，考试时间120分钟）注意事项：1. 本试卷分选择题和非选择题两部分. 在本试题卷上作答无效．．．．．．．．．．；2. 答题前，请认真阅读答题．．．．．．．卷．上的注意事项．．．．．．；3. 考试结束后，将本试卷和答题．．．．．．．卷一并交回．．．．. 一、选择题（本大题满分36分，每小题3分. 在下列各题的四个备选答案中，只有一个是正确的，请在答题卷上把你认为正确的答案的字母代号按要求用2B 铅笔涂黑） 1. 2 sin 60°的值等于 A. 1B.23C.2D.32. 下列的几何图形中，一定是轴对称图形的有A. 5个B. 4个C. 3个D. 2个3. 据2013年1月24日《桂林日报》报道，临桂县2012年财政收入突破18亿元，在广西各县中排名第二. 将18亿用科学记数法表示为A. 1.8×10B. 1.8×108C. 1.8×109D. 1.8×10104. 估计8-1的值在 A. 0到1之间 B. 1到2之间 C. 2到3之间 D. 3至4之间5. 将下列图形绕其对角线的交点顺时针旋转90°，所得图形一定与原图形重合的是 A. 平行四边形 B. 矩形 C. 正方形 D. 菱形6. 如图，由5个完全相同的小正方体组合成一个立体图形，它的左视图是7. 为调查某校1500名学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况，随机抽取部分学生进行调查，并结 合调查数据作出如图所示的扇形统计图. 根据统计图提供的 信息，可估算出该校喜爱体育节目的学生共有 A. 1200名 B. 450名 C. 400名 D. 300名8. 用配方法解一元二次方程x 2 + 4x – 5 = 0，此方程可变形为A. （x + 2）2 = 9B. （x - 2）2 = 9C. （x + 2）2 = 1D. （x - 2）2 =1 9. 如图，在△ABC 中，AD ，BE 是两条中线，则S △EDC ∶S △ABC =A. 1∶2B. 1∶4C. 1∶3D. 2∶310. 下列各因式分解正确的是A. x 2 + 2x -1=（x - 1）2B. - x 2 +（-2）2 =（x - 2）（x + 2）C. x 3- 4x = x （x + 2）（x - 2）D. （x + 1）2 = x 2 + 2x + 111. 如图，AB 是⊙O 的直径，点E 为BC 的中点，AB = 4， ∠BED = 120°，则图中阴影部分的面积之和为 A.3 B. 23C.23D. 1圆弧 角 扇形 菱形 等腰梯形A. B.C. D.（第9题图）（第11题图）（第7题图）12. 如图，△ABC 中，∠C = 90°，M 是AB 的中点，动点P 从点A出发，沿AC 方向匀速运动到终点C ，动点Q 从点C 出发，沿 CB 方向匀速运动到终点B. 已知P ，Q 两点同时出发，并同时 到达终点，连接MP ，MQ ，PQ . 在整个运动过程中，△MPQ 的面积大小变化情况是 A. 一直增大B. 一直减小C. 先减小后增大D. 先增大后减小二、填空题（本大题满分18分，每小题3分，请将答案填在答题卷上，在试卷上答题无效） 13. 计算：│-31│= . 14. 已知一次函数y = kx + 3的图象经过第一、二、四象限，则k 的取值范围是 .15. 在10个外观相同的产品中，有2个不合格产品，现从中任意抽取1个进行检测，抽到合格产品的概率是 .16. 在临桂新区建设中，需要修一段全长2400m 的道路，为了尽量减少施工对县城交通所造成的影响，实际工作效率比原计划提高了20%，结果提前8天完成任务，求原计划每天修路的长度. 若设原计划每天修路x m ，则根据题意可得方程 .17. 在平面直角坐标系中，规定把一个三角形先沿着x 轴翻折，再向右平移2个单位称为1次变换. 如图，已知等边三角形 ABC 的顶点B ，C 的坐标分别是（-1，-1），（-3，-1），把 △ABC 经过连续9次这样的变换得到△A ′B ′C ′，则点A 的对 应点A ′ 的坐标是 .18. 如图，已知等腰Rt △ABC 的直角边长为1，以Rt △ABC 的斜边AC 为直角边，画第二个等腰Rt △ACD ，再以Rt △ACD 的 斜边AD 为直角边，画第三个等腰Rt △ADE ……依此类推直 到第五个等腰Rt △AFG ，则由这五个等腰直角三角形所构成 的图形的面积为 . 三、解答题（本大题8题，共66分，解答需写出必要的步骤和过程. 请将答案写在答题卷上，在试卷上答题无效）19. （本小题满分8分，每题4分）（1）计算：4 cos45°-8+(π-3) +(-1)3；（2）化简：（1 - n m n+）÷22nm m -.20. （本小题满分6分）21. （本小题满分6分）如图，在△ABC 中，AB = AC ，∠ABC = 72°. （1）用直尺和圆规作∠ABC 的平分线BD 交AC 于点D （保留作图痕迹，不要求写作法）；（2）在（1）中作出∠ABC 的平分线BD 后，求∠BDC 的度数.22. （本小题满分8分）在开展“学雷锋社会实践”活动中，某校为了解全校1200名学生参加活动的情况，随机调查了50名学生每人参加活动的次数，并根据数据绘成条形统计图如下：3121--+x x ≤1， ……① 解不等式组：3（x -1）＜2 x + 1. ……②（第12题图）（第17题图）（第18题图） （第21题图）°（1）求这50个样本数据的平均数、众数和中位数；（2）根据样本数据，估算该校1200名学生共参加了多少次活动. 23. （本小题满分8分）如图，山坡上有一棵树AB ，树底部B 点到山脚C 点的距离BC 为63米，山坡的坡角 为30°. 小宁在山脚的平地F 处测量这棵树的高，点 C 到测角仪EF 的水平距离CF = 1米，从E 处测得树 顶部A 的仰角为45°，树底部B 的仰角为20°，求树 AB 的高度.（参考数值：sin20°≈0.34，cos20°≈0.94，tan20°≈0.36）24. （本小题满分8分）如图，PA ，PB 分别与⊙O 相切于点A ，B ，点M 在PB 上，且OM ∥AP ，MN ⊥AP ，垂足为N. （1）求证：OM = AN ；（2）若⊙O 的半径R = 3，PA = 9，求OM 的长.25. （本小题满分10分）某中学计划购买A 型和B 型课桌凳共200套. 经招标，购买一套A 型课桌凳比购买一套B 型课桌凳少用40元，且购买4套A 型和5套B 型课桌凳共需1820元. （1）求购买一套A 型课桌凳和一套B 型课桌凳各需多少元？（2）学校根据实际情况，要求购买这两种课桌凳总费用不能超过40880元，并且购买A 型课桌凳的数量不能超过B 型课桌凳数量的32，求该校本次购买A 型和B 型课桌凳共有几种方案？哪种方案的总费用最低？26. （本小题满分12分）在平面直角坐标系中，现将一块等腰直角三角板ABC 放在第二象限，斜靠在两坐标轴上，点C 为（-1，0）. 如图所示，B 点在抛物线y =21x 2 -21x – 2图象上，过点B 作BD ⊥x 轴，垂足为D ，且B 点横坐标为-3. （1）求证：△BDC ≌ △COA ； （2）求BC 所在直线的函数关系式；（3）抛物线的对称轴上是否存在点P ，使△ACP 是以AC 为直角边的直角三角形？若存在，求出 所有点P的坐标；若不存在，请说明理由.2013年初三适应性检测参考答案与评分意见（第23题图）（第24题图） （第26题图）一、选择题说明：第12题是一道几何开放题，学生可从几个特殊的点着手，计算几个特殊三角形面积从而降低难度，得出答案. 当点P ，Q 分别位于A 、C 两点时，S △MPQ =21S △ABC ；当点P 、Q 分别运动到AC ，BC 的中点时，此时，S △MPQ =21×21AC. 21BC =41S △ABC ；当点P 、Q 继续运动到点C ，B 时，S △MPQ =21S △ABC ，故在整个运动变化中，△MPQ 的面积是先减小后增大，应选C. 二、填空题 13.31； 14. k ＜0； 15. 54（若为108扣1分）； 16. x 2400-x%)201(2400+ = 8； 17. （16，1+3）； 18. 15.5（或231）. 三、解答题19. （1）解：原式 = 4×22-22+1-1……2分（每错1个扣1分，错2个以上不给分） = 0 …………………………………4分（2）解：原式 =（n m n m ++-n m n +）·m n m 22- …………2分= nm m +·m n m n m ))((-+ …………3分= m – n …………4分 20. 解：由①得3（1 + x ）- 2（x -1）≤6， …………1分 化简得x ≤1. …………3分 由②得3x – 3 ＜ 2x + 1， …………4分 化简得x ＜4. …………5分 ∴原不等式组的解是x ≤1. …………6分21. 解（1）如图所示（作图正确得3分）（2）∵BD 平分∠ABC ，∠ABC = 72°， ∴∠ABD =21∠ABC = 36°， …………4分 ∵AB = AC ，∴∠C =∠ABC = 72°， …………5分 ∴∠A= 36°，∴∠BDC =∠A+∠ABD = 36° + 36° = 72°. …………6分 22. 解：（1）观察条形统计图，可知这组样本数据的平均数是 _x =50551841737231⨯+⨯+⨯+⨯+⨯　=3.3， …………1分∴这组样本数据的平均数是3.3. …………2分∵在这组样本数据中，4出现了18次，出现的次数最多， ∴这组数据的众数是4. …………4分∵将这组样本数据按从小到大的顺序排列，其中处在中间的两个数都是3，有233 = 3. ∴这组数据的中位数是3. ………………6分（2）∵这组数据的平均数是3.3，∴估计全校1200人参加活动次数的总体平均数是3.3，有3.3×1200 = 3900. ∴该校学生共参加活动约3960次. ………………8分23. 解：在Rt △BDC 中，∠BDC = 90°，BC = 63米，∠BCD = 30°，∴DC = BC ·cos30° ……………………1分 = 63×23= 9， ……………………2分 ∴DF = DC + CF = 9 + 1 = 10，…………………3分 ∴GE = DF = 10. …………………4分 在Rt △BGE 中，∠BEG = 20°， ∴BG = CG ·tan20° …………………5分 =10×0.36=3.6， …………………6分 在Rt △AGE 中，∠AEG = 45°，∴AG = GE = 10， ……………………7分 ∴AB = AG – BG = 10 - 3.6 = 6.4.答：树AB 的高度约为6.4米. ……………8分24. 解（1）如图，连接OA ，则OA ⊥AP . ………………1分∵MN ⊥AP ，∴MN ∥OA. ………………2分 ∵OM ∥AP ，∴四边形ANMO 是矩形.∴OM = AN. ………………3分（2）连接OB ，则OB ⊥AP ，∵OA = MN ，OA = OB ，OM ∥BP ， ∴OB = MN ，∠OMB =∠NPM.∴Rt △OBM ≌Rt △MNP . ………………5分 ∴OM = MP .设OM = x ，则NP = 9- x . ………………6分 在Rt △MNP 中，有x 2 = 32+（9- x ）2.∴x = 5. 即OM = 5 …………… 8分25. 解：（1）设A 型每套x 元，则B 型每套（x + 40）元. …………… 1分 ∴4x + 5（x + 40）=1820. ……………………………………… 2分∴x = 180，x + 40 = 220.即购买一套A 型课桌凳和一套B 型课桌凳各需180元、220元. ……………3分（2）设购买A 型课桌凳a 套，则购买B 型课桌凳（200 - a ）套.a ≤32（200 - a ）， ∴ …………… 4分 180 a + 220（200- a ）≤40880.解得78≤a ≤80. …………… 5分∵a 为整数，∴a = 78，79，80∴共有3种方案. ………………6分 设购买课桌凳总费用为y 元，则y = 180a + 220（200 - a ）=-40a + 44000. …………… 7分 ∵-40＜0，y 随a 的增大而减小，∴当a = 80时，总费用最低，此时200- a =120. …………9分 即总费用最低的方案是：购买A 型80套，购买B 型120套. ………………10分。

2013年初中毕业生学业文化考试适应性练习数学试题卷考生须知：1．全卷分试题卷和答题卡两部分．全卷满分150分，考试时间120分钟．试题卷共6页，答题卡共6页．2．答题前，先用钢笔在答题卡规定位置上填写学校、班级、姓名、准考证号. 3.答题时,将试卷Ⅰ选择题的答案用2B 铅笔在答题卡上对应的选项位置涂黑、涂满，试卷Ⅱ填空题的答案写在答题卡上对应的横线上.解答题的答案或解答过程直接做在答题卡上.参考公式：二次函数c bx ax y ++=2(0≠a )图象的顶点坐标是)44,2(2ab ac a b --． 温馨提示：细心审题，认真答题，相信你定有出色表现！试卷I (选择题，共40分)请将本卷的答案，用2B 铅笔在答题卡上对应的选项位置涂黑、涂满．一．选择题(本大题有10小题，每小题4分，共40分．请选出每小题中一个符合题意的正确选项，不选、多选、错选，均不给分) 1.下列各组数中，互为相反数的是（ ▲ ）A.2和2-B.2-和21 C.2-和21- D.21和2 2． 2.5PM 是指空气中直径小于等于5.2微米（0000025.0米）的可吸入颗粒物，号称“灰霾杀手”．0000025.0用科学记数法表示为（ ▲ ）A ．62.510⨯ B ．62.510-⨯ C ．52510-⨯D ．52.510-⨯3．如图，已知CD AB //,若015=∠A ,025=∠E ，则C ∠等于（ ▲ ）.A.015 B.025 C.035 D.0404．如图是由4个大小相同的正方体搭成的几何体，则其俯视图是（ ▲ ）5.使分式22xx -+无意义的x 的值是（ ▲ ） A.2x = B.2x =- C.2x ≠ D.2x ≠- 6.已知两圆的半径分别是3和2，圆心的坐标分别是)2,0(和)4,0(-，那么这两圆的位置关系是（ ▲ ）A.内含B.相交C.相切D.外离7．不透明袋中装有编号为3,2,1的三个质地均匀、大小相同的球，从中随机取出一球记下编号后，放入袋中搅匀，再从袋中随机取出一球，则两次所取球的编号相同的概率为( ▲ )A.19B.16C.13D.12 8．如图，Rt ABC ∆中，090C ∠=，以点B 为圆心，适当长为半径画弧，与ABC ∠的两边相交于点F E ,，分别以点E 和点F 为圆心，大于EF 21的长为半径画弧，两弧相交于点M ，作射线BM ，交AC 于点D ．若BDC ∆的面积为10，A ABC ∠=∠2，则ABC ∆的面积为（ ▲ ）A ．25B ．30C ．35D ．409．小聪和小明分别从相距30公里的甲、乙两地同时出发相向而行，小聪骑摩托车到达乙地后立即返回甲地，小明骑自行车从乙地直接到达甲地，函数图象1()y km 和2()y km 分别表示小聪离甲地的距离和小明离乙地的距离与已用时间()t h 之间的关系,如图所示.则下列叙述中错误的是( ▲ )A ．折线段OAB 是表示小聪的函数图象1y ,线段OC 是表示小明的函数图象2y .B ．小聪去乙地和返回甲地的平均速度相同.C ．两人在出发80分钟后第一次相遇.D ．小明骑自行车的平均速度为15公里/小时.10．已知二次函数221y x bx =++，当b 取不同的值时，其图象构成一个“抛物线系”，如图中的实线型抛物线分别是b 取三个不同的值时二次函数的图象，它们的顶点在一条抛物线上（图中虚线型抛物线），则这条虚线型抛物线的解析式是（ ▲ ）A.21y x =-+B.221y x =-+C.2112y x =-+ D.241y x =-+试卷Ⅱ(填空题和解答题，共110分)请将本卷答案或解答过程用签字笔或钢笔写在答题卡对应答题区域内．二．填空题(本大题有6小题，每小题5分，共30分．) 11.分解因式：34x x -= ▲ ．12.某校为选拔学生参加市教育部门组织的中学生头脑运动会，教练对甲、乙两名选手平时的五次训练成绩进行统计，两选手的平均成绩均为76分，方差分别是251S =甲，212S =乙.则两选手中，成绩比较稳定的是 ▲ 选手.13.将底面周长为20cm π的圆锥的侧面展开后，所得扇形的圆心角为0120，则该圆锥的母线长是▲ cm ．14.如图,将量角器和含030角（图中的BAC ∠）的一块直角三角板紧靠着放在同一平面内,使,,D C B 三点在同一条直线上,量角器的非圆弧边DC 的长恰好是该三角板一边BC 的2倍,过点A 作量角器圆弧所在圆的切线,切点为E ,则点E 所对应的量角器上的刻度数是 ▲ 度(只要求写出锐角的度数).15.如图，矩形ABCD 中放置9个形状、大小都相同的小矩形,相关数据图中所示,则图中阴影部分的面积为 ▲ (平方单位)．16．如图，AOB ∆为等边三角形，点B 的坐标为(2,0)-，过点(2,0)C 作直线l 交AO 于点D ，交AB 于E ，点E 在反比例函数(ky x x=＜0)的图象上，若ADE ∆和DCO ∆（即图中两阴影部分）的面积相等，则k 值为 ▲ .三．解答题(本大题有8小题，第17～20小题每小题8分，第2l 小题10分，第22、23小题每小题12分，第24小题14分，共80分．解答需写出必要的文字说明、演算步骤或证明过程.)17．（1）计算：121(2)sin 45(21)()2---︒+---. （2）解不等式：3(1)2(12)x x -<+.（温馨提示：此空白处不答题）18．如图，已知平面直角坐标系中两点(1)A -，5、(41)B -，． （1）将A B 、两点沿x 轴分别向右平移5个单位，得到点11A B 、，请画出四边形11ABB A ,并直接写出这个四边形的面积；（2）画一条直线，将四边形11ABB A 分成两个全等的图形，并满足这两个图形都是轴对称图形.19．如图，在我市岭光燧道建设工程中，工程队沿AC 方向凿山洞建路，为了加快施工进度，要在山的另一边同时施工.该工程队设计了如下方案:在AC 上取一点B ,使0145,ABD ∠=500BD m =,055D ∠=.要使,,A C E 三点成一直线,求开挖点E 离点D 的距离(精确到1m )20．“保护眼睛，从我做起”.我市教育部门为了解本市在校生的视力状况，随机抽取了我市的1000名小学生和若干名初中生，对他们的视力状况进行调查，并把调查结果绘制成如下统计图1和2.（近视程度分为轻度、中度、高度三种）.请根据题中信息解答下列问题:（1）填空:本次调查中抽取的1000名小学生．．．患近视的百分比是 ▲ ；本次调查的初中生有 ▲ 人；（2）我市在校初中生约有2.5万人，小学生约有4.8万人，请分别估计我市初中生与小学生中患“中度和高度近视．．．．．．．”的人数.并根据计算结果，请你对同学提一条温馨提示语.(字数限20个以内)21.欣欣商铺计划用地面砖铺设营业用房的矩形地面ABCD ，已知该矩形地面的长10米，宽8米.铺设图案设计如图所示：矩形的四角为小正方形，阴影部分为四个矩形，四个矩形的宽都为小正方形的边长，阴影部分铺绿色地面砖，其余部分铺白色地面砖.（1）要使铺白色地面砖的面积为52平方米，那么矩形地面四角的小正方形的边长应为多少米？（2）如果铺白色地面砖的费用为每平方米30元，铺绿色地面砖的费用为每平方米20元.当地面四角小正方形的边长为多少米时，铺设地面的总费用最少？最少费用是多少？22.已知坐标平面上的线段AB 及点P ，任取AB 上一点Q ，线段PQ 长度的最小值称为点P 到线段AB 的距离，记作()d P AB →.(1)如图所示，已知长度为2个单位的线段MN 在x 轴上，M 点的坐标为(1,0)，求点(1,1)P 到线段MN 的距离()d P MN →；(2)已知坐标平面上点G 到线段DE :y x =(0≤x ≤3)的距离()2d G DE →=,且点G 的横坐标为1,试求点G 的纵坐标.23.复习完“四边形”内容后，老师出示下题：如图1，直角三角板的直角顶点P 在正方形ABCD 的对角线BD 上移动，一直角边始终经过点C ，另一直角边交直线AB 于点Q ，连结QC .求证:PQC DBC ∠=∠．（1）请你完成上面这道题；（2）完成上题后，同学们在老师的启发下进行了反思，提出许多问题，如：①如图2，若将题中的条件“正方形ABCD ”改为“矩形ABCD ”，其余条件都不变,是否仍能得到PQC DBC ∠=∠？②如图3，若将题中的条件“正方形ABCD ”改为“直角梯形ABCD ”，其余条件都不变,是否仍能得到PQC DBC ∠=∠？……请你对上述反思①和②作出判断，在下列横线上填写“是”或“否”：① ▲ ；② ▲ ．并对①、②中的判断，选择．．其中．．一个．．说明理由． （温馨提示：此空白处不答题）24．如图，已知抛物线c bx ax y ++=21与抛物线5622++=x x y 关于y 轴对称，并与y 轴交于点M ，与x 轴交于A 、B 两点.(1)求抛物线1y 的解析式；（2）若AB 的中点为C ，求CMB ∠sin ；（3）若一次函数y kx h =+的图象过点M ，且与抛物线1y 交于另一点),(n m N ，其中n m ≠，同时满足02=+-t m m 和02=+-t n n （t 为常数）.①求k 值；②设该直线交x 轴于点D ，P 为坐标平面内一点，若以O 、D 、P 、M 为顶点的四边形是平行四边形，试求P 点的坐标.（只需直接写出点P 的坐标，不要求解答过程）（温馨提示：此空白处不答题）2013年初中毕业生学业文化考试适应性练习数学卷评分标准一、选择题：（每题选对得4分） 题号 1 2 3 4 5 6 7 8 9 10 答案 A B D A BDCBCB二、填空题：（每题填对得5分）11．(2)(2)x x x +- 12.乙 13.30 14.60 15.82 16.334-说明:第11小题只提出了公因式x ,不再分解下去,得2分.第14小题只得到一个答案得3分. 三、解答题：（共80分） 17.(本题8分) (1)解:原式=221422-+- (各1分,共4分) =-3 (2)解:33x -＜24x +(1分) 34x x --＜23-(2分) 7x -＜1-(3分) x ＞174分 18.(本题8分)结论:如图所示的四边形11ABB A 即为要求画的四边形,直线1AB 即为所要求画的直线（也可以是直线1BA ）.四边形11ABB A 的面积是20(平方单位). 说明:所画四边形和直线正确各得3分,共6分,面积计算正确得2分,合计共8分.19.(本题8分)解:∵,,A C E 三点成一直线,点B 在AC 上, ∴在BDE ∆中,由于0145,ABD ∠=055D ∠=, ∴01455590E ∠=-=.∴BDE ∆为直角三角形. …………………………………………………………………………3分又∵500BD m =,∴0cos555000.57285DE DB =⋅≈⨯=. ………………………………………………7分答:开挖点E 离点D 的距离约为285米. ……………………………………………8分20.(本题8分)(1)38%；1000. ………………………………………………各2分，共4分 (2)解:34556100%25000100251000+⨯⨯=,10424100%4800061441000+⨯⨯=,…各1分，共2分所以可估计我市初中生与小学生中患“中度和高度近视”的人数分别有10025人和6144人. 温馨提示语:答案不唯一,如可以是“请注意读书、写字姿势要正确，用眼讲究卫生哟”等.只要合理,能围绕主题即可视为得满分. ……………………………………………………………………2分 21.(本题10分) 解:(1)设小正方形的边长为x 米, ………………………………………………1分 则24(102)(82)52x x x +--=,即22970x x -+=, …………………………………………3分解得1271,2x x ==.经检验均符合题意. ………………………………………………4分 答:小正方形的边长为1米或3.5米. ………………………………………………5分 (2)设铺设地面的总费用为W 元,则22304(102)(82)201084(102)(82)W x x x x x x ⎡⎤⎡⎤=⨯+--+⨯⨯----⎣⎦⎣⎦ ………………2分=2803602400x x -+=2980()19954x -+ ………………………………………………3分 ∵80＞0,∴W有最小值.当94x =米时,W最小值=1995元. ………………………………………4分 答:当小正方形的边长为94米时,铺设地面的总费用最少,最少费用为1995元. ………………5分22.(本题12分)解:(1)∵M 点的坐标为(1,0)，点P 的坐标为(1,1),根据定义可得PM 就是点P 到线段MN 的距离. ∴()d P MN →=1. ………………………………………………3分(2)在坐标平面内作出线段DE:y x=(≤x≤3). ……………………………………………1分∵点G 的横坐标为1，∴点G 在直线1x =上，设直线1x =交x 轴于点H ，交DE 于点K. …2分①如图,过点1G 作1G F DE ⊥于点F,则1G F 就是点1G 到线段DE 的距离. ∵线段DE :y x =(0≤x ≤3),∴1,G FK DHK ∆∆均为等腰直角三角形, …………4分 ∵1()2d G DE →=,∴2,KF =由勾股定理得2GK =. ………………5分 又∵1KH OH ==,∴13HG =.即1G 的纵坐标为3. …6分 ②如图,过点O 作2G O OE ⊥交直线1x =于点2G ,由题意知2OHG ∆为等腰直角三角形,∵1OH =,∴22G O =. ∴点2G 同样是满足条件的点. ∴点2G 的纵坐标为1-. ………………………………………………9分综上,点2G 的纵坐标为3或1-.23.(本题12分)证明：（1）∵四边形ABCD 为正方形，∴∠ABC ＝90°，∠ABD ＝∠DBC ＝12∠ABC ＝45°. ……………………………………1分过点P 作PM ⊥BC ，PN ⊥AB ，垂足分别为M 、N ．则∠PNB ＝∠PMB ＝90°，MP ＝NP ．∴∠MPN ＝90°，即∠QPN ＋∠QPM ＝90°． ………………………………………………3分∵∠CPM ＋∠QPM ＝∠QPC ＝90°，∴∠CPM ＝∠QPN ，又∵MP ＝NP ，∠PMC ＝∠PNQ ＝90°，∴△MPC ≌△NPQ ． ………………………………………………4分 ∴PC ＝PQ ．∴∠PQC ＝∠PCQ ＝45°＝∠DBC ． ………………………………………………5分（2）①是；②是． ………………………………………………各1分,共2分①的证明：如图2，过点P 作PM ⊥BC ，PN ⊥AB ，垂足分别为M 、N ．易得四边形PNBM 为矩形，则MB ＝NP ，∠MPN ＝90°． ………………………………1分∵∠CPM ＋∠QPM ＝∠QPC ＝90°，∠QPN ＋∠QPM ＝∠MPN ＝90°，∴∠CPM ＝∠QPN ，又∵∠PMC ＝∠PNQ ＝90°，∴△MPC ∽△NPQ ， ………………………………………………………………………………2分 ∴,PC MP PQ NP= ∵PN MB =，∴,PC MP MP PQ NP MB== ……………………………………………………………………………3分在Rt PBM ∆中，tan ,PM PBM BM ∠=在Rt PQC ∆中，tan ,PC PQC PQ∠=∴tan tan PBM PQC ∠=∠， ………………………………………………4分∴∠PQC ＝∠DBC ． ………………………………………………5分 说明：若选择②进行证明，则辅助线如图所作，基本上可采用类似方法进行证明，同样按步给分.24.(本题14分)解:(1)对于函数5622++=x x y 来说,令0x =,则5y =,∴(0,5)M . …………………1分令0y =,则2650x x ++=,∴121,5x x =-=-.∴抛物线2y 与x 轴两交点的坐标为(1,0),(5,0)--. ………………………………………………2分∵抛物线1y 、2y 关于y 轴对称,∴(1,0),(5,0)A B . ………………………………………………3分故可设1(1)(5),y a x x =--将点(0M 代入,得1(1)(5),y x x =--即2165y x x =-+. ……………………………………4分(2)∵(1,0),(5,0)A B ,(0,5)M ,C 为AB 的中点, ∴(3,0),2,34C CB MC ==. ………………………………………………1分∴1125522CMB S CB OM ∆=⋅⋅=⨯⨯=. ∵5OM OB ==,∴由勾股定理可得52MB =. ………………………………………………2分过点C 作CH MB ⊥于点H ,则1525, 2.2CH CH ⨯⋅=∴= ………………………………3分 ∴在R ∆中，217s i n .1734CH CMB MC ∠===……………………………………………4分 （3）①∵直线y kx h =+过点(0,5)M ，∴5h =.∵(,)N m n 在抛物线1y 上,∴26 5.n m m =-+ ………………………………………………1分又∵02=+-t m m ,02=+-t n n ,故两式相减,得:220.m n m n --+=即()(1)0m n m n -+-=.∵n m ≠,∴10m n +-=,即1n m =-. ………………………………………………2分将1n m =-代入265n m m =-+得:2540m m -+=.∴121, 4.m m ==从而120, 3.n n ==-∴12(1,0),(4,3).N N - ………………………………………………3分故将它们的坐标分别代入5y kx =+中,得125, 2.k k =-=-………………………………………4分②当15k =-时,直线为55y x =-+,此时,D N 与A 点重合.因此满足条件的P 点有三个:123(1,5),(1,5),(1,5).P P P -- ………………………………………………1分当12k =-时,直线为25y x =-+,此时5(,0)2D .因此满足条件的P 点也有三个:456555(,5),(,5),(,5).222P P P -- ………………………………………………2分综上,满足条件的P 点共有六个:123(1,5),(1,5),(1,5),P P P --456555(,5),(,5),(,5).222P P P --。

2013年中考适应性考试英语试题（本试卷共8页，满分120分，考试时间120分钟）注意事项：1．答卷前，考生务必将自己的姓名、考试号填写在试题卷和答题卡上，并将考试号条形码粘贴在答题卡上指定位置。

2．选择题每小题选出答案后，用2B铅笔将答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号，答在试题卷上无效。

3．非选择题（主观题）用0.5毫米的黑色墨水签字笔直接答在答题卡上每题对应的答题区域内，答在试题卷上无效。

4．考试结束后，请将本试题卷和答题卡一并上交。

选择题（共70分）一、听力测试（本大题满分25分，每小题1分）做题时，先将答案划在试卷上。

录音内容结束后再将试卷上的答案转涂到答题卡上。

第一节听下面的8段短对话。

每段对话后有一个小题，从每小题A、B、C三个选项中选出一个最佳答案。

听完每段对话后，你有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话只播一遍。

1. When is the boy’s birthday?A. On June 8th.B. On June 20th.C. On July 20th.2. What animal does the woman like best?A. Tigers.B. Elephants.C. Pandas.3. What time is it now?A. Seven o'clock.B. Eight o'clock.C. Seven thirty.4. How often does Linda surf the internet?A. Every day.B. Never.C. Once a week.5. Where was Sarah last night?A. At home.B. At school.C. We don't know.6. Who does the red T-shirt belong to?A. Alice.B. Linda.C. Lucy.7. What does the woman mean?A. She’d like green tea rather than black tea.B. She wants to drink two cups of tea.C. Either green tea or black tea is OK for her.8. How long has Susan lived in Shanghai?A. For ten years.B. For two months.C. For seven years.英语试题第1页（共8页）第二节下面你将听到5段对话或独白。

2013年初中毕业生学业考试数学 第一次适应性考试试题卷亲爱的同学：欢迎参加考试！请你认真审题，积极思考，细心答题，发挥最佳水平．答题时，请注意以下几点：1． 全卷共4页，有三大题，24小题．全卷满分150分．考试时间120分钟． 2． 答案必须写在答题纸相应的位置上，写在试题卷、草稿纸上均无效． 3． 答题前，认真阅读答题纸上的《注意事项》，按规定答题． 祝你成功！参考公式：抛物线2(0)y ax bx c a =++≠的顶点坐标是24(,)24b ac b a a--． 卷Ⅰ一、选择题（本题有10小题，每小题4分，共40分．每小题只有一个选项是正确的，不选、多选、错选，均不给分） 1. 在下列实数中，最小的数是（ ▲ ）A ．0B ．3C ．2D ．π- 2．温州市拟在温州汽车东站、汽车西站间建造约10公里的空中轨道，总造价预计需要人民币2 000 000 000元，将这个造价用科学记数法表示应为（ ▲ ） A ．2×107元 B ．2×108元 C ．2×109元 D. 2×1010元 3．如图所示的是零件三通的立体图，则这个几何体的主视图是（ ▲ ）A B C D4．如图，在△ABC 中，∠C =Rt ∠，AB =5，BC =3，则sin A 的值是（ ▲ ）A ．43 B ．53 C ．54 D ．355．不等式3x ≤6的解在数轴上表示为 （ ▲ ）6．九（1）班班长统计去年1～8月“书香校园”活动中全主视方向（第3题图）（第4题图）班同学的课外阅读数量（单位：本），绘制了如图所示 的折线统计图，阅读数量变化率最大的两个月是（ ▲ ） A ．1月与2月 B ．4月与5月 C ．5月与6月 D ．6月与7月 7．下列运算中，计算正确的是（ ▲ ）A ．236()a a =B ．3362a a a +=C ．632a a a ÷=D ．3332a a a ⋅=8. 反比例函数6y x=的图象上有两个点为1(1,)y ，2(2,)y ，则y 1与y 2的关系是（ ▲ ）A ．12y y >B ．12y y <C ．12y y =D ．不能确定 9．如图，A ⊙，B ⊙的半径分别为1cm ，2cm ，圆心距AB 为5cm ．如果A ⊙由图示位置沿直线AB 向右平 移2cm ，则此时该圆与B ⊙的位置关系是（ ▲ ）A ．外离B ．相交C ．外切D ．内含10．如图，在△ABC 中，AB =BC ，将△ABC 绕点B 顺时针旋转α度，得到△A 1BC 1，A 1B 交AC 于点E ，A 1C 1分别交AC ，BC 于点D ，F ，下列结论： ①∠CDF =α；②A 1E =CF ；③DF =FC ；④BE =BF ． 其中正确的有（ ▲ ）A ．②③④B ．①③④C ．①②④D ．①②③卷Ⅱ二、填空题（本题有6小题，每小题5分，共30分） 11．分解因式：m 2－1＝ ▲ ．12. 二次函数y ＝ax 2＋bx ＋c 的部分图象如图所示，由图象可知该二次函数的图象的对称轴是直线x ＝ ▲ ．13．如图AB ∥CD ，CE 交AB 于点A ，AD ⊥AC 于点A ，若∠1＝48°，则∠2＝ ▲度．14．如图，在△ABC 中，∠ACB =90°，∠A =30°，点D 是AB 的中点，连结CD ．若AC，则图中长度等于1cm 的线段有 ▲ 条．（第14题图）（第13题图）D（第9题图）AB（第12题图）（第10 题图）C 1BA15．我县开展“四边三化”工作，某街道产生m 立方米的拆违垃圾需要清理，某工程队承包了清理工作，计划每天清理60立方米，考虑到还有其他地方的垃圾需要清理，该工程队决定增加人手以提高50%的清理效率，则完成整个任务的实际时间比原计划时间少用了 ▲ 天（用含m 的代数式表示）． 16．如图，Rt △ABC 中，∠B =Rt ∠，点D 在边AB 上，过点D 作DG ∥AC 交BC于点G ，分别过点D ，G 作DE ∥BC ，FG ∥AB ，DE 与FG 交于点O ．当阴影面积等于梯形ADOF 的面积时，则阴影面积与△ABC 的面积之比为 ▲ ．三、解答题（本题有8小题，共80分） 17.（本题10分）（1）计算：()()201320131-+-；（2）先化简，再求值：(m -n )(m +n )+(m +n )2 - 2m 2，其中21-==n m ，． 18．（本题8分）如图，E ，F 是平行四边形ABCD 的对角线AC 上的点，CE ＝AF ，请你猜想：BE 与DF证明． 猜想： 证明：19．（本题8分）图①，图②（图在答题卷上）均为76⨯的正方形网格，点A ，B ，C 在格点（小正方形的顶点）上．（1）在图①中确定格点D ，并画出一个以A ，B ，C ，D 为顶点的四边形，使其为轴对称图形；（2）在图②中确定格点E ，并画出一个以A ，B ，C ，E 为顶点的四边形，使其为中心对称图形．20．（本题8分）小刚和小明两位同学玩“石头，剪刀，布”游戏．游戏规则为：两人同时出拳，其中石头胜剪刀、剪刀胜布、布胜石头；若两人出拳相同，则为平局．（1）一次出拳小刚出“石头”的概率是多少？（2）如果用A ，B ，C 分别表示小刚出的石头，剪刀，布，用A 1，B 1，C 1分别表示小明的石头，剪刀，布，那么一次出牌小刚胜小明的概率是多少？用列表法或画树状图法加以说明；（第18题图）B（3）你认为这个游戏对小刚和小明公平吗？为什么？21．（本题10分）我县各学校九年级学生在体育测试前，都在积极训练自己的考试项目，王强就本班同学“自己选测的体育项目”进行了一次调查统计，下面是他通过收集数据后，绘制的两幅不完整的统计图．请你根据图中提供的信息，解答以下问题：（1）该班共有 ▲ 名学生； （2）补全条形统计图；（3）求扇形统计图中“篮球”部分所对应的圆心角的度数；（4）若该校九年级有360名学生，请计算出该校九年级“其他”部分的学生人数．22．（本题10分）如图，在△ABC 中，∠C =90°，∠ACB 的平分线交AB 于点O ，以O 为圆心的⊙O 与AC 相切于点D ．（1）求证: ⊙O 与BC 相切；（2）当AC =3，BC =6时，求⊙O 的半径．23．（本题12分）我县绿色和特色农产品在国际市场上颇具竞争力．外贸商胡经理按市场价格10元/千克在我县收购了6000千克蘑菇存放入冷库中．请根据胡经理提供的预测信息（如右图）帮胡经理解决以下问题：（1）若胡经理想将这批蘑菇存放x 天后一次性出售，则x 天后这批蘑菇的销售单价为 ▲ 元， 这批蘑菇的销售量是 ▲ 千克； （2）胡经理将这批蘑菇存放多少天后，一次性出售所得的销售总金额．．．．．为100000元； （销售总金额＝销售单价×销售量）．（第21题图）（3）将这批蘑菇存放多少天后一次性出售可获得最大．．利润．．？最大利润是多少？（第23题图）24．（本题14分）如图，在矩形ABCD中，AB=3，BC=4．动点P从点A出发沿AC向终点C运动，同时动点Q从点B出发沿BA向点A运动，到达A点后立刻以原来的速度沿AB返回．点P，Q运动速度均为每秒1个单位长度，当点P到达点C时停止运动，点Q也同时停止．连结PQ，设运动时间为t（t >0）秒．（1）求线段AC的长度；（2）当点Q从B点向A点运动时（未到达A点），求△APQ的面积S关于t 的函数关系式，并写出t的取值范围；（3）伴随着P，Q两点的运动，线段PQ的垂直平分线为l：①当l经过点A时，射线QP交AD于点E，求AE的长；②当l经过点B时，求t的值．ABCEABC A BD ABCDC2013年初中毕业生学业考试第一次适应性考试数学参考答案一、选择题(每小题4分, 共40分)二、 填空题（每小题5分, 共30分)11.(m ＋1)(m －1) 12.2 13.42° 14.4 15.180m 16. 165三. 解答题（8小题共80分) 17.（1）解：()()8120132013--+-2211--= ……………3分(每化对一个给1分) 22-=…………………2分(2 )解：原式＝2222222m n mn m n m -+++-…………………2分＝mn 2………………………1分当2-=mn 时，原式＝4)2(22-=-⨯=mn ………………………2分 18．解：猜想BE ∥DF ，BE =DF …………2分证明：∵四边形ABCD 是平行四边形 ∴BC =AD ，∠1=∠2又CE =AF ，∴⊿BCE ≌⊿DAF ……3分 ∴BE =DF ，∠3=∠4 …………2分 ∴BE ∥DF ……………………1分 19．解：（1）有以下答案供参考：……………4分（2）有以下答案供参考：……………4分20．解：（1）P （一次出牌小刚出“石头”牌）=13； ……2分 （2）树状图：……3分 或列表：由树状图（树形图）或列表可知，可能出现的结果有9种，而且每种结果出现的可能性相同，其中小刚胜小明的结果有3种． 所以，P （一次出牌小刚胜小明）=13． ……1分 （3）由树状图（树形图）或列表可求得：P （一次出牌小明胜小刚）=13． P （一次出牌小刚胜小明）= P （一次出牌小明胜小刚），即两人获胜的概率相等， 这个游戏对小刚和小明公平． ……2分21．解：（1）50………………2分（2）…………4分A 1B 1C 1 AA 1B 1C 1 BA 1B 1C 1 C开始小刚小明（3）︒=⨯︒2.1155016360………………2分（4）725010360=⨯名 答：“其他”部分学生人数有72名．…………2分 （不答不扣分）22．解：（1）证明：如图，连结OD ，作OE ⊥BC 于点E , …………1分∵⊙O 与AC 相切于点D ，∴OD ⊥AC .…………1分 ∵OC 是∠ACB 的平分线，∴OD ＝OE .…………1分 ∴⊙O 与BC 相切…………2分（2）解：∵OD ⊥AC ，∠ACB =90°，∴OD ∥CB ，∴△AOD ∽△ABC ，1分 解法1 ∴ ,BC ODAC AD =即,2163===BC AC OD AD ……………………2分∴,2121CD OD AD ==∴，232===AC OD CD 即圆的半径为2．……2分 解法2 ∴,BCODAC AD =设半径为x , ∵OC 是∠ACB 的平分线, ∴∠DCO =45° ∴CD =OD =x ，∴AD = AC －CD =3-x ，……………………2分,633xx =-解得x =2，即圆的半径为2．……………………2分 23．解：（1）()x 1.010+ ()x 106000- ………………4分（2）()()1000001060001.010=-+x x ……………………1分化简得0400005002=+-x x解得x 1=100，……………1分x 2=400(舍去) ……………1分胡经理销售将这批蘑菇存放100天后，一次性出售所得的销售总金额达到100000元．……………1分（3）设最大利润为W ，由题意得W()()x x x 2406000101060001.010-⨯--+=x x 2602+-=16900)130(2+--=x ，……………2分∵x ≤110，∴当x =110时，W 最大值＝16500……………1分答：存放110天后出售这批香菇可获得最大利润16500元．……………1分24．解：（1）在矩形ABCD中，5AC ==……2分（2）如图①，过点P 作PH ⊥AB 于点H ，AP=t ，AQ =3－t ，由△AHP ∽△ABC ，得BC PH AB AP =，∴PH=45t ，……2分 t t t t S 565254)3(212+-=⋅-=，…………2分)30(<<t .…………1分(3) ①如图②，线段PQ 的垂直平分线为l 经过点A ，则AP=AQ ，即3－t=t ，∴t=1.5，∴AP=AQ=1.5，…………………………1分 延长QP 交AD 于点E ，过点Q 作QO ∥AD 交AC 于点O ， 则,BC QO AB AQ AC AO ==25=⋅=∴AC AB AQ AO ， 2=⋅=BC ABAQ OQ ，∴PO=AO －AP=1．由△APE ∽△OPQ ，得3,=⋅=∴=OQ OPAPAE OP AP OQ AE ．……2分 ②（ⅰ）如图③，当点Q 从B 向A 运动时l 经过点B ， BQ ＝CP ＝AP ＝t ，∠QBP ＝∠QAP∵∠QBP ＋∠PBC ＝90°，∠QAP ＋∠PCB ＝90° ∴∠PBC ＝∠PCB CP ＝BP ＝AP ＝t ∴CP ＝AP ＝21AC ＝21×5＝2.5 ∴t ＝2.5． ………2分 （ⅱ）如图④，当点Q 从A 向B 运动时l 经过点B ，BP ＝BQ ＝3－（t －3）＝6－t ，AP ＝t ，PC ＝5－t ， 过点P 作PG ⊥CB 于点G 由△PGC ∽△ABC ， 得()t AB AC PC PG BC GC AB PG AC PC -=⋅=∴==553, ()t BC AC PC CG -=⋅=554,BG ＝4－()t -554=t 54由勾股定理得222PG BG BP +=，即图②()222553)54()6(⎥⎦⎤⎢⎣⎡-+=-t t t ，解得1445=t ．………2分。

2013年南平市初中毕业班适应性考试参考答案
一、单项选择题（每小题2分，共50分）
二、综合题（本题5小题，每空1分，共50分）
26.（每空1分，共10分）
（1）山谷N流经地区等高线密集，河流落差大，流速快
（2）耕地林地（或草地、湖泊）（任写其中一种即可）少（小）减小
（3）东北大（较大）降水较多，房顶坡度大有利于排水
27.（每空1分，共9分）
（1）乙丙甲甲（2）④
（3）①人口集中，耕地面积比较大，工农业发达，水资源需求量大②水资源分布较少（①②顺序可对调）南水北调推广节水器具；一水多用等（言之有理均可
得分）
28.（每空1分，共9分）
（1）①⑤
（2）西地形平坦、水源充足、交通便利等（言之有理均可得分）
（3）位于板块交界处，地壳活跃
（4）丁注意节约用电；选乘公共交通；选用低排放低污染的交通工具；不使用一次性产品等（言之有理都可得分）。

29.（每空1分，共12分）
（1）淮华北麦地
（2）甲（3）森林草原自东向西降水逐渐减少
（4）乙牦牛高（5）三（一～三）④
30.（除特殊标注外，其余每空1分，共10分）
（1）俄罗斯 2
（2）人口众多（或人口自然增长率高、人口增长快）
旱涝、地震、台风、泥石流、滑坡等；
（3）中国俄罗斯②③俄罗斯中国①④
（4）气候湿热（或全年高温多雨）
（5）全年高温，分干、湿两季（气温、降水各1分，共2分，其他答案合理也可得分）（6）巴西
八年级适应性质量检测地理参考答案第1页（共1页）。

四川省南充市中考2013年适应性考试数学试卷一、选择题（本大题共10个小题，每小题3分，共30分）每小题都有代号为A、B、C、D 的四个答案选项，其中只有一个是正确的，请把正确选项的代号用2B铅笔涂在答题卡上．涂正确记3分，不涂、涂错或涂出的代号超过一个记0分．1．（3分）（2013•南充模拟）﹣2的倒数是（）A．B．2C．D．一 2考点：倒数分析：根据乘积是1的两个数叫做互为倒数解答．解答：解：∵（﹣2）×（﹣）=1，∴﹣2的倒数是﹣．故选A．点评：本题考查了倒数的定义，是基础题，熟记概念是解题的关键．2．（3分）（2013•南充模拟）如图，立体图形的主视图是（）A．B．C．D．考点：简单几何体的三视图．3718684分析：根据主视图的定义，找到从正面看所得到的图形即可．解答：解：从正面可看到一个长方形．故选：A．点评：本题考查了三视图的知识，主视图是从物体的正面看得到的视图．3．（3分）（2013•南充模拟）等腰三角形的两边为2和3，则周长为（）A．7B．8C．7或8 D．9考点：等腰三角形的性质；三角形三边关系分析：根据等腰三角形的性质，分两种情况：①当腰长为2时，②当腰长为3时，解答出即可．解答：解：根据题意，①当腰长为2时，周长=2+2+3=7；②当腰长为3时，周长=3+3+2=8．故选C．点评：本题主要考查了等腰三角形的性质，注意本题要分两种情况解答．注意满足三角形三边关系．4．（3分）（2013•南充模拟）下列各式中，能用完全平方公式分解因式的是（）A．16x2+1 B．x2+2x﹣1 C．a2+2ab+4b2D．，考点：因式分解-运用公式法分析：根据完全平方公式的结构特点：必须是三项式，其中有两项能写成两个数（或式）的平方和的形式，另一项是这两个数（或式）的积的2倍，对各选项分析判断后利用排除法求解．解答：解：A、16x2+1只有两项，不符合完全平方公式；B、x2+2x﹣1其中有两项x2、﹣1不能写成平方和的形式，不符合完全平方公式；C、a2+2ab+4b2另一项不是a、2b的积的2倍，不符合完全平方公式；D、符合完全平方公式．故选D．点评：本题主要考查了完全平方公式，熟记公式结构是解题的关键．完全平方公式：a2±2ab+b2=（a±b）2；5．（3分）（2013•南充模拟）关于x的方程的解是正数，则a的取值范围是（）A．a＞0 B．a＜3 C．0＜a＜3 D．a＞3考点：分式方程的解专题：计算题．分析：将a看做已知数，将分式方程去分母转化为整式方程，求出整式方程的解得到x的值，根据解为正数列出关于a的不等式，求出不等式的解集即可得到a的范围．解答：解：分式方程去分母得：3x﹣3a=ax，解得：x=，根据题意得：＞0，解得：0＜a＜3．故选C．点评：此题考查了分式方程的解，弄清题意是解本题的关键．6．（3分）（2013•南充模拟）甲、乙两同学五次测试数学的平均成绩相同，方差分别为，甲、乙两同学数学成绩较稳定的是（）A．甲B．乙C．甲、乙一样D．不能确定考点：方差分析：方差是反映一组数据的波动大小的一个量，方差越小，稳定性越好．解答：解：∵S2甲＜S2乙，∴甲同学数学成绩较稳定．故选A．点评：本题考查了方差的知识，解答本题关键是掌握方差越小，稳定性越好．7．（3分）（2013•南充模拟）抛掷一枚硬币，两次都出现正面向上的概率是（）A．B．C．D．考点：列表法与树状图法专题：计算题．分析：列表得出抛掷一枚硬币两次所有等可能的情况数，找出两次都为正面的情况数，即可求出所求的概率．解答：解：列表如下：正反正（正，正）（反，正）反（正，反）（反，反）所有等可能的情况有4种，其中两次都出现正面向上的情况有1种，则P=．故选C．点评：此题考查了列表法与树状图法，用到的知识点为：概率=所求情况数与总情况数之比．8．（3分）（2013•南充模拟）如图是一个以O为对称中心的中心对称图形，若∠A=30°，∠C=90°，AC=1，则AB的长为（）A．4B．C．D．考点：中心对称分析：在直角△ABC中根据AO=，得出AO的长，进而得出AB的长．解答：解：∵在Rt△AOC中，∠A=30°，∠C=90°，AC=1，∴AO===，∴BA=2AO=．故选：D．点评：本题主要考查了中心对称图形的性质以及锐角三角函数的应用，根据已知得出AO的长是解题关键．9．（3分）（2013•南充模拟）如果直线y=x+b与双曲线有一个交点为A（1，m），则b的值为（）A．1B．﹣1 C．2D．3考点：反比例函数与一次函数的交点问题分析：将点A的坐标代入双曲线，求出m的值，得出点A的坐标，然后代入直线解析式可求出b的值．解答：解：将点A（1，m）代入双曲线可得：m==2，将点（1，2）代入直线解析式可得：2=1+b，解得：b=1．故选A．点评：本题考查了反比例函数与一次函数的交点问题，解答本题关键是求m的值，难度一般．10．（3分）（2013•南充模拟）如图，⊙O与AB切于点C，∠BCE=60°，DC=6，DE=4，则S△CDE为（）A．B．C．D．6考点：切线的性质；含30度角的直角三角形专题：计算题．分析：过C作CF垂直于DE，由AB为圆O的切线，利用弦切角等于夹弧所对的圆周角，得到∠CDE=∠BCE=60°，再直角三角形CDF中，由DC的长，利用锐角三角函数定义求出CF的长，由DE为底边，CF为高，求出三角形CDE的面积即可．解答：解：过C作CF⊥DE，交DE于点F，∵AB与圆O相切，CE为圆O的弦，∴∠CDE=∠BCE=60°，在Rt△CDF中，DC=6，∠CDE=60°，∴CF=DCsin60°=3，又DE=4，则S△CDE=DE•CF=6．故选B点评：此题考查了切线的性质，锐角三角函数定义，以及三角形的面积求法，熟练掌握切线的性质是解本题的关键．二、填空题（本大题共4个小题，每小题3分，共12分）请将答案直接填写在答题卡横线上11．（3分）（2013•南充模拟）分解因式：2x2﹣2x﹣12= 2（x﹣3）（x+2）．考点：因式分解-十字相乘法等；因式分解-提公因式法分析：首先提取公因式2，再根据所给多项式的系数特点，可以用十字相乘法进行因式分解．解答：解：2x2﹣2x﹣12=2（x2﹣x﹣6）=2（x﹣3）（x+2）．故答案为：2（x﹣3）（x+2）．点评：本题考查了十字相乘法分解因式，十字左边相乘等于二次项系数，右边相乘等于常数项，交叉相乘再相加等于一次项系数．12．（3分）（2013•南充模拟）一圆锥的底面圆半径为2cm，母线长为3cm，则侧面积为6πcm2．考点：圆锥的计算专题：计算题．分析：由于圆锥的侧面展开图为扇形，扇形的弧长等于圆锥底面圆的周长，扇形的半径等于圆锥的母线长，所以根据扇形的面积公式可求解．解答：解：圆锥的侧面积=×3×2π×2=6π（cm2）．故答案为6πcm2．点评：本题考查了圆锥的计算：圆锥的侧面展开图为扇形，扇形的弧长等于圆锥底面圆的周长，扇形的半径等于圆锥的母线长．也考查了扇形的面积公式．13．（3分）（2013•南充模拟）第一盒乒乓球中有2 个白球 2 个黄球，第二盒乒乓球中有1个白球3个黄球，分别从每个盒中随机地取出1个球，则取出的两个球中有一个白球和一个黄球的概率是．考点：列表法与树状图法分析：画出树状图，然后根据概率公式列式计算即可得解．解答：解：根据题意，画出树状图如下：一共有16种情况，一个白球和一个黄球的情况有8种，所以，P（一个白球和一个黄球）==．故答案为：．点评：本题考查了列表法与树状图法，用到的知识点为：概率=所求情况数与总情况数之比．14．（3分）（2013•南充模拟）如图，在Rt△ABC中，AB=AC，D，E是斜边BC上两动点，∠DAE=45°，将△ADC绕点A顺时针旋转90°后得到△AFB，连接EF．下列结论：①△AED≌△AEF，②△ABE∽△ACD，③BE+CD＞DE，④cos∠BEF=．一定成立的有①②④．考点：相似三角形的判定与性质；全等三角形的判定与性质；旋转的性质分析：首先根据等腰直角三角形的性质，可求得顶角与底角的度数；根据旋转的性质，可得对应角与对应边相等；根据全等三角形的判定定理即可求得①正确；当∠1=∠3时，△ABE∽△ACD，由此可以推知②不一定正确；根据勾股定理与等量代换可得③正确；由①中的全等三角形的性质推知EF=ED，则根据余弦三角函数的定义证得④正确．解答：解：∵在Rt△ABC中，AB=AC，∴∠BAC=90°，∠ABC=∠C=45°，∵∠DAE=45°，即∠2=45°，∴∠1+∠3=45°，∵将△ADC绕点A顺时针旋转90°后，得到△AFB，∴∠4=∠3，AF=AD，∴∠EAF=∠1+∠4=∠1+∠3=45°，∴∠EAF=∠2，①∵在△AED与△AEF中，，∴△AED≌△AEF（SAS），故①正确；②当∠1≠∠3时，△ABE∽△ACD不成立．故②错误；③由△AED≌△AEF知DE=EF．根据旋转的性质知，∠5=∠C=45°，∴∠FBE=∠5+∠ABC=90°，∴根据勾股定理得到BE2+BF2=EF2，即BE2+BF2=DE2，∵BE＞EF﹣BF，即BE＞DE﹣BF∴BE2+DC2=DE2；∴BE+DC＞DE．故③正确；④由①知△AED≌△AEF，则DE=EF．∵∠FBE=90°，∴cos∠BEF==，即cos∠BEF=．故④正确．综上所述，正确的选项是：①③④．故填：①③④．点评：此题考查了相似三角形的判定定理、全等三角形的判定定理、等腰直角直角三角形的性质以及旋转的性质．此题涉及的知识面比较广，解题时要注意仔细分析．三、（本大题共3个小题，每小题6分，共18分）15．（6分）（2013•南充模拟）计算：．考点：实数的运算；负整数指数幂；特殊角的三角函数值分析：根据实数混合运算的法则进行计算即可．解答：解：原式=﹣4+3+4﹣8×=﹣4+3+4﹣4=﹣1．点评：本题考查的是实数的运算，熟知在进行实数运算时，和有理数运算一样，要从高级到低级，即先算乘方、开方，再算乘除，最后算加减，有括号的要先算括号里面的，同级运算要按照从左到有的顺序进行是解答此题的关键．16．（6分）（2013•南充模拟）如图，▱ABCD的BC边的中点E，延长AE交DC的延长线于点F．求证：DC=CF．考点：平行四边形的性质；全等三角形的判定与性质专题：证明题．分析：根据平行四边形性质得出AB=CD，AB∥CD，求出∠B=∠FCE，∠F=∠BAE，BE=CF，证△ABE≌△FCE，推出AB=CF即可．解答：证明：∵四边形ABCD是平行四边形，∴AB=CD，AB∥CD，∴∠B=∠FCE，∠F=∠BAE，∵E为BC中点，∴BE=CF，在△ABE和△FCE中∴△ABE≌△FCE，∴AB=CF，∵AB=DC，∴DC=CF．点评：本题考查了平行四边形性质，平行线性质，全等三角形的性质和判定的应用，关键是求出AB=CF．17．（6分）（2013•南充模拟）某校为了促进体育活动的开展，组建了足球、篮球、乒乓球、羽毛球、田径五个体育活动小组，经调查九（ l ）班各活动小组参加人数的条形统计图和扇形统如下：（1）该班有多少学生？（2）请你将条形统计图补充完整；（3）对扇形统计图中，乒乓球小组所对应的扇形圆心角比羽毛球小组所对应的扇形圆心角大多少度？考点：条形统计图；扇形统计图分析：（1）根据足球组有16人，占20%，据此即可求得；（2）总人数乘以对应的百分比即可求得对应的组的人数；（3）求得乒乓球小组与羽毛球小组的人数的差占总数的比例乘以360度即可求解．解答：解：（1）16÷20%=80（人）；（2）篮球小组的人数是：80×25%=20（人），羽毛球小组的人数：80﹣12﹣16﹣20﹣28=4（人）．；（3）乒乓球小组与羽毛球小组的人数的差是：28﹣4=24，则乒乓球小组所对应的扇形圆心角比羽毛球小组所对应的扇形圆心角大360×=108°．点评：本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．四、（本大题共2个小题，每小题8分，共16分）18．（8分）（2013•南充模拟）已知关于x的方程（x﹣3）（x﹣2）﹣p2=0．（1）求证：这个方程总有两个不相等的实数根；（2）若二实根x1，x2满足，求p的值．考点：根的判别式；根与系数的关系专题：计算题．分析：（1）先把方程整理为一般式，再计算出△=1+4p2，根据非负数的性质得到△＞0，然后根据判别式的意义得这个方程总有两个不相等的实数根；（2）根据根与系数的关系得到得x1+x2=5，x1x2=6﹣p2，由已知条件变形得到（x1+x2）2﹣4x1x2=9，即25﹣4（6﹣p2）=9，然后解p的方程即可．解答：（1）证明：方程整理为x2﹣5x+6﹣p2=0，△=（﹣5）2﹣4×1×（6﹣p2）=1+4p2，∵4p2≥0，∴△＞0，∴这个方程总有两个不相等的实数根；（2）根据题意得x1+x2=5，x1x2=6﹣p2，∵，∴（x1+x2）2﹣4x1x2=9，即25﹣4（6﹣p2）=9，∴p=±2．点评：本题考查了一元二次方程ax2+bx+c=0（a≠0）的根的判别式△=b2﹣4ac：当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．也考查了一元二次方程的根与系数的关系．19．（8分）（2013•南充模拟）如图，已知矩形ABCD中，E为AD上一点，BE⊥CE．（1）求证：△EAB∽△CDE；（2）若AB=3，AD=8，求AE的长．考点：相似三角形的判定与性质；矩形的性质分析：（1）根据“矩形的四个角都是直角”、“同角的余角相等”推知△EAB和△CDE中的对应角∠A=∠D=90°，∠ABE=∠DEC，则由相似三角形的判定定理可以证得结论；（2）根据（1）中的相似三角形的对应边成比例来求线段AE的长度．解答：（1）证明：如图，在矩形ABCD中，∠A=∠D=90°．∵BE⊥CE，∴∠BEC=90°，∴∠ABE=∠DEC，∴△EAB∽△CDE；（2）解：如图，在矩形ABCD中，AB=CD=3．由（1）知，△EAB∽△CDE．则=，即=，解得，AE=4±．即AE的长度是4±．点评：本题考查了相似三角形的判定与性质，矩形的性质．解题时，利用了“矩形的四个角都是直角”、“矩形的对边相等”的性质．五、（本题满分8分）20．（8分）（2013•南充模拟）某商场购进一批单价为16元的商品，经市场调查发现若按20元/件销售，每月能售出360件，若按25元/件销售，何月能售出210件，设每月销售量y（件）是售价x（元/件）的一次函数．（1）求y与x之间的函数关系式；（2）销售价定为多少时，才能使月利润最大，月最大利润是多少？考点：二次函数的应用分析：（1）设出一次函数解析式y=kx+b，用待定系数法求解即可．（2）按照等量关系“每月获得的利润=（销售价格﹣进价）×销售件数”列出二次函数，并求得最值．解答：解：（1）依题意设y=kx+b，则有解得：．所以y=﹣30x+960（16≤x≤32）；（2）每月获得利润：P=（﹣30x+960）（x﹣16）=30（﹣x+32）（x﹣16）=30（﹣x2+48x﹣512）=﹣30（x﹣24）2+1920．所以当x=24时，P有最大值，最大值为1920．答：当价格为24元时，才能使每月获得最大利润，最大利润为1920元．点评：本题考查了二次函数在实际生活中的应用，重点是掌握求最值的问题．注意：数学应用题来源于实践，用于实践，在当今社会市场经济的环境下，应掌握一些有关商品价格和利润的知识，总利润等于总收入减去总成本，然后再利用二次函数求最值．六、（本题满分8分）21．（8分）（2013•南充模拟）如图，四边形ABCD是矩形，将△BCD沿BD折叠为△BED，连接AE．（1）求证：四边形ABDE是等腰梯形；（2）若∠BDC=60°，BC=6，求AE的长．考点：等腰梯形的判定；矩形的性质；翻折变换（折叠问题）专题：探究型．分析：（1）先由矩形及折叠的性质得出∠ODB=∠OBD，则OB=OD，易得OA=OE，则在等腰△OAE与等腰△OBD 中，有一对对顶角相等，可得∠OAE=∠ODB，证得AE∥BD，又由AB=DE，则可得四边形ABDE是等腰梯形；（2）先根据Rt△BCD中∠BDC=60°，BC=6求出CD及BD的长，再由图形反折变换的性质得出∠CBD=∠DBK，故可得出∠ABK的度数，根据锐角三角函数的定义可求出AK的长度，由（1）可知四边形ABDE 是等腰梯形，所以AK=EK，BK=DK，△AKB∽△BKD，根据相似三角形的对应边成比例即可求出AE的长．解答：（1）证明：∵四边形ABCD是矩形，∴AD∥BC，∴∠ODB=∠DBC，∵∠OBD=∠DBC，∴∠ODB=∠OBD，∴OB=OD，∵AD=BC=BE，∴OA=OE，∴∠OAE=∠OEA，∵∠AOE=∠BOD，∴∠OAE=∠ODB，∴AE∥BD，∵AB=CD=DE，∴四边形ABDE是等腰梯形；（2）∵Rt△BCD中∠BDC=60°，BC=6，∴∠DBC=30°，CD===2，BD=2CD=4，∵△BED由△BCD反折而成，∴∠CBD=∠DBK=30°，∴∠ABK=30°，在Rt△ABK中，∵∠ABK=30°，AB=CD=2，∴AK=AB•tan30°=2×=2，∴DK=AD﹣AK=6﹣2=4，∵由（1）可知四边形ABDE是等腰梯形，∴AK=EK，BK=DK，△AKB∽△BKD，∴=，即=，解得AE=2．点评：本题考查的是等腰梯形的判定与性质，熟知等腰梯形的判定与性质、矩形的性质及相似三角形的判定与性质是解答此题的关键．七、（本题满分8分）22．（8分）（2013•南充模拟）如图，已知抛物线与x轴交于点A（﹣2，0），B（4，0），与y轴交于点C （0，8）．（1）求抛物线的解析式及其顶点D的坐标；（2）设直线CD交x轴于点E．在线段OB的垂直平分线上是否存在点P，使得点P到直线CD的距离等于点P到原点O的距离？如果存在，求出点P的坐标；如果不存在，请说明理由；（3）过点B作x轴的垂线，交直线CD于点F，将抛物线沿其对称轴平移，使抛物线与线段EF总有公共点．试探究：抛物线向上最多可平移多少个单位长度？向下最多可平移多少个单位长度？考点：二次函数综合题专题：压轴题．分析：（1）由抛物线过A、B、C三点可求出抛物线表达式；（2）假设存在，设出P点，解出直线CD的解析式，根据点P到CD的距离等于PO可解出P点坐标；（3）应分两种情况：抛物线向上或下平移，设出解析式，代入点求出平移的单位长度．解答：解：（1）设抛物线解析式为y=a（x+2）（x﹣4）．把C（0，8）代入，得a=﹣1．∴y=﹣x2+2x+8=﹣（x﹣1）2+9，顶点D（1，9）；（2分）（2）假设满足条件的点P存在．依题意设P（2，t）．由C（0，8），D（1，9）求得直线CD的解析式为y=x+8，它与x轴的夹角为45°．设OB的中垂线交CD于H，则H（2，10）．则PH=|10﹣t|，点P到CD的距离为．又．（4分）∴．平方并整理得：t2+20t﹣92=0，解之得t=﹣10±8．∴存在满足条件的点P，P的坐标为（2，﹣10±8）．（6分）（3）由上求得E（﹣8，0），F（4，12）．①若抛物线向上平移，可设解析式为y=﹣x2+2x+8+m（m＞0）．当x=﹣8时，y=﹣72+m．当x=4时，y=m．∴﹣72+m≤0或m≤12．∴0＜m≤72．（8分）②若抛物线向下平移，可设解析式为y=﹣x2+2x+8﹣m（m＞0）．由，有﹣x2+x﹣m=0．∴△=1+4m≥0，∴m≥﹣．∴向上最多可平移72个单位长，向下最多可平移个单位长．（10分）点评：此题考查待定系数求抛物线解析式，第二问考查垂直平分线性质，利用距离相等解题，最后一问考抛物线的平移，要注意已知条件和技巧．。

2013年初中学业水平适应性考试英语第Ⅰ卷（共三部分满分95分）第一部分听力（共四节，满分30 分）第一节听句子，选出与所听句子相关的图片。

注意每个句子听两遍。

（共5小题，每小题1分，满分5 分）第二节听句子，选出与所听句子内容相符的正确大雨。

每个句子听两遍。

（共五小题，每小题1分，满分5分）6. A. Me, too . B. Really? C. I’d like to.7. A. Well done. B. Quite well. C. They’re fine.8. A. In a month. B. About a month. C. Once a month.9. A. I’m afraid not. B. Sorry to hear that. C.I don’t think so.10. A. Thanks. B. Don’t say so. C. No ,thanks.第三节听对话，选出能回答问题的的正确选项。

每段对话听两遍。

（共10小题，每小题1分，满分10分）听第一段对话，回答第11—12题。

11. Does Mike exercise every day ?A. Yes, he does.B. No, he doesn’tC. We don’t know .12. What does the woman think of Mike’s living habit?A. Healthy .B. UnhealthyC. Terrible. 听第二段对话，回答第13—14题。

13. Where are they talking ?A. In a school.B. In a shop.C. At home.14. What is boy’s mother ?A. A teacher.B. A soccer player.C. A housewife.听第三段对话，回答第15—17题。

2013年11月19初中毕业会考适应性考试英 语本试卷分第一卷(选择题)和第二卷(非选择题)两部分。

第一卷第1至8页，第二卷第9至10页。

考生作答时，第一卷(选择题)须将答案答在机读答题卡上，第二卷(非选择题) 须将答案答在答题卡上。

在本试卷、草稿纸上答题无效。

满分150分。

考试时间120分钟。

考试结束后，将机读答题卡和答题卡一并上交。

第一卷（选择题，共105分）注意事项：1. 选择题必须用2B 铅笔将答案标号填涂在机读答题卡对应题目的位置上。

2. 第一卷共三部分，共计100分。

第一部分：听力（共三节，满分30分）做题时，请先将答案标在试卷上。

听力内容结束后，你将有两分钟的时间将试卷上的答案转涂到答题卡上。

第一节 （共5小题；每小题1.5分，满分7.5分）听下面5段对话。

每段对话后有一个小题，从题中所给的A 、B 、C 三幅图中，选出一个与你所听到的内容相符合的选项，并标在试卷的相应位置。

每段对话读两遍。

1. A B C2. A B C3. A B C.4. A B C5. A B C第二节（共5小题；每小题1.5分，满分7.5分）听下面5段对话。

每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

每段对话读两遍。

6. What would the man like for breakfast?A. Cakes.B. Bread.C. Rice.7. Whose coat is this?A. Kate's.B. Li Lei’s.C. Jim's.8. How often does Tom write to his pen friend?A. Once a year.B. Once a month.C. Once a week.9. What subject did the woman fail?A. Math.B. English.C. Chinese.10. Where does the grandpa probably live?A. In a city.B. In a factory.C. On a farm.第三节（共10小题；每小题1.5分，满分15分）听下面3段对话或独白。

2013年中考适应性考试1．序幕奔腾浪漫（3分）2. 孜孜不倦（1分）3. 将“就收获将来大希望”修改为“才能收获将来大希望”（2分）4.不设统一答案，有对青春的理解1分，修辞1分。

示例：青春，是人生痛苦蜕变的过程，更是成长中快乐的丰碑。

青春让我们在跌倒中长大，有些青涩，也有些灿烂。

5．（1）“光盘”是一个形象的说法，表面意思是说把盘子里的菜吃得只剩下“光”盘子的行为。

（2分）（2）如：①克勤于邦，克俭于家。

②历览前贤国与家，成由勤俭破由奢。

③取之有度，用之有节，则常足。

（可以引用名家名言，也可以自己创作）（2分）（3）注意称谓和劝说的内容，语言得体，语意连贯即可。

（3分）6.①禅房花木深②一览众山小③何当共剪西窗烛④便引诗情到碧霄⑤燕然未勒归无计⑥希望是本无所谓有，无所谓无的。

⑦忽如一夜春风来千树万树梨花开⑧吴楚东南坼乾坤日夜浮（每格1分）7.皎洁的月光朗照着一望无际的荞麦田，远远望去，灿烂耀眼，如同一片晶莹的白雪。

（2分）8.言之有理即可。

示例一：苍苍霜草，点出秋色的浓重；切切虫吟，渲染了秋夜的凄清。

行人绝迹，万籁无声，透露出诗人孤独寂寞的感情；示例二：月明荞麦花如雪，大自然的如画美景感染了诗人，情不自禁地发出不胜惊喜的赞叹。

（3分）9．见客/ 而有惭色（2分）10．①，称赞，以……为美②正③用眼睛看，看④向来，一向（每个1分，共4分）11．①妻子奇怪地询问他这样做的原因，（他）始终不肯告诉（妻子）。

（2分）②现在子伯的富贵哪如（哪里比得上）您的高尚呢？（2分）12．令狐之子“车马服从，雍容如也”，而自己却“耕于野”“蓬发历齿”。

（2分）13．她规劝丈夫：“你从小就重清廉、节操，不顾荣华利禄。

令狐的高贵怎能跟你的高洁相比呢？为什么要忘记原来的志向而感到对儿女有点惭愧呢？”可见她能积极看问题，善于发现别人的长处，注重引导和规劝等。

（4分）14.示例：晨读就是早晨读书，摆脱虚空和焦灼（或激活慵懒和困倦），精神饱满地耕耘奋斗和打拼的心路。

A B C D2013年11月19初中毕业会考适应性考试理综试卷（物理·化学）本试卷分为第Ⅰ卷（选择题）和第II 卷（非选择题）两部分，为理化合卷.满分150分（其中物理80分、化学70分）；考试时间120分钟. 第一卷第1至8页，第二卷第9至12页。

考生作答时，第一卷(选择题)须将答案答在机读答题卡上，第二卷(非选择题) 须将答案答在答题卡上。

考试结束后，将机读答题卡和答题卡一并上交.第Ⅰ卷（选择题75分）注意事项：1.答第Ⅰ卷前考生务必将自己的姓名、考号、考试科目用铅笔涂写在机读卡上.2.每小题选出答案后，用铅笔把机读卡上的对应题目的答案标号涂黑，如需改动需用橡皮擦干净后，再选涂其它答案；直接答在试卷上不能得分.一、选择题 （每题只有一个正确选项；1—16题为物理，17—30题为化学. 每小题2.5分，共75分）） 1．下列星球中，属于恒星的是 A 地球。

B 月球。

C 土星。

D 太阳。

2．在下图所示的光现象中，属于光的折射现象的是3．使用MP3时，调节音量按钮是为了改变声音的 A 响度。

B 音调。

C 音色。

D 频率。

4．四冲程内燃机工作时，机械能转化成内能的冲程是 A 吸气冲程。

B 压缩冲程。

C 做功冲程。

D 排气冲程。

5．（烟台）两个相同的容器分别装满了质量相同的甲、乙两种液体．用同一热源分别加热，液体温度与加热时间关系如图所示A ．甲液体的比热容大于乙液体的比热容B ．如果升高相同的温度，两液体吸收的热量相同C ．加热相同的时间，甲液体吸收的热量大于乙液体吸收的热量D ．加热相同的时间，甲液体温度升高的比乙液体温度升高的多6．质量相同的甲、乙两小车同时同地做匀速直线运动，它们运动的s-t 图像如图所示。

由图像可知，甲小车A. 具有的惯性大B. 所受的合力大C . 具有的动能大 D. 具有的势能大。

7．如下图左所示，三个底面积不同的圆柱形容器内分别盛有A 、B 、C 三种液体，它们对容器底部的压强相等，现分别从三个容器内抽出相同深度的液体后，剩余液体对容器底部的压强P a 、P b 、P c 的大小关系是FA. P a ＞P b ＞P cB. P a ＝P b ＝P c 。