2.2.1 算术平方根
- 格式:pptx
- 大小:1.58 MB
- 文档页数:14


常用的平方根表立方根表在数学的世界里,平方根和立方根是非常重要的概念。
它们在各种数学计算、科学研究以及实际生活中都有着广泛的应用。
为了方便计算和查询,人们常常会编制平方根表和立方根表。
平方根,简单来说,就是一个数的平方等于另一个数,那么这个数就是另一个数的平方根。
例如,2 的平方是 4,所以 2 是 4 的平方根。
同时,因为(-2) 的平方也是 4,所以-2 也是 4 的平方根。
一个正数有两个平方根,它们互为相反数;0 的平方根是 0;负数在实数范围内没有平方根。
立方根则是指一个数的立方等于另一个数,那么这个数就是另一个数的立方根。
比如,2 的立方是 8,所以 2 是 8 的立方根。
与平方根不同的是,任何实数都有唯一的一个立方根。
平方根表通常列出了从 1 到某个较大整数的平方根的值。
以常见的平方根表为例,它会依次给出 1 到 100 这些整数的平方根。
比如,1 的平方根是 1,4 的平方根是 2,9 的平方根是 3 等等。
在实际使用中,如果我们要计算一个不是整数的数的平方根,比如 25 的平方根,我们可以先找到最接近 25 的两个整数的平方根,然后通过插值的方法来估算。
立方根表的编制方式与平方根表类似,也是列出从 1 到一定整数的立方根的值。
比如,1 的立方根是 1,8 的立方根是 2,27 的立方根是3 等等。
那么,这些平方根表和立方根表在哪些方面有用呢?在数学计算中,它们可以大大提高计算速度和准确性。
特别是在一些复杂的计算中,如果需要多次用到某个数的平方根或立方根,直接从表中查找可以节省时间,避免繁琐的计算过程。
在科学研究中,平方根和立方根的概念经常出现。
比如在物理学中,计算物体的速度、加速度等常常会涉及到平方根;在化学中,计算物质的密度、体积等可能会用到立方根。
有了平方根表和立方根表,科学家们可以更高效地进行数据处理和分析。
在工程领域,如建筑、机械制造等,也经常需要用到平方根和立方根的计算。

2.2.1平方根【学习目标】1、掌握算术平方根的定义.2、会求一个数的算术平方根.【温故知新】1、回顾无理数的概念.2、计算:42= ; 72= ;92 = ;112 = .3、填底数:( )2=16,()2=49,( )2=81, ( )2=121.【设疑导学】阅读课本P26页,回答下列问题:1、完成课本问题(1)(2)2、如果_________________,即____,则这个正数x就叫做a的算术平方根.记为“_____”读作“_____”.即_____a.=例如:22=4,则2就是4算术平方根,记为_____4=.特别地规定0的算术平方根是_______,即0=0.3、由算术平方根的定义可知:只有_____和______才有算术平方根,_______数没有算术平方根,即在a中a______0.4、课本问题(2)中的无理数可表示为x=_____,y=______,w=______.这些数都是 _______数.5、阅读例题1和2.由此我们可以看出求一个正数的平方与求_________________是互为逆运算.归纳:(1)式子a中的双重非负性:一是a_______,二是a______.(2)算术平方根的性质:一个正数的算术平方根是_______;0的算术平方根是___;负数___________.【适时检测】1、根据算术平方根的定义填空:①因为202=400,所以400的算术平方根是______,即400=________; ②因为252=625,所以625的算术平方根是______,即625=_________; ③因为172=289,所以289的算术平方根是_______,即289=_________; ④因为232⎪⎭⎫ ⎝⎛=94所以94的算术平方根是_______,即94=________; ⑤0、1、7、13的算术平方根分别是__________________;⑥0.0004的算术平方根是______________;⑦-10_______算术平方根;⑧259的算术平方根是_____________;⑨32的算术平方根是______________. 2、 填空(1)若一个数的算术平方根是7,那么这个数是 ;(2)(2)9的算术平方根是 ;(3)2)32(的算术平方根是 ;(4)若22=+m ,则2)2(+m = .3、求下列各数的算术平方根。

教师学科教案[ 20 – 20 学年度第__学期]任教学科:_____________任教年级:_____________任教老师:_____________xx市实验学校《平方根》基于标准的教学设计教材来源:义务教育教科书《数学》/北师大版课时:第一课时授课对象:八年级学生设计者:目标1:结合上一章勾股定理及上节无理数,能准确的说出算数平方根的概念,会用根号表示一个数的算术平方根并求出它的算术平方根。
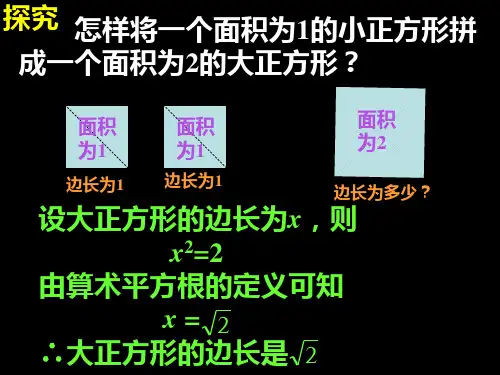
(1)结合图形完成填空:=2x,=2y,=2z,=2w.(2)在x,y,z,w中哪些是有理数?哪些是无理数?你能表示它们吗?你还能构造出几个这样的无理数吗?巩固勾股定理,引入本节算术平方根。
回答问题,教师自主学习仔细阅读课本26页内容,请回答下列问题:1.算术平方根的概念是什么?2.什么数有算术平方根?负数有算术平方根吗?通过独立思考,会用自己的语言叙述算术平方根的概念结论:只有非负合作交流一:例1.求下列各数的算术平方根。
900, 1,144121, 1495%的学生与他人合作交流后能够准确求出一个数的算术平方根。
找四名学生到讲评。
自主检测一1、填空:64的算术平方根是________,0的算术平方根是______,0.004的算术平方根是_____,7的算术平方根是______2,求下列各数的算术平方根:36,15,410-,)65(,610,259,(-3.9)2,2.25;95%的学生准确做出自主检一学生做完教师批改组员的。
合作交流二:(课本26页问题)例2.自由下落物体的高度h(米)与下落时间t(秒)的90%的学生通过教师巡视倾听,目标2: 利用算术平方根能解决实际关系为h=4.9t2.有一铁球从19.6米高的建筑物上自由下落,到达地面需要多长时间?与他人合作交流,能够利用算术平方根解决实际问题。
回答问题,然后点评。




初中数学平方根口诀表
平方根又叫二次方根,其中属于非负数的平方根称之为算术平方根。
下面整理了记忆平方根的口诀,供大家参考。
平方根表
巧记平方根口诀
负数方根不能行,零取方根仍为零。
正数方根有两个,符号相反值相同。
2 作根指可省略,其它务必要写明。
负数只有奇次根,算术方根零或正。
注:方根均指平方根。
平方根公式
如果一个非负数x的平方等于a,即x²=a,(a≥0),那么这个非负数x叫做a的算术平方根。
a的算术平方根记为√a ,读作“根号a”,a叫做被开方数。
求一个非负数a的平方根的运算叫做开平方。
结论:被开方数越大,对应的算术平方根也越大(对所有正数都成立)。
一个正数如果有平方根,那么必定有两个,它们互为相反数。
显然,如果知道了这两个平方根的一个,那么就可以及时的根据相反数的概念得到它的另一个平方根。
负数在实数系内不能开平方。
只有在复数系内,负数才可以开平方。
负数的平方根为一对共轭纯虚数。
例如:-1的平方根为±i,-9的平方根为±3i,其中i为虚数单位。
规定:i²=-1或i=√-1,-i=-√-1。
一般地,“√ ̄”仅用来表示算术平方根,即非负数的非负平方根。
规定:0的算术平方根为0。

§2.2.1算术平方根【学习目标】1、能述数的算术平方根的概念,会用根号表示一个数的算术平方根;2、掌握求一个正数的算术平方根与平方是互逆的运算,会利用这个互逆运算关系求某些非负数的算术平方根;3、会应用算术平方根的性质。
【学习活动】学习准备:1、计算:24=_______;27=_______;29=_______;211=_______.2、填底数:()216=;()249=;()281=;()2121=.3、根据右图填空:2x=______;2y=______;2z=______;2w=______.【探究活动一】算术平方根的概念一般地,如果一个_______x的平方等于a,即2x a=,那么这个数x就叫做a的_____________,记为_______________,读作_________.特别地,我们规定:0的算术平方根是_________.即:若2x a=()0x≥,则x=______.例题解析例1、求下列各数的算术平方根:(1)900;(2)1;(3)4964;(4)14;(5)610;(6)27.4.实践练习:求下列各数的算术平方根,并用符号表示出来.(1)1.96;(2)124;(3)410-;(4)()23.9-.例2、自由下落物体的高度h (米)与下落时间t (秒)的关系为24.9h t =.有一铁球从19.6米高的建筑物上自由下落,到达地面需要多长时间?实践练习:如图,从帐篷支撑竿AB 的顶部A 向地面拉一根绳子AC 固定帐篷.若绳子的长度为5.5米,地面固定点C 到帐篷支撑竿底部B 的距离是4.5米,则帐篷支撑竿的高是多少米?【探究活动二】算术平方根的性质若2x a =()0x ≥,则x =______.易知:a ______0a . 例3、求下列各式中x 的取值范围.(125x + (23443x x --; (32x -实践练习:已知223y x x =--,求x y 的值.例4、已知1y -和12x -互为相反数,且0x ≠,求yx 的值.实践练习:如果 450x x y -++-=,求:(1)x 、y 的值;(2)xy 的算术平方根.【学习评价】(1)若一个数的算术平方根是5,则这个数是_________.(2)49的算术平方根是_________.(3)若一个数的算术平方根等于它本身,这个数是_______.(4)正数_________的平方为25144,971的算术平方根为_________.(5)()21.44-的算术平方根为_________.(6)81的算术平方根为_________,04.0=_________.(7)若1-x 有算术平方根,则x 的取值范围是_________.2、下列数中没有算术平方根的是( )A .0B .1-C .10D .23)(-3、求下列各式的值(141294 (2)216 (3)216 (4))2(22>x x )-(4、已知a、b满足6b=+,求a b+的算术平方根.5、已知()2++++=.340x y。

常用的平方根表立方根表在数学的世界里,平方根和立方根是非常重要的概念。
为了更方便地进行计算和解决问题,人们常常会用到平方根表和立方根表。
平方根,简单来说,就是一个数的平方的逆运算。
比如,如果一个数的平方是 9,那么这个数就是 9 的平方根,即 3 或者-3。
平方根表就是把一些常见数字的平方根整理在一起,方便我们查阅和使用。
立方根呢,则是一个数的立方的逆运算。
例如,若一个数的立方是8,那么这个数就是 8 的立方根,即 2。
立方根表就是将常见数字的立方根罗列出来的表格。
平方根表通常包含从 1 到一定数值范围内数字的平方根。
比如说,对于数字 1,它的平方根就是 1;数字 4 的平方根是 2;数字 9 的平方根是 3。
当数字不是完全平方数时,平方根就会是一个无理数,这时候平方根表中会给出其近似值。
比如,2 的平方根约为 1414,3 的平方根约为 1732 等等。
立方根表的构成和平方根表类似,只不过是关于数字的立方根。
像1 的立方根还是 1,8 的立方根是 2,27 的立方根是 3。
对于不是完全立方数的数字,立方根表也会给出相应的近似值。
这些平方根表和立方根表在很多领域都有着广泛的应用。
在数学计算中,当我们需要快速得到一个数的平方根或立方根的值时,它们可以节省我们大量的计算时间。
特别是在一些复杂的数学问题中,或者在需要精确计算的科学研究中,这些表格能发挥重要作用。
在工程领域,平方根和立方根的计算也经常出现。
比如在建筑设计中,计算结构的受力、材料的用量等,都可能会用到平方根和立方根。
有了平方根表和立方根表,工程师们能够更高效地完成设计和计算工作,确保工程的准确性和安全性。
在物理学中,平方根和立方根的概念同样不可或缺。
例如在研究物体的运动、能量的转换等方面,常常需要进行相关的计算。
此时,平方根表和立方根表可以为物理学家们提供便利,帮助他们更专注于理论的研究和实验的分析。
在日常生活中,平方根和立方根的应用也并不少见。
常用的平方根表立方根表在数学的世界里,平方根和立方根是非常重要的概念。
它们在各种数学计算、科学研究以及实际生活中都有着广泛的应用。
为了方便计算和查询,人们常常会编制平方根表和立方根表。
平方根,简单来说,就是一个数的平方等于另一个数,那么这个数就是另一个数的平方根。
例如,因为 2 的平方等于 4,所以 2 是 4 的平方根。
同时,-2 也是 4 的平方根,因为(-2) 的平方也等于 4。
正数有两个平方根,它们互为相反数;0 的平方根是 0;负数在实数范围内没有平方根。
立方根则是一个数的立方等于另一个数,那么这个数就是另一个数的立方根。
比如,因为 2 的立方等于 8,所以 2 是 8 的立方根。
与平方根不同的是,任何实数都有唯一的立方根。
平方根表通常列出了从 1 到一定数值(比如 1000)的整数的平方根。
以常见的平方根表为例,它会按照数字的顺序依次列出每个数的平方根。
例如,1 的平方根是 1,2 的平方根约为 1414,3 的平方根约为1732 等等。
这些数值都是经过精确计算得出的,为我们在计算中提供了极大的便利。
立方根表的形式与平方根表类似,也是按照数字顺序列出一定范围内整数的立方根。
比如 1 的立方根是 1,2 的立方根约为 1260,3 的立方根约为 1442 等等。
那么,这些平方根表和立方根表在哪些方面能帮助我们呢?首先,在数学计算中,如果我们需要频繁计算某个数的平方根或立方根,直接查询表格可以节省大量的计算时间。
特别是在一些复杂的数学问题中,快速准确地获取平方根和立方根的值能够提高解题的效率。
其次,在科学研究和工程领域,很多数据的处理和分析都涉及到平方根和立方根的计算。
例如,物理学中的力学、电学计算,化学中的浓度计算,以及工程学中的结构设计等。
有了平方根表和立方根表,科研人员和工程师们可以更快速地得到准确的结果,从而推进研究和项目的进展。
在日常生活中,平方根和立方根的应用也不少。
比如在建筑施工中,计算房间的面积、体积时就可能用到;在制定预算时,计算成本的平方根或立方根来评估价格的合理性等等。