上海交通大学理论力学考试样题(34学时)
- 格式:pdf
- 大小:169.10 KB
- 文档页数:23

目 录
2007年上海交通大学420理论力学考研真题
2006年上海交通大学420理论力学考研真题
2005年上海交通大学420理论力学考研真题
2004年上海交通大学420理论力学考研真题
2003年上海交通大学420理论力学考研真题
2002年上海交通大学420理论力学考研真题
2001年上海交通大学420理论力学考研真题
2000年上海交通大学420理论力学考研真题
1999年上海交通大学理论力学考研真题
1998年上海交通大学理论力学考研真题
1997年上海交通大学理论力学考研真题
1996年上海交通大学理论力学考研真题。
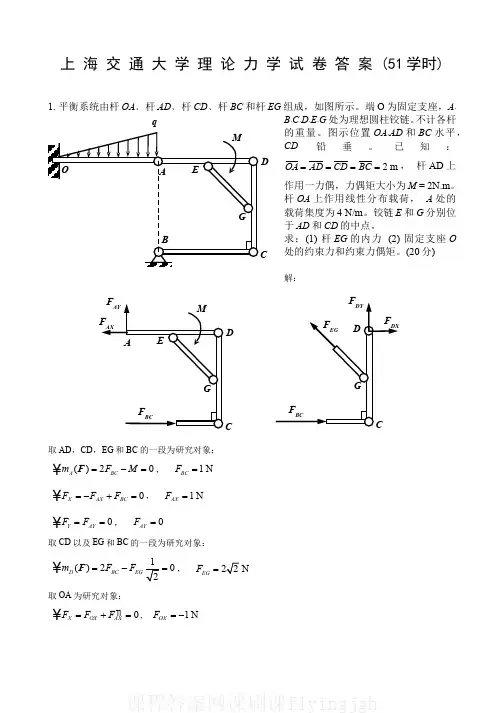
上 海 交 通 大 学 理 论 力 学 试 卷 答 案 (51学时)1. 平衡系统由杆OA ﹑杆AD ﹑杆CD ﹑杆BC 和杆EG 组成,如图所示。
端O 为固定支座,A ﹑B ﹑C ﹑D ﹑E ﹑G 处为理想圆柱铰链。
不计各杆的重量。
图示位置OA ﹑AD 和BC 水平,CD 铅垂。
已知:2m OA AD CD BC ====, 杆AD 上作用一力偶,力偶矩大小为M = 2N.m 。
杆OA 上作用线性分布载荷, A 处的载荷集度为4 N/m 。
铰链E 和G 分别位于AD 和CD 的中点。
求:(1) 杆EG 的内力 (2) 固定支座O 处的约束力和约束力偶矩。
(20分)解:取AD ,CD ,EG 和BC 的一段为研究对象:()20ABC m F M =-=¥F , 1N BC F =0XAX BC F F F =-+=¥, 1N AX F =0YAY FF ==¥, 0AY F =取CD 以及EG 和BC的一段为研究对象:()20D BC EGm F F =-=¥F, N EG F =取OA 为研究对象:0XOX AXFF F ᄁ=+=¥, 1N OX F =-CDCqD0YOY FF Q =-=¥, 4NOY F Q ==4()03O O m M Q =-=¥F , 416N.m 33OM Q ==2. 如图所示,杆AO 和杆AB 重量不计,铰O 为固定铰支座,杆OA 与杆AB 以圆柱铰A 铰接,杆AB 的端B 搁置在粗糙的地面上,端B的极限摩擦系数为4。
杆AO 和杆AB 的长度均为l 。
大小为W 的集中载荷作用点在杆AB 的点C ,令点C 与点B 的距离为x ,杆AB 上作用一水平力F,大小为2W 。
求系统平衡时x 的范围。
(20分)F’AX==A2WA杆OA 是两力杆,设OA F 为两力杆的内力,取杆AB 为研究对象,对B点取矩1()022B OA xm F l F W=-+=¥v ,得到 OA xF W l=ᅲ0yN FF W =-=¥, N F W=当B点处于右滑的临界状态024X OA N F F F F W l m =-+=-+=�¥解得:4lx =当B点处于左滑的临界状态024X OA N F F F F W l m =--=--=�¥解得:34x l =系统平衡时x 的范围:1344l x l ᆪᆪA3. 如图所示,圆弧杆B 1搁置在高为h 的平台上。


《理论力学》试题库第一部分填空题:第一类:1,已知某质点运动方程为x=2bcoskt,y=2bsinkt,其中b、k均为常量,则其运动轨迹方程为-—————-———--,速度的大小为——-—————-———,加速度的大小为—————————-—-。
2、已知某质点运动方程为x=2cos3t,y=2sin3t,z=4t则其运动速度的大小为,加速度的大小为 .3、已知某质点运动方程为r=e ct,θ=bt,其中b、c是常数,则其运动轨道方程为——-———-—-——-———-————--,其运动速度的大小为--———————-,加速度的大小为———-————————。
4、已知某质点的运动方程为x=2bcos2kt,y=bsin2kt,则其运动轨道方程为;速度大小为 ;加速度大小为。
5、已知质点运动的参数方程为y=bt,θ=at,其中a、b为常数,则此质点在极坐标系中的轨道方程式为,在直角坐标系中的轨道方程式为。
6、已知某质点的运动方程为r=at,θ=bt,其中a、b是常数,则其运动轨道方程为—-———-——-——-——————————,其运动速度的大小为——-———————,加速度的大小为—-—-———-————。
7、已知某质点运动方程为r=at,θ=b/t,其中a、b是常数,则其运动轨道方程为---—-———--————-,其运动速度的大小为—-—-—--———,加速度的大小为———-—————.8、已知某质点的运动方程为x=at,y=a(e t-e-t)/2,其中a为常数,则其运动轨道方程为—-—-——-—---—————---———,曲率半径为——-———————。
第二类:9、质点在有心力作用下,其————————————-—-—-———均守恒,其运动轨道的微分方程为—--——-——-——————--—————,通常称此轨道微分方程为比耐公式。
10、柯尼希定理的表达式为—-——-——————--————-—-,其中等式右边第一项和第二项分别为——————————————————————---—-—————-——————-——-——-———。

大学理论力学期末考试题库及答案一、选择题(每题2分,共20分)1. 质点系的质心位置取决于()。
A. 质点系的总质量B. 质点系中各质点的质量C. 质点系中各质点的位置D. 质点系中各质点的速度答案:C2. 刚体的转动惯量与()有关。
A. 质量B. 质量分布C. 质量分布和形状D. 形状3. 两个质点组成的系统,若两质点间的作用力大小相等,方向相反,则这两个力()。
A. 是一对平衡力B. 是一对作用力和反作用力C. 是一对内力D. 不能确定答案:B4. 质点沿直线做匀加速运动,加速度为a,初速度为v0,则经过时间t后的速度v为()。
A. v = v0 + atB. v = v0 - atC. v = v0 + 1/2atD. v = v0 - 1/2at5. 两个质点组成的系统,若两质点间的作用力大小相等,方向相反,则这两个力()。
A. 是一对平衡力B. 是一对作用力和反作用力C. 是一对内力D. 不能确定答案:B6. 刚体绕固定轴转动时,其转动惯量与()有关。
A. 质量B. 质量分布C. 质量分布和形状D. 形状答案:C7. 质点沿直线做匀加速运动,加速度为a,初速度为v0,则经过时间t后的位移s为()。
A. s = v0t + 1/2at^2B. s = v0t - 1/2at^2C. s = v0t + at^2D. s = v0t - at^2答案:A8. 刚体绕固定轴转动时,其角加速度与()有关。
A. 质量B. 质量分布C. 质量分布和形状D. 形状答案:B9. 质点沿直线做匀加速运动,加速度为a,初速度为v0,则经过时间t后的位移s为()。
A. s = v0t + 1/2at^2B. s = v0t - 1/2at^2C. s = v0t + at^2D. s = v0t - at^2答案:A10. 两个质点组成的系统,若两质点间的作用力大小相等,方向相反,则这两个力()。
A. 是一对平衡力B. 是一对作用力和反作用力C. 是一对内力D. 不能确定答案:B二、填空题(每题2分,共20分)1. 质点系的质心位置取决于质点系中各质点的________和________。


《理论力学》——期末考试答案一、单选题1.力对点之矩决定于( )。
A.力的大小B.力臂的长短C.力的大小和力臂的长短D.无法确定正确答案:C2.动点相对于动坐标系的运动称为( )的运动。
A.牵连运动B.相对运动C.绝对运动D.圆周运动正确答案:B3.动点的牵连速度是指该瞬时牵连点的速度,它相对的坐标系是( )。
A.动坐标系B.不必确定的C.静坐标系D.静系或动系都可以正确答案:C4.在质点系动能定理中,应注意外力或内力做的功之和不等于合外力或( )做的功。
A.重力B.浮力C.合内力D.牵引力正确答案:C5.将平面力系向平面内任意两点进行简化,所得主矢量和主矩都相等,且主矩不为零,则该力系简化的最后结果为( )。
A.合力偶B.合力C.平衡力系D.无法进一步合成正确答案:A6.超静定结构的超静定次数等于结构中( )。
A.约束的数目B.多余约束的数目C.结点数D.杆件数正确答案:B7.静不定系统中,多余约束力达到3个,则该系统静不定次数为( )A.3次B.6次C.1次D.不能确定正确答案:A8.关于平面力偶系、平面汇交力系、平面一般力系,最多能够得到的相互独立的平衡方程的个数依次是( )。
A.2、1、3B.2、2、3C.1、2、2D.1、2、3正确答案:D9.平面任意力系向一点简化,应用的是( )。
A.力的平移定理B.力的平衡方程C.杠杆原理D.投影原理正确答案:A10.对于平面力系,一个平衡方程可解( )未知量。
A.1个B.2个C.3个D.不一定正确答案:A11.一平面力系由两组平面平行力系组成(这两组平面平行力系之间互不平行),若力系向某A点简化结果为一合力,下述说法正确的是( )。
A.这两组平面平行力系必然都各自向A点简化为一合力B.这两组平面平行力系可能都各自简化为一力偶C.可能一组平面平行力系向A点简化得到一个力和一个力偶,而另一组平面平行力系向A点简化得到一合力D.可能这两组平面平行力系都各自向A点简化得到一个力和一个力偶正确答案:D12.在任何情况下,在几何可变体系上增加一个二元体后构成的体系是几何( )体系。
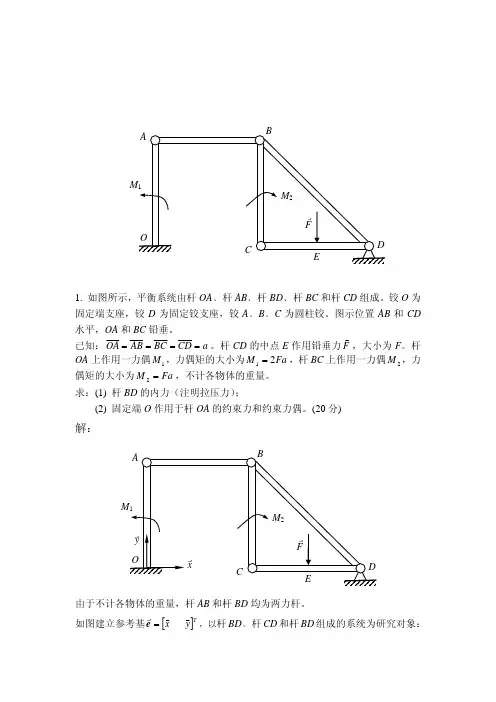
1. 如图所示,平衡系统由杆OA ﹑杆AB ﹑杆BD ﹑杆BC 和杆CD 组成。
铰O 为固定端支座,铰D 为固定铰支座,铰A ﹑B ﹑C 为圆柱铰。
图示位置AB 和CD 水平,OA 和BC 铅垂。
已知:a CD BC AB OA ====。
杆CD 的中点E 作用铅垂力F v,大小为F 。
杆OA 上作用一力偶1M ,力偶矩的大小为Fa M 21=,杆BC 上作用一力偶2M ,力偶矩的大小为Fa M =2,不计各物体的重量。
求:(1) 杆BD 的内力(注明拉压力);(2) 固定端O 作用于杆OA 的约束力和约束力偶。
(20分) 解:由于不计各物体的重量,杆AB 和杆BD 均为两力杆。
如图建立参考基[]Ty x v v r =e , 以杆BD ﹑杆CD 和杆BD 组成的系统为研究对象:0)(1=∑=i n i z D F M v0212=+−a S M aF AB (3分) 解得:2FS AB =(拉力)(1分)以杆BD 为研究对象:0)(1=∑=i n i z C F M v0212=−−M a S a S BD AB (3分)解得:F S BD 22−=(压力)(1分)ABS r BDS rDABS r以杆OA 为研究对象:01=∑=ni ixF,0=+AB x O S F (2分)01=∑=n i iyF,0=y O F (2分)0)(1=∑=i ni z O F M v01=++−O AB M M a S (3分)解得:F F x O 21−=,0=y O F ,Fa M O 23−=(2分)2. 如图所示,梯子由杆OA 和杆AB 组成,铰O 为固定铰支座,铰A 为圆柱铰,杆AB 搁置在地面上,接触点为端点B 。
杆OA 和杆AB 的长度均为l ,图示位置杆OA 和杆AB 的倾角均为60o 。
杆AB 与地面接触点B的静摩擦因数为321=s f 。
人的重量为W ,不计杆OA 和杆AB 的重量。
设梯子始终保持平衡,计算(1) 人到达的最高点P 与点B 的距离x 。


理论力学部分第一章静力学基础一、是非题(每题3分,30分)1.力有两种作用效果,即力可以使物体的运动状态发生变化,也可以使物体发生变形。
()2.在理论力学中只研究力的外效应。
()3.两端用光滑铰链连接的构件是二力构件。
()4.作用在一个刚体上的任意两个力成平衡的必要与充分条件是:两个力的作用线相同,大小相等,方向相反。
()5.作用于刚体的力可沿其作用线移动而不改变其对刚体的运动效应。
()6.三力平衡定理指出:三力汇交于一点,则这三个力必然互相平衡。
()7.平面汇交力系平衡时,力多边形各力应首尾相接,但在作图时力的顺序可以不同。
()8.约束力的方向总是与约束所能阻止的被约束物体的运动方向一致的。
()9. 力偶只能使刚体发生转动,不能使刚体移动。
()10.固定铰链的约束反力是一个力和一个力偶。
()二、选择题(每题4分,24分)1.若作用在A点的两个大小不等的力F1和F2,沿同一直线但方向相反。
则其合力可以表示为。
①F1-F2;②F2-F1;③F1+F2;2.作用在一个刚体上的两个力F A、F B,满足F A=-F B的条件,则该二力可能是。
①作用力和反作用力或一对平衡的力;②一对平衡的力或一个力偶。
③一对平衡的力或一个力和一个力偶;④作用力和反作用力或一个力偶。
3.三力平衡定理是。
①共面不平行的三个力互相平衡必汇交于一点;②共面三力若平衡,必汇交于一点;③三力汇交于一点,则这三个力必互相平衡。
4.已知F1、F2、F3、F4为作用于刚体上的平面共点力系,其力矢关系如图所示为平行四边形,由此。
①力系可合成为一个力偶;②力系可合成为一个力;③力系简化为一个力和一个力偶;④力系的合力为零,力系平衡。
5.在下述原理、法则、定理中,只适用于刚体的有。
①二力平衡原理;②力的平行四边形法则;③加减平衡力系原理;④力的可传性原理;⑤作用与反作用定理。
6.关于约束的说法正确的是 。
① 柔体约束,沿柔体轴线背离物体。
② 光滑接触面约束,约束反力沿接触面公法线,指向物体。
理论力学期末考试试题1-1、自重为P=100kN的T字形钢架ABD,置于铅垂面内,载荷如图所示。
其中转矩M=20kN.m,拉力F=400kN,分布力q=20kN/m,长度l=1m。
试求固定端A的约束力。
解:取T型刚架为受力对象,画受力图.1-2 如图所示,飞机机翼上安装一台发动机,作用在机翼OA上的气动力按梯形分布:q=60kN/m,2q=40kN/m,机翼重1p=45kN,发动机1重p=20kN,发动机螺旋桨的反作用力偶矩M=18kN.m。
求机翼处于平2衡状态时,机翼根部固定端O所受的力。
解:1-3图示构件由直角弯杆EBD以及直杆AB组成,不计各杆自重,已知q=10kN/m,F=50kN,M=6kN.m,各尺寸如图。
求固定端A处及支座C的约束力。
1-4 已知:如图所示结构,a, M=Fa, 12F F F ==, 求:A ,D 处约束力.解:1-5、平面桁架受力如图所示。
ABC为等边三角形,且AD=DB。
求杆CD的内力。
1-6、如图所示的平面桁架,A端采用铰链约束,B端采用滚动支座约束,各杆件长度为1m。
在节点E和G上分别作用载荷F=10kN,G F=7EkN。
试计算杆1、2和3的内力。
解:2-1 图示空间力系由6根桁架构成。
在节点A上作用力F,此力在矩形ABDC平面内,且与铅直线成45º角。
ΔEAK=ΔFBM。
等腰三角形EAK,FBM和NDB在顶点A,B和D处均为直角,又EC=CK=FD=DM。
若F=10kN,求各杆的内力。
2-2 杆系由铰链连接,位于正方形的边和对角线上,如图所示。
在节点D沿对角线LD方向作用力F。
在节点C沿CH边铅直向下作用力F。
D如铰链B,L和H是固定的,杆重不计,求各杆的内力。
2-3 重为1P =980 N ,半径为r =100mm 的滚子A 与重为2P =490 N 的板B 由通过定滑轮C 的柔绳相连。
已知板与斜面的静滑动摩擦因数s f =0.1。
滚子A 与板B 间的滚阻系数为δ=0.5mm ,斜面倾角α=30º,柔绳与斜面平行,柔绳与滑轮自重不计,铰链C 为光滑的。