《固体物理基础教学课件》第3章.ppt
- 格式：ppt
- 大小：3.93 MB
- 文档页数：36
下载文档原格式
合集下载
固体物理课件
e 2 晶体中有3N个振动模 晶体中有 个振动模 C = k ( ∑ B k T ) (eℏω j / kBT − 1)2 V 1） 爱因斯坦模型 ） j =1 B 假设N个原子构成的晶体 个原子构成的晶体， 假设 个原子构成的晶体，
所有的原子以相同的频率 ω0振动 2） 德拜模型 ） 以连续介质的弹性波来代表格 波，将晶格看作是各向同性的 连续介质
V (r + R) = V (r )
布洛赫定理
具有晶格周期性时， 布洛赫定理 —— 势场 V ( r ) 具有晶格周期性时，电子的波 函数满足薛定谔方程 ℏ2 2 [− ∇ + V ( r )]ψ ( r ) = E ψ ( r ) 2m —— 方程的解具有以下性质
ψ ( r + Rn ) = e ik ⋅R ψ ( r )
ω = 2
−
− i (ωt − naq )
2
β
m
ω
aq sin m 2
−π a
β
π π < q ≤ a a
q=
µn = µn+ N 2π
Na
× h —— h为整数 为整数
π a o 晶格振动波矢的数 目=晶体的原胞数 晶体的原胞数
能量本征值 ε n = ( n q + 1 ) ℏ ω q
q
晶格振动的能量量子； 声子 —— 晶格振动的能量量子；或格波的能量量子 当这种振动模处于 系统能量本征值
原子的振动 —— 晶格振动在晶体中形成了各种模式的波
模型 运动方程 试探解
m µ n = − β (µ n − µ n−1 ) − β (µ n − µ n+1 )
..
一维晶格振动 一维无限长原子链， ， ， 一维无限长原子链，m，a，β
2021固体物理第三章最新PPT资料
固体物理第三章
第三章 晶格振动和晶体热学性质
本章主要内容 用最近邻原子间谐力模型来讨论晶格振动的本征频率； 用格波来描写晶格原子的集体运动； 用量子理论来表述格波相应的能量量子；
在此基础上处理固体的热学性质。
§3.1 一维晶格的振动
晶格振动的根本原因: 原子间存在着相互作用力。 对于一对原子而 言，可以用彼此间的相互作用势能来表示。
设想边界条件：无限多个相同晶体相联接，各晶体中相对应的原子 的运动情况都一样。
玻恩－卡门边界条件：
u1 uN1
德国理论物理学家，量 子力学的奠基人之一玻 恩，M.(Max Born 1882～1970). 1954年荣 获诺贝尔物理学奖
通常采用试解的方法求解。假设上式具有简谐波形式的试解：
unAie(qnat)
q为波矢，qna是序号为n的原子在t=0时刻的振动位相。
序号为n’的原子的位移：
u n A i ( q n a t ) e A i ( q t n ) q e ( n a n a ) u n e i( n q n )a
频率－波矢关系（称为色散关系）。
表明试解代表一种简正模型（即一个ω和一个q值）的格波。
格波： Aei(tnaq)
连续介质弹性波： Aei(txq)
从形式看，格波与连续介质弹性波完全类似。但连续介质弹性 波中的X是可连续取值的；而在格波中只能取na（原子位置），这 是一系列周期排列的点。
一个格波解表示所有原子同时作频率为 的振动，不同原子有
将简谐波形式的试解代入运动学方程
mdd2u 2tn (un1un12un)
m 2 u n u n ( e iq e a iq 2 a ) 2 u n (c q ) o 1 a )s
第三章 晶格振动和晶体热学性质
本章主要内容 用最近邻原子间谐力模型来讨论晶格振动的本征频率； 用格波来描写晶格原子的集体运动； 用量子理论来表述格波相应的能量量子；
在此基础上处理固体的热学性质。
§3.1 一维晶格的振动
晶格振动的根本原因: 原子间存在着相互作用力。 对于一对原子而 言，可以用彼此间的相互作用势能来表示。
设想边界条件：无限多个相同晶体相联接，各晶体中相对应的原子 的运动情况都一样。
玻恩－卡门边界条件：
u1 uN1
德国理论物理学家，量 子力学的奠基人之一玻 恩，M.(Max Born 1882～1970). 1954年荣 获诺贝尔物理学奖
通常采用试解的方法求解。假设上式具有简谐波形式的试解：
unAie(qnat)
q为波矢，qna是序号为n的原子在t=0时刻的振动位相。
序号为n’的原子的位移：
u n A i ( q n a t ) e A i ( q t n ) q e ( n a n a ) u n e i( n q n )a
频率－波矢关系（称为色散关系）。
表明试解代表一种简正模型（即一个ω和一个q值）的格波。
格波： Aei(tnaq)
连续介质弹性波： Aei(txq)
从形式看，格波与连续介质弹性波完全类似。但连续介质弹性 波中的X是可连续取值的；而在格波中只能取na（原子位置），这 是一系列周期排列的点。
一个格波解表示所有原子同时作频率为 的振动，不同原子有
将简谐波形式的试解代入运动学方程
mdd2u 2tn (un1un12un)
m 2 u n u n ( e iq e a iq 2 a ) 2 u n (c q ) o 1 a )s
第三章 固体物理ppt课件
§2
三维晶格的振动
设实际三维晶体沿基矢a1、a2、a3方向的初基原胞数分 别为N1、N2、N3，即晶体由N＝N1·N2·N3个初基原胞组成， 每个初基原胞内含s个原子。 一维情况下，波矢q和原子振动方向相同，所以只有纵波。 三维情况下，有纵波也有横波。
原则上讲，每支格波都描述了晶格中原子振动的一类运动 形式。初基原胞有多少个自由度，晶格原子振动就有多少种 可能的运动形式，就需要多少支格波来描述。
一个波矢为K的第S支模式处在第N个激发态，我们就说在晶 体中存在着N个波矢为K的第S支声子（因为给定了K与第S支模 式则ω可由色散关系唯一确定），在晶体中波矢为K的纵声学支 模式处于N激发态，我们就说晶体中有N个波矢为K的纵声学支 声子。
声子这个名词是模仿光子而来（因为电磁波也是一种简谐振 动）。声子与光子都代表简谐振动能量的量子。所不同的是光子 可存在于介质或真空中，而声子只能存在于晶体之中，只有当晶 体中的晶格由于热激发而振动时才会有声子，在绝对零度下，即 在0K时，所有的简正模式都没有被激发，这时晶体中没有声子， 称之为声子真空。声子与光子存在的范围不同，即寄居区不同。
每一组整数（L1,L2,L3 ）对应一个波矢量q。将这些波矢在倒空 间逐点表示出来，它们仍是均匀分布的。每个点所占的“体积” 等于“边长”为(b1/N1)、（b2/N2）、(b3/N3)的平行六面体的 “体积”，它等于： b b b 3 1 2 N N N 1 N 2 3 式中Ω*是倒格子初原胞的“体积”，也就是第一 布里渊区的“体积”，而Ω*＝（2π）3/Ω ，所以每个波 矢q在倒空间所占的“体积”为：
子的位移构成了波，这个波称之为格波，把寻求到的
运动方程的解带入运动方程就能找出ω 与q的关系即
固体物理基础第3章 晶格振动理论
第3章 晶格振动理论
第3章 晶格振动理论
3.1 一维单原子链 3.2 一维双原子链 3.3 三维晶格的振动 3.4 声子 3.5 晶格振动谱的实验测定 3.6 晶格热容的量子理论 3.7 晶体的非简谐效应 热膨胀和热传导
1
第3章 晶格振动理论
2
第3章 晶格振动理论
3
第3章 晶格振动理论
图3.1 一维单原子链模型
6
第3章 晶格振动理论 将μ(x-Δx，t)和μ(x+Δx，t)在x处泰勒展开，并且只保留到二 阶项，这种假设称为简谐近似，于是有
(x-x, t)(x, t)-12dd(xt,t)x-12d2d(t2x,t)x2 (x+x, t)(x, t)+12dd(xt,t)x+12d2d(t2x,t)x2
把这些连续量带入方程(3.1)整理后即可得到：
率。
根据这种长波近似的极限情形，就可以设想，当长波近
似的条件λ>>a不成立时，方程(3.1)的解仍应具有类似的形式，
即只需在式(3.4)的简谐波的解中用na替代x即可，也就是式
(3.2)
8
第3章 晶格振动理论
3.1.3 色散关系 为了进一步研究一维单原子链振动的特点，可以将式
(3.2)所示的格波ห้องสมุดไป่ตู้式的解代入振动方程(3.1)，得：
10
第3章 晶格振动理论
-π＜qa≤π
即
-π q π
(3.6)
a
a
而
-
π a
，π a
正好是一维单原子链的第一布里渊区。该范围以
外的q并不能提供其他不同的波。晶体中的格波之所以具有
这样的特点，可以用图3.2来说明。为了便于图示，图中把
第3章 晶格振动理论
3.1 一维单原子链 3.2 一维双原子链 3.3 三维晶格的振动 3.4 声子 3.5 晶格振动谱的实验测定 3.6 晶格热容的量子理论 3.7 晶体的非简谐效应 热膨胀和热传导
1
第3章 晶格振动理论
2
第3章 晶格振动理论
3
第3章 晶格振动理论
图3.1 一维单原子链模型
6
第3章 晶格振动理论 将μ(x-Δx，t)和μ(x+Δx，t)在x处泰勒展开，并且只保留到二 阶项，这种假设称为简谐近似，于是有
(x-x, t)(x, t)-12dd(xt,t)x-12d2d(t2x,t)x2 (x+x, t)(x, t)+12dd(xt,t)x+12d2d(t2x,t)x2
把这些连续量带入方程(3.1)整理后即可得到：
率。
根据这种长波近似的极限情形，就可以设想，当长波近
似的条件λ>>a不成立时，方程(3.1)的解仍应具有类似的形式，
即只需在式(3.4)的简谐波的解中用na替代x即可，也就是式
(3.2)
8
第3章 晶格振动理论
3.1.3 色散关系 为了进一步研究一维单原子链振动的特点，可以将式
(3.2)所示的格波ห้องสมุดไป่ตู้式的解代入振动方程(3.1)，得：
10
第3章 晶格振动理论
-π＜qa≤π
即
-π q π
(3.6)
a
a
而
-
π a
，π a
正好是一维单原子链的第一布里渊区。该范围以
外的q并不能提供其他不同的波。晶体中的格波之所以具有
这样的特点，可以用图3.2来说明。为了便于图示，图中把
固体物理学 ppt课件
第1章 晶体的结构
阐明晶体中原子排列的几何规律性
PPT课件
1
内 容
1.1 晶体的特征 1.2 空间点阵 1.3 晶格的周期性、基矢 1.4 密勒指数 1.5 倒格子 1.6 晶体的特殊对称性、对称操作 1.7 晶系、布喇菲原胞 1.8 密堆积、配位数 1.9 X射线衍射方程、反射球
PPT课件 2
1.1 晶体的特征
问题一 体心立方晶胞中含有几个原子？ 原子引基矢。 问题二 体心立方原胞如何选取？ 问题三 问题四
8 1 2 个原子 以体心原子为顶 8 点，分别向三个顶角
1 3 a1 a 2 a 3 a 原胞的基矢形式？ 2
a1
k
a a 1 ( i j k ) 原胞体积？ 2 a a 2 (i j k ) 2 a a 3 (i j k ) 2
1.3.3 三维情况
布喇菲格子：最小重复单元（原胞）只含有一个原子的晶格 复式格子：原胞中含有两个或两个以上原子的晶格
（1）三维布喇菲晶格原胞：是三边长等于各方向基矢， 结点为顶点的平行六面体。基矢（a1,a2 ,a3 ）
a3 a2 a1
PPT课件
20
晶格周期性：设r为重复单元中任意一处的位矢
简立方(SC)
体心立方(BCC) 面心立方(FCC)
PPT课件
22
简立方（Simple Cubic，简称 SC ）
三个基矢等长并且互相垂直。
a3
a a2
原胞与晶胞相同。
a1
a 1 ai a 2 aj a 3 ak
PPT课件
23
体心立方(Body Centered Cubic, 1 BCC)
阐明晶体中原子排列的几何规律性
PPT课件
1
内 容
1.1 晶体的特征 1.2 空间点阵 1.3 晶格的周期性、基矢 1.4 密勒指数 1.5 倒格子 1.6 晶体的特殊对称性、对称操作 1.7 晶系、布喇菲原胞 1.8 密堆积、配位数 1.9 X射线衍射方程、反射球
PPT课件 2
1.1 晶体的特征
问题一 体心立方晶胞中含有几个原子？ 原子引基矢。 问题二 体心立方原胞如何选取？ 问题三 问题四
8 1 2 个原子 以体心原子为顶 8 点，分别向三个顶角
1 3 a1 a 2 a 3 a 原胞的基矢形式？ 2
a1
k
a a 1 ( i j k ) 原胞体积？ 2 a a 2 (i j k ) 2 a a 3 (i j k ) 2
1.3.3 三维情况
布喇菲格子：最小重复单元（原胞）只含有一个原子的晶格 复式格子：原胞中含有两个或两个以上原子的晶格
（1）三维布喇菲晶格原胞：是三边长等于各方向基矢， 结点为顶点的平行六面体。基矢（a1,a2 ,a3 ）
a3 a2 a1
PPT课件
20
晶格周期性：设r为重复单元中任意一处的位矢
简立方(SC)
体心立方(BCC) 面心立方(FCC)
PPT课件
22
简立方（Simple Cubic，简称 SC ）
三个基矢等长并且互相垂直。
a3
a a2
原胞与晶胞相同。
a1
a 1 ai a 2 aj a 3 ak
PPT课件
23
体心立方(Body Centered Cubic, 1 BCC)
《固体物理基础教学课件》第3章
原子n离开平衡位置位移μn 原子n和原子n+1间相对位移
n1 n
平衡位置 非平衡位置
a 3
3-1 原子作用力的处理：简谐近似
忽略高阶项，简谐近似考虑原子 V 振动，相邻原子间相互作用势能
v(a)12(ddr2v2)a2
相邻原子间作用力
O
a
r
f ddv, (d dr2v2)a
只考虑相邻原子的作用，第n个原
第2n+1个M原子的方程 M d2 dt2 2n1(22n12n22n)
ቤተ መጻሕፍቲ ባይዱ 第2n个m原子的方程 mdd 2t22n(22n2n12n1)
解也具有平面波 的形式
两种原子振动的 振幅（m取A， M取B）一般来说 是不同的
a 13
3-2 声学波与光学波
色散关系有不同的两种
2(m m M M ) 11(m 4 m M M )2sin2aq12
a 2
3-1 一维单原子链模型
一维单原子链：最简单的晶格模型
晶格具有周期性，晶格的振动具有波的形式 —— 格波
格波的研究方法：
计算原子之间的相互作用力 根据牛顿定律写出原子运动方程，并求解方程
一维单原子链模型：
平衡时相邻原子间距为a （即原胞体积为a）
原子质量为m 原子限制在沿链方向运动
声子
0.1
1 100 10000
a 11
3-2 一维双原子链模型
一维双原子链模型 声学波与光学波 声学波与光学波的长波极限 长光学波的特性
a 12
3-2 一维双原子链模型
两种原子m和M (M > m) 构成一维复式格子 M原子位于2n-1, 2n+1, 2n+3 … m原子位于2n, 2n+2, 2n+4… 晶格常数、同种原子间的距离：2a
n1 n
平衡位置 非平衡位置
a 3
3-1 原子作用力的处理：简谐近似
忽略高阶项，简谐近似考虑原子 V 振动，相邻原子间相互作用势能
v(a)12(ddr2v2)a2
相邻原子间作用力
O
a
r
f ddv, (d dr2v2)a
只考虑相邻原子的作用，第n个原
第2n+1个M原子的方程 M d2 dt2 2n1(22n12n22n)
ቤተ መጻሕፍቲ ባይዱ 第2n个m原子的方程 mdd 2t22n(22n2n12n1)
解也具有平面波 的形式
两种原子振动的 振幅（m取A， M取B）一般来说 是不同的
a 13
3-2 声学波与光学波
色散关系有不同的两种
2(m m M M ) 11(m 4 m M M )2sin2aq12
a 2
3-1 一维单原子链模型
一维单原子链：最简单的晶格模型
晶格具有周期性，晶格的振动具有波的形式 —— 格波
格波的研究方法：
计算原子之间的相互作用力 根据牛顿定律写出原子运动方程，并求解方程
一维单原子链模型：
平衡时相邻原子间距为a （即原胞体积为a）
原子质量为m 原子限制在沿链方向运动
声子
0.1
1 100 10000
a 11
3-2 一维双原子链模型
一维双原子链模型 声学波与光学波 声学波与光学波的长波极限 长光学波的特性
a 12
3-2 一维双原子链模型
两种原子m和M (M > m) 构成一维复式格子 M原子位于2n-1, 2n+1, 2n+3 … m原子位于2n, 2n+2, 2n+4… 晶格常数、同种原子间的距离：2a
固体物理基础第3章 晶格振动理论
14
第3章 晶格振动理论
基于如下的物理考虑：首先，晶体的宏观热性质取决于 组成晶体的绝大多数原子的运动状态；其次，晶体边界(表 面)原子的数目远小于晶体内部原子数目，因此对晶体热性 质的影响很小；第三，按照近邻作用近似，边界原子对内部 原子运动状态的影响很小。于是，玻恩-卡曼提出了这样的 周期性边界条件：假定由数目巨大的N个原子组成的一维单 原子链首尾衔接(间距也为a)，构成一个如图3.3所示的半径 很大的圆环，局部范围内原子沿环方向的振动仍然可以看做
2
第3章 晶格振动理论 μn+2，…表示，第n个原子的实际位移为Xn=na+μn，如图 3.1(b)所示。尽管晶格中任一原子都会受到其他(n-1)个原子 的作用，但是这种作用会随着原子间距的增加而快速减小， 这是比较容易理解的，因此，为了使问题进一步简化，可以 进行近邻作用近似，即假定晶格中任一原子只受到其最近邻 原子的作用。这样的话，由于晶格中相邻原子间的相互作用 (化学键)都相同，就可以把一维单原子链想象成N个原子由 完全相同的弹簧连接的情况，如图3.1(c)所示，于是对于第n 个原子，只受到前后两个原子的作用fn-1，fn+1，它们与原子 的相对位移成正比，并且具有相同的弹性系数(或者叫回复 力系数)β。
把这些连续量带入方程(3.1)整理后即可得到：
m 2 ( t2 x ,t) 2 x (x 2 ,t)a 2 2 ( t2 x ,t)0 2 2 x (x 2 ,t)
(3.3)
7
第3章 晶格振动理论
这是数理方程中的波动方程，其中
2 0
程的特解为
a2 m
为波速度，该方
(x,t)Aei(tqx)
这是由2N个方程组成的联立方程组。同样，该方程组 应该具有下列形式的格波解，只是由于P原子和Q原子质量 的不同，其格波解的振幅不同：
第3章 晶格振动理论
基于如下的物理考虑：首先，晶体的宏观热性质取决于 组成晶体的绝大多数原子的运动状态；其次，晶体边界(表 面)原子的数目远小于晶体内部原子数目，因此对晶体热性 质的影响很小；第三，按照近邻作用近似，边界原子对内部 原子运动状态的影响很小。于是，玻恩-卡曼提出了这样的 周期性边界条件：假定由数目巨大的N个原子组成的一维单 原子链首尾衔接(间距也为a)，构成一个如图3.3所示的半径 很大的圆环，局部范围内原子沿环方向的振动仍然可以看做
2
第3章 晶格振动理论 μn+2，…表示，第n个原子的实际位移为Xn=na+μn，如图 3.1(b)所示。尽管晶格中任一原子都会受到其他(n-1)个原子 的作用，但是这种作用会随着原子间距的增加而快速减小， 这是比较容易理解的，因此，为了使问题进一步简化，可以 进行近邻作用近似，即假定晶格中任一原子只受到其最近邻 原子的作用。这样的话，由于晶格中相邻原子间的相互作用 (化学键)都相同，就可以把一维单原子链想象成N个原子由 完全相同的弹簧连接的情况，如图3.1(c)所示，于是对于第n 个原子，只受到前后两个原子的作用fn-1，fn+1，它们与原子 的相对位移成正比，并且具有相同的弹性系数(或者叫回复 力系数)β。
把这些连续量带入方程(3.1)整理后即可得到：
m 2 ( t2 x ,t) 2 x (x 2 ,t)a 2 2 ( t2 x ,t)0 2 2 x (x 2 ,t)
(3.3)
7
第3章 晶格振动理论
这是数理方程中的波动方程，其中
2 0
程的特解为
a2 m
为波速度，该方
(x,t)Aei(tqx)
这是由2N个方程组成的联立方程组。同样，该方程组 应该具有下列形式的格波解，只是由于P原子和Q原子质量 的不同，其格波解的振幅不同：
固体物理基础学：第3章 晶格振动与晶体的热学性质
晶格振动在晶体中形成了各种模式的波（格波），这些模式 是相互独立的，各模式的波所取的能量是分立的 简谐近似下，通过一些数学手段处理，可以用一系列独立的 简谐振子来描述这些相互独立、能量分立的振动模式 这些谐振子的能量量子，成为声子 晶格振动的总体可看做是声子的系宗
3-0 本章导读
热容量 热运动在宏观性 质的表现
v f （ n1 - n） （ n - n 1） n
平衡位置
牛顿第二定律 F=ma
力与两个原 子的位移有关
d 2 n （ n1 - n） （ n - n 1） m dt 2
(1)
非平衡位置
这即是第n个原子的运动方程！
3-2 一维单原子链模型
dv f d
d 2v 其中 ( 2 )a dr
3-1 一维单原子链模型
现考虑第n-1和第n+1个原子对第n个原子的双重作用 同样，写出简谐近似后的相互作用势v，如下：
v
1 2 2 （ ） （ ） n n 1 n 1 n 2
对位移求偏导，得到力：
杜隆－珀替经验规律： 一摩尔固体有N个原子，有3N个振动自由度，按能量均分 定律，每个自由度平均热能为kT，摩尔热容量 3Nk＝3R
—— 实验表明在较低温度下，热容量随着温度的降低而下降 爱因斯坦模型与德拜模型
研究晶格振动的意义远不限于热学性质。晶格振动是 研究固体 宏观性质和微观过程的重要基础。对晶体的热学性质、电学性 质、光学性质、超导电性、磁性、结构相变有密切关系。
其中任意一个简正坐标方程解
Qi Asin(it )
可化为 i
—— ωi是振动的圆频率，当只考察某一个 的振动时：
方程
3-2-讲稿-第三章-固体物理2004.11.28ppt-...
B m ( ) A M
离子晶体中光学波的共振能 够引起对红外光在 附近 的强烈吸收，这是红外光谱学的点， 格波支被称 为光学波。 作业：P580 3.2
GaN红外光谱
AlN薄膜的红外光谱
第三章 补充作业
1：将P93（3-55）式代入（3-53）式中求出A和B。 2：为什么将W+和W-说成是光学波和声学波 。 3：双原子链中长声子波的两种原子运动为什么是完全一致 （即振幅和相位没差别）？ 4：为什么说长光学中mM两格子上的原子在作相对振动并振动 保持质心不变？ 5：为什么是杜隆—珀替定律？ 6：什么是爱因斯坦量子假设？ 7：爱因斯坦假设下的热 量公式是什么？与实验比较会怎样？ 它的缺陷在何处？ 9：什么是德拜模型？德拜模型的得出的热 量形式如何？他 与实验符合的情况如何？ 10、简述晶格状态方程的推导过程。
| q |
2
=1
具有 平方和 的形式
首先看势能的计算： 因为势能：
不计高阶项和V(a)＝0，得到： 其中：
同一种原子具有相同的位相。
由（3-62）: 式表明：q 0 时，两种原子振动具有完全相反 的位相。如P97图3-7所示。 长光学波的极限实际上是P、Q两个格子的 相对振动，保持质心不变。
离子晶体中光学波的共振能 够引起对红外光在 附近 的强烈吸收，这是红外光谱学的点， 格波支被称 为光学波。 作业：P580 3.2
GaN红外光谱
AlN薄膜的红外光谱
第三章 补充作业
1：将P93（3-55）式代入（3-53）式中求出A和B。 2：为什么将W+和W-说成是光学波和声学波 。 3：双原子链中长声子波的两种原子运动为什么是完全一致 （即振幅和相位没差别）？ 4：为什么说长光学中mM两格子上的原子在作相对振动并振动 保持质心不变？ 5：为什么是杜隆—珀替定律？ 6：什么是爱因斯坦量子假设？ 7：爱因斯坦假设下的热 量公式是什么？与实验比较会怎样？ 它的缺陷在何处？ 9：什么是德拜模型？德拜模型的得出的热 量形式如何？他 与实验符合的情况如何？ 10、简述晶格状态方程的推导过程。
| q |
2
=1
具有 平方和 的形式
首先看势能的计算： 因为势能：
不计高阶项和V(a)＝0，得到： 其中：
同一种原子具有相同的位相。
由（3-62）: 式表明：q 0 时，两种原子振动具有完全相反 的位相。如P97图3-7所示。 长光学波的极限实际上是P、Q两个格子的 相对振动，保持质心不变。
固体物理(第3章)讲解
2
—— 每一个原子运动方程类似 —— 方程的数目和原子数相同
§ 3-2简谐近似和简正坐标 一维单原子链 —— —— 晶格振动与晶体的热学性质 § 3-1 晶格振动与晶体的热学性质
方程解和振动频率 设方程组的解 naq — 第n个原子振动相位因子
得到 应用三角公式
4 2 aq sin ( ) m 2
—— 常数
—— 平衡条件
§ 3-2简谐近似和简正坐标 一维单原子链 —— —— 晶格振动与晶体的热学性质 § 3-1 晶格振动与晶体的热学性质
dv 1 d v v (a ) v (a ) ( )a ( 2 )a 2 High items dr 2 dr
简谐近似 —— 振动很微弱，势能展式中只保留到二阶项
2 1 2 2 任意一个简正坐标 [ 2 i Qi ] (Qi ) i (Qi ) 2 2 Qi
1 能量本征值 i ( ni ) i 2
本征态函数
—— 谐振子方程
n (Qi )
i
i
exp(
2
2
) H ni ( )
— 厄密多项式
§3-1 简谐近似和简正坐标 ——
格波 波矢的取值和布里渊区 相邻原子相位差 格波1的波矢
—— 原子的振动状态相同
相邻原子相位差
§ 3-2简谐近似和简正坐标 一维单原子链 —— —— 晶格振动与晶体的热学性质 § 3-1 晶格振动与晶体的热学性质
格波 格波2的波矢
aq1 / 2
相邻原子的位相差
—— 两种波矢q1和q2的格波中，原子的振动完全相同
原子位移宗量
N个原子的位移矢量 —— 体系的势能函数在平衡位置按泰勒级数展开
—— 每一个原子运动方程类似 —— 方程的数目和原子数相同
§ 3-2简谐近似和简正坐标 一维单原子链 —— —— 晶格振动与晶体的热学性质 § 3-1 晶格振动与晶体的热学性质
方程解和振动频率 设方程组的解 naq — 第n个原子振动相位因子
得到 应用三角公式
4 2 aq sin ( ) m 2
—— 常数
—— 平衡条件
§ 3-2简谐近似和简正坐标 一维单原子链 —— —— 晶格振动与晶体的热学性质 § 3-1 晶格振动与晶体的热学性质
dv 1 d v v (a ) v (a ) ( )a ( 2 )a 2 High items dr 2 dr
简谐近似 —— 振动很微弱，势能展式中只保留到二阶项
2 1 2 2 任意一个简正坐标 [ 2 i Qi ] (Qi ) i (Qi ) 2 2 Qi
1 能量本征值 i ( ni ) i 2
本征态函数
—— 谐振子方程
n (Qi )
i
i
exp(
2
2
) H ni ( )
— 厄密多项式
§3-1 简谐近似和简正坐标 ——
格波 波矢的取值和布里渊区 相邻原子相位差 格波1的波矢
—— 原子的振动状态相同
相邻原子相位差
§ 3-2简谐近似和简正坐标 一维单原子链 —— —— 晶格振动与晶体的热学性质 § 3-1 晶格振动与晶体的热学性质
格波 格波2的波矢
aq1 / 2
相邻原子的位相差
—— 两种波矢q1和q2的格波中，原子的振动完全相同
原子位移宗量
N个原子的位移矢量 —— 体系的势能函数在平衡位置按泰勒级数展开
精品课件-固体物理基础教程(贾护军)-第3章
2
第3章 晶格振动理论 μn+2，…表示，第n个原子的实际位移为Xn=na+μn，如图 3.1(b)所示。尽管晶格中任一原子都会受到其他(n-1)个原子 的作用，但是这种作用会随着原子间距的增加而快速减小，这 是比较容易理解的，因此，为了使问题进一步简化，可以进行 近邻作用近似，即假定晶格中任一原子只受到其最近邻原子的 作用。这样的话，由于晶格中相邻原子间的相互作用(化学键) 都相同，就可以把一维单原子链想象成N个原子由完全相同的 弹簧连接的情况，如图3.1(c)所示，于是对于第n个原子，只 受到前后两个原子的作用fn-1，fn+1，它们与原子的相对位移 成正比，并且具有相同的弹性系数(或者叫回复力系数)β。
3
第3章 晶格振动理论
图3.1Байду номын сангаас一维单原子链模型
4
第3章 晶格振动理论
经过上面的分析，就可以根据牛顿第二定律直接建立第n 个原子的运动状态方程，即
m
d2n
dt 2
fn1
fn1
(n1 n ) (n1 n )
(3.1)
(n1 n1 2n )
每一个原子对应一个这样的方程，因此式(3.1)实际上代
(3.4)
这是一个简谐波，其中A为振幅， q= 2π为波数，ω为角频率。
根据这种长波近似的极限情形，就可 以设想，当长波近似
的条件λ>>a不成立时，方程(3.1)的解仍应具有类似的形式，
即只需在式(3.4)的简谐波的解中用na替代x即可，也就是式
(3.2)
8
第3章 晶格振动理论
3.1.3 色散关系 为了进一步研究一维单原子链振动的特点，可以将式
(3.2)所示的格波形式的解代入振动方程(3.1)，得：
第3章 晶格振动理论 μn+2，…表示，第n个原子的实际位移为Xn=na+μn，如图 3.1(b)所示。尽管晶格中任一原子都会受到其他(n-1)个原子 的作用，但是这种作用会随着原子间距的增加而快速减小，这 是比较容易理解的，因此，为了使问题进一步简化，可以进行 近邻作用近似，即假定晶格中任一原子只受到其最近邻原子的 作用。这样的话，由于晶格中相邻原子间的相互作用(化学键) 都相同，就可以把一维单原子链想象成N个原子由完全相同的 弹簧连接的情况，如图3.1(c)所示，于是对于第n个原子，只 受到前后两个原子的作用fn-1，fn+1，它们与原子的相对位移 成正比，并且具有相同的弹性系数(或者叫回复力系数)β。
3
第3章 晶格振动理论
图3.1Байду номын сангаас一维单原子链模型
4
第3章 晶格振动理论
经过上面的分析，就可以根据牛顿第二定律直接建立第n 个原子的运动状态方程，即
m
d2n
dt 2
fn1
fn1
(n1 n ) (n1 n )
(3.1)
(n1 n1 2n )
每一个原子对应一个这样的方程，因此式(3.1)实际上代
(3.4)
这是一个简谐波，其中A为振幅， q= 2π为波数，ω为角频率。
根据这种长波近似的极限情形，就可 以设想，当长波近似
的条件λ>>a不成立时，方程(3.1)的解仍应具有类似的形式，
即只需在式(3.4)的简谐波的解中用na替代x即可，也就是式
(3.2)
8
第3章 晶格振动理论
3.1.3 色散关系 为了进一步研究一维单原子链振动的特点，可以将式
(3.2)所示的格波形式的解代入振动方程(3.1)，得：
固体物理课件3.1
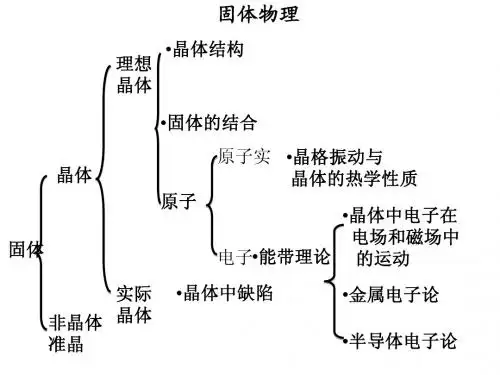
引言在第一章介绍晶体的微观结构中在第一章介绍晶体的微观结构中，，为了便于显示出晶体微观结构的内禀特征显示出晶体微观结构的内禀特征，，将组成晶体的各原子集团各用一个位置固定的几何点来代替构成Ｂravais 格子或将组成晶体的各个原子各用一个位置固定的小球来代替构成晶格个位置固定的小球来代替构成晶格，，这里显然忽略了原子的运动略了原子的运动。
实际上实际上，，大量的实验现象表明，组成晶体的原子并不是静止在晶格格点上固定不动的定不动的，，各原子是在围绕其晶格格点这一平衡位置永不停息地振动着位置永不停息地振动着。
第三章晶格振动与晶体热学性质晶格振动的研究——晶体的热学性质固体热容量——热运动是晶体宏观性质的表现晶格振动——研究固体宏观性质和微观过程的重要基础晶格振动——晶体的热学性质晶体的热学性质、、电学性质电学性质、、光学性质光学性质、、超导电性导电性、、磁性磁性、、结构相变有密切关系原子的振动——晶格振动在晶体中形成了各种模式的波——简谐近似下简谐近似下，，系统哈密顿量是相互独立简谐振动哈密顿量之和——这些谐振子的能量量子这些谐振子的能量量子，，称为声子——晶格振动的总体可看作是声子的系综——用一系列独立的简谐振子来描述这些独立而又分立的振动模式——这些模式是相互独立的这些模式是相互独立的，，模式所取的能量值是分立的§3.1 一维晶格的振动由于晶体中原子数目巨大由于晶体中原子数目巨大，，原子与原子之间存在相互关系原子与原子之间存在相互关系，，任一原子的位移至少与相邻原子任一原子的位移至少与相邻原子、、次近邻原子的位移有关次近邻原子的位移有关，，所以严格求解晶格振动是极其困难的所以严格求解晶格振动是极其困难的。
为了探讨晶格振动的基本特征基本特征，，需要采用一些近似的方法需要采用一些近似的方法。
晶格具有周期性晶格具有周期性，，晶格的振动具有波的形式——格波格波的研究——先计算原子之间的相互作用力——根据牛顿定律写出原子运动方程根据牛顿定律写出原子运动方程，，最后求解方程一维晶格——每个相同原子的质量m ，平衡时原子间距a 个原子和第n ＋1个原子间的相对位移nx ＋1个原子间的距离1n na x x ++−nn n x x a x −++−111、一维简单格子——原子之间的作用力du f dx =−平衡位置时平衡位置时，，两个原子间的互作用势能()u a ()u a δ+发生相对位移后，相互作用势能1n n x x δ+=−2221()()()()2a a du d u u a u a High itemsdr drδδδ+=+++常数——平衡条件nn n x x a x −++−112221()()()2a d u u a u a High itemsdrδδ+=++简谐近似——振动很微弱振动很微弱，，势能展式中只保留到二阶项βδ——恢复力系数nn n x x a x −++−11原子的运动方程——只考虑相邻原子的作用只考虑相邻原子的作用，，第n 个原子受到的作用力1111()()(2)n n n n n n n x x x x x x x βββ+−+−−−−=+−第n 个原子的运动方程1,2,3,)N ⋯每一个原子运动方程类似方程的数目和原子数相同nn n x x a x −++−11最近邻近似方程解和振动频率2112(2)nn n n d x m x x x dtβ+−=+−设方程组的解()i qna t n x Aeω−=qna —第n 个原子振动相位因子1)]1)]1aq t aq t n x Aeωω−−+−+=)2(2−+=−−iaqiaqeem βω得到224sin ()2aq m βω=应用三角公式)2sin(2aq m βω=)2sin(2aqm βω=1）波矢q 增加倒格矢的整数倍的整数倍，，频率不变不变，，即格波的频率在波矢空间内是以倒格矢为波矢的取值范围波矢的取值范围：：aa2a π2a πωω换成-q ，频率不变不变，，即格波的频率在波矢空间内具有反演对称性在波矢空间内具有反演对称性。
固体物理课件ppt完全版
角引8条对角线，在其中互不相邻的 4条对角线的中点，各加一个原子 — 得到金刚石晶格结构！
B A
特点：每个原子有4个最近邻，它们
正好在正四面体的顶角位置！
τ
金刚石晶格结 构的典型单元
三、 晶胞(单胞)
晶胞：为反映晶格的对称性，在结晶学中选择较大 的周期单元 → 称为晶体学原胞
晶胞的基矢：沿晶胞的三个棱所作的三个矢量，常
A
a
c
A层
B
六角密排晶格结构的典型单元
B层
A层内原子的上、下各3个最 近邻原子所分别形成的正三 角形的空间取向，不同于B 面内原子的上、下各3个最 近邻原子所分别形成的正三 角形的空间取向！
五、金刚石晶体结构
1· 特点：每个原子有4 个最近邻，它们正 好在一个正四面体的顶角位置 2· 堆积方式：立方单元体内对角线上的原子 — A 面心立方位置上的原子 — B 金刚石晶格 A、B 两个面心 立方晶格套成 相对位移 = 对角线的1/4
33
3
4
6· 判断此原胞为fcc格子的最小周期性单元 3 a 原胞 a1 a2 a3 ∵ fcc 格子的一个立方单元体积中含的原子数： 4 4 a 1 又∵ 原胞 fcc 4 a a ∴原胞中只包含一个原子 → 因而为最小周期性单元 注： fcc 晶格方式是一种最紧密的排列方式 — 立方密排晶格！
3· 原胞： a , a 在密排面内，互成1200角，a 沿垂直
1 2
3
密排面的方向构成的菱形柱体 → 原胞
B A
六角密排晶格的堆积方式 a A
a3
B
c
a1
a2
六角密排晶格结构的原胞
六角密排晶格结构的典型单元
B A
特点：每个原子有4个最近邻，它们
正好在正四面体的顶角位置！
τ
金刚石晶格结 构的典型单元
三、 晶胞(单胞)
晶胞：为反映晶格的对称性，在结晶学中选择较大 的周期单元 → 称为晶体学原胞
晶胞的基矢：沿晶胞的三个棱所作的三个矢量，常
A
a
c
A层
B
六角密排晶格结构的典型单元
B层
A层内原子的上、下各3个最 近邻原子所分别形成的正三 角形的空间取向，不同于B 面内原子的上、下各3个最 近邻原子所分别形成的正三 角形的空间取向！
五、金刚石晶体结构
1· 特点：每个原子有4 个最近邻，它们正 好在一个正四面体的顶角位置 2· 堆积方式：立方单元体内对角线上的原子 — A 面心立方位置上的原子 — B 金刚石晶格 A、B 两个面心 立方晶格套成 相对位移 = 对角线的1/4
33
3
4
6· 判断此原胞为fcc格子的最小周期性单元 3 a 原胞 a1 a2 a3 ∵ fcc 格子的一个立方单元体积中含的原子数： 4 4 a 1 又∵ 原胞 fcc 4 a a ∴原胞中只包含一个原子 → 因而为最小周期性单元 注： fcc 晶格方式是一种最紧密的排列方式 — 立方密排晶格！
3· 原胞： a , a 在密排面内，互成1200角，a 沿垂直
1 2
3
密排面的方向构成的菱形柱体 → 原胞
B A
六角密排晶格的堆积方式 a A
a3
B
c
a1
a2
六角密排晶格结构的原胞
六角密排晶格结构的典型单元
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
3-1 边界条件
一维单原子晶格看作无限长，所有原子是等价的，每个原 子的振动形式都一样
实际的晶体为有限，形成的链不是无穷长，链两头的原子 不能用中间原子的运动方程来描述
但如果用与其它原子不同的运动方程描述两端的少数原子， 则会导致相互联立的方程求解更加复杂
采用玻恩－卡曼周期性边界条件避免这种情况 含义：原子链首尾的振动情况必须复原 玻恩－卡曼周期性
才能在一维单原子链晶体中传播，其它频率的格波将被强 烈衰减
3-1 格波取值的长波极限
长波极限情况 (q 0, a)
sin( aq ) aq , a q
22
m
一维单原子格波相当于波速为 a / m 的连续介质波
相邻两个原子之间的位相差 趋于0，晶体内所有原子振动 情况相同
3-1 声子
2
(m M mM
)
1
1
4mM (m M
)2
sin2
1 aq
2
2
(m M mM
)
1
1
4mM (m M
)2
sin2
1
aq
2
即一维复式晶格中存在两种 独立的格波：
声学波（频率较低）
光学波（频率较高）
命名主要根据两种格波在长 波极限 ( q→0 ) 的性质
3-2 声学波的长波极限
ω和q满足以下的色散关系
2 4 sin2 ( aq)
m
2
连续介质中的波（如声波）可表示为
i
Ae
(t
2
x
)，则可看出
格波和连续介质波具有完全类似的形式
一个格波表示的是所有原子同时做频率为ω的振动
aq取值任意加减2π的整数倍对所有原子的振动没有影响，所
以可将波数q取值限制为
a
q
a
3-1 简约布里渊区
原子n离开平衡位置位移μn 原子n和原子n+1间相对位移
n1 n
非平衡位置
3-1 原子作用力的处理：简谐近似
忽略高阶项，简谐近似考虑原子 V
振动，相邻原子间相互作用势能
v(a
)
1 2
(
d2 dr
v
2
)a
2
相邻原子间作用力
O
a
r
f
dv
d
,
d 2v ( dr2 )a
只考虑相邻原子的作用，第n个原
长声学波的频率太低，无法 与电磁波作用
c c0q
长光学波可与远红外光作用
离子晶体中光学波的共振能引 起对远红外光的强烈吸收，可 应用于红外光谱学
频率
q 0,
2 sin(aq) a
mM
2 q
mM
两种原子振幅比值
B A
1
两种原子的振幅和位
相趋于一致，运动方
式没有差别
长声学波代表原胞质 心（原胞整体）振动
3-2 光学波的长波极限
频率
q 0,
2
mM mM
两种原子振幅比值
B A
m M
同种原子振动位相一致，
子受到的作用力
(n1 n ) (n n1) (n1 n1 2n )
平衡位置
第n个原子的运动方程
m
d 2n
dt 2
(n1 n1 2n )
非平衡位置
3-1 格波的物理意义
上式的解（原子振动位移）具有平面波的形式
n Aei(tnaq)
naq是第n个原子的振动位相因子 A是原子振动振幅，为常数 ω是格波的角频率，为常数；q是格波的波数
边界条件限制波数 在简约布里渊区内 取均匀分布的N个 分立值
3-1 格波的色散关系
2 4 sin2 ( aq)
(q)
m
2
ω取正值，则有
2 sin(aq)
m2 频率是波数的偶函数
色散关系曲线具有周期性，
q
- - 2 0 2
aa
aa
仅取简约布里渊区的结果即可
由正弦函数的性质可知，只有满足 0 2 / m 的格波
aq取值任意加减2π的整数倍对 所有原子的振动没有影响
红线：q=π/2a
绿线：q=5π/2a
将波数q取值限制为 q
a
a
即波数q取值在简约布里渊区
（第一布里渊区）中
第一章内容： 简约布里渊区内的全部波矢代 表了晶体中所有的状态，区外 的波矢都可通过平移倒格矢在 该区内找到等价状态点；讨论 固体性质时，可以只考虑第一 布里渊区。
晶格常数、同种原子间的距离：2a
第2n+1个M原子的方程
M
d 22n1
dt 2
(22n1 2n2
2n )
第2n个m原子的方程
m
d 22n
dt 2
(22n 2n1 2n1)
解也具有平面波
的形式
两种原子振动的 振幅（m取A， M取B）一般来说 是不同的
3-2 声学波与光学波
色散关系有不同的两种
第3章 晶格振动与晶体的热学性质
3-1 一维单原子链模型 3-2 一维双原子链模型 3-3 确定晶格振动谱的实验方法 3-4 晶体热容的量子理论 3-5 非谐作用产生的晶体热学性质
掌握 了解
3-1 一维单原子链模型
一维单原子链模型 格波及其色散关系 简约布里渊区 长波极限下的格波 声子
相邻原子振动相反
长光学波代表原胞质心 保持不变的振动，原胞 中不同原子做相对运动
3-2 长光学波的特性
长声学波的频率正比于波数，相当于把一维原子链看做连 续介质时的弹性波，类似于声波
长光学波代表晶格的高频振动，实际晶体中在1013~1014Hz， 对应于远红外光波
电磁波只与波数相同的格波 发生相互作用
晶格振动 可通过引入简正坐标进行量子化处理，其结论可 用“声子”描述
振动能量的本征值为
n
声子含义：晶格振动（格波）的能量量子
声子是一种元激发，可与电子或光子发生作用 声子具有能量、动量，看作是“准粒子”
晶格振动的问题转化为声子系统问题的研究
20赫兹---20000赫兹，高于20000赫兹的叫超声波
能量(eV) 0.01
声子
0.1
1 100 10000
3-2 一维双原子链模型
一维双原子链模型 声学波与光学波 声学波与光学波的长波极限 长光学波的特性
3-2 一维双原子链模型
两种原子m和M (M > m) 构成一维复式格子
M原子位于2n-1, 2n+1, 2n+3 … m原子位于2n, 2n+2, 2n+4…
3-1 一维单原子链模型
一维单原子链：最简单的晶格模型
晶格具有周期性，晶格的振动具有波的形式 —— 格波
格波的研究方法：
计算原子之间的相互作用力
根据牛顿定律写出原子运动方程，并求解方程
一维单原子链模型：
平衡时相邻原子间距为a （即原胞体积为a）
平衡位置
原子质量为m
原子限制在沿链方向运动