正多面体与平面的展开图

展开图如下所示：若以正二十面体的中心为原点，各顶点的坐标分别为Φ,0,±1)}，在此Φ = (1+正十二面体是正二十面体的对偶多面体。

建立模型的基本过程如下：void CTestView::ReadPoint()//点表{double a=180;//长方形的宽double b=a*(1+sqrt(5))/2;//黄金分割的矩形的长double half=0.5;//第一个长方形的各个顶点P[0].x=half*a;P[0].y=0;P[0].z=half*b;P[1].x=-half*a;P[1].y=0;P[1].z=half*b;P[2].x=half*a;P[2].y=0;P[2].z=-1/2.0*b;P[3].x=-1/2.0*a;P[3].y=0;P[3].z=-half*b;//第二个长方形的各个顶点P[4].x=half*b;P[4].y=-half*a;P[4].z=0;P[5].x=half*b;P[5].y=half*a;P[5].z=0;P[6].x=-half*b;P[6].y=half*a;P[6].z=0;P[7].x=-half*b;P[7].y=-half*a;P[7].z=0;//第三个长方形的各个顶点P[8].x=0;P[8].y=-half*b;P[8].z=half*a;P[9].x=0;P[9].y=-half*b;P[9].z=-half*a;P[10].x=0;P[10].y=half*b;P[10].z=half*a;P[11].x=0;P[11].y=half*b;P[11].z=-half*a;}void CTestView::ReadFace()//面表{//面的边数、面的顶点编号F[0].SetEN(3) ;F[0].p[0]=0 ;F[0].p[1]=5 ;F[0].p[2]=10 ;F[1].SetEN(3) ;F[1].p[0]=5 ;F[1].p[1]=2 ;F[1].p[2]=11 ;F[2].SetEN(3) ;F[2].p[0]=11 ;F[2].p[1]=3 ;F[2].p[2]=6 ;F[3].SetEN(3) ;F[3].p[0]=6 ;F[3].p[1]=1 ;F[3].p[2]=10 ;F[4].SetEN(3) ;F[4].p[0]=7 ;F[4].p[1]=1 ;F[4].p[2]=6 ;F[5].SetEN(3) ;F[5].p[0]=1 ;F[5].p[1]=0 ;F[5].p[2]=10 ;F[6].SetEN(3) ;F[6].p[0]=8 ;F[6].p[1]=0 ;F[6].p[2]=1 ;F[7].SetEN(3) ;F[7].p[0]=0 ;F[7].p[1]=4 ;F[7].p[2]=5 ;F[8].SetEN(3) ;F[8].p[0]=4 ;F[8].p[1]=2 ;F[8].p[2]=5 ;F[9].SetEN(3) ;F[9].p[0]=2 ;F[9].p[1]=3;F[9].p[2]=11 ;F[10].SetEN(3);F[10].p[0]=2 ;F[10].p[1]=9;F[10].p[2]=3 ;F[11].SetEN(3);F[11].p[0]=3 ;F[11].p[1]=7 ;F[11].p[2]=6;F[12].SetEN(3);F[12].p[0]=4 ;F[12].p[1]=9;F[12].p[2]=2;F[13].SetEN(3);F[13].p[0]=9;F[13].p[1]=7 ;F[13].p[2]=3 ;F[14].SetEN(3);F[14].p[0]=7 ;F[14].p[1]=8;F[14].p[2]=1 ;F[15].SetEN(3);F[15].p[0]=8;F[15].p[1]=4 ;F[15].p[2]=0;F[16].SetEN(3);F[16].p[0]=10 ;F[16].p[1]=5 ;F[16].p[2]=11;F[17].SetEN(3);F[17].p[0]=6;F[17].p[1]=10;F[17].p[2]=11;F[18].SetEN(3);F[18].p[0]=4 ;F[18].p[1]=8;F[18].p[2]=9 ;F[19].SetEN(3);F[19].p[0]=8 ;F[19].p[1]=7 ;F[19].p[2]=9;}正十二面体正十二面体是五个柏拉图立体之一,共有二十个顶点、三十条边和十二个面,而每一个面皆是正五边形正十二面体是由12 个正五边形所组成的正多面体。

11中正方体展开图正方体的十一种平面展开图可记忆成下面口诀：一三二，一四一，一在同层可任意，两个三，日状连，三个二，成阶梯，相邻必有日，整体没有田。

相对的两个面之间总隔着一个面正方体：中间四个面，上下各一面（6种摆法-141）中间三个面，一二隔河见（3种摆法-132/231）中间二个面，楼梯天天见（1种摆法-222)中间没有面，三三连一线（1种摆法-33）例1 在图13中（每个小四边形皆为全等的正方形），可以是一个正方体表面展开图的是( ).例2图14是一个正方体包装盒的表面展开图，若在其中的三个正方形A、B、C内分别填上适当的数,使得这个表面展开图沿虚线折成正方体后,相对面上的两个数互为相反数,则填在A、B、C内的三个数依次是( ).A.0,-2,1B.0,1,-2C.1,0,-2D.-2,0,1例3图15所示的是一个正方体包装盒的表面展开图，各个面上标注的数字分别为1，2，3，4，5，6。

现将表面展开图复原为正方体包装盒，则标注数字1和3的两个面是互相平行的，请你写出另一组相互平行的面上所对应的数字：_______。

注：例1、例2、例3的答案分别为：C;A;2与5或4与6。

是不是有点多此一举？例4 一个无盖的正方体纸盒，将它展开成平面图形，可能情况总共有（）。

A．12种 B.11种 C.9种 D.8种千万注意，你可不要选B呦！选D才对。

我又在炫耀了，不过你能很快画出这8个平面展开图吗？下面是示意图，黑方块表示展开图，白方块表示空缺。

（一）□■□■■■□■□（二）■■■■■□□□（三）■■■■□■□□（四）■■■■□□■□（五）■■■■□□□■（六）□■□■■■□□■（七）□□■■■■□□■（八）■□□■■■□□■。

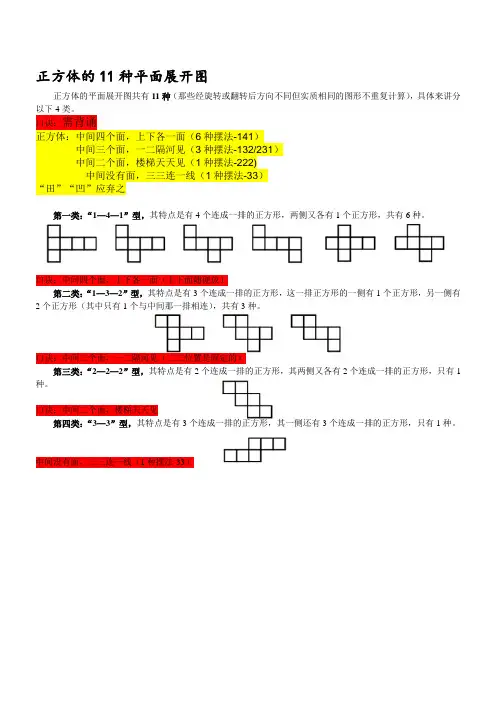
正方体的11种平面展开图
正方体的平面展开图共有11种（那些经旋转或翻转后方向不同但实质相同的图形不重复计算），具体来讲分以下4类。

口诀：需背诵
正方体：中间四个面，上下各一面（6种摆法-141）
中间三个面，一二隔河见（3种摆法-132/231）
中间二个面，楼梯天天见（1种摆法-222)
中间没有面，三三连一线（1种摆法-33）
“田”“凹”应弃之
第一类：“1—4—1”型，其特点是有4个连成一排的正方形，两侧又各有1个正方形，共有6种。

口诀：中间四个面，上下各一面（上下面随便放）
第二类：“1—3—2”型，其特点是有3个连成一排的正方形，这一排正方形的一侧有1个正方形，另一侧有2个正方形（其中只有1个与中间那一排相连），共有3种。

口诀：中间三个面，一二隔河见（二三位置是固定的）
第三类：“2—2—2”型，其特点是有2个连成一排的正方形，其两侧又各有2个连成一排的正方形，只有1种。

口诀：中间二个面，楼梯天天见
第四类：“3—3”型，其特点是有3个连成一排的正方形，其一侧还有3个连成一排的正方形，只有1种。

中间没有面，三三连一线（1种摆法-33）。