(完整版)中考专题一-折叠问题题型方法归纳,推荐文档

初中数学中的折叠问题折叠问题（对称问题）是近几年来中考出现频率较高的一类题型，学生往往由于对折叠的实质理解不够透彻，导致对这类中档问题失分严重。

本文试图通过对在初中数学中经常涉及到的几种折叠的典型问题的剖析，从中抽象出基本图形的基本规律，找到解决这类问题的常规方法。

其实对于折叠问题，我们要明白： 1、折叠问题（翻折变换）实质上就是轴对称变换．2、折叠是一种对称变换，它属于轴对称．对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．3、对于折叠较为复杂的问题可以实际操作图形的折叠，在画图时，画出折叠前后的图形，这样便于找到图形之间的数量关系和位置关系．4、在矩形（纸片）折叠问题中，重合部分一般会是一个以折痕为底边的等腰三角形5、利用折叠所得到的直角和相等的边或角，设要求的线段长为x ，然后根据轴对称的性质用含x 的代数式表示其他线段的长度，选择适当的直角三角形，运用勾股定理列出方程求解．一、矩形中的折叠1．将一张长方形纸片按如图的方式折叠，其中BC ，BD 为折痕，折叠后BG 和BH 在同一条直线上，∠CBD= 度．折叠前后的对应角相等2．如图所示，一张矩形纸片沿BC 折叠，顶点A 落在点A ′处，再过点A ′折叠使折痕DE ∥BC ，若AB=4，AC=3，则△ADE 的面积是 ．对称轴垂直平分对应点的连线3．如图，矩形纸片ABCD 中，AB=4，AD=3，折叠纸片使AD 边与对角线BD 重合，得折痕DG ，求AG 的长．根据对称的性质得到相等的对应边和对应角，再在直角三角形中根据勾股定理列方程求解即可GA'C D4．把矩形纸片ABCD 沿BE 折叠，使得BA 边与BC 重合，然后再沿着BF 折叠，使得折痕BE 也与BC 边重合，展开后如图所示，则∠DFB 等于（ ）注意折叠前后角的对应关系5．如图，沿矩形ABCD 的对角线BD 折叠，点C 落在点E 的位置，已知BC=8cm ，AB=6cm ，求折叠后重合部分的面积．重合部分是以折痕为底边的等腰三角形6．将一张矩形纸条ABCD 按如图所示折叠，若折叠角∠FEC=64°，则∠1= 度；△EFG 的形状 三角形．对折前后图形的位置变化，但形状、大小不变，注意一般情况下要画出对折前后的图形，便于寻找对折前后图形之间的关系，注意以折痕为底边的等腰△GEF8．如图，正方形纸片ABCD 的边长为8，将其沿EF 折叠，则图中①②③④四个三角形的周长之和为折叠前后对应边相等321FEDCBA54132G D‘FC‘DBCAE9．如图，将边长为4的正方形ABCD 沿着折痕EF 折叠，使点B 落在边AD 的中点G 处，求四边形BCFE 的面积注意折叠过程中的变与不变，图形的形状和大小不变，对应边与对应角相等10．如图，将一个边长为1的正方形纸片ABCD 折叠，使点B 落在边AD 上 不与A 、D 重合．MN 为折痕，折叠后B’C’与DN 交于P ．(1)连接BB’，那么BB’与MN 的长度相等吗？为什么？ (2)设BM=y ，AB’=x ，求y 与x 的函数关系式；(3)猜想当B 点落在什么位置上时，折叠起来的梯形MNC’B’面积最小？并验证你的猜想．PC'NB CADMB'QPH C'N BCADM B'二、纸片中的折叠11．如图，有一条直的宽纸带，按图折叠，则∠α的度数等于（）题考查的是平行线的性质，同位角相等，及对称的性质，折叠的角与其对应角相等，和平角为180度的性质，注意△EAB是以折痕AB为底的等腰三角形12．如图，将一宽为2cm的纸条，沿BC，使∠CAB=45°，则后重合部分的面积为在折叠问题中，一般要注意折叠前后图形之间的联系，将图形补充完整，对于矩形（纸片）折叠，折叠后会形成“平行线+角平分线”的基本结构，即重叠部分是一个以折痕为底边的等腰三角形ABC13．将宽2cm的长方形纸条成如图所示的形状，那么折痕PQ的长是注意掌握折叠前后图形的对应关系．在矩形（纸片）折叠问题中，会出现“平行线+角平分线”的基本结构图形，即有以折痕为底边的等腰三角形APQa2130°BEFACD14．如图a 是长方形纸带，∠DEF=20°，将纸带沿EF 折叠成图b ，再沿BF 折叠成图c ，则图c 中的∠CFE 的度数是（ ）本题考查图形的翻折变换，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变．由题意知∠DEF=∠EFB=20°图b ∠GFC=140°，图c 中的∠CFE=∠GFC -∠EFG15．将一张长为70 cm 的长方形纸片ABCD ，沿对称轴EF 折叠成如图的形状，若折叠后，AB 与CD 间的距离为60cm ，则原纸片的宽AB 是（ ）16．一根30cm 、宽3cm 的长方形纸条，将其按照图示的过程折叠（阴影部分表示纸条的反面），为了美观，希望折叠完成后纸条两端超出点P 的长度相等，则最初折叠时，求MA 的长图c 图b图aCDGFEAC GDFEAFDBCAEB BGE F D A EF D B C AB C60c m三、三角形中的折叠17．如图，把Rt△ABC（∠C=90°），使A，B两点重合，得到折痕ED，再沿BE折叠，C点恰好与D点重合，则CE：AE=（3）如图（3）把△CDE沿DE斜向上折叠，探求∠1、∠2、∠C的关系．（1）根据折叠前后的图象全等可知，∠1=180°-2∠CDE，∠2=180°-2∠CED，再根据三角形内角和定理比可求20．观察与发现：将三角形纸片ABC（AB＞AC）沿过点A的直线折叠，使得AC落在AB边上，折痕为AD，展开纸片（如图①）；在第一次折叠的基础上第二次折叠该三角形纸片，使点A和点D重合，折痕为EF，展平纸片后得到△AEF（如图②）．小明认为△AEF是等腰三角形，你同意吗？请说明理由．实践与运用：(1)将矩形纸片ABCD沿过点B的直线折叠，使点A落在BC边上的点F处，折痕为BE（如图③）；再沿过点E的直线折叠，使点D落在BE上的点D’处，折痕为EG（如图④）；再展平纸片（如图⑤）．求图⑤中∠α的大小．在第一次折叠中可得到∠EAD = ∠FAD在第二次折叠中可得到EF是AD的垂直平分线，则AD⊥EF∴∠AEF = ∠AFE∴△AEF是等腰三角形(1)由折叠可知∠AEB = ∠FEB，∠DEG = ∠BEG而∠BEG = 45°+ ∠α因为∠AEB + ∠BEG + ∠DEG = 180°所以 45°+ 2（45°+∠α）= 180°∠α = 22.5°由于角平分线所在的直线是角的对称轴，所以在三角形中的折叠通常都与角平分线有关。

精选全中考数学中的折叠问题文完整版（可编辑修改）近年来，在各地中考数学命题时，十分重视对图形语言、文字语音、符号语言的理解运用及相互之间的关系，相互之间的转化能力以及动手操作能力的考查。

这样，图形的折叠问题就成为一个亮点，有关翻折的考题日趋增加。

翻折问题的解决方法，抓住翻折后与翻折的图形是以折痕为轴的轴对称图形这一关键，并运用代数方程，一般均可求得。

下面我们以中考题为例，谈谈翻折问题的几例类型及解法，供大家参考。

一、以矩形为母体的翻折这种类型最多，以折痕的不同位置又可分下面几种：1、沿对角线翻折例1、(2000年山西省)已知：如图1，将矩形ABCD沿直线BD折叠，使点C 落在C’处，BC’交AD于E，AD=8，AB=4，求△BED的面积。

分析：因为BD是对称轴，∴∠CBD=∠C’BD，又AD∥BC，∴∠CBD=∠ADB，得：∠C’BD=∠ADB，∴ED=EB设ED=x，∴AD=8-x在Rt△ABE中，AB2+AE2=BE2，即42+(8-x)2=x2，∴x=5，∴ED=EB=5又BD=∴S△BED==10方法2：过E作EF⊥BD，垂足F，在得到BE=5，BD=4后，在Rt△BEF中，EF=，得S△BED=BD×EF=×4×=10方法3：∵Rt△BEF∽Rt△BDC’，∴EF：DC’=BF：BC’，得EF==(以下略)2、沿一直线翻折，使一顶点落在对边上例2、(2000年山东省)已知矩形ABCD的两边AB与BC的比为4：5，E是AB 上一点，沿CE将△EBC向上翻折，若B点恰好落在边AD上的F点，如图2，则tg∠DCF=______。

A、B、C、D、分析：因为CF=CB，∴CF：CD=5：4，得CD：DF=4：3，∴tg∠DCF==，应选(A)。

例3、(1998年台州市)如图3，矩形ABCD的长、宽分别为5和3，将顶点C 折过来，使它落在AB上的C’点(DE为折痕)，那么阴影部分的面积是______。

中考数学——六种类型折叠问题类型1 直角三角形的翻折或翻折后产生直角三角形的问题例1．如图，Rt△ABC中，AB＝9，BC＝6，∠B＝90°，将△ABC折叠，使点A与BC的中点D重合，折痕为MN，则线段BN的长为（）【分析】设BN＝x，则由折叠的性质可得DN＝AN＝9﹣x，根据中点的定义可得BD＝3，在Rt△BND中，根据勾股定理可得关于x的方程，解方程即可求解．【解答】设BN＝x，由折叠的性质可得DN＝AN＝9﹣x，∵D是BC的中点，∴BD＝3，在Rt△NBD中，x +3 ＝（9﹣x），解得x＝4．即BN＝4．故选：A．例1变式1．如图，在Rt△ABC中，直角边AC＝6，BC＝8，将△ABC按如图方式折叠，使点B与点A重合，折痕为DE，则CD的长为（）A．25/4 B．22/3 C．7/4 D．5/3【解析】由题意得DB＝AD；设CD＝x，则AD＝DB＝（8﹣x），∵∠C＝90°，∴AD ﹣CD ＝AC ,（8﹣x）﹣x ＝36，解得x＝7/4；即CD＝7/4．故选：C．例1变式2．如图，矩形ABCD中，AB＝4，AD＝6，点E为BC上一点，将△ABE沿AE折叠得到△AEF，点H为CD上一点，将△CEH沿EH折叠得到△EHG，且F落在线段EG上，当GF＝GH时，则BE的长为_____．【解析】由折叠可得∠AEH＝1/2∠BEC＝90°，进而得出Rt△AEH中，AE +EH2 ＝AH ，设BE＝x，则EF＝x，CE＝6﹣x＝EG，再根据勾股定理，即可得到方程x +4 +（6﹣x）+（6﹣2x）＝（2x﹣2）+6 ，解该一元二次方程，即可得到BE的长．BE的长为2．【点评】本题主要考查的是翻折的性质、矩形的性质、勾股定理以及解一元二次方程的综合运用，解决问题的关键是连接AH构造直角三角形AEH，这种折叠问题常设要求的线段长为x，然后根据折叠和轴对称的性质用含x的代数式表示其他线段的长度，选择适当的直角三角形，运用勾股定理列出方程求出答案．方法策略模式：在折叠后产生的直角三角形中，把某条边设成未知数根据勾股定理列方程求解。

专题01特殊平行四边形中的折叠问题全梳理目录【方法归纳】 (1)【考法一、三角形翻折问题】 (1)【考法二、四边形翻折问题】 (16)【课后练习】 (28)【方法归纳】1.折叠的基本性质：翻折前后对应的边与角相等；2.对于翻折都不确定的情况，注意分类讨论，避免漏掉解；3.方程思想：灵活设未知数，通过勾股定理建立方程，解出答案4.综合性：把折叠性质与四边形性质相结合，建立边角之间的关系。

【考法一、矩形翻折问题】例．如图，在矩形OABC 中8AB =，4BC =，点D 为对角线OB 中点，点E 在OC 所在的直线上运动，连结DE ，把ODE 沿DE 翻折，点O 的对应点为点F ，连结BF ．(1)当点F 在OC 下方时（如图1），求证：DE BF ∥．(2)当点F 落在矩形的对称轴上时，求EF 的长．(3)是否存在点E ，使得以D ，E ，F ，B 为顶点的四边形是平行四边形？若存在，求OE 的长；若不存在，请说明理由．当四边形△中，在Rt ABO222=+=OB AB AO8BC OC⊥∴∥，且D为OBDM BC中位线，DM∴为OCBOE EF BD DO ∴==，，25OE OD ∴==；如图，当四边形DEBF 为平行四边形时，DF OD BE ∴=，25BE ∴=，在Rt BEC △中，EC =826OE ∴=-=；DF OD BD DF == ，25BE OD ∴==，在Rt BCE 中，2CE BE =-在矩形ABCD 中，8AB =，6AD =，现将纸片折叠，点D 的对应点记为点P ，折痕为EF （点E 、F 是折痕与矩形的边的交点），再将纸片还原．【初步思考】（1）若点P落在矩形ABCD的边AB上（如图①）当点P与点A重合时，DEF∠=_____︒，当点E与点A重合时，DEF∠=______︒；【深入探究】（2）若点P落在矩形ABCD的内部（如图②），且点E、F分别在AD、DC边上，AP的最小值是______；【拓展延伸】（3）若点F与点C重合，点E在AD上，射线BA与射线FP交于点M（如图③）在各种不同的折叠位置中，是否存在某一情况，使得线段AM与线段DE的长度相等？若存在，请求出线段AE的长度；若不存在，请说明理由．【答案】（1）90；45（2）2（3）存在某一情况，使得线段AM与线段DE的长度相等，线段AE的长度为65或4211【分析】（1）当点P与点A重合时，画出图形可得结论；当点E与点A重合时，则EF平分DAB∠，即可得出答案；（2）当F与C重合，点P在对角线AC上时，AP有最小值，根据折叠的性质求8CD PC==，由勾股定理求10AC=，即可得出结果；（3）分两种情况根据全等三角形的判定和性质以及勾股定理解答即可．【详解】解：（1）四边形ABCD是矩形，90DAB D∴∠=∠=︒，当点P与点A重合时，EF是AD的中垂线，90DEF∴∠=︒，当点E与点A重合时，如图，则EF平分DAB∠，==，则AF=设DF PF x当A，P，F在一直线上时，当x最大为8时，AP最小值为四边形ABCD是矩形，A ADC B∴∠=∠=∠=90∠由折叠的性质得：EPM ，AM DE=∴=，AM EP四边形ABCD是矩形，∴∠=∠=∠=︒，DAM ADC B90∠=∠由折叠的性质得：EPC ADC ∴∠=∠=︒，GAM GPE90变式2．【问题情境】折纸操作简单，富有数学趣味，我们可以通过折纸开展数学探究，探索数学奥秘，下面是折纸过程．【动手操作】步骤1：对折矩形纸片ABCD ，使AD 与BC 重合，得到折痕EF ，展平纸片；步骤2：点M 为边AD 上任意一点（与点A ，D 不重合），ABM 沿BM 折叠得到A BM '△，折痕BM 交EF 于点N ．【问题探究】（1）如图1，当点A 的对称点A '落在EF 上时，连接AN ．求证：四边形ANA M '为菱形；（2）已知2BC AB =，继续对折矩形纸片ABCD ，使AB 与DC 重合，折痕GH 与EF 交于点O ．将ABM 沿BM 折叠，连接MO ，若点A 的对称点A '恰好落在线段MO 上，此时2AM =．①尺规作图：请在图2中用直尺和圆规，作点A 的对称点A '（保留作图痕迹，不写作法）；②求AB 的长度；【拓展迁移】如图3，在矩形纸片ABCD 的边AB 上取一点P ，折叠纸片，使P ，B 两点重合，展平纸片，得到折痕EF ；点B '为EF 上任意一点（与点E ，F 不重合），折叠纸片使B ，B '两点重合，得到折痕l 及点P 的对应点P '，折痕l 交EF 于点K ，展平纸片，连接BP '，KP '．（3）猜想P B K ∠'与BC P '∠的数量关系，并证明．【答案】（1）见解析；（2）①见解析；②6AB =；（3）3P BC BP K ''∠∠＝，理由见解析【分析】（1）根据折叠可得出NA NA '=，MA MA '=，AMB A MB '∠=∠，，证明AD EF ∥，利用平行线的性质得出AMB MNA '∠=∠，则A MB MNA ''∠=∠，利用等角对等边得出MA NA ''=，即可得证；（2）①以M 为圆心，MA 为半径画弧交MO 于A '即可；②利用折叠的性质，矩形的判定与性质可得出2BH AB A B AG OG '====，证明()HL OA B OHB ' ≌，得出OA OH OG '==，在Rt MGO △中，根据勾股定理，可求出OG ，进而求出AB ；（3）连接PK ，BK ，延长BK 交P B ''于点M ，可证明EB B MBB ''≌ ，得出BE B M '=，90FEB BMB '∠=∠=︒，由折叠可得BK PK P K B K ''===，利用等边对等角和三线合一的性质可得出P BK BP K ''∠=∠，KBB KB B ''∠=∠，MB MP ''=，利用线段垂直平分线的性质BP BB ''=，利用三线合一性质可得出P BK KBB ''∠=∠，则P BK BP K KBB KB B ''''∠=∠=∠=∠，由（1）中BC EF ∥，可得出B BC KB B ''∠=∠，即可得证．【详解】（1）证明：连接AA '，∵ABM 沿BM 折叠，得到A BM '△，∴BM 垂直平分AA '，∴NA NA '=，MA MA '=，AMB A MB '∠=∠，由折叠可知：AEF BEF ∠=∠，∵180AEF BEF ∠+∠=︒，∴90BEF ∠=︒，∵四边形ABCD 为矩形，∴90DAB ∠=︒，∴90BEF DAB ∠=∠=︒，∴AD EF ∥，∴AMB MNA '∠=∠，∴A MB MNA ''∠=∠，∴MA NA ''=，∴MA NA NA MA ''===，∴四边形ANA M '为菱形；点A'即为所求，解：连接BO，由折叠可知：AB A B'=，MA 由（1）得90∠=∠=︒GHB HGA∵l为折痕，∴P B B PBB'''∠=∠，BP B P''=，l ∴KP KP'=，=，KB KB'∴KBB KB B''∠=∠，∵B B BB''=，∴BE B M '=，90FEB BMB '∠=∠=︒，由折叠可知：KP KB =，EP EB =，90FEB ∠=︒，∴KP KB '=，KP KB ''=∴P BK BP K ''∠=∠，MB MP ''=∴BP BB ''=，∴P BK BP K KBB KB B ''''∠=∠=∠=∠，由（1）可知BC EF ∥，∴B BC KB B ''∠=∠，∴3P BC BP K ''∠=∠．【点睛】本题考查了矩形与折叠，等腰三角形的判定与性质，全等三角形的判定与性质，线段垂直平分线的性质等知识，明确题意，灵活运用所学知识解决问题是解题的关键．变式3．如图1，在矩形ABCD 中，点E 是边AB 上的一点，连接DE ．(1)若DE 平分ADC ∠，点G 是CD 上的一点，连接EC ，EG ，且EC EG =．过点C 作CQ EG⊥于Q ，CQ 延长线交ED 于H ，过点H 作HP CD ⊥于P ，如图．①填空：AED △的形状是______三角形；②求证：PHC BEC△△≌(2)将图1的矩形ABCD 画在纸上，若DE 平分ADC ∠，沿过点E 的直线折叠，点C 恰好落在AD 上的点C '处，点B 落在点B '处，得到折痕EF ，B C ''交AB 于点M ，如图．求证：MC ME '=．(3)如图，延长DE 交CB 的延长线于点K 使得AB BK =，此时恰好BE BC =，连接AC 交DK 于点J ，连接BJ ．请证明：KJ AJ BJ >+．【答案】(1)①等腰直角；②见解析(2)见解析(3)见解析【分析】（1）①根据矩形的性质和角平分线的性质可得45AED ADE ∠=∠=︒，进而得出结果；②可证得BCE PCH ∠=∠，EC HC =，90HPC B ︒∠=∠=，进而得出结论；（2）连接C E '，可证得Rt Rt EC A C EB ''' ≌，可得C EA EC B '''∠=∠，根据等角对等边即可得出结论；（3）在线段EK 上取点I ，使得KI AJ =，连接BI ，可证KBE ABC ≌△△，得BKE BAC ∠=∠，在证KBI ABJ ≌△△，得KBI ABJ ∠=∠，90IBJ KBA ︒∠=∠=，得出IJ BJ >，进一步得出结论．【详解】（1）① 四边形ABCD 是矩形，∴90A ADC ∠=∠=︒，DE 平分ADC ∠，∴1452ADE ADC ∠=∠=︒，∴9045AED ADE ∠=︒-∠=︒，∴AED ADE ∠=∠，∴AE DE =，∴AED △等腰直角三角形，故答案为：等腰直角②证明：如图，过点E 作EW CD ⊥于W ．EC EG = ，EGC ECG ∴∠=∠，CH EG ⊥ ，90HCP EGC ∴∠+∠=︒，90BCE ECG ∠︒∠+= ，BCE PCH ∴∠=∠，45EDW DEW ∠︒∠== ，45EHC EDW PCH PCH ∴∠=∠︒+∠=+∠，DEC DEW CEW ∠=∠+∠，EW BC ∥，BCE CEW PCH ∴∠=∠=∠，DEC EHC ∴∠=∠，EC HC ∴=，90HPC B ∠=∠=︒PHC BEC ∴△△≌．（2）证明：如图，连接C E '，由（1）知，AED △为等腰直角三角形，AD AE ∴=，四边形ABCD 是矩形，AD BC ∴=，90EAC B '∠=∠=︒，由折叠知，B C BC ''=，B B '∠=∠，AE B C ''∴=，EAC B ''∠=∠，又EC C E ''=，在Rt EC A '△和Rt C EB ''△中，EC C E ''=，AE B C ''=，∴Rt Rt EC A C EB ''' ≌，C EA EC B '''∴∠=∠，MC ME '∴=．（3）如图，在线段EK 上取点I ，使得KI AJ =，连接BI ，在AJB 与KIB △中，BK AB =，ABC ABK ∠=∠，BE BC =，KBE ABC ∴△△≌，BKE BAC ∴∠=∠．KI AJ = ，BK AB =，BKE BAC ∠=∠，KBI ABJ ∴△△≌，KBI ABJ ∴∠=∠，90IBJ IBA ABJ IBA KBI KBA ∴∠=∠+∠=∠+∠=∠=︒，IBJ ∴△为直角三角形，IJ BJ ∴>，KJ AJ BJ ∴>+．【点睛】本题是四边形综合题，考查了等腰直角三角形的判定和性质，矩形的性质，全等三角形的判定和性质，轴对称的性质，准确添加常用辅助线，构造特殊三角形和证明全等三角形是解本题的关键。

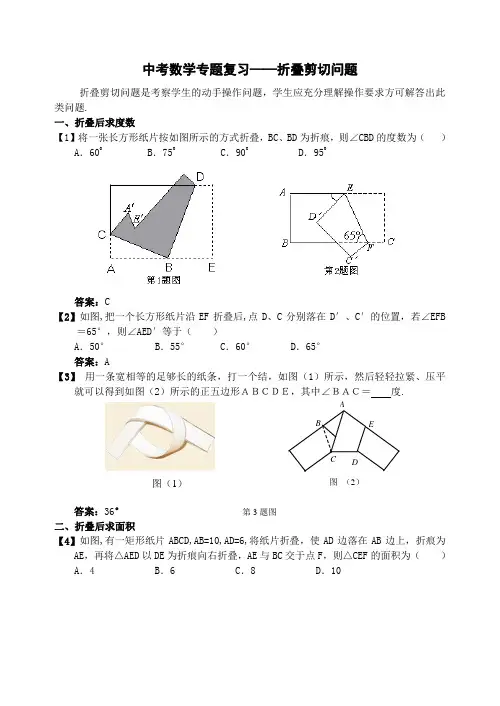
C DEB A 图 （2） 中考数学专题复习——折叠剪切问题折叠剪切问题是考察学生的动手操作问题，学生应充分理解操作要求方可解答出此类问题.一、折叠后求度数【1】将一张长方形纸片按如图所示的方式折叠，BC 、BD 为折痕，则∠CBD 的度数为（ ）A ．600B ．750C ．900D ．950答案：C【2】如图,把一个长方形纸片沿EF 折叠后,点D 、C 分别落在D ′、C ′的位置，若∠EFB＝65°，则∠AED ′等于（ ）A ．50°B ．55°C ．60°D ．65° 答案：A【3】 用一条宽相等的足够长的纸条，打一个结，如图（1）所示，然后轻轻拉紧、压平就可以得到如图（2）所示的正五边形ＡＢＣＤＥ，其中∠ＢＡＣ＝ 度.答案：36° 二、折叠后求面积【4】如图,有一矩形纸片ABCD,AB=10,AD=6,将纸片折叠，使AD 边落在AB 边上，折痕为AE ，再将△AED 以DE 为折痕向右折叠，AE 与BC 交于点F ，则△CEF 的面积为（ ） A ．4 B ．6 C ．8 D ．10图（1） 第3题图答案：C【5】如图，正方形硬纸片ABCD 的边长是4，点E 、F 分别是AB 、BC 的中点，若沿左图中的虚线剪开，拼成如下右图的一座“小别墅”，则图中阴影部分的面积是A ．2B ．4C ．8D ．10答案：B【6】如图a ，ABCD 是一矩形纸片，AB ＝6cm ，AD ＝8cm ，E 是AD 上一点，且AE ＝6cm 。

操作：（1）将AB 向AE 折过去，使AB 与AE 重合，得折痕AF ，如图b ；（2）将△AFB 以BF 为折痕向右折过去，得图c 。

则△GFC 的面积是（ ）E A A A B B C C C GD D D F F 图a 图b 图c 第6题图A.1cm 2B.2 cm 2C.3 cm 2D.4 cm 2答案：B三、折叠后求长度【7】如图，已知边长为5的等边三角形ABC 纸片，点E 在AC 边上，点F 在AB 边上，沿着EF 折叠，使点A 落在BC 边上的点D 的位置，且ED BC ⊥，则CE 的长是（ ） （A ）10315-（B ）1053- （C ）535- （D ）20103-答案：D 四、折叠后得图形【8】将一张矩形纸对折再对折（如图），然后沿着图中的虚线剪下，得到①、②两部分，将①展开后得到的平面图形是（ ）A ．矩形B ．三角形C ．梯形D ．菱形答案：D【9】在下列图形中，沿着虚线将长方形剪成两部分，那么由这两部分既能拼成平行四边形又能拼成三角形和梯形的是（ ）A. B. C. D.答案：D【10】小强拿了张正方形的纸如图（1），沿虚线对折一次如图（2），再对折一次得图（3），然后用剪刀沿图（3）中的虚线（虚线与底边平行）剪去一个角，再打开后的形状应是( )AB CEF第7题图第8题图 第9题图第10题图答案：D 【11】将一圆形纸片对折后再对折，得到图1，然后沿着图中的虚线剪开，得到两部分，其中一部分展开后的平面图形是（ ）答案：C【12】如图1所示，把一个正方形三次对折后沿虚线剪下，则所得的图形是（ ）答案：C【13】 如图，已知BC 为等腰三角形纸片ABC 的底边，AD ⊥BC ，AD=BC. 将此三角形纸片沿AD 剪开，得到两个三角形，若把这两个三角形拼成一个平面四边形，则能拼出互不全等的四边形的个数是（ ） A. 1 B. 2A B C D 图3图1第12题图C. 3D. 4答案：D五、折叠后得结论【14】亲爱的同学们，在我们的生活中处处有数学的身影.请看图，折叠一张三角形纸片，把三角形的三个角拼在一起，就得到一个著名的几何定理，请你写出这一定理的结论：“三角形的三个内角和等于_______°.”答案：180【15】从边长为a 的正方形内去掉一个边长为b 的小正方形(如图1)，然后将剩余部分剪拼成一个矩形(如图2)，上述操作所能验证的等式是（ ）A.a 2–b 2 =(a+b)(a-b) Ｂ.(a –b)2 = a 2–2ab+b 2Ｃ.(a+b)2 = a 2 +2ab+ b 2 Ｄ.a 2+ ab = a (a+b) 答案：A【16】如图，一张矩形报纸ABCD 的长AB ＝a cm ，宽BC ＝b cm ，E 、F 分别是AB 、CD 的中点，将这张报纸沿着直线EF 对折后，矩形AEFD 的长与宽之比等于矩形ABCD 的长与宽之比，则a ∶b 等于（ ）． A ．1:2 B ．2:1 C ．1:3 D ．3:1答案：A六、折叠和剪切的应用【17】将正方形ABCD 折叠，使顶点A 与CD 边上的点M 重合，折痕交AD 于E ，交BC 于F ，边AB 折叠后与BC 边交于点G （如图）.（1）如果M 为CD 边的中点，求证：DE ∶DM ∶EM=3∶4∶5；第15题图（1） 第17题图 （2）ABCDEF MG 第19题图（2）如果M 为CD 边上的任意一点，设AB=2a ，问△CMG 的周长是否与点M 的位置有关？若有关，请把△CMG 的周长用含DM 的长x 的代数式表示；若无关，请说明理由.答案：（1）先求出DE=AD 83，AD DM 21=，AD EM 85=后证之. （2）注意到△DEM ∽△CMG ，求出△CMG 的周长等于4a ，从而它与点M 在CD 边上的位置无关.【18】同学们肯定天天阅读报纸吧?我国的报纸一般都有一个共同的特征:每次对折后,所得的长方形和原长方形相似,问这些报纸的长和宽的比值是多少?答案：2∶1.【19】用剪刀将形状如图1所示的矩形纸片ABCD 沿着直线CM 剪成两部分,其中M 为AD 的中点.用这两部分纸片可以拼成一些新图形,例如图2中的Rt △BCE 就是拼成的一个图形.(1)用这两部分纸片除了可以拼成图2中的Rt △BCE外,还可以拼成一些四边形.请你试一试,把拼好的四边形分别画在图3、图4的虚框内.(2)若利用这两部分纸片拼成的Rt △BCE 是等腰直角三角形,设原矩形纸片中的边AB 和BC 的长分别为a 厘米、b 厘米,且a 、b 恰好是关于x 的方程01)1(2=++--m x m x 的两个实数根,试求出原矩形纸片的面积.答案：（1）如图（2）由题可知AB ＝CD ＝AE ，又BC ＝BE ＝AB ＋AE∴BC ＝2AB ， 即a b 2=由题意知 a a 2,是方程01)1(2=++--m x m x 的两根E B A C B A M C D M 图3 图4 图1 图2 第21题图 BACBAMCE M图3图4E第21题答案图∴⎩⎨⎧+=⋅-=+1212m a a m a a消去a ，得 071322=--m m 解得 7=m 或21-=m 经检验：由于当21-=m ，0232<-=+a a ，知21-=m 不符合题意，舍去. 7=m 符合题意.∴81=+==m ab S 矩形答：原矩形纸片的面积为8cm 2.【20】电脑CPU 蕊片由一种叫“单晶硅”的材料制成，未切割前的单晶硅材料是一种薄型圆片，叫“晶圆片”。

HistudyjiftS7^i viPTUk帮助预子個建持续迸步的孚刃力几何图形折叠问题【疑难点拨】1. 折叠（翻折）问题常常出现在三角形、四边形、圆等平面几何问题中，其实质是轴对称性质的应用•解题 的关键利用轴对称的性质找到折叠前后不变量与变量， 运用三角形的全等、相似及方程等知识建立有关线段、角之间的联系.2. 折叠（翻折）意味着轴对称，会生成相等的线段和角，这样便于将条件集中•如果题目中有直角，则通常 将条件集中于较小的直角三角形，利用勾股定理求解.3. 矩形中的一次折叠通常利用折叠性质和平行线性质求角的度数，或者利用折叠性质以及勾股定理求线段 长度•矩形中的两次或多次折叠通常出现“一线三直角”的模型 （如图），从而构造相似三角形，利用相似三角形求边或者角的度数.4. 凡是在几何图形中出现“折叠”这个字眼时，第一反应即存在一组全等图形，其次找出与要求几何量相 关的条件量.1.常见的轴对称图形：等腰三角形、矩形、菱形、正方形、圆 .2.折叠的性质：折叠的实质是轴对称，折叠前后的两图形全等，对应边和对应角相等. 【基础篇】 一、选择题：1. . （2018?四川凉州？ 3分）如图将矩形 ABCD&对角线BD 折叠，使C 落在C'处，BC'交AD 于点E ,则下到结 论不一定成立的是（）AD=BCB .Z EBD=/ EDB C.A ABE^A CBD D sin / ABE*A.IHistudyjlftS7^l viPTUk帮助预子個建持续iS步的孚刃力2. （2017山东烟台）如图1，将一圆形纸片向右、向上两次对折后得到如图2所示的扇形AOB已知OA=6取OA的中点C,过点C作CD L OA交理于点D,点F是上一点.若将扇形BOD沿OD翻折，点B恰好与点F重合，用剪刀沿着线段BD, DF, FA依次剪下，则剪下的纸片（形状同阴影图形）面积之和为（___________ .A. 36 n -108 B . 108-32 n C. 2 n D.nABC AB=AC / BAC=90，点E为AB中点.沿过点E的直线折5. （2017乌鲁木齐）如图，在矩形ABCD中，点F在AD上,点E在BC上，把这个矩形沿EF折叠后，使点D恰好落在BC边上的G点处，若矩形面积为4胚且/ AFG=60 , GE=2BG则折痕EF的长为（）A. 1B.说C. 2D.加如图，矩形纸片ABCD中, AB=4, BC=6将厶ABC沿AC折叠，使点B落在点E处，CE交AD 叠，使点B与点A重合，折痕现交于点F.已知E一，则BC的长是（3. （2017浙江衢州）于点F,则DF的长等于（）4. （2018 •山东青岛• 3分）如图，三角形纸片B. 3.2C. 3HiSMldy」畅字刃VIPT住叱帮朗预子陶建持续进步的孚刃门二、填空题:6. （2018 •辽宁省盘锦市）如图，已知Rt△ ABC中，/ B=90°, / A=60°, AC=2三+4,点M N分别在线段AC.ABD恰好落在线段BC上，当△ DCM为直角三角形时，折痕MN勺长为.ABCD（纸片）折叠，使点B与AD边上的点K重合，EG为折痕；点C2=75°, EF= + 1,则BC的长-3分）如图，将矩形ABCD沿 EF折叠，使点B落在AD边上的点G处，点C落在点H处,BG 则/ AGB=三、解答与计算题：9. （2018 •广东• 7分）如图，矩形ABCD中, AB> AD,把矩形沿对角线AC所在直线折叠，使点B落在点E处,上，将厶ANM沿直线Mr折叠，使点A的对应点8. （2018 •湖南省常德7. （2018 •山东威海• 8分）如图，将矩形已知/ DGH=30，连接(1)求证：△ ADE^A CEDAE交CD于点F,连接DEHistudyjlftS7^]l viPTUk|帮助预子陶建持续进步的孚刃力|10—（ 2018?山东枣庄？ 10分）如图，将矩形— D 交AF 于点G,连接DG（1） 求证：四边形EFDG 是菱形；（2） 探究线段EG GF AF 之间的数量关系，并说明理由； （3） 若 AG=6 EG=2E ，求 BE 的长.【能力篇】一、选择题： 11.（ 2018 •辽宁省阜新市）如图，将等腰直角三角形ABC （/ B=90°）沿EF 折叠，使点A 落在BC 边的中点A处，BC=8,那么线段AE 的长度为（）12.（ 2018 •四川省攀枝花・3分）如图，在矩形 ABCD 中, E 是AB 边的中点，沿 EC 对折矩形ABCD 使B 点落 在点P 处，折痕为EC 连结AP 并延长AP 交CD 于 F 点，连结CP 并延长CP 交AD 于Q 点.给出以下结论： ① 四边形AECF 为平行四边形； ② / PBA=Z APQ③ 厶FPC 为等腰三角形； ④ 厶 APB^A EPC 其中正确结论的个数为（）A . 1 B. 2 C. 3D. 4C. 6D. 7D GECEB .A .亠13. （2018 •湖北省武汉• 3分）如图，在O O 中，点C 在优弧-I.上，将弧「■沿BC 折叠后刚好经过 AB 的中点 D.若O O 的半径为 匚AB=4,则BC 的长是（、填空ABCD 中，点E 是CD 的中点，将△ BCE 沿BE 折叠后得到△ BEF14. （2018 •辽宁省葫芦岛市 ） 如图，在矩形15. （ 2018 •四川宜宾• 3分）如图，在矩形 ABCD 中, AB=3 CB=2,点E 为线段AB 上的动点，将△ CBE 沿 CE ①当E 为线段AB 中点时，AF// CE; ②当E 为线段AB 中点时，AF=9 ;5④当 A F 、C 三点共线时，△ CEF ^A AEF.DG 1且点F 在矩形ABCD 勺内部，将 BF 延长交AD 于点G.若 =' ，则折叠，使点B 落在矩形内点F 处，下列结论正确的是 （写出所有正确结论的序③当A F 、C 三点共线时,AE='HiSMiaa快乐字刃I VIPT 性叱帮朗滋子陶建持续进步的孚刃门GvPEDU !BCEDCA'B三、解答与计算题:16. (2018 •湖北省宜昌• 11分)在矩形 ABCD 中, AB=12 P 是边AB 上一点，把△ PBC 沿直线PC 折叠，顶点B 的对应点是点 G,过点B 作BEL CG 垂足为E 且在AD 上, BE 交PC 于点F . (1)如图1,若点E 是AD 的中点，求证：△ AEB^A DEC (2)如图2,①求证：BP=BF③当BP=9时，求 BE?EF 的值.②当 AD=25 且 AE v DE 时，求 cos / PCB 的值; 17. (2018 •广东• 7分)如图，矩形ABCC 中，AB> AD,把矩形沿对角线 AC 所在直线折叠，使点B 落在点E 处, AE 交CD 于点F ,连接DE (1)求证：△ ADE^A CED (2)求证：△ DEF 是等腰三角形.HiSMc!®快S 字刃丄VIP 亍性比 帮朗预子陶建持续进步的孚刃门■ BC *HiStUCU快乐字刃VIPT性比帮助预子问建持续迸步的字刃力18. （2018?江苏盐城？10分）如图，在以线段二5■为直径的上取一点，连接、就•将_二弓匚沿.止翻折后得到□.（1 ）试说明点在上；（2）在线段.：「的延长线上取一点，使上厂—」一丄.求证：三壬为①门的切线；（3）在（2）的条件下，分别延长线段、匚吕相交于点，若m厂=J，二匸=-,求线段的长•【探究篇】19. （2018年江苏省泰州市？12分）对给定的一张矩形纸片ABCD进行如下操作：先沿CE折叠，使点B落在CD 边上（如图①），再沿CH折叠，这时发现点E恰好与点D重合（如图②）（2）将该矩形纸片展开.①如图③，折叠该矩形纸片，使点C与点H重合，折痕与AB相交于点P,再将该矩形纸片展开.求证：/ HPC=90 ;②不借助工具，利用图④探索一种新的折叠方法，找出与图③中位置相同的P点，要求只有一条折痕，且点P 在折痕上，请简要说明折叠方法•（不需说明理由）（1）根据以上操作和发现，求的值;设四边形BEFC 的面积为S ,求S 与x 之间的函数表达式，并求出 S 的最小值.(2) 随着点M 在边AD 上位置的变化，△ PDM 的周长是否发生变化？如变化，请说明理由；如不变，请求出该定值;(3) 沿直线EF 折叠，使点B 的对应点M 始终落在边AD 上（点M 不与点A D 重合），点C 落在点N 处，MN W CD 交3 .....HistudyjlftS7^l VIPTlik帮助预子陶建持续iS步的孚刃力几何图形折叠问题【疑难点拨】1. 折叠（翻折）问题常常出现在三角形、四边形、圆等平面几何问题中，其实质是轴对称性质的应用•解题的关键利用轴对称的性质找到折叠前后不变量与变量，运用三角形的全等、相似及方程等知识建立有关线段、角之间的联系.2. 折叠（翻折）意味着轴对称，会生成相等的线段和角，这样便于将条件集中•如果题目中有直角，则通常将条件集中于较小的直角三角形，利用勾股定理求解.3. 矩形中的一次折叠通常利用折叠性质和平行线性质求角的度数，或者利用折叠性质以及勾股定理求线段长度•矩形中的两次或多次折叠通常出现“一线三直角”的模型（如图），从而构造相似三角形，利用相似三角形求边或者角的度数.4. 凡是在几何图形中出现“折叠”这个字眼时，第一反应即存在一组全等图形，其次找出与要求几何量相关的条件量.1.常见的轴对称图形：等腰三角形、矩形、菱形、正方形、圆.2.折叠的性质：折叠的实质是轴对称，折叠前后的两图形全等，对应边和对应角相等.【基础篇】一、选择题：1. . （2018?四川凉州？3分）如图将矩形ABCD&对角线BD折叠，使C落在C'处，BC'交AD于点E,则下到结论不一定成立的是（）A. AD=BCB.Z EBD=/ EDBC.A ABE^A CBD D sin / ABE*ED【分析】主要根据折叠前后角和边相等找到相等的边之间的关系，即可选出正确答案.【解答】解：A、BC=BC, AD=BC二AD=BC，所以正确.B、 / CBD2 EDB / CBD=/ EBD EBD2 EDB正确.AED、T sin / ABE』,BE•••Z EBD=/ EDB••• BE=DEHistudyjlftS7^l VIPTlik帮助预子陶建持续iS步的孚刃力• sin / ABE^.ED故选：C.HistudyjlftS7^ll viPTUk|帮助预子詞11持续进步的字刃力|【点评】本题主要用排除法，证明 A , B , D 都正确，所以不正确的就是—C,排除法也是数学中一种常用的解题方 法. 2.（2017山东烟台）如图1，将一圆形纸片向右、向上两次对折后得到如图2所示的扇形AOB 已知OA=6取OA 的中点C,过点C 作CDL OA 交丽于点D,点F 是廳上一点.若将扇形BOD 沿 OD 翻折，点B 恰好与点F 重合， 用剪刀沿着线段 BD, DF , FA 依次剪下，则剪下的纸片（形状同阴影图形）面积之和为（ __________ . A . 36 n -108 B . 108-32 n C . 2 n D.n【考点】MO 扇形面积的计算；P9:剪纸问题.1【分析】先求出/ ODC M BOD=30，作DEL OB 可得DE= OD=3先根据S 弓形BD =S 扇形BOD - & BOD 求得弓形的面积,2再利用折叠的性质求得所有阴影部分面积.【解答】解：如图，••• CD L OA•••/ DCO M AOB=90 ,•••/ ODC M BOD=30 ,则剪下的纸片面积之和为 12X （ 3 n- 9） =36 n- 108, 故答案为： 36 n- 108 .故选 A 3.（2017浙江衢州）如图，矩形纸片 ABCD 中, AB=4, BC=6将厶ABC 沿 AC 折叠，使点B 落在点E 处，CE 交AD于点F ,则DF 的长等于（）…S 弓形B[=S 扇形X 6X 3=3n- 9,•/ OA =OD =OB =6OC |OA作DE L OB 于点E ,则 DE= OD=3c Mg 心BOD _d BOD=His【udy 』?i 乐字刃］vi 卩卞性比帮朗预子陶建持续迸步的孚刃门【考点】PB 翻折变换（折叠问题）；LB :矩形的性质.【分析】根据折叠的性质得到 AE=AB / E=Z B=90°,易证Rt △ AEF ^ Rt △ CDF ,即可得到结论 设FA=x ,则FC=x , FD=6- x ,在Rt △ CDF 中利用勾股定理得到关于 x 的方程x 2=42+（ 6-x ）【解答】解：•••矩形 ABCD 沿对角线AC 对折，使△ ABC 落在厶ACE 的位置, ••• AE=AB / E=Z B=90°,又•••四边形ABCD 为矩形， • AB=CD • AE=DC 而/ AFE=Z DFC•••在△ AEF 与厶CDF 中，ZAFE-ZCFD•••△ AEF ^A CDF ( AAS ,• EF=DF ；•••四边形ABCD 为矩形， • AD=BC=6 CD=AB=4 •/ Rt △ AEF ^ Rt △ CDF • FC=FA设 FA=x ,贝U FC=x , FD=6- x , 13 在 Rt △ CDF 中，CF=C D+DF ,即 x 2=42+ (6 - x ) 2,解得 x= , 则 FD=6- x=. 故选：B.HiStUdyjl?iS7^l VIPTUk帮朗预子陶建持续进步的孚刃门D.5, 7EF=DF ；易得FC=FA,解方程求出x .B- AC4. （2018 •山东青岛• 3分）如图，三角形纸片ABC AB=AC / BAC=90，点E为AB中点.沿过点E的直线折叠，使点B与点A重合，折痕现交于点F.已知EF=，贝U BC的长是（）2A. .B. 3、2C. 3D. 3 3【分析】由折叠的性质可知/ B=Z EAF=45，所以可求出/ AFB=90，再直角三角形的性质可知EF丄AB,所以AB=AC!的长可求，再利用勾股定理即可求出BC的长.【解答】解：•••沿过点E的直线折叠，使点B与点A重合，•••/ B=Z EAF=45 ,•••/ AFB=90° ,•••点E为AB中点，1 3•EF= —AB, EF= ,2 2•AB=AC=3•••/ BAC=90 ,•BC=3.2 ,故选：B.【点评】本题考查了折叠的性质、等腰直角三角形的判断和性质以及勾股定理的运用，求出/ AFB=9C°是解题的关键.5. （2017乌鲁木齐）如图，在矩形ABCD中，点F在AD上,点E在BC上，把这个矩形沿EF折叠后，使点D恰好落在BC边上的G点处，若矩形面积为4胚且/ AFG=60 , GE=2BG则折痕EF的长为（）HiStUdyjl?iS7^l VIPTUk帮朗预子陶建持续is步的孚刃门【考点】PB:翻折变换（折叠问题）；LB:矩形的性质.【分析】由折叠的性质可知，DF=GF HE=CE GH=DC/ DFE=/ GFE结合/ AFG=60即可得出/ GFE=60，进而可得出△ GEF为等边三角形，在Rt△ GHE中,通过解含30度角的直角三角形及勾股定理即可得出GE=2EC DC= EC,再由GE=2BG吉合矩形面积为4 ，即可求出EC的长度，根据EF=GE=2EC卩可求出结论.【解答】解：由折叠的性质可知，DF=GF HE=CE GH=DC Z DFE=Z GFE•••/ GFE+Z DFE=180 -Z AFG=120 ,•••/ GFE=60 .•/ AF// GE Z AFG=60 ,•Z FGE=/ AFG=60 ,•△ GEF为等边三角形，•EF=GE•••/ FGE=60，/ FGE+Z HGE=90 ,•Z HGE=30 .在Rt△ GHE中, Z HGE=30 ,•GE=2HE=C,•GH= =*$HE= CE•/ GE=2BG•BC=BG+GE+EC=4EC•••矩形ABCD勺面积为 4 ,•4EC?^EC=4 ,•EC=1, EF=GE=2故选C.二、填空题：6. （2018 •辽宁省盘锦市）如图，已知Rt△ ABC中，Z B=90°, Z A=60°, AC=2 :;+4,点M N分别在线段AC.AB上，将△ ANM沿直线MN折叠，使点A的对应点D恰好落在线段BC上，当△ DCM为直角三角形时，折痕MN勺长为 .帮朗滋子陶建持续迸步的孚刃门①如图，当/ CDM=90时，△ CDM是直角三角形,•••在Rt△ ABC中，/ B=90°, / A=60° AC=^+4, /-Z C=30°, AB^ AC五+-,由折叠可得:Z MDN Z A=60°1_ 1_Z BDN=30，•/ BN空DN爰AN •/丄術+卸BN= AB= ：,■2硬+4•• AN=2BN="Z DNB=60 , /Z ANM Z DNM=60，/•/ AMN=60 , •師+4•• AN=MN=";【解答】解：分两种情况：②如图，当/ CMD=90时，△ CDM是直角三角形,帮助预子问il持续迸步的孚刃力I □ ~I] ■由题可得：/ CDM=60 , / A=Z MDN=60 , /-Z BDN=60 , / BND=30 BD空DN= AN, BN庐BD\1AB巫+2 ,1_/• AN=2, BN^3,过N 作NH L AM于H,贝UZ ANH=30 , /• AH空AN=1, HN昉,由折叠可得：Z AMN Z DMN=45 ,/•△ MNH是等腰直角三角形，/• HM=HN= :,/ MN= ■.故答案为：'或；7. （2018 •山东威海• 8分）如图，将矩形ABCD（纸片）折叠，使点B与AD边上的点K重合，EG为折痕；点C与AD边上的点K重合，FH为折痕.已知Z 仁67.5 ° ,Z 2=75°, EF= + 1,求BC的长.【分析】由题意知Z 3=180 ° - 2 Z 1=45°、Z 4=180°- 2Z 2=30 °、BE=KE KF=FC 作KM L BC,设KM=x 知EM=x MF= x,根据EF的长求得x=1，再进一步求解可得.【解答】解：由题意，得：Z 3=180 °- 2 Z 1=45°,Z 4=180°- 2Z 2=30 °, BE=KE KF=FC设KM=x 贝U EM=x MF^J x,x+ V3x^3+1,解得：x=1,••• EK=J办KF=2,.BC=BE+EF+FC=EK+EF+KF=3++J：,• BC的长为【点评】本题主要考查翻折变换，解题的关键是掌握翻折变换的性质：折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等.8. （2018 •湖南省常德・3分）如图，将矩形ABC［沿EF折叠，使点B落在AD边上的点G处，点C落在点H处, 已知Z DGH=30，连接BG 则Z AGB= 75如图，过点K作KM L BC于点M帮朗预子陶建持续进步的孚刃门/ EBC-Z EBG即：/ GBC M BGH由平行线的性质可知/ AGB=Z GBC从而易证/ AGB2 BGH据此可得答案.【解答】解：由折叠的性质可知：GE=BE / EGH M ABC=90 ,•••/ EBG=Z EGB•••/ EGH-Z EGB玄EBC-Z EBG 即：/ GBC=/ BGH又••• AD// BC•Z AGB=Z GBC•Z AGB=Z BGHvZ DGH=30 ,•Z AGH=150 ,•Z AGB二Z AGH=75 ,2故答案为：75°.【点评】本题主要考查翻折变换，解题的关键是熟练掌握翻折变换的性质：折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等.三、解答与计算题：9. (2018 •广东• 7分)如图，矩形ABCD中, AB> AD,把矩形沿对角线AC所在直线折叠，使点B落在点E处,AE交CD于点F,连接DE(1)求证：△ ADE^A CED(2)求证：△ DEF是等腰三角形.【分析】(1)根据矩形的性质可得出AD=BC AB=CD结合折叠的性质可得出AD=CE AE=CD进而即可证出△ ADE◎ △ CED( SSS ;(2)根据全等三角形的性质可得出Z DEF=Z EDF利用等边对等角可得出EF=DF由此即可证出△ DEF是等腰三角形.HiSMlda快乐字刃I VI PT住叱帮朗预子陶建持续进步的孚刃门【解答】证明：(1)：四边形ABCD是矩形，••• AD=BC AB=CD由折叠的性质可得：BC=CE AB=AE•AD=CE AE=CDC AD=CE在厶人。

折叠专题（轴对称变换）折叠问题是近几年中考常考题型，但学生往往对折叠的本质理解不透，造成失分严重。

折叠问题题型多样，变化灵活，从考察学生空间想象能力与动手操作能力的实践操作题，到直接运用折叠相关性质的说理计算题，发展到基于折叠操作的综合题，甚至是压轴题。

考查的着眼点日趋灵活，能力立意的意图日渐明显。

这对于识别和理解几何图形的能力、空间思维能力和综合解决问题的能力都提出了比以往更高的要求.一、折叠本质折叠问题实际就是轴对称变换。

折叠重合部分一定全等，折叠前后对应边和对应角相等。

折痕所在直线就是这两个全等形的对称轴。

二、方法点拨1、考查问题：求折点位置、求线段长度、求重叠面积、求角度。

2、注意有一个等腰三角形。

通常设X，用方程解题。

3、出题位置：选择题、填空压轴题、或22、23题（22题可能性大些）。

4、折叠对象主是三角形和四边形①三角形折叠模型：②四边形折叠模型：三、典例解析【例题1】（2018广西贵港）如图将矩形ABCD折叠，折痕为EF，BC的对应边B'C′与CD 交于点M，若∠B′MD=50°，则∠BEF的度数为．提示：连接ME可解或设∠EFC=X度，则x+(x-50)=180可解（2018 广西桂林）如图，在正方形ABCD 中，AB=3，点 M 在 CD 的边上，且DM=1，△AEM 与△ADM 关【例题2】于A M 所在的直线对称，将△ADM 按顺时针方向绕点A旋转90°得到△ABF，连接E F，则线段EF 的长为（）（提示：EF=BM）A.2B．C．D．【例3】如图，在矩形纸片A BCD 中，AB=4，AD=12，将矩形纸片折叠，使点C落（考点：勾股定理）在A D 边上的点M处，折痕为P E，此时P D=3．（1）求M P 的值；（2）在A B 边上有一个动点F，且不与点A，B 重合．当A F 等于多少时，△MEF的周长最小？（考点：折叠性质将军饮马）总结解题步骤：1、将已知条件标在图上；2、设未知数，将未知数标在图上；3、列方程，多数情况可通过勾股定理解决。

初中数学中的折叠问题一、矩形中的折叠1．将一张长方形纸片按如图的方式折叠，其中BC ，BD 为折痕，折叠后BG 和BH 在同一条直线上，∠CBD= 度．2．如图所示，一张矩形纸片沿BC 折叠，顶点A 落在点A ′处，再过点A ′折叠使折痕DE ∥BC ，若AB=4，AC=3，则△ADE 的面积是 ．3．如图，矩形纸片ABCD 中，AB=4，AD=3，折叠纸片使AD 边与对角线BD 重合，得折痕DG ，求AG 的长．根据对称的性质得到相等的对应边和对应角，再在直角三角形中根据勾股定理列方程求解即可4．把矩形纸片ABCD 沿BE 折叠，使得BA 边与BC 重合，然后再沿着BF 折叠，使得折痕BE 也与BC 边重合，展开后如图所示，则∠DFB 等于（ ）注意折叠前后角的对应关系5．如图，沿矩形ABCD 的对角线BD 折叠，点C 落在点E 的位置，已知BC=8cm ，AB=6cm ，求折叠后重合部分的面积．重合部分是以折痕为底边的等腰三角形321FEDCBAGA'C A B D6．将一张矩形纸条ABCD 按如图所示折叠，若折叠角∠FEC=64°，则∠1= 度；△EFG 的形状 三角形．对折前后图形的位置变化，但形状、大小不变，注意一般情况下要画出对折前后的图形，便于寻找对折前后图形之间的关系，注意以折痕为底边的等腰△GEF7．如图，将矩形纸片ABCD 按如下的顺序进行折叠：对折，展平，得折痕EF （如图①）；延CG 折叠，使点B 落在EF 上的点B ′处，（如图②）；展平，得折痕GC （如图③）；沿GH 折叠，使点C 落在DH 上的点C ′处，（如图④）；沿GC ′折叠（如图⑤）；展平，得折痕GC ′，GH （如图 ⑥）．（1）求图 ②中∠BCB ′的大小；（2）图⑥中的△GCC ′是正三角形吗？请说明理由．理清在每一个折叠过程中的变与不变8．如图，正方形纸片ABCD 的边长为8，将其沿EF 折叠，则图中①②③④四个三角形的周长之和为折叠前后对应边相等9．如图，将边长为4的正方形ABCD 沿着折痕EF 折叠，使点B 落在边AD 的中点G 处，求四边形BCFE 的面积注意折叠过程中的变与不变，图形的形状和大小不变，对应边与对应角相等 10．如图，将一个边长为1的正方形纸片ABCD 折叠，使点B 落在边AD 上 不与A 、D 重合．MN 为折痕，折叠后B ’C ’与DN 交于P ．(1)连接BB ’，那么BB ’与MN 的长度相等吗？为什么？ (2)设BM =y ，AB ’=x ，求y 与x 的函数关系式； (3)猜想当B 点落在什么位置上时，折叠起来的梯形MNC ’B ’面积最小？并验证你的猜想．54132G D‘F C‘DB CA E二、纸片中的折叠11．如图，有一条直的宽纸带，按图折叠，则∠α的度数等于（ ）题考查的是平行线的性质，同位角相等，及对称的性质，折叠的角与其对应角相等，和平角为180度的性质，注意△EAB 是以折痕AB 为底的等腰三角形12．如图，将一宽为2cm 的纸条，沿BC ，使∠CAB=45°，则后重合部分的面积为在折叠问题中，一般要注意折叠前后图形之间的联系，将图形补充完整，对于矩形（纸片）折叠，折叠后会形成“平行线+角平分线”的基本结构，即重叠部分是一个以折痕为底边的等腰三角形ABC13．将宽2cm 的长方形纸条成如图所示的形状，那么折痕PQ 的长是注意掌握折叠前后图形的对应关系．在矩形（纸片）折叠问题中，会出现“平行线+角平分线”的基本结构图形，即有以折痕为底边的等腰三角形APQ14．如图a 是长方形纸带，∠DEF=20°，将纸带沿EF 折叠成图b ，再沿BF 折叠成图c ，则图c 中的∠CFE 的度数是（ ）图c 图b图aCDGFEAC GDFEAFDBCAEB Ba 2130°B EF AC D本题考查图形的翻折变换，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变．由题意知∠DEF=∠EFB=20°图b ∠GFC=140°，图c 中的∠CFE=∠GFC-∠EFG15．将一张长为70 cm 的长方形纸片ABCD ，沿对称轴EF 折叠成如图的形状，若折叠后，AB 与CD 间的距离为60cm ，则原纸片的宽AB 是（ ）16．一根30cm 、宽3cm 的长方形纸条，将其按照图示的过程折叠（阴影部分表示纸条的反面），为了美观，希望折叠完成后纸条两端超出点P 的长度相等，则最初折叠时，求MA 的长三、三角形中的折叠17．如图，把Rt △ABC （∠C=90°），使A ，B 两点重合，得到折痕ED ，再沿BE 折叠，C 点恰好与D 点重合，则CE ：AE=18．在△ABC 中，已知AB=2a ，∠A=30°，CD 是AB 边的中线，若将△ABC 沿CD 对折起来，折叠后两个小△ACD 与△BCD 重叠部分的面积恰好等于折叠前△ABC 的面积的14．（1）当中线CD 等于a 时，重叠部分的面积等于 ；GEFD AEF DBC A B C 60cm（2）有如下结论（不在“CD 等于a ”的限制条件下）：①AC 边的长可以等于a ；②折叠前的△ABC 的面积可以等于32a 2；③折叠后，以A 、B 为端点的线段AB 与中线CD 平行且相等．其中， 结论正确（把你认为正确结论的代号都填上，若认为都不正确填“无”）．注意“角平分线+等腰三角形”的基本构图，折叠前后图形之间的对比，找出相等的对应角和对应边19．在△ABC 中，已知∠A=80°，∠C=30°，现把△CDE 沿DE 进行不同的折叠得△C ′DE ，对折叠后产生的夹角进行探究：（1）如图（1）把△CDE 沿DE 折叠在四边形ADEB 内，则求∠1+∠2的和； （2）如图（2）把△CDE 沿DE 折叠覆盖∠A ，则求∠1+∠2的和；（3）如图（3）把△CDE 沿DE 斜向上折叠，探求∠1、∠2、∠C 的关系．（1）根据折叠前后的图象全等可知，∠1=180°-2∠CDE ，∠2=180°-2∠CED ，再根据三角形内角和定理比可求出答案；（2）连接DG ，将∠ADG+∠AGD 作为一个整体，根据三角形内角和定理来求；（3）将∠2看作180°-2∠CED ，∠1看作2∠CDE-180°，再根据三角形内角和定理来求．B'C DA B 231E B'CDB A 21图(1)C'ACBDE12C'ABCDE21GC'A BC DE由于等腰三角形是轴对称图形，所以在折叠三角形时常常会出现等腰三角形20．观察与发现：将三角形纸片ABC（AB＞AC）沿过点A的直线折叠，使得AC落在AB边上，折痕为AD，展开纸片（如图①）；在第一次折叠的基础上第二次折叠该三角形纸片，使点A和点D重合，折痕为EF，展平纸片后得到△AEF（如图②）．小明认为△AEF是等腰三角形，你同意吗？请说明理由．实践与运用：(1)将矩形纸片ABCD沿过点B的直线折叠，使点A落在BC边上的点F处，折痕为BE（如图③）；再沿过点E的直线折叠，使点D落在BE上的点D’处，折痕为EG（如图④）；再展平纸片（如图⑤）．求图⑤中∠α的大小．由于角平分线所在的直线是角的对称轴，所以在三角形中的折叠通常都与角平分线有关。

初中数学专题：折叠问题(推荐完整)编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（初中数学专题：折叠问题(推荐完整)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为初中数学专题：折叠问题(推荐完整)的全部内容。

初中数学专题：折叠问题(推荐完整）编辑整理：张嬗雒老师尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布到文库,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是我们任然希望初中数学专题:折叠问题（推荐完整）这篇文档能够给您的工作和学习带来便利.同时我们也真诚的希望收到您的建议和反馈到下面的留言区，这将是我们进步的源泉,前进的动力。

本文可编辑可修改，如果觉得对您有帮助请下载收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为〈初中数学专题：折叠问题（推荐完整)> 这篇文档的全部内容.专题八折叠问题学习要点与方法点拨：出题位置：选择、填空压轴题或压轴题倒数第二题折叠问题中，常出现的知识时轴对称。

折叠对象有三角形、矩形、正方形、梯形等；考查问题有求折点位置、求折线长、折纸边长周长、求重叠面积、求角度、判断线段之间关系等;轴对称性质——-—-折线，是对称轴、折线两边图形全等、对应点连线垂直对称轴、对应边平行或交点在对称轴上。

压轴题是由一道道小题综合而成，常常伴有折叠；解压轴题时,要学会将大题分解成一道道小题;那么多作折叠的选择题填空题，很有必要。

基本图形：在矩形ABCD中，将△ABF沿BE折叠至△FBE，可得何结论？结论：（1）全等；（2）垂直。

（1）基本图形练习：如图,将三角形纸片ABC沿过点A的直线折叠,使得AC落在AB上，折痕为AD，展开纸片;再次折叠，使得A和D点重合，折痕为EF，展开纸片后得到△AEF,则△AEF是等腰三角形，对吗？（2）折叠中角的考法与做法：将矩形纸片ABCD沿过点B的直线折叠，使得A落在BC边上的点F处，折痕为BE（图1）；再沿过点E的直线折叠，使点D落在BE边上的点D’，折痕为EG（图2）,再展开纸片，求图(3）中角a的大小.（3）折叠中边的考法与做法：如图，将边长为6cm的正方形ABCD折叠，使点D 落在AB边中点E处,折痕为FH,点C落在Q处,EQ与BC交于点G，则△EBG的周长是多少？模块精讲例1.（2014•扬州）已知矩形ABCD的一条边AD=8，将矩形ABCD折叠,使得顶点B落在CD边上的P点处．★解题步骤：第一步：将已知条件标在图上；第二步：设未知数，将未知数标在图上；第三步：列方程，多数情况可通过勾股定理解决。

专题：漫谈折叠问题（二）一、折叠问题小技巧A 要注意折叠前后线段、角的变化，全等图形的构造；B 通常要设求知数；C 利用勾股定理构造方程。

二、折叠问题常见考察点（一）求角的度数1.如图，在折纸活动中，小明制作了一张△ABC纸片，点D、E分别是边AB、AC上，将△ABC 沿着DE折叠压平，A与A′重合，若∠A=75°，则∠1+∠2=【】A．150°B．210°C．105°D．75°【考点】翻折变换（折叠问题），三角形内角和定理。

2. 如图，在平行四边形ABCD中，∠A=70°，将平行四边形折叠，使点D、C分别落在点F、E处（点F、E都在AB所在的直线上），折痕为MN，则∠AMF等于【】A．70° B．40° C．30° D．20°3. 如图，在等腰△ABC中，AB＝AC，∠BAC＝50°．∠BAC的平分线与AB的中垂线交于点O，点C沿EF折叠后与点O重合，则∠CEF的度数是__________．【考点】翻折变换(折叠问题)，等腰三角形的性质，三角形内角和定理，线段垂直平分线的判定和性质。

4. 如图，将正方形ABCD 沿BE 对折，使点A 落在对角线BD 上的A′处，连接A′C，则∠BA′C=__________度．5.如图,在△ABC 中，D,、E 分别是边AB 、AC 的中点, ∠B=50°º.现将△ADE 沿DE 折叠，点A 落在三角形所在平面内的点为A 1,则∠BDA 1的度数为__________°.【考点】翻折变换（折叠问题），折叠对称的性质，三角形中位线定理，平行的性质。

（二）求线段长度1.如图，正方形纸片ABCD 的边长为3，点E 、F 分别在边BC 、CD 上，将AB 、AD 分别和AE 、AF 折叠，点B 、D 恰好都将在点G 处，已知BE=1，则EF 的长为【 】A ．B ．C ．D ．3【考点】翻折变换（折叠问题），正方形的性质，折叠的性质，勾股定理。

方法归纳利用勾股定理解决折叠问题一、利用勾股定理解决平面图形的折叠问题【例1】如图，有一张直角三角形纸片，两直角边AC=5 cm，BC=10 cm，将△ABC折叠，使点B与点A重合，折痕为DE，则CD的长为( )A.252cm B.152cm C.254cm D.154cm【分析】图中CD在Rt△ACD中，由于AC已知，要求CD，只需求AD，由折叠的对称性，得AD=BD，注意到CD+BD=BC，利用勾股定理即可解之.【方法归纳】折叠问题是近几年来中考中的常见题型.解折叠问题关键是抓住对称性.勾股定理的数学表达式是一个含有平方关系的等式，求线段的长时，可由此列出方程，运用方程思想分析问题和解决问题，以便简化求解.1.如图所示，有一块直角三角形纸片，∠C=90°，AC=4 cm，BC=3 cm，将斜边AB翻折，使点B落在直角边AC的延长线上的点E处，折痕为AD，则CE的长为( )A.1 cmB.1.5 cmC.2 cmD.3 cm2.(2014·青岛)如图，将长方形ABCD沿EF折叠，使顶点C恰好落在AB边的中点C′上，若AB＝6，BC＝9，则BF 的长为( )A.4 C.4.5 D.53.如图，长方形纸片ABCD中，已知AD=8，折叠纸片使AB边与对角线AC重合，点B落在点F处，折痕为AE，且EF=3，则AB的长为( )A.3B.4C.5D.64.如图，长方形ABCD的边AD沿折痕AE折叠，使点D落在BC上的F处，已知AB=6，△ABF的面积是24，则FC 等于( )A.1B.2C.3D.45.如图，四边形ABCD是边长为9的正方形纸片，将其沿MN折叠，使点B落在CD边上的B′处，点A对应点为A′，且B′C=3，则AM的长为( )A.1.5B.2C.2.25D.2.56.如图所示，在△ABC中，∠B=90°，AB=3，AC=5，将△ABC折叠，使点C与点A重合，折痕为DE，则△ABE的周长为__________.7.如图，在Rt△ABC中，∠C=90°，BC=6 cm，AC=8 cm，按图中所示方法将△BCD沿BD折叠，使点C落在AB边的C′点，那么△ADC′的面积是__________.8.如图，已知Rt△ABC中，∠C=90°，AC=6，BC=8，将它的锐角A翻折，使得点A落在BC边的中点D处，折痕交AC边于点E，交AB边于点F，则DE的值为__________.二、利用勾股定理解决立体图形的展开问题【例2】如图，圆柱形玻璃杯，高为12 cm，底面周长为18 cm，在杯内离杯底4 cm的点C处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿4 cm与蜂蜜相对的点A处，则蚂蚁到达蜂蜜的最短距离为__________cm.【分析】将圆柱形平面展开，将A、C两点放在同一平面内,然后利用勾股定理进行计算.【方法归纳】在曲面上求两点之间的最短距离，根据“两点之间线段最短”和“化曲面为平面”两种思想，利用勾股定理解决.解决本题时要注意展开后有一直角边长是9 cm而不是18 cm.9.如图，一圆柱体的底面周长为24 cm，高AB为5 cm，BC是直径，一只蚂蚁从点A出发沿着圆柱体的表面爬行到点C的最短路程是( )A.6 cmB.12 cmC.13 cmD.16 cm10.如图，在一个长为2 m，宽为1 m的长方形草地上，放着一根长方体的木块，它的棱和场地宽AD平行且棱长大于AD，木块从正面看是边长为0.2 m的正方形，一只蚂蚁从点A处到达C处需要走的最短路程是__________m（精确到0.01 m）.11.一位同学要用彩带装饰一个长方体礼盒.长方体高6 cm，底面是边长为4 cm的正方形，从顶点A到顶点C′如何贴彩带用的彩带最短？最短长度是多少？12.如图，一个长方体形状的木柜放在墙角处(与墙面和地面均没有缝隙)，有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C1处.(1)请你画出蚂蚁能够最快到达目的地的可能路径；(2)当AB=4，BC=4，CC1=5时，求蚂蚁爬过的最短路径的长.参考答案例1要使A，B两点重合，则折痕DE必为AB的垂直平分线.设CD=x，则AD=BD=10-x.在Rt△ACD中，由勾股定理，得x2+52=(10-x)2.解得x=15 4.故应选D. 变式练习1.A2.A3.D4.B5.B6.77.6 cm28.13 3例2如图，圆柱形玻璃杯展开（沿点A竖直剖开）后，侧面是一个长18 cm，宽12 cm的长方形，作点A关于杯上沿MN的对称点B，连接BC交MN于点P，连接BM，过点C作AB的垂线交剖开线MA于点D.由轴对称的性质和三角形三边关系知AP+PC为蚂蚁到达蜂蜜的最短距离，且AP=BP.由已知和长方形的性质，得DC=9,BD=12.在Rt△BCD中，由勾股定理得∴AP+PC=BP+PC=BC=15.即蚂蚁到达蜂蜜的最短距离为15 cm.变式练习9.C 10.2.6011.把长方体的面DCC′D′沿棱C′D′展开至面ABCD上，如图.构成矩形ABC′D′，则A到C′的最短距离为AC′的长度，连接AC′交DC于O，易证△AOD≌△C′OC.∴OD=OC.即O为DC的中点，由勾股定理得AC′2=AD′2+D′C′2=82+62=100,∴AC′=10 cm.即从顶点A沿直线到DC中点O，再沿直线到顶点C′，贴的彩带最短，最短长度为10 cm.12.(1)如图，木柜的表面展开图是两个矩形ABC1′D1和ACC1A1.蚂蚁能够最快到达目的地的可能路径有如图所示的AC1′和AC1两种.(2)蚂蚁沿着木柜表面经线段A1B1到C1′，爬过的路径的长l1.蚂蚁沿着木柜表面经线段BB1到C1，爬过的路径的长l2∵l1>l2，鱼儿，在水中串上串下，吐着顽皮的泡泡；鸟儿从荷叶上空飞过，想亲吻荷花姑娘的芳泽。