下载文档原格式
数字信号处理教程课后习题答案目录第一章离散时间信号与系统第二章Z变换第三章离散傅立叶变换第四章快速傅立叶变换第五章数字滤波器的基本结构第六章无限长单位冲激响应（IIR）数字滤波器的设计方法第七章有限长单位冲激响应（FIR）数字滤波器的设计方法第八章数字信号处理中有限字长效应第一章 离散时间信号与系统1 .直接计算下面两个序列的卷积和)n (h *)n (x )n (y =请用公式表示。
分析：①注意卷积和公式中求和式中是哑变量m （ n 看作参量）， 结果)(n y 中变量是 n ,; )()()()()(∑∑∞-∞=∞-∞=-=-=m m m n x m h m n h m x n y ②分为四步 （1）翻褶（ -m ），（2）移位（ n ）,（3）相乘，; )( )( 4n y n n y n 值的，如此可求得所有值的）相加，求得一个（③ 围的不同的不同时间段上求和范一定要注意某些题中在 n00 , 01()0 , ,()0,n n n a n N h n n n n x n n n β-⎧≤≤-=⎨⎩⎧≤⎪=⎨<⎪⎩其他如此题所示，因而要分段求解。
)(5.0)(,)1(2 )()4()(5.0)(,)2( )()3()()(,)( )()2()()(,)( )()1(3435n u n h n u n x n R n h n n x n R n h n R n x n R n h n n x n n n =--==-=====δδ2 .已知线性移不变系统的输入为)n (x ,系统的单位抽样响应 为)n (h ,试求系统的输出)n (y ,并画图。
分析：①如果是因果序列)(n y 可表示成)(n y ={)0(y ，)1(y ，)2(y ……}，例如小题（2）为)(n y ={1，2，3，3，2，1} ;②)()(*)( , )()(*)(m n x n x m n n x n x n -=-=δδ ;③卷积和求解时，n 的分段处理。
数字信号处理第三版习题答案数字信号处理（Digital Signal Processing，简称DSP）是一门研究如何对数字信号进行处理和分析的学科。
它在现代通信、音频处理、图像处理等领域有着广泛的应用。
为了更好地理解和掌握数字信号处理的知识，许多人选择了《数字信号处理（第三版）》这本经典教材。
本文将为大家提供一些《数字信号处理（第三版）》习题的答案，以帮助读者更好地学习和巩固所学知识。
第一章：离散时间信号和系统1.1 习题答案：a) 离散时间信号是在离散时间点上取值的信号，而连续时间信号是在连续时间上取值的信号。
b) 离散时间系统是对离散时间信号进行处理的系统，而连续时间系统是对连续时间信号进行处理的系统。
c) 离散时间信号可以通过采样连续时间信号得到。
1.2 习题答案：a) 线性系统满足叠加性和齐次性。
b) 时不变系统的输出只与输入的时间延迟有关，与输入信号的具体形式无关。
c) 因果系统的输出只与当前和过去的输入有关，与未来的输入无关。
第二章：离散时间信号的时域分析2.1 习题答案：a) 离散时间信号的能量是信号幅值的平方和，而功率是信号幅值的平方的平均值。
b) 离散时间信号的能量和功率可以通过计算信号的幅值序列的平方和和平方的平均值得到。
2.2 习题答案：a) 离散时间信号的自相关函数是信号与其自身经过不同时间延迟的乘积的和。
b) 离散时间信号的自相关函数可以用于确定信号的周期性和频率成分。
第三章：离散时间信号的频域分析3.1 习题答案：a) 离散时间信号的频谱是信号在频率域上的表示，可以通过对信号进行傅里叶变换得到。
b) 离散时间信号的频谱可以用于分析信号的频率成分和频谱特性。
3.2 习题答案：a) 离散时间信号的频谱具有周期性，其周期等于采样频率。
b) 离散时间信号的频谱可以通过对信号进行离散傅里叶变换得到。
第四章：离散时间系统的频域分析4.1 习题答案：a) 离散时间系统的频率响应是系统在不同频率下的输出与输入之比。
第1章 时域离散信号和时域离散系统 1.1.2 重要公式（1） ∞-∞==-=m n h n x m n h m x n y )(*)()()()( 这是一个线性卷积公式， 注意公式中是在－∞~∞之间对m 求和。
如果公式中x(n)和h(n)分别是系统的输入和单位脉冲响应， y(n)是系统输出， 则该式说明系统的输入、 输出和单位脉冲响应之间服从线性卷积关系。
（2）x(n)=x(n)*δ(n)该式说明任何序列与δ(n)的线性卷积等于原序列。
x(n －n0)=x(n)*δ(n －n0)（3）∞-∞=-=k a n k X T X )j j (1)j (ˆs ΩΩΩ这是关于采样定理的重要公式， 根据该公式要求对信号的采样频率要大于等于该信号的最高频率的两倍以上， 才能得到不失真的采样信号。
∞-∞=--=n a a T nT t T nT t nt x t x /)(π]/)(πsin[)()(这是由时域离散信号理想恢复模拟信号的插值公式。
1.2 解线性卷积的方法解线性卷积是数字信号处理中的重要运算。
解线性卷积有三种方法， 即图解法（列表法）、 解析法和在计算机上用MA TLAB 语言求解。
它们各有特点。
图解法（列表法）适合于简单情况， 短序列的线性卷积， 因此考试中常用， 不容易得到封闭解。
解析法适合于用公式表示序列的线性卷积， 得到的是封闭解， 考试中会出现简单情况的解析法求解。
解析法求解过程中， 关键问题是确定求和限， 求和限可以借助于画图确定。
第三种方法适合于用计算机求解一些复杂的较难的线性卷积， 实验中常用。
解线性卷积也可用Z 变换法，以及离散傅里叶变换求解， 这是后面几章的内容。
下面通过例题说明。
设x(n)=R 4(n), h(n)=R 4(n)， 求y(n)=x(n)*h(n)。
该题是两个短序列的线性卷积， 可以用图解法（列表法）或者解析法求解。
表1.2.1给出了图解法（列表法）， 用公式可表示为y(n)={…, 0, 0, 1, 2, 3, 4, 3, 2, 1, 0, 0, …}下面用解析法求解， 写出卷积公式为∑∞-∞=∞-∞=-=-=m m m n R m R m n h m x n y )()()()()(44在该例题中， R 4(m)的非零区间为0≤m ≤3， R 4(n －m)的非零区间为0≤n －m ≤3，或写成n －3≤m ≤n ，这样y(n)的非零区间要求m 同时满足下面两个不等式：0≤m ≤3 m －3≤m ≤n上面公式表明m 的取值和n 的取值有关， 需要将n 作分段的假设。
·1·第1章 时域离散信号和系统1.1 引 言本章内容是全书的基础。
学生从学习模拟信号分析与处理到学习数字信号处理，要建立许多新的概念，数字信号和数字系统与原来的模拟信号和模拟系统不同，尤其是处理方法上有本质的区别。
模拟系统用许多模拟器件完成，数字系统用运算方法完成。
如果对本章中关于数字信号与系统的若干基本概念不清楚，那么在学习数字滤波器时，会感到不好掌握，因此学好本章是很重要的。
1.2 本章学习要点(1) 关于信号● 模拟信号、时域离散信号、数字信号三者之间的区别。
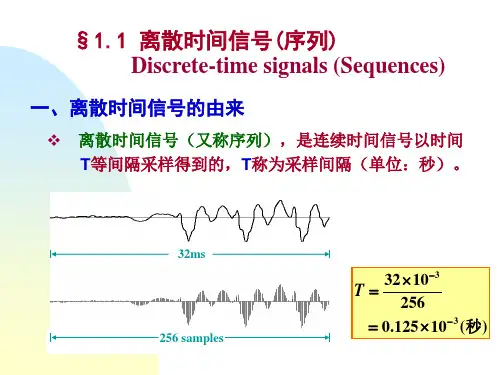
● 如何由模拟信号产生时域离散信号。
● 常用的时域离散信号。
● 如何判断信号是周期性的，其周期如何计算。
(2) 关于系统● 什么是系统的线性、时不变性，以及因果性、稳定性；如何判断。
● 线性、时不变系统输入和输出之间的关系；求解线性卷积的图解法、列表法、解析法，以及用MA TLAB 工具箱函数求解。
● 线性常系数差分方程的递推解法。
● 用MA TLAB 求解差分方程。
● 什么是滑动平均滤波器，它的单位脉冲响应是什么。
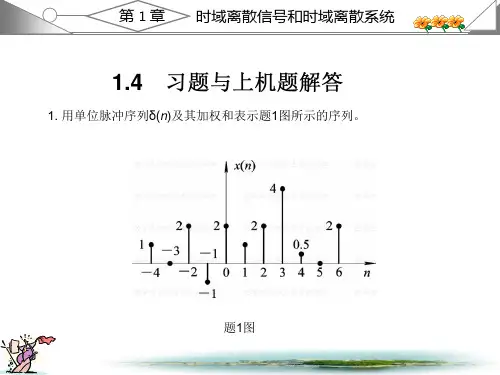
1.3 习题与上机题解答1.1 用单位脉冲序列及其加权和表示图P1.1所示的序列。
解：()(2)(1)2()(1)2(2)3(3)(4)2(6)x n n n n n n n n n δδδδδδδδ=+-+++-+-+-+-+-1.2 给定信号24,4≤≤1()4,0≤≤40,n n x n n +--⎧⎪=⎨⎪⎩其他(1) 画出x (n )的波形，标上各序列值；(2) 试用延迟的单位脉冲序列及其加权和表示x (n )序列； (3) 令1()2(2)x n x n =-，画出1()x n 的波形； (4) 令2()(2)x n x n =-，画出2()x n 的波形。
·2·解：(1) 画出x (n )的波形，如图S1.2.1所示。
图P1.1 图S1.2.1(2) ()4(4)2(3)2(1)4()4(1)4(2)4(3)4(4)x n n n n n n n n n δδδδδδδδ=+-+++++-+-+-+--。
