正弦型曲线
- 格式:doc
- 大小:445.00 KB
- 文档页数:6



用博途生成正弦曲线-概述说明以及解释1.引言1.1 概述概述本文将介绍如何使用博途软件生成正弦曲线。
正弦曲线是一种常见的曲线形式,具有许多应用场景。
通过博途软件,我们可以轻松地生成并调整正弦曲线的各种参数,如振幅、频率和相位等,从而实现对正弦曲线的个性化定制。
在本文中,我们将首先介绍博途软件的基本概念和功能,以及正弦曲线的定义。
随后,我们将详细讲解使用博途软件生成正弦曲线的步骤,并提供一些实例演示。
最后,我们将总结博途软件生成正弦曲线的优势,探讨它的应用前景,并展望未来发展方向。
通过本文的阅读,读者将能够全面了解博途软件的使用方法和正弦曲线的生成过程,以及正弦曲线在不同领域的应用。
无论是对于学术研究还是工程实践,掌握使用博途生成正弦曲线的技能都将是一项有价值的能力。
接下来,让我们开始介绍博途软件及其强大的正弦曲线生成功能。
文章结构是指文章整体的组织架构和章节安排。
一个清晰的文章结构可以帮助读者更好地理解和获取信息。
本文将按照以下结构进行论述:1. 引言1.1 概述:介绍博途生成正弦曲线的重要性和应用背景。
1.2 文章结构:说明本文的章节组织和内容安排。
1.3 目的:明确本文的目标和意义。
2. 正文2.1 博途软件介绍:简要介绍博途软件的功能和特点。
2.2 正弦曲线的定义:详细解释正弦曲线的概念和数学表达式。
2.3 使用博途生成正弦曲线的步骤:具体介绍在博途软件中生成正弦曲线的方法和操作步骤。
3. 结论3.1 总结博途生成正弦曲线的优势:回顾使用博途生成正弦曲线的优点和好处。
3.2 应用前景:展望博途生成正弦曲线在各个领域的应用前景,如教育、工程等。
3.3 未来发展方向:探讨博途生成正弦曲线在功能和性能上的改进和拓展方向。
通过以上的文章结构,读者可以清晰地了解到本文的主要内容,并根据自己的需求选择性地阅读相关章节。
同时,文章结构也有助于作者逻辑清晰地展开论述,使整篇文章更具条理性和可读性。
1.3 目的:本文旨在介绍如何通过博途软件生成正弦曲线,探讨其在工程领域中的应用和优势。

正弦相位曲线
正弦相位曲线(或称为正弦波)是描述平稳周期振荡的数学曲线,它在基础数学、应用数学、物理、工程、信号处理和许多其他领域都有广泛的应用。
正弦波是以正弦函数命名的,它是正弦函数的图像。
正弦曲线的函数表达式通常为y = Asin(ωx + φ) + k,其中 A 表示振幅,ω 表示角频率,φ 表示初相位,x 表示自变量,y 表示因变量,k 是偏距。
正弦曲线的形状由这些参数共同决定,不同的参数组合会得到不同的曲线形状。
正弦函数的相位指的是波形在水平方向上平移的距离,也可以理解为信号的时间偏移。
对于一般的正弦函数y = A sin (ωx + φ),φ 就是正弦曲线左右平移的距离。
当φ=0 时,正弦函数图像没有经过平移。
正弦曲线是一种周期性函数,其值在一定的时间或角度范围内以一定频率反复变化。
此外,正弦曲线还是一种偶函数,即y = sin(x) = -sin(-x)。
正弦曲线的最大值为1,最小值为-1,周期为2π。
正弦曲线和余弦曲线是不同相位的正弦曲线,因为余弦波可以被视为相移为π/2 弧度的正弦波。
以上是正弦相位曲线的基本概念和性质,希望对你有所帮助。
如果你需要更深入的理解或有其他相关问题,欢迎继续提问。

高中数学正弦型曲线教案
一、教学目标
1. 了解正弦函数的定义及性质。
2. 掌握正弦函数的图像特征。
3. 能够利用正弦函数解决实际问题。
二、教学重点和难点
1. 正弦函数的定义及性质。
2. 正弦函数的图像特征。
三、教学准备
1. 教材课本及教辅材料。
2. 教学投影仪及相关幻灯片。
四、教学步骤
1. 引入:介绍正弦函数的定义及性质,引导学生了解正弦函数的基本概念。
2. 讲解:讲解正弦函数的图像特征,包括振幅、周期、相位等概念。
3. 实例演练:通过例题演练,让学生掌握正弦函数的应用方法。
4. 课堂练习:让学生进行课堂练习,加深对正弦函数的理解。
5. 拓展应用:引导学生将正弦函数应用于实际问题中,加深对正弦函数的理解。
五、教学反馈
1. 对学生进行课堂讨论,让学生分享自己的理解和体会。
2. 收集学生反馈意见,及时调整教学方式。
六、教学延伸
1. 鼓励学生研究正弦函数的更深层次的知识,拓展数学思维。
2. 引导学生自主学习,探索正弦函数的更多应用场景。
七、课后作业
1. 完成课后习题,巩固所学知识。
2. 拓展阅读相关教材,加深对正弦函数的理解。
八、教学总结
1. 总结本节课的重点内容,引导学生对学习进行反思和总结。
2. 展望下节课内容,激发学生学习兴趣。
以上是本节课的教案范本,希望能对你的教学有所帮助。
祝教学顺利!。

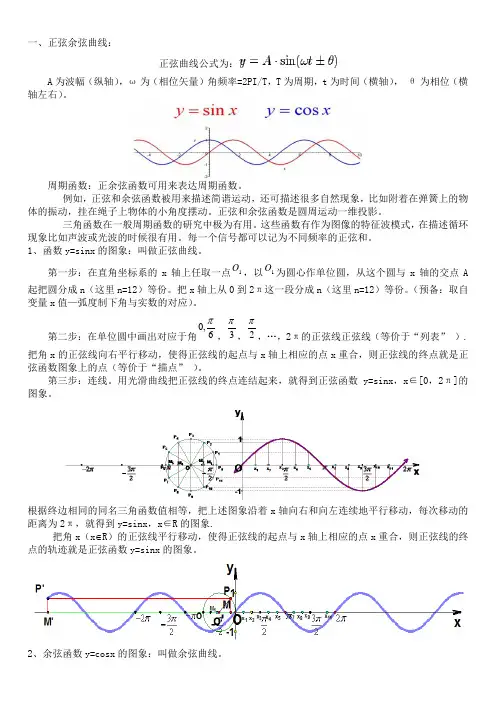
一、正弦余弦曲线: 正弦曲线公式为:A 为波幅(纵轴),ω为(相位矢量)角频率=2PI/T ,T 为周期,t 为时间(横轴), θ为相位(横轴左右)。
周期函数:正余弦函数可用来表达周期函数。
例如,正弦和余弦函数被用来描述简谐运动,还可描述很多自然现象,比如附着在弹簧上的物体的振动,挂在绳子上物体的小角度摆动。
正弦和余弦函数是圆周运动一维投影。
三角函数在一般周期函数的研究中极为有用。
这些函数有作为图像的特征波模式,在描述循环现象比如声波或光波的时候很有用。
每一个信号都可以记为不同频率的正弦和。
1、函数y=sinx 的图象:叫做正弦曲线。
第一步:在直角坐标系的x 轴上任取一点1O ,以1O 为圆心作单位圆,从这个圆与x 轴的交点A 起把圆分成n (这里n=12)等份。
把x 轴上从0到2π这一段分成n (这里n=12)等份。
(预备:取自变量x 值—弧度制下角与实数的对应)。
第二步:在单位圆中画出对应于角6,0π,3π,2π,…,2π的正弦线正弦线(等价于“列表” ).把角x 的正弦线向右平行移动,使得正弦线的起点与x 轴上相应的点x 重合,则正弦线的终点就是正弦函数图象上的点(等价于“描点” )。
第三步:连线。
用光滑曲线把正弦线的终点连结起来,就得到正弦函数y=sinx ,x ∈[0,2π]的图象。
根据终边相同的同名三角函数值相等,把上述图象沿着x 轴向右和向左连续地平行移动,每次移动的距离为2π,就得到y=sinx ,x ∈R 的图象.把角x (x ∈R )的正弦线平行移动,使得正弦线的起点与x 轴上相应的点x 重合,则正弦线的终点的轨迹就是正弦函数y=sinx 的图象。
2、余弦函数y=cosx 的图象:叫做余弦曲线。
根据诱导公式,可以把正弦函数y=sinx的图象向左平移2π单位即得余弦函数y=cosx的图象。
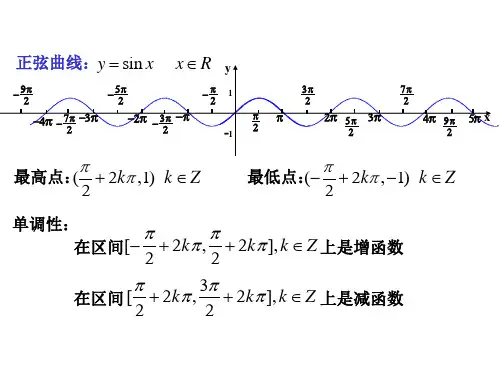
3、用五点法作正弦函数和余弦函数的简图(描点法):正弦函数y=sinx,x∈[0,2π]的图象中,五个关键点是:(0,0)、(2π,1)、(π,0)、(23π,-1)、(2π,0)。


拓扑学家的正弦曲线
拓扑学是研究几何图形在连续变形下保持不变的性质的一门学科。
在拓扑学中,一些简单的几何图形,如圆、球、矩形等,被视为基本图形。
而复杂的图形则可以由这些基本图形通过“粘合”、“切割”等方式得到。
正弦曲线是一个典型的由连续函数生成的复杂图形。
正弦曲线是周期函数,它的形状会随着参数的变化而变化。
想象一下,当一个球被无限拉伸时,它可能会变成一个圆;而当一个圆被挤压时,它可能会变成一个椭圆。
这些变化都是连续的,也即在拓扑学中,它们被认为是同胚的。
正弦曲线也可以看作是这种连续变化的产物。
在数学上,正弦曲线可以用函数y=sin(x)来表示。
这个函数在-π到π之间是周期性的,形状类似于波浪。
这个波浪可以看作是由无数个小的三角形组成,每个三角形的高就是正弦函数的值。
当我们考虑正弦曲线的拓扑性质时,我们会发现它其实是一个封闭的图形,也就是说,它的起点和终点是相连的。
这与球体相似,但与线段不同。
线段有两个端点,而正弦曲线的“端点”是相连的。
此外,正弦曲线还有一个重要的性质,那就是它是连续的。
这意味着如果你在正弦曲线上取任意两点,你可以通过一系列连续的变换将它们连接起来。
这与球体和线段的性质类似,但与矩形不同,因为矩形的对角线不是连续的。
总的来说,正弦曲线是一个非常有趣的几何图形,它具有许多独特的拓扑性质。
通过对正弦曲线的深入研究,我们可以更好地理解拓扑学的基本概念和原理。
美术鉴赏正弦曲线
正弦曲线是一种基本的数学曲线,也是美术创作中常用的造型元素之一。
它的形状优美而和谐,给人一种舒适和平静的感觉。
在美术鉴赏中,正弦曲线常常被用来描绘自然界中的曲线形态,例如海浪、山脉等。
正弦曲线的特点是周期性重复,即在一定的距离上呈现相同的形状。
这种特性使得它在美术创作中具有较大的灵活性和表现力。
艺术家们可以利用正弦曲线的周期性特点,创造出丰富多样的艺术作品。
在绘画中,正弦曲线可以用来描绘人物的体态和姿势。
人体的肌肉和骨骼结构常常呈现出曲线的形态,而正弦曲线恰好可以捕捉到这种动态和流畅感。
通过运用正弦曲线,艺术家可以更加准确地表现人物的形态和动作,使作品更富有生命力。
在雕塑中,正弦曲线常被用来塑造曲线优美的雕塑形态。
雕塑家可以通过运用正弦曲线的技巧,赋予作品流动感和动态感。
正弦曲线的曲折与平滑变化,可以使雕塑作品更富有变化和层次感,给人一种自然和谐的审美体验。
此外,正弦曲线在建筑设计中也有广泛的应用。
建筑师可以借鉴正弦曲线的形态,设计出曲线流畅的建筑外观。
这种曲线的运用可以使建
筑更加具有艺术感和吸引力,在城市景观中成为独特的标志。
总的来说,美术鉴赏中的正弦曲线是一种具有优美形态和丰富表现力的元素。
在绘画、雕塑和建筑等艺术领域中,正弦曲线都能够为作品增添美感和艺术价值。
通过对正弦曲线的运用和创造,艺术家们可以展现出自己独特的艺术风格和创造力。
正弦曲线运动轨迹是一种周期性变化的运动,其路径可以被描述为一个正弦函数的图形。
正弦曲线通常用来描述具有周期性往复特点的运动,例如简谐振动。
在数学上,正弦曲线可以表示为 y = A sin(ωx + φ) 的形式,其中:1. 振幅(A):表示运动的最大偏离量,即峰值到平衡位置的距离。
在直线往复运动中,振幅等于行程的一半。
2. 角频率(ω):与运动的周期和速度有关,决定了每单位时间内完成周期的次数。
3. 相位(ωx+φ):反映了运动状态的变化,包括初相(φ),它决定了在t=0时刻曲线的位置。
4. 周期(T):完成一个完整循环所需的时间。
此外,在物理世界中,正弦曲线运动轨迹可以体现在多种场合,比如钟摆的摆动、弹簧振子的运动,甚至是天体观测中的星下点轨迹等。
总之,正弦运动的特点是开始时速度最快,随着接近极值点速度逐渐减慢直至为零,然后再返回。
因此,这种运动轨迹在工程学、物理学和许多其他科学领域中都有广泛的应用。
在工程领域,正弦曲线运动被广泛应用于设计和控制各种机械设备。
例如,在汽车工程中,正弦曲线可以帮助优化发动机的点火系统和燃油喷射系统,以提高燃烧效率。
在建筑领域,正弦曲线可以指导建筑物的抗震设计,通过模拟地震波的运动轨迹,预测和减小地震对建筑物的影响。
在生物学中,正弦曲线也有其独特的应用。
生物体内的许多生理过程,如心跳、呼吸和肌肉收缩,都具有周期性往复的特点。
正弦曲线可以帮助研究人员了解这些生理过程的规律,为疾病的预防和治疗提供理论依据。
此外,正弦曲线还可以用于生物信号的处理和分析,如脑电图、心电图等。
在通信领域,正弦曲线运动轨迹在无线电信号的传输和处理中起到关键作用。
无线通信信号通常采用正弦波形,通过调整正弦波的频率、相位和振幅,实现多路信号的复用和干扰抑制。
正弦曲线在这一领域的研究,有助于提高通信系统的性能和容量。
在艺术领域,正弦曲线运动轨迹也为艺术家提供了丰富的创作灵感。
例如,在音乐中,正弦波是基本音高的基础,通过不同频率的正弦波叠加,可以合成出丰富多彩的音乐旋律。
正弦型函数的图象与性质
1. 三角函数图象变换路线:sin y x =ϕ−−−−−→左移个单位
sin()y x ϕ=+ ω
−−−−−→横坐标变为倍
sin()y x ωϕ=+A −−−−−
→纵坐标变为倍
sin()y A x ωϕ=+. 或:sin y x = ω
−−−−−→1
横坐标变为倍
sin y x ω=ϕ
ω
−−−−−
→左移个单位
sin ()y x ϕωω
=+A −−−−−
→纵坐标变为倍
sin()y A x ωϕ=+. 注意:()y=sin x+ y=sin x+ϕϖϕϖϖ
⎛⎫ ⎪⎝
⎭
应先化为 图象平移:x 左加右减、y 上加下减。
例如:向左平移1个单位,解析式变为])1(sin[ϕω++=x A y 向下平移3个单位,解析式变为3)sin(-+=ϕωx A y
3. 三角函数的值域的求法:y=asinx+bcosx 型,引入辅助角ϕ ,化为y=22b a +sin
(x+ϕ),利用函数()1sin ≤+ϕx 即可求解。
Y=asin 2
x+bsinxcosx+mcos 2
x+n 型
亦可以化为此类。
4. 绝对值或平方对三角函数周期性的影响:一般说来,某一周期函数解析式加绝对值
或平方,其周期性是:弦减半、切不变.既为周期函数又是偶函数的函数自变量加
绝对值,其周期性不变,其它不定。
如x y x y sin ,sin 2==的周期都是π,
|tan |y x =的周期不变; 但sin cos y x x =+x x y cos sin +=的周期为
2
π
, y=|tan x |的周期不变,
5. 辅助角公式(化一公式)
)sin(cos sin 22ϕ++=+=x b a x b x a y 其中a
b =
ϕtan
常用结论: sin cos )4
π
ααα+=
+
sin 2sin()3
π
ααα=+
cos 2sin()6
π
ααα+=+
6. 求三角复合函数的对称性的通法,
一般是将其化归成研究基本三角函数sin y α=、cos y α=、tan y α=的对称性。
7. 求三角函数的单调区间问题的通法是,直接观察基本三角函数sin y x =、
cos y α=、tan y α=的单调区间,从而得到三角复合函数的单调区间。
本
题中函数的单调区间是是在特定的区间内的,一般是先求出所有的单调
区间,然后在看哪些区间落在规定区域内。
()f x x
=)
4
π
-
,令
]2
2,22[4π
ππππ+-∈-
k k x Z k ∈) 则[2x k π∈3,2]44k πππ-+,由于]2,0[π∈x ,则
)(x f 在]2,0[π内单调递增区间为]4
3,0[π和]2,4
7[ππ
;
8. 求函数()sin )f x A x ωϕ=+(在某个给定的区域内的最值问题通用的方法是:
根据自变量限定的区域,求出x ωϕ+的整体的取值范围,从而把问题转化成求sin y A α=的值域问题。
【练习】:
1. 函数)cos (sin cos 2x x x y +=的图象的对称中心和对称轴分别是__________、
____________(答:128k (
,)(k Z )ππ-∈、28
k x (k Z )ππ
=+∈)
;
2. 已知f (x )sin(x )x )θθ=+++为偶函数,求θ的值。
(答:
6
k (k Z )π
θπ=+∈)
3. 函数2
5f (x )sin x cos x x =-x R )∈的单调递增区间为___________(答:512
12
[k ,k ](k Z )π
π
ππ-+
∈) 4. 关于函数)
(),32sin(4)(R x x x f ∈+=π
有下列命题:
①由f(x 1)=f(x 2)=0可得x 1-x 2必是π的整数倍;
②y =f(x)的表达式可改写为
)6
2sin(4)(π-=x x f ; ③y =f(x)的图像关于点)0,6
(π-对称;
④y =f(x)的图像关于直线x =6
π-对称。
其中正确的命题的序号是2、3。
(注:把你认为正确的命题的序号都填上) 5. 函数y=sin(x-6
π)·cosx 的最小值是_______。
-4
3
解:利用积化和差公式(注:今后高考试卷中会提供公式),得
y=21[sin(2x-6
π)]+sin(-6π)]
=21sin(2x-6π)-4
1。
∵sin(2x-6
π)∈[-1,1],
∴y min =-4
3
注:若试卷中没给出积化和差公式,则应将sin(x-
6
π
)展开进行化简。