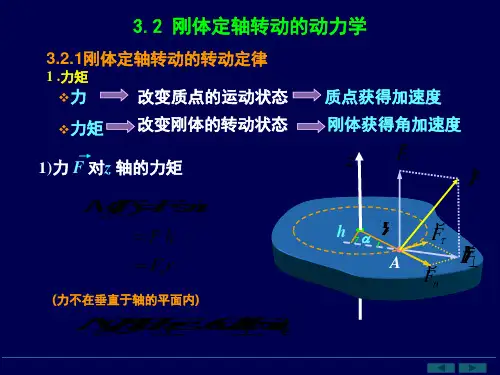
刚体定轴转动的转动定律
- 格式:ppt
- 大小:671.56 KB
- 文档页数:35


刚体转动定律引言刚体转动定律是描述刚体绕固定轴进行旋转时运动规律的物理定律。
在刚体力学中,刚体是指其内部各点的相对位置保持不变的物体。
刚体转动定律主要包括角动量守恒、角加速度与力矩之间的关系以及转动惯量等内容。
本文将从这些方面对刚体转动定律进行详细介绍。
角动量守恒角动量是描述旋转物体运动状态的重要物理量,定义为质点或刚体绕某一轴线旋转时,其线性动量相对于该轴线的偏离程度。
在没有外力作用下,系统的角动量守恒。
角动量L可以表示为L = Iω,其中I是物体的转动惯量,ω是物体的角速度。
根据角速度ω = Δθ/Δt可以得到L = IΔθ/Δt。
当一个刚体受到外力矩作用时,根据牛顿第二定律可以得到F = ma,同样地,在角度上也有τ = Iα。
其中τ表示力矩,I表示物体的转动惯量,α表示物体的角加速度。
当刚体绕固定轴转动时,如果外力矩为零,则根据牛顿第二定律可以得到τ = 0,进而推导出Iα = 0。
由此可见,在没有外力矩作用下,刚体的角加速度为零,即角动量守恒。
转动惯量转动惯量是描述物体对于旋转运动的惯性大小的物理量。
对于一个质点来说,其转动惯量可以表示为I = mr²,其中m是质点的质量,r是质点到轴线的距离。
对于一个复杂形状的刚体来说,其转动惯量则需要通过积分计算得到。
对于连续分布的物体来说,其转动惯量可以表示为I = ∫r²dm。
不同形状和布局的刚体具有不同的转动惯量。
例如,对于一个围绕自身中心垂直旋转的圆盘来说,其转动惯量可以表示为I = ½MR²,其中M是圆盘的质量,R是圆盘半径。
角加速度与力矩之间的关系当刚体受到外力矩作用时,根据牛顿第二定律可以得到τ = Iα。
这个关系描述了力矩和角加速度之间的关系。
对于一个质点来说,其角加速度可以表示为α = τ/I,其中τ是作用在质点上的力矩,I是质点的转动惯量。
对于一个复杂形状的刚体来说,其转动惯量不仅与质量有关,还与物体的形状和布局有关。

刚体定轴转动定律公式刚体定轴转动定律是描述刚体绕定轴做转动运动的数学公式。
本文将详细介绍刚体定轴转动定律的公式及相关参考内容。
1.刚体定轴转动定律公式1.1角位移公式刚体绕定轴做转动运动时,它的每一个质点都有一个角位移,角位移是一个标量,用Δθ表示。
角位移与刚体绕定轴转动的弧长有关,它们之间的关系可以用以下公式表示:Δθ = Δl / r其中,Δl表示弧长的长度,r表示刚体绕定轴的半径。
1.2角速度公式角速度是描述刚体绕定轴的旋转速度的物理量,用ω表示,角速度是一个矢量,它的方向垂直于刚体绕定轴的平面,符号和方向由右手定则确定。
角速度与角位移之间的关系可以用以下公式表示:ω = Δθ / Δt其中,Δt表示时间间隔。
1.3角加速度公式角加速度是描述刚体绕定轴转动加速度的物理量,用α表示,角加速度是一个矢量,它的方向也垂直于刚体绕定轴的平面,符号和方向由右手定则确定。
角加速度与角速度之间的关系可以用以下公式表示:α = Δω / Δt其中,Δt表示时间间隔。
1.4力矩公式力矩是描述外力对刚体绕定轴转动影响的物理量,用M表示,力矩是一个矢量,它的方向垂直于刚体绕定轴的平面,符号和方向由右手定则确定。
力矩与角加速度之间的关系可以用以下公式表示:M = I α其中,I表示刚体绕定轴的转动惯量,α表示角加速度。
2.参考内容2.1转动惯量的定义转动惯量是描述刚体绕定轴转动惯性的物理量,用I表示,它反映了刚体对于绕定轴转动的惯性大小。
转动惯量的计算方法取决于刚体的形状和密度分布。
常见的刚体的转动惯量计算公式:(1)矩形薄板绕转轴的转动惯量Izz = 1/12m(a²+b²)其中,m表示薄板的质量,a和b表示薄板的长和宽。
(2)圆环绕轴的转动惯量Izz = mr²其中,m表示圆环的质量,r表示圆环的半径。
2.2角动量的定义角动量是描述刚体绕定轴转动动量的物理量,用L表示,它反映了刚体绕定轴转动的惯性大小和角速度大小。


![[理学]第5章 刚体的定轴转动_OK](https://uimg.taocdn.com/1edbe6d74b35eefdc8d333f9.webp)