黄金分割(正)

黄金分割黄金分割概念把一条线段分割为两部分，使其中一部分与全长之比等于另一部分与这部分之比。

其比值是(√5-1)/2，取其前三位数字的近似值是0.618。

由于按此比例设计的造型十分美丽柔和，因此称为黄金分割，也称为中外比。

这是一个十分有趣的数字，我们以0.618来近似，通过简单的计算就可以发现：1÷0.618≈1.618 (1-0.618)÷0.618≈0.618这个数值的作用不仅仅体现在诸如绘画、雕塑、音乐、建筑等艺术领域，而且在管理、工程设计等方面也有着不可忽视的作用。

黄金分割发现关于黄金分割比例的起源大多认为来自毕达哥拉斯，据说在古希腊，有一天毕达哥拉斯走在街上，在经过铁匠铺前他听到铁匠打铁的声音非常好听，于是驻足倾听。

他发现铁匠打铁节奏很有规律，这个声音的比例被毕达哥拉斯用数理的方式表达出来。

被应用在很多领域，后来很多人专门研究过，开普勒称其为“神圣分割”也有人称其为“金法”。

在金字塔建成1000年后才出现毕达哥拉斯定律，可见这很早就存在。

只是不知这个谜底。

编辑本段算路率简介理笔录百算分制胜法规律计策，观测远古的几轮计算，黄金轮算法不一样数字，论发展发现史，由于公元前6世纪古希腊的毕达哥拉斯学派研究过正五边形和正十边形的作图，因此现代数学家们推断当时毕达哥拉斯学派已经触及甚至掌握了黄金分割。

公元前4世纪，古希腊数学家欧多克索斯第一个系统研究了这一问题，并建立起比例理论。

公元前300年前后欧几里得撰写《几何原本》时吸收了欧多克索斯的研究成果，进一步系统论述了黄金分割，成为最早的有关黄金分割的论著。

中世纪后，黄金分割被披上神秘的外衣，意大利数家帕乔利称中末比为神圣比例，并专门为此著书立说。

德国天文学家开普勒称黄金分割为神圣分割。

到19世纪黄金分割这一名称才逐渐通行。

黄金分割数有许多有趣的性质，人类对它的实际应用也很广泛。

最著名的例子是优选学中的黄金分割法或0.618法，是由美国数学家基弗于1953年首先提出的，70年代在中国推广。

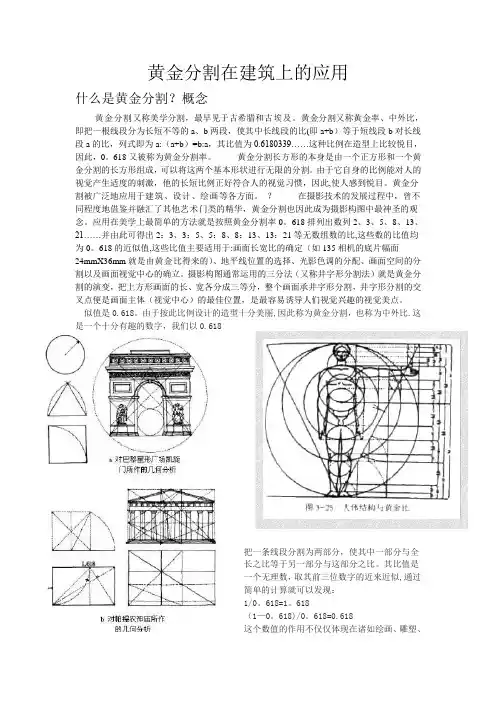
黄金分割在建筑上的应用什么是黄金分割？概念黄金分割又称美学分割，最早见于古希腊和古埃及。

黄金分割又称黄金率、中外比，即把一根线段分为长短不等的a、b两段，使其中长线段的比(即a+b）等于短线段b对长线段a的比，列式即为a:（a+b）=b:a，其比值为0.6180339……这种比例在造型上比较悦目，因此，0。

618又被称为黄金分割率。

黄金分割长方形的本身是由一个正方形和一个黄金分割的长方形组成，可以将这两个基本形状进行无限的分割。

由于它自身的比例能对人的视觉产生适度的刺激，他的长短比例正好符合人的视觉习惯，因此,使人感到悦目。

黄金分割被广泛地应用于建筑、设计、绘画等各方面。

？在摄影技术的发展过程中，曾不同程度地借鉴并融汇了其他艺术门类的精华，黄金分割也因此成为摄影构图中最神圣的观念。

应用在美学上最简单的方法就是按照黄金分割率0。

618排列出数列2、3、5、8、13、21……并由此可得出2：3、3：5、5：8、8：13、13：21等无数组数的比,这些数的比值均为0。

618的近似值,这些比值主要适用于:画面长宽比的确定（如135相机的底片幅面24mmX36mm就是由黄金比得来的）、地平线位置的选择、光影色调的分配、画面空间的分割以及画面视觉中心的确立。

摄影构图通常运用的三分法（又称井字形分割法）就是黄金分割的演变，把上方形画面的长、宽各分成三等分，整个画面承井字形分割，井字形分割的交叉点便是画面主体（视觉中心）的最佳位置，是最容易诱导人们视觉兴趣的视觉美点。

似值是0.618。

由于按此比例设计的造型十分美丽,因此称为黄金分割，也称为中外比.这是一个十分有趣的数字，我们以0.618把一条线段分割为两部分，使其中一部分与全长之比等于另一部分与这部分之比。

其比值是一个无理数，取其前三位数字的近来近似,通过简单的计算就可以发现：1/0。

618=1。

618（1—0。

618)/0。

618=0.618这个数值的作用不仅仅体现在诸如绘画、雕塑、音乐、建筑等艺术领域，而且在管理、工程设计等方面也有着不可忽视的作用.让我们首先从一个数列开始,它的前面几个数是：1、1、2、3、5、8、13、21、34、55、89、144…。

黄金分割-正五边形
图（一）图（二）
图（三）图（四）
正五边形中包含着美妙的黄金分割，在一个正五边形里（如图（一））画出一个星形（如图（二）），这个星形是由五条对角线构成，每一条对角线的长度恰好是正五边形每一边长的倍，继续在星形中间的五角形再画上一个小星形（如图（三）），在小星形中再画上一个更小的星形（如图（四）），如此这般一直画下去，可得到一个碎形图形，而这些小星形的边长比例也都和有关呢！
利用GSP画出黄金分割一正五边形的作法如下：
1.画一线段AB，以AB为一边，作正五边形ABCDE，连
对角线AC、AD、BD、BE、CE
2.利用Iterate将A、B两点分别用F、G两点取代，即可得出如图
（三），再按Ctrl+〝+〞可得出如图（四），如此这般一直画下去，理论上可以无限作下去，即可作出黄金分割一正五边形。

2
5
1+
2
5
1+。

黄金分割的应用什么是黄金分割黄金分割（Golden Ratio），又称黄金比例、黄金均衡、黄金分割比等，是一种数学比例关系，常用希腊字母φ（phi）表示。

其数值约为1.6180339887。

黄金分割在艺术、建筑、设计等领域有广泛的应用，被认为是一种极具美感的比例关系。

黄金分割在艺术中的应用黄金分割在艺术中的应用可以追溯到古希腊时期。

许多古希腊的雕塑、绘画和建筑作品都使用了黄金分割作为设计基准。

例如，著名的雕塑家波利克列托斯创造的雕塑《斯特拉卡斯女孩》就使用了黄金分割比例。

黄金分割可以产生一种令人愉悦和和谐的美感，让人们对艺术作品产生更深的共鸣。

黄金分割在建筑设计中的应用黄金分割在建筑设计中也拥有重要的应用价值。

许多古代建筑，如帕台农神殿、金字塔和水立方等，都采用了黄金分割比例来确定建筑元素的大小和位置关系。

黄金分割可以使建筑物更加谐调和和谐，给人一种平衡稳定的感觉。

现代建筑设计中，一些设计师仍然使用黄金分割来提高建筑的美感和观赏性。

黄金分割在设计中的应用黄金分割也被广泛应用于各种设计领域，如平面设计、产品设计和网页设计等。

设计师可以使用黄金分割比例来确定设计元素的大小、位置和比例关系，以达到视觉上的平衡和谐。

在平面设计中，将设计元素放置在黄金分割线上或黄金分割点附近，可以使设计更加吸引人。

在产品设计中，黄金分割可以帮助设计师确定产品的比例和形状，使产品更加美观和符合人体工程学。

在网页设计中，应用黄金分割可以改善网页的布局和排版，使用户更容易阅读和理解内容。

黄金分割在摄影中的应用黄金分割在摄影中也被广泛运用。

摄影师可以使用黄金分割线将画面分割成三个垂直或水平的部分，将主要主题放置在黄金分割线上，从而使画面更加平衡和吸引人。

黄金分割还可以用来确定景物在画面中的位置和比例关系，以达到更好的构图效果。

总结黄金分割作为一种数学比例关系，在艺术、建筑、设计和摄影等领域都有广泛的应用。

它可以产生一种美感和和谐感，被认为是一种理想的比例关系。

黄金分割的正确计算方法再谈一下空间的黄金分割（大盘5522 点--1664 点）对当前行情的定义：阶段高位高点:低点:周线位: + 位:+ 位:+ 位:+再看一下周线:81 周线90 周线99如下跌不破81 周线就可买股（以收盘价为准）再从时间周期: 我讲7月7日左右要变盘，还有7月23日要变盘,从7月7 日到7 月23 日有12 个交易日，你取一半看一下, 如你从7 月15 日左右再看一下，当然如果你的股票有时与大盘不同步，你一定找一下你买的理由，你卖出的理由，你赚钱只能靠你自己，再说一下时间周期:2008年1月14日---2008 年10月28日共下降192交易日:从2008 年10 月29 日到2009 年6 月17 日共计155 个交易日从2008 年10 月29 日到2009 年8 月7 日共计192 个交易日（到此完成一个上升周期，感觉有点难）个人认为调整后观察上海40月线的支撑, 如收盘不破，在时间周期内，就可找一个目标股操作了，一定记住，市场永远是对的.在这里，我们将说明如何得到黄金分割线，并根据它们指导下一步的买卖股票的操作以下就是方法：画单点有两个因素（一是黄金数字，二是最高或最低点）画黄金分割线的第一步是记住若干个特殊的数字：最为重要，股价极容易在由这4 个数产生的黄金分割线处产生支撑和压力。

第二步是找到一个点。

这个点是上升行情结束，调头向下的最高点，或者是下降行情结束，调头向上的最低点。

当然，我们知道这里的高点和低点都是指一定的范围，是局部的。

只要我们能够确认一趋势（无论是上升还是下降）已经结束或暂时结束，则这个趋势的转折点就可以作为进行黄金分割的点。

这个点一经选定，我们就可以画出黄金分割线了。

在上升行情开始调头向下时，我们极为关心这次下落将在什么位置获得支撑。

黄金分割提供的是如下几个价位。

它们是由这次上涨的顶点价位分别乘上上面所列的几个特殊数字中的几个。

假设，这次上涨的顶点是10 元，则这几个价位极有可能成为支撑，其中和的可能性最大同理，在下降行情开始调头向上时，我们关心上涨到什么位置将遇到压力。

黄金分割的正确计算方法
黄金分割是一种美学比例，也是一种数学比例，它是指一条线段分为两部分，使整条线段与较短部分之比等于较短部分与较长部分之比。

黄金分割比例被广泛运用在建筑、绘画、雕塑等艺术领域，被认为是最具美感的比例之一。

在数学中，黄金分割比例被表示为Φ（phi），其值约为1.618。

黄金分割的正确计算方法可以通过以下步骤进行：
1. 设定问题，首先，我们需要明确需要计算黄金分割的线段长度，例如线段AB的长度为x。

2. 建立等式，根据黄金分割的定义，我们可以建立如下等式，(x-a)/a = a/x，其中a为较短部分的长度。

3. 解方程，将等式进行变形，得到x^2 ax a^2 = 0。

然后，我们可以使用一元二次方程的求根公式来解这个方程，得到x = (1+√5)a/2 或 x = (1-√5)a/2。

4. 计算结果，根据上述公式，我们可以计算出黄金分割的两个部分的长度。

需要注意的是，黄金分割比例是一个无理数，无法用有限的小数表示，因此在实际计算中，我们可以采用近似值来进行计算。

通常情况下，我们可以取Φ的近似值1.618进行计算。

除了通过数学方法计算黄金分割外，我们还可以通过绘图的方式来构造黄金分割。

通过绘制正方形和正三角形，我们可以很容易地构造出黄金分割比例。

总之，黄金分割是一种重要的美学比例和数学比例，它在艺术和设计中具有广泛的应用。

掌握黄金分割的正确计算方法，可以帮助我们更好地理解和运用这一比例，从而创作出更具美感和和谐的作品。

黄金分割的正确计算方法黄金分割，又称黄金比例，是一种被广泛应用于艺术、建筑、设计等领域的比例关系。

它被认为是一种美学上的完美比例，具有对称、和谐、美感等特点。

在数学上，黄金分割的比例大约是1:1.618，这个比例在很多自然界和人类创造的事物中都可以找到。

在本文中，我们将介绍黄金分割的正确计算方法，希望能帮助大家更好地理解和应用这一美学原理。

首先，我们来介绍黄金分割的基本原理。

黄金分割是指一条线段，被分割成两部分，使整体与较大部分之间的比例等于较大部分与较小部分之间的比例。

数学上可以用如下的表达式来表示：（a + b）/ a = a / b = φ。

其中，a为整体的长度，b为较小部分的长度，φ为黄金分割比例，约等于1.618。

根据这个表达式，我们可以得到黄金分割的计算方法。

计算黄金分割的方法如下：1. 已知整体长度，求较大部分和较小部分的长度：假设整体长度为x，较大部分为a，较小部分为b，根据黄金分割的定义，我们可以得到以下等式：x / a = a / b = φ。

解方程组，可以得到：a = x / φ。

b = x a。

2. 已知较大部分或较小部分的长度，求另一部分的长度：如果已知较大部分a的长度，我们可以通过以下公式求得较小部分b的长度：b = a / φ。

如果已知较小部分b的长度，我们可以通过以下公式求得较大部分a的长度：a =b φ。

通过以上的计算方法，我们可以准确地得到黄金分割的两个部分的长度，从而应用到设计、艺术等领域中去。

在实际应用中，黄金分割的比例被广泛应用于建筑、绘画、摄影、设计等领域。

例如，在建筑设计中，黄金分割比例被用来确定建筑物的比例尺度，使建筑物看起来更加和谐美观。

在绘画和摄影中，黄金分割比例被用来构图，使画面更加吸引人。

在设计中，黄金分割比例被用来布局，使设计更加美观大方。

总之，黄金分割是一种美学上的完美比例，它在艺术、设计等领域有着广泛的应用。

通过本文介绍的黄金分割的正确计算方法，希望能帮助大家更好地理解和应用这一美学原理，从而创作出更加美观和和谐的作品。

黄金分割是一个古老的数学方法。

对它的各种神奇的作用和魔力，数学上至今还没有明确的解释，只是发现它屡屡在实际中发挥我们意想不到的作用。

数学家法布兰斯在13世纪写了一本书，关于一些奇异数字的组合。

这些奇异数字的组合是1、1、2、3、5、8、13、21、34、55、89、144、233┅┅ 任何一个数字都是前面两数字的总和 2＝1＋1、3＝2＋1、5＝3＋2、8＝5＋3┅┅，如此类推。

有人说这些数字是他从研究金字塔所得出。

金字塔和上列奇异数字息息相关。

金字塔的几何形状有五个面，八个边，总数为十三个层面。

由任何一边看入去，都可以看到三个层面。

金字塔的长度为5813寸（5-8-13），而高底和底面百分比率是0． 618，那即是上述神秘数字的任何两个连续的比率，譬如55/89＝0．618，89/144＝0．618，144/233＝0．618。

另外，一个金字塔五角塔的任何一边长度都等于这个五角型对角线（Diagonal）的0．618。

还有，底部四个边的总数是36524．22寸，这个数字等于光年的一百倍！这组数字十分有趣。

0．618的倒数是1．618。

譬如14/89＝1．168、233/144＝1．168，而0．618×1．168＝就等于1。

另外有人研究过向日葵，发现向日葵花有89个花辫，55个朝一方，34个朝向另一方。

神秘？不错，这组数字就叫做神秘数字。

而0．618，1．618就叫做黄金分割率（Golden Section）。

在这里，我们将说明如何得到黄金分割线，并根据它们指导下一步的买卖股票的操作。

黄金分割线分为两种:单点的黄金分割线和两点黄金分割线.以下就是方法：画单点有两个因素（一是黄金数字，二是最高或最低点）画黄金分割线的第一步是记住若干个特殊的数字：0.191 0.382 0.618 0.809最为重要，股价极容易在由这4个数产生的黄金分割线处产生支撑和压力。

第二步是找到一个点。

这个点是上升行情结束，调头向下的最高点，或者是下降行情结束，调头向上的最低点。

黄金分割是一个古老的数学方法。

对它的各种神奇的作用和魔力，数学上至今还没有明确的解释，只是发现它屡屡在实际中发挥我们意想不到的作用。

数学家法布兰斯在13世纪写了一本书，关于一些奇异数字的组合。

这些奇异数字的组合是1、1、2、3、5、8、13、21、34、55、89、144、233┅┅ 任何一个数字都是前面两数字的总和 2＝1＋1、3＝2＋1、5＝3＋2、8＝5＋3┅┅，如此类推。

有人说这些数字是他从研究金字塔所得出。

金字塔和上列奇异数字息息相关。

金字塔的几何形状有五个面，八个边，总数为十三个层面。

由任何一边看入去，都可以看到三个层面。

金字塔的长度为5813寸（5-8-13），而高底和底面百分比率是0． 618，那即是上述神秘数字的任何两个连续的比率，譬如55/89＝0．618，89/144＝0．618，144/233＝0．618。

另外，一个金字塔五角塔的任何一边长度都等于这个五角型对角线（Diagonal）的0．618。

还有，底部四个边的总数是36524．22寸，这个数字等于光年的一百倍！这组数字十分有趣。

0．618的倒数是1．618。

譬如14/89＝1．168、233/144＝1．168，而0．618×1．168＝就等于1。

另外有人研究过向日葵，发现向日葵花有89个花辫，55个朝一方，34个朝向另一方。

神秘？不错，这组数字就叫做神秘数字。

而0．618，1．618就叫做黄金分割率（Golden Section）。

在这里，我们将说明如何得到黄金分割线，并根据它们指导下一步的买卖股票的操作。

黄金分割线分为两种:单点的黄金分割线和两点黄金分割线.以下就是方法：画单点有两个因素（一是黄金数字，二是最高或最低点）画黄金分割线的第一步是记住若干个特殊的数字：0.191 0.382 0.618 0.809最为重要，股价极容易在由这4个数产生的黄金分割线处产生支撑和压力。

第二步是找到一个点。

这个点是上升行情结束，调头向下的最高点，或者是下降行情结束，调头向上的最低点。

研究报告黄金分割在生活中的应用东北育才学校马艺宸一．黄金分割的定义黄金分割又称黄金律，是指事物各部分间一定的数学比例关系，即将整体一分为二，较大部分与较小部分之比等于整体与较大部分之比，其比值为1∶0.618或1.618∶1，即长段为全段的0.618。

0.618被公认为最具有审美意义的比例数字。

上述比例是最能引起人的美感的比例，因此被称为黄金分割。

二．黄金分割在生活中的应用（一）艺术中的黄金分割1.人体上的黄金分割。

最完美的人体：肚脐到脚底的距离/头顶到脚的距离=0.618。

最漂亮的脸庞：眉毛到脖子的距离/头顶到脖子的距离=0.618。

达·芬奇的《蒙娜丽莎》、拉斐尔笔下温和俊秀的圣母像，都有意无意地用上了这个比值。

人们公认的最完美的脸型——“鹅蛋”形，脸宽与脸长的比值约为0.618，如果计算一下翩翩欲仙的芭蕾演员的优美身段，可以得知，他们的腿长与身长的比值也大约是0.618，组成了人体的美。

2. 中国最古老的古琴，处处透着黄金分割的神奇，琴背两池，左龙右凤。

控制琴弦发音的枢纽有三：轸，凫掌，凤嗉。

琴有五弦，音有八度，琴节为徽。

“以琴长全体三分损一，又三分益一，而转相增减”，全弦共有十三徽。

把这些排列到一起，二池，三纽，五弦，八音，十三徽。

多么奇妙的排列，恰是费波那奇数，而两个相邻费波那奇数比率则越来越接近黄金分割率，是有意还是巧合?看来，中国古人对黄金分割的领悟与运用，与西方确有异曲同工之妙。

3.1483年左右，达芬奇画的一副未完成的油画，包围着圣杰罗姆躯体的黑线，就是一个黄金分割的矩形，当时达芬奇似乎有意利用这一黄金分割的比值。

“检阅”是法国印象派画家舍勒特的一副油画，它的画杠结构比例也正是0.618的比值。

英国在画家斐拉克曼的名著《希腊的神话和传说》一书中，工绘有96幅美人图。

每一幅画上的美人都妩媚无比婀娜多姿。

如果仔细量一下她们的比例也都也雅典娜相似。

4. 音乐家发现，二胡演奏中，“千金”分弦的比符合0.618∶1时，奏出来的音调最和谐、最悦耳。

黄金分割--数学家斐波纳奇黄金分割的历史背景和数学背景黄金分割的推销员--数学家斐波纳奇斐波纳奇是中世纪最伟大的数学家。

正是他把黄金分割的数学思想发扬光大。

他出版了三本重要的数学著作：献给罗马皇帝的《计算书》、1220年出版的《实用几何学（Practica Geometriae）》，以及《求积法（Liber Quadratorum）》。

钦佩他的比萨共和国的公民们把他记载成一位"言行谨慎，学识渊博的人",《大英百科全书》的资深编辑约瑟夫o基斯认为，未来的学者迟早会"公正地对待比萨的斐波纳奇，他是世界上伟大的学术先驱之一。

"尽管后来的世界几乎忘却了斐波纳奇，但他无疑是他那个时代的伟人。

斐波纳奇的名声是如此之大，以致于本身也是一位科学家和学者的罗马帝国皇帝弗里德里克二世（Frederic Ⅱ）为了寻找他，特别安排去比萨城访问。

斐波纳奇与弗里德里克二世的会见发生在公元1225年，这是当时比萨城的一件圣事。

皇帝一马当先，带领着由号兵、侍臣、骑士、官员和一大群野兽组成的长长的队伍。

皇帝在这位举世闻名的数学家面前提出的一些问题在《计算的书》中有详尽的记载。

斐波纳奇显然是解决了皇帝提出的问题，后来皇帝在宫廷热烈欢迎了他。

公元1228年，当斐波纳奇修订《计算的书》时，他把修订版题献给了弗里德里克二世。

斐波纳奇对金融市场的最伟大贡献就是斐波纳奇序列，也称黄金分割序列。

他的名声是如此之大，以至于人们也把黄金分割分析称为斐波纳奇分析。

黄金比例无所不在1.618(或0.618)即所谓黄金比例(Golden Ratio)或黄金平衡(Golden Mean)。

它的比例令眼睛和耳朵感到和谐。

它在生物、音乐、绘画和建筑中都有表现。

威廉·霍法(William Hoffet)在为1975年12月号的《史密森人(Smithsonian Magazine)》杂志撰写的文章中说：……0.618034与1之比是纸牌与巴台农神庙(Parthenon)、向日葵与蜗牛壳、希腊花瓶与外宇宙的螺旋星系的形状的数学基础。