磁介质习题解答

第十二章 磁介质一 选择题1. 磁介质有三种，用相对磁导率r μ表征它们各自的特征时，（ ） A ．顺磁质0r >μ，抗磁质0r <μ，铁磁质1r >>μ。

B ．顺磁质1r >μ，抗磁质1r =μ，铁磁质1r >>μ。

C ．顺磁质1r >μ，抗磁质1r <μ，铁磁质1r >>μ。

D ．顺磁质0r >μ，抗磁质0r <μ，铁磁质1r >μ。

解：选（C ）2. 关于稳恒磁场的磁场强度H 的下列几种说法中哪个是正确的？（ ） A ． H 仅与传导电流有关。

B ． 若闭合曲线内没有包围传导电流，则曲线上各点的H 必为零。

C ． 由于闭合曲线上各点H 均为零，则该曲线所包围传导电流的代数和为零。

D ． 以闭合曲线L 为边界的任意曲面的H 通量均相等。

解：由⎰∑=⋅L i I l H d ，H 的环流仅与闭合曲线内的传导电流I 有关，而不是H 仅与传导电流有关，所以A 不对。

同样，若闭合曲线内没有包围传导电流，则H 的环流为零，而不是H 为零，B 不对。

H 通量的正负与环路的积分方向有关，所以H 通量并不相同，D 不对所以选（C ）二 填空题1. 一个单位长度上密绕有n 匝线圈的长直螺线管，每匝线圈中通有强度为I 的电流，管内充满相对磁导率为μr 的磁介质，则管内中部附近磁感应强度B 的大小= ，磁场强度H 的大小= 。

解：B =nI r μμ0，H =nI2. 图示为三种不同的磁介质的B-H 关系曲线，其中虚线表示的是B =μ0H 的关系，说明a 、b 、c 各代表哪一类磁介质的B-H 关系曲线：a 代表 的B-H 关系曲线；b 代表 的B-H 关系曲线；填空题2图c 代表 的B-H 关系曲线。

解：铁磁质、顺磁质、抗磁质3． 长直电缆由一个圆柱导体和一共轴圆筒状导体组成，两导体中有等值反向均匀电流I 通过，其间充满磁导率为μ的均匀磁介质，介质中离中心轴距为r 的某点处的磁场强度的大小 H = ，磁感应强度的大小B = 。

第15章 磁介质的磁化一、选择题1(C)，2(B)，3(B)，4(C)，5(D)二、填空题(1). －8.88×10-6 ，抗 .(2). 铁磁质，顺磁质，抗磁质.(3). 7.96×105 A/m ， 2.42×102 A/m.(4). 各磁畴的磁化方向的指向各不相同，杂乱无章.全部磁畴的磁化方向的指向都转向外磁场方向.(5). 矫顽力大，剩磁也大；例如永久磁铁．(6). 磁导率大，矫顽力小，磁滞损耗低． 变压器，交流电机的铁芯等．三 计算题1. 一根同轴线由半径为R 1的长导线和套在它外面的内半径为R 2、外半径为R 3的同轴导体圆筒组成．中间充满磁导率为μ的各向同性均匀非铁磁绝缘材料，如图．传导电流I 沿导线向上流去，由圆筒向下流回，在它们的截面上电流都是均匀分布的．求同轴线内外的磁感强度大小B 的分布．解：由安培环路定理： ∑⎰⋅=i I l H d0< r <R 1区域： 212/2R Ir rH =π212R Ir H π=， 2102R Ir B π=μ R 1< r <R 2区域： I rH =π2r I H π=2， rI B π=2μ R 2< r <R 3区域： )()(22223222R R R r I I rH ---=π )1(22223222R R R r r I H ---π= )1(2222322200R R R r r IH B ---π==μμ r >R 3区域： H = 0，B = 02. 一根很长的同轴电缆，由一导体圆柱(半径为a )和同轴的导体圆管(内、外半径分别为b ，c )构成，使用时，电流I 从一导体流出，从另一导体流回．设电流都是均匀地分布在导体的横截面上，求∶导体圆柱内(r <a )和两导体之间(a <r <b )的磁场强度H 的大小．解∶由电流分布的轴对称性可知，在同一横截面上绕轴半径为r 的圆周上各点的B 值相等，其方向是沿圆周的切线方向．用H 的环路定律可求出．(1) r <a 222ar I r H ππ=π⋅ ∴ 22a Ir H π=(2) a <r <b I r H =π⋅2， rI H π=23. 螺绕环中心周长l = 10 cm ，环上均匀密绕线圈N = 200匝，线圈中通有电流I = 0.1 A ．管内充满相对磁导率μr = 4200的磁介质．求管内磁场强度和磁感强度的大小．解： ===l NI nI H /200 A/m===H H B r μμμ0 1.06 T4. 一铁环的中心线周长为0.3 m ，横截面积为1.0×10-4 m 2，在环上密绕300匝表面绝缘的导线，当导线通有电流3.2×10-2 A 时，通过环的横截面的磁通量为2.0×10-6 Wb ．求：(1) 铁环内部的磁感强度；(2) 铁环内部的磁场强度；(3) 铁的磁化率；(4) 铁环的磁化强度．解：(1) 2102-⨯==S B Φ T(2) n = 1000 m -1， H = nI 0＝32 A/m(3) 相对磁导率 4970==HB r μμ ∴ 磁化率 χm = μr ­1 = 496(4) 磁化强度 M = χm H ＝1.59×104 A/m四 研讨题1. 顺磁质和铁磁质的磁导率明显地依赖于温度，而抗磁质的磁导率则几乎与温度无关，为什么？参考解答：顺磁质的磁性主要来源于分子的固有磁矩沿外磁场方向的取向排列。

•••导体内任一点的磁场强度0Ir 2ttR2再由B = pH ,有导体内任一点的磁感应强度：12TT R21 jL/Ir Ir I r 2N(2) H =—I = 200A/m f (―-1);习题1515-1. 一圆柱形无限长导体，磁导率为“，半径为/?,通有沿轴线方向的均匀电流/ ,求: （1）导体内任一点的H、B和（2）导体外任一点的片、B。

解：如图，面电流密度为：i二厶。

7T R2（1）当r<R时，利用：（方•（" =》/,利用公式M =--H，有磁化强度：M °。

“（）“（）2TT R~ 2TT R- 2TT R-〃（）（2）当r>R时，利用：J方/有：导体外任-点的磁场强度：心总，磁感应强度：15・2・螺绕环平均周长l = lOcm，环上绕有线圈N = 200|di,通有电流I = 100/H A«试求: （1）管内为空气时〃和丹的大小；（2）若管内充满相对磁导率“，=4200的磁介质，〃和H的大小。

解：（1）B = ^nl = ;/0—/ =4^xl0-7 xlOOxlO"3 =2.5X10_4T,LDH =——=200 Ajm；A）B = pH =“o“月=4兀x 10一7 x 4200x200 = 1.057\ 15-3.螺绕环内通有电流20 A,环上所绕线圈共400匝,环的平均周长为40cm ,环内磁感应强度为1.0T,计算：（1）磁场强度；（2）磁化强度；（3）磁化率；（4）磁化面电流和相对磁导率。

解：（1）磁场强度：H = —/ = —x20 = 2xl04Aim；L 0.4D 1（2） ---------------------------------------- 磁化强度：M =——H = -2xl04 = 7.76x 10sA/m；“o4^-xlO-7（3）磁化率：乙”=“，一1,而;/r=—, .•.^=-^—-1 = 39.8-1=38.8；（4）磁化面电流密度：cr =M =--H =7.76xio5 A//n ,“o则磁化面电流:i s = s L=7.76X105X0.4=3.1X1O5A,相对磁导率：/=丄=39.8【或儿=%”+1 = 38.8 + 1=39.8】“0〃解：利用介质磁场的安培环路定理:' —工I ,考虑到导线内电流密度为:7TR-可求出磁场分布。

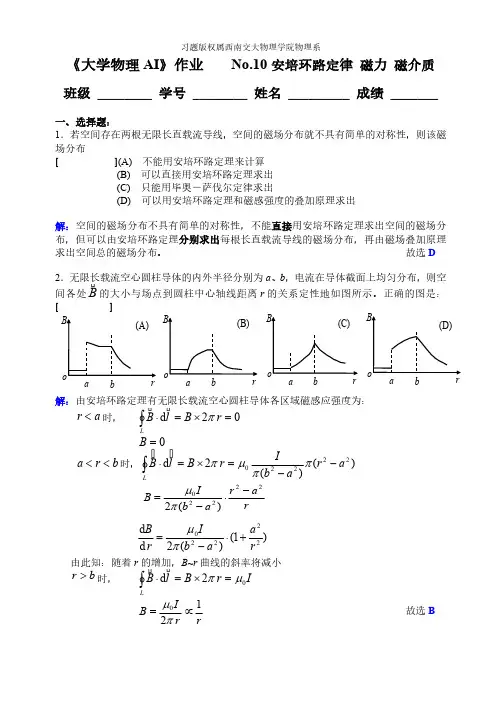
习题版权属西南交大物理学院物理系《大学物理AI 》作业No.10安培环路定律 磁力 磁介质班级 ________ 学号 ________ 姓名 _________ 成绩 _______一、选择题：1．若空间存在两根无限长直载流导线，空间的磁场分布就不具有简单的对称性，则该磁场分布 [ ](A) 不能用安培环路定理来计算 (B) 可以直接用安培环路定理求出 (C) 只能用毕奥－萨伐尔定律求出 (D) 可以用安培环路定理和磁感强度的叠加原理求出解：空间的磁场分布不具有简单的对称性，不能直接用安培环路定理求出空间的磁场分布，但可以由安培环路定理分别求出每根长直载流导线的磁场分布，再由磁场叠加原理求出空间总的磁场分布。

故选D 2．无限长载流空心圆柱导体的内外半径分别为a 、b ，电流在导体截面上均匀分布，则空间各处的大小与场点到圆柱中心轴线距离r 的关系定性地如图所示。

正确的图是：B 内[]解：由安培环路定理有无限长载流空心圆柱导体各区域磁感应强度为：时，a r <02d =⨯=⋅⎰r B l B Lπ内内0=B 时，b r a <<)()(2d 22220a r ab I r B l B L--=⨯=⋅⎰ππμπ内内r a r a b IB 22220)(2-⋅-=πμ)1()(2d d 22220ra ab I r B +⋅-=πμ由此知：随着r 的增加，B ~r 曲线的斜率将减小时，b r >I r B l B L02d μπ=⨯=⋅⎰内内故选Brr I B 120∝=πμ3．如图，线固定不动，则载流三角形线圈将：[ ] (A) 向着长直导线平移(B) (C) 转动(D) 不动解：建立如图所示的坐标轴，无限长直载流导线在x >0应强度为：方向xI B πμ20１=⊗由安培定律可得不同位置a 为：l aII AB a I I F AB πμπμ22210210==30cos d 2d 30cos 2102x x I I l BI F F l a aCABC AC =︒⋅===⎰⎰︒+πμ式中为三角形边长，各力方向如图所示，则载流三角形线圈所受合力为：l 令，有)0(>=λλal0)23111(2231233321[2d )(d 210210<+--=+⨯--=∑λπμλπμλI I I I F x 又（无穷远处），所以载流线圈所受合力始终向着长直电流，可见载流三角0|0==∑λx F形线圈不可能转动，只能向着长直导线平动。

大学物理第十五章磁介质的磁化习题解答第十五章磁介质的磁化习题解答（仅作为参考）15．1 一均匀磁化的磁介质棒，直径为25mm ，长为75mm ，其总磁矩为12000A·m 2．求棒的磁化强度M 为多少？[解答] 介质棒的面积为S = πr 2，体积为V = Sl = πr 2l ，磁矩为p m = 12000A·m 2，磁化强度为m m p p M V V∑==? 32312000(2510/2)7510π--= =3.26×108(A·m -1)．15．3 一螺绕环中心周长l = 10cm ，线圈匝数N = 200匝，线圈中通有电流I = 100mA ．求：（1）管内磁感应强度B 0和磁场强度H 0为多少？（2）设管内充满相对磁导率μr = 4200的铁磁质，管内的B 和H 是多少？（3）磁介质内部由传导电流产生的B 0和由磁化电流产生的B`各是多少？[解答]（1）管内的磁场强度为302200100101010NI H l --??==? = 200(A·m -1)．磁感应强度为B = μ0H 0 = 4π×10-7×200 = 2.5×10-4(T)．（2）当管内充满铁磁质之后，磁场强度不变H = H 0 =200(A·m -1)．磁感应强度为B = μH = μr μ0H= 4200×4π×10-7×200 = 1.056(T)．（3）由传导电流产生的B 0为2.5×10-4T ．由于B = B 0 + B`，所以磁化电流产生的磁感应强度为B` = B - B 0 ≈1.056(T)．15．5 一根磁棒的矫顽力为H c = 4.0×103A·m -1，把它放在每厘米上绕5匝的线圈的长螺线管中退磁，求导线中至少需通入多大的电流？[解答]螺线管能过电流I 时，产生的磁感应强度为B = μ0nI ．根据题意，螺线管产生的磁场强度至少要与磁棒的矫顽力大小相等，但方向相反，因此B = μ0H c ，所以电流强度为I = H c /n = 4.0×103/500 = 8(A)．。

高中物理奥林匹克竞赛专题15.磁介质习题（有答案）磁化面电流密度 m A H μB M σs 501076.7⨯=-==磁化面电流 AL σi s s 55101.34.01076.7⨯=⨯⨯== 15-4. 一永磁环的磁化强度为M ，磁环上开有一很窄的细缝。

求图中1、2点处的磁感应强度B 值和磁场强度H 值。

解：H B M 0-=μ由于是一个永磁环 0=•⎰c d l H 所以 02=H15-5. 图a 为铁氧体材料的H B -磁滞曲线，图b 为此材料制成的计算机存贮元件的环形磁芯。

磁芯的内、外半径分别为mm 5.0和mm 8.0，矫顽力为A/m 500π=C H 。

设磁芯的磁化方向如图b 所示，欲使磁芯的磁化方向翻转，试问：（1）轴向电流如何加？至少加至多大时，磁芯中磁化方向开始翻转？（2）若加脉冲电流，则脉冲峰值至少多大时，磁芯中从内而外的磁化方向全部翻转？解：（1）内r i H c π2max=（2）A H r i c 8.0500108.0223max =⨯⨯⨯==-πππ外思考题15-1. 何谓顺磁质、抗磁质和铁磁质，它们的区别是什么？答：顺磁质：磁介质在磁场中磁化后，产生的附加磁场的方向与原来的磁场方向相同。

抗磁质：磁介质在磁场中磁化后，产生的附加磁场的方向与原来的磁场方向相反。

铁磁质：磁介质在磁场中磁化后，产生的附加磁场的方向与原来的磁场方向相同，并且附加磁场远远大于原来磁场。

15-2. 将电介质与磁介质加以比较.答：略15-3. 何谓磁滞回线？答：对于铁磁质来说，磁感应强度B 随磁场强度H 的变化而变化所形成的闭合曲线就叫磁滞回线。

见教材P107页图15-11。

15-4. 在两个分界面，磁感应强度和磁场强度的关系如何？答：在两个分界面磁场强度的法向分量是连续的，磁感应强度的法向分量不连续。

磁介质测试题及答案一、选择题1. 磁介质的磁性能主要取决于以下哪一项？A. 材料的化学成分B. 材料的微观结构C. 材料的制备工艺D. 外部磁场强度答案：B2. 以下哪种类型的磁介质具有最高的磁导率？A. 软磁材料B. 硬磁材料C. 铁磁材料D. 反铁磁材料答案：A3. 磁介质的磁滞回线反映了材料的哪些特性？A. 磁导率B. 磁饱和度C. 磁滞损失D. 所有上述选项答案：D二、填空题4. 磁介质的_______是指材料在没有外磁场作用时，内部磁畴的排列状态。

答案：初始磁化状态5. 磁介质的_______是指材料在外加磁场作用下，磁化强度达到最大值的能力。

答案：磁饱和度三、简答题6. 简述磁介质在存储设备中的应用及其重要性。

答案：磁介质在存储设备中主要用于数据的存储。

由于磁介质具有较高的磁导率和磁饱和度，它们能够存储大量的数据信息。

此外，磁介质的稳定性和可重复写入特性使其在硬盘驱动器、磁带和其他存储设备中得到广泛应用。

磁介质的性能直接影响存储设备的容量、速度和可靠性。

7. 描述磁介质的磁滞回线，并解释其物理意义。

答案：磁滞回线是描述磁介质在外加磁场作用下磁化强度与磁场强度之间关系的曲线。

当外加磁场逐渐增大时，磁介质的磁化强度随之增加，但存在一定的滞后现象。

当磁场减小到零时，磁介质的磁化强度不会立即回到零，而是存在一个剩余磁化强度。

这个剩余磁化强度与外加磁场的相互作用导致了磁滞损失，这是磁介质在反复磁化过程中能量损耗的来源。

磁滞回线的形状和位置反映了磁介质的磁性能，如磁导率、磁饱和度和磁滞损失等。

四、计算题8. 假设有一磁介质样品，其磁化强度M随外加磁场H的变化关系为M = 0.5H。

如果外加磁场从0增加到2000 A/m，计算磁介质样品的磁化强度变化范围。

答案：根据给定的关系M = 0.5H，当外加磁场H从0增加到2000 A/m时，磁化强度M的变化范围是从0增加到1000 A/m（即0.5 * 2000 A/m）。

磁介质一章习题答案习题10—1 将一有限长圆柱形的均匀抗磁质放在一无限长直螺线管内，其螺线管线圈的电流方向如图所示。

在a 、b 、c 三点的磁感应强度与未放入抗磁质前相比较其增减情况是：［ ］(A) a 点增加，b 点减小，c 点不变。

(B) a 点增加，b 点增加，c 点增加。

(C) a 点减小，b 点减小，c 点增加。

(D) a 点减小，b 点增加，c 点减小。

解：抗磁质放在一无限长直螺线管内，相当于把它放在均匀的外磁场中。

现 已知外场0B 方向向右。

对磁介质中的a 点来说，其本身磁化电流产生的附加磁场B '的方向与外场方向相反，叠加的结果使a 点的场减小；对介质外的b 点来说，外场0B 方向仍旧向右，这时的抗磁质相当于N 极在左、S 极在右的磁铁，其附加磁场B '的方向在b 点向左，因此，b 点的场也减小；对介质外侧的c 点来说，外场0B 方向仍旧向右，但是在该处B '的方向也向右，与外场同向，故c 点的场是增加的。

综上所述，应该选择答案(C)。

习题10—2 图示三种不同磁介质的磁化曲线，虚线表示真空中的B —H 关系。

则表示铁磁质的是曲线 ；表示抗磁质的是曲线 ；表示顺磁质的是曲线 。

解：真空中的B —H 关系为：H B 0μ=；对一般弱磁介质的B —H 关系为：H H B r μμμ0==，式中r μ为常数，若为顺磁质，则1>r μ因而0μμ>；若为抗磁质，则1<r μ因而0μμ<，所以若以真空中的B —H关系曲线为参考，则曲线Ⅱ表示的是顺磁质，曲线Ⅲ表示的是抗磁质。

对于铁磁质其B —H关系仍然为：H H B r μμμ0==，但是，由于其r μ不是常数，即)(H r r μμ=，因此其B —H 关系是非线性的，相应的B —H 关系曲线亦非直线，故而表示铁磁质的应是曲线Ⅰ。

习题10—3 关于稳恒磁场的磁场强度H 的下列几种说法中哪一个是正确的? (A) H 仅与传导电流有关。

第八章 磁场中的磁介质8－1一螺绕环的平均半径为R=0.08m ，其上绕有N=240匝线圈，电流强度为I=0.30A 时管内充满的铁磁质的相对磁导率μr ＝5000，问管内的磁场强度和磁感应强度各为多少？ 解：（1）由I d =⋅⎰l H L 得I R N H NI R H π=→=π22代入数值为 m A H /1043.108.014.323.02402⨯=⨯⨯⨯= （2）T H B r 9.01043.150********=⨯⨯⨯⨯π=μμ=-8－2在图11－8所示的实验中，环型螺绕环共包含500匝线圈，平均周长为50cm ，当线圈中的电流强度为2.0A 时，用冲击电流计测得介质内的磁感应强度为2.0T ，求这时（1）待测材料的相对磁导率μr ；（2）磁化电流线密度j s 。

解：（1）I R N H π=2代入数值m A H /2000105025002=⨯⨯=- 7962000104270=⨯⨯π=μ=μ-H B r （2）m A nI j r s /1056.121050500)1796()1(62⨯=⨯⨯⨯-=-μ=- 8－3如图所示，一根长圆柱型同轴电缆，内、外导体间充满磁介质，磁介质的相对磁导率为μr （μr <1），导体的磁化可以略去不计，电缆沿轴向有稳定电流I 通过，内外导体上的电流的方向相反，求（1）空间各区域的磁感应强度和磁化强度；（2）磁介质表面的磁化电流。

解：依题意，内圆柱的电流密度21R I j π=（1）r<R 时： 根据∑⎰=⋅I d l H L得21121222R Ir jr H r j r H π==→π=π 2101012R Ir H B πμ=μ= 0)1(11=-μ=H M r （导体的μr =1）R 1<r<R 2时：根据∑⎰=⋅I d l H L 得rI H I r H π=→=π2222 r I H B r r πμμ=μμ=20202习题8－3图r I H M r r π-μ=-μ=2)1()1(22 R 2<r<R 3时： )(2223R R I j -π= 根据∑⎰=⋅I d l H L 得222322332223)(2)(2R R r R r I H R r j I r H --π=→-π-=π 22232230303)(2R R r R r I H B --πμ=μ= 0)1(33=-μ=H M r （导体的μr =1）r>R 3时：H=0, B=0, M=0（2）I I r s )1(-μ=8－4一个截面为正方形的环形铁心，其中磁介质的相对磁导率为μr ，若在此环形铁心上绕有N 匝线圈，线圈中的电流为I ，设环的平均半径为r ，求此铁心的磁化强度。