理论力学复习题
- 格式:docx
- 大小:553.80 KB
- 文档页数:27
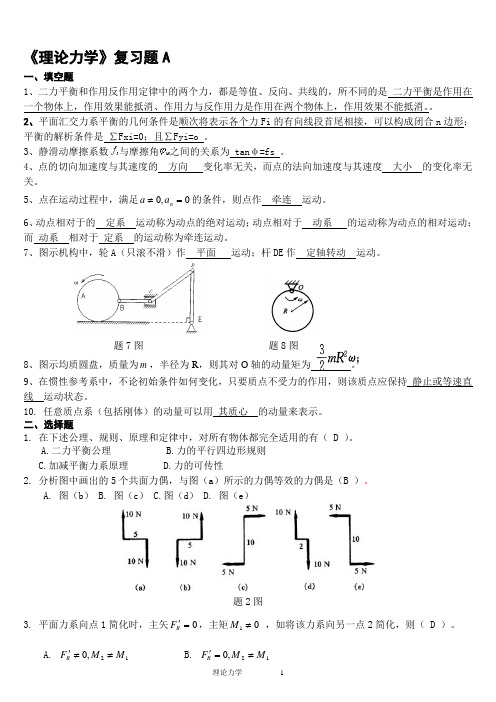
《理论力学》复习题A一、填空题1、二力平衡和作用反作用定律中的两个力,都是等值、反向、共线的,所不同的是 二力平衡是作用在一个物体上,作用效果能抵消、作用力与反作用力是作用在两个物体上,作用效果不能抵消。
2、平面汇交力系平衡的几何条件是顺次将表示各个力Fi 的有向线段首尾相接,可以构成闭合n 边形;平衡的解析条件是 ∑Fxi=0;且∑Fyi=o 。
3、静滑动摩擦系数与摩擦角之间的关系为 tanφ=fs 。
4、点的切向加速度与其速度的 方向 变化率无关,而点的法向加速度与其速度 大小 的变化率无关。
5、点在运动过程中,满足0,0=≠n a a 的条件,则点作 牵连 运动。
6、动点相对于的 定系 运动称为动点的绝对运动;动点相对于 动系 的运动称为动点的相对运动;而 动系 相对于 定系 的运动称为牵连运动。
7、图示机构中,轮A (只滚不滑)作 平面 运动;杆DE 作 定轴转动 运动。
题7图 题8图8、图示均质圆盘,质量为m ,半径为R ,则其对O 轴的动量矩为 。
9、在惯性参考系中,不论初始条件如何变化,只要质点不受力的作用,则该质点应保持 静止或等速直线 运动状态。
10. 任意质点系(包括刚体)的动量可以用 其质心 的动量来表示。
二、选择题1. 在下述公理、规则、原理和定律中,对所有物体都完全适用的有( D )。
A.二力平衡公理B.力的平行四边形规则C.加减平衡力系原理D.力的可传性2. 分析图中画出的5个共面力偶,与图(a )所示的力偶等效的力偶是(B )。
A. 图(b ) B. 图(c ) C.图(d ) D. 图(e )题2图3. 平面力系向点1简化时,主矢0='RF ,主矩01≠M ,如将该力系向另一点2简化,则( D )。
A. 12,0M M F R≠≠' B. 12,0M M F R ≠='C. 12,0M M F R=≠' D. 12,0M M F R ==' 4. 将大小为100N 的力F 沿x 、y 方向分解,若F 在x 轴上的投影为86.6 N ,而沿x 方向的分力的大小为115.47 N ,则F 在y 轴上的投影为( B )。

1、如图所示结构,求支座反力。
2、组合梁AC和CE用铰链C相连,支承和荷载情况如图所示,已知跨度l=8m,F=5kN,均布荷载q=2.5kN/m,力偶矩M=5kNm。
求各支座的约束反力。
3、如图所示结构,求支座反力。
4、如图所示结构,q=10kN/m,求支座反力1、如图所示机构,杆OC与轮Ⅰ在轮心O处铰接,并以匀速v水平向左平移,起始时点O与点A相距l,AB杆可绕A轴定轴转动,与轮Ⅰ在D点接触,接触处有足够的摩擦使之不打滑,轮Ⅰ的半径为r。
求:θ=30°时,轮Ⅰ的角速度ω1和AB杆的角速度ω。
2、图示半径R=3r的凸轮以匀速v沿水平面向右移动,其中r为顶杆滚轮半径,顶杆O1O2沿铅直导轨滑动,假设滚轮与凸轮接触处无相对滑动,求当θ=30°,且B,O1,O2在同一直线上时,滚轮的角速度以及轮缘边上B点的速度。
3、图示机构,曲柄OA长为r,绕O轴转动,连杆AB=3r 始终与角点D保持接触,在图示位置时,曲柄的角速度为ω0,角加速度为α0,方向如图,求这时AB杆的:(1)角速度ωAB;(2)B点的速度v B。
)4、图示机构中,曲柄OA以匀角速度ω0绕O轴转动,通过齿条AB带动齿轮O1。
已知OA=R,齿轮O1半径r=0.5R,求当θ=60°时,齿条AB的角速度和齿轮O1的角速度。
1、如图所示,半径为r的均质圆盘,在半径为R的圆弧面上只滚不滑。
初瞬时θ=θ0,圆盘由静止开始纯滚动。
求均质圆盘脱离圆弧之前:(1)圆盘的角加速度(表示为θ的函数);(2)圆弧面作用于圆轮上的法向反力和摩擦力(表示为θ的函数)。
2、均质圆盘半径为r,质量为m,在初始角度θ0时静止释放后,在半径为R的圆弧轨道上做纯滚动。
求圆盘在任意位置θ时:(1)圆盘滚动的角加速度;(2)圆弧轨道的法向反力和摩擦力。
3、如图所示,均质杆AB长度为l,放在铅锤平面内,在角φ0时杆由静止状态倒下,墙与地面均光滑。
求(1)杆在脱离墙前之前的任意位置时的角速度和角加速度;(2)杆脱离墙面时与水平面的夹角。

理论力学试题库及答案(通用篇)一、理论力学试题库(通用篇)试题一:已知一质点在平面直角坐标系中的运动方程为 x = 2t² + 3,y = 4t² - t + 1。
求该质点在t = 2s 时的速度和加速度。
试题二:一质点沿圆周运动,其半径为 r,角速度为ω,角加速度为α。
求质点在任意时刻 t 的速度和加速度。
试题三:一质点从静止开始沿直线运动,受到恒力F 的作用。
求质点在任意时刻 t 的速度和位移。
试题四:一质点在平面内做匀速圆周运动,半径为r,角速度为ω。
求质点在任意时刻 t 的速度和加速度。
试题五:一质点在平面内做匀速运动,速度大小为v,方向与水平方向成θ 角。
求质点在任意时刻 t 的位移。
试题六:一质点在重力作用下做自由落体运动,求质点在任意时刻 t 的速度和位移。
试题七:一质点在水平地面上受到一斜向上的拉力F,拉力与水平方向的夹角为θ。
求质点在任意时刻 t 的速度和加速度。
试题八:一质点在平面内做匀速圆周运动,半径为r,角速度为ω。
求质点在任意时刻 t 的切向加速度和法向加速度。
试题九:一质点在平面内做匀速运动,速度大小为v,方向与水平方向成θ 角。
求质点在任意时刻 t 的位移和速度。
试题十:一质点在水平地面上受到一恒力 F 的作用,力与水平方向的夹角为θ。
求质点在任意时刻 t 的速度和位移。
二、答案答案一:t = 2s 时,速度 v = (4t, 8t - 1) = (8, 15) m/s;加速度 a = (8, 8) m/s²。
答案二:质点在任意时刻 t 的速度v = (rω, 0),加速度a = (0, rα)。
答案三:质点在任意时刻 t 的速度 v = (F/m)t,位移 s = (F/m)t²/2。
答案四:质点在任意时刻 t 的速度 v =(rωcos(ωt), rωsin(ωt)),加速度 a = (-rω²sin(ωt), rω²cos(ωt))。

理论力学题库及答案一、理论力学题库(一)选择题1. 在牛顿力学中,物体的运动状态可以用以下哪个物理量来描述?A. 力B. 动量C. 动能D. 动能定理2. 以下哪个物理量是守恒量?A. 动量B. 动能C. 力D. 功3. 一个物体做直线运动,以下哪个条件是物体做匀速直线运动的必要条件?A. 合外力为零B. 合外力恒定C. 速度恒定D. 加速度恒定(二)填空题4. 牛顿第二定律的表达式为______。
5. 动量的定义为______。
6. 功的计算公式为______。
7. 动能定理的表达式为______。
(三)计算题8. 一质量为2kg的物体在水平地面上受到一个水平力F的作用,力F与物体运动方向相同。
已知物体从静止开始运动,经过3秒后速度达到6m/s。
求力F的大小。
9. 一质量为4kg的物体从静止开始沿着光滑的斜面下滑,斜面倾角为30°,求物体下滑3秒后的速度。
10. 一质量为5kg的物体在水平地面上以10m/s的速度运动,遇到一个斜面,斜面倾角为45°,物体沿着斜面上滑,求物体上滑的最大距离。
二、理论力学题库答案(一)选择题答案1. B. 动量2. A. 动量3. A. 合外力为零(二)填空题答案4. F=ma5. 动量 = 质量× 速度6. 功 = 力× 位移× cosθ7. 动能定理:动能的增量 = 外力做的功(三)计算题答案8. 解:根据牛顿第二定律,F=ma,其中a为加速度,m为质量。
由题意知,a=(6m/s - 0m/s) / 3s = 2m/s²。
代入公式,F=2kg × 2m/s² = 4N。
9. 解:根据动能定理,动能的增量 = 外力做的功。
由于物体从静止开始下滑,初始动能为0。
下滑过程中,重力做功,即mgh,其中h为下滑的高度。
由斜面倾角可知,h =lsin30°,其中l为下滑的距离。
因此,mgh = (4kg ×9.8m/s²) × (l × sin30°) = 4kg × 9.8m/s² × (l × 0.5)。

理论力学复习题理论力学是物理学的一个重要分支,它主要研究物体在力的作用下的运动规律。
以下是一些理论力学的复习题,可以帮助同学们巩固和检验学习效果。
1. 牛顿运动定律- 描述牛顿第一定律的内容。
- 根据牛顿第二定律,解释力与加速度之间的关系。
- 牛顿第三定律在实际问题中的应用。
2. 静力学基础- 解释什么是平衡状态。
- 描述如何使用力的合成和分解来解决平衡问题。
- 举例说明摩擦力在静力学问题中的作用。
3. 动力学分析- 解释什么是惯性参考系。
- 描述牛顿运动定律在非惯性参考系中的应用。
- 举例说明如何使用牛顿定律解决动力学问题。
4. 功和能- 定义功和能,并解释它们之间的关系。
- 描述保守力和非保守力的区别。
- 举例说明如何应用机械能守恒定律解决实际问题。
5. 角动量和角动量守恒定律- 定义角动量,并解释它在物理系统中的重要性。
- 描述角动量守恒定律的应用条件。
- 举例说明如何使用角动量守恒定律解决旋转问题。
6. 刚体的转动- 解释刚体转动的基本原理。
- 描述转动惯量的概念及其计算方法。
- 举例说明如何使用转动定律解决刚体转动问题。
7. 振动和波动- 描述简谐振动的基本特征。
- 解释波的传播和波速的概念。
- 举例说明如何分析机械波的传播特性。
8. 拉格朗日力学- 介绍拉格朗日方程的基本概念。
- 描述如何使用拉格朗日方程解决复杂系统的动力学问题。
- 举例说明拉格朗日力学在物理问题中的应用。
9. 哈密顿力学- 解释哈密顿原理和哈密顿方程。
- 描述哈密顿量和拉格朗日量之间的关系。
- 举例说明哈密顿力学在解决动力学问题中的优势。
10. 非线性动力学和混沌理论- 描述非线性动力学的特点。
- 解释混沌理论的基本概念。
- 举例说明如何识别和分析混沌系统。
通过这些复习题,同学们可以检验自己对理论力学各个主题的理解程度,并为进一步的学习打下坚实的基础。
希望这些题目能够帮助同学们更好地掌握理论力学的知识点。

理论力学复习题一、 填空1、质点沿空间曲线232()(32)(24)r t t i t j t t K =++−+− 运动在2t S =时,质点的速度V =__________________;加速度a = __________________,速度大小为V =__________________;加速度大小为a =__________________。
2、质量为m 的质点运动规律为j t i t a r ωωsin cos +=,式中a 、b ,ω均为常数,则质点的轨道道方程为 ,质点从(a ,0)运动到(b ,0),在这一过程中动量的增量=ΔP,动能的增量Δ=K E 。
3、已知点的运动方程为t R y t R x ωωcos ,sin ==,其中R ,W 为常量,点的运动轨迹为__________________,速度为v =__________________,加速度a =__________________。
4、在极坐标中,其径向和横向单位矢量j ,i 的时间导数分别为=dti d =dtj d 。
5、质点的运动速度为(1)kt V A e −=−,其中A ,K 均为常数。
当0t =时质点位于坐标的原点,则质点的运动方程为__________________;加速度为__________________。
6、某质点运动方程为r=e at,θ=bt;该质点径向速率V r =_____________,横向速率V=________________;径向加速度的值αr =________________,横向加速度的值αθ=_______________,加速度的值α=________________。
7、在自然坐标系中,切向加速度ιa 和法向加速度n a 的计算公式为ιa =___________,n a =________________;8、在极坐标中加速度的两个分量为(1)__________________,(2)__________________。
理论力学练习题一、是非题(每题2分。
正确用√,错误用×,填入括号内。
)1、作用在一个物体上有三个力,当这三个力的作用线汇交于一点时,则此力系必然平衡。
()2、力对于一点的矩不因力沿其作用线移动而改变。
()3、在自然坐标系中,如果速度υ= 常数,则加速度α= 0。
()4、虚位移是偶想的,极微小的位移,它与时间,主动力以及运动的初始条件无关。
()5、设一质点的质量为m,其速度 与x轴的夹角为α,则其动量在x轴上的投影为mv x =mvcos a。
()6、作用于刚体的力可在刚体范围内沿其作用线移动而不改变其对刚体的运动效应。
()7、平面汇交力系平衡时,力的多边形各力应首尾相接,但在作图时力的顺序可同。
()8、约束力的方向总是与约束所能阻止的被约束物体的运动方向一致的。
()9、切向加速度只表示速度方向的变化率,而与速度的大小无关。
()10、刚体平移时,若刚体上任一点的运动已知,则其它各点的运动随之确定。
()11、刚体作平面运动时,绕基点转动的角速度和角加速度与基点的选取无关。
()12、二力构件是指只受两个力作用的构件。
()13、刚体在3个力的作用下平衡,这3个力不一定在同一个平面内。
()14、只要全约束力与支撑面法线的夹角小于摩擦角,则两物体间不会产生滑动。
()15、在自然坐标系中,如果速度=常数,则加速度a = 0。
()16、两自由运动质点,其微分方程完全相同,但其运动规律不一定相同。
二、选择题(每题3分。
请将答案的序号填入划线内。
)1、如图所示系统只受力F作用而处于平衡。
欲使A支座约束反力的作用线与AB成30o角,则斜面的倾角应为()A、30o;B、150o;C、90o;D、60o。
2、杆AB 长2m ,C 是其中点(尺寸如图(d )所示)。
分别受图示四个力系作用,则和图(d )是等效力系的是。
( )A 、图(a )所示的力系;B 、图(b )所示的力系;C 、图(c )所示的力系;D 、图(a )、图(b )、图(c )都不能。
理论力学复习题一、填空题1、力对物体的作用效果一般分为力的外效应和力的内效应。
2、作用在刚体上的力可沿其作用线任意移动,而不改变该力对刚体的作用效果。
3、质点动力学的三个基本定律:惯性定律、力与加速度之间的关系定律、作用力与反作用力定律4、质点系动能定理建立了质点系动能的改变量和作用力的功之间的关系。
5、一对等值、反向、不共线的平行力组成的特殊力系,称为力偶6、两个或两个以上力偶的组合称为力偶系。
7、力矩与矩心的位置有关,力偶矩与矩心的位置无关。
8、物体质量的改变与发生这种改变所用合外力的比值叫做加速度。
9、力的三要素为大小、方向和作用点。
10、物体相对于地球静止或作匀速直线运动称为平衡状态。
11、作用在一个物体上的两个力使物体平衡,这两个力一定是大小相等、方向相反、作用在同一条直线上。
12、平面运动的速度分析法有三种方法基点法、速度瞬心法和速度投影法。
13、在刚体的平面运动中,刚体的平移和转动是两种最基本运动。
14、动力学的三个基本定律:动量定理、动量矩定理、动能定理。
15、空间力系分为空间汇交力系和空间力偶。
16、带传动中,带所产生的约束力属于柔性约束,带只能承受拉约束。
17、质点动力学的三个基本定律:惯性定律、力与加速度之间的关系定律、作用力与反作用力定律18、质点系动能定理建立了质点系动能的改变量和作用力的功之间的关系。
19、当力为零或力的作用线过矩心时,力矩为零,物体不产生效果。
二、判断题1实际位移和虚位移是位移的两种叫法(×)2.作用力和反作用力等值、反向、共线、异体、且同时存在。
(√)3.力偶无合力。
(×)4.运动物体的加速度大,它的速度也一定大。
(×)5.平面任意力系的合力对作用面内任一点之矩等于力系中各分力对于同一点之矩的代数和。
(√)6.若力偶有使物体顺时针旋转的趋势,力偶矩取正号;反之,取负号。
(×)7.既不完全平行,也不完全相交的力系称为平面一般力系(√)8.二力构件是指两端用铰链连接并且只受两个力作用的构件。
理论力学考试题及答案**理论力学考试题及答案**一、单项选择题(每题2分,共20分)1. 质点系中,内力的矢量和为零,这是基于()。
A. 牛顿第三定律B. 牛顿第二定律C. 牛顿第一定律D. 动量守恒定律答案:D2. 质心的位置由()决定。
A. 质点的质量B. 质点的位置C. 质点的加速度D. 质点的速度答案:B3. 刚体的转动惯量是关于()的量。
A. 质量B. 距离C. 力D. 速度答案:B4. 角动量守恒的条件是()。
A. 外力矩为零B. 外力为零C. 内力矩为零D. 内力为零答案:A5. 两质点组成的系统,若两质点质量相等,它们之间的万有引力为F,则系统的质心位置位于()。
A. 两质点连线的中点B. 质量较大的质点处C. 质量较小的质点处D. 无法确定答案:A6. 刚体绕固定轴的转动惯量I与()有关。
A. 质量分布B. 轴的位置C. 轴的方向D. 以上都是答案:D7. 刚体的平行轴定理表明,刚体绕任意轴的转动惯量等于绕通过质心的平行轴的转动惯量加上()。
A. 刚体的质量B. 刚体的转动惯量C. 刚体质量与两轴间距离的平方的乘积D. 刚体质量与两轴间距离的乘积答案:C8. 刚体的平面运动可以分解为()。
A. 任意两个不同的平面运动的叠加B. 平移和旋转的叠加C. 两个垂直平面内的旋转D. 任意两个不同的旋转的叠加答案:B9. 刚体的瞬时转轴是()。
A. 刚体上所有点速度相同的直线B. 刚体上所有点加速度相同的直线C. 刚体上所有点角速度相同的直线D. 刚体上所有点线速度为零的直线答案:D10. 刚体的定轴转动中,角速度的大小和方向()。
A. 与参考系的选择有关B. 与参考系的选择无关C. 与参考系的选择有关,但大小无关D. 与参考系的选择无关,但方向有关答案:B二、填空题(每题2分,共20分)1. 牛顿第二定律的数学表达式为:\( F = ma \),其中F表示力,m表示质量,a表示________。
理论力学期末复习题一一、单选题1、F= 100N 方向如图示,若将F 沿图示x ,y 方向分解,则x 向分力大小为( )。
A) 86.6 N ; B) 70.7 N ; C) 136.6 N ; D) 25.9 N 。
2、某平面任意力系F1 =4KN ,F2=3 KN ,如图所示,若向A 点简化,则得到( )A .F ’=3 KN ,M=0.2KNmB .F ’=4KN ,M=0.3KNmC .F ’=5 KN ,M=0.2KNmD .F ’=6 KN ,M=0.3 KNm第1题图 第2题图3、实验测定摩擦系数的方法,把物体放在斜面上,逐渐从零起增大斜面的倾角φ直到物体刚开始下滑为止,这时的φ就是对应的摩擦角φf ,求得摩擦系数为( )4、直角杆自重不计,其上作用一力偶矩为M 的力偶,图(a )与图(b )相比,B 点约束反力的关系为( )。
A 、大于B 、小于C 、相等D 、不能确定图(a ) 图(b )5、圆轮绕固定轴O 转动,某瞬时轮缘上一点的速度为v ,加速度为a ,如图所示。
试问哪些情况是不可能的?( )A 、(a)、(b)B 、(b)、(c)C 、(c)、(d)D 、(a)、(d)6、杆AB 的两端可分别沿水平、铅直滑道运动,已知B 端的速度为vB ,则图示瞬时B 点相对于A 点的速度为____________________。
A) B v sinθ; B) B v cosθ; C) B v ⁄ sinθ; D) B v ⁄ cosθ.第6题图 第7题图二、填空题7、图示物块重G=100N ,用水平力P 将它压在铅垂墙上,P=400N ,物块与墙间静摩擦系数fs=0.3,物块与墙间的摩擦力为F= 。
8、鼓轮半径R=0.5m ,物体的运动方程为x=52t (t 以s 计,x 以m 计),则鼓轮的角速度ω= ,角加速度α= 。
第8题图 第9题图 9、平面图形上任意两点的加速度A a 、B a 与A 、B 连线垂直,且A a ≠ B a ,则该瞬时,平面图形的角速度ω= 和角加速度α应为 。
理论力学复习题1一、是非题1、力有两种作用效果,即力可以使物体的运动状态发生变化,也可以使物体发生变形。
(√)2、在理论力学中只研究力的外效应。
(√)3、两端用光滑铰链连接的构件是二力构件。
(×)4、作用在一个刚体上的任意两个力成平衡的必要与充分条件是:两个力的作用线相同,大小相等,方向相反。
(√)5、作用于刚体的力可沿其作用线移动而不改变其对刚体的运动效应。
(×)6、三力平衡定理指出:三力汇交于一点,则这三个力必然互相平衡。
(×)7、平面汇交力系平衡时,力多边形各力应首尾相接,但在作图时力的顺序可以不同。
(√)8、约束力的方向总是与约束所能阻止的被约束物体的运动方向一致的。
(×)9、在有摩擦的情况下,全约束力与法向约束力之间的夹角称为摩擦角。
(×)10、用解析法求平面汇交力系的平衡问题时,所建立的坐标系x,y轴一定要相互垂直。
(×)11、一空间任意力系,若各力的作用线均平行于某一固定平面,则其独立的平衡方程最多只有3个。
(×)12、静摩擦因数等于摩擦角的正切值。
(√)13、一个质点只要运动,就一定受有力的作用,而且运动的方向就是它受力方向。
(×)14、已知质点的质量和作用于质点的力,质点的运动规律就完全确定。
(×)15、质点系中各质点都处于静止时,质点系的动量为零。
于是可知如果质点系的动量为零,则质点系中各质点必都静止。
(×)16、 作用在一个物体上有三个力,当这三个力的作用线汇交于一点时,则此力系必然平衡。
( × )17、 力对于一点的矩不因力沿其作用线移动而改变。
( √ )18、 在自然坐标系中,如果速度υ = 常数,则加速度α = 0。
( × )19、 设一质点的质量为m ,其速度 与x 轴的夹角为α,则其动量在x 轴上的投影为mvx =mvcos a 。
(√)20、 用力的平行四边形法则,将一已知力分解为F1和F2两个分力,要得到唯一解答,必须具备:已知F1和F2两力的大小;或已知F1和F2两力的方向;或已知F1或F2中任一个力的大小和方向。
( √ )21、 某力在一轴上的投影与该力沿该坐标轴的分力其大小相等,故投影就是分力。
( × )22、 图示结构在计算过程中,根据力线可传性原理,将力P 由A 点传至B 点,其作用效果不变。
( × )23、24、 作用在任何物体上的两个力,只要大小相等,方向相反,作用线相同,就一定平衡。
( × )。
25、 在有摩擦的情况下,全约束力与法向约束力之间的夹角称为摩擦角。
(× )26、 加速度dt v d 的大小为dt dv。
(×)27、 已知质点的质量和作用于质点的力,质点的运动规律就完全确定。
(× )28、 质点系中各质点都处于静止时,质点系的动量为零。
于是可知如果质点系的动量为零,则质点系中各质点必都静止。
( × )29、 两个力合力的大小一定大于它分力的大小。
(× )30、 约束力的方向总是与约束所能阻止的被约束的物体的运动方向是一致的。
( × )。
31、 两平面力偶的等效条件是:这两个力偶的力偶矩相等。
( × )32、 刚体的运动形式为平动,若刚体上任一点的运动已知,则其它各点的运动随之确定。
( √ )二、选择题(每题2分。
请将答案的序号填入划线内。
)1、 空间力偶矩是 ④ 。
①代数量; ②滑动矢量; ③定位矢量; ④自由矢量。
2、一重W的物体置于倾角为α的斜面上,若摩擦系数为f,且tgα<f,则物体①,若增加物重量,则物体①;若减轻物体重量,则物体①。
①静止不动;②向下滑动;③运动与否取决于平衡条件。
3、一动点作平面曲线运动,若其速率不变,则其速度矢量与加速度矢量(b)。
A:平行; B:垂直; C:夹角随时间变化; D:不能确定4、质点系动量守恒的条件是( b )。
A:作用于质点系的内力主矢恒等于零; B:作用于质点系的外力主矢恒等于零;C:作用于质点系的约束反力主矢恒等于零;D:作用于质点系的主动力主矢恒等于零;5、若作用在A点的两个大小不等的力F1和F2,沿同一直线但方向相反。
则其合力可以表示为③。
①F1-F2;②F2-F1;③F1+F2;6、作用在一个刚体上的两个力F A、F B,满足F A=-F B的条件,则该二力可能是②。
①作用力和反作用力或一对平衡的力;②一对平衡的力或一个力偶。
③一对平衡的力或一个力和一个力偶;④作用力和反作用力或一个力偶。
7、三力平衡定理是①。
①共面不平行的三个力互相平衡必汇交于一点;②共面三力若平衡,必汇交于一点;③三力汇交于一点,则这三个力必互相平衡。
8、已知F1、F2、F3、F4为作用于刚体上的平面共点力系,其力矢关系如图所示为平行四边形,由此④。
①力系可合成为一个力偶;②力系可合成为一个力;③力系简化为一个力和一个力偶;④力系的合力为零,力系平衡。
9、在下述原理、法则、定理中,只适用于刚体的有①③④。
①二力平衡原理;②力的平行四边形法则;③加减平衡力系原理;④力的可传性原理;⑤作用与反作用定理。
10、图示四个力四边形中,表示力矢R是F1、F2和F3的合力图形是( BD )11、12、固定铰支座约束反力( C )13、 A.可以用任意两个相互垂直的通过铰心的力表示14、 B.可以用任意一个大小和方向未知的通过铰心的力表示15、 C.其反力的方向在标定时可以任意假设16、 D.其反力的方向在标定时不可以任意假设17、力对物体作用效果,可使物体( D )18、 A.产生运动19、 B.产生内力20、 C.产生变形21、 D.运动状态发生改变和产生变22、作用在刚体上的二力平衡条件是( B )23、 A.大小相等、方向相反、作用线相同、作用在两个相互作用物体上24、 B.大小相等、方向相反、作用线相同、作用在同一刚体上25、 C.大小相等、方向相同、作用线相同、作用在同一刚体上26、 D.大小相等、方向相反、作用点相同27、平面力系向点1简化时,主矢FR=0,主矩M1≠0,如将该力系向另一点2简化,则( B )。
A:FR≠0,M2≠0; B:FR=0,M2≠M1; C:FR=0,M2=M1; D:FR≠0,M2=M1。
28、光滑面对物体的约束反力,作用在接触点处,其方向沿接触面的公法线( a )A.指向受力物体,为压力B.指向受力物体,为拉力C.背离受力物体,为拉力D.背离受力物体,为压力29、图示三铰拱架中,若将作用于构件AC上的力偶M平移至构件BC上,则A、B、C三处的约束反力( D )A.只有C处的不改变B.只有C处的改变C.都不变D.都改变17、牵连运动是指( a )A.动系相对于静系的运动B.牵连点相对于动系的运动C.静系相对于动系的运动D.牵连点相对于静系的运动18、一物重P ,用细绳BA 、CA 悬挂如图所示,且角α=60°。
若将BA 绳突然剪断,则该瞬时CA 绳的张力为( b )19、构件在外力作用下平衡时,可以利用( b ) A.平衡条件求出所有未知力 B.平衡条件求出某些未知力C.力系的简化求未知力D.力系的合成或分解求未知力20、 物体在一个力系作用下,此时只能( d )不会改变原力系对物体的外效应。
A.加上由二个力组成的力系B.去掉由二个力组成的力系C.加上或去掉由二个力组成的力系D.加上或去掉另一平衡力系21、图示均质杆OA 质量为m 、长度为l ,则该杆对O 轴转动惯量为( D )A .12m lB .12m 2lC .3mlD .3m 2l22、当具有一定速度的物体作用到静止构件上时,物体的速度发生急剧改变,由于惯性,使构件受到很大的作用力,这种现象称为冲击,例如( d )A .电梯上升B .压杆受压C .齿轮啮合D .落锤打桩23、汽车以匀速率v 在不平的道路上行驶,如图所示。
当通过A 、B 、C 三个位置时,汽车对路面的压力分别为FA 、FB 、FC ,则( b )=FB=FC >FB>FC<FB<FC =FB>FC24、直角刚杆A O = 2m ,BO = 3m ,已知某瞬时A 点的速度 U A= 6m/s ;而B 点的加速度与BO 成α= 60°角。
则该瞬时刚杆的角度速度ω= ① rad/s ,角加速度?=④ rad/s2。
①3; ②3; ③53; ④93。
三、计算题1、 水平梁AB 的A 端固定,B 端与直角弯杆BEDC 用铰链相连,定滑轮半径R = 20cm ,CD = DE = 100cm ,AC = BE = 75cm ,不计各构件自重,重物重P=10kN ,求C,A 处的约束力。
(20分)2、一水平简支梁结构,约束和载荷如图所示,求支座A 和B 的约束反力。
解:对该梁作受力分析由0∑=A M ,有:由0=∑X ,有:由0=∑Y ,有:3、两根铅直杆AB 、CD 与梁BC 铰接,B 、C 、D 均为光滑铰链,A 为固定端约束,各梁的长度均为L=2m ,受力情况如图。
已知:P=6kN ,M=4kN ·m ,qO=3kN/m,试求固定端A 及铰链C 的约束反力。
4、求指定杆1、2、3的内力。
5、一均质杆AB 重为400N ,长为l ,其两端悬挂在两条平行等长的绳上处于水平位置,如图所示。
今其中一根绳子突然被剪断,求另一根绳AE 此时的张力。
解:运动分析绳子突然被剪断,杆AB 绕A 作定轴转动。
假设角加速度为α,AB 杆的质心为C ,由于A 点的绝对速度为零,以瞬心A 为基点,因此有: l a C α21= 方向如图所示受力分析:AB 利用动静法,对质心C 建立力矩方程:由 0=∑C M有 021=⨯-*l T M C即 0211212=-Tl ml α (1)由 0=∑Y有 0=-+*mg F T C即 021=-+mg lm T α (2)联立(1)(2)两式,解得:【注】本题利用质心运动定理和绕质心转动的动量矩定理也可求解6、边长b =100mm 的正方形均质板重400N ,由三根绳拉住,如图所示。
求:1、当FG 绳被剪断的瞬时,AD 和BE 两绳的张力;2、当AD 和BE 两绳运动到铅垂位置时,两绳的张力。
7、图中,均质梁BC 质量为4m 、长4R ,均质圆盘质量为2m 、半径为R ,其上作用转矩M ,通过柔绳提升质量为m 的重物A 。
已知重物上升的加速度为a=0.4g ,求固定端B 处约束反力。
8、均质杆AB 长为L=2.5m ,质量为50kg ,位于铅直平面内,A端与光滑水平面接触,B 端由不计质量的细绳系于距地面h 高的O 点,如图所示。