4.4.1对数函数的概念(原卷版)

对数函数的概念与计算数学中，对数函数是一种非常重要的函数，它与指数函数密切相关。

本文将介绍对数函数的概念及其计算方法。

一、对数函数的概念对数函数是数学中一种常用的函数，它是指数函数的逆运算。

数学中常用的对数函数有自然对数函数 ln(x) 和常用对数函数 log(x)。

1. 自然对数函数 ln(x)自然对数函数 ln(x) 是以常数 e 为底的对数函数。

其中，常数 e 是一个重要的数学常数，它的近似值约为2.71828。

自然对数函数的定义域为正实数集合(0, +∞)，值域为实数集合。

2. 常用对数函数 log(x)常用对数函数 log(x) 是以常数 10 为底的对数函数。

常用对数函数的定义域为正实数集合(0, +∞)，值域为实数集合。

二、对数函数的计算对数函数的计算方法主要涉及对数的性质和运算规则。

1. 对数的性质（1） ln(1) = 0，即以 e 为底的对数函数 ln(x) 在 x = 1 时取值为 0。

（2） ln(e) = 1，即以 e 为底的对数函数 ln(x) 在 x = e 时取值为 1。

（3） log(1) = 0，即以 10 为底的对数函数 log(x) 在 x = 1 时取值为0。

（4） log(10) = 1，即以 10 为底的对数函数 log(x) 在 x = 10 时取值为 1。

2. 对数的运算规则（1） ln(a * b) = ln(a) + ln(b)，即以 e 为底的对数函数 ln(x) 的乘法运算可以转化为两个对数的加法运算。

（2） ln(a / b) = ln(a) - ln(b)，即以 e 为底的对数函数 ln(x) 的除法运算可以转化为两个对数的减法运算。

（3） log(a * b) = log(a) + log(b)，即以 10 为底的对数函数 log(x) 的乘法运算可以转化为两个对数的加法运算。

（4） log(a / b) = log(a) - log(b)，即以 10 为底的对数函数 log(x) 的除法运算可以转化为两个对数的减法运算。

对数函数的定义和基本性质1. 对数函数的定义对数函数是实数域上的一个函数，通常用符号y = log_a(x)（其中a是底数，x是真数）表示。

对数函数是对数arithmetic和函数function的组合。

对数函数是一类重要的数学函数，在数学分析、高等数学、工程学等领域中都有广泛的应用。

2. 对数函数的基本性质（1）单调性对数函数y = log_a(x)在定义域（即真数集）内是单调递增的。

当底数a > 1时，随着真数x的增加，对数函数的值也增加；当底数0 < a < 1时，随着真数x的增加，对数函数的值减少。

（2）反函数对数函数y = log_a(x)（其中a是底数，x是真数）和函数y = a^x（其中a是底数，x是真数）是互为反函数的关系。

也就是说，对于任意一个正实数y，都存在一个正实数x使得log_a(y) = x，则有a^x = y。

（3）对数恒等式对数恒等式是指对数函数在不同底数之间可以进行转换。

具体来说，有以下两个恒等式：•对数换底公式：log_a(b) = log_c(b) / log_c(a)（其中a, b, c 都是正实数，且a != 1, c != 1）。

•对数性质公式：log_a(b^c) = c * log_a(b)（其中a, b, c都是正实数，且a != 1）。

（4）对数函数的图像对数函数的图像是一条经过点(1, 0)，且斜率在0和+∞之间的曲线。

当底数a > 1时，图像位于第一象限；当底数0 < a < 1时，图像位于第二象限。

（5）对数函数的渐近线对数函数没有水平渐近线，但有一条垂直渐近线，即x = 0。

当x趋近于0时，对数函数的值趋近于负无穷；当x趋近于正无穷时，对数函数的值趋近于正无穷。

（6）对数函数与指数函数的关系对数函数和指数函数是互为逆运算的关系。

具体来说，对于任意一个正实数y，如果y = log_a(x)，则有x = a^y。

1．若函数 f(x)＝xlg2＋x，1，x>x1≤，1， 则 f(f(10))＝( B )
A．lg 101 B．2 C．1
D．0 f(f(10))＝f(1)＝12＋1＝ 2.
2．已知函数 f(x)＝log2(x2＋a)，若 f(3)＝－1，则 a＝ －127 . 解析：f(3)＝log2(9＋a)＝－1，所以 9＋a＝12，所以 a＝－127.
解析：设 f(x)＝logax，则 loga9＝2，解得 a＝3， 所以 f(x)＝log3x，所以 f31＝log331＝－1.
确定对数函数解析式的步骤 (1)设：用待定系数法先设出对数函数的解析式 y＝logax(a>0，且 a≠1)； (2)列：通过已知条件建立关于参数 a 的方程； (3)求：求出 a 的值，代入解析式即可．
D．(0，＋∞)
解析：由二次根式及分式有意义的条件，结合对数函数定义域可得
x－2>0， x>0，
解不等式组可得 x>2，即 x∈(2，＋∞)．
(x∈[0，＋∞))．
二、提出问题 1．上述函数式是指数函数吗？ 2．根据指数式与对数式的互化，你能化成对数式吗？ 3．化成对数式后式子有什么特点？ 4．x 是 y 的函数吗？
1．理解对数函数的概念，会求对数函数的定义域．
2．了解对数函数与指数函数之间的联系，提升学生观察问题、分析 问题和归纳问题的能力以及数学交流能力.
2．若 f(x)＝logax＋(a2－4a－5)是对数函数，则 a＝ 5 .
a2－4a－5＝0，
解析：由对数函数的定义可知，a＞0， a≠1，
解得 a＝5.
题型 2◆对数函数的解析式及应用 典例 1 已知函数 y＝ax－2＋1(a>0 且 a≠1)的图象过定点 A，函数 y ＝logmx(m>0，且 m≠1)也经过点 A，则 m 的值为 2 .

【课堂思维激活】 一、综合性——强调融会贯通 1．若函数y＝loga(x＋a)(a＞0且a≠1)的图象过点(－1,0)．
(1)求a的值； (2)求函数的定义域． 解：(1)将(－1,0)代入 y＝loga(x＋a)(a＞0，且 a≠1)中， 有 0＝loga(－1＋a)，则－1＋a＝1，所以 a＝2. (2)由(1)知，y＝log2(x＋2)，由 x＋2＞0，解得 x＞－2， 所以函数的定义域为{x|x＞－2}．
[方法技巧] 实际问题中对数模型要建模准确，计算时应充分利用对数的运算性质，注意 变量的实际意义．
【对点练清】 某公司制订了一个激励销售人员的奖励方案：当销售利润不超过10万元时，按销 售利润的15%进行奖励；当销售利润超过10万元时，若超出A万元，则超出部分 按2log5(A＋1)进行奖励．记奖金为y(单位：万元)，销售利润为x(单位：万元)． (1)写出奖金y关于销售利润x的关系式； (2)如果业务员老江获得5.5万元的奖金，那么他的销售利润是多少万元？ 解：(1)由题意知 y＝01..155＋x，2lo0g≤5xx－≤910，，x＞10. (2)由题意知 1.5＋2log5(x－9)＝5.5， 即 log5(x－9)＝2，所以 x－9＝52，解得 x＝34. 所以老江的销售利润是 34 万元．
[解析] (1)∵①中自变量出现在底数上，∴①不是对数函数；∵②中底数
a∈R 不能保证 a>0，且 a≠1，∴②不是对数函数；∵⑤⑦的真数分别为(x＋2)，
(x＋1)，∴⑤⑦也不是对数函数；∵⑥中 log4x 的系数为 2，∴⑥也不是对数函 数．只有③④符合对数函数的定义．
(2)∵函数 f(x)＝(a2＋a－5)logax 为对数函数，
解：要使函数 f(x)有意义， 只需ax＋－3a－≥x0>，0， 解得 a≤x<a＋3，即 A＝[a，a＋3)． 由14≤2x≤32，得－2≤x≤5，即 B＝[－2,5]． 选择第②个条件：当 a＝－3 时，A＝[－3,0)， ∴A∩B＝[－2,0)，满足条件． ∵∁UB＝(－∞，－2)∪(5，＋∞)，∴A∩(∁UB)＝[－3，－2)． 选择第③个条件： 当 a＝2 时，A＝[2,5)，∴A∩B＝[2,5)，满足条件． ∵∁UB＝(－∞，－2)∪(5，＋∞)，∴A∩(∁UB)＝∅.

第9讲 对数函数（原卷版）考点内容解读要求 常考题型 1．对数函数的图像和性质 理解对数函数的定义图象及性质 Ⅰ 选择题，填空题 2．对数函数的应用 对数函数性质的归纳与运用Ⅱ选择题，填空题1．对数1．对数的概念：一般地，如果N a x=)1,0(≠>a a ，那么数x 叫做以a 为底N 的对数，记作：Nx a log =（a — 底数，N — 真数，Na log — 对数式）说明：① 注意底数的限制0>a ，且1≠a ； ②xN N a a x =⇔=log ；③ 注意对数的书写格式． 两个重要对数：① 常用对数：以10为底的对数N lg ；② 自然对数：以无理数 71828.2=e 为底的对数的对数N ln ． 2．对数函数的特征特征⎩⎪⎨⎪⎧log a x 的系数：1log a x 的底数：常数，且是不等于1的正实数log a x 的真数：仅是自变量x判断一个函数是否为对数函数，只需看此函数是否具备了对数函数的特征．比如函数y ＝log7x 是对数函数，而函数y ＝－3log4x 和y ＝logx2均不是对数函数，其原因是不符合对数函数解析式的特点． 3．对数的运算性质如果0>a ，且1≠a ，0>M ，0>N ，那么： ①Ma (log ·=)N ；②=N M alog ；③ n a M log n =M a log )(R n ∈．注意：换底公式a bb c c a log log log =（0>a ，且1≠a ；0>c ，且1≠c ；0>b ）．利用换底公式推导下面的结论（1）b m n b a na m log log =；（2）a b b a log 1log =．2．对数函数及其性质 1．对数函数的定义：函数 x y a log =)10(≠>a a 且叫做 。

2．对数函数的性质：（1）定义域、值域：对数函数x y a log =)10(≠>a a 且的定义域为 ，值域为 ．（2）图象：由于对数函数是指数函数的 ，所以对数函数的图象只须由相应的指数函数图象作关于 的对称图形，即可获得。

对数函数的定义与性质1. 定义对数函数是指可以将正实数映射到实数集上的函数。

常用的对数函数有自然对数函数和常用对数函数。

自然对数函数以数学常数e为底的对数函数，通常以ln(x)表示，其中x为正实数。

常用对数函数以10为底的对数函数，通常以log(x)表示，其中x为正实数。

2. 性质2.1 对数函数的定义域和值域自然对数函数ln(x)的定义域是正实数集(0, +∞)，值域是实数集(-∞, +∞)。

常用对数函数log(x)的定义域是正实数集(0, +∞)，值域是实数集(-∞, +∞)。

2.2 对数函数的性质（1）对数函数的图像：自然对数函数ln(x)和常用对数函数log(x)的图像都是单调递增的曲线。

（2）基本性质：对数函数具有以下基本性质：•ln(1) = 0，即自然对数函数ln(x)在x=1处的函数值为0。

•ln(e) = 1，即自然对数函数ln(x)在x=e处的函数值为1。

•log(1) = 0，即常用对数函数log(x)在x=1处的函数值为0。

•log(10) = 1，即常用对数函数log(x)在x=10处的函数值为1。

（3）对数函数的性质：对数函数具有以下性质：•ln(x y) = ln(x) + ln(y)，即自然对数函数ln(x y)等于自然对数函数ln(x)和ln(y)的和。

•ln(x/y) = ln(x) - ln(y)，即自然对数函数ln(x/y)等于自然对数函数ln(x)和ln(y)的差。

•ln(x^n) = n * ln(x)，即自然对数函数ln(x^n)等于n乘以自然对数函数ln(x)。

•log(x y) = log(x) + log(y)，即常用对数函数log(x y)等于常用对数函数log(x)和log(y)的和。

•log(x/y) = log(x) - log(y)，即常用对数函数log(x/y)等于常用对数函数log(x)和log(y)的差。

•log(x^n) = n * log(x)，即常用对数函数log(x^n)等于n乘以常用对数函数log(x)。

对数函数知识点总结对数函数是指可以用对数形式表示的函数，它的定义域为正实数集合，值域为实数集合。

对数函数具有一些特殊的性质和运算规则，在数学中得到广泛应用。

本文将对对数函数的定义、性质、运算规则以及常见的应用进行总结。

一、对数函数的定义与性质：1. 对数的定义：对于任意的正实数a和b (a ≠ 1)，对数函数 y = loga(b) 表示满足 a^y = b 的唯一实数y。

2.对数函数的定义域为正实数集合，值域为实数集合。

3. 常见的对数函数是以自然常数e为底的自然对数函数 y = ln(x)和以常数10为底的常用对数函数 y = log10(x)。

4. 对数函数与指数函数是互逆变换关系，即 loga(a^x) =a^(loga(x)) = x。

5. 对数函数的图像特点：以对数函数 y = loga(x) 为例，当 a > 1 时，函数图像过点(1,0)，在区间(0,+∞)上是单调递增的，当x趋于0时，y趋于负无穷；当 a < 1 时，函数图像过点(1,0)，在区间(0,+∞)上是单调递减的，当x趋于0时，y趋于正无穷。

6. 对数函数具有对称性，即 loga(a/x) = -loga(x)。

二、对数函数的运算规则：1. 对数的乘法规则：loga(mn) = loga(m) + loga(n)。

2. 对数的除法规则：loga(m/n) = loga(m) - loga(n)。

3. 对数的幂次规则：loga(m^p) = p * loga(m)。

4. 对数的换底公式：loga(b) = logc(b) / logc(a)，其中c为任意的正实数（c ≠ 1）。

5. 对数函数的反函数：对于对数函数 y = loga(x)，其反函数为指数函数 x = a^y。

三、对数函数的应用：1.解指数方程和指数不等式：对于形如a^x=b或a^x<b的方程或不等式，可以通过取对数将其转化为对数方程或对数不等式进行求解。

∵log23<log24=2,∴log23-1<1.
又log34>log33=1,∴log34>log23-1,
即c>a,∴c>a>b,故选B.
5 | 如何解对数不等式
对数不等式的类型及解题方法 (1)形如loga f(x)>logab的不等式,借助函数y=logax的单调性求解,如果a的取值不确 定,需分a>1与0<a<1两种情况进行讨论; (2)形如loga f(x)>b的不等式,应将b化成以a为底数的对数式的形式(即b=logaab),借 助函数y=logax的单调性求解; (3)形如logf(x)a>logg(x)a的不等式,利用换底公式化为同底的对数进行求解,或利用图 象求解.
已知函数f(x)=loga(3-ax)(a>0). (1)当x∈[0,2]时,函数f(x)恒有意义,求实数a的取值范围; (2)是否存在这样的实数a,使得函数f(x)在区间[1,2]上为减函数,并且最大值为1? 如果存在,求出a的值;如果不存在,请说明理由. 解析 (1)设t(x)=3-ax,∵a>0, ∴t(x)=3-ax为减函数, 当x∈[0,2]时,t(x)的最小值为3-2a, 当x∈[0,2]时,f(x)恒有意义,即x∈[0,2]时,3-ax>0恒成立,∴3-2a>0,∴a3< .
2
2
2
综上,原不等式的解集为
1 2
,1.
对数函数的概念 对数函数的图象和性质
1 | 对数函数的概念
一般地,函数① y=logax(a>0,且a≠1) 叫做对数函数,其中x是自变量,定义 域是② (0,+∞) .
2 |对数函数的图象与性质

(1)ln 0.3,ln 2;
(2)loga3.1,loga5.2(a>0,且a≠1);
(3)log30.2,log40.2;
(4)log3π,logπ3.
解:(1)因为函数y=ln x在定义域内是增函数,且0.3<2,所以ln
.
2 -2-8 = 0,
解析:(1)由题意可知 + 1 > 0, 解得 a=4.
+ 1 ≠ 1,
(2)设对数函数为f(x)=logax(a>0,且a≠1).
则由题意可得f(8)=-3,即loga8=-3,
所以
a-3=8,即
1
3
-
a=8 =
1
.
2
所以 f(x)=log 1 x,故由 B(n,2)在函数图象上可得 f(n)=log 1 n=2,
2
是
.
课堂篇
探究学习
探究一
探究二
探究三
探究四
探究五
思想方法
随堂演练
解析:(1)由题意得x2-x>0,
解得x>1或x<0,
故函数的定义域是(-∞,0)∪(1,+∞).故选A.
(2)∵已知函数 f(x)=2log1 x 的值域为[-1,1],
2
∴-1≤2log1 x≤1,
2
即 log 1 1
≤2log1 x≤log1 1
(3)
)
课堂篇
探究学习
探究一
探究二
探究三
探究四
探究五
思想方法
对数函数的概念
例1 (1)已知对数函数f(x)=(m2-3m+3)·logmx,则m=
1
随堂演练

对数函数的基本概念对数函数是数学中常见且重要的一种函数类型。

它在各个领域中广泛应用，包括科学、工程、经济等。

本文将介绍对数函数的基本概念，包括对数的定义、性质以及常见的对数函数。

1. 对数的定义对数是数学中一个重要的概念，它描述了某个数在指定底数下的幂运算结果。

常见的对数有自然对数（以常数e为底数）和常用对数（以常数10为底数）。

自然对数常用符号ln表示，定义为ln(x) = y，其中x是指数，y是底数为e的对数。

常用对数常用符号log表示，定义为log(x) = y，其中x是指数，y是底数为10的对数。

对数函数将指数和底数之间的关系转化为指数和对数之间的关系，更加方便进行数值计算和问题求解。

2. 对数的性质对数具有一些特定的性质，便于在数学计算中应用。

（1）对数的底数必须大于0且不等于1，指数必须大于0；（2）对数的底数越大，对数的值越小；（3）对数的底数在(0,1)之间时，对数的值为负数；（4）对数的底数为1时，对数的值为0；（5）对数的底数为0时，对数的值是无穷大；（6）对数的指数乘积可以转化为对数之间的和；（7）对数的指数相除可以转化为对数之间的差；（8）对数的指数幂可以转化为对数之间的乘法；（9）对数的指数幂可以转化为对数之间的除法。

通过这些性质，可以方便地化简和计算对数的表达式。

3. 常见的对数函数（1）自然对数函数自然对数函数是以自然常数e为底数的对数函数，通常用符号ln表示。

自然对数函数在数学中有广泛的应用，尤其在微积分和指数函数中。

自然对数函数的图像是一个上升的曲线，其特点是具有水平渐进线y=0和y轴为渐进线。

它的导数是它自身的倒数，即(ln x)' = 1/x。

（2）常用对数函数常用对数函数是以常数10为底数的对数函数，通常用符号log表示。

常用对数函数在实际应用中比较常见，尤其在计算中常被使用。

常用对数函数的图像也是一个上升的曲线。

与自然对数函数不同的是，常用对数函数有一个特殊的点log(1) = 0。

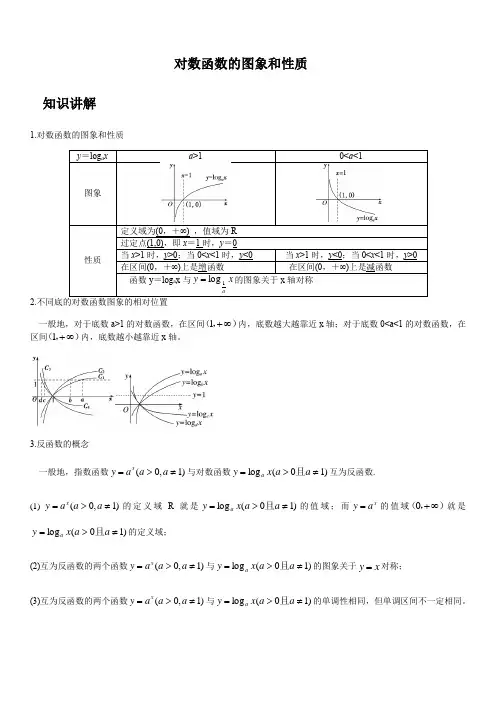
1.对数函数的图象和性质a>10<a<1定义域为(0，＋∞) ，值域为R2.一般地，对于底数a>1的对数函数，在区间），（∞+1内，底数越大越靠近x轴；对于底数0<a<1的对数函数，在区间），（∞+1内，底数越小越靠近x轴。

3.反函数的概念一般地，指数函数)1,0(≠>=aaay x与对数函数)1(log≠>=aaxya且互为反函数.(1))1,0(≠>=aaay x的定义域R就是)1(log≠>=aaxya且的值域；而x ay=的值域），（∞+0就是)1(log≠>=aaxya且的定义域；(2)互为反函数的两个函数)1,0(≠>=aaay x与)1(log≠>=aaxya且的图象关于xy=对称；(3)互为反函数的两个函数)1,0(≠>=aaay x与)1(log≠>=aaxya且的单调性相同，但单调区间不一定相同。

对数函数的图象和性质知识讲解一、选择题 1.已知函数y=log a (x+c )(a ,c 为常数,且a>0,a ≠1)的图象如图所示,则下列结论成立的是( )A.a>1,c>1B.a>1,0<c<1C.0<a<1,c>1D.0<a<1,0<c<12.下列关于函数)4(log )(31-=x x f 的单调性叙述正确的是（ ）A.在R 上为增函数B.在R 上为减函数C.在区间），（∞+4上为增函数 D.在区间），（∞+4上为减函数 3.函数12()log (2)f x x =-的单调递增区间是( ) A ．(,2)-∞ B ．(,0)-∞ C ．(2,)+∞D ．(0,)+∞ 4. 设a ，b ，c 均为正数，且a a 21log 2=，b b 21log 21=⎪⎭⎫ ⎝⎛，c c2log 21=⎪⎭⎫ ⎝⎛，则( )A ．a<b<cB ．c<b<aC ．c<a<bD ．b<a<c5.函数y=log a (x+2)+1(a>0,且a ≠1)的图象过定点( )A.(1,2)B.(2,1)C.(-2,1)D.(-1,1)6.若函数f (x )=log 2(x 2-ax -3a )在区间(-∞,-2]上是减函数,则实数a 的取值范围是( )A.(-∞,4)B.(-4,4]C.(-∞,4)∪[2,+∞)D.[-4,4) 7.函数2()log ()a f x ax x =-在[2,4]上是增函数，则实数a 的取值范围是（ ）A ．112a <<或1a > B ．1a > C ．114a << D ．108a <<同步练习8.已知函数f(x)={(a −1)x +4−2a, x <11+log 2x, x ⩾1，若f(x)的值域为R ，则实数a 的取值范围是( ) A.(1,2] B.(－∞，2] C.(0,2] D.[2，＋∞)9.已知a>0且a ≠1,函数y=log a x ,y=a x ,y=x+a 在同一坐标系中的图象可能是( )10.y=2x 与y=log 2x 的图象关于( )A.x 轴对称B.直线y=x 对称C.原点对称D.y 轴对称11.已知f (x )为R 上的增函数，且f (log 2x )>f (1)，则x 的取值范围为( )A.⎝⎛⎭⎫12，2B.⎝⎛⎭⎫0，12∪(2，＋∞) C ．(2，＋∞) D ．(0，1)∪(2，＋∞)12.（2020·福建安溪·高二期末）已知函数()f x 为R 上的偶函数，当0x ≥时，())2020log f x x =，则关于x 的不等式()()122f x f -<的解集为（ ）． A ．1,2⎛⎫-+∞ ⎪⎝⎭ B ．3,2⎛⎫-∞ ⎪⎝⎭C ．13,22⎛⎫- ⎪⎝⎭D ．30,2⎛⎫ ⎪⎝⎭13.已知a >0，且a ≠1，则函数y ＝x ＋a 与y ＝log a x 的图象只可能是( )14.函数f (x )＝log a |x |＋1(a ＞1)的图象大致为( )15.图中曲线是对数函数log ay x =的图象，已知a 43，35，110四个值，则相应于1C ，2C ，3C ，4C 的a 值依次为( )A ，43，35，110B 43，110，35C ．4335，110 D ．43，110，35 二、填空题1.函数()log (43)(0a f x x a =->且1)a ≠的图象所过定点的坐标是________.2.设a >1，若仅有一个常数c 使得对于任意的x ∪[a ，2a ]，都有y ∪[a ，a 2]满足方程log a x ＋log a y ＝c ，则a 的值为________．3.已知函数f (x )={log 2x,x >0,3x ,x ≤0,直线y=a 与函数f (x )的图象恒有两个不同的交点,则a 的取值范围是 .4.已知函数y ＝log 12()x 2－ax ＋a 在区间(2，＋∞)上是减函数，则实数a 的取值范围是____________．三、解答题1.比较下列各组数的大小；(1)log 0.90.8，log 0.90.7，log 0.80.9；(2)log 32，log 23，log 413.2.已知实数x 满足21log 321-≤≤-x .求函数y ＝⎝⎛⎭⎫log 2x 2·⎝⎛⎭⎫log 2x 4的值域．3.已知函数f (x )＝log 4(ax 2＋2x ＋3)．(1)若f (1)＝1，求f (x )的单调区间；(2)是否存在实数a ，使f (x )的最小值为0？若存在，求出a 的值；若不存在，说明理由．4.已知0m >，函数()lg(2)f x x m =-．（1）当1m =时，解不等式()0f x ；（2）若对于任意31,,()2t f x ⎡⎤∈⎢⎥⎣⎦在区间[,2]t t 上的最大值与最小值的和不大于1，求m 的取值范围．。

互为反函数, 定义域和值域互换, 对应法则互逆
例3.求下列函数的定义域： (1)y＝loga(9－x)(a>0，a≠1)；(2)y＝log(x－1)(3－ x)．
【思路点拨】 列出不等式组 → 解不等式
→ 写出定义域
自我挑战 求下列函数的定义域： 1
(1) y＝lgx＋ 1－3； (2) y＝ log x(2－x)．
y=3x-2 y x
∴x= y 2
y
3
∴函数y=3x-2(x∈R)
的反函数为
y= x 2
x∈R3
1 -2 -1-1 1
-2
y x2 3
x
例.求函数y=x3(x∈R)的反函数，并画出
原来的函数和它的反函数的图象.
解： y x3 x 3 y
y
y 3 x(x R)
1
y x3 y x
y3 x
x M´(b,a).
温馨提示：
(1)只有一一映射确定的函数才有反函数． (2)求反函数的步骤可概括为一解、二换、三写． (3)互为反函数的两个函数，它们的图像关于直线y ＝x对称． (4)互为反函数的两个函数的定义域与值域互换． (5)互为反函数的两函数单调性一致． (6)奇函数的反函数仍是奇函数，偶函数无反函数．
2
重要结论:
函数y=f(x)的图象和它的反函数 y=f-1(x)的图象
关于直线y=x对称。
应用思路：
已知函数的图像利用对称性可以 画出它的反函数的图像。
y
(0, 2) A
· · 3 1 · B-(22-, 01)-1
1A
(
2 3
,
0)
·-2 B (0, 2)
yx
原函数过

ab 2b
2
.
11
（2）. 求下列函数的定义域： 1
(1)f(x)＝lg(x－2)＋x－3；(2)f(x)＝log(x＋1)(16－4x)． 【解析】 (1)要使函数有意义,需满足Error!解得 x>2 且 x≠3, 所以函数定义域为(2,3)∪(3,＋∞)． (2)要使函数有意义,需满足Error!解得－1<x<0 或 0<x<4, 所以函数定义域为(－1,0)∪(0,4)．
底数,N 叫做真数.
重难点二 对数的性质、换底公式与运算性质
(1)对数的性质：①alogaN＝N；②logaab＝b(a>0,且 a≠1). (2)对数的运算法则
如果 a>0 且 a≠1,M>0,N>0,那么 ①loga(MN)＝logaM＋logaN；
M ②loga N ＝logaM－logaN；
B． y ln(2 x) C． y ln(1 x)
D．
3
y ln(2 x)
（3）．函数 f(x)＝ax－b 的图象如图所示,其中 a,b 为常数,则下列结论正确的是( )
A．a>1,b<0
B．a>1,b>0
C．0<a<1,b>0
D．0<a<1,b<0
（4）．当 a>1 时,在同一坐标系中,函数 y＝a－x 与 y＝logax 的图象为( )
例 2 求下列函数的定义域：
1
1
(1)f(x)＝
；(2)f(x)＝ ＋ln(x＋1)；
1
2－x
log x＋1
2
1
1
【解析】(1)要使函数 f(x)有意义,则 log x＋1>0,即 log x>－1,解得 0<x<2,即函数 f(x)的定义

指数函数性质
当底数为负数时，指数函数的图象关于原点对称；当底数 为1时，其图象为直线；当底数为正数时，其图象向右上 方倾斜且为连续的曲线。
对数函数性质
对数函数的图象与底数a的取值有关，a>1时，函数图象 单调递增；0<a<1时，函数图象单调递减。
指数函数与对数函数的图象及性质
指数函数图象
根据不同的底数a，指数函数的图象形状不 同。当a>1时，图象为连续的曲线且单调递 增；当0<a<1时，图象也为连续的曲线但 单调递减。
常用对数
以10为底数的对数，如log10(1000) = 3。
反对数
对于任何一个正实数x，都存在一个唯一的实数y ，使得xy = e^y = x。
对数函数的定义
定义域
对数函数的自变量可以是正实数，也可以是正无穷大，但不能取 负值和零。
函数表达式
y = log(a)x（其中a是底数，x是自变量，y是因变量）。
性质
指数函数具有连续性、非线性、递增等特性，当底数大于1时，函数值随自变量的增加而增加，当底 数小于1时，函数值随自变量的增加而减少。
对数函数与指数函数的转换
对数函数与指数函数是相互转化的，对数函数$y = log_a(x)$（其中$a > 0$且$a \neq 1$）可以看作是以$a$ 为底数的指数函数$y = a^x$的反函数。
值域
对数函数的值域为实数集，即y属于R。无论底数为何值，对数函数均有正值，这是因为任何正数的对数值均为实 数。
定义域
对数函数的定义域为正实数集，即x>0。这是因为只有当x为正数时，才能确保对数值有意义。
03
指数函数与对数函数的关系
指数函数的定义和性质

对数函数 1.对数函数的概念由于指数函数y=a x在定义域(-∞，+∞)上是单调函数，所以它存在反函数，我们把指数函数y=a x(a ＞0，a ≠1)的反函数称为对数函数，并记为y=log a x(a ＞0，a ≠1).因为指数函数y=a x的定义域为(-∞，+∞)，值域为(0，+∞)，所以对数函数y=log a x 的定义域为(0，+∞)，值域为(-∞，+∞).2.对数函数的图像与性质对数函数与指数函数互为反函数，因此它们的图像对称于直线y=x . 据此即可以画出对数函数的图像，并推知它的性质.为了研究对数函数y=log a x(a ＞0，a ≠1)的性质，我们在同一直角坐标系中作出函数y=log 2x ，y=log 10x ，y=log 10x,y=log 21x,y=log101x 的草图由草图，再结合指数函数的图像和性质，可以归纳、分析出对数函数y=log a x(a ＞0，a ≠1)的图像的特征和性质.见下表. 图 象a ＞1a ＜1性 质(1)x ＞0(2)当x=1时，y=0 (3)当x ＞1时，y ＞0 0＜x ＜1时，y ＜0 (3)当x ＞1时，y ＜0 0＜x ＜1时，y ＞0 (4)在(0，+∞)上是增函数 (4)在(0，+∞)上是减函数补充 性质①底都大于1时，底大图低（即在1>x 的部分底越大图象就越接近x 轴）②底都小于1时，底大图高（即在10<<x 的部分底越大图象就越远离x 轴）比较对数大小的常用方法有：(1)若底数为同一常数，则可由对数函数的单调性直接进行判断.(2)若底数为同一字母，则按对数函数的单调性对底数进行分类讨论. (3)若底数不同、真数相同，则可用换底公式化为同底再进行比较. (4)若底数、真数都不相同，则常借助1、0、-1等中间量进行比较.3.指数函数与对数函数对比名称 指数函数 对数函数 一般形式 y=a x(a ＞0，a ≠1) y=log a x(a ＞0，a ≠1)定义域 (-∞，+∞) (0，+∞) 值域 (0，+∞) (-∞，+∞)函 数 值 变 化 情 况当a ＞1时，⎪⎩⎪⎨⎧<<==>>)0(1)0(1)0(1x x x a x 当0＜a ＜1时，⎪⎩⎪⎨⎧<>==><)0(1)0(1)0(1x x x a x 当a ＞1时⎪⎩⎪⎨⎧<<==>>)1(0)1(0)1(0log x x x x a当0＜a ＜1时，⎪⎩⎪⎨⎧<>==><)1(0)1(0)1(0log x x x x a单调性 当a ＞1时，a x是增函数；当0＜a ＜1时，a x是减函数.当a ＞1时，log a x 是增函数； 当0＜a ＜1时，log a x 是减函数.图像 y=a x的图像与y=log a x 的图像关于直线y=x 对称.1．对数(1)对数的概念如果)1,0(≠>=a a N a b,那么b 叫做以a 为底N 的对数,记)1,0(log ≠>=a a N b a (2)对数的性质：①零与负数没有对数 ②01log =a ③1log =a a (3)对数的运算性质N M MN ①a a a log log log +=N M NM②a a alog log log -= M n M ③a n a log log =其中a>0,a ≠0,M>0,N>0(4)对数换底公式：)10,10,0(log log log ≠>≠>>=m m a a N aNN m m a 且且2．对数函数一般形式： y =a log x (a>0且a≠1)定义域：(0,+ ∞) 值域：(0,+ ∞) 过定点：（1，0）图象：单调性： a> 1,在(-∞,+ ∞)上为增函数０＜a<1, 在(-∞,+∞)上为减函数值分布： 当时且1,1>>x a y>0 当时且1,10><<x a y<0时且10,1<<>x a y<0 时且10,10<<<<x a y>0二、题型剖析1．对数式的化简和运算题组①指数式与对数式的互化 ⑴将下列指数式改写成对数式；1624=；27133=-；205=a ；45.021=⎪⎭⎫⎝⎛b⑵将下列对数式改写成指数式；3125log 5=； 23log 31-=；699.1lg -=a题组②计算：（1）1log 2log 2a a +； （2）33log 18log 2-； （3）1lg lg 254-；（4）552log 10log 0.25+； （5）522log 253log 64+； （6）22log (log 16)。

() A．y＝2＋log3x
logax(a> 0 且 a≠1)可知 D 正确．]
B．y＝loga(2a)(a>0，且 a≠1)
C．y＝logax2(a>0，且 a≠1)
D．y＝ln x
35
3．函数 f(x)＝ lg x＋lg(5－3x) 的定义域是( )
C [由l5g－x≥3x>0，0， 得
A.0，53 B.0，53 C.1，53
24
【例 3】 (1)当 a>1 时，在同一坐标系中，函数 y＝a－x 与 y＝logax
的图象为( )
A
B
C
D
(2)已知 f(x)＝loga|x|，满足 f(－5)＝1，试画出函数 f(x)的图象．
[思路点拨] (1)结合 a>1 时 y＝a－x＝1ax 及 y＝logax 的图象求解．
(2)由 f(－5)＝1 求得 a，然后借助函数的奇偶性作图．
27
C [∵在 y＝loga(－x)中，－x＞0，∴x＜0， ∴图象只能在 y 轴的左侧，故排除 A，D； 当 a＞1 时，y＝loga(－x)是减函数， y＝a－x＝1ax 是减函数，故排除 B； 当 0＜a＜1 时，y＝loga(－x)是增函数， y＝a－x＝1ax 是增函数，∴C 满足条件，故选 C.]
解得－1<x<0 或 0<x<4， 所以函数定义域为(－1,0)∪(0,4)．
23
对数函数的图象问题
[探究问题] 1．如图，曲线 C1，C2，C3，C4 分别对应 y＝loga1x， y＝loga2x，y＝loga3x，y＝loga4x 的图象，你能指出 a1， a2，a3，a4 以及 1 的大小关系吗？ 提示：作直线 y＝1，它与各曲线 C1，C2，C3，C4 的交点的横坐标就 是各对数的底数，由此可判断出各底数的大小必有 a4>a3>1>a2>a1>0. 2．函数 y＝ax 与 y＝logax(a>0 且 a≠1)的图象有何特点？ 提示：两函数的图象关于直线 y＝x 对称．

突破14 对数与对数函数重难点突破一、基础知识【知识点一、对数】 1．对数的概念（1）对数：一般地，如果x a N =(0,1)a a >≠且，那么数 x 叫做以a 为底 N 的对数，记作_______，其中a 叫做对数的底数，N 叫做真数．（2）常用对数：通常我们将以_______为底的对数叫做常用对数，并把10log N 记为lg N ．（3）自然对数：在科学技术中常使用以无理数e=2．718 28……为底数的对数，以e 为底的对数称为自然对数，并把e log N 记为ln N ． 2．对数与指数的关系当a >0，且a ≠1时，log ba a Nb N =⇔=．即3．对数的性质根据对数的概念，知对数log (0,1)a N a a >≠且具有以下性质： （1）负数和零没有对数，即0N >； （2）1的对数等于0，即log 10a =； （3）底数的对数等于1，即log 1a a =． 【知识点二、对数的运算】 1．基本性质若0,1,0a a N >≠>且，则 （1）log a Na=______；（2）log ba a =______．2．对数的运算性质如果0,1,0,0a a M N >≠>>且，那么： （1）log _________a (M N)=⋅； （2）log ________aM=N； （3）log _______()n a M =n ∈R ． 【知识点三、换底公式及公式的推广】 1．对数的换底公式log log (0,1;0,1;0)log c b c NN b b c c N b=>≠>≠>且且．【注】速记口诀：换底公式真神奇，换成新底可任意， 原底加底变分母，真数加底变分子．2．公式的推广 （1）1log log a b b a=（其中a >0且1a ≠；b >0且1b ≠）；（2）log log n na ab b =（其中a >0且1a ≠；b >0）；（3）log log n m a a mb b n=（其中a >0且1a ≠；b >0）； （4）1log log a ab b =-（其中a >0且1a ≠；b >0）；（5）log log log log a b c a b c d d ⋅⋅=（其中a ，b ，c 均大于0且不等于1，d >0）． 【知识点四、对数函数】 1．对数函数的概念一般地，我们把函数log (0,1)a y x a a =>≠且叫做对数函数，其中x 是自变量，函数的定义域是_____． 2．对数函数(0,1)xy a a a =>≠且的结构特征 （1）对数符号前面的系数是1；（2）对数的底数是不等于1的正实数（常数）； （3）对数的真数仅有自变量x ． 【知识点五、对数函数的图象与性质】1．一般地，对数函数log (0,1)a y x a a =>≠且的图象和性质如下表所示：01a << 1a >图象定义域 (0,)+∞值域 R奇偶性 非奇非偶函数过定点 过定点(1,0)，即1x =时，0y =单调性 在(0,)+∞上是___函数 在(0,)+∞上是___函数 函数值的变化情况当01x <<时，0y >； 当1x >时，0y <当01x <<时，0y <； 当1x >时，0y >【注】速记口诀：对数增减有思路，函数图象看底数； 底数只能大于0，等于1了可不行； 底数若是大于1，图象从下往上增； 底数0到1之间，图象从上往下减； 无论函数增和减，图象都过（1，0）点．2．对数函数log (0,1)a y x a a =>≠且中的底数对其图象的影响在直线x =1的右侧，当a >1时，底数越大，图象越靠近x 轴；当0<a <1时，底数越小，图象越靠近x 轴，即“底大图低”．【知识点六、反函数】根据指数与对数的关系，将指数式(0,1)xy a a a =>≠且（其中x 是自变量，且x ∈R ，y 是x 的函数，(0,)y ∈+∞）化成对数式，即log a x y =，于是对于任意一个(0,)y ∈+∞，通过式子log a x y =都有唯一一个x ∈R 与之对应，这样将y 看成自变量，x 是y 的函数，这时我们就说log ((0,))a x y y =∈+∞是函数()x y a x =∈R 的反函数．由于习惯上将x 看成自变量，而将y 看成因变量，因此，我们将log a x y =中的x ，y 互换，写成log ((0,))a y x x =∈+∞，即对数函数log ((0,))a y x x =∈+∞是指数函数()x y a x =∈R 的反函数，它们的图象关于直线y x =对称．二、题型分析1．对数的概念解决使对数式有意义的参数问题，只要注意满足底数和真数的条件，然后解不等式（组）即可．对数的概念是对数式和指数式互化的依据，在互化过程中应注意对数式和指数式之间的对应关系． 【例1】在对数式(1)log (3)x x --中，实数x 的取值范围应该是 A ．1<x <3B ．x >1且x ≠2C ．x >3D ．1<x <3且x ≠2【变式训练1】在M ＝log （x ﹣3）（x +1）中，要使式子有意义，x 的取值范围为（ ） A ．（﹣∞，3] B ．（3，4）∪（4，+∞） C ．（4，+∞）D ．（3，4）【变式训练2若对数ln （x 2﹣5x +6）存在，则x 的取值范围为 ．2．对数运算性质的应用对数的运算性质是进行对数运算和化简的基础，所以要熟记对数的运算性质以及对数恒等式，化简的原则是：（1）尽量将真数化为 “底数”一致的形式；（2）将同底的多个对数的和（差）合成积（商）的对数；（3）将积（商）的对数分成若干个对数的和（差）．运算时要灵活运用对数的相关公式求解，如log a a =1(0,1)a a >≠且，log log 1a b b a ⋅=等．【例2】计算：（1）9log 32162)23(log --+； （2）2(lg 5)lg 2lg 5lg 2+⨯+．【变式训练1】（2019春•东莞市期末）计算（1）2﹣（）+lg+（）lg 1（2）lg 52+lg 8+lg 5lg 20+（lg 2）2【变式训练2】（2019•西湖区校级模拟）计算： （1）；（2）．3．换底公式的应用换底公式即将底数不同的对数转化为底数相同的对数，进而进行化简、计算或证明．换底公式应用时究竟换成什么为底，由已知条件来确定，一般换成以10为底的常用对数或以e 为底的自然对数．【例3】已知711,log 473ab ⎛⎫== ⎪⎝⎭，试用,a b 表示49log 48．【变式训练1】（2019秋•中江县校级期中）利用对数的换底公式化简下列各式： （1）log a c •log c a ；（2）log 23•log 34•log 45•log 52； （3）（log 43+log 83）（log 32+log 92）．【变式训练2】利用对数的换底公式化简下列各式：（log 43+log 83）（log 32+log 92）4．对数方程的求解解对数方程时，（1）等号两边为底数相同的对数式，则真数相等；（2）化简后得到关于简单对数式的一元二次方程，再由对数式与指数式的互化求解． 【例4】方程1122log (95)log (32)2x x ---=-+的解为 ．【变式训练1】求下列各式中x 的值： （1）log 4x ＝﹣，求x ；（2）已知log 2（log 3x ）＝1，求x ．【变式训练2】求下列各式中x 的值： （1）log x 27＝； （2）4x ＝5×3x ．【变式训练3】先将下列式子改写指数式，再求各式中x 的值． ①log 2x ＝﹣ ②log x 3＝﹣．5．与对数函数有关的函数的定义域和值域定义域是使解析式有意义的自变量的取值集合，求与对数函数有关的定义域问题时，要注意对数函数的概念，若自变量在真数上，则必须保证真数大于0；若自变量在底数上，应保证底数大于0且不等于1．同时还要注意偶次方根的被开方数非负，分母不能为零等．求值域时，一方面要抓住对数函数的定义域和单调性，另一方面，若是复合函数，则要抓住中间变量的取值范围．【例5】已知函数33()log (2)log (6)f x x x =-++． （1）求函数()f x 的定义域； （2）求函数()f x 的最大值．【变式训练1】（2019•西湖区校级模拟）函数的定义域是（ ） A ．B ．C ．D ．【变式训练2】（2018秋•宜宾期末）函数y ＝的定义域是（ ）A ．（，+∞）B ．（，1]C ．（﹣∞，1]D ．[1，+∞）【变式训练3】（2018春•连城县校级月考）函数y ＝的定义域是（ ）A ．[1，+∞）B ．（，+∞）C ．（1，+∞）D ．（，1]6．对数函数的图象对数函数=log (0,1)a y x a a >≠且的图象过定点（1，0），所以讨论与对数函数有关的函数的图象过定点的问题，只需令真数为1，解出相应的,x y ，即可得到定点的坐标．当底数1a >时，对数函数()log a f x x =是(0,)+∞上的增函数，当1x >时，底数a 的值越小，函数图象越“陡”，其函数值增长得越快；当底数01a <<时，对数函数()log a f x x =是(0,)+∞上的减函数，当01x <<时，底数a 的值越大，函数图象越“陡”，其函数值减小得越快．也可作直线y =1与所给图象相交，交点的横坐标即为各个底数，依据在第一象限内，自左向右，图象对应的对数函数的底数逐渐变大，可比较底数的大小．【例6】设0,1a a >≠且，函数2log (2)a y x =++的图象恒过定点P ，则P 点的坐标是 A ．(1,2)- B ．(2,1)- C ．(3,2)-D ．(3,2)【变式训练1】（2019•西湖区校级模拟）若当x ∈R 时，函数f （x ）＝a |x |始终满足0＜|f （x ）|≤1，则函数y ＝log a ||的图象大致为（ ）A ．B ．C ．D ．【变式训练2】（2018秋•船营区校级月考）函数f （x ）＝的图象可能是（ ）A ．B ．C ．D ．【变式训练3】（2019秋•洛南县期末）函数y ＝|lg （x +1）|的图象是（ ）A ．B ．C ．D ．7．对数函数单调性的应用（1）比较对数式的大小：若比较同底数的两个对数式的大小，可直接利用对数函数的单调性；若比较底数不同、真数相同的两个对数式的大小，可以先用换底公式化为同底后，再进行比较，也可以利用顺时针方向底数增大画出对数函数的图象，再进行比较；若比较底数与真数都不同的两个对数式的大小，常借助1，0等中间量进行比较．（2）解简单的对数不等式：形如log log a a x b >的不等式，常借助=log a y x 的单调性求解，如果a 的取值不确定，需分1a >与01a <<两种情况进行讨论；形如log a x b >的不等式，应将b 化为以a 为底数的对数式的形式，再借助=log a y x 的单调性求解． 【例7】已知13212112,log ,log 33a b c -===，则 A ．a b c >> B ．a c b >> C ．c a b >>D ．c b a >>【变式训练1】（2019秋•沙坪坝区校级月考）已知a ＝log 30.3，b ＝30.3，c ＝0.30.2，则（ ） A ．a ＜b ＜cB ．a ＜c ＜bC ．c ＜a ＜bD ．b ＜c ＜a【变式训练2】（2019•西湖区校级模拟）下列关系式中，成立的是（ ） A ．B ．C ．D ．8．对数型复合函数的性质及其应用 （1）对数复合函数的单调性复合函数y =f [g （x ）]是由y =f （x ）与y =g （x ）复合而成，若f （x ）与g （x ）的单调性相同，则其复合函数f [g （x ）]为增函数；若f （x ）与g （x ）的单调性相反，则其复合函数f [g （x ）]为减函数．对于对数型复合函数y =log a f （x ）来说，函数y =log a f （x ）可看成是y =log a u 与u =f （x ）两个简单函数复合而成的，由复合函数单调性“同增异减”的规律即可判断．另外，在求复合函数的单调性时，首先要考虑函数的定义域．（2）对于形如y =log a f （x ）（a >0，且a ≠1）的复合函数，其值域的求解步骤如下： ①分解成y =log a u ，u =f （x ）两个函数； ②求f （x ）的定义域； ③求u 的取值范围；④利用y =log a u 的单调性求解．【例8】讨论函数()2log 32()1a f x x x =--的单调性．【变式训练1】（2018秋•宜宾期末）函数y ＝的定义域是（ ）A ．（，+∞）B ．（，1]C ．（﹣∞，1]D ．[1，+∞） 【变式训练2】（2018春•连城县校级月考）函数y ＝的定义域是（ ）A ．[1，+∞）B ．（，+∞）C ．（1，+∞）D ．（，1]【变式训练3】（2019秋•南昌校级期中）函数y ＝log 4（2x +3﹣x 2）值域为 ． 【变式训练4】函数y ＝（x ）2﹣x 2+5 在 2≤x ≤4时的值域为 ．9．忽略真数大于0【例9】已知()lg lg 2lg 23x y x y +=-，求32log xy的值．10．忽略对底数的讨论【例10】不等式1log (4)log a ax x ->-的解集是_______．三．课后作业1．222log log 63+等于 A ．1B ．2C ．5D ．62．实数01()lg42lg52-++的值为 A ．1B ．2C ．3D ．43．已知函数f （x ）=log 2（3+x ）+log 2（3–x ），则f （1）= A ．1 B ．log 26C ．3D ．log 294．若212log log 2a b +=，则有A ．a =2bB ．b =2aC ．a =4bD ．b =4a5．设()()2log 20xf x x =>，则f （3）的值是A ．128B ．256C ．512D ．86．log 513+log 53等于 A ．0 B ．1C ．–1D ．log 51037．若a =3412（），b =1234（），c =log 23，则a ，b ，c 大小关系是 A ．a <b <c B ．b <a <cC ．b <c <aD ．c <b <a8．若a =30.4，b =0.43，c =log 0.43，则 A ．b <a <c B ．c <a <bC ．a <c <bD ．c <b <a9．若25210cab==且abc ≠0，则c c a b+= A ．2B ．1C ．3D ．410．已知1122log log a b <，则下列不等式一定成立的是A ．11()()43a b < B ．11a b> C ．ln （a –b ）>0D ．3a –b <111．函数y =__________．12．函数y =lg x 的反函数是__________．13．函数f （x ）的定义域为__________． 14．设2x =5y =m ，且11x y+=2，则m 的值是__________． 15．方程log 2（2–x ）+log 2（3–x ）=log 212的解x =__________． 16．已知f （x ）=lg （10+x ）+lg （10–x ），则f （x ）是 A ．f （x ）是奇函数，且在（0，10）是增函数 B ．f （x ）是偶函数，且在（0，10）是增函数 C ．f （x ）是奇函数，且在（0，10）是减函数 D ．f （x ）是偶函数，且在（0，10）是减函数 17．设正实数a ，b 满足6a =2b ，则A ．01ba << B ．12ba <<C ．23ba<<D ．34b a<<18．根据有关资料，围棋状态空间复杂度的上限M 约为3361，而可观测宇宙中普通物质的原子总数N 为1080，则下列各数中与MN最接近的是 A ．1033 B ．1053C ．1073D ．109319．若log 2（log 3a ）=log 3（log 4b ）=log 4（log 2c ）=1，则a ，b ，c 的大小关系是 A ．a >b >c B ．b >a >cC ．a >c >bD ．b >c >a20．若正实数x ，y 满足log 2（x +3y ）=log 4x 2+log 2（2y ），则x +3y 的最小值是 A ．12 B ．10C ．8D ．621．对任意的正实数x ，y ，下列等式不成立的是 A ．lg y –lg x =lg y xB ．lg （x +y ）=lg x +lg yC ．lg x 3=3lg xD ．lg x =ln ln10x22．设函数y =f （x ）的图象与y =log 2（x +a ）的图象关于直线y =–x 对称，且f （–2）+f （–1）=2，则a = A ．3B ．1C ．2D ．423．已知函数f （x ）=ln （–x 2–2x +3），则f （x ）的增区间为 A ．（–∞，–1） B ．（–3，–1）C ．[–1，+∞）D ．[–1，1）24．已知函数()()212log 45f x x x =--，则函数f （x ）的减区间是A ．（–∞，2）B ．（2，+∞）C ．（5，+∞）D ．（–∞，–1）25．已知R 上的奇函数f （x ）满足当x <0时，f （x ）=log 2（1–x ），则f （f （1））= A ．–1 B ．–2C ．1D ．226．若实数a ，b 满足a >b >1，m =log a （log a b ），2(log )a n b =，2log a l b =，则m ，n ，l 的大小关系为A ．m >l >nB ．l >n >mC ．n >l >mD ．l >m >n27．函数f （x ）=log a （3–ax ）（a >0且a ≠1）在区间（a –2，a ）上单调递减，则a 的取值范围为__________． 28．已知函数f （x ）=a •2x +3–a （a ∈R ）的反函数为y =f –1（x ），则函数y =f –1（x ）的图象经过的定点的坐标为__________．29．若函数f （x ）=log a （x 2–ax +1）（a >0且a ≠1）没有最小值，则a 的取值范围是__________． 30．（1）5log 3333322log 2log log 8259-+-；（2）7log 23log lg 25lg 47+++．31．求函数f（x）=log13（x2–3）的单调区间．32．已知函数f（x）=lg（x+1）–lg（1–x）．（1）求函数f（x）的定义域；（2）判断函数f（x）的奇偶性．33．已知函数f（x）=log a（1+x）–log a（1–x），其中a>0且a≠1．（1）求函数f（x）的定义域；（2）判断f（x）的奇偶性，并说明理由；（3）若f（35）=2，求使f（x）>0成立的x的集合．34．（2018•天津）已知a=log2e，b=ln2，c=121log3，则a，b，c的大小关系为A ．a >b >cB ．b >a >cC ．c >b >aD ．c >a >b35．（2018•天津）已知a =log 372，b =1314（），c =131log 5，则a ，b ，c 的大小关系为A ．a >b >cB ．b >a >cC ．c >b >aD ．c >a >b36．（2018•新课标Ⅲ）设a =log 0.20.3，b =log 20.3，则 A ．a +b <ab <0 B ．ab <a +b <0C ．a +b <0<abD ．ab <0<a +b37．（2018•上海）设常数a ∈R ，函数f （x ）=1og 2（x +a ）．若f （x ）的反函数的图象经过点（3，1），则a =__________．38．【2018年全国卷Ⅲ文】已知函数())ln1f x x =+，()4f a =，则()f a -=__________．。