极点极线及高中圆锥曲线必备公式

圆锥曲线极点极线定理圆锥曲线极点极线定理1. 引言圆锥曲线是平面解析几何中的重要概念之一，它包括椭圆、双曲线和抛物线三种类型。

在研究圆锥曲线的性质时，极点和极线是不可避免的概念。

本文将介绍圆锥曲线的极点极线定理，该定理是描述圆锥曲线中极点和极线之间关系的重要结论。

2. 极点和极线的定义在平面直角坐标系中，设有一条直线L和一个点P(x0,y0)。

若从P到L上每一点所引的直线与L垂直，则称P为L的极点，L为P的极线。

3. 圆锥曲线的定义设有一个平面内固定点F（称为焦点）和一条固定直线d（称为准线）。

对于任意一点P，分别以PF和PD（D为d上任意一点）为半径作两个圆，并将这两个圆相切于P处。

则所有这样的P所构成的集合称为圆锥曲线。

4. 圆锥曲线中极点与极轴间关系对于任意一条圆锥曲线，设其焦点为F，准线为d，P为任意一点，则有以下结论：（1）若P在焦点F上，则其极线为准线d；（2）若P在准线d上，则其极线为过该点且垂直于准线的直线；（3）若P不在焦点F和准线d上，则其极轴为PF的中垂线。

5. 圆锥曲线中极轴与极径间关系对于任意一条圆锥曲线，设其焦点为F，准线为d，O为坐标系原点，则有以下结论：（1）若O在焦点F上，则其极径是任意一条过O的直线；（2）若O在准线d上，则其极径是与准线垂直且经过O的直线；（3）若O不在焦点F和准线d上，则其极径是从O出发经过圆锥曲线上任意一点P的直线。

6. 圆锥曲线中两个互异的定理对于任意一条圆锥曲线，设其焦点为F，准线为d，P(x,y)为任意一点。

则有以下两个互异的定理：（1）以FP和PD分别为半径的两个圆相交于点P，则P在圆锥曲线上；（2）以FP和PD分别为半径的两个圆相切于点P，则P在圆锥曲线上。

7. 结论综上所述，圆锥曲线极点极线定理是描述圆锥曲线中极点和极线之间关系的重要结论。

在研究圆锥曲线的性质时，该定理具有重要意义。

线犾 上任一点作抛物线的两条切线 ， 则直 犕， 犖 为切 点 ， 线 犕犖 恒过定点 ． 解析 ： 因为 抛 物 线 的 准 线 和 焦 点 刚 好 是 一 对 极 点 和极线 ， 由定理第 （ ） 条知直线 犕犖 恒过焦点 犉（ ） ４ １， ０ ．
， 动 直 线犾 与 椭 圆 犫＞０） 只有一个公共 点 犘， 且 犆 点 犘 在第一象限 ． （ Ⅰ ）已 知 直 线 犾 的 斜率为犽， 用 犪， 犫， 犽表示 点 犘 的坐标 ； 图１
） 所对应的准线 ． 对于双曲线和抛物线结论类似 ． 犉（ 犮， ０ 焦点与准线 是 圆 锥 曲 线 的 统 一 定 义 ， 我们很多人 只知道它的存在 ， 却不知道 它 们 内 在 的 联 系 ， 教材中潜 形匿迹 ， 但 我 们 也 不 能 对 此 视 而 不 见， 我们也可借此 解题 ．
２ 例 ２ 已知抛物线 狔 过直 ＝４ 狓 和 直 线犾： 狓＝ －１，
１ １ ２ ２ ） 即２ 犕犖 的方程为 （ 狋 ＝ ·２ 狋 狓＋１， 狋 狓－狔－ 狋 狔＋ ２ ２
２ ２ ２ ４ 狋 － 狋 ＋２－ 狋 ｜ 于是 犱＝｜ ＋２＝０， ＝２ ２ １＋４ 狋 槡 ２ （ ） ， 则 犱＝ ＝１＋４ 狋 狊 ≥１
槡
２ ２ （ ） １＋ 狋 令 ２ ． 狊 １＋４ 狋
— —极 点 与 极 线 在 高 考 解 题 中 的 ３ 洗 尽 铅 华 — 应用
在近年的各地 高 考 模 拟 试 题 中 ， 有关圆锥 事实上 ， 曲线的极点与 极 线 问 题 也 屡 见 不 鲜 ． 用普通方法可以
·６ ４·
数学教育研究
２ ０ １ ５ 年第 １ 期
求解 ， 但过程相对繁杂 ， 如果 用 极 点 和 极 线 的 视 角 看 问 题， 则事半功倍 ． 定值问题 ３． １ 可以解决圆锥曲线中的定点 、 例 ３ （ ２ ０ １ ４稽阳联谊 学校 高 三 数 学 联 考 ２ １ 题）

圆锥曲线的几大大题特征公式：焦半径、准线、弦长、切线方程、弦中点公式、极线方程/*另外，针对“计算不好”的同学，本人提供“硬解定理”供大家无脑使用。

具体的请参考本目录下的【硬解定理的推导和使用】文章。

*/圆锥曲线的切线方程在历年高考题中出现，但是在高中教材及资料都涉及较少。

本文主要探索圆锥曲线的切线方程及其应用。

从而为解这一类题提供统一、清晰、简捷的解法。

【基础知识1：切线方程、极线方程】【1-0】公式小结：x 2换成xx 0，y 2换成yy 0，x 换成(x+x 0)/2,y 换成(y+y 0)/2.【1-1】椭圆的切线方程： ①椭圆12222=+y x上一点),(00y x P 处的切线方程是12020=+yy xx 。

(【1-2【1-3 【1-41、第入原始式，最后得切线方程式1)()(2202202020=+=+by a x b yy a xx （注:k 的表达式可以在草稿中巧用点差法求,具体见下）2、第2种证明思路：点差法(求斜率，其余跟第一种方法一样)证明：设某直线与曲线C 交于M 、N 两点坐标分别为),(11y x 、),(22y x ，中点P ),(00y x则有⎪⎪⎩⎪⎪⎨⎧=+=+)2(.1)1(,1222222221221 b y a x b y a x ⇒)2()1(-，得.022********=-+-b y y a x x2212121212ab x x y y x x y y -=++⋅--∴又.22,000021211212x y x y x x y y x x y y k MN ==++--= 2200a b x y k MN -=⋅∴(弦中点公式的椭圆基本表达式。

双曲线则是2200ab x y k MN =⋅) 当M 、N 无限趋近时，P 在椭圆C 上。

即得切线斜率0022y x a b k ⋅-= 3、第三种证明思路(注意：仅供理解，考试使用可能分证明：由2（圆锥曲线切线证明）（同一目录下文章）可知圆上一点的切线方程。

备战 2019 年高考数学二轮复习常用的圆锥曲线公式总结圆锥曲线包含圆，椭圆，双曲线，抛物线。

以下是常用的圆锥曲线公式总结，请考生实时学习。

抛物线： y = ax *+ bx + c就是 y 等于 ax 的平方加上bx 再加上ca0 时张口向上a0 时张口向下c = 0 时抛物线经过原点b = 0 时抛物线对称轴为y 轴还有极点式y = a(x+h)* + k就是 y 等于 a 乘以 (x+h) 的平方 +k-h 是极点坐标的xk 是极点坐标的y一般用于求最大值与最小值抛物线标准方程:y^2=2px它表示抛物线的焦点在x 的正半轴上 ,焦点坐标为 (p/2,0) 准线方程为 x=-p/2因为抛物线的焦点可在随意半轴,故共有标准方程y^2=2px y^2=-2px x^2=2py x^2=-2py圆：体积 =4/3(pi)(r^3)面积 =(pi)(r^2)周长 =2(pi)r圆的标准方程(x-a)2+(y-b)2=r2注：(a,b)是圆心坐标语文课本中的文章都是优选的比较优异的文章 ,还有许多名家名篇。

假如有选择顺序渐进地让学生背诵一些优异篇目、出色段落 ,对提升学生的水平会大有裨益。

此刻 ,许多语文教师在剖析课文时 ,把文章解体的支离破裂 ,总在文章的技巧方面下功夫。

结果教师费力 ,学生头疼。

剖析完以后 ,学生见效甚微 ,没过几日便忘的干干净净。

造成这类事半功倍的难堪局面的重点就是对文章读的不熟。

常言道“书读百遍 ,其义自见”,假如有目的、有计划地指引学生频频阅读课文,或细读、默读、跳读 ,或听读、范读、轮读、分角色朗诵,学生便能够在读中自然意会文章的思想内容和写作技巧,能够在读中自然增强语感 ,增强语言的感觉力。

长此以往,这类思想内容、写作技巧和语感就会自然浸透到学生的语言意识之中,就会在写作中自觉不自觉地加以运用、创建和发展。

唐宋或更早以前，针对“经学”“律学”“算学”和“书学”各科目，其相应教授者称为“博士”，这与此刻“博士”含义已经相去甚远。

圆锥曲线的极坐标方程、焦半径公式、焦点弦公式一、圆锥曲线的极坐标方程椭圆、双曲线、抛物线可以统一定义为：与一个定点(焦点)的距离和一条定直线(准线)的距离的比等于常数e 的点的轨迹．以椭圆的左焦点(双曲线的右焦点、抛物线的焦点)为极点，过点F 作相应准线的垂线，垂足为K ，以FK 的反向延长线为极轴建立极坐标系．椭圆、双曲线、抛物线统一的极坐标方程为： θρcos 1e ep -=. 其中p 是定点F 到定直线的距离，p ＞0 ．当0＜e ＜1时，方程表示椭圆；当e ＞1时，方程表示双曲线，若ρ＞0，方程只表示双曲线右支，若允许ρ＜0，方程就表示整个双曲线；当e=1时，方程表示开口向右的抛物线.二、圆锥曲线的焦半径公式设F 为椭圆的左焦点(双曲线的右焦点、抛物线的焦点)，P 为椭圆(双曲线的右支、抛物线)上任一点，则 ∵PQ e PF =，∴)cos (p PF e PF +=θ，其中FH p =，=θ〈x 轴，FP 〉 ∴焦半径θcos 1e ep PF -=． 当P 在双曲线的左支上时，θcos 1e ep PF +-=. 推论：若圆锥曲线的弦MN 经过焦点F ，则有ep NF MF 211=+.三、圆锥曲线的焦点弦长若圆锥曲线的弦MN 经过焦点F ，1、椭圆中，cb c c a p 22=-=，θθπθ2222cos 2)cos(1cos 1c a ab e ep e ep MN -=--+-=. 2、双曲线中，若M 、N 在双曲线同一支上，θθπθ2222cos 2)cos(1cos 1c a ab e ep e ep MN -=--+-=； 若M 、N 在双曲线不同支上，2222cos 2cos 1cos 1a c ab e ep e ep MN -=--+-=θθθ. 3、抛物线中，θθπθ2sin 2)cos(1cos 1p p p MN =--+-=. 四、直角坐标系中的焦半径公式设P （x,y ）是圆锥曲线上的点，1、若1F 、2F 分别是椭圆的左、右焦点，则ex a PF +=1，ex a PF -=2；2、若1F 、2F 分别是双曲线的左、右焦点，当点P 在双曲线右支上时，a ex PF +=1，a ex PF -=2；当点P 在双曲线左支上时，ex a PF --=1，ex a PF -=2；3、若F 是抛物线的焦点，2p x PF +=.。

一
ｂ ０、 ＞ ）抛物线 一２ｘ ＞ ｏ ） ｐ（ ） 的一个极点 ， 它
对应 的极线 为 Ｌ， Ｐ任 意引一条 直线 ， ｒ于点 过 交 Ａ、 交 Ｌ于点 Ｑ， Ｂ， 若点 Ａ 是位于 Ｐ、 Ｑ间 的点 ， 则 （ ）当 Ｐ在 ｒ 外时 ， １
０
．
２
—
２
—
２Ｉ ２ｏｏ￣ ｏｉ ｂＸ ｃｓ ＋ｎＹｓ ａＩ ｎ
一
一பைடு நூலகம்
一Ｔ
＝
⑤
２ ２
中 学数 学 教 学
２１ ０ ０年 第 ４期
圆锥 曲线极 点 与 极 线 的 一组 性 质
湖 北 省 阳 新 县 高 级 中 学 邹 生 书 （ 编 ：３ ２ ０ 邮 ４５０ ）
１ 圆 锥 曲线 极 点 和 极 线 的定 义 已 知圆锥 曲线 Ｃ： 。 ＋ ２ ｘ＋２ ｖ＋ ＋ Ｄ Ｅ Ｆ 一 ０ Ａ ＋ Ｃ ≠ ０ ， 称 点 Ｐ ｘ ，。 和 直 线 ｚ （。 。 ）则 （ 。ｙ ） ：
（ ） Ｐ 在 椭 圆 ｒ 内 ， ０ 的 延 长 线 取 点 １ 若 在 Ｐ
由参数 方程 中 ｔ 的几 何意 义知 ｔ 一 Ｐ ｔ 一 Ｐ Ａ， Ｂ． 由韦达 定理 ，
一
，
Ｄ Ｃ０ Ｓ ａ 十 口 Ｓ１ 。 ｎ 口
＋ ＋ 一
一
ｂｚ ２ ＋ 口 Ｙ 。 一 口 ｂ 。
‘
Ｑ， ｌ Ｐ １ Ｉ Ｉ Ｉ Ｒ Ｉ Ｒ为 Ｏ 使 ． ∞ — Ｏ Ｏ （ Ｐ延 长线 与 ｒ的交点 ） 过 Ｑ引 ｒ的 两条切线 ， ， 连结 两切 点 的
直 线 即 为 Ｌ ．
如 图 １ 由 于 Ｐ 在 ，
Ｊ
椭圆外， 此 Ｐ 、 Ｂ 因 Ａ Ｐ

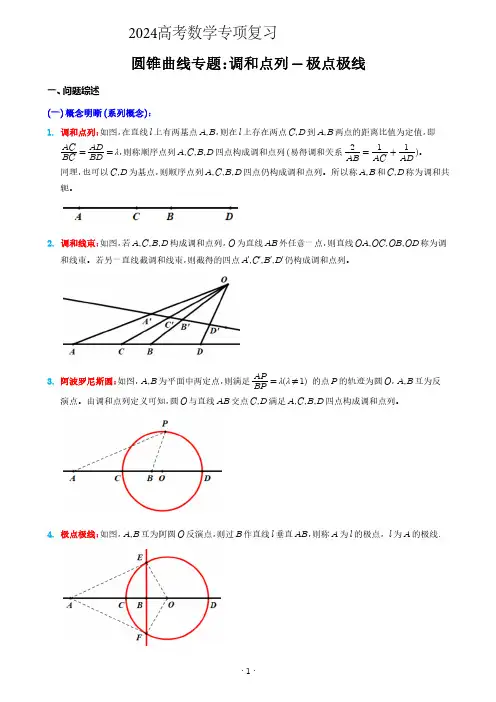
圆锥曲线专题：调和点列-极点极线一、问题综述(一)概念明晰(系列概念)：1.调和点列：如图，在直线l上有两基点A,B，则在l上存在两点C,D到A,B两点的距离比值为定值，即AC BC =ADBD=λ，则称顺序点列A,C,B,D四点构成调和点列(易得调和关系2AB=1AC+1AD)。

同理，也可以C,D为基点，则顺序点列A,C,B,D四点仍构成调和点列。

所以称A,B和C,D称为调和共轭。

2.调和线束：如图，若A,C,B,D构成调和点列，O为直线AB外任意一点，则直线OA,OC,OB,OD称为调和线束。

若另一直线截调和线束，则截得的四点A ,C ,B ,D 仍构成调和点列。

3.阿波罗尼斯圆：如图，A,B为平面中两定点，则满足APBP=λ(λ≠1)的点P的轨迹为圆O，A,B互为反演点。

由调和点列定义可知，圆O与直线AB交点C,D满足A,C,B,D四点构成调和点列。

4.极点极线：如图，A,B互为阿圆O反演点，则过B作直线l垂直AB，则称A为l的极点，l为A的极线.2024高考数学专项复习5.极点极线推广(二次曲线的极点极线)：(1).二次曲线Ax 2+By 2+Cxy +Dx +Ey +F =0极点P (x 0,y 0)对应的极线为Ax 0x +By 0y +Cx 0y +y 0x 2+D x 0+x2+E y 0+y 2+F =0x 2→x 0x ,y 2→y 0y ,xy →x 0y +y 0x 2,x →x 0+x2,y →y 0+y 2(半代半不代)(2)圆锥曲线的三类极点极线(以椭圆为例)：椭圆方程x 2a 2+y 2b 2=1①极点P (x 0,y 0)在椭圆外，PA ,PB 为椭圆的切线，切点为A ,B 则极线为切点弦AB :x 0xa 2+y 0yb 2=1；②极点P (x 0,y 0)在椭圆上，过点P 作椭圆的切线l ，则极线为切线l :x 0x a 2+y 0y b 2=1；③极点P (x 0,y 0)在椭圆内，过点P 作椭圆的弦AB ，分别过A ,B 作椭圆切线，则切线交点轨迹为极线x 0xa 2+y 0yb 2=1；(3)圆锥曲线的焦点为极点，对应准线为极线.(二)重要性质性质1：调和点列的几种表示形式如图，若A ,C ,B ,D 四点构成调和点列，则有AC BC =AD BD =λ⇔2AB =1AD +1AC⇔OC 2=OB ⋅OA ⇔AC ⋅AD =AB ⋅AO ⇔AB ⋅OD =AC ⋅BD性质2：调和点列与极点极线如图，过极点P作任意直线，与椭圆及极线交点M,D,N则点M,D,N,P成调和点列(可由阿圆推广)性质3：极点极线配极原则若点A的极线通过另一点D，则D的极线也通过A．一般称A、D互为共轭点．推广：如图，过极点P作两条任意直线，与椭圆分别交于点MN,HG，则MG,HN的交点必在极线上，反之也成立。

PART ONE
01 典 例 导 引
高考真题
曲线的极点极线理论
设椭圆 C :
x2 a2
y2 b2
1(a
b
0) 过点 M (
2,1) ，且着焦点为 F1(
2, 0)
（1）求椭圆 C 的方程；
（2）当过点 P(4,1) 的动直线 l 与椭圆 C 相交与两不同点 A, B 时，在线段 AB 上取点 Q ，
则 PA QA ；反之，若 PA QA 成立，则称点 P 与 Q 关于 调和共轭.
PB QB
PB QB
P 关于圆锥曲线 的调和共轭点的轨迹是一条直线，这条直线就是点 P 的极线.
推论 1 设点 P 关于圆锥曲线 的调和共轭点为点 Q ，则有 2 1 1 PQ PA PB
反之，若 2 1 1 成立，则点 P 与 Q 关于 调和共轭. PQ PA PB
推论 2： P,Q 是圆锥曲线 的一条对称轴 l 上两点（不在 上），若 P,Q 关于是圆锥 曲线 调和共轭，过 Q 任作 的一条割线，交 于点 A, B ，则 APQ BPQ
推论 3：设点 P 关于有心圆锥曲线 （设其中心为 O ）的调和共轭点为点 Q ，直线 PQ 经过 圆锥曲线的中心，则有 OR2 OP OQ ，反之若有 OR2 OP OQ ，则点 P 与 Q 关于 有心圆锥曲线 调和共轭.
PB QB
又 A，P，B，Q 四点共线，从而 AP PB, AQ QB
于是 4 x1 x2 ， 1 y1 y2 ； x x1 x2 ， y y1 y2
1
1
1
1
从而 x12 2 x22 4x ，
①
y12
2y2
2
y
，
②

圆锥曲线的极坐标方程知识点精析 椭圆、双曲线、抛物线可以统一定义为：与一个定点(焦点)的距离和一条定直线(准线)的距离的比等于常数e 的点的轨迹．以椭圆的左焦点(双曲线的右焦点、抛物线的焦点)为极点，过点F 作相应准线的垂线，垂足为K ，以FK 的反向延长线为极轴建立极坐标系．椭圆、双曲线、抛物线统一的极坐标方程为： θρcos 1e ep-=.其中p 是定点F 到定直线的距离，p ＞0 ． 当0＜e ＜1时，方程表示椭圆；当e ＞1时，方程表示双曲线，若ρ＞0，方程只表示双曲线右支，若允许ρ＜0，方程就表示整个双曲线；当e=1时，方程表示开口向右的抛物线.引论（1）若 1+cos epe ρθ=则0＜e ＜1当时，方程表示极点在右焦点上的椭圆 当e=1时时，方程表示开口向左的抛物线 当e ＞1方程表示极点在左焦点上的双曲线 （2 ）若1-sin epe ρθ=当 0＜e ＜1时，方程表示极点在下焦点的椭圆 当e=1时，方程表示开口向上的抛物线 当 e ＞1时!方程表示极点在上焦点的双曲线 （3）1+sin epe ρθ=当 0＜e ＜1时，方程表示极点在上焦点的椭圆 当e=1时，方程表示开口向下的抛物线当 e ＞1时!方程表示极点在下焦点的双曲线（2）圆锥曲线弦长问题若圆锥曲线的弦MN 经过焦点F ，1、椭圆中，cb c c a p 22=-=，θθπθ2222cos 2)cos(1cos 1c a ab e ep e ep MN -=--+-=.2、双曲线中，（注释：双曲线问题比较特殊，很多参考书上均有误解。

）若M 、N 在双曲线同一支上，θθπθ2222cos 2)cos(1cos 1c a ab e ep e ep MN -=--+-=； 若M 、N 在双曲线不同支上，2222cos 2cos 1cos 1a c ab e ep e ep MN -=--+-=θθθ.3、抛物线中，θθπθ2sin 2)cos(1cos 1pp p MN =--+-=例1过双曲线22x y -145=的右焦点，引倾斜角为3π的直线，交双曲线与A 、B 两点，求AB ｜｜解：根据题意，建立以双曲线右焦点为极点的极坐标系 即得 所以 又由得 注释：求椭圆和抛物线过焦点的弦长时，无需对 v 加绝对值，但求双曲线的弦长时，一定要加绝对值，这是避免讨论做好的方法。

圆锥曲线基础知识技巧套路题型结论极点极线圆锥曲线是解析几何中的重要组成部分，它包括椭圆、双曲线和抛物线。

掌握圆锥曲线的基本知识和解题技巧，对提高数学素养和解题能力具有重要意义。

本文将为您详细介绍圆锥曲线的基础知识、技巧套路、题型结论以及极点极线的应用。

一、基础知识1.定义：圆锥曲线是平面与圆锥面的交线。

根据平面与圆锥面的相对位置关系，可分为椭圆、双曲线和抛物线三种类型。

2.标准方程：- 椭圆：x^2/a^2 + y^2/b^2 = 1（a > b > 0）- 双曲线：x^2/a^2 - y^2/b^2 = 1（a > 0, b > 0）- 抛物线：y^2 = 2px（p > 0）或x^2 = 2py（p > 0）3.基本性质：- 椭圆：对称性、有界性、顶点、焦点、准线等；- 双曲线：对称性、无界性、顶点、焦点、准线等；- 抛物线：对称性、有界性、顶点、焦点、准线等。

二、技巧套路1.椭圆：- 求解椭圆上的点P(x, y)到焦点F1、F2的距离之和：|PF1| + |PF2| = 2a（椭圆的长轴）- 椭圆的切线方程：y = kx + m，代入椭圆方程，求解k和m。

2.双曲线：- 求解双曲线上的点P(x, y)到焦点F1、F2的距离之差：|PF1| - |PF2| = 2a（双曲线的实轴）- 双曲线的切线方程：y = kx + m，代入双曲线方程，求解k和m。

3.抛物线：- 抛物线的焦点：F(p/2, 0)（对于y^2 = 2px）或F(0, p/2)（对于x^2 = 2py）- 抛物线的切线方程：y = kx + m，代入抛物线方程，求解k和m。

三、题型结论1.椭圆：- 线段长度的最大值和最小值：与椭圆的长轴和短轴有关；- 面积的最大值和最小值：与椭圆的长轴和短轴有关。

2.双曲线：- 线段长度的最大值和最小值：与双曲线的实轴和虚轴有关；- 面积的最大值和最小值：与双曲线的实轴和虚轴有关。

圆锥曲线中的极点极线问题考情探究命题规律及备考策略【命题规律】本节内容是新高考卷的选考内容，设题不定，难度中等或偏难，分值为5-17分【备考策略】1.理解、掌握圆锥曲线极点极线的定义2.理解、掌握圆锥曲线的极点极线问题及其相关计算【命题预测】本节内容是新高考卷的常考内容，小题和大题都会作为载体命题，同学们要会结合公式运算，需强化训练复习知识讲解1.极点极线的定义如图,设P 是不在圆雉曲线上的一点,过P 点引两条割线依次交圆锥曲线于四点E ,F ,G ,H ,连接EH ,FG 交于N ,连接EG ,FH 交于M ,则直线MN 为点P 对应的极线.若P 为圆雉曲线上的点,则过P 点的切线即为极线.同理,PM 为点N 对应的极线,PN 为点M 所对应的极线.因而将△MNP 称为自极三点形.设直线MN 交圆锥曲线于点A ,B 两点,则P A ,PB 恰为圆锥曲线的两条切线.2.其他定义对于圆锥曲线C :Ax 2+Bxy +Cy 2+Dx +Ey +F =0,已知点P x 0,y 0 (非中心)及直线l :Ax 0x +B ⋅x 0y +y 0x 2+Cy 0y +D ⋅x +x 02+E ⋅y 0+y 2+F =0,则称点P x 0,y 0 是直线l 关于圆锥曲线C 的极点,直线l 称为点P 关于圆锥曲线C 的极线。

配极原则:共线点的极线必共点,共点线的极点必共点。

3.替换原则x0x →x 2,x 0y +y 0x 2→xy ,y 0y →y 2,x +x 02→x ,y +y 02→y .4.极点极线的几何意义(以椭圆为例)已知椭圆方程:x2a2+y2b2=1,设点P x0,y0的极线l:x0xa2+y0yb2=1.(1)当点P x0,y0在椭圆上时,极线l是以点P为切点的切线。

(极点在极线上)(2)当点P在椭圆外时,极线l与椭圆相交,且为由P点向椭圆所引切线的切点弦所在直线。

(3)当点P在椭圆内时,极线l与椭圆相离,极线l为经过点P的弦在两端点处的切线交点的轨迹,且极线l与以点P为中点的弦所在的直线平行。

压轴题05圆锥曲线中的极点、极线问题“极点极线”是射影几何中的内容，不属于高考考查的范围，但极点极线是圆锥曲线的一种基本特征，自然成为命题人命题的背景知识和方向，可以肯定的说“极点极线”为背景的考题是出题人思维中的定势方向，学生掌握了极点极线的相关知识，就可以从“高观点下”看待高中圆锥曲线的相关内容，更容易抓住问题的本质，虽然高考解答题不能用相关结论，但是我们可以将它作为辅助手段，快速的找到正确答案，然后再用初等方法写过程解题。

也就是说只有熟练“二级结论”才能明确运算方向、提高运算效率.○热○点○题○型1椭圆中的极点与极线问题○热○点○题○型2双曲线中的极点与极线问题○热○点○题○型3抛物线中的极点与极线问题极点极线的定义4.极点极线的配极性质①点P关于二次曲线ϕ的极线p 经过点Q ⇔点Q 关于二次曲线ϕ的极线q 经过点P ．②直线p 关于二次曲线ϕ的极点P 在直线q 上⇔直线q 关于二次曲线ϕ的极点Q 在直线p 上．①②说白了，就是点P 和点Q 是二次曲线的一组调和共轭点．1.若椭圆22221x y a b +=的焦点在x 轴上，过点11,2⎛⎫⎪⎝⎭作圆22+=1x y 的切线，切点分别为A 、B ，直线AB 恰好经过椭圆的右焦点和上顶点，则椭圆方程是．解利用替换法则，易得直线AB 为：112x y +=，故1c =，2b =，椭圆方程是22154x y +=2.如图所示，内外两个椭圆的离心率相同，从外层椭圆顶点向内层椭圆引切线AC 、BD ，设内层椭圆方程为()222210x y ab a b +=>>，若直线AC 与BD 的斜率之积为14-，则椭圆的离心率为()．A ．12B ．22C ．D ．34解(1)法一选C ；不妨特殊化，设切线BD 关于y 轴的对称切线为BE ，令切线AC 和BE 恰好重合为切线AB ，则222114b e a ==-，即32e =．法二设11(,)C x y ，22(,)D x y ，外层椭圆为()22222211x y m m a m b+=>，则(,0)A ma，(0,)B mb ．椭圆在点C 处的切线为：11221xx yy a b +=，代入(,0)A ma ，可得1ax m=，1y =；椭圆在点D 处的切线为：22221xx yy a b +=，代入(0,)B mb ，可得2bym=，2x =-因此，2244221212224421212114ACBD b x b x x x b b b k k e a y a y a y y a a ⎛⎫=--===-=-=-⎪⎝⎭ ，即32e =．法三设直线AC 为：()y k x ma =-，利用等效判别式：222222a k b k m a +=，解得AC k =；同理可得：BDk a=，因此，2214AC BDbk ka=-=-．3.如图，已知A、B分别为椭圆()222210x y a ba b+=>>的右顶点和上顶点，直线l∥AB，l与x轴、y轴分别交于C、D两点，直线CE、DF为椭圆的切线，则CE与DF的斜率之积CE DFk k等于()．A．22ab±B．222a ba-±C．22ba±D．222a bb-±ABCDyxOABCDyEFO xl解选C；不妨在第一象限，令CD与该椭圆相切于点H，则切点F与H关于y轴对称，切点E与H关于x轴对称，此时有22CE DFbk ka=．4.如图，O是坐标原点，过(,0)E p的直线分别交抛物线22(0)y px p=>于A、B两点，直线BO与过点A平行于x轴的直线相交于点M，过点M与此抛物线相切的直线与直线x p=相交于点N．则22ME NE-=()．A．22p B．2p C．4p D．pyxO EN BAM答案选A．法一设211,2yA yp⎛⎫⎪⎝⎭，222,2yB yp⎛⎫⎪⎝⎭，则直线AB的方程为：1212()2y y y px y y+=+，代入点E可得：2122y y p=-．直线OB的方程为：22py xy=，令1y y=，可得x p=-，即点M的坐标为1(,)p y-．设3(,)N p y，则22222134ME NE p y y-=+-，只需要再得到一个关于1y、3y的式子即可．直线MN的两点式方程为：1313()2()0y y x py p y y-+-+=，与抛物线方程联立：2221313()42()0y y y p y p y y-+-+=，令2221313(4)4()2()0p y y p y y ∆=+-+= ，可得222132y y p -=-，故2222ME NE p -=．法二利用到点00(,)M x y 对抛物线22y px =的双切线方程为：[]2220000(2)(2)()y px y px yy p x x --=-+，代入点1(,)M p y -、3(,)N p y ，可得：[]222223131(2)(2)()y p y p y y p p p -+=--，解得222132y y p -=-．5.设a 、b 是关于t 的方程2cos sin 0t t θθ+=的两个不等实根，则过2(,)A a a ，2(,)B b b 两点的直线与双曲线22221cos sin x y θθ-=的公共点的个数为()．A ．0B ．1C ．2D ．3解易知直线AB 的方程为cos sin 0y x θθ+=，又双曲线的渐近线为cos sin x y θθ=±，则直线AB 为双曲线的渐近线，故选A ．6.过椭圆22194x y +=上一点M 作圆222x y +=的两条切线，点A 、B 为切点．过A 、B的直线l 与x 轴、y 轴分别交于P 、Q 两点，则△POQ 的面积的最小值为()．A ．12B ．23C ．1D ．43解(1)选B ；设00(,)M x y ，则直线l 的方程为：002xx yy +=，易得02,0P x ⎛⎫⎪⎝⎭，020,Q y ⎛⎫ ⎪⎝⎭．又2200001943x y x y +=≥，即003x y ≤，故00223POQ S x y =≥△．7.已知双曲线()222210,0x y a b a b-=>>，圆222C x y a +=：，过双曲线的任意一点000(,)(0)P x y y ≠作圆C 的两条切线，其切点分别为A 、B ．若直线AB 与x 轴、y 轴分别交于M 、N 两点，则2222b a OMON-=．A ．22b aB ．22b a-C ．22a b D ．22c a 解选A ；直线AB 为：200xx yy a +=，令0y =，20a x x =，20a OM x =；令0x =，20a y y =，20a ON y =，因此，22222220022442b x a y b a b a a aOMON-=-=．8.圆221x y +=的切线与椭圆22143x y +=交于两点A 、B ，分别以A 、B 为切点的椭圆22143x y +=的切线交于点P ，则点P 的轨迹方程为．解设00(,)P x y ，则极点P 对应的极线（切点弦）AB 的方程为：00143xx yy+=，又直线AB1=，即22001169x y +=，即点P 的轨迹方程为221169x y +=．9.设1A 、2A 、3A 、4A 是平面直角坐标系中两两不同的四点，若1312()A A A A λλ=∈R，1412()A A A A μμ=∈R ，且112λμ+=,则称3A 、4A 调和分割1A 、2A ，已知平面上的点C 、D 调和分割A 、B ，则下面说法正确的是()．A ．C 可能是线段AB 的中点B ．D 可能是线段AB 的中点C ．C 、D 可能同时在线段AB 上D ．C 、D 不可能同时在线段AB 的延长线上解对调和点列背景熟悉的话，此题是送分题，显然选D ．10.过点(1,1)M -的动直线l 交圆2220C x y x +-=：于点A 、B ，O 为坐标原点，若在线段AB 上的点Q 满足112MA MB MQ+=，则min OQ =．答案55；Q 点的轨迹就是极点M 对应的极线！。

通俗来讲:对于圆锥曲线Γ外或内一点K 来说,其对应的极线即为:过点K 作Γ的两条割线所交的四个点两两相连再延长后,形成的除K 以外的两个交点所在的直线. 注1：若点K 在圆锥曲线Γ上,则在点K 处的切线即为极线注2：若FH//EG ,即交不到点M ,则点K 对应的极线过点N 且与FH 或EG 平行. 第二几何定义：(i)P (x 0,y 0)在圆锥曲线上,极线即为点P 处的切线；(ii)P (x 0,y 0)在圆锥曲线外,极线即为过点P 处的两条切线的切点弦；(iii)点P (x 0,y 0)在圆锥曲线Γ内,其极线l 是曲线Γ过点P 的割线两端点处的切线交点的轨迹 代数定义：已知圆锥曲线C:Ax 2+Cy 2+Dx +Ey +F =0，一点P (x 0,y 0)， 直线l:Ax 0x +Cy 0y +Dx 0+x 2+Ey 0+y 2+F =0，则l 为P 关于C 的极线，P 为l 关于C 的极点．P (x 0,y 0)是平面上任一点,点P (x 0,y 0)对应的极线为数学复习：极点极线第一几何定义：如图过圆锥曲线Γ外一点上P 作两条割线依次交圆锥曲线Γ于E,F,G,H 四点,且EH ∩FG =N ,延长FH,EG 交于M ,则直线MN 即为点P 对应的极线,同理,极点M 对应的极线为NP ,极点N 对应的极线为PM,ΔMNP 称为自极三点形.l(1)椭圆x2a 2+y 2b2=1,极线l:x 0x a 2+y 0y b 2=1(2)双曲线:x 2a 2−y 2b2=1,极线l:x 0x a 2−y 0y b 2=1(3)抛物线:y 2=2px ,极线l:y 0y =p (x 0+x )特殊的极点与极线(1)椭圆:x 2a 2+y 2b 2=1(a >b),点M(m,0)在椭圆中对应的极线方程为x =a 2m(2)双曲线:x 2a 2−y 2b 2=1,点M(m,0)对应的极线方程为x =a 2m(3)抛物线:y 2=2px ,点M(m,0)对应的极线方程为x =−m更特别地,圆锥曲线的焦点与其相应的准线是该圆锥曲线的一对极点与极线 (1)对于椭圆x 2a 2+y 2b 2=1(a >b),焦点F(±c,0)对应的极线方程为x =±a 2c (2)对于双曲线x 2a 2−y 2b 2=1,焦点F(±c,0)对应的极线方程为x =±a 2c(3)对于抛物线y 2=2px ,焦点F (p 2,0)对应的极线方程为x =−p 2核心性质1：配极原理给定平面内一圆锥曲线 C ，若点 P 关于 C 的极线过点 Q ，则点 Q 关于 C 的极线也过点 P ，如所示 .配极原则的一个等价命题：已知一圆锥曲线C，如果平面内有一直线d，直线d上有一动点P，P点关于C的极线为l，如图所示 .核心性质2：调和点列给定圆锥曲线T,点P(不在T上)对应的极线为lp ,过点P任意作一条直线1交lp于点Q,交r于A,B,则点P,A,Q,B为调和点列.调和点列定义已知点P,A,Q,B为直线上依次四点,且满足|AP||PB|=|AQ||QB|(等价于2|PQ|=1 |PA|+1|PB|或者2|QP|=1|QA|−1|QB|), 则称P,A,Q,B为调和点列。

上 ，所 以有 ＋ Ｃｙ ＋２Ｄｘ。＋２Ｅｙ。＋Ｆ一 ０，代
入 切 线 方 程 ，化 简 得 切 线 方 程 为 。ｚ＋ Ｃｙ。 ＋
Ｄ（ｘ＋ 。）＋Ｅ（ｙ＋ｙ。）＋ Ｆ一 ０，极线 ｚ就是 曲线
Ｃ 在 点 Ｐ 处 的 切 线 ；
（２）设 Ｍ（ ，Ｙ ）、Ｎ（ｘ２，Ｙ２），由（１）得 曲线在点
ｂ＞ ０）、抛物线 Ｙ 一 ２ｐｘ（Ｐ＞ ０））的一个极 点 ，
它对 应 的极 线为 Ｌ． （１）若 ｒ为椭 圆或双 曲线 ，ＯＰ（０为中心 ）或
０Ｐ 的 延 长 线 交 ｒ 于 Ｒ，交 Ｌ 于 点 Ｑ，则 ｌ（＿）Ｐ ｌ·ｌ∞ ｌ— ｌ ＯＲ ｌ ；
（２）若 Ｉ１为抛 物线 ，ｌ是 ｒ在顶 点 ０处 的切 线 （即 Ｙ轴 ），过 点 Ｐ 作 ｆ的 垂 线 ，交 Ｌ于 Ｑ，交 ｒ于 Ｒ，则 ｌ ＰＲ ｌ— ｌ ＱＲ １．
一 ０，又 点 Ｑ（ ，Ｙ ）在 直 线 ｚ上 ，所 以 Ａｘ。ｚ ＋
Ｃｙ ０Ｙｌ＋ Ｄ（ｘｌ ４－ｚ。）＋ Ｅ（ｙｌ＋ Ｙ。）＋ Ｆ 一 ０，由 以
上两 式 知 点 Ｑ（ ，ｙ ）在 直 线 ＭＮ 上 ，即 直 线
ＭＮ 必 过 极 点 Ｐ．
例 １ 已 知 圆 ＋ Ｙ 一 １和 圆 外 一 点 Ｐ（２，
直 线 ＭＮ 过 点 Ｐ，所 以 有 Ａｌｎｘ。＋ Ｃｎｙ ｏ十 Ｄ（ｘｏ＋
）＋Ｅ（Ｙ。＋ ）＋Ｆ— Ｏ，故 曲线 Ｃ在 Ｍ 、Ｎ 两 点
处 的 两 条 切 线 的 交 点 Ｑ 在 极 线 ｚ上 ．
（４）设 点 Ｑ（ ，Ｙ ），由 （２）知 直 线 ＭＮ 的 方
程 为 Ａｘｌ ＋ ＣｙｌＹ＋ Ｄ（ ＋ １）＋ Ｅ（ｙ＋ ｙ１）＋ Ｆ
（４）若 过极 线 上一点 Ｑ 可作 Ｃ的两条 切线 ， Ｍ 、．Ｎ 为切点 ，则直线 ＭＮ 必过 极点 Ｐ．

椭圆、 曲线、抛物线统一的极坐标方程为
ρ = ep . 1 − e cosθ
其中 p 是定点 F 到定直线的距离，p＞0 ．
当 0 e 1 时，方程表示椭圆
当 e＞1 时，方程表示 曲线，若ρ＞0，方程只表示 曲线右支，若允
许ρ 0，方程就表示整个 曲线
当 e=1 时，方程表示开口向右的抛物线.
二、圆锥曲线的焦半径公式
推论 若圆锥曲线的弦 MN 过焦点 F，则有 1 + 1 = 2 . MF NF ep
、圆锥曲线的焦点弦长 若圆锥曲线的弦 MN 过焦点 F，
1、椭圆中， p = a 2 − c = b2 ， MN = ep +
ep
= 2ab2 .
c
c
1− ecosθ 1− ecos(π −θ) a2 − c2 cos2 θ
圆锥曲线的极坐标方程、焦半径公式、焦点弦公式
湖北省天门中学 薛德斌
一、圆锥曲线的极坐标方程
椭圆、 曲线、抛物线可以统一定义为 一个定点(焦点)的距离和一条定
直线(准线)的距离的比等于常数 e 的点的轨迹．
以椭圆的左焦点( 曲线的右焦点、抛物线的焦点)为极点，过点 F 作相
应准线的垂线，垂足为 K，以 FK 的 向延长线为极轴建立极坐标系．
3、抛物线中， MN = p +
p
= 2p .
1 − cosθ 1 − cos(π − θ ) sin 2 θ
四、直角坐标系中的焦半径公式 设 P x,y 是圆锥曲线 的点，
1、若 F1、F2 分别是椭圆的左、右焦点，则 PF1 = a + ex ，、 F2 分别是 曲线的左、右焦点，
设 F 为椭圆的左焦点( 曲线的右焦点、抛物线的焦点)，P 为椭圆( 曲线 的右支、抛物线) 任一点，则

圆锥曲线的极坐标方程、焦半径公式、焦点弦公式 湖北省天门中学 薛德斌一、圆锥曲线的极坐标方程椭圆、 曲线、抛物线可以统一定义为 一个定点(焦点)的距离和一条定直线(准线)的距离的比等于常数e 的点的轨迹．以椭圆的左焦点( 曲线的右焦点、抛物线的焦点)为极点，过点F 作相应准线的垂线，垂足为K，以FK 的 向延长线为极轴建立极坐标系．椭圆、 曲线、抛物线统一的极坐标方程为 θρcos 1e ep −=. 其中p 是定点F 到定直线的距离，p＞0 ．当0 e 1时，方程表示椭圆当e＞1时，方程表示 曲线，若ρ＞0，方程只表示 曲线右支，若允许ρ 0，方程就表示整个 曲线当e=1时，方程表示开口向右的抛物线.二、圆锥曲线的焦半径公式设F 为椭圆的左焦点( 曲线的右焦点、抛物线的焦点)，P 为椭圆( 曲线的右支、抛物线) 任一点，则 PQ e PF =， )cos (p PF e PF +=θ，其中FH p =，=θ x 轴，FP 焦半径θcos 1e ep PF −=． 当P 在 曲线的左支 时，θcos 1e ep PF +−=. 推论 若圆锥曲线的弦MN 过焦点F，则有epNF MF 211=+.、圆锥曲线的焦点弦长若圆锥曲线的弦MN 过焦点F， 1、椭圆中，cb c c a p 22=−=，θθπθ2222cos 2)cos(1cos 1c a ab e ep e ep MN −=−−+−=. 2、 曲线中，若M、N 在 曲线同一支 ，θθπθ2222cos 2)cos(1cos 1c a ab e ep e ep MN −=−−+−= 若M、N 在 曲线 同支 ，2222cos 2cos 1cos 1a c ab e ep e ep MN −=−−+−=θθθ. 3、抛物线中，θθπθ2sin 2)cos(1cos 1p p p MN =−−+−=. 四、直角坐标系中的焦半径公式设P x,y 是圆锥曲线 的点，1、若1F 、2F 分别是椭圆的左、右焦点，则ex a PF +=1，ex a PF −=22、若1F 、2F 分别是 曲线的左、右焦点，当点P 在 曲线右支 时，a ex PF +=1，a ex PF −=2 当点P 在 曲线左支 时，ex a PF −−=1，ex a PF −=23、若F 是抛物线的焦点，2p x PF +=.。

当0 e 1, ep 为椭圆，并且为任意角 1- ecos
当e 1,
ep 1- e cos
为双曲线
双曲线右支 双曲线左支
（，2 -） （-，）
圆锥曲线统一的极坐标方程
课堂反思
江西省2020年春季延期开学期间线上教育课程
圆锥曲线统一的极坐标方程
课后作业
习题1：判断方程 6 为哪类圆锥曲线？ 2 cos
江西省2020年春季延期开学期间线上教育课程
谢谢
12/9/2020
圆锥曲线统一的极坐标方程
探究应用
例1：方程为 = 6 表示什么曲线？ 1 2 cos
变式：方程为= 5 表示什么曲线？ 3 2cos
分析：已知方程完全符合圆锥曲线极坐标方程 结构形式.因此判断可以寻找e.
分析：方程并非符合圆锥曲线统一极坐标方程 构造称为圆锥曲线的极坐标方程
ep 1 e cos
习题2：判断方程 5 为哪类圆锥曲线？ 3 3cos
江西省2020年春季延期开学期间线上教育课程
圆锥曲线统一的极坐标方程
课后作业
习题1：判断方程 6 为哪类圆锥曲线. 2 cos
解析： e 1，该曲线为椭圆 2
习题2：判断方程 5 为哪类圆锥曲线？ 3 3cos
解析： e 1，该曲线为抛物线
sin2
江西省2020年春季延期开学期间线上教育课程
圆锥曲线统一的极坐标方程
温故知新
圆锥曲线
l
统一的名称：圆锥曲线
统一的方程：
思考一：能否找到统一的特征求出统一 的方程？
与一个定点的距离和一条定直线 （定点不在定直线上）的距离的比
等于常数e 的轨迹. 其中当e 1时，轨迹为抛物线
令e 1，直线l为定直线，F为定点，M 为动点 MF 为动点到定点的距离 MA 为动点到定直线的距离