初中物理：机车启动问题

机车起动的两种方式分析机车起动问题是指汽车、火车、轮船、摩托等动力机械的起动问题，而起动过程分为以恒定功率起动和恒力起动（先匀加速起动至额定功率后再变加速运动）两种情况，因起动过程中各物理量相互关联而又发生变化，过程比较复杂，有一定的难度．1．以恒定功率起动在此过程中，机车不断加速，因为开始时机车已经达到额定功率，根据P=Fv 可知在速度v 不断增大的时候，牵引力F 会不断减小，加速度F-f=ma （f 表示机车运动过程中受到的阻力）也不断减小，但因为加速度的方向和速度的方向相同，所以无论加速度a 怎样小，速度v 也是增加的．即机车一直做加速度减小的加速运动，直到F f =时，达到最大速度m P P v F f==，此后以v m 做匀速直线运动．起动过程结束的标志就是“速度不变”． 例1．汽车发动机的额定功率为60kw,汽车质量为5t,汽车在水平路面上行驶时，阻力是车中的0.1倍，g=10m/s 2问（1）汽车保持以额定功率从静止启动能达到的最大速度是多少？解析：由P =F·v 可知，汽车在额定功率下行驶，牵引力与速度成反比．速度增大，牵引力减小，当汽车的牵引力与所受阻力相等时，速度达到最大．所以v m =P /F f=60000/0.1×5000×10m/s = 12m/s ． 说明：此类问题主要把握住机车作加速度减小的加速运动，最终匀速的运动特点，利用F f =时，达到最大速度m P P v F f==来解题． 2．先以恒力起动至额定功率后再恒功率起动该起动过程分为两个阶段：阶段１是匀加速过程，在此过程中，速度v 由零开始不断增加，功率P 也由零开始逐渐增加；由F-f=ma ，因为加速度a 是不变的，所以在此过程中牵引力F 也是不变的．此过程的结束就是第二个过程的开始，以“功率P 达到最大即额定功率，但速度没有达到最大”为标志．阶段２中因为还有加速度的存在，所以速度v 会继续增加，在功率P 不变的情况下，根据P =Fv ，可知牵引力F 不断减小，加速度a 也相应减小．第二过程结束的标志就是“机车的功率P 最大，速度v 也是最大”，到此为止，整个起动过程结束．再以后，机车将以v m 做匀速直线运动，功率不变．例2．汽车发动机的额定功率为60 kW ，汽车的质量为4 t ，当它行驶在坡度为0.02的长直公路上时，如图１，所受阻力为车重的0.1倍(g ＝10 m/s 2)，求：⑴汽车所能达到的最大速度v m =？⑵若汽车从静止开始以0.6 m/s 2的加速度做匀加速直线运动，则此过程能维持多长时间？解析： ⑴汽车在坡路上行驶，所受阻力由两部分构成，即f ＝kmg ＋mg sin α=4000＋800N=4800 N ． 又因为F ＝f 时达到最大速度，且P =f·v m ，所以36010/12.5/sin 4800m P v m s m s kmg mg α⨯===+． ⑵汽车从静止开始，以a =0.6 m/s 2匀加速行驶，由F ＝ma ，有F ′－f －mg sin α＝ma ．故 3sin 7.210F kmg mg ma N α'=++=⨯ 保持这一牵引力，汽车匀加速行驶到速度mv '，此时达到额定功率，据P Fv =有图１8.33/m m P v m s F '=='． 由运动学规律可以求出匀加速行驶的时间8.3313.90.6m v t s s a '===． 说明：此后汽车将做加速度减小的加速运动，直到达到12.5m/s,而后匀速直线运动． ３．两种启动方式的共同点对同一机车，在相同条件下，两种启动方式最终都是F =f ，匀速时的速度v m 相同．v -t 图像如图２所示．例3．电动机通过一绳子吊起质量为8 kg 的物体，绳的拉力不能超过120 N ，电动机的功率不能超过1200 W ，要将此物体由静止起用最快的方式吊高90 m （已知此物体在被吊高接近90 m 时，已开始以最大速度匀速上升）试分析应如何吊起物体？达到最大功率的最短时间是多少？匀速时的速度是多少？解析： 此题可以采用机车起动类问题的思路，即将物体吊高分为两个过程处理：第一过程是以绳所能承受的最大拉力拉物体，使物体匀加速上升，第一个过程结束时，电动机刚达到最大功率．第二个过程是电动机一直以最大功率拉物体，拉力逐渐减小，当拉力等于重力时，物体开始匀速上升.在匀加速运动过程中加速度为a =8108120m ⨯-=-m mg F m/s 2=5 m/s 2 末速度v t =1201200=m m F P =10 m/s 上升的时间t 1=510=a v t s=2 s 此即达到最大功率的最短时间．在功率恒定的过程中，最后匀速运动的速率为v m =1081200⨯==mg F F P m m =15 m/s 说明：本题考查对机车启动两类问题的理解及迁移应用的创新能力．同学们往往对整个过程分析不透，若开始即以最大功率拉，绳会被拉断．v v 2。

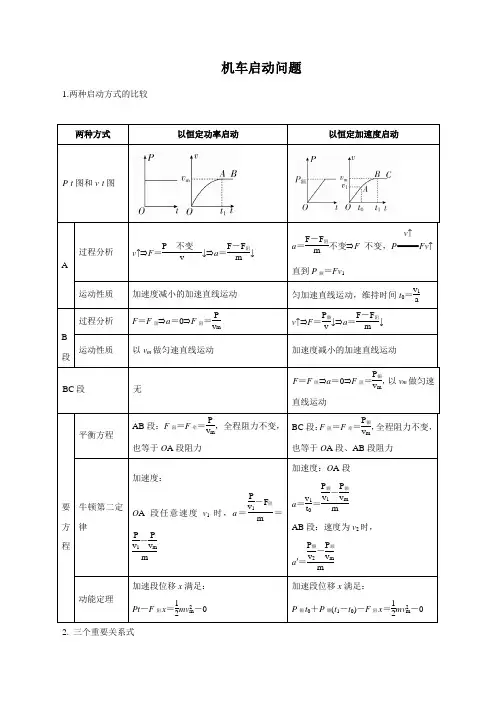
机车启动问题1.两种启动方式的比较两种方式以恒定功率启动以恒定加速度启动P -t 图和v -t 图OA段过程分析 v ↑⇒F ＝P不变v ↓⇒a ＝F －F 阻m↓ a ＝F －F 阻m 不变⇒F 不变，P =====v ↑Fv ↑直到P 额＝Fv 1运动性质 加速度减小的加速直线运动 匀加速直线运动，维持时间t 0＝v 1aA B 段过程分析 F ＝F 阻⇒a ＝0⇒F 阻＝Pv mv ↑⇒F ＝P 额v ↓⇒a ＝F －F 阻m↓运动性质以v m 做匀速直线运动加速度减小的加速直线运动BC 段 无F ＝F 阻⇒a ＝0⇒F 阻＝P 额v m ，以v m 做匀速直线运动重要方程平衡方程AB 段：F 阻＝F 牵＝P v m ，全程阻力不变，也等于O A 段阻力 BC 段：F 阻＝F 牵＝P 额v m，全程阻力不变，也等于O A 段、AB 段阻力 牛顿第二定律 加速度：O A 段任意速度v 1时，a ＝Pv 1－F 阻m ＝P v 1－P v mm加速度：O A 段 a ＝v 1t 0＝P 额v 1－P 额v m mAB 段：速度为v 2时， a ′＝P 额v 2－P 额v m m动能定理加速段位移x 满足：Pt －F 阻x ＝12mv 2m－0加速段位移x 满足：P 额t 0＋P 额(t 1－t 0)－F 阻x ＝12mv 2m－02. 三个重要关系式(1) 无论哪种启动过程，机车的最大速度都等于其匀速运动时的速度，即v m ＝PF 阻。

(2) 机车以恒定加速度启动时，匀加速过程结束后功率最大，速度不是最大，即v ＝P F <v m ＝PF 阻。

(3) 机车以恒定功率运行时，牵引力做的功W ＝Pt ，由动能定理得Pt －F 阻x ＝ΔE k ，此式经常用于求解机车以恒定功率启动过程的位移或速度。

【典例】一列火车总质量m ＝500 t ，发动机的额定功率P ＝6×105 W ，在水平轨道上行驶时，轨道对火车的阻力f 是车重的0.01倍，g 取10 m/s 2。

1 二、P ＝F v 的应用 机车的两种启动方式(1)机车以恒定功率启动的过程分析由P ＝F v 知，随速度的增加、牵引力减小，又由a ＝F －F f m 知加速度逐渐减小，故汽车以恒定功率启动，实际上是做加速度逐渐减小的加速运动，当加速度a ＝0时，汽车达到速度的最大值，此时F ＝F f ，v m ＝PF f .这一启动过程的v －t 图象如图2所示．图2(2)机车以恒定加速度启动的过程分析此过程牵引力F ＝ma ＋F f ，开始保持不变，由P ＝F v 知随速度的增大，P 逐渐增大，当达到额定功率时，匀加速过程结束，此时速度为v 0＝P F ，之后，保持功率不变继续加速(与1中过程相同)，最后仍有v m ＝PF f .这一运动过程的v －t 图象如图3所示．图3说明 (1)以恒定加速度启动时，匀加速结束时速度并未达到最大速度v m . (2)两种启动方式最终最大速度的计算均为v m ＝PF f.抓住两个基本公式：①功率公式P ＝F v ；②牛顿第二定律，即F －F 阻＝ma .1 在水平路面上运动的汽车的额定功率为100 kW ，质量为10 t ，设阻力恒定，且为车重的0.1倍(g 取10 m/s 2)，求：(1)若汽车以0.5 m/s 2的加速度从静止开始做匀加速直线运动，汽车的功率如何变化？这一过程能维持多长时间？(2)若汽车以不变的额定功率从静止启动，汽车的加速度如何变化？当汽车的加速度为2 m/s 2时，速度为多大？(3)汽车在运动过程中所能达到的最大速度的大小．解析 (1)汽车从静止开始做匀加速直线运动的过程中，a 1不变，则牵引力F 不变，由P ＝F v 知，v 变大，P 也变大，当P ＝P 额时，此过程结束． F 1＝F f ＋ma 1＝(0.1×104×10＋104×0.5) N ＝1.5×104 Nv 1＝P 额F 1＝1051.5×104 m/s ＝203 m/s ， 则t ＝v 1a 1＝2030.5 s ＝403s.(2)汽车以不变的额定功率从静止启动，v 变大，由P ＝F v 知，牵引力F 减小，故汽车的加速度减小．F 2＝F f ＋ma 2＝(0.1×104×10＋104×2) N ＝3×104 N v 2＝P 额F 2＝1053×104 m/s ＝103m/s. (3)当汽车速度最大时，a 3＝0，F 3＝F f ，P ＝P 额，故 v max ＝P 额F f ＝1050.1×104×10 m /s ＝10 m/s.答案 (1)功率逐渐变大 403s (2)加速度逐渐减小 103m /s (3)10 m/s2．汽车发动机的额定功率P ＝60 kW ，若其总质量为m ＝5 t ，在水平路面上行驶时，所受阻力恒为F ＝5.0×103 N ，则：(1)汽车保持恒定功率启动时：①求汽车所能达到的最大速度v max .②当汽车加速度为2 m/s 2时，速度是多大？③当汽车速度是6 m/s 时，加速度是多大？(2)若汽车以a ＝0.5 m/s 2的加速度由静止开始做匀加速运动，这一过程能维持多长时间？3．一辆重5 t 的汽车，发动机的额定功率为80 kW.汽车从静止开始以加速度a ＝1 m /s 2做匀加速直线运动，车受的阻力为车重的0.06倍．(g 取10 m/s 2)求： (1)汽车做匀加速直线运动的最长时间；(2)汽车开始运动后，5 s 末和15 s 末的瞬时功率．4．一质量为5 000 kg的汽车，以额定功率由静止启动，它在水平面上运动时所受的阻力为车重的0.1倍，发动机额定功率为50 kW.则汽车在此路面上行驶的最大速度为()A．5 m/s B．7 m/s C．8 m/s D．10 m/s5. 汽车发动机的额定功率为80kW，它以额定功率在平直公路上行驶的最大速度为20m／s，那么汽车在以最大速度匀速行驶时所受的阻力是.. .. ..A. 8000NB. 4000NC. 2500ND. 1600N-6.一辆汽车在平直公路上以额定功率行驶，设所受阻力不变。

机车启动问题（附解析功、功率、动能定理二轮专题）2.机车启动问题一、基础知识回顾1．机车输出功率P＝Fv，其中F为机车牵引力．2．恒定功率启动(1)机车先做加速度逐渐减小的变加速直线运动，后做匀速直线运动，速度—时间图象如图所示，当F＝F阻时，vm＝PF＝PF阻.(2)动能定理Pt－F阻x＝12mv2m－0.3．恒定加速度启动(1)速度—时间图象如图所示．机车先做匀加速直线运动，当功率增大到额定功率后获得匀加速的最大速度v1.之后做变加速直线运动，直至达到最大速度vm后做匀速直线运动．(2)常用公式：F－F阻＝maP＝FvP额＝F阻vmv1＝at1二、典型例题[例1](多选)一辆汽车在平直的公路上运动，运动过程中先保持某一恒定加速度，后保持恒定的牵引功率，其牵引力和速度的图象如图所示．若已知汽车的质量m、牵引力F1和速度v1及该车所能达到的最大速度v3，运动过程中所受阻力恒定，则根据图象所给的信息，下列说法正确的是()A．汽车行驶中所受的阻力为F1v1v3B．汽车匀加速运动的过程中牵引力的冲量大小为mv1v3&#61480;v3－v1&#61481;C．速度为v2时的加速度大小为F1v1mv2D．若速度为v2时牵引力恰为F12，则有v2＝2v1解析根据牵引力和速度的图象和功率P＝Fv得汽车运动中的最大功率为F1v1.该车所能达到的最大速度时加速度为零，所以此时阻力等于牵引力，所以阻力f＝F1v1v3，选项A正确；根据牛顿第二定律，有恒定加速时，加速度a′＝F1－fm＝F1m－F1v1mv3，加速的时间：t＝v1a＝mv1v3F1&#61480;v3－v1&#61481;，则汽车匀加速运动的过程中牵引力的冲量大小为I＝F1t＝mv1v3&#61480;v3－v1&#61481;，故B正确．速度为v2时的牵引力是F1v1v2，对汽车受力分析，受重力、支持力、牵引力和阻力，根据牛顿第二定律，有速度为v2时加速度大小为a＝F1v1mv2－F1v1mv3，故C错误．若速度为v2时牵引力恰为F12，则F1v1v2＝F12，则v2＝2v1，选项D正确；故选ABD.答案ABD[例2]．(多选)某汽车在平直公路上以功率P、速度v0匀速行驶时，牵引力为F0.在t1时刻，司机减小油门，使汽车的功率减为P2，此后保持该功率继续行驶，t2时刻，汽车又恢复到匀速运动状态．有关汽车牵引力F、速度v的几种说法，其中正确的是()A．t2后的牵引力仍为F0B．t2后的牵引力小于F0C．t2后的速度仍为v0D．t2后的速度小于v0解析：选AD.由P＝F0v0可知，当汽车的功率突然减小为P2时，瞬时速度还没来得及变化，则牵引力突然变为F02，汽车将做减速运动，随着速度的减小，牵引力逐渐增大，汽车做加速度逐渐减小的减速运动，当速度减小到使牵引力又等于阻力时，汽车再做匀速运动，由P2＝F0v2可知，此时v2＝v02，故A、D正确．[例3]．一汽车在平直公路上行驶．从某时刻开始计时，发动机的功率P随时间t的变化如图所示．假定汽车所受阻力的大小f恒定不变．下列描述该汽车的速度v随时间t变化的图线中，可能正确的是()解析：选A.由P&shy;t图象知：0～t1内汽车以恒定功率P1行驶，t1～t2内汽车以恒定功率P2行驶．设汽车所受牵引力为F，则由P＝Fv得，当v增加时，F减小，由a＝F－fm知a减小，又因速度不可能突变，所以选项B、C、D错误，选项A正确．[例4]．如图甲所示，用固定的电动机水平拉着质量m＝2kg的小物块和质量M＝1kg的平板以相同的速度一起向右匀速运动，物块位于平板左侧，可视为质点．在平板的右侧一定距离处有台阶阻挡，平板撞上后会立刻停止运动．电动机功率保持P＝3W不变．从某时刻t＝0起，测得物块的速度随时间的变化关系如图乙所示，t＝6s后可视为匀速运动，t＝10s时物块离开平板．重力加速度g＝10m/s2，求：(1)平板与地面间的动摩擦因数μ为多大？(2)物块在1s末和3s末受到的摩擦力各为多大？(3)平板长度L为多少？解析：(1)由图可知，前2s内物块和平板一起做匀速运动，对整体分析，在水平方向上受到水平向右的拉力和地面给平板的滑动摩擦力，此二力的合力为零．拉力大小为：FT1＝Pv1滑动摩擦力大小为：Ff＝μ(M＋m)g由平衡条件可得：Pv1＝μ(M＋m)g可得：μ＝0.2(2)物块在1s末时与平板一起做匀速运动，合力为零．物块受到水平向右的拉力与水平向左的静摩擦力，因此静摩擦力大小为：Ff1＝FT1＝Pv1＝6N物块在2s末之后与平板发生相对运动，之后物块与平板间的摩擦力为滑动摩擦力且大小保持不变．物块在6s后可视为匀速运动，此时物块受到的合力为零，即拉力与滑动摩擦力大小相等方向相反，即：Ff2＝FT2＝Pv＝10N 物块在3s末时受到的滑动摩擦力大小与6s后受到的摩擦力大小相等，为10N.(3)依题意，物块在2s末之后一直到10s时，物块从平板的一端运动到另一端，对物块由动能定理得：PΔt－Ff2L＝12mv22－12mv21代入解得：L＝PΔt－12mv22＋12mv21Ff2＝2.42m.答案：(1)0.2(2)6N10N(3)2.42m三、方法总结解决机车启动问题时的四点技巧1．分清是匀加速启动还是恒定功率启动．2．匀加速启动过程中，机车功率是不断改变的，但该过程中的最大功率是额定功率，匀加速运动阶段的最大速度小于机车所能达到的最大速度，达到额定功率后做加速度减小的加速运动．3．以额定功率启动的过程中，机车做加速度减小的加速运动，速度最大值等于PFf，牵引力是变力，牵引力做的功W＝Pt.4．无论哪种启动方式，最后达到最大速度时，均满足P ＝Ffvm，P为机车的额定功率．。

多练出技巧 巧思出硕果 机车启动专题1.机车以恒定功率加速启动（阻力是车重的k 倍） 过程分析：汽车以恒定功率起动时，它的牵引力F 将随速度v 的变化而变化，其加速度a 也随之变化，具体变化过程可采用示意图表示：由此可得汽车速度达到最大时，a=0，kmgP v v F P kmg f F m m =⇒⎭⎬⎫⋅=== p-t 图像如图a ，v-t 图像如图b 针对训练1. 质量为2×103kg 的汽车发动机的额定功率为80kW ，若汽车在平直公路上行驶所受阻力大小恒为4×103N ，那么A. 汽车在公路上以额定功率行驶的最大行驶速度为20m/sB. 汽车以额定功率起动，当汽车速度为5m/s 时，加速度为6m/s2C. 汽车以2m/s 2的加速度起动做匀加速运动，第2s 末发动机实际功率为32kWD. 汽车以2m/s 2的加速度起动做匀加速运动，匀加速运动所能维持的时间为5s2. 质量为 m 的汽车，启动后沿平直路面行驶，如果发动机的功率恒为P ，且行驶过程中受到的摩擦阻力大小一定，汽车速度能够达到的最大值为v ，那么当汽车的车速为v/4时，汽车的瞬时加速度的大小 A. P/mv B. 2P/mv C. 3P/mv D. 4P/mv3.汽车以恒定功率P 由静止出发，沿平直路面行驶，最大速度为v ，则下列判断正确的是A.汽车先做匀加速运动，最后做匀速运动B.汽车先做加速度越来越大的加速运动，最后做匀速运动C.汽车先做加速度越来越小的加速运动，最后做匀速运动D.汽车先做加速运动，再做减速运动，最后做匀速运动4.飞机在飞行时受到的空气阻力与速率的平方成正比，若飞机以速率v 匀速飞行时，发动机的功率为P ，则当飞机以速率n v 匀速飞行时，发动机的功率为A.npB.2npC.n 2pD.n 3p5. 质量为2×103kg 的汽车，发动机输出功率为3×104W ，在水平公路上能达到的最大速度为15m/s ，当汽车的速度为10m/s 时，其加速度为_________m/s 2。

机车的两种启动方式江苏省淮安市阳光学校223300 冯新波通常讲机车的功率是指机车的牵引力的功率，P＝F v恒成立，与阻力f无关，与P是否为额定功率无关，与机车的运动状态无关。

机车可通过油门控制功率，可通过换档调整速度从而改变牵引力。

机车起动通常有两种方式，下面把这两种启动方式的规律总结如下：一、机车以恒定功率启动的运动过程1、机车以恒定的功率P启动后，若运动过程中所受的阻力不变，由于牵引力F＝P／v，根据牛顿第二定律：F－f＝ma 即P／v－f＝ma所以：当速度v增大时，加速度a减小。

当加速度a＝0时，机车的速度达到最大，此时有：。

以后，机车已v m做匀速直线运动。

2、这一过程，F、v、a3、用v－t图，这一过程可表示为右下图：最大速度之前是一段曲线。

4、以恒定功率启动的特点：（1）汽车在启动过程中先做加速度不断减小的加速运动，同时牵引力变小，当牵引力等于阻力时，开始以最大速度匀速运动。

（2）汽车在启动过程中的功率始终等于汽车的额定功率。

（3）汽车的牵引力和阻力始终满足牛顿第二定律F－f＝ma。

（4）汽车的牵引力和瞬时速度始终满足P－P额＝F v。

（5）在启动过程结束时，因为牵引力和阻力平衡，此时有P额＝F v m＝f v m。

（6）从能的角度看，启动过程中牵引力所做的功一方面用以克服阻力做功，另一方面增加汽车的动能。

二、机车以恒定加速度启动的运动过程1、机车以恒定的加速度a启动时，牵引力F、阻力f均不变，此时有：F－f＝ma。

机车匀加速运动的瞬时功率：P＝Fv＝（f＋ma）•v＝（f＋ma）•a t≤P额。

匀加速阶段的最长时间t＝P额／［（ma＋f）a］；匀加速运动的末速度为vt＝P额／（ma＋f）。

当机车达到这一速度时，其瞬时功率等于它的额定功率。

然后机车又做变加速运动。

此时加速度a和第一种启动过程一样变化；这时的最大速度还是。

而变加速阶段的位移应该用动能定理来计算：2=amfmvP－fPFPv m额额＝==↓⇒=↑⇒avPFv保持匀速直线运动⇒变加速运动匀速运动∙∙∙∙∙∙fPFPv m额额＝=2t2mmv21mv21s ftP－＝－额↑⇒Pv＝不变、fF－＝，mfFa⇒=↓⇒=avPF额保持匀速直线运动⇒匀速运动∙∙∙∙∙∙v3、用v －t 图，这一过程可表示为右图： 起初匀加速运动是一段倾斜的直线，紧接着是一段曲线，最后是平行于时间轴的直线。

专题课：机车启动问题1．(多选)一辆汽车以恒定的输出功率以某一初速度冲上一斜坡，在上坡过程中，它的运动情况可能是( )A ．先加速，后匀速B ．先加速，后减速C ．一直加速且加速度越来越小D ．一直减速且加速度越来越大2．以恒定功率从静止开始运动的汽车，经时间t 1后速度达到最大值v m ，在此过程中汽车通过的位移为x ，则( )A ．x>v m t 12B ．x ＝v m t 12C ．x<v m t 12D ．无法判断3．汽车的质量为m ，其发动机的额定功率为P.当汽车开上一个倾角为θ的斜坡时，受到的阻力为重力的k 倍，重力加速度为g ，则它的最大速度为( )A .P mg sin θ B .P cos θmg （k ＋sin θ）C .P cos θmgD .P mg （k ＋sin θ）4．一辆小车在水平面上做匀速直线运动，从某时刻起，小车所受的牵引力和阻力随时间变化规律如图LZ 3­1所示，则作用在小车上的牵引力F 1的功率随时间变化的图像是图LZ 3­2中的( )图LZ3­1图LZ3­25．(多选)一辆轿车在平直公路上运行，启动阶段轿车牵引力保持不变，而后以额定功率继续行驶，经过时间t0，其速度由零增大到最大值v m.若轿车所受的阻力f为恒力，关于轿车的速度v、牵引力F、功率P随时间t变化的情况，图LZ3­3中正确的是()图LZ3­36．(多选)火车从车站开出做匀加速运动，若阻力与速度成正比，则() A．火车发动机的功率一定越来越大，牵引力越来越大B．火车发动机的功率恒定不变，牵引力越来越小C．当火车达到某一速率时，若要保持此速率做匀速运动，则发动机的功率这时应减小D．当火车达到某一速率时，若要保持此速率做匀速运动，则发动机的功率一定跟此时速率的二次方成正比7．质量为m、发动机的额定功率为P0的汽车沿平直公路行驶，当它的加速度为a时，速度为v，测得发动机的实际功率为P1.假设运动中所受阻力恒定，则它在平直公路上匀速行驶的最大速度是()A．vB.P1 maC.P0vP1－mavD.P1vP0－mav8．图LZ3­4为修建高层建筑常用的塔式起重机．在起重机将质量m＝5×103 kg的重物竖直吊起的过程中，重物由静止开始向上做匀加速直线运动，加速度a ＝0.2 m/s2，当起重机输出功率达到其允许的最大值时，保持该功率直到重物做速度为v m＝1.02 m/s的匀速运动．g取10 m/s2，不计额外功．求：图LZ3­4(1)起重机允许输出的最大功率；(2)重物做匀加速运动所经历的时间和起重机在第2 s末的输出功率．9．汽车的额定功率为60 kW，总质量为2×103kg；运动中所受阻力恒为2000 N．若汽车在额定功率下运动，求：(1)当汽车的加速度是1 m/s2时的速度大小；(2)汽车行驶的最大速度；(3)10 s内牵引力做的功．10．一辆重5 t、额定功率为80 kW的车以a＝1 m/s2的加速度由静止开始做匀加速直线运动，车受的阻力为车重的0.06倍，g取10 m/s2.(1)分析车从静止开始至刚匀速运动过程中车的牵引力和发动机的功率如何变化．(2)车做匀加速直线运动能维持多长时间？(3)车做匀加速直线运动过程的平均功率为多少？(4)车加速10 s末的瞬时功率为多少？(5)车速的最大值为多少？11．汽车的质量为2 t，额定功率为80 kW，在平直的公路上行驶的最大速度为20 m/s.如果汽车从静止开始以2 m/s2的加速度做匀加速直线运动，运动过程中阻力不变，则：(1)汽车受到的阻力为多大？(2)3 s末汽车的瞬时功率为多大？(3)汽车维持匀加速运动的时间为多长？专题课：机车启动问题1．AC[解析] 设汽车牵引力为F，斜坡倾角为θ，汽车质量为m，摩擦力为F f，当F>F f＋mg sinθ时，有可能先加速后匀速到达坡顶，选项A正确，B 错误；若坡较短，则可能在变加速过程中到达坡顶，选项C正确；当F<F f＋mg sinθ时，汽车则减速上升，由F＝Pv可知，v减小，则F增大，而F f＋mg sinθ－F＝ma，故加速度越来越小，a＝0时，v最小，选项D错误．2．A[解析] 汽车的速度图像如图所示，假定汽车做匀变速直线运动，其速度图像是直线，直线与横轴包围的面积即v m t12，由于汽车以恒定功率开始运动，则其加速度应逐渐减小，实际速度图线如图中曲线所示，由图像可知，曲线与横轴所包围的面积较大，故A选项正确．3．D[解析] 当汽车速度最大时，加速度a＝0，牵引力F＝mg sinθ＋kmg，故此时最大速度v m＝PF＝Pmg（k＋sinθ），选项D正确．4．D[解析] 小车所受的牵引力和阻力恒定，所以小车做匀加速直线运动，牵引力的功率P＝F1v＝F1(v0＋at)，对应图D.5．BCD[解析] 轿车以恒定的牵引力F启动，由a＝F－fm得，轿车先做匀加速运动，由P＝Fv知，轿车的输出功率均匀增加，当功率达到额定功率时，牵引力逐渐减小，加速度逐渐减小，轿车做加速度逐渐减小的加速运动，当F＝f时，速度达到最大，之后轿车做匀速运动，选项B、C、D正确．6．ACD[解析] 根据P＝Fv、F－F f＝ma、F f＝kv得P＝(kv＋ma)v＝kv2＋mav，故在题设条件下，火车发动机的功率和牵引力都随速率v的增大而增大，则选项A正确；当火车达到某一速率时，欲使火车做匀速运动，则a＝0，此时P ＝kv2，故选项C、D正确．7．C[解析] 当加速度为a时，由F＝F f＋ma＝P1v得，阻力F f＝P1v－ma，当F＝F f时，速度最大，为v m，则v m＝P0F f＝P0vP1－mav.8．(1)5.1×104W(2)5 s 2.04×104W[解析] (1)设起重机允许输出的最大功率为P0，重物达到最大速度时，拉力F 等于重力，有P0＝Fv m，F＝mg，代入数据，得P0＝5.1×104W.(2)匀加速运动结束时，起重机达到允许输出的最大功率，设此时重物受到的拉力为F，速度为v1，匀加速运动经历的时间为t1，有P0＝Fv1，F－mg＝ma，v 1＝at 1联立以上各式并代入数据，得t 1＝5 st ＝2 s 时，重物处于匀加速运动阶段，设此时速度为v 2，输出功率为P ，则有v 2＝at ，P ＝Fv 2联立以上各式并代入数据，得P ＝2.04×104 W .9．(1)15 m /s (2)30 m /s (3)6×105 J[解析] (1)由牛顿第二定律得F 牵－F 阻＝ma又P ＝F 牵v两式联立解得v ＝15 m /s .(2)当汽车做匀速运动时，汽车的速度最大，此时F 牵＝F 阻由P ＝F 牵v max 得v max ＝P F 牵＝P F 阻＝60×1032000 m /s ＝30 m /s . (3)牵引力做功W ＝Pt ＝60×103×10 J ＝6×105 J .10．(1)匀加速过程，牵引力不变，功率逐渐增大；变加速过程，牵引力逐渐减小，功率不变(2)10 s (3)40 kW (4)80 kW (5)26.7 m /s[解析] (1)由题意，f ＝kmg ＝0.06×5000×10 N ＝3×103 N .从静止开始的匀加速直线运动过程，牵引力F 1是定值，由牛顿第二定律得F 1－f ＝ma ，得F 1＝8×103 N ，而功率在不断增大．达到额定功率后，车做变加速直线运动直至刚匀速运动，牵引力逐渐变小，直到和阻力相等，而功率则保持不变．(2)由P m ＝F 1v 1＝F 1at 1得t 1＝10 s .(3)设t 1＝10 s 末的速度为v 1，t 1时间内的平均速度为v ，则v 1＝at 1＝10 m /s ，v ＝v 12＝5 m /s ，所以P ＝F 1v ＝40 kW .(4)P＝F1v1＝80 kW.(5)由P m＝fv m得v m＝26.7 m/s.11．(1)4×103N(2)48 kW(3)5 s[解析] (1)在输出功率等于额定功率的条件下，当牵引力F等于阻力f时，汽车的加速度减小到0，汽车的速度达到最大．汽车所受的阻力为f＝Pv max＝8×10420N＝4×103N.(2)设汽车做匀加速运动时需要的牵引力为F′，根据牛顿第二定律有F′－f＝ma，解得F′＝f＋ma＝4×103N＋2×103×2 N＝8×103N因为3 s末汽车的瞬时速度为v3＝at＝2×3 m/s＝6 m/s，所以汽车在3 s末的瞬时功率为P3＝F′v3＝8×103×6 W＝48 kW.(3)汽车做匀加速运动时，牵引力F′恒定，随着车速增大，输出功率逐渐增大，输出功率等于额定功率时的速度是汽车做匀加速运动的最大速度，其数值为v′max＝PF′＝8×1048×103m/s＝10 m/s根据运动学公式，汽车维持匀加速运动的时间t＝v′maxa＝102s＝5 s.。