第六章单相对流传热的实验关联式
- 格式:pdf
- 大小:948.39 KB
- 文档页数:26




西交《传热学》第六章单相对流传热的关联式前言各位同学,以下是西交《传热学》第六章单相对流传热的关联式的,单相对流传热试验关联式,这个标题提醒了我们这一章的主要学习内容:单相状态,对流传热,试验,关联式。
单相是指没有相变的发生,怎么理解呢,就是在传热过程中传热的双方的状态没有变化,比如说在一块冰融化的过程中就存在状态的变化。
试验,每一个理论的产生和技术的应用都要经过研究人员在大量试验的基础上加以总结,因此试验是一种的重要的研究手段,从实验中可以推算出该项试验现象遵循的试验方程式即试验关联式。
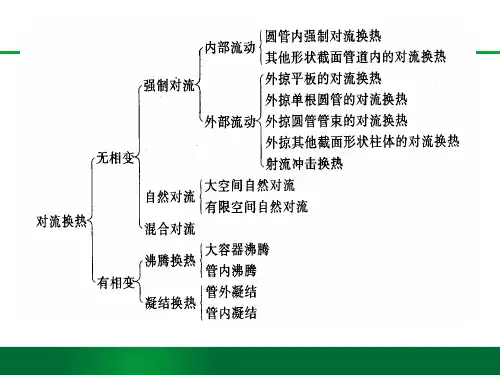
主要介绍单相对流传热的实验结果,本章将按内部流动、外部流动、大空间自然对流及有限空间自然对流的顺序展开讨论。
为了通过有限次数的实验测定而得出具有一定通用性的换热规律,在进行实验以及整理实验数据时,都必须遵循一定的原则,即相似原理。
本章将先对相似原理进行较深入的介绍基础上,再逐一介绍各类具体的实验关联式。
一、微细尺度通道内的流动与换热及纳米流体换热简介产生背景:20世纪80年代初期由于高新科学技术的发展在机械、电子、控制与能源领域,一门新兴交叉学科-微机电系统(micro-electro-mechanical system-MEMS)迅速崛起。
这里的所谓“微”是指工作部件的特征尺度在1毫米(10-3 m)到微米(10-6 m)的尺度范围。
目前微型热交换器、微尺度作用器、微尺度控制器件、微尺度生物芯片等不少已经成为商业产品。
在这样微细尺度的通道内,流体的流动与热交换出现了许多与常规尺度通道中的流动与传热过程不同的特点(统称为尺度效应,size effects)。
微细尺度传热学的研究也成为传热学研究的一个前沿重要分支领域。
气体在微细尺度通道中流动时,气体分子的平均自由程λ与通道的特征尺度L(对圆管取为直径)之比称为Knudsen(努森)数,是表征流动区域的重要参数:KnLλ=根据Kn数大小的不同,可以将气体的流动划分为以下四个区域连续介质区(continuum region):0.001Kn≤根据Kn数大小的不同,可以将气体的流动划分为以下四个区域连续介质区(continuum region):0.001Kn≤速度滑移与温度跳跃区(velocity slip and temperature jump r egion):0.0010.1Kn<<过渡区(transition region): 0.110Kn <<自由分子区(free-molecular region): 10Kn ≥Navier -Stokes 方程与能量方程以及无速度滑移(即固体壁面上流体速度等于当地的固体表面速度)与无温度跳跃即(固体壁面上流体的温度等于当地的固体表面的温度)边界条件仅适用于Knudsen 数小于 的连续介质区;在 0.0010.1Kn <<的范围内,上述控制方程仍然适用,但必须采用速度滑移与温度跳跃的条件;在过渡区与自由分子区基于连续介质假定而导出的Navier -Stokes 方程与能量方程不再适用,对流动与传热过程的数学描述需要采用基于分子动力论的有关原理与方程。




第六章 单相流体对流换热及准则关联式第一节 管内受迫对流换热本章重点:准确掌握准则方程式的适用条件和定性温度、定型尺寸的确定。
1-1 一般分析),,,,,,,,(l c t t u f h p f w μαρλ=流体受迫在管内对流换热时,还应考虑以下因素的影响:① 进口段与充分发展段,② 平均流速与平均温度,③ 物性场的不均匀性,④ 管子的几何特征。
一、进口段与充分发展段1.流体在管内流动的主要特征是,流动存在着两个明显的流动区段,即流动进口(或发展)段和流动充分发展段,如图所示。
(1)从管子进口到边界层汇合处的这段管长内的流动称为管内流动进口段。
(2)进入定型流动的区域称为流动充分发展段。
在流动充分发展段,流体的径向速度分量v 为零,且轴向速度u 不再沿轴向变化,即:0=∂∂xu, 0=v 2.管内的流态(1)如果边界层在管中心处汇合时流体流动仍然保持层流,那么进入充分发展区后也就继续保持层流流动状态,从而构成流体管内层流流动过程。
2300Re <用νdu m =Re 判断流态, 式中 m u 为管内流体的截面平均流速, d 为管子的内直径,ν为流体的运动黏度。
(2)如果边界层在管中心处汇合时流体已经从层流流动完全转变为紊流流动,那么进入充分发展区后就会维持紊流流动状态,从而构成流体管内紊流流动过程。
410Re >(3)如果边界层汇合时正处于流动从层流向紊流过渡的区域,那么其后的流动就会是过渡性的不稳定的流动,称为流体管内过渡流动过程。
410Re 2300<<3.热进口段和热充分发展段当流体温度和管壁温度不同时,在管子的进口区域同时也有热边界层在发展,随着流体向管内深入,热边界层最后也会在管中心汇合,从而进入热充分发展的流动换热区域,在热边界层汇合之前也就必然存在热进口区段。
随着流动从层流变为紊流, 热边界层亦有层流和紊流热边界层之分。
热充分发展段的特征对常物性流体,在常热流和常壁温边界条件下,热充分发展段的特征是:)(1x f t f =及)(2x f t w =与管内任意点的温度),(r x f t =组成的无量纲温度⎪⎪⎭⎫⎝⎛--x f x w w t t t t ,,x ,随管长保持不变,即: 0,,x ,=⎪⎪⎭⎫ ⎝⎛--∂∂x f x w w t t t t x 式中,t —管内任意点的温度,),(r x f t = ⇒xf x w w t t tt ,,x ,--仅是r 的函数。


第6章单相对流传热的实验关联式主要研究内容:
相似原理及其应用;
典型的单相流体对流换热过程及其
特征数关联式;
由于对流传热本身是一个非常复杂的物理问题,现
在用牛顿冷却定律把复杂简单表示,把复杂问题转到计算对流传热系数上面。
所以,对流传热系数大小的确定成为了一个复杂问题,其影响因素非常多。
目前还不能对对流传热系数从理论上来推导它的计算式,只能通过实验得到其经验关联式。
✓通过因次分析,建立特征数(准数)关系式;
✓通过实验,测定各准数的指数。
经验关联式的获取方法:
对流传热研究进展及方法
试验是不可或缺的手段,然而,经常遇到如下两个问题:
(1) 变量太多§6.1相似原理
)
, , , , , , , ,(l c t t v f h p f w ηαρλ 1 问题的提出
A 实验中应测哪些量(是否所有的物理量都测)
B 实验数据如何整理(整理成什么样函数关系)
(2) 实物试验很困难或太昂贵的情况,如何进行试验?
相似原理将回答上述两个问题
•
同类物理现象•
同名的已定特征数相等•单值性条件相似:初始条件、边界条件、几何条件、物理条件实验中只需测量各特征数所包含的物理量,避免了测量的盲目性——解决了实验中测量哪些物理量的问题
按特征数之间的函数关系
之间的函数关系整理实验数据,得到实用关联式——解决了实验中实验数据如何整理的问题
因此,我们需要知道某一物理现象涉及哪些无量纲数?它们之间的函数关系如何?
可以在相似原理的指导下采用模化试验——解决了实物试验很困难或太昂贵的情况下,如何进行试验的问题
4 物理现象相似的条件
§6.2相似原理的应用
4)圆形直管内的层流
层流时对流传热的特点:
✓物性特别是粘度受管内温度不均匀性的影响,导致速度分布受热流方向影响。
✓层流的对流传热系数受自然对流影响严重使得对流传热系数提高。
✓层流要求的进口段长度长,实际进口段小时,对流传热系数提高。
无限空间的自然对流换热:
n
(⋅
Nu Pr)
=
C
Gr
注意事项:
1.无限空间中自然对流换热的定性温度为流体与壁面的平均温度Tm=(Tw+Tf)/2。
2.无限空间中自然对流换热准则方程式中的系数C和指数n可根据放热表面的形状、位置及Gr数值范围由表6-10选取。
定型尺寸(特征尺寸)
•定型尺寸——相似准则中表示几何特征的尺寸,如Re、Nu中的l和d。
一般是:
(1)流体沿平壁流动取流动方向平壁的长度。
沿
竖壁作自然流动时取竖壁高度。
(2)流体绕流圆管或圆柱时,取圆管或圆柱的外
径。
(3)壁流体在管内流动取圆管内径。
对于非圆形截
面的管道则取当量直径,即
de=4F/U
注:式中F为管道的流通截面积;U为被流体润湿
的周长
(1)流体平均温度T f 。
对于管内流动,常取T f =(T f1+T f2)/2,T f1和T f2分别表示进出口截面上流体的平均温度。
(2)边界层流体的平均温度T m 。
如果用T w 和T f 分别表示壁面和流体温度则T m =(T w +T f )/2。
(3)壁面平均温度Tw 。
定性温度
自然对流换热例题讲解:
•一块0.6m×0.6m的薄板放在温
度为30℃的室内。
板的一面保持
在74℃,另一面绝热,计算下述
条件下此平板自然对流换热的热流
量:
•(1)平板垂直放置;
•(2)平板热面朝上水平放置;
•(3)平板热面朝下水平放置。
垂直放置
热面朝下热面朝上
•解:
–假设
– 1.换热为稳定态;
– 2.空气为理想气体;
– 3.大气压力为1atm
•
定性温度为•
T m =(T s +T ∞)/2=(74+30)/2=52℃=325K •
空气的热物性参数为•
λ=0.0279W/m ℃, ν=1.815×10-5m 2/s ,Pr=0.709, •β=1/T m =1/325K=0.00308K -1
•讨论:在本例中平板除通过自然对流换热外,还通过辐射向周围环境散热。
假设平板表面为黑体(黑度系数ε=1)并且室内墙壁的温度与室温相同(30℃),则通过辐射换热的热流量为:
•这比上面任何一种自然对流换热的换热强度都大。
因此在实际计算物体表面通过自然对流换热时,通过辐射散发的热量也是很显著的,必须予以考虑。
W
K K K m W m T T A Q s 124])27330()27374)[(/1067.5)(36.0)(1()(44428244
=+-+⋅⨯=-=-∞
σε。