医药数理统计方法7-1方差分析的基本原理

方差分析（ANOVA）简介方差分析（Analysis of Variance，简称ANOVA）是一种统计方法，用于比较两个或多个样本均值之间的差异是否显著。

它是通过分析样本之间的方差来判断均值是否存在差异。

ANOVA广泛应用于实验设计、医学研究、社会科学等领域，是一种重要的统计工具。

一、方差分析的基本原理方差分析的基本原理是通过比较组内变异和组间变异的大小来判断样本均值之间的差异是否显著。

组内变异是指同一组内个体之间的差异，组间变异是指不同组之间的差异。

如果组间变异显著大于组内变异，就可以认为样本均值之间存在显著差异。

二、方差分析的假设方差分析的假设包括以下几个方面：1. 观测值是独立的。

2. 观测值是正态分布的。

3. 各组的方差是相等的。

三、方差分析的步骤方差分析的步骤主要包括以下几个方面：1. 确定研究问题和目标。

2. 收集数据并进行数据清洗。

3. 计算组内平方和、组间平方和和总平方和。

4. 计算均方和。

5. 计算F值。

6. 进行显著性检验。

四、方差分析的类型根据研究设计的不同，方差分析可以分为单因素方差分析和多因素方差分析。

1. 单因素方差分析：适用于只有一个自变量的情况，用于比较不同水平下的均值差异。

2. 多因素方差分析：适用于有两个或两个以上自变量的情况，用于比较不同因素和不同水平下的均值差异。

五、方差分析的应用方差分析广泛应用于各个领域，包括实验设计、医学研究、社会科学等。

它可以用于比较不同治疗方法的疗效、不同教学方法的效果、不同产品的质量等。

六、方差分析的优缺点方差分析的优点包括：1. 可以同时比较多个样本均值之间的差异。

2. 可以通过显著性检验来判断差异是否显著。

3. 可以通过计算效应量来评估差异的大小。

方差分析的缺点包括：1. 对数据的正态性和方差齐性有一定要求。

2. 只能用于比较均值差异，不能用于比较其他统计指标的差异。

七、总结方差分析是一种重要的统计方法，通过比较组内变异和组间变异的大小来判断样本均值之间的差异是否显著。

方差分析的基本原理是什么
方差分析是一种统计方法，用于比较两个或多个不同组之间的平均值是否存在显著差异。

其基本原理是通过对数据的方差进行分解，将总平方和分解为组内平方和和组间平方和，从而判断不同组之间的差异是否超过了由随机因素引起的差异。

具体步骤如下：
1. 假设组间和组内的观测值都来自于正态分布的总体，并且方差相等（方差齐性）。

2. 计算组内平方和（误差平方和），即每个组内观测值与该组的平均值之差的平方和。

3. 计算组间平方和（效应平方和），即每组平均值与总体均值之差的平方和乘以每组样本量。

4. 比较组间和组内的方差大小，通过计算F统计量来衡量两
者之间的差异。

5. 根据显著性水平（如α=0.05），比较计算得到的F值与临
界F值进行比较，判断差异是否显著。

6. 若差异显著，则可以得出结论：不同组之间的平均值存在显著差异。

方差分析能够帮助研究者确定实验结果的可靠性和效应的大小，以及不同因素对结果的影响程度。

它广泛应用于各个领域的实验设计和数据分析中。

方差分析的原理方差分析（ANOVA）是一种统计方法，用于比较三个或三个以上组的均值是否相等。

它是一种用于检验组间差异是否显著的方法，通常用于实验设计和数据分析中。

方差分析的原理基于对组间差异和组内差异的分解，通过比较组间变异和组内变异的大小来判断组间均值是否有显著差异。

方差分析的原理可以通过以下步骤来解释，首先，假设我们有多个组，每个组都有一定的样本量和均值。

我们想要知道这些组的均值是否有显著差异。

方差分析的原理就是通过计算组间变异和组内变异来判断这一点。

具体来说，方差分析的原理包括以下几个步骤：1. 计算组内变异，首先，我们计算每个组内观察值与该组均值的偏差平方和。

这个偏差平方和反映了每个组内观察值与该组均值之间的差异程度。

2. 计算组间变异，然后，我们计算每个组均值与总体均值的偏差平方和。

这个偏差平方和反映了每个组均值与总体均值之间的差异程度。

3. 比较组间变异和组内变异，接下来，我们比较组间变异和组内变异的大小。

如果组间变异显著大于组内变异，说明组间均值存在显著差异；反之，如果组间变异远小于组内变异，说明组间均值之间没有显著差异。

4. 判断显著性，最后，我们通过F检验或t检验来判断组间均值是否有显著差异。

如果F值或t值大于一定的临界值，我们就可以拒绝原假设，认为组间均值存在显著差异；反之，如果F值或t值小于临界值，我们就不能拒绝原假设，认为组间均值之间没有显著差异。

方差分析的原理是基于对组间差异和组内差异的分解，通过比较组间变异和组内变异的大小来判断组间均值是否有显著差异。

它是一种常用的统计方法，可以帮助研究者判断不同组之间的差异是否显著，对于实验设计和数据分析具有重要意义。

通过深入理解方差分析的原理，我们可以更好地应用这一方法，从而更准确地进行数据分析和实验设计。

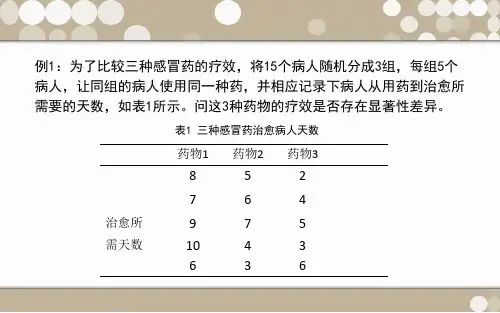
方差分析是用于两个及两个以上样本均数差别的显著性检验。

由于各种因素的影响，研究所得的数据呈现波动状，造成波动的原因可分成两类，一是不可控的随机因素，另一是研究中施加的对结果形成影响的可控因素。

方差分析的基本思想是：通过分析研究不同来源的变异对总变异的贡献大小，从而确定可控因素对研究结果影响力的大小。

方差分析主要用途：①均数差别的显著性检验，②分离各有关因素并估计其对总变异的作用，③分析因素间的交互作用，④方差齐性检验。

在科学实验中常常要探讨不同实验条件或处理方法对实验结果的影响。

通常是比较不同实验条件下样本均值间的差异。

例如医学界研究几种药物对某种疾病的疗效；农业研究土壤、肥料、日照时间等因素对某种农作物产量的影响；不同化学药剂对作物害虫的杀虫效果等，都可以使用方差分析方法去解决。

方差分析原理方差分析的基本原理是认为不同处理组的均数间的差别基本来源有两个：(1) 随机误差，如测量误差造成的差异或个体间的差异，称为组内差异，用变量在各组的均值与该组内变量值之偏差平方和的总和表示，记作SS w，组内自由度df w。

(2) 实验条件，实验条件，即不同的处理造成的差异，称为组间差异。

用变量在各组的均值与总均值之偏差平方和表示，记作SS b，组间自由度df b。

总偏差平方和 SS t = SS b + SS w。

组内SS t、组间SS w除以各自的自由度(组内dfw =n-m，组间dfb=m-1，其中n为样本总数，m为组数)，得到其均方MS w和MS b，一种情况是处理没有作用，即各组样本均来自同一总体，MS b/MS w≈1。

另一种情况是处理确实有作用，组间均方是由于误差与不同处理共同导致的结果，即各样本来自不同总体。

那么，MS b>>MS w(远远大于)。

MS b/MS w比值构成F分布。

用F值与其临界值比较，推断各样本是否来自相同的总体。

方差分析的假设检验假设有m个样本，如果原假设H0：样本均数都相同即μ1=μ2=μ3=…=μm=μ，m个样本有共同的方差。

方差分析的原理及依据
方差分析是一种统计学方法，用于比较两个或多个组的平均值是否有显著差异。

方差分析的原理及依据是基于正态分布的假设，即每个组的数据符合正态分布，并且组间、组内的方差相等。

方差分析的原理：
方差分析的原理是通过比较组间方差与组内方差来判断不同组别之间是否有显著差异。

其中组间方差是指各组样本均值与总均值之间的差异，而组内方差则是指各样本值与对应组样本均值之间的差异。

在正态分布假设下，这两种方差是服从F分布的，因此可以通过计算组间方差与组内方差的比值F值，来确定不同组别之间是否有显著差异。

方差分析的依据：
方差分析的依据主要是基于以下假设：
1. 各组的数据是独立的。

2. 各组的数据符合正态分布。

3. 各组的方差相等。

基于这些假设，方差分析可以推导出各组均值之间的差异是否为随机变异的结果。

如果差异不是由随机变异引起的，而是由于不同组别之间确实存在差异，那么这些差异就是有意义的，需要对其进行进一步分析。

通过方差分析，可以找出不同组别之间的差异，并确定哪些因素对组别之间的差异产生了影响。

例如，在生产过程中，通过分析不同生产批次之间的质量差异，可以找出影响质量的因素，并进一步进行改进。

在医学研究中，通过比较不同药物治疗组之间的效果，可以找出哪种药物最为有效，并为临床应用提供依据。

总之，方差分析作为一种统计学方法，在各个领域都具有重要的应用价值。

通过对不同组别之间的差异进行分析，可以为相关领域的决策和实践提供有力的支持。

方差分析的统计原理
方差分析是一种用于比较三个或多个总体均值是否具有显著差异的统计方法。

在进行方差分析时，我们假设所比较的各组数据是来自于正态分布总体的简单随机样本。

方差分析的基本原理是比较组间差异与组内差异的大小。

组间差异反映不同组别之间的均值差异，而组内差异反映各组内观察值与各组均值之间的差异。

具体而言，方差分析通过计算组间的均方（组间平方和除以自由度）与组内的均方（组内平方和除以自由度）来进行比较。

如果组间均方较大，且组内均方较小，就说明组间差异较显著，即存在组别之间的均值差异。

利用F检验可以判断组间均方
和组内均方是否具有显著差异。

在进行方差分析时，需要检验一些假设，包括总体均值相等的原假设和各组之间均值相等的原假设。

通过计算方差分析所得到的F值与临界F值进行比较，可以判断是否拒绝原假设。

方差分析可以应用于许多实际问题，例如比较不同药物治疗组的效果、不同教学方法对学生成绩的影响等。

方差分析的主要优点是可以同时比较多个组别的差异，适用于研究多因素对结果的影响。

而且，方差分析结果也可以提供各组均值之间的比较信息，进一步帮助我们理解差异的来源和性质。

方差分析原理及其应用方差分析是一种统计方法，用于比较两个或多个样本的均值是否存在显著差异。

它可以帮助我们判断不同因素对观测结果的影响程度，进而做出合理的决策。

本文将介绍方差分析的原理，并探讨其在实际应用中的价值。

一、方差分析的原理方差分析的核心思想是通过比较组间差异与组内差异的大小来判断各个因素对观测结果的影响有无显著性差异。

具体原理可概括为以下步骤：1. 建立假设：首先，我们需要明确研究的问题，并根据问题建立相应的假设。

一般来说，我们会设立原假设（H0）和备择假设（H1），用以描述观测数据之间存在的差异。

2. 计算总体方差和组内方差：方差分析需要计算总体方差和组内方差。

总体方差是指所有观测数据与整体均值之间的差异，而组内方差则是指同一组内观测数据与组内均值之间的差异。

3. 计算组间方差：通过比较组间方差与组内方差的大小，判断不同因素对观测结果的影响是否显著。

组间方差较大且显著时，说明不同组之间存在明显的差异。

4. 判断显著性：根据计算得到的统计量和显著水平，进行显著性判断。

若计算得到的统计量大于临界值，且显著水平小于设定的显著性水平，则可以拒绝原假设，得出结论。

二、方差分析的应用方差分析在很多领域都有广泛的应用。

下面将以实际案例来说明方差分析的应用价值。

假设有一家公司的销售部门希望了解不同销售方法对销售额的影响。

为了达到这个目的，他们选择了三种不同的销售方法，并随机选取了一组销售人员分别采用这三种方法进行销售。

他们收集了每位销售人员在一个月内的销售额数据，然后使用方差分析来比较这三种方法的销售额差异。

根据方差分析的原理，我们首先建立假设：H0：三种销售方法对销售额没有显著影响；H1：三种销售方法对销售额有显著影响。

然后，通过计算得到总体方差和组内方差，进而计算组间方差。

假设计算结果显示组间方差较大且显著，即不同销售方法对销售额存在显著影响。

最后，利用所得的统计量和显著水平进行显著性判断。

若统计量大于临界值，显著水平小于设定的显著性水平，我们可以拒绝原假设，得出结论：不同销售方法对销售额有显著影响。

方差分析知识点总结方差分析的基本原理是利用总体均值之间的变异性来进行假设检验。

它的基本思想是：通过对数据的变异性进行分解，我们可以得到与总体均值之间的比较，以判断它们是否存在显著差异。

方差分析将总体的变异性分为两部分：组内变异性和组间变异性。

组内变异性是指同一组内个体间的差异，而组间变异性是不同组之间的差异。

方差分析的基本假设包括：1. 各总体均值相等的原假设（H0）：μ1 = μ2 = ... = μk2. 各总体均值不全相等的备择假设（H1）：μi ≠ μj（i ≠ j）方差分析适用的条件包括：1. 各总体的总体分布应是正态分布2. 各组的方差应相等3. 各个样本应是相互独立的方差分析的类型主要包括一元方差分析（One-way ANOVA）和二元方差分析（Two-way ANOVA）。

其中，一元方差分析通过比较一个自变量对一个因变量的影响；而二元方差分析则同时考虑了两个以上的自变量对一个因变量的影响。

一元方差分析的过程包括以下几个步骤：1. 提出假设：提出总体均值相等的原假设和不全相等的备择假设。

2. 收集数据：收集不同组的样本数据。

3. 方差分解：计算组间变异性和组内变异性。

4. 计算统计量：计算F统计量。

5. 判断显著性：根据F统计量判断原假设的接受或拒绝。

二元方差分析则在一元方差分析的基础上加入了第二个自变量，其过程相对复杂一些。

方差分析的计算过程包括了方差分解和F统计量的计算。

在实际操作中，方差分析可以使用统计软件进行计算，如SPSS、R等。

方差分析的结果解释主要依据F统计量来判断原假设的接受或拒绝。

若F值大于临界值，则拒绝原假设，认为各组的均值存在显著差异；若F值小于临界值，则接受原假设，认为各组的均值相等。

方差分析的应用领域非常广泛，其中包括医学、社会科学、经济学等。

在医学研究中，方差分析可用于比较不同药物治疗对患者健康状况的影响；在社会科学中，方差分析可用于比较不同教育水平对收入的影响；在经济学中，方差分析可用于比较不同地区对GDP的影响等。

医学统计学方差分析方差分析是一种统计学方法，用于比较三个或三个以上的组之间的平均值是否存在显著差异。

在医学研究中，方差分析常用于比较不同治疗方法或不同个体群体之间的差异，以确定是否存在统计学上的显著差异。

方差分析的基本原理是比较组间离散程度与组内离散程度的比值，即组间均方与组内均方的比值。

组间方差表示不同组之间的差异性，组内方差表示同一组内个体之间的变异程度。

如果组间离散程度显著大于组内离散程度，即组间均方大于组内均方，就可以得出组间存在显著差异的结论。

在医学研究中，方差分析可以应用于很多不同的情况。

举例来说，我们可以使用方差分析来比较不同药物对同一疾病的治疗效果，或者比较不同药物剂量对同一疾病的治疗效果。

我们还可以使用方差分析比较不同年龄组、性别组或不同地区患者之间的其中一种疾病发病率。

方差分析的核心是比较组间差异与组内差异。

组间差异可以通过计算组间均方来得到。

组间均方的计算公式为组间平方和除以组间自由度。

组间平方和是每个组内数据与该组均值之差的平方的总和。

组间自由度等于组数减1、组内差异可以通过计算组内均方来得到。

组内均方的计算公式为组内平方和除以组内自由度。

组内平方和是每个组内数据与该组均值之差的平方的总和。

组内自由度等于总体样本量减去组数。

计算得到组间均方和组内均方之后，即可计算F值。

F值等于组间均方除以组内均方。

F值的计算结果可以与F分布的临界值进行比较，以判断组间均方是否显著大于组内均方。

如果F值大于F分布的临界值，就可以得出组间存在显著差异的结论。

除了F值，方差分析还可以计算一些其他的统计量。

例如，可以计算每个组的均值和标准差，以了解不同组之间的差异程度。

还可以计算方差分析表，其中包含了组间平方和、组间自由度、组间均方、组内平方和、总平方和、总自由度、组内自由度和组内均方等统计量。

需要注意的是，在进行方差分析之前，需要检验数据的正态性和方差齐性。

正态性检验可通过绘制正态概率图、Shapiro-Wilk检验或Kolmogorov-Smirnov检验进行。

第六章方差分析第一节方差分析的基本原理上章介绍了1个或两个样本平均数的假设测验方法.本章将介绍k（k≥3)个样本平均数的假设测验方法，即方差分析(analysis of variance).方差分析就是将总变异剖分为各个变异来源的相应部分,从而发现各变异原因在总变异中相对重要程度的一种统计分析方法。

其中，扣除了各种试验原因所引起的变异后的剩余变异提供了试验误差的无偏估计，作为假设测验的依据。

因而，方差分析象上章的t测验一样也是通过将试验处理的表面效应与其误差的比较来进行统计推断的，只不过这里采用均方来度量试验处理产生的变异和误差引起的变异而已。

方差分析是科学的试验设计和分析中的一个十分重要的工具。

本章将在介绍方差分析基本原理和方法的基础上进一步介绍数学模型和基本假定。

一、自由度和平方和的分解方差是平方和除以自由度的商。

要将一个试验资料的总变异分解为各个变异来源的相应变异,首先必须将总自由度和总平方和分解为各个变异来源的相应部分.因此，自由度和平方和的分解是方差分析的第一步。

下面先从简单的类型说起。

设有k组数据，每组皆具n个观察值,则该资料共有nk个观察值,其数据分组如表6。

1.表6.1 每组具n个观察值的k组数据的符号表组别观察值(，i=1，2，…,k；j=1，2,…,n) 总和平均均方1 ……2 …………i…………k……在表6.1中，总变异是nk个观察值的变异，故其自由度,而其平方和则为：（6·1)（6·1）中的C称为矫正数：（6·2)这里，可通过总变异的恒等变换来阐明总变异的构成。

对于第i组的变异,有总变异为第1，2，…,k组的变异相加，利用上式总变异（6·1)可以剖分为:（6·3）即总平方和=组内(误差)平方和+处理平方和组间变异由k个的变异引起，故其自由度,组间平方和为:(6·4)组内变异为各组内观察值与组平均数的变异,故每组具有自由度和平方和；而资料共有组，故组内自由度，组内平方和为：（6·5）因此,得到表6.1类型资料的自由度分解式为：(6·6）总自由度DF T=组间自由度DF t+组内自由度DF e求得各变异来源的自由度和平方和后，进而可得:(6·7)若假定组间平均数差异不显著(或处理无效)时，(6·7)中与是的两个独立估值,均方用表示，也用表示，两者可以互换。

方差分析的原理
（1）方差分析的概念
方差分析的目的是推断多组资料的总体均数是否相同，也即检验多组数据之间的均数差异是否有统计意义。

当我们用多个t 检验来完成这一过程时，相当于从t 分布中随机抽取多个t 值，这样落在临界范围之外的可能大大增加，从而增加了Ⅰ型错误的概率。

我们可以把方差分析看作t 检验的增强版。

（2）方差的可分解性
方差分析依据的基本原理就是方差的可加性原则。

作为一种统计方法，方差分析把实验数据的总变异分解为若干个不同来源的分量。

数据的变异由两部分组成： 组内变异：由于实验中一些希望加以控制的非实验因素和一些未被有效控制的未知因素造成的变异，如个体差异、随机误差
组内变异是具体某一个处理水平之内的，因此在对总体变异进行估计的时候不涉及研究的处理效应。

组间差异：不仅包括组内变异的误差因素，还包括了是不同组所接受的实验处理不同造成的影响
如果研究数据的总变异是由处理效应造成的，那么组间变异在总变异中应该占较大比例。

B M S 表示组间方差，B B B
SS M S df =，1B df k =-，k 表示实验条件的个数 W
M S 表示组内方差，W
W W SS M S df =，()1W df k n =-，n 表示每种实验条件中的被试个数
（3）方差分析的基本假定
①样本必须来自正态分布的总体
②每次观察得到的几组数据必须彼此独立 ③各实验处理内的方差应彼此无显著差异
为了满足这一假定，我们可采用最大F 比率法2m ax m ax 2m in s F s ，求出各样本中方差最
大值与最小值的比，通过查表判断。

文章来源：博仁教育。