离散数学第九章树

在离散数学中，图是一个由点和边组成的抽象数学模型。

其中，树是一种特殊的图，它是一个无环连通图。

在图论中，树扮演了重要的角色，它具有许多有趣的性质和应用。

而生成树则是树的一个特殊子集，它由给定图中的所有顶点和部分边构成。

本文将介绍图的树的基本概念，并探讨生成树的计数方法。

首先，让我们来看看图的树。

树是一种无环连通图，其中任意两个顶点之间存在唯一一条路径。

它具有以下性质：1.n个顶点的树有n-1条边。

这可以通过归纳法证明：当n=1时，结论成立；假设n=k时成立，那么n=k+1时，只需要添加一个顶点和一条边，即可构成n=k+1个顶点的树。

因此，结论成立。

2.连接树上任意两个顶点的边都是桥。

即如果一条边被删除，那么树就会变成两个或更多个不相连的子树。

3.树是一个高度平衡的结构。

对于一个n个顶点的树，任意两个叶子结点之间的路径长度至多相差1。

4.树的任意两个顶点之间有唯一一条路径，路径长度为顶点之间的边数。

接下来，让我们来讨论生成树的计数方法。

生成树是树的一个特殊子集，它是由给定图中的所有顶点和部分边构成。

生成树的计数在图论中具有重要的意义和应用。

对于一个具有n个顶点的连通图来说，其生成树的个数可以通过Cayley公式计算得到。

Cayley公式是由亚瑟·凯利于1889年提出的，它给出了完全图的生成树数目。

据此，我们可以得到生成树的计数公式为：T = n^(n-2)，其中T表示生成树的个数。

此外，还有一种常见的计数方法是基于度数矩阵和邻接矩阵的矩阵树定理。

矩阵树定理由高斯于1847年提出，它提供了一种计算图的生成树个数的方法。

根据矩阵树定理，一个无向图G的生成树数目等于该图度数矩阵的任意一个(n-1)阶主子式的行列式的值。

其中，度数矩阵是一个对角矩阵，它的对角线上的元素为各个顶点的度数。

邻接矩阵则是一个关于顶点间连接关系的矩阵，其中1表示相邻顶点之间存在边，0表示不存在边。

除了数学方法，还存在一种基于图的遍历的计数方法，称为Kirchhoff矩阵树定理。

第9章习题解答9. 1有5片树叶.分析设T有x个1度顶点(即树叶)•则T的顶点数n = 3 + 2 + x = 5 + x,T的边数m = n- \ =4 + x.由握手定理得方程.2m = 2(4 + x) = y^J(v f) = 3x3 + 2x2 + l- x = 13 + x./=1由方程解出*5.所求无向树T的度数列为1, 1, 1, 1, 1, 2, 2, 3, 3, 3.由这个度数列可以画多棵非同构的无向树，图9. 6给出的4棵都具有上述度数列，且它们是非同构的.9.2 T中有5个3度顶点.分析设T中有x个3度顶点，则T中的顶点数n = l + x,边数加= "-l = 6 + x,由握手定理得力程.2m = 12 + 2x =》d（片）=3x + 7/=!rtl方程解出x=5.所求无向树T的度数列为1, 1, 1, 1, 1, 2, 2, 3, 3, 3.由这个度数列可以画多棵非同构的无向树，图9.6给出的4棵都具有上述度数列，且它们是非同构的.9.2 T中有5个3度顶点.要析设T中有x个3度顶点，则T中的顶点数"7 +小边数加1=6 + .由握手定理得方程.由此解出"5,即T中有5个3度顶.T的度数列为1, 1, 1, 1, 1, 1, 1, 3, 3, 3, 3, 3.由于T中只有树叶和3度顶点, 因而3度顶点可依次相邻，见图9. 7所示.还有棵与它非同构的树，请读者自己i田i出.9. 3力肛-1条新边才能使所得图为无向树.分析设具有£个连通分支的森林为G,则G有k个连通分支人込，…八/全为树，心1,2,…&加新边不能在7；内部加，否则必产生回路.因而必须在不同的小树之间加新边.每加一条新边后，所得到的森林就减少一个连通分支.恰好加-1条新边，就使得图连通且无回路，因而是树•在加边过程屮，只需注意，不在同一人连通分支中加边.下面给出一种加边方法,取v,为7；中顶点，加新边(v,,v,+l)z = l,2,---J-l,则所得图为树, 见图9. 8给出的一个特例.图中虚线边为新加的边.9. 4不一定.分析n阶无向树T具有“-I条边，这是无向树T的必要条件，但不是充公条件•例如，阶圈(即“-1个顶点的初级回路) 和一个孤立点组成无向简单图具有”-1条边，但它显然不是树.图9.89. 5非同构的无向树共有2棵，如图9. 9所示.困9.9分析由度数列1, 1, 1, 1,2,2, 4不难看出，唯一的4度顶点必须与2度顶点相邻，它与1个2度顶点相邻，还是与两个2度顶点都相邻，所得树是非同构的，再没有其他情况. 因而是两棵非同构的树. o 、O O9.6有两棵非同构的生I ，——V(1) (2)成树，见图9. 10所示. 图9.10分析图9. 10是5阶图(5个顶点的图)，5阶非同构的无向树只有3棵，理由如下.5 阶无向树中，顶点数"=5,边数加=4,各顶点度数Z和为&度数分配方案有3种,分别为①1, 1, 1, 1,4;②1, 1, 1,2,3;③1, 1,2, 2. 2.每种方案只有一棵非同构的树•图9.10所示的5阶图的非同构的生成树的度数列不能超出以上3种，也就是说，它至多有3棵非同构的生成树，但由于图中无4度顶点，所示，不可能有度数列为①的生成树，于是该图最多有两棵非同构的生成树.但在图9. 10中已经找出了两个非同构的生成树, 其中(1)的度数列为③，(2)的度数列为②，因而该图准确地有两棵非同构的牛成树.9. 7 基本回路为：C c = cbad,C e = ead,C g = gfa,C h =hfab.基本回路系统为{C c,C e,C g,C h}.基本回路系统为{S a,S h,S d,S f}.分析1°注意基本回路用边的序列表示，而基本割集用边的集合表示.2°基本回路中，只含一条弦，其余的边全为树枝，其求法是这样的：设弦e = (fj),则％,Vj在生成树T中，且在T中, 之间存在唯一的路径「订与e = (v,,v y)组成的回路为G中对应弦e的基本回路.3°基本割集中，只含一条树枝，其余的边都是弦，其求法是这样的:设树枝e = (i;,Vj),则e为T中桥,于是T-e (将e从T 中支掉)，产生两棵小树7；和0，则={e \e在G中且e的两端点分别在7；和3中} S。

在离散数学中，生成树（Spanning Tree）是一个图（Graph）的子图，它包含图中的所有顶点，并且是一个树（Tree）。

生成树的一个重要性质是它不包含任何环（Cycle）。

求一个给定图的生成树个数是一个经典问题，通常使用矩阵树定理（Matrix Tree Theorem）来解决。

矩阵树定理给出了一个图的生成树个数的计算公式，它基于图的拉普拉斯矩阵（Laplacian Matrix）的行列式。

拉普拉斯矩阵是一个方阵，其大小为图的顶点数，矩阵的元素定义如下：•如果i和j是不同的顶点，则矩阵的第i行第j列的元素是顶点i和j之间的边的权重（如果存在边的话），否则是0。

•对于每个顶点i，矩阵的第i行第i列的元素是顶点i的度（即与顶点i相邻的边的数量）的负值。

矩阵树定理指出，图的生成树个数等于其拉普拉斯矩阵的任何一个n-1阶主子式的行列式值的绝对值。

n是图的顶点数，n-1阶主子式意味着去掉矩阵中的一行和一列后得到的矩阵。

下面是一个简单的例子，说明如何使用矩阵树定理计算生成树的个数：假设有一个包含4个顶点的简单图，其边和权重如下：A -- 2 -- B| |1 3 1| |C -- 4 -- D1 -3 1 00 1 -3 40 0 1 -4主子式的行列式值。

去掉第一行和第一列后，我们得到：1 01 -3 40 1 -4x3矩阵的行列式，我们得到：1 * 1) - (0 * 0) = 12 - 1 = 11过程可能涉及复杂的行列式计算，特别是对于大型图来说。

在实际应用中，通常会使用专门的数学软件或库（如Python中的NumPy或SciPy）来进行这些计算。

此外，还有一些算法（如Kruskal算法和Prim算法）可以用来构造生成树，但它们并不直接计算生成树的总数。

这些算法通常用于找到图的一个生成树，而不是计算所有可能的生成树的数量。

离散数学树
离散数学中的树(Tree)是一种常见的图论结构，它是一种无向、连通且没有简单回路的无向图，或者是一个有向连通图，其中每个节点都只有唯一一个父节点（除了根节点）。

树形结构中的每一个节点都可以视为一个子树的根节点，因为它下面连接了若干个子节点，这样就形成了一棵向下生长的树状结构。

树形结构还有一个重要的特点就是它具有很好的递归性质，因为每个节点下面都可以再建立一棵子树，这样就可以逐层递归地构建出整棵树。

在离散数学中，树被广泛应用于算法设计、数据结构以及对计算机网络和信息系统进行建模等领域。

树的深度和广度优先遍历、树的一些基本性质(如高度、度、叶子节点等)以及树的遍历应用在图的搜索算法、排序、哈夫曼编码、抽象语法树等算法中都有广泛的应用。

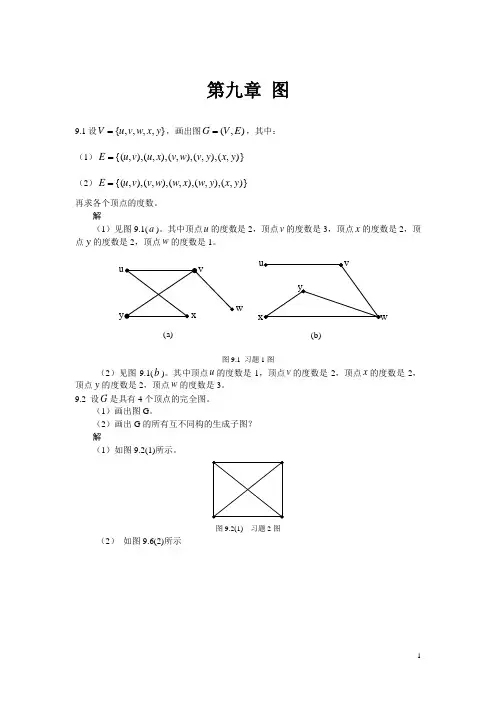
第九章 图9.1设},,,,{y x w v u V =，画出图),(E V G =，其中：（1）)},(),,(),,(),,(),,{(y x y v w v x u v u E =（2）)},(),,(),,(),,(),,{(y x y w x w w v v u E =再求各个顶点的度数。

解（1）见图9.1(a )。

其中顶点u 的度数是2，顶点v 的度数是3，顶点x 的度数是2，顶点y 的度数是2，顶点w 的度数是1。

图9.1 习题1图（2）见图9.1(b )。

其中顶点u 的度数是1，顶点v 的度数是2，顶点x 的度数是2，顶点y的度数是2，顶点w 的度数是3。

9.2 设G 是具有4个顶点的完全图。

（1）画出图G 。

（2）画出G 的所有互不同构的生成子图？解（1）如图9.2(1)所示。

图9.2(1) 习题2图（2） 如图9.6(2)所示﹒ ﹒ ﹒ ﹒ ﹒ ﹒图9.2(2) 习题2图9.3 一个无向简单图，如果同构于它的补图，则称这个图为自互补图。

（1）试画出五个顶点的自互补图。

（2）证明一个自互补图一定只有k 4或14+k 个顶点（k 为整数）。

解（1）(a) (b)图9.3 习题3图 （2）因为n 个顶点的无向完全图有)1(21-n n 条边，所以自互补图有)1(41-n n 条边，因此，k n 4=或14+k 。

9.4 画出两个不同构的简单无向图。

每一个图都仅有6个顶点，且每个顶点都均是3度，并指出这两个图为什么不同构。

解图9.4 习题9.4图9.5 证明任意两个同构的无向图，一定有一个同样的顶点度序列。

顶点度序列是一组按大小排列的正整数。

每一个数对应某一个顶点的度数。

证明两个同构的无向图，度数相同的顶点数目一定相同，这样才能够建立起顶点之间的一一对应关系，进而建立起边的对应关系。

所以，任意二个同构的无向图，一定有一个同样的顶点度序列。

9.6图9.6中所给的图(a )与图(b )是否同构？为什么？(a )(b ) 图9.6 习题6图 解左图9.2（a ）中次数为4的点，与3个度数为1，一个度数为2的顶点相邻接，右图9.2（b ）中度数为4的点，却与3个度数为1，一个度数为3的顶点相邻接。

第9章 习题解答9.1 有5片树叶.分析 设T 有x 个1度顶点(即树叶).则T 的顶点数Tx x n ,523+=++=的边数.41x n m +=-=由握手定理得方程.∑=+=⋅+⨯+⨯==+=ni ix x vd x m 1.1312233)()4(22由方程解出.5=x所求无向树T 的度数列为1,1,1,1,1,2,2,3,3,3.由这个度数列可以画多棵非同构的无向树,图9.6给出的4棵都具有上述度数列,且它们是非同构的.9.2 T 中有5个3度顶点.分析 设T 中有x 个3度顶点,则T 中的顶点数,7x n +=边数x n m +=-=61,由握手定理得方程.∑=+==+=ni ix v d x m 173)(2122由方程解出x=5.所求无向树T 的度数列为1,1,1,1,1,2,2,3,3,3.由这个度数列可以画多棵非同构的无向树,图9.6给出的4棵都具有上述度数列,且它们是非同构的.9.2 T 中有5个3度顶点.要析 设T 中有x 个3度顶点,则T 中的顶点数x n +=7,边数x n m +=-=61,由握手定理得方程.∑=+==+=ni ix v d x m 173)(2122.由此解出5=x ,即T 中有5个3度顶.T 的度数列为1,1,1,1,1,1,1,3,3,3,3,3.由于T 中只有树叶和3度顶点,因而3度顶点可依次相邻,见图9.7所示. 还有一棵与它非同构的树,请读者自己画出.9.3 加1-k 条新边才能使所得图为无向树.分析 设具有k 个连通分支的森林为G,则G 有k 个连通分支i K T T TT ,,,21全为树,.,,2,1k i =加新边不能在i T 内部加,否则必产生回路.因而必须在不同的小树之间加新边. 每加一条新边后,所得到的森林就减少一个连通分支. 恰好加1-k 条新边,就使得图连通且无回路,因而是树.在加边过程中,只需注意,不在同一人连通分支中加边. 下面给出一种加边方法,取iv 为iT 中顶点,加新边1,,2,1),(1-=+k i vv i i,则所得图为树,见图9.8 给出的一个特例.图中虚线边为新加的边.9.4 不一定.分析 n 阶无向树T 具有1-n 条边,这是无向树T 的必要条件,但不是充公条件.例如, 阶圈(即1-n 个顶点的初级回路)和一个孤立点组成无向简单图具有1-n 条边, 但它显然不是树.9.5 非同构的无向树共有2棵,如图 9.9所示.分析由度数列1,1,1,1,2,2,4不难看出，唯一的4度顶点必须与2度顶点相邻，它与1个2度顶点相邻，还是与两个2度顶点都相邻，所得树是非同构的，再没有其他情况.因而是两棵非同构的树.9.6 有两棵非同构的生成树,见图9.10所示.分析图9.10 是5阶图(5个顶点的图), 5阶非同构的无向树只有3棵,理由如下. 5阶无向树中,顶点数5=n,边数4=m,各顶点度数之和为8,度数分配方案有3种,分别为①1,1,1,1,4;②1,1,1,2,3;③1,1,2,2.2.每种方案只有一棵非同构的树.图9.10所示的5阶图的非同构的生成树的度数列不能超出以上3种,也就是说,它至多有3棵非同构的生成树, 但由于图中无4度顶点,所示,不可能有度数列为①的生成树,于是该图最多有两棵非同构的生成树. 但在图9.10 中已经找出了两个非同构的生成树,其中(1)的度数列为③,(2) 的度数列为②,因而该图准确地有两棵非同构的生成树.9.7 基本回路为: .,,,hfab C gfa C ead C cbad C h g e c====基本回路系统为}.,,,{h g e cC C C C基本割集为:},,{},,{},,,{},,,,,{h g f Sc ed S h c b S h g ce a S fd b a ====基本回路系统为},,,{f d b aS S S S.分析 1°注意基本回路用边的序列表示,而基本割集用边的集合表示.2° 基本回路中,只含一条弦,其余的边全为树枝,其求法是这样的: 设弦),(j iv ve =,则jiv v,在生成树T 中,且在T 中,ji v v ,之间存在唯一的路径ji ,Γ与),(j iv ve =组成的回路为G 中对应弦e 的基本回路.3° 基本割集中,只含一条树枝,其余的边都是弦,其求法是这样的:设树枝),(j iv ve =,则e 为T 中桥,于是eT-(将e 从T中支掉),产生两棵小树1T 和2T ,则}|{21'''中和的两端点分别在中且在T T e G e e S e =e S 为树枝e 对应的基本割集. 显然ee S S e ,∈中另外的边全是弦. 注意,两棵小树1T 和2T ,中很可能有平凡的树(一个顶点).aT -得两棵小树如图9.11中(1) 所示. G 中一个端点在i T 中,另一个端点在2T 中的边为a(树枝), h g c e ,,,,它们全是弦,于是},,,,{h g c e a Sa=bT - 得两棵小树如图9.11中(2) 所示, 其中有一棵为平凡树. G 中一个端点在1T 中,另一个端点在2T 中的边数除树枝b 外,还有弦,,h c 所以, },,{h c b Sb=dT -产生的两棵小树如图9.11中(3) 所示 . G 中一个端点在1T 中,另中一个端点在2T 中的边,除树枝d 外,还有两条弦e c ,,所示, },,{e c d Sd=fT -产生的两棵小树如图9.11中(4) 所示. 由它产生的基本割集为},,{h g f Sf=9.8 按Kruskal 求最小生成树的算法,求出的图9.3(1)的最小生成树T 为图9.12中(1) 所示, 其7)(=T W .(2) 的最小生成树T 为图9.12中(2)所示,其.11)(=T W9.9 421,,B B B为前缀码.分析 在421,,B B B中任何符号串都不是另外符号串的前串,因而它们都是前缀码.而在3B 中, 1是11,101的前缀,因而3B不是前缀码. 在5B 中,,a 是ac aa ,等的前缀,因而5B 也不是前缀码.9.10 由图9.4 (1) 给出的2元前缀码.}11,011,01010,0100,00{1=B由(2) 给出的3元前缀码为.}.2,1,022,0202,0201,0200,01,00{2=B分析 1B 是2元树产生的2元前缀码(因为码中的符号串由两个符号0,1组成),类似地,2B 是由3元树产生的3元前缀码(因为码中符号串由3个符号0,1,2组成).一般地,由r 元树产生r 元前缀码.9.11 (1) 算式的表达式为ji h g f e d c b a *)*()()*)*((((++÷-+.由于使其成为因而可以省去一些括号优先于,,,*,-+÷ji h g f e d c b a **)()*)*((++÷-+.(2) 算式的波兰符号法表达式为.****hij fg bcde a ++-÷+(3) 算式的逆波兰符号法表达式为.****+÷+-+jI hi fg e d abc9.12 答案 A:①; B ②; C:④; D:⑨.分析 对于每种情况都先求出非同构的无向树,然后求出每棵非同构的无向树派生出来的所有非同构的根树.图9.13 中,(1),(2),(3),(4)分别画出了2阶,3阶,4阶,5阶所有非同构的无向树,分别为1棵,1棵,2棵和3棵无向树.2阶无向树只有1棵,它有两个1度顶点,见图9.13中(1)所示,以1个顶点为树根,1个顶点为树叶,得到1棵根树.3阶非同的无向树也只有1棵,见图9.13中(2)所示.它有两个1度顶点,1个2度顶点,以1度顶点为根的根树与以2度顶点为根的树显然是非同构的根树,所以2个阶非同构的根树有两棵.4阶非同构的无向树有两棵,见图9.13中(3)所示. 第一棵树有3片树叶,1个3度顶点, 以树叶为根的根树与以3度顶点为根的树非同构.所以,由第一棵树能生成两个非同构的根树, 见图9.14 中(1)所示. 第二棵树有两片树叶,两个2度顶点,由对称性,以树叶为根的根树与2度顶点为根的根树非同构,见图9.14中(2) 所示. 所以,4阶非同构的根树有4棵.5阶非同构的无向树有3棵,见图9.13中(4)所示. 由第一棵能派生两棵非同构的根树, 由第二棵能派生4棵非同构的根树,由第三棵能派生3棵非同构的根树,所以,5阶非同构的根树共有9棵,请读者将它们都画出来.9.13 答案 A:②; B:②; C:③; D:③; E:③;F:④; G: ④; H:③.分析 将所有频率都乘100,所得结果按从小到大顺序排列:.35,20,15,10,10,5,5=======a b c d e f g w w w w w w w以以上各数为权,用Huffman 算法求一棵最优树,见图9.15所示.对照各个权可知各字母的前缀码如下:a ——10，b ——01，c ——111，d ——110，e ——001，f ——0001，g ——0000.于是，a,b 的码长为e d c ,,,2的码长为g f ,,3的码长为4. W(T)=255(各分支点的权之和),W(T)是传输100按给定频率出现的字母所用的二进制数字,因则传输104个按上述频率出现的字母要用25500⨯个二进制数字..24=1055最后还应指出一点,在画最优树叶, 由于顶点位置的不同,所得缀码可能不同,即有些字母的码子在不同的最优树中可能不同,但一般说来码长不改变.特别是,不同的最优树,它们的权是固定不变的.9.14 答案 A:②; B:④分析用2元有序正则树表示算式,树叶表示参加运算的数,分支点上放运算符,并将被减数(被除数)放在左子树上,所得2元树如图9.16所示.用前序行遍法访问此树,得波兰符号表示法为abc-++de-*.**ghf用后序行遍法访问此树,得逆波兰符号表示法为dec*fghab--++**。

习题91. 设G 是一个(n ，m)简单图。

证明：，等号成立当且仅当G 是完全图。

证明：（1）先证结论：因为G 是简单图，所以G 的结点度上限 max(d(v)) ≤ n-1, G 图的总点度上限为 max(Σ(d(v)) ≤ n ﹒max(d(v)) ≤ n(n-1) 。

根据握手定理，G 图边的上限为 max(m) ≤ n(n-1)/2,所以。

（2） =〉G 是完全图 因为G 具有上限边数，假设有结点的点度小于n-1,那么G 的总度数就小于上限值，边数就小于上限值，与条件矛盾。

所以，G 的每个结点的点度都为n-1，G 为完全图。

G 是完全图 =〉 因为G 是完全图，所以每个结点的点度为n-1, 总度数为n(n-1)，根据握手定理，图G 的边数 。

■2. 设G 是一个（n ，n +1）的无向图，证明G 中存在顶点u ，d （u ）≥3。

证明：反证法，假设,则G 的总点度上限为max(Σ(d(u)) ≤2 n ，根据握手定理，图边的上限为max(m) ≤ 2n/2=n 。

与题设m = n+1，矛盾。

因此，G 中存在顶点u ，d （u ）≥3。

■3．确定下面的序列中哪些是图的序列，若是图的序列，画出一个对应的图来: （1）（3，2，0，1，5）； （2）（6，3，3，2，2） （3）（4，4，2，2，4）； （4）（7，6，8，3，9，5）解：除序列（1）不是图序列外，其余的都是图序列。

因为在（1）中，总和为奇数，不满足图总度数为偶数的握手定理。

可以按如下方法构造满足要求的图：序列中每个数字ai 对应一个点，如果序列数字是偶数，那么就在对应的点上画ai/2个环，如果序列是奇数，那么在对应的点上画(ai-1)/2个环。

最后，将奇数序列对应的点两两一组，添加连线即可。

下面以（2）为例说明：(6 , 3, 3, 2, 2 ) 对应图G 的点集合V= { v 1,v 2,v 3,v 4,v 5}每个结点对应的环数(6/2, (3-1)/2, (3-1)/2, 2/2,2/2) = (3,1,1,1,1)将奇数3，3 对应的结点v 2,v 3一组，画一条连线其他序列可以类式作图，当然大家也可以画图其它不同的图形。

第九章树9.1 无向树及其性质定义9.1 连通无回路的无向图称为无向树, 或简称树, 常用T表示树(Tree);平凡图称为平凡树;若无向图G至少有两个连通分支, 每个连通都是树, 则称G为森林(Forest);在无向图中, 悬挂顶点称为树叶(Leaf);度数大于或等于2的顶点称为分支点(Node)无向树有许多性质, 它们是树的充要条件, 因此它们都可看作是树的定义。

定理9.1 设G = <V, E>是n阶m条边的无向图, 则下面各命题是等价的:(1) G是树(2) G中任意两个顶点之间存在唯一的路径(3) G中无回路, 且m = n-1(4) G是连通的, 且m = n-1(5) G是连通的, 且G中任何边均为桥(6) G中没有回路, 但在任何两个不同的顶点之间加一条新边, 在所得图中得到唯一一个含新边的圈证：(1) ⇒ (2)由G的连通性和定理14.5的推论可知: ∀u,v∈V, u与v之间存在路径。

若路径不是唯一的, 设Γ1与Γ2都是u到v的路径。

显然必存在由Γ1和Γ2上边构成的回路, 这就与G中无回路矛盾。

(2) ⇒ (3)先证明: G中无回路。

若G中存在关联某顶点v的环, 则v到v存在长为0和1的两条路经, 这与已知矛盾。

若G中存在长度大于或等于2的圈, 则圈上任何两个顶点之间都存在两条不同的路径, 这与已知条件矛盾。

下面用归纳法证明: m = n-1。

1) n = 1时, G为平凡图, 结论显然成立。

2) 设n ≤ k(k ≥ 1)时, 结论成立。

3) 当n = k+1时设e = (u, v)为G中的一条边, 由于G中无回路, 所以, G-e有两个连通分支G1和G2。

设n i和m i分别为G i中的顶点数和边数, 则n i≤ k(i = 1, 2)。

由归纳假设可知: m i = n i-1, 于是, m=m1+m2+1=n1+n2+1-2=n-1。

(3) ⇒ (4)假设: G不是连通的。

离散数学知识点总结（9）-树⼀、⽆向树和有向树对于任何⽆向图，若图中不存在简单回路，则 m≤n-1⽆向图是⽆向树的四个条件互相等价：连通、不存在简单回路、m=n-1满⾜⾄少2个 每⼀对相异顶点之间存在唯⼀的简单道路 极⼩连通（每⼀条边都是桥） 极⼤⽆圈因此⽆向树必定不含重边和⾃环，⼀定是简单图，⼀定是平⾯图。

⽆向树中度数为1的顶点称为叶⼦，度数⼤于1的顶点称为分枝点。

平凡树：⼀阶简单图，既⽆叶⼦⼜⽆分枝点任何⾮平凡树⾄少有2个叶⼦顶点证明：设n(n≥2) 阶⽆向连通图G的边数满⾜m=n-1，设图中度数为1的顶点数为t，则2m=deg(v1)+...+dev(v n)≥t+2(n-t)，得t≥2 或者设⽆向树中存在着a i个度为i的顶点，a1+2a2+...=2m，a1+a2+...=n=m+1，故叶⼦数=a3+2a4+3a5+...+2≥2森林：不含任何简单回路的图。

森林的每个连通分⽀都是树⼆、有向树和根树有向树：不考虑边的⽅向时是⼀棵⽆向树的有向图根树：只有⼀个⼊度为0的顶点，其它顶点⼊度均为1的有向树根树中出度为0的顶点称为叶⼦，出度⼤于0的顶点称为分枝点在根树中，从根到任⼀其它顶点都存在唯⼀的简单道路以v为根的根树：有向图中存在顶点v，使得从v到图中任意其它顶点都存在唯⼀简单道路，⽽且不存在从v到v的简单回路在根树中，由根到顶点v的道路长度称作v的层数（level） ；所有顶点的层数的最⼤值称为根树的⾼度（height）若T的每个分⽀点最多m个⼉⼦，则称T为m叉树；若其每个分⽀点都恰好m个⼉⼦，则称T为m叉正则树正则m叉树，其叶⼦数为t，分枝点数为i，则所有顶点出度之和为mi=所有顶点的⼊度之和t+i-1，故(m-1)i=t-1三、标号树前序遍历结果-+×421×÷632称作前缀表⽰、波兰式将波兰式压栈，当插⼊到×42时将其替换为8后序遍历结果42×1+63÷2×-称作后缀表⽰、逆波兰式将波兰式压栈，当插⼊到42×时将其替换为8中序遍历表达式4×2+1-6÷3×2称作中缀表⽰由前缀表⽰或后缀表⽰可以唯⼀构造表⽰运算式的有序树，但是由中缀表⽰则不⾏此外还有⼀些关于遍历、哈夫曼编码的知识点，数据结构中就有。