当前位置：文档之家 › 第二章 信源与信息熵

第二章 信源与信息熵

  • 格式：ppt
  • 大小：448.50 KB
  • 文档页数：26

下载文档原格式

  / 26

合集下载

信息论第二章(2)

信息论第二章(2)
5 联合自信息量：
若有两个消息xi，yj 同时出现，它们所带有的信息量， 称为联合自信息量
I ( xi y j ) log p( xi y j ) (bit)
6 条件自信息量：
事件xi在事件yj给定的条件下的自信息量，称为条件自 信息量
I ( xi y j ) log p( x｜y j ) （bit） ｜ i

i

j
1 H (( X ))＝(p( xy) log p( xy) H XY H X | Y ) X ,Y
平均互信息与各类熵之间关系的集合图（维拉图）表示：
I(X;Y) = H(X) - H(X|Y) = H(Y) - H(Y|X) = H(X)+H(Y)-H(XY) 图中，左边的圆代表 H(XY)= H(X)+H(Y)- I(X;Y) 随机变量X的熵，右 边的圆代表随机变量 Y的熵，两个圆重叠 H(X|Y) 部分是平均互信息 H(Y|X) I(X;Y)。每个圆减去 =H(X)-I(X;Y) =H(Y)-I(X;Y) I(X;Y)后剩余的部分 代表两个条件熵。 I(X;Y)
i 1 i
n
★定义自信息的数学期望为平均自信息量H
n 1 H ( X ) E log p ( xi ) log p ( xi ) (bit/符号) p ( xi ) i 1
(X)，称为信息熵：
★熵的含义：
① 熵是从整个集合的统计特性来考虑的，它从平均意义上来表征 信源的总体特征。 ② 在信源输出后，信息熵H(X)表示每个消息提供的平均信息量；
复习
3 离散信源的数学模型：
x2 x3 ... ... xn X x1 P ( x) P ( x ) P ( x ) P ( x ) ... ... P( x ) 1 2 3 n 要满足的条件： P ( xi ) 0,

《信息论与编码》课件1第2章

《信息论与编码》课件1第2章
I(ai)是一个随机变量并不难理解。因为ai发生可以使收 信者获得大小为I(ai)的自信息，然而在信源未发出消息之 前，收信者不仅对ai是否发生具有不确定性，而且对于能 够获得多少自信息也是不确定的。因此，伴随着X=ai的随 机发生而发生的自信息I(ai)是一个随机变量，并且与随机 变量X具有相同的概率分布, 即自信息I(ai)是一个发生概率 为P(X=ai)
如果消息ai已发生，则该消息发生所含有的自信息定 义为
1
1
I (ai ) log P(ai ) log pi
(2.4)
第2章 离散无记忆信源与信息熵
可以很容易地证明, 自信息的定义满足上面提出的四个
(1) 此自信息的定义是根据消息发生的概率建立的一个 工程定义，而不是根据这个消息对人的实际意义而建立的 定义。这一纯粹技术性的定义仅仅抓住了“信息”一词在
(2) 自信息I(ai) 在消息ai发生之前，自信息I(ai)表示ai发生的不确定性; 在消息ai发生以后，自信息I(ai)表示ai所含有的（或提
第2章 离散无记忆信源与信息熵
(3) 在式(2.4)中关于对数的底未作明确规定。这是 因为对数的底仅仅影响到度量的单位，实际中可根据
如果取对数的底为2，则所得信息量的单位为比特 （bit， binary unit），此时logx用lbx
第2章 离散无记忆信源与信息熵
第2章 离散无记忆信源与信息熵
2.1 离散无记忆信源 2.2 自信息和熵 2.3 熵函数的性质 2.4 联合事件的熵及其关系 2.5 连续信源的信息测度 习题2
第2章 离散无记忆信源与信息熵
信息理论的研究对象是以各类信息的获取、表示、 传输和处理为目的的信息系统。图2-1给出了一个典型 的通信系统物理模型。在这样的通信系统中，一个贯 穿始终的、最基本的问题便是信息，即信源输出的是 信息，在系统中传输的是信息，接收者获得的也是信 息。可见，在信息理论的学习和研究中，首先需要对

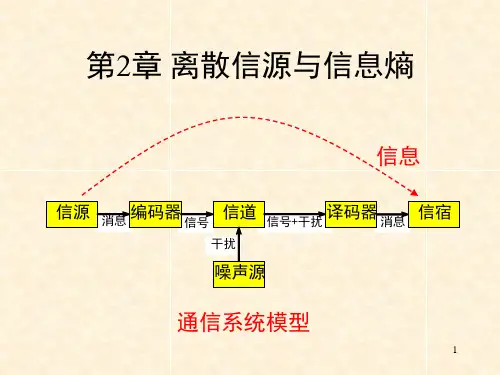
2015秋.信息论.第2章离散信源与信息熵

2015秋.信息论.第2章离散信源与信息熵

第2章离散信源与信息熵信号 信号+干扰 消息干扰消息 信源 编码器 信道 译码器 信宿 噪声源通信系统模型信息2.1 信源的分类和描述信源是信息的发源地，可以是人、生物、机器或其他事物。

信源的输出是包含信息的消息。

消息的形式可以是离散的或连续的。

信源输出为连续信号形式（如语音），可用连续随机变量描述。

连续信源←→模拟通信系统信源输出是离散的消息符号（如书信），可用离散随机变量描述。

离散信源←→数字通信系统离散信源…X i…X j…离散无记忆信源：输出符号Xi Xj之间相互无影响；离散有记忆信源：输出符号Xi Xj之间彼此依存。

3离散信源无记忆有记忆发出单个符号发出符号序列马尔可夫信源非马尔可夫信源y j将一粒棋子随意地放在棋盘中的某列；棋子放置的位置是一个随机事件；可看做一个发出单个符号的离散信源。

x i1212,,...,(),(),...,()m m x x x X P p x p x p x ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦就数学意义来讲，信源就是一个概率场，可用概率空间来描述信源。

由离散随机变量X 表示棋子位置：10()1,()1m i ii p x p x =≤≤=∑i x 其中，代表随机事件的某一结果。

2.2离散信源的信息熵信息的可度量性是信息论建立的基础；香农的信息论用事件发生概率的对数来描述事件的不确定性，得到消息的信息量，建立熵的概念。

2.2.1自信息量–定义2.1 任意随机事件x i 的自信息量定义为：i i i 1(x )log log (x )(x )I P P ==-小概率事件所包含的不确定性大，自信息量大。

大概率事件所包含的不确定性小，自信息量小。

概率为1的确定性事件，自信息量为零。

i i i 1(x )log log (x )(x )I P P ==-信息量的单位与公式中的对数取底有关。

以2为底，单位比特（bit ）；以e 为底，单位奈特（nat ）；()22log log ,log log ln log c a c b b x e x a==⋅–例：棋盘共8列，甲随手一放，将一枚棋子放在了第3列。

4第二章3-熵的计算

4第二章3-熵的计算

q
q
（3）根据概率关系，可以得到联合熵与条件熵的关系： 根据概率关系，可以得到联合熵与条件熵的关系： 联合熵与条件熵的关系
H ( X1 X 2 ) = −∑∑ P(ai a j ) logP(ai a j )
i =1 j =1
q q
q
qபைடு நூலகம்
= −∑∑ P (ai a j ) log( P (ai )P (a j | ai ))
得：
H ( X ) = −∑ P(ai ) logP(ai ) = 1.542( Bit / Symbol)
i =1 3
H ( X 2 / X 1 ) = −∑∑ P(ai a j ) logP(a j / ai ) = 0.87(Bit / Symbol)
i =1 j =1 3
3
3
H ( X 1 X 2 ) = −∑∑ P(ai a j ) logP(ai a j ) = 2.41( Bit / Symbols)
0.71比特/符号
•
从另一角度（来研究信源X的信息熵的近似值） 从另一角度（来研究信源X的信息熵的近似值）：
（ 1 ） 由于信源 X 发出的符号序列中前后两个符号之间有依 由于信源X 赖性，可以先求出在已知前面一个符号X 已知前面一个符号 赖性， 可以先求出在已知前面一个符号Xl＝ai时，信源输出 下一个符号的平均不确定性 的平均不确定性： 下一个符号的平均不确定性：
0.71比特/符号
二维平稳信源X：
条件熵H(X2|X1） 平均符号熵H2(X) 简单信源X符号熵H(X)
H(X2|X1) ≤H2(X) ≤H(X) H(X1X2)=H(X1)+H(X2|X1)=2H2(X)
有记忆平稳信源的联合熵、条件熵、 有记忆平稳信源的联合熵、条件熵、平均符号熵 与无记忆信源熵之间的定量关系。 与无记忆信源熵之间的定量关系。

第2章 信源熵 第1讲 自信息量 与 互信息量

第2章 信源熵 第1讲 自信息量 与 互信息量

余 映 云南大学
17/38
计算举例
• 对于 2n 进制的数字序列, 假设每一符号的出现完 全随机且概率相等，求任一符号的自信息量。 解：设任一码元 xi 出现概率为 p(xi)，根据题意， p(xi) = 1/ 2n I (xi) = –log(1/ 2n) = n (bit) • 事件的自信息量只与其概率有关，而与它的取值 无关。
余 映 云南大学
18/38
信息量与不确定性的关系
• 信源中某一消息发生的不确定性越大，一旦它发生，并为 收信者收到后，消除的不确定性就越大，获得的信息也就 越大。 • 由于各种原因（例如噪声太大），收信者接收到受干扰的 消息后，对某信息发生的不确定性依然存在或者一点也未 消除时，则收信者获得较少的信息或者说一点也没有获得 信息。
余 映 云南大学 21/38
信息量与不确定性的关系
• 自信息量和不确定度的含义又有区别
– 不确定度只与事件的概率有关，是一个统计量，在静 态状态下也存在； – 自信息量只有该随机事件出现时才给出，不出现时不 给出，因此它是一个动态的概念。
余 映 云南大学
22/38
自信息的含义
• 在事件 xi 发生前：表示事件 xi 发生的不确定性。 • 在事件 xi 发生后：表示事件 xi 所提供的信息量。
余 映 云南大学
19/38
信息量与不确定性的关系
• 信息量的直观定义：
收到某消息获得的信息量＝不确定性减少的量 ＝(收到此消息前关于某事件发生的不确定性) －(收到此消息后关于某事件发生的不确定性) • 在无噪声时，通过信道传输，可以完全不失真地收到消息， 收到此消息后关于某事件发生的不确定性完全消除，此项 为零。因此得 收到某消息获得的信息量 ＝收到此消息前关于某事件发生的不确定性 ＝信源输出的某消息中所含有的信息量

第二章_离散信源与信息熵的关系

第二章_离散信源与信息熵的关系

给出，为了书写方便以后写成： 和
y1 , y2 , Y q1 , q2 , ym qm
xn Y y1, y2 , Q q( y ), q( y ), p( xn ) ； 1 2
ym q ( ym )
一. Definition of the self-mutual information:
«信 息 论 基 础 »
第二章：信息的度量与信息熵
( The measure of Information &Entropy) §2. 1 自信息与条件自信息
( self—information & conditional self— information) §2. 2 自互信息与条件自互信息 (self—mutual
p ( x ) 则表达当收端已收到某种消息后, 再统计发端的发送 率： y 概率，所以此条件概率称为后验概率(Posterior Probability) 。
§2. 1 自信息与条件自信息 因此我们说事件 xi 以及它所对应的先验概率P( x )而定
i
义出的自信息 I [ p( xi )] ，所表达的不论事件是否有人接收这 个事件它所固有的不确定度，或者说它所能带来的信息 xi p ( ) 量。而消息事件 y j xi nk 它所对应的条件概率 yj 是在收端接收到已干扰的消息后的后验概率,如果当它为1 xi p ( ) 则属于透明传输；若 y j <1，则属于有扰传输。而当 xi p ( ) 后验概率大于先验概率是 y j > P( xi )，说明事件 y j 发生之后多少也解除了事件 xi 的部分不定度，即得到 了事件 X xi 的部分信息。由于概率越大，不定度越小。 从客观上讲，条件自信息一定不会大于无条件的自信息。 同时也反映出要得知一些条件，原事件的不定度一定会 减少，最坏的情况也不过保持不变，即条件与事件无关。

第二章信源及其信息量

第二章信源及其信息量
X 1 q( X ) 1 3 1 6
2
1 2
3
计算出各事件Байду номын сангаас自信息量列表2-1如下：
消息xi 概率分布q (xi) 自信息量I (xi)
x1 1/3 log 3
x2 1/6 log 6
x3 1/2 log 2
自信息量I(ai)代表两种含义：
1.事件ai发生以前，表示事件发生的先验不确定性
x1 x2 x3 X 3 x0 （3）信源三: 等概信源 q ( X ) 0 . 25 0 . 25 0 . 25 0 . 25 3 熵 H(X3) = -4×0.25 log 0.25 = log4 = 2（比特/符号）
（4）信源四： 信源为确定事件
⑵.平均互信息量
定义xi ∈ X和yj ∈ Y之间的互信息量为I(xi ;yj )，在集合X上对 I(xi ;yj )进行概率加权统计平均，可得I(X;yj)为：
I ( X ; y j ) p xi y j I ( xi ; y j ) p xi y j log
i i




p ( xi y j ) p ( xi )
第2章 离散信源及其信息熵
内容提要： 根据香农对于信息的定义，信息是一个系 统不确定性的度量，尤其在通信系统中， 研究的是信息的处理、传输和存储，所以 对于信息的定量计算是非常重要的。本章 主要研究离散信源下各种信息的定量计算 ，讨论它们的性质和相互关系。
2.1 信源基本分类及其数学模型
在通信系统中，收信者在未收到信息以前， 对信源发出什么样的消息是不确定的，是随机的， 所以可以用随机变量、随机矢量或随机过程来描 述信源输出的消息，或者说用一个样本空间及其 概率测度来描述信源。 不同的信源根据其输出消息的不同的随机性 质进行分类。

2信源与信息熵2

2信源与信息熵2
i 1 j 1 n m
• 联合自信息量
I ( xi y j ) log2 p( xi y j )
• 条件自信息量和联合自信息量同样满足非负 性和单调递减性。 • 关系
I ( xi y j ) log2 p( xi ) p( y j / xi ) I ( xi ) I ( y j / xi ) log2 p( y j ) p( xi / y j ) I ( y j ) I ( xi / y j )
信源熵与自信息量的关系1:定性
• 信源熵用以表征信源的平均不确定性：一个 信源，无论是否输出符号，由于具有特定的 概率统计特性，因此具有特定的熵值。 • 信息量则只有当信源输出的符号被接收者收 到后才有意义。平均自信息量是能够消除信 源不确定性时所需信息的量度，即收到一个 信源符号，全部解除了这个符号的不确定性。 或者说获得这样大的信息量后，信源不确定 性就被消除了。
• 平均自信息量：表示信源中发出每个符号平均所能 提供的信息量。它只与信源中各个符号出现的概率 有关，可以用来表示信源输出信息的总体量度。 • 信源X的平均不确定度：表示总体平均意义上的信 源符号的不确定度(不管是否发出)。数值上等于平 均自信息量。 • 这个平均自信息量的表达式和统计物理学中热熵的 表达式很相似。在统计物理学中，热熵是一个物理 系统杂乱性(无序性)的度量。这在概念上也有相似 之处。所以，可以把信源X的平均不确定度称为 “信源熵”。
例2-5/6
• 例2-5(P19):
• 例2-6(P19): • 由于符号间通常存在关联性，实际信息量往 往远远小于理论值。
例2-7
• 例2-7(P19):二元信源的信息熵。
• 自信息量是针对无条件概率计算的，可以在 数学上进行简单的推广：将无条件概率换为 条件概率或联合概率。

信源及信源熵

信源及信源熵

2.1 单符号离散信源
数学模型：
X P( X
)
x1 p( x1 )
0 p(xi ) 1,
xi p(xi )
xn
p(
xn
)
n
p(xi ) 1
i 1
单符号离散信源
常用旳概率论旳基本概念和性质
先验概率、联合概率、条件概率及其相互关系：
（1）0 p(xi )、p( y j ) 、p( y j / xi ) 、p(xi / y j ) 、p(xi y j ) 1
离散无记忆信源旳N次扩展信源旳数学模 型是信源空间X旳N重空间。
信源旳描述与分类
有记忆信源
一般情况下，信源在不同步刻发出旳符号之间是相互依
赖旳。即信源输出旳平稳随机序列X中，各随机变量Xi
之间是有依赖旳。如：在中文构成旳中文序列中，只有 根据中文旳语法、习常用语、修辞制约和体现实际意义 旳制约所构成旳中文序列才是有意义旳中文句子或文章。 所以，在中文序列中前后文字旳出现是有依赖旳，不能 以为是彼此不有关旳。这种信源称为有记忆信源。
因为每个随机变量UL有n种取值，则U 有n L
种可能取值。
信源旳描述与分类
离散序列信源
例：最简朴L=3旳三位PCM信源：这 时L=3, n=2, 即i={0,1}，则有：
U 3 u 000 u 001
p(u)
p03
p02 p1
u 111
p13
当p0 p1 12时 000, 001, 010, ,111
假如上述条件概率与时间起点i无关，即信源 输出旳符号序列可看成为时齐马尔可夫链， 则此信源称为时齐马尔可信源。
信源旳描述与分类
离散序列信源总结
离散序列信源

第二章信源与信息熵

第二章信源与信息熵
j i, j
I ( X ; Y ) p( yj ) I ( X ; yj ) p( xiyj ) log
p( xi / yj ) p( xi )
I(X;Y)=H(X)-H(X/Y)；I(Y;X)=H(Y)-H(Y/X)=I(X;Y)．
• 3.疑义度或损失熵
条件熵H(X/Y)信道上的干扰和噪声所造成的对信源符号x的平均不确定度．
X 0 P p
二元信源熵为
1 q
H (X ) p log p q log q p log p (1 p ) log(1 p ) H ( p)
信源信息熵H(X)是概率p的函数，通常用 H(p)表示。函数曲线如图
i i
I ( xi) 0; P( xi) 0;0 p( xi) 1
H(X ) 0
• 2.信源熵：表征信源的平均不确定度． 3.平均自信息：平均每个信源符号所能提供的信息 量.大小与信源熵相同.
• 例2.2.3二元信源是离散信源的一个特例。该信源X输出符号只 有两个，设为0和1。输出符号发生的概率分别为p和q，p+q=1。 即信源的概率空间为可得二元信源熵为
2.概率空间
一个离散信源发出的各个符号消息的集合 例如：
X＝｛x1，x2，…，xn｝
它们的概率分别为 P＝｛p(x1)，p(x2)，…，p(xn)｝ p(xi)称为符号xi的先验概率。 把他们写到一起就是概率空间:
X x1 P p( x1)
x2
n
...xn
xiyi 所包含的不确定度在数值上也等于它们的自信息量。
4.条件自信息量:当二者不独立 在给定y条件下，随机事件x所包含的不确定度在数值 上与条件自信息量相同，但两者含义不同。

信源及其熵

信源及其熵

如果被告知摸出的是红球，那么获得的信息量是：
I (a1) ＝－log p(a1) ＝－log0.8= 0.32 （比特） 如被告知摸出来的是白球，所获得的信息量应为：
I (a2) ＝ －log p(a2) ＝ －log0.2 = 2.32 （比特） 平均摸取一次所能获得的信息量为 ：
H(X)= p(a1) I (a1) + p(a2) I (a2) =0.72（比特/符号）
二. 信息熵
对一个信源发出不同的消息所含有的信息量也不同。
所以自信息I(ai)是一个随机变量，不能用它来作为
整个信源的信息测度
定义自信息的数学期望为平均自信息量Hr(X)，称为 信息熵：

Hr (X ) Elogr
1 p(ai
)



q i 1
p(ai
) log r
... ...
qN P( qN
)
N
其中，P( i ) P(aik ), ik (1,2,..., q) k 1
有记忆信源
信源在不同时刻发出的符号之间是相互依赖的， 即信源输出的平稳随机序列X中，各随机变量Xi之 间相互依赖。
例：汉字组成的中文序列中，只有根据中文的语法、
P(X) P( X1X 2 X N ) P( Xi )
i 1
设各随机变量Xi取值同样符号集A:{a1,a2,…,aq}，则
N
P(x i ) P(ai1ai2 ,..., aiN ) P(aik ), ik (1,2,..., q)
k 1
N维随机矢量的一个取
由于信源发送什么消息预先是不可知的，只能 用概率空间来描述信源
2.1 信源的数学模型及分类

第 2 章 信源与信息熵

第 2 章 信源与信息熵
• 布袋摸球实验，如先取一球记下颜色后不放回布袋 再取另一球，则组成消息的两个球的颜色之间有关 联性。
一般情况下，信源在不同时刻发出的符号之间是相 互依赖的，即信源输出的平稳随机序列 X 中，各随机变 量 X l 之间是有依赖的。
例如在汉字组成的中文消息中，前后文字的出现是 有依赖的，不能认为是彼此不相关的，放在L维随机矢 量的联合概率分布中，就必然要引入条件概率分布来说 明它们之间的关联。这种信源即有记忆信源。
第 2 章 信源与信息熵
2.1 信源的描述与分类 2.2 离散信源熵和互信息 2.3 离散序列信源的熵 2.4 连续信源的熵和互信息 2.5 冗余度
概率论基础
无条件概率、条件概率、联合概率的性质和关系
(1) 0 ≤ p( x i )， p( y j )， p( y j | x i )， p( x i | y j )， p( x i y j )≤1
设信源输出的Ｌ维随机序列（随机矢量）为
序列中的随机变量 X l ∈ A ( l =1, 2, …, L ) 信源的概率空间：
??
?
2010-3-30
例：
∵ 序列无记忆
若为平稳随机序列，则
L l=1
这种由信源 X 输出的 L 长随机序列 X 所描述的信 源叫做离散无记忆信源 X 的 L 次扩展信源。
(2)
n
m
n
i
=
p
1
(
x
i
)
=
1
,
∑
j=
p
1
(
y
j
)
=
1
,
∑p
i=1
(
x
i
|
y
j
)

信息论基础第2章

信息论基础第2章

若
U
(t
,

)
a.e.

0，

a.e.
当t T /2时
U (t,) U (t,), 当 t T / 2时
这里，U (t, )为一周期性随机过程；
“a.e.”为almost everywhere, 几乎处处含义下相等（收敛）
2019/10/14
P.10
常用的展开式 (续）：
类似于周期性确知信号，在时域内可做下列付氏级数展开：当 t T / 2 时，
b
a R(t1t2 ) (t2 )dt2 (t1 )
下面简要介绍积分方程的概念，所谓积分方程，是指未知函数在积 分号内的方程式，我们这里讨论的是最常见的线性积分方程。即一 般积分方程可写为：
b
a(x)(x) f (x) a K (x, )( )d
2019/10/14
对消息序列信源有：

UL
pu


U u1U unL p(u1) p(unL )

2019/10/14
P.5
2）实际信源 （续）
例：最简单L=3的三位PCM信源：这时L=3, n=2, 即i={0,1}，则有：

U3 p(u)


U
000,U p03 ,
2019/10/14
P.14
常用的展开式 (续）：


U
(t
,

)
a.e


ai ()i (t)
则

i 1
ቤተ መጻሕፍቲ ባይዱi
(
)
a.e

b
a U (t,)i (t)dt

第二章信源信息熵(第二讲)

第二章信源信息熵(第二讲)

第二章 信源与信息熵（第二讲）（2课时）主要内容：（1）信源的描述（2）信源的分类 重点：信源的分类，马尔可夫信源。

难点：信源的描述，马尔可夫信源。

作业：2.1, 2.2, 2.3说明：本堂课推导内容较多，枯燥平淡，不易激发学生兴趣，要注意多讨论用途。

另外，注意，解题方法。

多加一些内容丰富知识和理解。

2．1 信源的描述与分类在通信系统中收信者在未收到消息以前对信源发出什么消息是不确定的，是随机的，所以可用随机变量、随机序列或随机过程来描述信源输出的消息，或者说用一个样本空间及其概率测度——概率空间来描述信源。

信源：产生随机变量、随机序列和随机过程的源。

信源的基本特性：具有随机不确定性。

信源的分类离散信源：文字、数据、电报——随机序列 连续信源：话音、图像——随机过程离散信源：输出在时间和幅度上都是离散分布的消息。

消息数是有限的或可数的，且每次只输出其中一个消息，即两两不相容。

发出单个符号的无记忆信源离散无记忆信源： 发出符号序列的无记忆信源离散信源离散有记忆信源： 发出符号序列的有记忆信源发出符号序列的马尔可夫信源 概率论基础：无条件概率，条件概率和联合概率的性质和关系： 非负性0()()(/)(/)()1i j j i i j i j p x p y p y x p x y p x y ≤≤，，，， 完备性111111()1,()1,(/)1,(/)1,()1n m nijiji j i mm nji i j j j i p x p y p x y p yx p x y ===========∑∑∑∑∑∑11()(),()()n mijjijii j p x y p y p x y p x ====∑∑联合概率()()(/)()(/)()()()(/)()(/)()i j i j i j i j i j i j j i j i j i p x y p x p y x p y p x y X Y p x y p x p y p y x p y p x y p x =====当与相互独立时，，贝叶斯公式11()()(/)(/)()()i j i j i j j i nmijiji j p x y p x y p x y p y x p x y p x y ====∑∑，2.1.1 无记忆信源：例如扔骰子，每次试验结果必然是1～6点中的某一个面朝上。

第2章 -1信源与信息熵1【单符号离散信源】

第2章 -1信源与信息熵1【单符号离散信源】
y信道传输的平均信息量有扰离散信道结论因信道有扰而产生的平均信息量称噪声熵反映了信道中噪声源的不确定度唯一地确定信道噪声所需要的平均信息量hyy的先验不确定度hyx发出x后关于y的后验不确定度在已知x的条件下对于随机变量y存在的平均不确定度发出x前后y不确定度的平均减少量可看作在有扰离散信道上传递消息时唯一地确定接收符号y所需要的平均信息量hy减去当信源发出符号x为已知时需要确定接收符号y所需要的平均信息量hyx
1. 离散信源熵 (平均自信息量/无条件熵)
[定义] 自信息量的数学期望为信源的平均信息量，记为：H（X）。
H(X)=E[I(xi)]= –∑p(xi)log2 p(xi)
——平均不确定度的度量、体现: 总体平均
[单位]
二进制:bit/(信源)符号，或bit/(信源)序列 [含义]信息熵具有以下三方面物理含义： ⑴ 表示信源输出前，信源的平均不确定性 ⑵ 表示信源输出后，每个符号所携带的平均信息量 ⑶ 表示信源的的随机性（不同的信源有不同的统计特性） 信息熵的意义： 信源的信息熵是从整个信源的统计特性来考虑的。它是从 平均意义上来表征信源的总体特性的。对于某特定的信源， 其信息熵只有一个。不同的信源因统计特性不同，其信息熵 也不同。
√
（后续章节）
一、概述
⒈ 信息的一般概念 一个人获得消息→消除不确定性→获得信息。 ⒉ 信息度量的定性分析 事件发生的概率越大，不确定性越小，该事件 包含的信息量越小； 事件发生的概率越小，不确定性越大，该事件 包含的信息量越大； 如果一个事件发生的概率为1，那么它包含的 信息量为0； 两个相互独立事件所提供的信息量应等于它们 各自提供的信息量之和。
2.2.1
自信息量
1.自信息量 [定义] 若信源发出符号xi，由于信道无干扰，收到的就

第二章信源和信息熵

第二章信源和信息熵
即：收信者所获得的信息量应等于信息传输前 后不确定性的减少的量。
例：设一条电线上串联8个灯泡，且损坏的可 能性为等概，若仅有一个坏灯泡，须获知多少 信息量才可确认？ 第二章信源和信息熵
第二章 信源和信息熵
例解：
测量前，P1(x)＝1/8，存在不确定性： I(P1(x))＝log8＝3bit
第一次测量获得信息量： 第二次测量获得信息量： 第三次测量获得信息量： 每次测量获得1bit信息量，需三次测量可确定坏灯泡
第二章信源和信息熵
第二章 信源和信息熵
（2）信源发出的符号间彼此是否独立： 无记忆信源：随机矢量的各分量相互独立 有记忆信源：随机矢量的各分量不相互独立
表述有记忆信源比无记忆信源困难的多，实际中，信 源发出的符号往往只与前若干符号的依赖关系强，与 更前面的符号依赖关系弱，这类信源可用马尔可夫信 源表示。 不同统计特性的信源可用随机变量、随机矢量以及随 机过程描述其输出的消息。
自信息的两种含义：信源输出消息x1之前，自信息 I(x1)是关于x1发生地不确定性的度量；而在信源输出 消息x1后，自信息I(x第1二)章表信源示和信x息1熵所含有的信息量。
第二章 信源和信息熵
注意：信息单位比特（表示以2为底的对数） 与计算机术语中的比特（表示二进制数的位） 的意义是不同的。
▪收到某消息获得的信息量＝收到此消息前关于 某事件发生的不确定性－收到此消息后关于某 事件发生的不确定性
例：扔一颗质地均匀的正方体骰子，研究其下落后， 朝上一面的点数。每次试验结果必然是1点、2点、3点、 4点、5点、6点中的某一个面朝上。每次试验只随机出 现其中一种消息，不可能出现这个集合以外的消息， 考察此事件信源的数学模型。
解：数学模型为：
且满足：

第2章 信源与信息熵(3)

第2章 信源与信息熵(3)
平均互信息的物理意义
互信息量实质是通信中实际传送的有用信息量。 互信息量实质是通信中实际传送的有用信息量。 显然，互信息越大越好， 显然，互信息越大越好，极限是 H ( X ) 能否将发送端X的信息量全部传送？ 能否将发送端 的信息量全部传送？ 的信息量全部传送 要求通信过程中没有信息量损失，而实际传输过程中， 要求通信过程中没有信息量损失，而实际传输过程中，信 道中的噪声会淹没一定的信息，即信息有损失。 道中的噪声会淹没一定的信息，即信息有损失。 通信过程中，信息量损失了多少？ 通信过程中，信息量损失了多少？ X的信息量减去实际传输的信息量，即 的信息量减去实际传输的信息量， 的信息量减去实际传输的信息量
I ( X ; Y ) = I (Y ; X )
理论证明略（与单符号互信息相同）。 理论证明略（与单符号互信息相同）。
②非负性
I ( X ;Y ) ≥ 0 I ( X ;Y ) ≤ H ( X )
理论证明参考周荫清编的信息理论基础， 理论证明参考周荫清编的信息理论基础，直观理解
③极值性
直观理解！！ 直观理解！！
p ( xi | y j ) p ( xi )
= log 2
p ( xi ) p ( y j )
p ( xi , y j )
2 .2 离散信源熵和互信息
三、互信息
1、单符号之间的互信息量 性质： ③ 性质： 证明： 证明：
I ( xi ; y j ) = ( xi , y j )
p ( xi ) p ( y j )
p ( xi , y j )
= log 2
p ( xi ) p ( y j )
2 .2 离散信源熵和互信息
三、互信息
2、平均互信息 定义： 指单符号互信息量在X集合和 集合上的统计平均值。 定义： 指单符号互信息量在 集合和Y集合上的统计平均值。 集合和 集合上的统计平均值

信息论与编码曹雪虹著第二章

信息论与编码曹雪虹著第二章

16
2.1信源描述与分类

单符号无记忆信源的性质


它是最简单也是最基本的信源，是组成实际信源的基本 单元。 当信源给定，其相应的概率空间就已给定；反之，如果 概率空间给定，这就表示相应的信源已给定。所以，概 率空间能表征这离散信源的统计特性，因此有时也把这 个概率空间称为信源空间。 这些信源可能输出的消息数是有限的或可数的，而且每 次只输出其中一个消息。因此，可以用一个离散型随机 变量X来描述这个信源输出的消息。这个随机变量X的样 本空间就是符号集A；而X的概率分布就是各消息出现的 先验概率，信源的概率空间必定是一个完备集。
28
2.1信源描述与分类
18
2.1信源描述与分类
最简单L=2的情况，其概率分布为：
X (a1 , a1 ) (a1 , a2 ) P p(a , a ) p(a , a ) 1 1 1 2 (an , an ) p(an , an )
其中： 且
p(ai , a j ) 0, p(ai , a j ) 1
11
2.1信源描述与分类
（3）连续信源:输出消息取值是无限的，即可能出现的消
息数是不可数的无限值。 其数学模型为连续型的概率空间
U (a, b) p(u ) p(u )
u U (, ), p(u)为概率密度函数
b
且概率密度分布函数P(u)≥0, p (u )du 1 。符号集 a 中的取值是介于（a,b）之间连续值， P(u)概率密度分 布函数。
12
2.1信源描述与分类

例如：
一个袋中有很多干电池，随机摸出一个，测其电压值 作为输出符号，该信源每次输出一个符号，但符号取 值在[0，1.5]之间的所有实数，可用连续型随机变量 U来描述，连续信源的概率空间为

信息论导论-第2章_20131

信息论导论-第2章_20131
信息论导论-第2章
14
互信息量(简述)
1、互信息量的定义 2、互信息量的性质
信息论导论-第2章
15
互信息量

两个随机事件X和Y，分别取值于信源、信宿 发出的离散消息集合 a

信源X的数学模型
a2 , p (a2 ),
n i =1
X a1 , = P( X ) p (a1 ),
∴ I ( x1 ) = −lbP ( x1 ) = −lb(1/ 2) = lb 2 = 1(bit ) −lbP ( x2 ) = −lb(1/ 4) = I ( x2 ) = lb 4 = 2(bit ) I ( x3 ) = −lbP ( x3 ) = −lb(1/ 8) = lb8 = 3(bit ) I ( x4 ) = −lbP ( x4 ) = −lb(1/ 8) = lb8 = 3(bit )
0
logxP(x) P(x) 1
③I(xi)是P(xi)的单调递减函数。
信息论导论-第2章
11
一、自信息量

证明：
P( xi ) ∈ [0,1] dI ( xi ) d ∴ = [−lbP( xi )] dP( xi ) dP( xi ) −lbe d = −lbe <0 [ln P ( xi )] = dP( xi ) P( xi )
n
i =1
k = 1, 2, , n
信息论导论-第2章
21
二、单符号离散信源的信息熵
n n ∂ 即 {−∑ P( xi )lbP( xi ) + λ[∑ P( xi ) − 1]} ∂P( xk ) i 1 = i 1 =
= −[lbe + lbP( xk )] + λ = 0,

第2章 信源与信息熵(4)

第2章 信源与信息熵(4)
2、性质：
I X ; Y p xi p y j | xi log 2
i, j
px p y
i i
p y j | xi
j
/ xi
当p(xi)一定时，互信息是p(yj/xi)的U型函数，存在极小值。
信息率失真函数的理论基础。
当p(yj/xi)一定时，互信息是p(xi)的n型函数，存在极大值。
H（X/Y）
损失熵（疑义度）
发送端 H（X）
I（X；Y）
H（Y） 接收端
H(Y/X) 噪声熵
2 .2 离散信源熵和互信息
四、熵的性质
1.非负性： H ( X ) 0
例
2 .2 离散信源熵和互信息
四、熵的性质
2 对称性：
例
x1 X P 1 3
x2 1 2
四、熵的性质
5 最大熵定理： 离散无记忆信源输出M个不同消息符号，当且仅当各符 号出现的概率相等时，信源熵最大。
直观理解：
x1 X P 1 3
x2 1 3
x3 1 3
x1 X P 1 2
x2 1 4
x3 1 4
③


I xi ; y j I xi I y j I xi , y j
上节内容回顾
二、平均互信息
1、定义 指单符号互信息I(xi,yj)在X和Y集合上的统计平均值。
I X ; Y p xi , y j log 2
i, j
p xi | y j p xi
求：信源熵、二次扩展信源序列熵和平均符号熵
X2信源 的元素 对应的 消息序列
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
发出符号序列的无记忆信源
——每次发出1组含2个以上符号的符号序列来代表一 个消息的信源，且各符号之间没有统计关联性。
需要用随机序列（或随机矢量） X =(X1, X2,…, Xl, …, XL)来描 述信源输出的消息，用联合概率分布p(X1, X2,…, Xl, …, XL)来表 示信源特性。 p (X 1 ) p ( X 2 ) … p (X l ) … p (X L ) 若该信源输出的每个符号是统计独立的，且具有相同的概率 空间，则该信源是离散平稳无记忆信源，亦称为独立同分布 （independently identical distribution，i. i. d.）信源。
发出单个符号的无记忆信源
可用一个离散型随机变量X来描述这个信源输出的消息。 随机变量X的样本空间就是符号集：
A {a1 , a2 ,
X的概率分布为：
, an }
p(ai)是X =ai的先验概率
P { p(a1 ), p(a2 ),
, p(an )}
单符号离散信源的数学模型—概率空间
X a1 P p(a ) 1
——每次发出1组含2个以上符号的符号序列来代表一 个消息的信源。
需要用随机序列（或随机矢量） X =(X1, X2,…, Xl, …, XL)来描 述信源输出的消息，用联合概率分布p(X1, X2,…, Xl, …, XL)来表 示信源特性。 当L=2时，此时信源为X =(X1, X2) ，其概率空间为：
X (a1 , a1 ) P p(a , a ) 1 1
(a1 , a2 ) p(a1 , a2 )
n i , j 1 i j
(an , an ) p(an , an )
p(ai , a j ) 0
p(a , a ) 1
2.1.1 无记忆信源Fra bibliotek---信源的基本特性：具有随机不确定性。
2.1 信源的描述和分类
信源的分类
按照信源发出的消息在时间上和幅度上的分布情况可 将信源分成离散信源和连续信源两大类 离散信源: 文字、数据、电报—随机序列
信源
{ 连续信源: 话音、图像 随机过程
—
连续信源
指发出在时间和幅度上都是连续分布的连续消息 （模拟消息）的信源，如语言、图像、图形等都是 连续消息。
离散信源
指发出在时间和幅度上都是离散分布的离散消息的 信源，如文字、数字、数据等符号都是离散消息。
离散 离散无记忆信源 信源 离散有记忆信源
{
{发出符号序列的无记忆信源 发出符号序列的有记忆信源 { 发出符号序列的马尔可夫信源
发出单个符号的无记忆信源
2.1.1 无记忆信源
离散无记忆信源
所发出的各个符号是相互独立的，发出的符号序列 中的各个符号之间没有统计关联性，各个符号的出 现概率是它自身的先验概率。
发出单个符号的无记忆信源
——指信源每次只发出一个符号代表一个消息， 消息的数量是有限的。
例如扔骰子，每次实验结果必然是1～6点中的某一个面 朝上。每次实验的结果不随实验次数变化，也不与先前 的实验结果相关，因而该信源是单符号无记忆信源。可 用一个离散型随机变量X来描述这个信源输出的消息。
2.1.1 无记忆信源
p( X 1 , X 2 ,
Xl ,
X L ) p( X l ) [ p( X )]L
l 1
L
2.1.2 有记忆信源
发出符号序列的有记忆信源
——每次发出1组含2个以上符号的符号序列来代表一 个消息的信源，且各符号之间是相互依赖的。
此时的联合概率表示就需要引入条件概率来反映信源发出的 符号序列中各个符号之间的记忆特征：
2.1 信源的描述和分类
离散信源
指发出在时间和幅度上都是离散分布的离散消息的 信源，如文字、数字、数据等符号都是离散消息。
离散 离散无记忆信源 信源 离散有记忆信源
{
{发出符号序列的无记忆信源 发出符号序列的有记忆信源 { 发出符号序列的马尔可夫信源
发出单个符号的无记忆信源
2.1 信源的描述和分类
第二章 信源与信息熵
2.1 信源的描述和分类
信源 ---产生消息(符号)、消息序列和连续消息的来源。 ---产生随机变量、随机序列和随机过程的源。
在通信系统中收信者在未收到消息以前对信源发出 什么消息是不确定的,是随机的，所以可用随机变量、 随机序列或随机过程来描述信源输出的消息,或者说 用一个样本空间及其概率测度—概率空间来描述信源。
或
R p ( x) X
px ( x) 0,

b
a
pX ( x)dx 1 或

R
pX ( x)dx 1
解释：信源输出的消息也是单符号，但消息的数量是无限的。 符号集A的取值是介于a和b之间的一个连续值，或者取值 为实数集R等。
2.1.1 无记忆信源
发出符号序列的信源
a2 p(a2 )
an p(an )
p(ai ) 0
p (a ) 1
i 1 i
n
2.1.1 无记忆信源
连续信源
——输出在时间和幅度上都是连续分布的消息 。
单符号连续无记忆信源
概率空间： p ( x ) P X
X ( a, b)
——输出信号在幅度和时间上都是连续的。
某一时刻的取值是随机的，通常用随机过程 {x(t )} 来描述。
通信系统中的信号都是平稳遍历的随机过程。
对于确知的随机波形信号，可以进行采样、量化，使其变换 成时间和幅度都是离散的离散信号。
根据时域采样定理，一个频率受限（0 f fm）、时间受限 （0 t tB ）的任何随机波形完全可以由 2tB fm 个采样值来描述。 一般情况下，这些采样值之间是线性相关的，所以随机波形信 源也是一种有记忆信源。
p( x1 , x2 , x3 ,
xL ) x1 ) p( x1 , x2 , xL 1 ) x1 ) p( x1 , x2 , xL 2 ) x1 ) p( xL 1 | xL 2 ,
p( xL | xL 1 , p( xL | xL 1 ,
2.1.2 有记忆信源
随机波形信源