SPSS统计分析软件实例分析

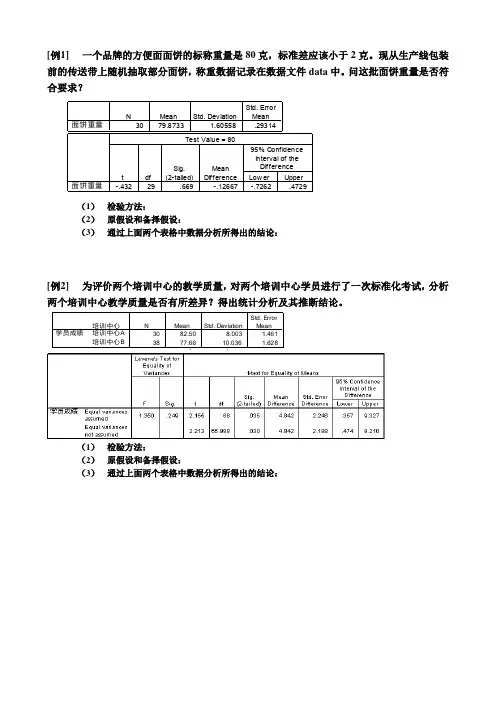
[例1]一个品牌的方便面面饼的标称重量是80克，标准差应该小于2克。

现从生产线包装前的传送带上随机抽取部分面饼，称重数据记录在数据文件data中。

问这批面饼重量是否符（1）检验方法：（2）原假设和备择假设：（3）通过上面两个表格中数据分析所得出的结论：[例2]为评价两个培训中心的教学质量，对两个培训中心学员进行了一次标准化考试，分析（1）检验方法：（2）原假设和备择假设：（3）通过上面两个表格中数据分析所得出的结论：[例3]某康体中心的减肥班学员入班时的体重数据和减肥训练一个月后的体重数据记录在数据文件data中，试分析一个月的训练是否有效。

（1）检验方法：（2）原假设和备择假设：（3）通过上面两个表格中数据分析所得出的结论：（4）可以绘制_________图，直观显示前后体重的变化趋势。

[例4]为了解非计算机专业对计算机课程教学的意见，在金融系和统计系本科生中进行了一次抽样调查，得到了390名学生的调查数据。

试据此推断两系本科生对计算机课程教学的意见是否一致。

（1）检验方法：（2）原假设和备择假设：（3）通过上面两个表格中数据分析所得出的结论：（4）可以通过_________图直观地比较不同系别的满意度。

[例5]为了试验某种减肥药物的性能，测量11个人在服用该药以前以及服用该药1个月后、2个月后、3个月后的体重。

那么请问在这4个时期，11个人的体重有无发生显著的变化？（1）通过上面输出结果表格，可判断使用的检验方法：（2）原假设和备择假设：（3）结论：[例6]数据文件“Employee data.sav”记录了474名职工的基本信息（1）绘制复式条形图来表示不同性别的雇佣类别情况；（2）对起始薪金绘制茎叶图，说明图中信息；（3）通过箱图描绘不同雇佣类别的职工当前薪金情况，得出结论；（4）分析起始薪金的确定与什么因素有关，说明下面两表分别用的分析方法，并比较两表的结果。

控制变量起始薪金教育水平（年）雇佣类别 & 经验（以月计）起始薪金相关性 1.000 .461显著性（双侧）. .000df 0 470 教育水平（年）相关性.461 1.000显著性（双侧）.000 .df 470 0[例7]考察数码相机成像元器件像素数是否会对产品销量产生显著影响（设显著性水平α=0.05）。

SPSS统计分析实例讲解引言在社会科学研究和商业分析中，统计分析是一个重要的工具，可以帮助我们理解数据背后的规律和关系。

SPSS（Statistical Package for the Social Sciences）是一种常用的统计分析软件，具有强大的数据处理和分析功能。

本文将通过一个实例，介绍如何使用SPSS进行统计分析。

实例背景假设我们是一家快餐连锁店的运营经理，我们想了解不同分店的顾客满意度与相关因素之间的关系。

为了实现这个目标，我们收集了以下三个变量的数据：1.顾客满意度：用于评估顾客对快餐店的满意程度，以1-10的等级进行评分。

2.服务质量：用于评估不同分店提供的服务质量，以1-5的等级进行评分。

3.价格水平：用于评估不同分店的价格水平，以1-5的等级进行评分。

我们希望通过分析这些数据，了解不同分店的服务质量和价格水平对顾客满意度的影响。

数据分析步骤步骤一：载入数据首先，我们需要将收集到的数据导入SPSS软件进行分析。

打开SPSS软件，点击菜单栏中的文件（File），选择导入（Import），然后选择收集到的数据文件进行导入。

步骤二：数据清洗在进行数据分析之前，我们需要对数据进行清洗，以确保数据的准确性和一致性。

一般来说，数据清洗包括以下几个方面的处理：•去除缺失值：检查数据中是否存在缺失值，如果有，可以删除含有缺失值的观测样本或者使用合适的方法进行填补。

•标准化变量：如果不同变量的测量单位和量级存在差异，可以对变量进行标准化处理，使得它们具有可比性。

•检查异常值：检查数据中是否存在异常值，如果有，可以进行修正或者删除。

•数据转换：对于非正态分布的变量，可以进行对数变换或者其他适当的转换，以满足统计分析的前提条件。

步骤三：描述性统计分析描述性统计分析是对数据的整体情况进行概括和描述的统计方法。

通过描述性统计分析，我们可以了解数据的中心趋势、离散程度和分布形态等。

在SPSS中，可以使用以下方法进行描述性统计分析：•平均值：计算变量的平均值，以反映数据的中心趋势。

SPSS概览数据分析实例详解SPSS（Statistical Package for the Social Sciences）是一种统计分析软件，被广泛应用于各个领域的数据分析。

在SPSS中，数据分析可以通过不同的统计方法、图表和输出来进行。

下面是一个关于如何使用SPSS进行数据分析的实例详解。

假设我们有一个关于一所大学学生的调查数据集，包括以下信息：性别、年龄、所在学院、GPA（平均绩点）、社交媒体使用时间和每周学习时间等变量。

我们想要使用SPSS对这些数据进行一些分析，以了解学生的特征与他们的学习表现之间是否存在关联。

首先，我们需要导入数据集到SPSS中。

在SPSS中，你可以点击“File”菜单，选择“Open”选项来导入数据集（通常是一个Excel或CSV文件）。

导入后，你将在SPSS的“Data Editor”窗口中看到你的数据。

然后，我们可以开始进行数据的概览。

在SPSS中，你可以使用“Frequencies”命令来查看变量的分布情况。

点击“Analyze”菜单，选择“Descriptive Statistics”选项，然后点击“Frequencies”选项。

在弹出的对话框中，你需要选择你想要分析的变量。

比如，你可以选择年龄、GPA和每周学习时间这三个变量。

点击“OK”按钮后，SPSS会生成一个报告，展示这些变量的频数、百分比和其他统计信息。

接下来，我们可以使用SPSS的图表功能来可视化数据。

在SPSS中，你可以点击“Graphs”菜单，选择“Chart Builder”选项来创建图表。

在“Chart Builder”窗口中，你可以选择不同的图表类型，例如柱状图、散点图或箱线图。

比如，你可以选择创建一个散点图来展示GPA与每周学习时间之间的关系。

然后，你需要将变量拖动到图表的相应位置上。

比如，你可以将GPA拖动到纵坐标（Y轴）上，将每周学习时间拖动到横坐标（X轴）上。

点击“OK”按钮后，SPSS会生成一个散点图，展示这两个变量之间的关系。

SPSS相关分析实例操作步骤-SPSS做相关分析SPSS（Statistical Product and Service Solutions）是目前在工业、商业、学术研究等领域中广泛应用的统计学软件包之一。

Correlation是SPSS的一个功能模块，可以用于分析两个或多个变量之间的关系。

下面是SPSS进行相关分析的具体步骤：1. 打开SPSS软件，选择“变量视图”（Variable View），输入相关的变量名，包括数字型变量和分类变量。

2. 进入“数据视图”（Data View），输入数据，并保存数据集。

3. 打开菜单栏中的“分析”（Analyze），选择“相关”（Correlate），再选择“双变量”（Bivariate）。

4. 在双变量窗口中，选择包含需要分析的变量的变量名，并将其移至右侧窗口中的变量框（Variables）。

5. 如果需要控制其他变量的影响，可以选择“控制变量”（Options）。

6. 点击“确定”（OK）按钮后，SPSS将输出结果，并将其显示在输出窗口中。

相关系数（Correlation Coefficient）介于-1和1之间，可以用来衡量两个变量之间的线性关系的强度。

7. 如果需要对结果进行图形化展示，可以选择“图”（Plots），并选择适当的图形类型。

需要注意的是，进行相关分析时需要确保变量之间存在线性关系。

如果变量之间存在非线性关系，建议使用其他统计方法进行分析。

同时，SPSS进行相关分析的结果只能描述变量之间的关系，不能用于说明因果关系。

以上是SPSS做相关分析的具体步骤，希望能对大家进行SPSS 数据分析有所帮助。

SPSS多元线性回归分析实例操作步骤多元线性回归是一种常用的统计分析方法，用于探究多个自变量对因变量的影响程度。

SPSS（Statistical Package for the Social Sciences）是一款常用的统计软件，可以进行多元线性回归分析，并提供了简便易用的操作界面。

本文将介绍SPSS中进行多元线性回归分析的实例操作步骤，帮助您快速掌握该分析方法的使用。

步骤一：准备数据在进行多元线性回归分析之前，首先需要准备好相关的数据。

数据应包含一个或多个自变量和一个因变量，以便进行回归分析。

数据可以来自实验、调查或其他来源，但应确保数据的质量和可靠性。

步骤二：导入数据在SPSS软件中，打开或创建一个新的数据集，然后将准备好的数据导入到数据集中。

可以通过导入Excel、CSV等格式的文件或手动输入数据的方式进行数据导入。

确保数据被正确地导入到SPSS中，并正确地显示在数据集的各个变量列中。

步骤三：进行多元线性回归分析在SPSS软件中，通过依次点击"分析"-"回归"-"线性"，打开线性回归分析对话框。

在对话框中，将因变量和自变量移入相应的输入框中。

可以使用鼠标拖拽或双击变量名称来快速进行变量的移动。

步骤四：设置分析选项在线性回归分析对话框中，可以设置一些分析选项，以满足具体的分析需求。

例如，可以选择是否计算标准化回归权重、残差和预测值，并选择是否进行方差分析和共线性统计检验等。

根据需要，适当调整这些选项。

步骤五：获取多元线性回归分析结果点击对话框中的"确定"按钮后，SPSS将自动进行多元线性回归分析，并生成相应的分析结果。

结果包括回归系数、显著性检验、残差统计和模型拟合度等信息，这些信息可以帮助我们理解自变量对因变量的贡献情况和模型的拟合程度。

步骤六：解读多元线性回归分析结果在获取多元线性回归分析结果之后，需要对结果进行解读，以得出准确的结论。

SPSS统计分析_实例宝典SPSS（Statistical Package for the Social Sciences）是一种统计分析软件，广泛应用于社科、商科、医学等领域的数据分析和统计研究中。

SPSS提供了丰富的统计方法和分析工具，能够对数据进行描述性统计、假设检验、回归分析、方差分析、因子分析等等统计分析。

下面以一个实例宝典来介绍SPSS的使用。

假设我们有一份调查数据，包括了一些样本的年龄、性别、收入等变量。

我们希望利用SPSS对这份数据进行分析，得出一些有关样本特征的结论。

首先，我们需要导入数据。

在SPSS的菜单栏中，选择"File"，然后点击"Open"，找到我们保存的数据文件，并进行导入。

导入完成后，我们可以在数据视图中看到导入的数据，包括了各个变量的取值。

接下来，我们可以对数据进行描述性统计分析。

在菜单栏中选择"Analyze"，然后点击"Descriptive Statistics"，再选择"Frequencies"。

在"Frequencies"对话框中，选择我们感兴趣的变量（如年龄、性别、收入），然后点击"OK"。

SPSS将会为我们输出每个变量的频数、均值、标准差等描述性统计结果。

通过这些统计量，我们可以对样本的整体特征进行了解。

接着，我们可以进行一些比较性的分析。

比如，我们可以对不同性别的样本进行回归分析，探究性别对收入是否有显著影响。

在菜单栏中选择"Analyze"，然后点击"Regression"，再选择"Linear"。

在"Linear Regression"对话框中，选择我们的自变量（性别）和因变量（收入），然后点击"OK"。

SPSS将会为我们输出回归模型的系数、截距、残差等结果，帮助我们了解性别对收入的作用。

将生存时间按从小到大顺序排列如下：
表1 BCG治疗组生存情况
死亡=1；删失=0
表2 药物和BCG结合治疗组生存情况
死亡=1；删失=0
按上述二表将数据输入SPSS软件,其中数据编号为i,列1即时间为t,列3即生存结局为status,表1为group1,表2为group2;
选择Analyze中的Survival里的Kaplan-Meier分析,将Time,Status,Factor依次选定,option和Compare Factor依次设定完成后,得到输出结果,结果分析如下：
Survival Table中：
1为BCG治疗组患者生存率Estimate及其标准误Std. Error的计算结果;
2为药物与BCG结合治疗组患者生存率Estimate及其标准误Std. Error的计算结果;
Overall Comparisons
Test of equality of survival distributions for the different levels of group.
两组生存率的log-rank检验
：两种疗法患者生存率相同
H
：两种疗法患者的生存率不同
H
1
α=
采用SPSS软件对两组生存率进行检验,得到上面Overall Comparisons表,其中第一
,还不能认为用BCG疗法和用药行为LogRank检验结果;即X2=,P=;按α=水准,不拒绝H
物与BCG结合疗法治疗黑色素瘤患者的生存率有差别;
生存曲线如上图所示,其中生存时间为横轴,生存率为纵轴;。

《SPSS 17中文版统计分析典型实例精粹》：以经典统计学软件SPSS 17中文版为写作平台，提供软件命令的中英对照基础篇学习软件基本操作和统计描述知识，实例篇详解案例应用原理、流程和操作技巧36个实例典型、丰富，涉及调查统计、市场研究、企业／政府数据分析和医学统计领域循序渐进、由浅入深，围绕SPSS应用的原理、流程和操作技巧娓娓阐述插图：1.3 SPSS的运行方式SPSS提供了三种基本的运行方式：完全窗口菜单运行方式、程序运行方式和批处理方式。

完全窗口菜单运行方式简单明了，除人工输入数据需要键盘外，大部分的操作命令、统计分析方法的实现都是通过菜单、图标按钮和对话框来完成的，使用者无需掌握编程知识就可以使用SPSS软件，适用于传统的统计分析人员。

程序运行方式和批处理方式则是从使用者特殊的分析需求出发，编写SPSS命令程序，通过语句直接运行的。

这两种运行方式要求使用者掌握专业的SPSS编程语法，对使用者的要求较高。

1.4 SPSS的主要界面1.4.1 SPSS的启动SPSS安装完毕后，系统会自动在Windows的【开始】菜单下创建快捷方式。

打开【开始】菜单，在“SPSS for Windows”下选中“SPSSl7.0 for Windows”并单击，即可启动SPSS。

当用户运行SPSS软件后，计算机屏幕上会出现一个SPSS启动操作对话框，如图1.10所示。

在该对话框中，用户可以选择打开数据的方式。

对话框中包括一个六选一的单选按钮组和一个复选框，分别说明如下：“您希望做什么？（What would you like to do？）”单选按钮组运行教程（Runthetutorial）：单击选中后，SPSS将打开帮助教程，在教程中，用户可选择不同模块的帮助说明进行有针对性的辅导。

输入数据（Type in data）：需要手动输入数据，建立新的数据文件时可选择此项。

选中后，即进入空白的SPSS数据编辑窗口。

SPSS因子分析(因素分析)——实例分析SPSS因子分析(因素分析)——实例分析SPSS（Statistical Package for the Social Sciences）是一种广泛应用于数据分析的软件工具，其中的因子分析（Factor Analysis）被广泛用于统计学和社会科学领域的研究。

本文将通过一个实例分析来介绍SPSS因子分析的基本原理和步骤。

1.研究背景在实施因子分析之前，首先需要明确研究背景和目的。

假设我们正在研究消费者购物行为，并希望确定出不同因素对于购物偏好的影响。

2.数据收集和准备在进行因子分析前，需要收集并准备相关数据。

假设我们已经收集到了100位消费者的关于购物行为的调查问卷数据，包括10个关于购物偏好的变量。

在SPSS中，我们可以将这些数据输入到一个数据矩阵中，每一行代表一个消费者，每一列代表一个变量。

3.因子分析设置在SPSS中，通过导航菜单选择适当的分析工具来进行因子分析。

在设置选项中，我们可以选择因子提取方法（如主成分分析、极大似然法等）和旋转方法（如方差最大旋转、斜交旋转等）等。

根据实际情况，我们可以调整这些参数以获得最佳结果。

4.因子提取在因子分析的第一步中，SPSS会计算每个变量的因子载荷矩阵，并根据设定的准则提取出主要因子。

因子载荷表示了每个变量与每个因子之间的关联程度，值越大表示关联程度越高。

通过因子载荷矩阵，我们可以判断每个变量对于哪个因子具有较高的影响。

5.因子旋转因子旋转可用于调整因子载荷矩阵，以使其更易于解释。

旋转后的因子载荷矩阵通常会呈现出更简洁、更有意义的结果。

在SPSS中，我们可以选择合适的旋转方法并进行旋转操作。

6.因子解释和命名在完成因子分析后，我们需要对结果进行解释和命名。

根据因子载荷矩阵和旋转结果，我们可以确定每个因子代表了哪些变量，并为每个因子赋予一个描述性的名称，以便于后续的数据分析和报告撰写。

7.结果解读最后，根据因子分析的结果，我们可以进行一系列的统计推断和解读。

SPSS与数据统计分析期末论文影响学生对学校服务满意程度的因素分析一、数据来源本次数据主要来源自本校同学,调查了同学们年级、性别、助学金申请情况、生源所在地、学院、毕业学校、游历情况、家庭情况、升高、体重、近视程度、学习时间、经济条件、兴趣、对学校各方面的评价、与对学校总评价以及建议等共41条信息，共收集数据样本724条。

我们将运用SPSS,对变量进行频数分析、样本T检验、相关分析等手段，旨在了解同学们对学校提供的满意程度与什么因素有关。

二、频数分析可靠性统计克隆巴赫 Alpha项数.98562对全体数值进行可信度分析本次数据共计724条，首先从可靠性统计来看，alpha值为0。

985,即全体数据绝大部分是可靠的，我们可以在原始数据的基础上进行分析与处理。

其中，按年级来看,绝大多数为大二学生填写(占了总人数的67。

13%)，之后分别依次为大二（23.76％)、大四（4。

14％）、大一（4。

97%)。

而从专业来看,占据了数据绝大多数样本所在的学院为机械、材料、经管、计通。

三、数据预处理拿到这份诸多同学填写的问卷之后，我们首先应对一些数据进行处理，对于数据的缺失值处理，由于我们对本份调查的分析重点方面是关于学生的经济情况的,因此对于确实的部分数据，升高、体重、近视度数、感兴趣的事等无关项我们均不需要进行缺失值的处理，而我们可能重点关注的每月家里给的钱、每月收入以及每月支出，由于其具有较强主观性,如果强行处理缺失值反而会破坏数据的完整性，因此我们筛去未填写的数据，将剩余数据当作新的样本进行分析.而对于一些关键的数据，我们需要做一些必要的预处理,例如一些调查项，我们希望得到数值型变量,但是填写时是字符型变量，我们就应该新建一个数字型变量并将数据复制，以便后续分析。

同时一些与我们分析相关的缺省值，一些明显可以看出的虚假信息，我们都需要先进行处理。

而具体预处理需要怎么做,这将会在其后具体分析时具体给出。

四、相关分析通过这份数据，我们可以直观地看到，最终同学给出了对学校总体的评价,而到底是什么影响了同学们的评价呢？我们小组打算从同学们的总体评价入手，分析同学们的家庭经济情况、学习成绩以及学校的各类资源完备程度是否会对同学们的评价造成影响。

SPSS因子分析——实例分析SPSS因子分析是一种统计方法，用于探索多个变量之间的相关性和结构。

它可以帮助研究者发现潜在的因素或维度，简化数据分析，并揭示变量之间的潜在关系。

本文将通过一个实例来介绍如何使用SPSS进行因子分析。

假设我们有一个关于消费者购买行为的调查问卷，包含了多个变量，如购买频率、购买金额、购买渠道等。

我们想要通过因子分析来探索这些变量之间的潜在结构，并识别出潜在的因素。

首先，我们需要将原始数据导入SPSS软件。

在SPSS的"变量视图"中，我们可以将每个变量名称输入到空白单元格中，并为每个变量选择适当的测量尺度（如定类尺度、定序尺度、定距尺度）。

然后，切换到"数据视图"，在每一行中输入被调查者的数据。

接下来，我们需要进行因子分析的前提检测。

在SPSS的"分析"菜单中，选择"数据采样"并点击"样本界限"，以确保我们选择的样本大小是否足够。

然后，我们选择"统计"中的"相关性"，点击"双变量"并检查变量之间是否存在显著的相关性。

如果我们的数据满足以上要求，我们可以继续进行因子分析。

在SPSS的"分析"菜单中，选择"数据准备"，点击"描述统计"并选择"频数"，以检查每个变量的分布情况。

然后，我们再次选择"分析"中的"数据准备"，点击"因子"并选择"提取方法"。

在弹出的对话框中，我们可以选择合适的提取方法，如主成分分析、极大似然估计等。

这些方法之间的选择要根据具体情况而定。

接下来，我们需要选择合适的因子数。

在"因子提取"对话框中，点击"因子"并输入我们认为合适的因子数。

SPSS多元线性回归分析实例操作步骤SPSS（Statistical Package for the Social Sciences）是一种统计分析软件，广泛应用于社会科学研究领域。

其中，多元线性回归分析是SPSS中常用的一种统计方法，用于探讨多个自变量与一个因变量之间的关系。

本文将演示SPSS中进行多元线性回归分析的操作步骤，帮助读者了解和掌握该方法。

一、数据准备在进行多元线性回归分析之前，首先需要准备好数据。

数据应包含一个或多个因变量和多个自变量，以及相应的观测值。

这些数据可以通过调查问卷、实验设计、观察等方式获得。

确保数据的准确性和完整性对于获得可靠的分析结果至关重要。

二、打开SPSS软件并导入数据1. 启动SPSS软件，点击菜单栏中的“文件（File）”选项；2. 在下拉菜单中选择“打开（Open）”选项；3. 导航到保存数据的文件位置，并选择要导入的数据文件；4. 确保所选的文件类型与数据文件的格式相匹配，点击“打开”按钮；5. 数据文件将被导入到SPSS软件中，显示在数据编辑器窗口中。

三、创建多元线性回归模型1. 点击菜单栏中的“分析（Analyse）”选项；2. 在下拉菜单中选择“回归（Regression）”选项；3. 在弹出的子菜单中选择“线性（Linear）”选项；4. 在“因变量”框中，选中要作为因变量的变量；5. 在“自变量”框中，选中要作为自变量的变量；6. 点击“添加（Add）”按钮，将自变量添加到回归模型中；7. 可以通过“移除（Remove）”按钮来删除已添加的自变量；8. 点击“确定（OK）”按钮，创建多元线性回归模型。

四、进行多元线性回归分析1. 多元线性回归模型创建完成后，SPSS将自动进行回归分析并生成结果；2. 回归结果将显示在“回归系数”、“模型总结”和“模型拟合优度”等不同的输出表中；3. “回归系数”表显示各个自变量的回归系数、标准误差、显著性水平等信息；4. “模型总结”表提供模型中方程的相关统计信息，包括R方值、F 统计量等；5. “模型拟合优度”表显示模型的拟合优度指标，如调整后R方、残差平方和等；6. 可以通过菜单栏中的“图形（Graphs）”选项，绘制回归模型的拟合曲线图、残差图等。

《数据统计分析软件SPSS的应用(五)——相关分析与回归分析》篇一数据统计分析软件SPSS的应用（五）——相关分析与回归分析一、引言在当今的大数据时代，数据统计分析成为了科学研究、市场调研、社会统计等众多领域的重要工具。

SPSS（Statistical Package for the Social Sciences）作为一款功能强大的数据统计分析软件，广泛应用于各种数据的处理与分析。

本文将重点介绍SPSS中的相关分析与回归分析，以及其在实际应用中的具体操作与作用。

二、相关分析1. 相关分析的概念与意义相关分析是研究两个或多个变量之间关系密切程度的一种统计方法。

在SPSS中，相关分析可以帮助我们了解变量之间的关联性，为后续的回归分析提供基础。

2. SPSS中相关分析的操作步骤（1）导入数据：将需要分析的数据导入SPSS软件中。

（2）选择相关分析：在SPSS的菜单栏中选择“分析”->“相关”->“双变量”，进行相关分析。

（3）选择变量：在选择变量界面，选择需要进行相关分析的变量。

（4）设置选项：设置相关系数的类型（如皮尔逊相关系数、斯皮尔曼等级相关系数等），以及是否需要进行双侧检验等。

（5）运行分析：点击“运行”按钮，SPSS将自动计算相关系数及显著性水平等统计量。

3. 相关分析的应用实例以某市房价与居民收入的关系为例，通过SPSS的相关分析，我们可以了解房价与居民收入之间的关联程度，为政策制定和房地产市场分析提供依据。

三、回归分析1. 回归分析的概念与意义回归分析是研究一个或多个自变量与因变量之间关系的一种统计方法。

在SPSS中，回归分析可以帮助我们了解自变量对因变量的影响程度，以及预测因变量的变化趋势。

2. SPSS中回归分析的操作步骤（1）导入数据：将需要进行回归分析的数据导入SPSS软件中。

（2）选择回归分析：在SPSS的菜单栏中选择“分析”->“回归”->“线性”，进行回归分析。

SPSS问卷数据分析操作实例在当今社会，数据的收集和分析对于了解各种现象、解决问题以及做出决策起着至关重要的作用。

问卷作为一种常见的数据收集工具，通过合理设计和有效发放，可以获取大量有价值的信息。

而 SPSS （Statistical Package for the Social Sciences）作为一款功能强大的统计分析软件，为我们处理和分析问卷数据提供了便捷和高效的途径。

接下来，我将通过一个具体的实例，为您详细介绍如何使用 SPSS 进行问卷数据分析。

假设我们进行了一项关于消费者对某品牌手机满意度的调查，共收集了 500 份有效问卷。

问卷中包含了消费者的个人信息（如年龄、性别、职业等）、对手机外观、性能、价格、售后服务等方面的满意度评价（采用 1-5 分的评分制，1 分为非常不满意，5 分为非常满意）以及是否会推荐给他人等问题。

首先，打开 SPSS 软件，将问卷数据导入到软件中。

SPSS 支持多种数据格式的导入，如 Excel、CSV 等。

在导入数据后，我们需要对数据进行初步的整理和检查，确保数据的完整性和准确性。

接下来，我们对消费者的个人信息进行描述性统计分析。

选择“分析” “描述统计” “频率”，将年龄、性别、职业等变量放入变量框中，点击“确定”。

这样，我们可以得到这些变量的频数分布、百分比、均值、中位数等统计量，从而了解调查对象的基本特征。

对于满意度评价的变量，我们可以计算其均值和标准差，以了解消费者对各方面的平均满意度水平和差异程度。

选择“分析” “描述统计” “描述”，将满意度评价变量放入变量框中，勾选“均值”和“标准差”，点击“确定”。

为了进一步探究不同性别、年龄或职业的消费者在满意度方面是否存在差异，我们可以进行方差分析或独立样本 t 检验。

例如，如果要比较男性和女性消费者在手机性能满意度上的差异，选择“分析” “比较均值” “独立样本 t 检验”，将性能满意度变量作为检验变量，性别变量作为分组变量，点击“确定”。