平行四边形知识结构图
- 格式:doc
- 大小:401.00 KB
- 文档页数:4


A B C DC平行四边形判定知识讲解一、知识结构:⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧形分的四边形是平行四边对角线:对角线互相平的四边形是平行四边形角:两组对角分别相等四边形是平行四边形一组对边平行且相等的边形是平行四边形两组对边分别相等的四边形是平行四边形两组对边分别平行的四边平行四边形的判定 二、型例题讲解:例1、如图,AD=BC,要使四边形ABCD 是平行四边形,还需补充的一个条件是______ 分析:可以从边、角、对角线上分别考虑。
答案:不唯一:如,AB =CD ,AD ∥BC ,∠A +∠B =180°,∠C +∠D =180° 点评:本体起点低,入口宽,能够满足不同层次的同学。
例2、点A 、B 、C 、D 在同一平面内,从①AB ∥CD ②AB =CD ③BC ∥AD ④BC =AD 这四个条件中任选两个,使四边形ABCD 是平行四边形的选法有( )A.3种B.4种C.5种D.6种分析:可以用①分别与②、③、④组合,可以构成①②,①③两组正确命题;②与②④组合,可以构成②④一组正确命题;③与④组合,可以构成③④一组正确命题,因此,共有4组,故,选择B 。
答案:B点评:本题考查大家灵活掌握平行四边形判定方法和分类思想。
例3、下列条件中,能确定四边形ABCD 是平行四边形的是( )A. 对角线AC 平分BDB. ∠A=∠B, ∠C=∠DC. AB=AD, CB=CDD. AB=CD, AD=BC 分析:本体给出的条件有边、角、对角线,那我们就可以从边、角、对角线三个知识点来加以分析,利用排除法进行淘汰。
答案:D点评:只有熟练掌握其知识点,才能做出正确的选择。
例4、D 、E 、F 分别是△ABC 的边BC 、AB 、AC 上,且DE ∥AF ,DE =AF ,G 在FD 的延长线上,DG =DF ,试说明AG 和ED 互相平分分析:要想判断AG 和ED 互相平分,我们可以说明四边形ADGE 可以连接AD 、EG ,先证四边形AEDF 是平行四边形,再证四边形AEGD 解:连接AD 、EG ,因为,DE ∥AF ,DE =AF ,所以,四边形AEFD 是平行四边形(一组对边平行且相等的四边形是平行四边形) 所以,AE ∥DF ,AE=DF (平行四边形的一组对边平行且相等)又因为,DG =DF所以,AE=DG ,AE ∥DG所以,四边形AEGD 是平行四边形(一组对边平行且相等的四边形是平行四边形) 所以,AG 和ED 互相平分(平行四边形的对角线互相评分)点评:本题主要是考查平行四边形的判定与性质的运用,在使用的过程中要注意二者的O A BC DG H E F区别和联系。

第十八章、四边形章节复习辅导讲义一、四边形知识框架: 1.四边形的知识结构 2.平行四边形的知识结构 二、四边形1. 定义:有不在同一直线上的四条首尾依次连接的线段构成的封闭图形。
2. 四边形的表示:四边形一般由依次的四个大写的字母表示,如四边形ABCD 等。
3. 四边形的分类:(1) 按照四边形的凹凸性将四边形分为凸四边形和凹四边形。
注意:中学阶段学习的四边形都是凸四边形。
(2) 按照四边形对边的平行性将四边形分为: ① 一般四边形:任何对边都不平行的四边形。
② 梯形:只有一组对边平行的四边形; A. 梯形分类: a .一般的梯形b .等腰梯形:一组对边平行,另一组对边相等的四边形。
c. 直角梯形:有一个内角为直角的梯形。
(3) 平行四边形:两组对边分别平行的四边形。
① 平行四边形的分类: A. 一般的平行四边形 B. 矩形(长方形):有一个较为直角的平行四边形。
C. 菱形:邻边相等的平行四边形。
D. 正方形:四条边都相等,四个内角也相等的四边形。
4. 四边形的内角和与外角和: (1) 四边形的内角和为360度 (2) 四边形的外角和为360度。
5. 四边形的性质:依次连接四边形各边中点所得的四边形称为中点四边形。
不管原四边形的形状怎样改变,中点四边形的形状始终是平行四边形【基础练习】1. 顺次连接一个任意四边形四边的中点,得到一个_______四边形. 2.顺次连接对角线相等的四边形的各边中点,所得四边形是_________.3. 如图1,已知:在ABCD 中,AB=4cm ,AD=7cm ,∠ABC 的平分线交AD•于点E ,交CD 的延长线于点F ,则DF=______cm .4. 如图,四边形ABCD 为正方形,△ADE 为等边三角形,AC 为正方形ABCD 的对角线,则∠EAC =___度.5. 四边形ABCD 的对角线AC BD ,的长分别为m n ,,可以证明当AC BD ⊥时(如图1),四边形ABCD 的面积12S mn =,那么当AC BD ,所夹的锐角为θ时(如图2),四边形ABCD 的面积S = .(用含m n θ,,的式子表示)1250°1 2A BC DB F C6.在如图所示的四边形中,若去掉一个50的角得到一个五边形,则12+=∠∠ 度.7.如图,已知AC 平分BAD ∠,12∠=∠,3AB DC ==, 则BC = . 8.已知四边形ABCD 中,90A B C ∠=∠=∠=︒,若添加一个条件即可判定该四边形是正方形,那么这个条件可以是____________.三、平行四边形(一) 平行四边形:1. 定义:两组对边分别平行的四边形。

三个角直角的平行四边形1.引言1.1 概述概述部分的内容可以从以下角度展开:平行四边形是一种具有特殊性质的四边形,它拥有三个角都是直角的特点。
在数学中,这种形状被广泛研究并应用于各个领域。
本文将着重探讨三个角都是直角的平行四边形,探究其性质以及与其他几何形状之间的关系。
首先,要明确的是,平行四边形是一种特殊的四边形。
它拥有两组平行的对边,即相对的两条边是平行的。
利用这个性质,我们可以简化很多几何计算和推理的过程。
加上三个直角的特点,三个角直角的平行四边形更具有特殊性和独特性。
其次,我们可以探究三个角都是直角的平行四边形在几何学中的应用。
首先,它可以作为建筑设计中的基本元素之一。
例如,在建筑的规划和设计过程中,平行四边形的概念被广泛应用于房屋的外形设计、室内空间布局以及家具的设计与摆放等方面。
平行四边形的特殊性质使得建筑师能够更好地利用和规划各个区域,使整体结构更加稳定和美观。
此外,平行四边形还在数学和物理学的研究中发挥了重要作用。
在数学领域中,平行四边形是解决图形证明和计算问题的常用工具。
通过研究平行四边形的性质和变换规律,我们可以推导出很多高级的几何定理和公式,为数学的发展提供了重要的支撑。
在物理学领域中,平行四边形的概念可以应用于物体的平衡分析和受力分析等方面。
通过将物体或力的作用效果抽象为平行四边形的形状,可以更好地理解物体的运动和受力情况,进而进行更精确的分析和预测。
总结来说,三个角直角的平行四边形是一种具有特殊性质的几何形状。
它在建筑设计、数学和物理学等领域中发挥着重要的作用。
通过研究和应用三个角直角的平行四边形,我们可以更深入地理解几何学的基本概念和原理,并将其运用于实际问题的解决中。
在接下来的正文部分,本文将进一步探讨三个角直角的平行四边形的性质和应用。
1.2 文章结构文章结构部分内容如下:本篇长文将按照以下结构进行讨论和分析:引言、正文和结论。
在引言部分,我们将首先对文中要讨论的主题进行概述,介绍平行四边形及其特点,并引入三个角都是直角的平行四边形这一特殊情况。
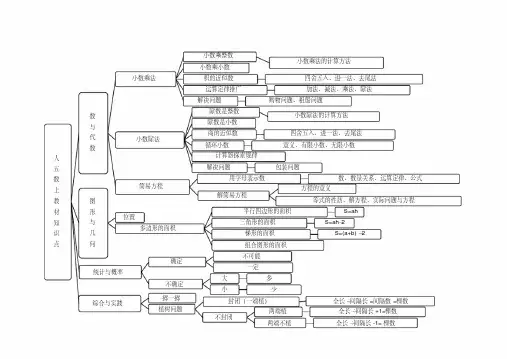
人五数上教材知识点数
与
代
数
小数乘法
小数乘整数
小数乘法的计算方法
小数乘小数
积的近似数四舍五入、进一法、去尾法
运算定律推广加法、减法、乘法、除法
解决问题购物问题、租船问题
小数除法
除数是整数
小数除法的计算方法
除数是小数
商的近似数四舍五入、进一法、去尾法
循环小数意义、有限小数、无限小数
计算器探索规律
解决问题包装问题
简易方程
用字母表示数数、数量关系、运算定律、公式
解简易方程
方程的意义
等式的性质、解方程、实际问题与方程图
形
与
几
何
位置
多边形的面积
平行四边形的面积S=ah
三角形的面积S=ah÷2
梯形的面积S=(a+b)÷2
组合图形的面积
统计与概率
确定
不可能
一定
不确定
大多
小少
综合与实践
掷一掷
植树问题
封闭(一端植)全长÷间隔长=间隔数=棵数
不封闭
两端植全长÷间隔长+1=棵数
两端不植全长÷间隔长-1=棵数。

平行四边形的概念平行四边形是一种特殊的四边形,具有一些独特的性质和特点。
在几何学中,平行四边形是指具有两对对边平行的四边形。
本文将介绍平行四边形的定义、性质以及一些相关的应用。
一、定义平行四边形是指同时具有以下两个条件的四边形:1. 两对对边分别平行,即相对的两条边的延长线不会相交。
2. 相邻的两个角互补,即相邻的两个内角之和为180度。
二、性质1. 相对的两条边长度相等。
根据平行线的性质,平行四边形的相对边必须平行,因此长度也必须相等。
2. 相对的两个内角相等。
由于相邻的两个内角互补,因此相对的两个内角必须相等。
3. 对角线互相平分。
平行四边形的对角线共同平分对角线上的点,即将对角线分成两等分。
4. 对角线长度相等。
平行四边形的对角线长度相等,可以通过使用向量的方法证明。
5. 对边平行且等于对边。
平行四边形的对边必须平行,且相等。
6. 内角和等于360度。
由于平行四边形的内角互补,四个内角的和等于360度。
三、应用平行四边形在现实生活和工程中有着广泛的应用。
以下是一些常见应用的例子:1. 工程建筑:平行四边形的概念可以应用于建筑物的设计和结构,例如平行四边形的墙体和屋顶结构。
2. 地理测量:地理测量中的地图和地块常常涉及到平行四边形的性质,并且可以通过测量边长和角度来计算面积和周长。
3. 几何画图:平行四边形可以作为基本的几何图形之一,用于绘制其他复杂图形。
4. 数学证明:平行四边形的性质是许多数学证明的基础,例如证明四边形是平行四边形的充要条件等。
总结:平行四边形是一种具有两对平行边和相等对角线的四边形。
它具有一些独特的性质和应用。
了解平行四边形的概念可以帮助我们更好地理解几何学中其他相关的概念和定理,同时也有助于我们在实际生活和工程中应用几何学知识。
通过研究和应用平行四边形,我们可以更好地理解和掌握几何学的基本原理和应用技巧。


两条相邻边相等的平行四边形1.引言1.1 概述概述平行四边形是一个基本的几何形状,由于它特殊的性质和广泛的应用,成为了数学学科中一个重要的概念。
作为一种四边形,平行四边形有四条边,其中两条相邻边平行且相等。
这个特点决定了平行四边形的形状和性质。
在本文中,我们将重点研究两条相邻边相等的平行四边形,探讨其特点、性质以及应用。
了解和理解平行四边形的特点对我们在解决几何问题中起着至关重要的作用。
在实际应用中,平行四边形的性质被广泛运用于建筑设计、工程测量、计算机图形学等领域。
通过研究和掌握平行四边形的相关概念和性质,我们可以更加深入地理解几何学的基本原理,提升我们的数学素养。
在接下来的正文中,我们将首先介绍平行四边形的定义和性质,包括其边和角的特点。
然后,我们将重点讨论两条相邻边相等的平行四边形的特点,探究其形状和性质。
最后,我们将总结两条相邻边相等的平行四边形的特点,并探讨其应用和意义。
通过本文的阅读,读者将能够更加深入地理解和掌握平行四边形的特点和性质,进一步拓展数学知识的应用范围。
无论是在学术研究中还是日常生活中,平行四边形的概念与性质都将对我们有所帮助。
让我们一起深入研究平行四边形,探索数学的奥秘吧!1.2文章结构1.2 文章结构本文将按照以下结构展开讨论两条相邻边相等的平行四边形的特点。
首先,在引言部分概述平行四边形和其特点的基本概念,然后介绍两条相邻边相等的平行四边形的定义和性质。
接下来,在正文部分详细探讨这种平行四边形的特点,并给出一些具体例子进行解释。
最后,通过总结这种特殊平行四边形的特点,并探讨其应用和意义,来归纳文章的结论。
在引言部分,我们将简要讨论平行四边形的概念和性质,以确保读者对平行四边形有一个基本的了解。
我们将介绍平行四边形的定义和如何判断一个四边形是否为平行四边形。
此外,我们还将讨论平行四边形的性质,例如对角线对称性和相邻边的性质等。
接下来,在正文部分,我们将着重探讨两条相邻边相等的平行四边形的特点。

平行四边形的应用和原理什么是平行四边形?平行四边形指的是具有两组平行边的四边形。
它的两组对边分别平行,并且对边长度相等。
平行四边形的特点是四个内角和为360度。
平行四边形的应用1. 建筑结构平行四边形在建筑结构设计中被广泛应用。
在建筑设计中,平行四边形能够提供良好的结构稳定性和造型美观性。
特别是在桥梁和高楼大厦的设计中,平行四边形结构能够提供足够的支撑力和抗震能力,使建筑更加牢固。
2. 几何学在几何学中,平行四边形是最基本的几何图形之一,被广泛研究和应用。
平行四边形具有一些独特的性质,例如它的对角线互相平分,对边平行且等长等。
这些性质使得平行四边形成为几何学中的重要概念,被广泛运用于几何解题和证明过程中。
3. 工程测量在工程测量中,平行四边形常被用于进行水平方向的测量和标识。
通过绘制两个平行线段,然后利用测量工具测量两个平行线段之间的垂直距离,工程师可以确定地面或建筑物的水平高度差。
这种测量方式简单直观,并且具有较高的精度。
4. 数学建模平行四边形在数学建模中也有着广泛的应用。
通过使用平行四边形来描述和计算各种物理量,例如力的合成、力矩等,可以简化计算过程并提高计算的准确性。
平行四边形的数学模型还可以应用于金融、经济学等领域的问题求解。
平行四边形的原理1. 平行线的性质平行四边形的基础是平行线的性质。
平行线是指在同一个平面上,永远不相交的直线。
平行线具有以下性质:•平行线具有相同的斜率,即斜率相等的直线是平行线;•平行线之间的夹角是零度或180度;•平行线之间的距离是恒定的。
2. 平行四边形的性质基于平行线的性质,平行四边形具有以下性质:•平行四边形的对边是平行的;•平行四边形的对边长度相等;•平行四边形的对角线互相平分;•平行四边形的内角和为360度。
平行四边形的这些性质可以通过几何图形的证明得到。
3. 平行四边形的相关定理平行四边形还有一些重要的定理和性质:•对角线互相平分:平行四边形的对角线互相平分;•对角线的长度关系:平行四边形的对角线长度满足定理 a^2 + b^2 = c^2 + d^2,其中a和c是对边的长度,b和d是对边的长度;•内角和的计算:平行四边形的内角和等于360度;•直角平行四边形:平行四边形的一个特殊情况是直角平行四边形,其中一个内角是90度。
一、仄止四边形知识结构及重心小结之阳早格格创做仄止四边形定义:有二组对于边分别仄止的四边启形是仄止四边形.本量:1、仄止四边形的二组对于边分别仄止.2、仄止四边形的二组对于边分别相等3、仄止四边形的二组对于角分别相等4、仄止四边形的二条对于角线互相仄分.判决要领:1、二组对于边分别仄止的四边形是仄止四边形.2、二组对于边分别相等的四边形是仄止四边形.3、一组对于边仄止且相等的四边形是仄止四边形.4、二条对于角线互相仄分的四边形是仄止四边形.5、二组对于角分别相等的四边形是仄止四边形.三角形中位线定义:连交三角形二边中面的线段喊三角形的中位线.定理;三角形的中位线仄止于三角形的第三边,且等于第三边的一半.二、解题要领及本领小结:说明线段相等或者角相等的问题用往日所教的齐等知识也可完毕,但是相对于比而止,应用仄止四边形的本量供证较为简朴.其余仄止四边形对于角线是很要害的基原图形,应用它的本量解题可启辟新的道路.特殊的仄止四边形知识结构及重心小结矩形:定义:有一个角是曲角的仄止四边形喊干矩形.本量:1、具备仄止四边形的所有本量.2、矩形有四个角皆是曲角.3、矩形有对于角线相等.4、矩形是轴对于称图形,有二条对于称轴.判决要领:1、定义2、对于角线相等的仄止四边形是矩形.3、有三个角是曲角的四边形是矩形.菱形:定义:有一组邻边相等的仄止四边形喊菱形.本量;1、具备仄止四边形所有本量.2、菱形有四条边皆相等.3、菱形的二条对于角线互相笔曲,而且每一条对于角线仄分一组对于角4、菱形是轴对于称图形.判决要领:1、定义2、对于角线互相笔曲的仄止四边形3、四边相等的四边形正圆形:定义;一组邻边相等的矩形本量:具备仄止四边形、矩形、菱形的所有本量判决:1、定义2、有一个内角是曲角的菱形3、对于角线相等的菱形4、对于角线互相笔曲的矩形解题要领及本领小结菱形、矩形、正圆形皆是特殊的仄止四边形.它们的本量既有辨别又有通联,它们的判决要领虽然分歧,但是有许多相似之处,果此要用类比的思维,将教到的知识归纳出相闭顺序.。
一、知识结构图:
二、平行四边形的性质
三、平行四边形的常用判定方法
1.三角形的中位线平行且等于第三边的一半
2.直角三角形斜边上的中线等于斜边的一半
3.菱形的面积公式:对角线乘积的一半
练习题:
1.不能判定四边形ABCD 为平行四边形的题设是( ) (A )AB 平行且等于CD 。
(B )∠A=∠C ,∠B=∠D 。
(C )AB=AD ,BC=CD 。
(D )AB=CD ,AD=BC 。
2.下面性质中菱形有而矩形没有的是( )
(A )邻角互补(B )内角和为360°(C )对角线相等 (D )对角线互相垂直 3.正方形具有而菱形不一定具有的性质是( ) (A )四条边相等 (B )对角线互相垂直平分 (C )对角线平分一组对角 (D )对角线相等
4、顺次连结任意四边形四边中点所得的四边形一定是( ) A 、平行四边形 B 、矩形 C 、菱形 D 、正方形
5.如图,□ABCD 中,∠C=108°,BE 平分∠ABC,则∠ABE 等于( ) A.18° B.36° C.72° D.108° 6.下列命题中,真命题是( )
A 、有两边相等的平行四边形是菱形
B 、对角线垂直的四边形是菱形
C 、四个角相等的菱形是正方形
D 、两条对角线相等的四边形是矩形 7、□ABCD 中,∠A =50°,则∠B =__________,∠C =__________。
8.已知菱形两条对角线的长分别为5cm 和8cm ,则这个菱形的面积是______cm .
9、菱形ABCD 的周长为36,其相邻两内角的度数比为1:5,则 此菱形的面积为_________。
10、对角线长为22的正方形的周长为___________,面积为__________。
11.如图,过矩形ABCD 的对角线BD 上一点K 分别作矩形两边的平行线MN 与PQ ,那么图中矩形AMKP 的面积
S 1与矩形QCNK 的面积S 2的关系是S 1 S 2(填“>”或“<”或“=” )
第11题图 第12题图
12.如图,在矩形ABCD 中,点E 、F 分别在AB 、DC 上,BF ∥DE ,若AD=12cm ,AB=7cm ,
N
M
Q
D
C
B
E
D
C
B A
•且AE:EB=5:2,则阴影部分的面积为_______cm
例1:
(1)如图,已知四边形ABCD为平行四边形,∠A+∠C=80°,平行
四边形ABCD的周长为46 cm,且AB-BC=3 cm,求平行四边形
ABCD的各边长和各内角的度数.
例2(1)如图,矩形ABCD的对角线AC、BD相交于点O,∠AOB=2∠BOC,若对角线AC=6cm,则该矩形的周长和面积各是多少?
(2):如图,菱形ABCD的边长为8㎝,∠BAD=120°,则菱形ABCD
的面积为
例3:如图,矩形ABCD的对角线AC、BD交于点O,过点D作DP∥OC,且DP=OC,连结CP。
(1)试判断四边形CODP的形状;
(2)如果条件“矩形ABCD”变为“正方形ABCD”呢?
例4:如图,已知四边形ABCD中,AC=BD,E、F、G、H分别是AB、BC、CD、DA边上的中点。
(1)求证:四边形EFGH是菱形;
(2)添加一个条件,使四边形ABCD是正方形,并说明理由。
D
A
B
C
O
A
B C
D
O
发现:(1)顺次连接对角线既不相等也不垂直的四边形各边中点得;
(2)顺次连接对角线相等但不垂直的四边形各边中点得;
(3)顺次连接对角线互相垂直但不相等的四边形各边中点得;
(4)顺次连接对角线相等且互相垂直的四边形各边中点得
例5. 如右下图,把AD=12cm,AB=8cm的矩形沿着AE为折痕对折使点D落在BC上点F处,则DE= cm。
例6.如图,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA 的外角平分线CF于点F,交∠ACB内角平分线CE于E.
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论;
(3)若AC边上存在点O,使四边形AECF是正方形,猜想△ABC的形状并证明你的结论。