静定梁内力图

静定梁的内力8.1 弯曲变形的概述弯曲是工程和生活实际中最常见的一种基本变形。

杆件由于受到某种作用,其轴线由直线变成曲线,这种变形称为弯曲。

以弯曲为主要变形的杆件在工程中称为梁。

梁是在工程中应用非常广泛的一种构件。

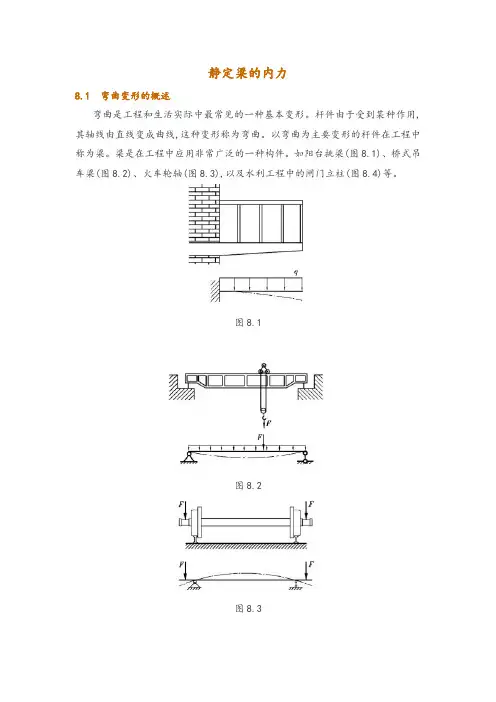
如阳台挑梁(图8.1)、桥式吊车梁(图8.2)、火车轮轴(图8.3),以及水利工程中的闸门立柱(图8.4)等。

图8.1图8.2图8.3图8.4工程中常见的梁,其横截面通常采用对称形状,如矩形、圆形、工字形及T形等,按照其截面形状可以相应地将其称为矩形截面梁、圆形截面梁以及工字形截面梁等。

建筑工程中以矩形截面梁最为常见,而在钢结构中以工字形截面梁较为常见。

在预制钢筋混凝土构件中存在T形截面梁;现浇钢筋混凝土结构中的矩形截面梁当考虑现浇板作为其翼缘时,在计算模式上也可称为T形截面梁。

上述各种截面的梁其横截面都具有一个竖向对称轴y(图8.5)。

该竖向对称轴与梁轴线所构成的平面称为纵向对称面(图8.6)。

图8.5图8.6具有纵向对称平面的梁,若其所受外力(荷载和支座反力)全部位于纵向对称平面内,则梁弯曲过程中轴线将始终保持在该纵向对称面内,这种弯曲称为平面弯曲。

本章只讨论平面弯曲梁。

梁的分类方式是多种多样的。

按照梁的轴线形状可以分为直梁和曲梁;按照梁的轴线与水平线的关系可以分为平梁和斜梁;按照梁的跨数可以分为单跨梁和多跨梁。

按照梁所在的几何不变体系是否有多余约束又可分为超静定梁和静定梁。

本章主要讨论单跨以及多跨平直静定梁在发生平面弯曲时其横截面上的内力。

8.2 单跨静定梁的内力计算1)剪力和弯矩内力与梁的强度、刚度等有着密切的关系。

内力可以随外力的增加而增大,内力越大,梁的变形也越大,当内力超过一定限度时,梁就会发生破坏。

讨论梁的强度、刚度问题,必须先求出梁的内力。

建筑力学通常研究的是梁横截面上的内力。

梁的内力与外力相关,要计算内力必须先统计梁上承受的外力作用。

统计出梁上的外力后,梁横截面上的内力可用截面法求得。

摘要：正确绘制梁的内力图，是正确计算截面应力、变形和对梁进行正确配筋的前提。

其绘制方法虽有多种，但在教学中采取何种方法能使学生快速掌握内力图的画法，有待进一步探索。

针对“三本”独立学院学生的特点，本文结合实例，阐述了快速掌握内力图画法的一般步骤。

关键词：“三本”独立学院《建筑力学》梁内力图绘制方法梁的内力图绘制指的是用图示法表示出剪力Q、弯矩M沿梁长变化的情况，是《建筑力学》教材中的一个重点和难点内容，也是建筑类专业学生必须掌握的基本功。

鉴于“三本”独立学院学生基础较差、学习兴趣不浓等特点，加上《建筑力学》是一门较枯燥的专业课程，为使学生掌握绘制梁内力图这项基本功，我根据《建筑力学》课程的教学经验，总结出下述绘制梁内力图的方法。

1.绘制梁内力图的基本步骤及原理1.1求梁的支座反力支座反力的求解是正确绘制内力图的重要依据。

支座反力一旦计算错误，接下来的各截面内力计算就会是错误，内力图的正确与否也就无从谈起。

求解支座反力时，先要对梁进行正确的受力分析，画出受力分析图，再根据静力学平衡方程即可得到正确值。

1.2对梁进行分段根据梁的荷载情况，假想把梁分成若干段，其原则是以荷载的作用点作为分段点，如集中荷载作用点、集中力偶作用点、均布荷载起止作用点，反力作用点。

1.3判断每段梁内力图形特征在正式绘制每段梁的内力图之前，预先判断出其图形特征是必要的。

主要是利用荷载集度、剪力与弯矩之间的微分关系，其数学表达式为：dQ(x) dx =q(x)（1）；dM(x)dx=Q(x)（2）；d2M(x)dx2=q(x)（3）；而在实际绘图过程中，往往只需要利用式1和式2的倒推关系式，即蘩q(x)dx=Q(x)（4）；蘩Q(x)dx=M(x)（5）；1.3.1当某段无荷载时，即q(x)=0，利用式4可得Q(x)为常数，则该段的剪力图形为水平直线，此时只需求出特征点（分段点）的剪力值便可绘制出剪力图。

1.3.2当某段有均布荷载时，即q(x)为常数，利用式4可得Q (x)为一次函数，则该段的剪力图形为倾斜直线，根据两点确定一条直线，此时只需求出特征点（两个分段点）的剪力值便可绘制出剪力图。

5.2 多跨静定梁的内力计算与内力图绘制一、多跨静定梁的组成单跨静定梁多使用于跨度不大的情况，如门窗、楼板、屋面大梁、短跨的桥梁以及吊车梁等。

通常将若干根单跨梁用铰相连，并用若干支座与基础连接而组成的静定结构称为多跨静定梁。

如图5. 19(a)所示为房屋建筑中一木檩条的结构图，在各短梁的接头处采用斜搭接加螺栓系紧。

由于接头处不能抵抗弯矩，因而视为铰结点。

其计算简图如图5. 19(b)所示。

从几何组成上看，多跨静定梁的组成部分可分为基本部分和附属部分。

如图5. 19(b)所示，其中梁AB 部分，有三根支座链杆直接与基础（屋架）相连，不依赖其它部分构成几何不变体系，称为基本部分；对于梁的EF 和IJ 部分，因它们在竖向荷载作用下，也能独立保持平衡，故在竖向荷载作用下，可以把它们当作基本部分；而短梁CD 和GH 两部分支承在基本部分之上，需依靠基本部分才能保持其几何不变性，故称为附属部分。

为了清楚地看到梁各部分之间的依存关系和力的传递层次，可以把基本部分画在下层，把附属部分画在上层，如图5.19(c)所示，称为层次图。

BCDEFG H I(f)(g)AB CD E F GHA BCDE F GHII(a)(b)(c)(d)(e)ABCDEF GHIA B C D E F G H I JABCD EFG H IJ檩条屋架上弦图5.19二、多跨静定梁的内力计算从受力分析看，由于基本部分能独立地承受荷载而维持平衡，故当荷载作用于基本部分时，由平衡条件可知，将只有基本部分受力，附属部分不受力。

而当荷载作用于附属部分时，则不仅附属部分受力，其反力将通过铰结处传给基本部分，使基本部分同时受力。

由上述基本部分和附属部分力的传递关系可知，多跨静定梁的计算顺序应该是先计算附属部分，后计算基本部分。

计算附属部分时，应先从附属程度最高的部分算起；计算基本部分时，把计算出的附属部分的约束力反其方向，作为荷载作用于基本部分。

第十章静定结构的内力分析本章主要讨论静定结构的内力计算。

它不仅是静定结构位移计算的基础，而且也是超静定结构计算的基础。

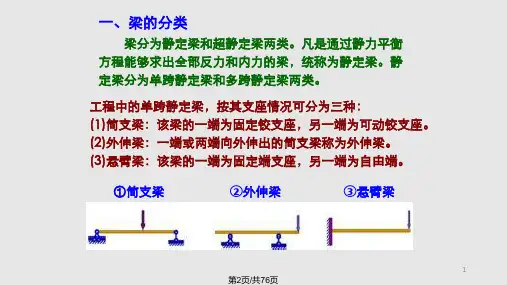
第一节静定梁的内力一、单跨静定梁单跨静定梁的力学简图有简支梁、悬臂梁和外伸梁三种形式，如图11-1所示。

图11-1梁内任意截面的内力的计算方法、内力图及弯矩图的做法在本书第六章中已有详细介绍，在此不再详述。

二、多跨静定梁若干根梁用铰相连，并和若干支座与基础相连而组成的静定梁，称为多跨静定梁。

在实际的建筑工程中，多跨静定梁常用来跨越几个相连的跨度。

图10-2(a)所示为一公路或城市桥梁中，常采用的多跨静定梁结构形式之一，其计算简图如图10-2(b)所示。

在房屋建筑结构中的木檩条，也是多跨静定梁的结构形式，如图10-3(a)所示为木檩条的构造图，其计算简图如图10-3(b)所示。

连接单跨梁的一些中间铰，在钢筋混凝土结构中其主要形式常采用企口结合(图10-2a)，而在木结构中常采用斜搭接并用螺栓连接(图10-3a)。

图10-2 图10-3从几何组成分析可知，图10-2(b)中AB梁是直接由链杆支座与地基相连，是几何不变的。

且梁AB本身不依赖梁BC和CD就可以独立承受荷载，称之为基本部分。

如果仅受竖向荷载作用，CD梁也能独立承受荷载维持平衡，同样可视为基本部分。

短梁BC是依靠基本部分的支承才能承受荷载并保持平衡，所以，称为附属部分。

同样道理在图10-3(b)中梁AB、CD和EF均为基本部分，梁BC和梁DE为附属部分。

为了更清楚地表示各部分之间的支承关系，把基本部分画在下层，将附属部分画在上层，如图10-2(c)和图10-3(c)所示，我们称它为关系图或层叠图。

计算多跨静定梁时，必须先从附属部分计算，再计算基本部分，按组成顺序的逆过程进行。

例如图10-2(c)，应先从附属梁BC计算，再依次考虑AB、CD梁。

这样便把多跨梁化为单跨梁，分别进行计算，从而可避免解算联立方程。

再将各单跨梁的内力图连在一起，便得到多跨静定梁的内力图。