下载文档原格式
2.4解:为计算简化,这里1R 与电容2C 的容抗之比π221=C X R 较大,可采用部分接入法公式 )(1002121pF C C C C C =+=∑电感 )(253.0)2(12mH C f L o ≈=∑π 接入系数 n=2121=+C C C 1R 在两端等效为)(20**Ω==k R n n R T 电感固有品质因数50,对应的固有谐振电阻)(58.792Ω≈=∑k C f Q R o oo π端等效电阻为)(16Ω≈+k R R R R oT oT有载品质因数10101623=⨯⨯=∑C f Q o L π习 题 第三章3.1 高频功率放大器的主要作用是什么?应对它提出哪些主要要求？答：高频功率放大器的主要作用是放大高频信号或高频已调波信号，将直流电能转换成交流输出功率。
要求具有高效率和高功率输出。
3.2 为什么丙类谐振功率放大器要采用谐振回路作负载？若回路失谐将产生什么结果？若采用纯电阻负载又将产生什么结果？答：因为丙类谐振功率放大器的集电极电流i c 为电流脉冲，负载必须具有滤波功能，否则不能获得正弦波输出。
若回路失谐集电极管耗增大，功率管有损坏的危险。
若采用纯电阻负载则没有连续的正弦波输出。
3.3 高频功放的欠压、临界和过压状态是如何区分的？各有什么特点？答：根据集电极是否进入饱和区来区分，当集电极最大点电流在临界线右方时高频功放工作于欠压状态，在临界线上时高频功放工作临界状态，在临界线左方时高频功放工作于过压状态。
欠压状态的功率和效率都比较低，集电极耗散功率也较大，输出电压随负载阻抗变化而变化，较少使用，但基极调幅时要使用欠压状态。
临界状态输出功率大，管子损耗小，放大器的效率也较高。
过压状态下，负载阻抗变化时，输出电压比较平稳且幅值较大，在弱过压时，效率可达最高，但输出功率有所下降，发射机的中间级、集电极调幅级常采用过压状态。
3.4 分析下列各种功放的工作状态应如何选择？ (1) 利用功放进行振幅调制时，当调制的音频信号加到基极或集电极时，如何选择功放的工作状态？(2) 利用功放放大振幅调制信号时，应如何选择功放的工作状态？ (3) 利用功放放大等幅度信号时，应如何选择功放的工作状态？答：(1) 当调制的音频信号加到基极时，选择欠压状态；加到集电极时，选择过压状态。
第二章 高频电路基础2－1对于收音机的中频放大器，其中心频率f 0=465 kHz ．B 0.707=8kHz ，回路电容C=200pF ，试计算回路电感和 Q L 值。
若电感线圈的 Q O =100，问在回路上应并联多大的电阻才能满足要求。
解2-1：答：回路电感为0.586mH,有载品质因数为58.125,这时需要并联236.66k Ω的电阻。
2－5 一个5kHz 的基频石英晶体谐振器， C q =2.4X10－2pF C 0=6pF ，，r o =15Ω。
求此谐振器的Q 值和串、并联谐振频率。
解2-5：答：该晶体的串联和并联频率近似相等，为5kHz ，Q 值为88464260。
2－7 求如图所示并联电路的等效噪声带宽和输出均方噪声电压值。
设电阻R=10k Ω，C=200 pF ，T=290 K 。
解：答：电路的等效噪声带宽为125kHz ，和输出均方噪声电压值为19.865μV2.2－10 接收机等效噪声带宽近似为信号带宽，约 10kHz ，输出信噪比为 12 dB ，要求接收机的灵敏度为 1PW ，问接收机的噪声系数应为多大？ 解2-10：根据已知条件答：接收机的噪音系数应为32dB 。
第三章 高频谐振放大器3－4 三级单调谐中频放大器，中心频率f 0=465 kHz ，若要求总的带宽B0.7=8 kHZ ，求每一级回路的 3 dB 带宽和回路有载品质因数Q L 值。
解3－4： 设每级带宽为B 1，则：答：每级带宽为15.7kHz,有载品质因数为29.6。
3－5 若采用三级临界耦合双回路谐振放大器作中频放大器（三个双回路），中心频率为f o =465 kHz ，当要求 3 dB 带宽为 8 kHz 时，每级放大器的3 dB 带宽有多大？当偏离中心频率 10 kHZ 时，电压放大倍数与中心频率时相比，下降了多少分贝？ 解3-5 设每级带宽为B 1，则：0226120611244651020010100.5864465200f L f C mHπππ-==⨯⨯⨯⨯=≈⨯⨯2由（）03034651058.125810LL 0.707f Q f Q B =⨯===⨯0.707由B 得：900312000000000010010171.222465102001024652158.1251171.22237.6610058.125L LLL L L L Q R k C C C Q Q R g g g R Q Q R R R k Q Q Q ΩωππωωΩ∑-===≈⨯⨯⨯⨯⨯⨯===++=-==⨯≈--因为：所以：（）0q q0q 00q0q 093120q C C 60.024C 0.024pF C C C 60.024f f f 0.998f 4.99kHz C 11122C 1110Q 884642602f Cr 25100.0241015 3.6-⨯==≈=++==≈=⎛⎫++ ⎪⎝⎭====ππ⨯⨯⨯⨯⨯π总电容串联频率品质因数20220002064121),11|()|11()11arctan(2)1(2)211101254410200108RH R j CR j C R H j df df H CR df fCR fCR CR kHz CR ωωωωωπππ∞∞∞∞-===++=+==+====⨯⨯⨯⎰⎰⎰0n 网络传输函数为H(j 则等效噪音带宽为B =22202343214444 1.3710290101251019.865()n n n n kTGB H kTB R kTRB R V μ-====⨯⨯⨯⨯⨯⨯=输出噪音电压均方值为U 121212234061015.85101015.8515.85 1.3710290101015883215.85 1.3729o i i F o S N S N kTB N S N dB---=====⨯⨯⨯⨯=≈≈⨯⨯。
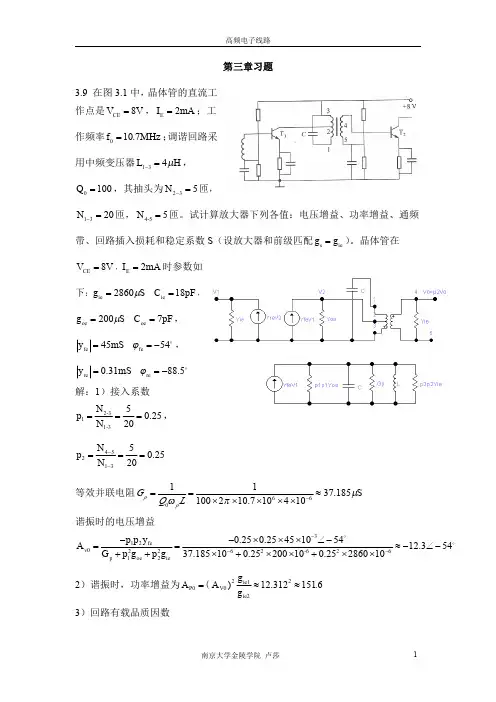
3．1 已知谐振功率放大电路U cc =24V ，P 0=5W 。
当ηc =60%时，试计算P c 和I co 。
若P o 保持不变，ηc 提高到80%，则P c 和I co 减小为多少？ 解：5258.33()0.63108.335 3.33()3250.35()72(2)80%,:6.251.250.26ηηηη⇒===∴=-=-==⋅⇒=====-===oo D D c c D o DD cc co co cc c o D cc D o Dco ccP P =P w w P P P P w w P P U I I A A U P P w P P P wP I AU (1)由由若提高到重复上面的计算得3．2 已知谐振功率放大电路工作在乙类状态，U cc =24V ，R ∑=53Ω，P o =5W 。
试求P D 、ηc 和集电极电压利用系数ξ。
解：22111010010111123222395.8%24,1:1(90)221(90)175.36%26.632:(11()22cm o c m cm cm cc D coc m cm cm c c m o c cm cm o c m cm c D c cc oD c c U P I R U V R U U P I I I I I I I I P I U P I U P P wg ξξηαπαπηηαηξθξ∑∑==⇒=∴===⎫==⎪⎪⇒=⎬⎪==⎪⎭∴======= (1)求由(2)求解法解法0)11275.36%()216.63o D c P P wθξαθπη====3．3 已知谐振功率放大电路的导通角θ分别为1800、900和600时都工作在临界状态，且三种情况下的U cc 和I cm 也都相同。
试计算三种情况下的效率ηc 的比值和输出功率P o 的比值。
解：00001111sin cos ()(1cos )11(180)0.5(90)0.318(60)0.2183sin cos ()(1cos )2(180)0.5(90)0.5(60)0.31932(180)(90)(60)(180)(90)(60)o o o o o oo o o cc cc cc o o o cm cm cm U U U I I I θθθαθπθαααππθθθαθπθαααπ-=-∴==≈=-≈-=-∴===-≈⎫==== 由1100111000112(180)(90)(60)()1122()(180)(90)(60)11(180):(90):(60):::1.57:1.792(180)(90)(60)211()22o o o cm cm cm o c m cm cm cm c D c cc cm cc o o o o o o c c c o o o o c m cm cm cm U U U P I U I U P I U I U P I U I U P αθηαθαααηηηααααθ⎪⇒==⎬⎪⎭===∴====∴ 又又11111(180):(90):(60)(180):(90):(60):1:0.7822o o o o o o o o o P P ααα==3．4 已知晶体管输出特性中饱和临界线跨导g cr =0.8A/V ，用此晶体管做成的谐振功放电路，U cc =24V ，θ=900，I cm =2.2A ，并工作在临界状态，试计算P o 、P D 、ηc 和R ∑。
3-1 若反馈振荡器满足起振和平衡条件，则必然满足稳定条件，这种说法是否正确？为什么？解：否.因为满足起振与平衡条件后，振荡由小到大并达到平衡。
但当外界因素(T 、V CC )变化时，平衡条件受到破坏，若不满足稳定条件，振荡器不能回到平衡状态，导致停振。
3-2 一反馈振荡器，欲减小因温度变化而使平衡条件受到破坏，从而引起振荡振幅和振荡频率的变化，应增大i osc)(V T ∂∂ω和ωωϕ∂∂)(T ，为什么？试描述如何通过自身调节建立新平衡状态的过程（振幅和相位）。
解：由振荡稳定条件知：振幅稳定条件：0)(iAi osc <∂∂VV T ω相位稳定条件：0)(oscT <∂∂=ωωωωϕ若满足振幅稳定条件，当外界温度变化引起V i 增大时，T(ωosc )减小，V i 增大减缓，最终回到新的平衡点。
若在新平衡点上负斜率越大，则到达新平衡点所需V i 的变化就越小，振荡振幅就越稳定。
若满足相位稳定条件，外界因素变化→ωosc ↑→ϕT (ω)↓最终回到新平衡点。
这时，若负斜率越大，则到达新平衡点所需ωosc 的变化就越小，振荡频率就越稳定。
3-3 并联谐振回路和串联谐振回路在什么激励下（电压激励还是电流激励）才能产生负斜率的相频特性？解：并联谐振回路在电流激励下，回路端电压V&的频率特性才会产生负斜率的相频特性，如图(a)所示。
串联谐振回路在电压激励下，回路电流I &的频率特性才会产生负斜率的相频特性，如图(b)所示。
3-5 试判断下图所示交流通路中，哪些可能产生振荡，哪些不能产生振荡。
若能产生振荡，则说明属于哪种振荡电路。
ωosc ↓ 阻止ωosc增大，解：(a) 不振。
同名端接反，不满足正反馈；(b) 能振。
变压器耦合反馈振荡器；(c) 不振。
不满足三点式振荡电路的组成法则；(d) 能振。
但L2C2回路呈感性，ωosc < ω2，L1C1回路呈容性，ωosc > ω1，组成电感三点式振荡电路。
(e) 能振。
计入结电容C b'e，组成电容三点式振荡电路。
(f) 能振。
但L1C1回路呈容性，ωosc > ω1，L2C2回路呈感性，ωosc > ω2，组成电容三点式振荡电路。
3-6 试画出下图所示各振荡器的交流通路，并判断哪些电路可能产生振荡，哪些电路不能产生振荡。
图中，C B、C C、C E、C D为交流旁路电容或隔直流电容，L C为高频扼流圈，偏置电阻R B1、R B2、R G不计。
解：画出的交流通路如图所示。
(a)不振，不满足三点式振荡电路组成法则。
(b) 可振，为电容三点式振荡电路。
(c) 不振，不满足三点式振荡电路组成法则。
(d) 可振，为电容三点式振荡电路，发射结电容C b'e为回路电容之一。
(e) 可振，为电感三点式振荡电路。
(f) 不振，不满足三点式振荡电路组成法则。
3-7 如图所示电路为三回路振荡器的交流通路，图中f01、f02、f03分别为三回路的谐振频率，试写出它们之间能满足相位平衡条件的两种关系式，并画出振荡器电路（发射极交流接地）。
解：(1) L2C2、L1C1若呈感性，f osc < f01、f02，L3C3 呈容性，f osc > f03，所以f03 < f osc < f01、f02。
(2) L2C2、L1C1若呈容性，f osc > f01、f02，L3C3 呈感性，f osc < f03，所以f03 > f osc > f01、f02。
3-8 试改正如图所示振荡电路中的错误，并指出电路类型。
图中C B、C D、C E均为旁路电容或隔直流电容，L C、L E、L S均为高频扼流圈。
解：改正后电路如图所示。
图(a)中L改为C1，C1改为L1，构成电容三点式振荡电路。
图(b)中反馈线中串接隔值电容C C，隔断电源电压V CC。
图(c)中去掉C E，消除C E对回路影响，加C B和C C以保证基极交流接地并隔断电源电压V CC；L2改为C1构成电容三点式振荡电路。
3-9 试运用反馈振荡原理，分析如图所示各交流通路能否振荡。
解：图(a)满足正反馈条件，LC 并联回路保证了相频特性负斜率，因而满足相位平衡条件。
图(b)不满足正反馈条件，因为反馈电压fV&比i1V &滞后一个小于90︒的相位，不满足相位平衡条件。
图(c)负反馈，不满足正反馈条件，不振。
3-13 在下图所示的电容三点式振荡电路中，已知L = 0.5 μH ，C l = 51 pF ，C 2 = 3300 pF ， C 3 =（12 ~ 250）pF ，R L = 5 k Ω，g m = 30 mS ，C b 'e = 20 pF ，β 足够大。
Q 0 = 80，试求能够起振的频率范围，图中C B 、C C 对交流呈短路，L E 为高频扼流圈。
解：在L E 处拆环，得混合Ⅱ型等效电路如图所示。
由振幅起振条件知，i L m 1ng g ng +'>(1)式中015.0211='+=C C C n ，其中mS 301pF 3320m ee b 22===+=''g r C C C ，。
代入(1)，得 mS 443.0L<'g 由eoL L11R R g +='，得k Ω115.4eo >R 则能满足起振条件的振荡频率为rad/s 109.1026o eo⨯>=LQ R ω。
由图示电路知，21213C C C C C C '+'+=∑。
当C 3 = 12pF 时，C ∑ = 62.23 pF ，rad/s 102.17916omax ⨯==∑LC ω当C 3 = 250pF 时，C ∑ = 300 pF 。
可见该振荡器的振荡角频率范围ωmin ~ ωmax = (102.9 ~ 179.2) ⨯ 106 rad/s ， 即振荡频率范围f min ~ f max = 16.38 ~ 28.52 MHz 。
3-15 一LC 振荡器，若外界因素同时引起ω0、ϕf 、Q e 变化，设o oωω>'，f f ϕϕ>'，e Q '分别大于Q e 或小于Q e ，试用相频特性分析振荡器频率的变化。
解：振荡回路相频特性如图，可见：(1)当o oωω>'时，osc osc ωω>'，且o osc ωω∆≈∆； (2)当f f ϕϕ>'时，设为oscω''，osc osc ωω>''； (3)当Q e 增加时，相频特性趋于陡峭，ϕf 不变，ωosc ↓ϕf 变化，Q e ↑→ ∆ ωosc ↓，Q e ↓→ ∆ ωosc ↑。
3-16 如图所示为克拉泼振荡电路，已知L = 2 μH ，C 1=1000 pF ，C 2 = 4000 pF ，C 3 = 70 pF ，Q 0 = 100，R L = 15 k Ω，C b 'e = 10 pF ，R E = 500 Ω，试估算振荡角频率ωosc 值，并求满足起振条件时的I EQmin 。
设 β 很大。
解：振荡器的交流等效电路如图所示。
由于C 1>> C 3，C 2 >> C 3，因而振荡角频率近似为rad/s 1052.84163osc ⨯=≈LC ω已知 R e0 = ωosc LQ 0 =16.9 k ΩpF 4010k Ω95.7//e b 22e0L L =+='==''C C C R R R ， 求得 pF 4.80021212,1='+'=C C C C C ，08.02,1332=+=C C C n Ω='≈''88.50L 22L R n R 又 m T EQ T EQ E e E i 2111112.0g V I V I R r R g C C C n =≈+=+=≈'+=， 根据振幅起振条件，，i Lm 1ng g ng +''> 即，)1(L T EQ n n g V I -''>求得I EQ > 3.21mA3-18 试指出如图所示各振荡器电路的错误，并改正，画出正确的振荡器交流通路，指出晶体的作用。
图中C B 、C C 、C E 、C S 均为交流旁路电容或隔直流电容。
解：改正后的交流通路如图所示。
图(a)L用C3取代，为并联型晶体振荡器，晶体呈电感。
图(b)晶体改接到发射极，为串联型晶体振荡器，晶体呈短路元件。
3-22 试判断如图所示各RC振荡电路中，哪些可能振荡，哪些不能振荡，并改正错误。
图中，C B、C C、C E、C S对交流呈短路。
解：改正后的图如图所示。
(a)为同相放大器，RC移相网络产生180︒相移，不满足相位平衡条件，因此不振。
改正：将反馈线自发射极改接到基极上。
(b)中电路是反相放大器，RC移相网络产生180︒相移，满足相位平衡条件，可以振荡。
(c)中放大环节为同相放大器，RC移相网络产生180︒相移，不满足相位平衡条件，因此不振。
改正：移相网络从T2集电极改接到T1集电极上。
(d)中放大环节为反相放大器，因为反馈环节为RC串并联电路，相移为0︒，所以放大环节应为同相放大。
改正：将T1改接成共源放大器。
3-23 图（a）所示为采用灯泡稳幅器的文氏电桥振荡器，图（b）为采用晶体二极管稳幅的文氏电桥振荡器，试指出集成运算放大器输入端的极性，并将它们改画成电桥形式的电路，指出如何实现稳幅。
解：电桥形式电路如图所示。
(a)中灯泡是非线性器件，具有正温度系数。
起振时，灯泡凉，阻值小(R t)，放大器增益大，便于起振。
随着振荡振幅增大，温度升高，R t增加，放大器增益相应减小，最后达到平衡。
(b)中D1、D2是非线性器件，其正向导通电阻阻值随信号增大而减小。
起振时，D1、D2截止，负反馈最弱，随着振荡加强，二极管正向电阻减小，负反馈增大，使振幅达到平衡。
