指数自回归模型

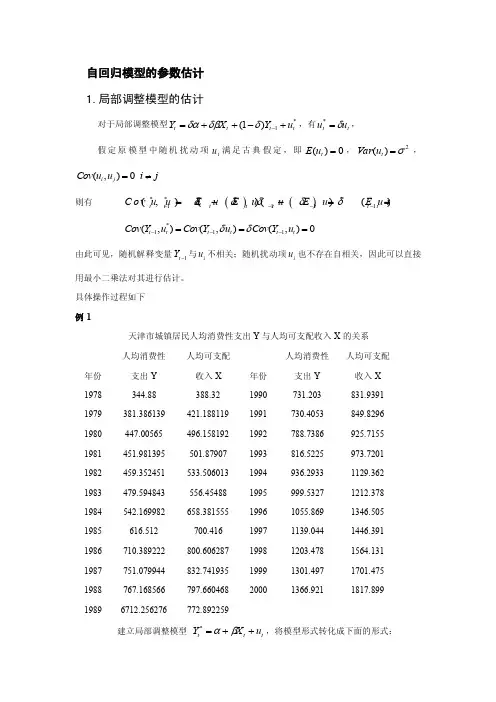
自回归模型的参数估计 1.局部调整模型的估计对于局部调整模型*1)1(t t t t u Y X Y +-++=-δδβδα，有t t u u δ=*，假定原模型中随机扰动项t u 满足古典假定，即0)(=t u E ，2)(σ=t u Var ，(,)0i j Cov u u i j =≠则有 ()()**21111(,)()()()0t t t t t tt t C o v u u E uE u uE u E u u δδδδδ----=--==*111(,)(,)(,)0t t t t t t Cov Y u Cov Y u Cov Y u δδ---===由此可见，随机解释变量1-t Y 与i u 不相关；随机扰动项i u 也不存在自相关，因此可以直接用最小二乘法对其进行估计。

具体操作过程如下 例1天津市城镇居民人均消费性支出Y 与人均可支配收入X 的关系 年份 人均消费性支出Y 人均可支配 收入X 年份 人均消费性支出Y 人均可支配收入X 1978 344.88 388.32 1990 731.203 831.9391 1979 381.386139 421.188119 1991 730.4053 849.8296 1980 447.00565 496.158192 1992 788.7386 925.7155 1981 451.981395 501.87907 1993 816.5225 973.7201 1982 459.352451 533.506013 1994 936.2933 1129.362 1983 479.594843 556.45488 1995 999.5327 1212.378 1984 542.169982 658.381555 1996 1055.869 1346.505 1985 616.512 700.416 1997 1139.044 1446.391 1986 710.389222 800.606287 1998 1203.478 1564.131 1987 751.079944 832.741935 1999 1301.497 1701.475 1988 767.168566 797.660468 2000 1366.9211817.89919896712.256276772.892259建立局部调整模型 t t t u X Y ++=βα*，将模型形式转化成下面的形式：*1*1*0*t t t t u Y X Y +++=-ββα然后直接用OLS 法估计模型参数。

指数回归和对数回归是数学模式中常用的两种回归方法。

在统计学和经济学中，这两种回归方法被广泛使用来研究和预测变量之间的关系。

本文将分别介绍指数回归和对数回归的基本概念和应用。

指数回归是一种采用指数函数作为自变量的回归方法。

指数回归的基本模型如下所示：y = a * exp(bx) + ε其中，y是因变量，x是自变量，a和b是回归系数，ε是误差项。

指数回归的特点是自变量的指数项具有较大的影响力，自变量的值越大，函数值增长的速度越快。

指数回归的应用十分广泛。

在自然科学领域中，指数回归可用于研究生物学中的生长模式、物理学中的指数衰减等现象。

在经济学中，指数回归可用于分析商品价格的变动、市场需求的变化等。

此外，指数回归还可用于研究社会科学中的扩散过程、疾病传播等。

对数回归是一种采用对数函数作为自变量的回归方法。

对数回归的基本模型如下所示：log(y) = a + bx + ε其中，y是因变量，x是自变量，a和b是回归系数，ε是误差项。

对数回归的特点是自变量的对数项具有较大的影响力，自变量的值越大，函数值的变化越小。

对数回归也有着广泛的应用。

在经济学中，对数回归可用于研究收入的增长模式、投资的回报率等。

在社会学中，对数回归可用于分析教育水平与收入之间的关系、人口增长的模式等。

此外，对数回归还可用于医学研究中，如分析治疗效果和疾病进程的关系。

指数回归和对数回归在数学模式中有着广泛的应用。

它们都是建立在基于指数函数和对数函数的模型之上，能够描述各种变量之间的关系。

无论应用于自然科学、社会科学还是经济学等领域，这两种回归方法都能为研究人员提供有用的工具。

在实际应用中，选择使用指数回归还是对数回归要根据具体的问题和数据来决定。

对数回归适用于自变量与因变量之间的关系是逐渐变化的情况，而指数回归则适用于自变量与因变量之间的关系具有快速变化的情况。

研究人员需要根据具体的研究需求和数据特点来选择合适的回归方法。

综上所述，指数回归和对数回归是数学模式中常用的两种回归方法。

自回归模型在金融预测中的应用自回归模型（Autoregressive Model）是一种经典的时间序列分析方法，被广泛应用于金融领域的预测和分析中。

通过对历史数据的分析和建模，自回归模型可以帮助金融从业者更好地理解市场走势、预测未来趋势，提高决策的准确性和效率。

本文将探讨自回归模型在金融预测中的应用，介绍其原理、优势以及实际案例。

### 原理介绍自回归模型是一种基于时间序列数据的统计模型，其基本思想是当前时刻的数值与前几个时刻的数值相关。

具体而言，自回归模型假设当前时刻的数值可以由前几个时刻的数值线性组合而成，即：$$X_t = \phi_1 X_{t-1} + \phi_2 X_{t-2} + \ldots + \phi_p X_{t-p} + \varepsilon_t$$其中，$X_t$表示当前时刻的数值，$X_{t-1}, X_{t-2}, \ldots, X_{t-p}$表示前几个时刻的数值，$\phi_1, \phi_2, \ldots,\phi_p$为模型参数，$\varepsilon_t$为误差项。

通过对历史数据进行拟合，可以估计出模型参数，进而用于未来数值的预测。

### 优势分析自回归模型在金融预测中具有以下优势：1. **考虑时间序列的相关性**：自回归模型能够充分利用时间序列数据的相关性，捕捉数据之间的动态关系，更好地反映市场的变化规律。

2. **简单易用**：自回归模型相对于其他复杂的预测方法来说，模型结构相对简单，参数较少，易于理解和实现。

3. **适用性广泛**：自回归模型适用于各种类型的时间序列数据，包括股票价格、汇率、利率等金融数据，具有较强的通用性。

4. **稳健性强**：自回归模型对异常值和噪声具有一定的鲁棒性，能够有效应对数据中的波动和干扰。

### 实际应用案例#### 股票价格预测自回归模型在股票价格预测中有着广泛的应用。

通过对历史股票价格数据的分析，可以建立自回归模型，利用过去若干个交易日的股价数据来预测未来的股价走势。

自回归模型法什么是自回归模型法自回归模型法（Autoregressive Model）是一种用于时间序列预测和分析的统计方法。

它基于时间序列中的自相关性，通过使用过去若干时间点的数据来预测未来的观测值。

自回归模型法广泛应用于经济学、金融学、气象学等领域，有助于我们理解时间序列数据的变化规律，进行预测和决策。

自回归模型法的基本原理自回归模型法的基本原理是建立一个线性模型，其中包括时间序列观测值和之前的观测值之间的关系。

它假设当前观测值与之前若干个观测值之间存在一种确定的关系，可以用线性方程来表示，其中过去的观测值是预测当前观测值的重要因素。

自回归模型法具体的形式可以表示为：其中，是当前观测值，是常数项，是自回归系数，是过去的观测值，是误差项。

自回归模型法的关键是确定自回归系数和误差项的取值。

通常使用最小二乘法来估计自回归系数，使得观测值和预测值之间的误差最小化。

通过对时间序列的历史数据进行拟合，可以得到一个自回归模型，用于预测未来观测值。

自回归模型法的应用举例1.经济预测：自回归模型法可以应用于经济领域的预测和决策。

例如，可以使用过去几个季度的经济数据，预测未来几个季度的经济增长率，以指导政府制定宏观经济政策。

2.股票价格预测：自回归模型法可以应用于股票市场的预测和交易决策。

通过分析历史股票价格数据，可以建立一个自回归模型，用于预测未来股票价格的涨跌趋势，帮助投资者做出买入或卖出的决策。

3.气象预测：自回归模型法可以应用于气象学中的天气预测。

通过分析过去几天或几周的气象数据，可以建立一个自回归模型，预测未来几天的气温、降雨量等天气指标，为农作物种植、航空运输等提供参考。

自回归模型法的优缺点自回归模型法具有以下优点：•能够捕捉时间序列数据中的自相关性，提供对未来观测值的预测。

•模型结构简单，易于理解和实现。

•可用于分析和理解时间序列数据的变化规律，揭示隐藏在数据背后的规律和趋势。

然而，自回归模型法也存在一些缺点：•假设观测值之间存在线性关系，可能无法准确描述非线性的时间序列数据。

python指数回归模型Python指数回归模型是一种统计学模型，用于分析自变量与因变量之间的非线性关系。

在统计学中，回归分析是一种重要的数据分析方法，用于研究变量之间的关系。

指数回归模型通过将自变量的指数函数引入回归模型中，能够更好地拟合非线性关系，提高模型的预测能力和解释力。

指数回归模型的基本形式为：Y = β0 + β1e^(β2X)，其中Y表示因变量，X表示自变量，β0、β1、β2为模型的参数。

该模型的关键在于指数函数e^(β2X)，它使得自变量X的变化对因变量Y的影响不是线性的，而是指数级的。

指数回归模型的应用非常广泛，特别是在经济学、金融学、市场营销等领域。

例如，在经济学中，指数回归模型可以用来分析经济指标（如GDP、通胀率等）与自变量（如时间、政策等）之间的关系。

在金融学中，指数回归模型可以用来分析股票价格与市场因素、公司基本面等因素之间的关系。

在市场营销中，指数回归模型可以用来分析产品销量与价格、促销活动等因素之间的关系。

在Python中，使用指数回归模型可以通过statsmodels库来实现。

首先，需要导入statsmodels库和pandas库（用于数据处理）。

然后，读取数据并进行预处理，确保自变量和因变量的数据类型正确。

接下来，使用statsmodels库的函数来拟合指数回归模型，并获取模型的参数估计值和拟合优度等统计指标。

最后，可以通过绘制拟合曲线和残差图等方式来评估模型的拟合效果。

在实际应用中，需要注意指数回归模型的一些限制和假设。

首先，指数回归模型假设自变量和因变量之间的关系是非线性的，并且变化率是指数级的。

其次，指数回归模型假设模型的误差项服从正态分布，并且误差项之间是独立的。

最后，指数回归模型假设自变量之间是线性无关的，不存在多重共线性的问题。

Python指数回归模型是一种强大的统计学工具，可以用于分析自变量与因变量之间的非线性关系。

通过合理地选择自变量和建立适当的模型，可以提高模型的预测能力和解释力，为决策提供有力的支持。

指数回归模型
模型形式
指数回归模型可以表示为以下形式：
$$y = a \cdot e^{bx} + c$$
其中，$y$ 是因变量，$x$ 是自变量，$a$、$b$、$c$ 是拟合参数。

模型分析
指数回归模型的优势之一是能够很好地拟合非线性关系。

通过指数函数的形式，该模型能够捕捉到数据中的递增或递减趋势。

模型参数 $a$ 表示随着自变量 $x$ 的增大，因变量 $y$ 的整体变化趋势。

当 $a$ 大于 1 时，表示 $y$ 的增长速度在加快；当
$a$ 小于 1 时，表示 $y$ 的增长速度在减缓。

参数 $b$ 表示指数函数的基底，决定了曲线的斜率。

如果
$b$ 大于 0，则曲线呈指数增长趋势；如果 $b$ 小于 0，则曲线呈指数下降趋势。

参数 $c$ 是一个偏移常数，用于调整曲线在纵向上的位置。

模型应用
指数回归模型在很多领域都有广泛的应用。

例如，经济学中的经济增长模型、生物学中的生物曲线拟合、市场分析中的销售预测等。

通过拟合实际数据，可以使用指数回归模型来预测未来的趋势和数值。

同时，通过模型的参数分析，可以了解自变量对因变量的影响程度和趋势。

总结
指数回归模型是一种用于拟合非线性关系的回归分析方法。

通过指数函数的形式，该模型能够很好地捕捉到递增或递减趋势。

模
型参数能够解释自变量对因变量的整体变化趋势和斜率变化。

指数回归模型在很多领域都有广泛应用，用于建模和预测自变量和因变量之间的关系。

自回归模型一、 预测方法综述预测方法大体上分为定性预测法、时间序列预测法和因果模型预测法。

定性预测法是在数据资料掌握不多的情况下，依靠人的经验和分析能力，用系统的、逻辑的思维方法，把有关资料加以综合、进行预测的方法。

定性预测法包括特尔斐法、主观概率预测法、判断预测法等方法。

时间序列预测法是依据预测对象过去的统计数据，找到其随时间变化的规律，建立时序模型，以判断未来数值的预测方法。

其基本思想是:过去的变化规律会持续到未来，即未来是过去的延伸。

时间序列预测法包括时间序列平滑法、趋势外推法、季节变动预测法等确定型时间序列的预测方法和马尔可夫法、随机型时间序列的预测方法。

因果模型预测法是把所要预测的对象同其他有关因素联系起来进行分析，制定出揭示因果关系的模型，然后根据模型进行预测。

因果模型预测法包括回归分析预测法、经济计量模型法、投入产出预测法等。

由于时间序列预测法和因果模型预测法都是以统计资料为依据，应用统计方法进行预测的，所以有时两者统称为统计预测。

到目前为止，已有近二百种预测方法。

1987年，Ledes和Farbor首次将神经网络引入到预测领域中，无论是从思想上、还是技术上都是一种拓宽和突破。

常用的分析和预测方法有下面几种:(1) 投资分析方法。

这是市场分析家常用的方法。

(2) 时间序列分析法。

这种方法主要是通过建立综合指数之间的时间序列相关辩识模型，如自回归移动平均模型(ARMA)、齐次非平稳模型(ARIMA)等来预测未来变化。

(3) 神经网络预测法。

神经网络是一种最新的时间序列分析方法。

(4) 其他预测方法。

如专家评估法和市场调查法等定性方法、季节变动法、马尔柯夫法和判别分析法等定量预测方法。

传统的预测方法大都采用线性模型来近似地表达预测对象的发展规律。

如最常用的AR模型预测，就是在时间序列平稳的假设基础之上，对其建立线性模型，然后采用模型外推的方法预测其未来值。

然而这些方法只适用于平稳时间序列的预测。

arima模型公式
ARIMA模型，也称为指数平滑自回归移动平均模型（Exponential Smoothing Autoregressive Moving Average Model，简称ARIMA），是最理想的求解时间序列问题的数学模型之一。

ARIMA模型是研究不同时期系统的变化趋势以及预测趋势未来变化的有效方法。

ARIMA模型是一种对非平稳时间序列进行预测分析的统计模型，其中的自回归与滑动平均相结合，从而利用历史变化趋势来预测时间序列未来的变化。

ARIMA模型能够捕捉历史数据中一些有形式的变化，例如周期性变化，这可能是由于季节性变化、土壤温度变化或季度销量变化等原因造成的，以确定未来的趋势。

ARIMA模型会考虑历史数据中出现的随机性，从而根据历史数据中出现的随机噪声梯度构建一个有效的数学模型，从而可以预测时间序列未来的变化趋势。

ARIMA模型的应用十分广泛，深受众多行业的青睐，特别是互联网领域。

互联网行业对高性能、快速、准确的数据预测分析解决方案有着极大的需求，ARIMA模型正是其最佳选择之一。

ARIMA模型可以分析用户访问路径行为、点击量转换率趋势、平台订单量、应用用户流失率等，从而帮助互联网企业更加针对性的采取有效措施，使企业有效提高运营效率，有效节省资源。

总之，ARIMA模型是一款无与伦比的预测分析工具，其应用范围广泛，在互联网行业尤其受到大家的钟爱，系统性的应用ARIMA模型，可以迅速帮助企业更加了解用户行为趋势，准确准确地把握运营策略，应保持龙头地位不负众望。

时间序列分析中常用的模型时间序列分析是一种重要的数据分析方法，用于研究随时间变化的数据。

在实际应用中，常常需要使用合适的模型来描述和预测时间序列数据。

本文将介绍时间序列分析中常用的几种模型，并对其原理和应用进行详细的讨论。

一、移动平均模型（MA模型）移动平均模型是时间序列分析中最简单的模型之一。

它基于时间序列在不同时刻的观测值之间存在一定的相关性，并假设当前的观测值是过去一段时间内的观测值的线性组合。

移动平均模型一般用“MA(q)”表示，其中q表示移动平均阶数，即过去q个观测值的影响。

二、自回归模型（AR模型）自回归模型是另一种常用的时间序列模型。

它假设当前的观测值与过去一段时间内的观测值之间存在线性关系，并通过自相关函数来描述观测值之间的相关性。

自回归模型一般用“AR(p)”表示，其中p表示自回归阶数，即过去p个观测值的影响。

三、自回归移动平均模型（ARMA模型）自回归移动平均模型是将移动平均模型和自回归模型相结合得到的一种模型。

它通过同时考虑观测值的移动平均部分和自回归部分来描述时间序列的相关性。

四、季节性模型在一些具有周期性波动的时间序列数据中，常常需要使用季节性模型进行分析。

季节性模型一般是在上述模型的基础上加入季节因素，以更准确地描述和预测数据的季节性变化。

五、自回归积分移动平均模型（ARIMA模型）自回归积分移动平均模型是时间序列分析中最常用的模型之一。

它通过引入差分运算来处理非平稳时间序列，并结合自回归模型和移动平均模型来描述残差项之间的相关性。

六、指数平滑模型指数平滑模型是一种常用的时间序列预测方法。

它假设未来的观测值与过去的观测值之间存在指数级的衰减关系，并通过平滑系数来反映不同观测值之间的权重。

七、ARCH模型和GARCH模型ARCH模型和GARCH模型是用于处理时间序列波动性的模型。

它们基于过去的方差序列来描述未来的波动性，并用于金融市场等领域的风险管理和波动率预测。

总结来说，时间序列分析中常用的模型包括移动平均模型、自回归模型、自回归移动平均模型、季节性模型、自回归积分移动平均模型、指数平滑模型、ARCH模型和GARCH模型等。

自回归模型原理
自回归模型（AutoregressiveModel）是一种常见的时间序列预测模型。

它的核心思想是用历史值预测未来值，可以用于任何连续性时间序列的预测问题。

自回归模型将当前时刻的值作为自变量，历史值作为因变量，通过建立历史值与当前值之间的函数关系，来预测未来值。

自回归模型通常用AR(p)表示，其中p代表历史值的个数。

自回归模型的原理是基于时间序列的稳定性和自相关性。

在稳定性方面，时间序列的各项统计指标在不同时间段内保持相对稳定的趋势；在自相关性方面，时间序列的前后各项指标之间存在一定的相关性关系。

自回归模型利用这种相关性，通过历史值来预测未来值，从而实现时间序列的预测。

自回归模型的建模过程，一般通过模型拟合和模型检验两个部分完成。

模型拟合阶段，需要通过选取合适的历史值个数p，以及确定适当的模型参数，来建立历史值与当前值之间的函数关系。

而模型检验阶段，则需要对模型进行稳定性、自相关性、残差等方面的检验，以验证模型的准确性和可靠性。

自回归模型在许多实际应用场景中都有广泛的应用，如股票价格预测、气象预报、经济数据预测等领域。

但同时，自回归模型也存在一些局限性，如对异常值比较敏感、样本量要求较高等。

因此，在实际应用中，需要结合具体问题和数据特征，选择合适的预测模型以及建模方法。

- 1 -。

自回归移动平均模型Autoregressive Integrated Moving Average Model,简记ARIMA什么是ARIMA模型ARIMA模型全称为自回归移动平均模型Autoregressive Integrated Moving Average Model,简记ARIMA,是由和于70年代初提出的一著名,所以又称为box-jenkins模型、博克思-詹金斯法;其中ARIMAp,d,q称为差分自回归移动平均模型,AR是自回归, p为自回归项; MA为移动平均,q 为移动平均项数,d为时间序列成为平稳时所做的差分次数;ARIMA模型的基本思想ARIMA模型的基本思想是：将预测对象随时间推移而形成的数据序列视为一个随机序列,用一定的来近似描述这个序列;这个模型一旦被识别后就可以从时间序列的过去值及现在值来预测未来值;现代统计方法、在某种程度上已经能够帮助企业对未来进行预测;ARIMA模型预测的基本程序一根据时间序列的、自相关函数和偏自相关函数图以ADF单位根检验其、趋势及其季节性变化规律,对序列的平稳性进行识别;一般来讲,经济运行的时间序列都不是平稳序列;二对非平稳序列进行平稳化处理;如果数据序列是非平稳的,并存在一定的增长或下降趋势,则需要对数据进行差分处理,如果数据存在异方差,则需对数据进行技术处理,直到处理后的数据的自相关函数值和偏相关函数值无显著地异于零;三根据时间序列模型的识别规则,建立相应的模型;若平稳序列的偏相关函数是截尾的,而自相关函数是拖尾的,可断定序列适合AR模型；若平稳序列的偏相关函数是拖尾的,而自相关函数是截尾的,则可断定序列适合MA模型；若平稳序列的偏相关函数和自相关函数均是拖尾的,则序列适合;四进行,检验是否具有统计意义;五进行,诊断残差序列是否为白噪声;六利用已通过检验的模型进行;相关链接各国的box-jenkins模型名称ARlMA模型案例分析案例一:ARlMA模型在海关税收预测中的应用2008年;海关税收预算计划8400亿元.比2007年实际完成数增加％,比2007年预算数增加％;为了对2008年江门海关税收总体形势进行把握,笔者尝试利用SAS软件的时间序列预测模块建立ARIMA模型,对2008年江门海关税收总值进行预测;从预测结果来看,预测模型拟合度较高,预测值也切合实际情况,预测模型具有一定的应用价值;现将预测的方法、原理以及影响税收工作的相关因素分析;一、ARlMA模型原理ARIMA模型全称为自回归移动平均模型Autoregressive Integrated Moving Average Model,简记ARIMA;是由博克思BoxfFfl詹金斯Jenkins于70年代初提出的一著名时问序列预测方法,所以又称为box--jenkins模型、博克思一詹金斯法;其中ARIMAp,称为差分自回归移动平均模型,AR是自回归,P为自回归项；MA为移动平均,q为移动平均项数,d为时间序列成为平稳时所做的差分次数;ARIMA模型可分为3种：1自回归模型简称AR模型；2简称MA模型；3简称ARIMA 模型;ARIMA模型的基本思想是：将预测对象随时问推移而形成的数据序列视为—个随机序列.以时间序列的自相关分析为基础.用一定的来近似描述这个序列;这个模型一旦被识别后就可以从时间序列的过去值及现在值来预测未来值;ARlMA模型在经济预测过程中既考虑了经济现象在时间序列上的依存性,又考虑了随机波动的干扰性,对于经济运行短期趋势的预测准确率较高,是近年应用比较广泛的方法之一;二、应用ARIMA模型进行预测每月税收数据.可以看作是随着时间的推移而形成的一个随机时间序列,通过对该时间序列上税款值的随机性、平稳性以及季节性等因素的分析,将这些单月税收值之间所具有的相关性或依存关系用数学模型描述出来,从而达到利用过去及现在的税收值信息来预测未来税收情况的目的;一对序列取对数和作差分处理,形成稳定随机序列ARIMA模型建模的基本条件是要求待预测的数列满足平稳的条件,即个体值要围绕序列均值上下波动,不能有明显的上升或下降趋势,如果出现上升或下降趋势,需要对原始序列进行差分平稳化处理;从上图可看出,江门海关自2002年以来的实际入库税收值数列波动性较明显,且呈现出一定的上升趋势,不能直接用AHIMA模型进行建模;取对数可以消除数据波动变大趋势,对数列进行一阶差分,可以消除数据增长趋势性和季节性;从下图可以看出,预测数列取对数并作一阶差分后的图形显示基本消除了性的影响,趋于平稳化,满足ARIMA模型建模的基本要求;二模型参数的估计时间序列预测模块的自相关分析包括对自和偏的分析,通过对比分析从而实现对时间序列特性的识别;从计算结果可知,自相关函数1步截尾,偏自相关函数2步截尾,白相关函数通过白噪声检验;根据变换数列的自相关函数和偏自相关函数的特点,并经过反复测试,对ARIMA模型的参数进行估计.三个参数定为d=l,p=2和q=l;对参数进行检验;从检验结果可知,参数估计全部通过.拟合优度统计量表中给出了残差序列的方差和,以及按AIC和SBC标准计算的和,这两个值都较小,表明对预测模型拟合得较好;从残差的自相关检验结果数据中.可以得知残差通过白噪声显著性检验;预测模型最终形式为：1+Z=1+Bu其中,Z=logX;B为后移算子,u为随机干扰项三应用模型预测;利用上面确定的模型进行预测;预测模型2007年税收的拟合值是亿元,跟实际税收值亿元比较,误差为％,表明预测模型拟合度较高,预测模型具有一定的应用fir值;把预测模型向前推12个月进行预测,得到2008年各月税收数据,全年累计税收预计均值为亿元,实际税收值会围绕此值上下波动;需要说明的是,由于利用模型向前预测1一12月的数据,预测时间越长,难度越大,也下降,若到年中再次预测时,预测精度将会进一步提高;这个税收预测值是基于当前水平、水平不变或提高的基础上,挖掘税收样本数据自身涵盖的信息.利用分析方法,建立预测模型得出的理论预测值,一旦实际外部环境和条件发生变化,例如国家实施、升值过快、大幅变动、对外的变化等,将对结果生一定的影响;三、其他可能对2008年税收工作产生影响的主要因素一个别商品税收变化影响巨大2007年占关区税收总值80％前20位大类税源,与2006年占关区税收总值80％前20位大类税源商品相比,新增了大豆、印刷和装订机械及零件、棉纱线,少了空气调节器、初级形状的聚丙烯和初级形状的聚乙烯.新增的三项收总值为亿元;占关区税收总值％,其中,大豆2007年税款高达亿元,2006年仅为15万元,影响巨大;另外,煤和钢材的税收值大幅增长;液化石油气、纺织品包括服装和纺织纱线、纸及纸板未切成形的税收下降幅度较大;主要税源商品的不稳定,为关区税收工作增加了难度;二本地企业异地纳税仍保持较大规模据统计,2007年江门关区企业在异地进口应税货值亿元人民币,比2006年增长％,应征税收为亿元,较2006年增长％.占江门区同期应征税收总额的四成多;从分布来看,大部分本地企业异地纳税进口行为分布在广州口岸;在广州口岸纳税亿元,下降占异地纳税总值的％;另外;在黄埔口岸纳税亿元,下降％；在拱北口岸纳税亿元,增加3倍从商品来看,异地纳税进口的商品主要是废塑料、废五金、木浆、冰乙酸、正丁醇、脂肪醇、冻猪杂碎、IEl挖掘机、初级形状聚乙烯等商品,税款均超过千万元,部分商品曾经在本关区口岸大量进口;废塑料进口3亿元,下降％；废五金进口亿元,增长％；木浆进口7783万元,增长％；冰乙酸进口6593万元,下降％；正丁醇进口3498万元,增长倍；脂肪醇进口3366万元;％；冻猪杂碎进口3313万元,增长倍；旧挖掘机进口3101万元,下降％；初级形状聚乙烯进口2539万元,下降54％;其中正丁醇、冻猪杂碎和废五金进口增长迅猛;三主要纳税大户变化较大2007年占关区税收总值60％前20位纳税企业,与2006年占关区税收总值60％前20位纳税企业相比,有12家企业新上榜,更新率为60％;新增的2家纳税企业嘉吉投资中国和北京华特安科经贸有限公司共纳税亿元,占关区税收总值的15％;影响巨大;而海洋石油阳江实业有限公司的纳税额从2006年的亿元下降到2783万元,该企业的税款下fl手x,l 2007年关区税收工作带来了较大的影响;主要纳税大户的不稳定,加大了2008年关区税收工作的不确定性;四加工贸易内销补税和出口征税的影响2007年,江门关区应征税收为亿元,增长％；内销补税不含后续补税为7909万元,增长％；后续补税为594万元,增长％;2007年江门关区品征税160万元,增长倍;江门关区的税收以一般贸易进口征税为主,但由于进出口值占关区进出口总值的比重超过一半.因而加强加工贸易内销征税工作,充分挖掘加贸内销补税潜力,可以为关区税收总量增长提供支持;虽然当前出口征税占关区税收总值的比重非常少,但由于国家不断调整外贸政策,2008年出口需要征收商品涉及300多个税号,而且相当多的商品率高达15—20％,预计江门关区出口关税将会保持大幅增长态势,为关区税收总量增长提供补充;综合来看,只要大类税源商品如己内酰胺、大豆、煤、钢材和废纸等保持2007年的进口规模,其他税源商品进口没有大幅下降,2008年的税收总额就能够保持甚至超过2007年的税收水平,如果液化石油气、纺织品和纸及纸板恢复2006年的进口水平,同时将本关区企业从异地报关引导回本关区,今年税收总额将比2007年小幅增长;结合应用前面的时间序列模型的预测结果,综合多方面因素,预计全年累计税收均值为亿元;案例二:基于ARIMA模型的备件消耗预测方法一、引言随着技术的进步和军事的变革,快速响应战场需求是装备战斗力的重要指标之一;要快速响应战场需求就要有强有力的后勤保障和支持,部队需要保证有一定数量备件;而实际中却常常由于没有足够的备件导致装备不能快速形成战斗力;由于造成备件短缺的重要原因是使用的备件需求预测方法和模型不够精确,故尝试用差分自回归滑动平均模型,即ARIMAp,d,q模型,对备件消耗进行预测;1备件消耗预测的ARIMAp,d,q模型求和自回归滑动平均模型AutoregressiveIntegrated Moving Average Model,简称ARIMA,由Box和Jenkins于70年代初提出的时间序列预测方法,又称为B-J模型、博克思-詹金斯法;其中ARIMAp,d,q称为差分自回归滑动平均模型,AR是自回归,MA为滑动平均,p、q分别为对应的阶数,d为时间序列成为平稳时所做的差分次数;1.基本思路首先需要明确建立模型的前提是在预测的这段时间内,影响该类备件消耗量的主要因素不发生大变故;在此前提下,将备件消耗的历史视为一个时间序列,即为一组依赖于时间t的随机变量序列;这些变量间有依存性和相关性,并表现出一定的规律性,如能根据这些消耗数据建立尽可能合理的统计模型,就能用这些模型来解释数据的规律性,就可利用已得到的备件消耗数据来预测未来消耗数据,也就能得出备件需求做好的备件供应;2.模型描述备件消耗预测ARIMAp,d,q模型实质是先对非平稳的备件消耗历史数据Yt进行dd＝0,1,dots,n次差分处理得到新的平稳的数据序列Xt,将Xt拟合ARMAp,q模型,然后再将原d次差分还原,便可以得到Y_t的预测数据;其中,ARMAp,q的一般表达式为：1式中,前半部分为自回归部分,非负整数p为自回归阶数,为自回归系数,后半部分为滑动平均部分,非负整数q为滑动平均阶数,为滑动平均系数；Xt为备件消耗数据相关序列,εt为WN0,σ2;当q=0时,该模型成为ARp模型：2当p＝0时,该模型成为MAq模型：33.备件消耗预测建模流程通过建立ARIMAp,d,q模型进行备件消耗预测的基本流程,如下图;1获取数据并进行预处理.收集装备使用阶段某备件消耗的数据序列,记为;利用游程检验法来判断该序列是否为平稳序列,如为非平稳序列,用差分的方法,即：,对序列进行平稳化预处理,每次差分后数据进行,直到差分所得数据可以通过平稳性检验,记为d次差分,得到新的平稳序列;取前N组或全部数据作为观测数据,进行零均值化处理,即：,得到一组预处理后的新序列;2ARMA模型的识别通过计算预处理后的序列的自相关函数ACF和偏自相关函数PACF来进行模型识别;具体的计算公式为：4;根据上述计算结果,并依据表1的模型识别原则,可以确定符合的模型;ARMAp,q模型识别原则模型ARp MAq ARMA自相关函数拖尾,指数衰减或振荡有限长度,截尾q步拖尾,指数衰减或振荡偏自相关函数有限长度,截尾p步拖尾,指数衰减或振荡拖尾,指数衰减或振荡3参数估计和模型定阶参数估计和模型定阶是建立备件消耗预测模型的重要内容,二者相互影响;在上述模型识别的基础上,利用样本矩估计法、最小二乘估计法或等对ARMAp,q的未知参数,即自回归系数、滑动平均系数以及白噪声方差进行估计,得出\widehat{\varphi}_1,\ldots,\widehat{\varphi}_p,\widehat{\theta}_1,\ldots,\widehat{\theta}_q,\wid ehat{\sigma}^2;利用AIC、BIC准则进行模型定阶;具体步骤;4模型检验首先要检验所建立模型是否能满足平稳性和可逆性,既要求下式6、式7根在单位圆外,具体公式如下：67再进一步判断上述模型的残差序列是否为白噪声,如果不是,则需要重新进行模型识别,如果是,则通过检验,得出软件模型：8 5备件消耗量预测根据上述预测模型,依据一步预测的方法对进行预测,并考虑前面所进行的d次差分,还原为备件消耗数据Yt的预测结果,根据该预测结果来进行备件的配置;二、案例应用1.原始数据及预处理以航空兵场站某种航材备件3年的消耗率件/1000h来进行分析和预测;取前30组数据建立模型,并用后面的几组数据对模型进行预测验证;3年的原始数据的时间序列如下图,是有关备件消耗统计时间2001年1月到2003年12月－备件消耗率件/1000h的某航材备件消耗数据;从上图中可以看出,数据有明显递增的趋势,为非平稳序列;尝试进行一次差分对数据进行平稳化处理,结果表明仍未平稳,然后再做一次差分,再对进行2次差分后的数据进行,可以通过检验,故接受数据具有平稳性的原假设;可得出d等于2,并将数据进行零均值化,下面进一步确定ARMAp,q模型;2.建立模型并进行参数估计计算零均值化后序列的自相关函数ACF和偏自相关函数PACF,结果如下图;其中,上下两条线为±;由图可以看出0≤p≤3,0≤q≤2;尝试建立ARMAp,q模型;对p、q可能的组合进行参数估计,并利用AIC准则进行定阶,并对估计出的参数进行平稳性和可逆性检验,结果表明都在单位圆外,可以初步确定满足要求的最佳模型为ARMA3,1模型,即：9式9中{εt}为WN0,;3.白噪声检验对已经通过平稳性和可逆性检验的模型9进行白噪声检验4≤m≤6,检验结果如图4;由上图中检验结果可看出,对应于上面m的值,都有m,可通过白噪声检验,模型合理;4.预测及结果分析根据模型9,用一步预测的方法对后4组数据进行预测,并与移动平均法进行对比,如表2;对预测结果进行多角度评价,具体选用的指标包括：平均绝对误差：10平均相对误差：11预测均方差：12其中,y_i为备件消耗序列的实际数据,为模型预测数据;预测结果对比移动平均法5 ARIMA模型时间真实值预测值MAE MRE MSE 预测值MAE MRE MSE129% %8注释：5是由上表预测结果及各项评价指标的对比可知,ARIMA模型预测结果明显优于移动平均法,从平均相对误差上来看,ARIMA模型为％,比移动平均法提高了将近15％,且预测的均方差也较小,仅;由此可见：该模型能较准确地预测出备件消耗的变化趋势,可为备件消耗量的预测提供依据;另由于ARIMA模型建立在历史数据的基础上,故搜集的历史数据越多,模型越准确;该建模方法能综合反映装备使用的实际情况,具有很好的模型适应性;模型具有较高的预测准确度,且有较成熟的软件支持SPSS、Matlab等,易于推广,可进行备件消耗预测,确定备件需求。

指数函数回归模型
指数函数回归模型是一类普遍用于分析时间序列和与时间相关
的数据分析模型。

该模型以指数函数为基本模型，以回归方法进行拟合，用于估计定义在一定时间范围内的一系列离散数据，并以回归曲线的形式来表达。

指数函数回归模型的基本思想是假设在某一时间段内，实际变量的变化也许是按某种规律即指数函数的形式发生的。

根据这种假设，指数函数回归模型建立的主要方法是：通过变量的实际取值，对指数函数参数进行估计和拟合。

指数函数回归模型可以有效地对时变数据进行拟合、增长趋势判断和预测，但由于指数函数表达能力有限，在一定程度上可能拟合出不精确的结果，精度可能会下降。

因此，使用指数函数回归模型时，应对模型中参数进行优化，提高模型拟合效果，从而实现效果更好的预测结果。

- 1 -。

自回归模型推导自回归模型是一种常用的时间序列分析方法，它可以用来预测未来的数据趋势。

本文将着重介绍自回归模型的推导过程。

首先，我们需要了解什么是自回归模型。

自回归模型是一种线性模型，它基于当前数据点的历史值来预测未来的值。

它的数学表达式为：y_t = β_0 + β_1*y_(t-1) + β_2*y_(t-2) + ... + β_p*y_(t-p) + ε_t其中，y_t是当前时间点的数值，y_(t-1)、y_(t-2)、...、y_(t-p)是t时刻之前的历史值，β_0、β_1、β_2、...、β_p是自回归系数，ε_t是误差项。

接下来，我们将介绍自回归模型的推导过程。

首先，我们需要对自回归模型进行变形，将其转化为矩阵形式。

我们将自回归模型中的历史值y_(t-1)、y_(t-2)、...、y_(t-p)构成一个p维的向量Y_t，将自回归系数β_1、β_2、...、β_p构成一个p维的向量β，将误差项ε_t构成一个1维的向量ε。

则自回归模型可以写成如下形式：y_t = β_0 + β*Y_t + ε_t接下来，我们需要确定自回归系数β。

我们使用最小二乘法来确定β，将误差项的平方和最小化。

我们将自回归模型中的所有数据点构成一个n×(p+1)的矩阵X，其中第一列为常数项1，后面p列是历史值。

则自回归模型可以写成如下形式：Y = X*β + ε其中，Y是一个n×1的列向量，X是一个n×(p+1)的矩阵，β是一个(p+1)×1的列向量，ε是一个n×1的列向量。

我们使用最小二乘法来确定β。

最小二乘法的目标是使误差项的平方和最小化，即：min(ε'*ε)对上式求导得到：2*X'*ε = 0解出β的值，即可得到自回归系数。

最后，我们需要检验自回归模型的拟合效果。

我们可以使用残差分析来检验模型的拟合效果，检验其是否符合高斯白噪声的分布。

如果残差符合高斯白噪声的分布，则说明自回归模型的拟合效果良好。

自回归模型的参数估计案例案例一：建立中国长期货币流通量需求模型。

中国改革开放以来，对货币需求量(Y)的影响因素，主要有资金运用中的贷款额(X)以及反映价格变化的居民消费者价格指数(P)。

长期货币流通量模型可设定为120e t t t t P Y X βμββ=+++ （1）其中，e t Y 为长期货币流通需求量。

由于长期货币流通需求量不可观测，作局部调整:11()e t t t t Y Y Y Y δ---=- （2）其中，t Y 为实际货币流通量。

将（1）式代入（2）得短期货币流通量需求模型：0121(1)t t t t t Y X P Y δβδβδβδδμ-=+++-+表1中列出了1978年到2007年我国货币流通量、贷款额以及居民消费者价格指数的相关数据。

表1年份 货币流通量Y （亿元）居民消费者价格指数P （1990年=100）贷款额X （亿元）1978212.046.2 1850.0 1979 267.7 47.1 2039.6 1980 346.2 50.6 2414.3 1981 396.3 51.9 2860.2 1982 439.1 52.9 3180.6 1983 529.8 54.0 3589.9 1984 792.1 55.5 4766.1 1985 987.8 60.6 5905.6 1986 1218.4 64.6 7590.8 19871454.569.39032.51988 2134.0 82.3 10551.3 1989 2344.0 97.0 14360.1 1990 2644.4 100.0 17680.7 1991 3177.8 103.4 21337.8 1992 4336.0 110.0 26322.9 1993 5864.7 126.2 32943.1 1994 7288.6 156.7 39976.0 1995 7885.3 183.4 50544.1 1996 8802.0 198.7 61156.6 1997 10177.6 204.2 74914.1 1998 11204.2 202.6 86524.1 1999 13455.5 199.7 93734.3 2000 14652.7 200.6 99371.1 2001 15688.8 201.9 112314.7 2002 17278.0 200.3 131293.9 2003 19746.0 202.7 158996.2 2004 21468.3 210.6 178197.8 2005 24031.7 214.4 194690.4 2006 27072.6 217.7 225347.2 200730375.2228.1261690.9对局部调整模型0121(1)t t t t t Y X P Y δβδβδβδδμ-=+++-+运用OLS 法估计结果如图1：图1 回归估计结果由图1短期货币流通量需求模型的估计式：1202.50.03577.45570.7236t t t t Y X P Y -=-+++由参数估计结果ˆ10.7236δ-=，得ˆ0.2764δ=。

指数型回归模型的渐近性质
指数型回归模型是利用数据对指数函数进行拟合，以构建出回归方程，常用来进行趋势分析和预测的数量分析方法。

该模型的渐进性质是由变量之间的联系导致的一种特殊的性质。

指数型回归模型的渐进性质表现出的是一种“渐进”的变化趋势。

它是指整个数据集中的变化率会系数不断加大或不断减小。

当心血模型的渐进性质大于零时，趋向总是会增加，当小于零时则会减少。

在一般情况下，该模型的渐进模型可以被表示为： y=
exp⁡(ax + b ) ，其中a为渐进系数。

渐进系数a可以用于决定模型整体变化率。

如果a 为正，则说明变量会向未来呈现一种稳定的正趋势，如果a为负则表示趋势变化会向负方向发展。

当回归拟合模型建立完成后，可以使用拟合达标度来分析指数型模型的渐进性质和系数的大小。

考察系数的大小可以判断模型的拟合质量，而考察模型的渐进性质则可以帮助分析研究者更好地实现具体的研究分析，从而更进一步地窥探建立起的回归模型的';背后的变化规律。

指数型回归模型的渐进性质实际上是一种复杂的性质，不仅需要对数据本身的特点有较深入的了解，而且还需要对整个模型有所把握，从所有变量中寻找准确较好的结论。

通过这种方法，研究者可以更有效地挖掘出数据背后变化的规律，从而可以更好地提供有效的预测、指导和决策。